
Mesh Alignment using Grid based PCA
David Kaye and Ioannis Ivrissimtzis
School of Engineering and Computing Sciences, Durham University, Durham, U.K.
Keywords:
Mesh Alignment, Principal Component Analysis, Grid Based Methods.
Abstract:
We present an algorithm for mesh alignment by performing Principal Components Analysis (PCA) on a set
of nodes of a regular 3D grid. The use of a 3D lattice external to both inputs increases the robustness of
PCA, particularly when dealing with meshes of different and possibly uneven vertex density. The proposed
algorithm was tested on meshes that have undergone standard mesh processing operations such as smooth-
ing, simplification and remeshing. In several cases the results indicate an improved robustness compared to
performing PCA directly on mesh vertices.
1 INTRODUCTION
It is often useful to compare two meshes, point clouds,
or a mixture of the two. For example, in shape recog-
nition one might compare two meshes or two point
clouds asking whether they belong to the same cate-
gory.
The comparison of two meshes usually starts with
their alignment. It should be noted that the exact way
in which two meshes are best aligned is not clearly de-
fined. In fact, the best alignment can be application-
dependent, and mesh alignment should be seen as an
ill-posed problem. Nevertheless, a good alignment al-
gorithm is expected to be able to align a mesh with a
version of it that has undergone common mesh pro-
cessing operations such as smoothing, simplification
or remeshing.
Alignment is typically done by computing a trans-
lation, a scaling and a rotation, which are then ap-
plied to one of the meshes to align it with the other.
The computation of the translation is usually done
by aligning barycentres, while the scaling is done by
aligning bounding boxes or bounding spheres (Sfikas
et al., 2014). Translation and scaling are both con-
sidered less challenging to compute than the rota-
tion, which is the focus of this paper. In some fields
such as medical imaging, the registration process re-
quires more than this simple pose normalisation, for
instance, an alignment between certain parts of the
two models (Postelnicu et al., 2009).
The simplest and most widely used method for the
rotational alignment of two meshes aligns the princi-
pal axes of the mesh vertex sets. Despite its popu-
larity, it is well documented that in demanding appli-
cations such as shape recognition the results of this
alignment method may not be satisfactory, especially
in the case when the mesh undergoes processing that
potentially disturbs the distribution of mesh vertices
such as simplification and remeshing.
One way around this problem is to voxelise the
mesh and then apply an alignment algorithm for vol-
umetric data. However, such a method can be compu-
tationally demanding, and the cost of the voxelisation
cannot be fully justified if it is used for mesh align-
ment only. A second approach would be to apply PCA
not on the mesh vertex set but on a more uniform point
set produced by a mesh sampling method. However,
such a method would depend on the quality of the tri-
angulation and for example, a large number of long
thin triangles in the mesh could cause problems.
Here, we propose a solution in between the above
two approaches, that is, a sampling method which,
without being a fully volumetric method, is based on
creating a subset of the nodes of a regular grid and
then performing PCA on that point set.
1.1 Contribution
We present a deterministic, fully automatic method
for mesh alignment based on performing PCA on a
point sample on a regular grid. The algorithm can also
process point clouds as inputs, allowing point clouds
to be aligned with meshes, or two point clouds to be
aligned. However, when connectivity exists, it is used
to increase the robustness of the usual PCA on the
mesh vertex set, which can be problematic when, for
instance, the mesh vertex set is very sparse.
174
Kaye D. and Ivrissimtzis I..
Mesh Alignment using Grid based PCA.
DOI: 10.5220/0005313801740181
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 174-181
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

1.2 Limitations
The main limitation of the algorithm is that since PCA
is applied to a subset of the nodes of a relatively
coarse grid, the method is less accurate than the usual
PCA on mesh vertices when the two meshes are iden-
tical or almost identical. In a sense, this larger error
is a trade-off for the increased robustness and our ex-
periments show that it is in a range that in most appli-
cations would be considered tolerable.
Since the method is underpinned by PCA, it is not
particularly well suited for inputs that have high levels
of rotational symmetry. Finally, since the algorithm is
highly geometric in nature, it could be challenging to
adapt to incorporate non-geometric primitives such as
colour (Roy et al., 2004).
2 RELATED WORK
Most of the work on mesh alignment focuses on and
enhances the Iterative Closest Point (ICP) algorithm,
which takes a set of points common to both input
meshes and iteratively rotates the mesh until the com-
mon points are aligned as closely as possible. A va-
riety of modifications and enhancements to the orig-
inal ICP algorithm have been developed and stud-
ied; to make it geometrically stable (Gelfand and
Rusinkiewicz, 2003), and to make it work with ap-
proximate nearest neighbouring points or with added
noise (Maier-Hein et al., 2010). Other ICP based
methods require an explicitly defined initial guess,
which prevents the method being used in a completely
automated manner (Besl and McKay, 1992).
Due to the variants of the ICP algorithms requiring
subset inputs, and possibly some manual intervention,
they are not directly comparable to the algorithm pre-
sented here. In reality, many practitioners use PCA
directly on the vertices of the input meshes in order
to provide an alignment that is good enough to work
with. PCA is a robust statistical method that is used
extensively for non-geometric problems requiring di-
mensionality reduction. It is also efficient, since it is
essentially a quadratic optimisation problem based on
variance maximisation. A technique that is similar in
spirit, called Independent Component Analysis (ICA)
(Hyv
¨
arinen et al., 2001), is based on quartic optimi-
sation and has been used for 3D object recognition
(Sahambi and Khorasani, 2003).
Despite its popularity, PCA has been reported to
perform poorly when aligning meshes for 3D model
recognition and this has been cited as motivation
for developing rotationally invariant mesh descrip-
tors (Kazhdan et al., 2003). Nevertheless, several
important shape descriptors, such as (Cantoni et al.,
2013), shape histograms (Ankerst et al., 1999) and de-
scriptors based on higher order moments (Elad et al.,
2002), are not rotationally invariant and thus require
alignment. Extensions to PCA to overcome its short-
comings include PCA performed on the normals of
a surface (Papadakis et al., 2007), and a continuous
version of PCA applied to whole mesh triangles rather
than just their vertices (Vranic et al., 2001). The latter
is independent from the distribution of vertices within
the mesh and thus, overcomes some of the limitations
of PCA the same way the method proposed here does.
However, it requires a triangle mesh as input and has
no obvious extensions to point clouds.
In our implementation, we used the Point Cloud
Library (Rusu and Cousins, 2011) for PCA and Mesh-
Lab (Cignoni et al., 2008) for the various geomet-
ric operations we performed as part of our testing;
smoothing, simplification, adding noise and remesh-
ing.
3 ALIGNMENT ALGORITHM
We begin with two meshes (A and B), assuming that
mesh B has been obtained from mesh A after a rota-
tion by an unknown angle around an unknown axis
and that some mesh processing operation may have
been applied to B. Each mesh is centred on the origin
as a preprocessing step. The translation can be stored
and the reverse operation applied at the end of the pro-
cedure. The basic alignment algorithm first creates
a regular grid around each mesh, then computes the
subset of the grid nodes that are near to the mesh, and
finally applies PCA to this subset of nodes.
3.1 The Basic Algorithm
For each mesh M, we first create a regular 3D lattice,
L
M
, around the mesh M. The dimension of the grid
is given by the user and trades-off the speed of the
algorithm against the accuracy of the alignment. We
then cycle through all the faces in M, and perform the
following for each face f ∈ M:
• Calculate the smallest rectangular subgrid, P
f
in
L
M
that completely contains f .
• To increase robustness, P
f
is expanded by one
node in each direction along each axis, for exam-
ple, a 2 × 2 × 3 subgrid becomes 4 × 4 × 5.
• For each lattice node, n ∈ P
f
, determine the short-
est distance from n to f .
• If the distance from n to f is less than 2 times the
edge of a grid cell, export the node to list I
M
(the
MeshAlignmentusingGridbasedPCA
175

Figure 1: Left: the black nodes are the smallest subgrid
that completely contains the red face. Centre: the smallest
subgrid is extended to decrease discontinuities. Right: the
nodes highlighted in green are the imprint of the red face on
the lattice.
Figure 2: Left, solid: eigenbasis of mesh A. Centre, dashed:
eigenbasis of mesh B. Right, dotted: eigenbasis of mesh B
0
.
‘imprint’ of the mesh M on the lattice).
For each mesh imprint (from Figure 1; the collec-
tion of green nodes from every face in the mesh), we
perform PCA on the nodes’ coordinates and sort the
output eigenvectors in decreasing order of eigenvalue
magnitude. Note that a more sophisticated implemen-
tation of the algorithm would apply a weighted PCA,
with the weight of each node derived from its dis-
tances to the mesh triangles that pushed it in I
M
. How-
ever, we have found experimentally that this would
not have a significant effect on the results and thus,
we opted for the much simpler unweighted PCA.
Between the two eigenbases (one for each mesh),
pairs of eigenvectors are formed based on them hav-
ing the largest, middle, or smallest eigenvalue magni-
tude (blue, green, and red correspondingly in Figure
2). Since PCA does not provide oriented principal
components, we have to ensure that the two eigen-
bases are consistently oriented. Where an inconsis-
tent orientation was detected, as we discuss in Sec-
tion 3.3, the sign of the eigenvector with the smallest
eigenvalue was flipped in one of the meshes.
For the actual mesh alignment, we start with the
first pair of principal components, a
1
, b
1
, (those with
the largest eigenvalues; blue). The rotation aligning
a
1
with b
1
(blue) is computed and applied to mesh B
to produce mesh B
0
. Lattice imprinting and PCA is
then performed on B
0
. The rotation around a
1
(or,
equivalently at this point, b
1
) aligning a
2
with b
0
2
(green) is then computed and applied to B
0
to produce
a mesh B
00
which is in alignment with A.
Note that it would have been possible to work out
both rotations (or even, a single rotation) from the ini-
tial PCA, however this is likely to be less accurate, as
the imprints of the meshes B and B
0
are different. In-
stead, by imprinting for a second time, the alignment
of the second eigenvector uses a dataset that is closer
to B
0
.
3.2 Iterative Algorithm
The basic algorithm can be repeated on mesh A and
the mesh B
00
(which has been aligned with A). The
procedure usually leads to a closer alignment, but the
decrease is not monotonic, and in some cases it could
even lead to poorer alignment.
We believe that the reason for the non-monotonic
decrease is the discrete nature of the grid relative to
the mesh itself, which means that even a tiny rotation,
which can change the position of any mesh vertex by
no more than an arbitrary small distance ε, may never-
theless change the position of a grid node marked for
processing by a distance equal to the edge of a grid
cell.
3.3 Eigenvector Orientation
In order for the method to work, the principal com-
ponents of meshes A and B must be consistently ori-
ented. However, PCA does not define a consistent
orientation. In order to align the two principal com-
ponents a
i
and b
i
consistently we evaluated a sum of
distances function on the two extreme mesh vertex
projections on the principal axis. For each of these
points, the distance to every data point was summed.
Then the principal axis was oriented in the direction
of the point with the largest associated sum.
Consistent orientation of principal components is
a particularly challenging problem. In our experi-
ments we noticed instances where the method was not
successful, causing large deviations (approximately π
radians) from the true alignment.
3.4 Input Types
The algorithm can, with minimal alteration, be used to
align a mesh with a point cloud, or even to align two
point clouds. Each point in the cloud is simply inter-
preted as a face with zero area. Here, the benefit of
using the lattice instead of performing PCA directly
on the point cloud is the increased robustness of the
calculations due to the external reference. Which al-
lows, for example, the alignment of a point cloud and
a simplified version thereof.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
176

Table 1: Mean errors (in degrees) when recovering angles
from a set of known rotations.
Mesh Mesh Imprint Vertex PCA
Bunny 0.45407 0.00648
Armadillo 0.18480 0.01150
Fandisk 1.11274 0.00075
Blade 0.93554 0.00650
Statuette 5.62708 0.01968
Figure 3: Standard Armadillo results. Left: initial rotation,
middle: original, unrotated mesh, right: four iterations.
When working with a point cloud, the same pro-
cedure would be followed, but treating each point as a
face with no area, so the initial containing subgrid (P
f
above) would always be a single cube, which would
become a 3 × 3 × 3 subgrid after expansion.
4 RESULTS
In the first experiment, each mesh had its principal
components computed by mesh imprinting and was
rotated by a known angle around the largest principle
component. The proposed algorithm was then used
to recover the rotation angle. This was then repeated
using vertex PCA and the results were compared. The
results are summarised in Table 1.
Since mesh alignment is an ill-posed problem, in a
second experiment we evaluated the visual relevance
of the reported errors by rotating the test meshes by
an unknown angle around an unknown axis. The
algorithm was used to bring them back into align-
ment. The results for the Armadillo and Statuette,
with the smallest and largest mean error respectively,
are shown in Figures 3 - 4.
4.1 Robustness against Mesh Processing
Operations
Smoothed versions of the models were obtained by
applying three iterations of Laplacian smoothing.
Simplified versions were obtained by using clustering
decimation with a cell size of 1% of the diagonal of
the bounding box. The decimation results are shown
Figure 4: Standard Statuette results. Left: initial rotation,
middle: original, unrotated mesh, right: four iterations.
Table 2: Number of faces in the original and decimated
meshes.
Mesh Original faces Decimated faces
Bunny 35,947 9,588
Armadillo 172,974 7,540
Blade 1,765,388 16,088
Statuette 10,000,000 18,330
in Table 2. Noisy meshes were obtained by randomly
displacing vertices by 1% of the bounding diagonal.
Finally, for remeshed models, surfaces were recon-
structed using the Poisson method (Kazhdan et al.,
2006) with 10 octree subdivisions.
The algorithms were then run against the each
mesh and the processed variants thereof. For each
method, the angular deviation between correspond-
ing principal components of the original and the pro-
cessed mesh were computed. The results are sum-
marised in Tables 3 - 6.
The proposed algorithm performed well on the
remeshed and simplified variants, but the noisy and
Table 3: Average deviation of principal components (in ra-
dians) when models were remeshed.
Remeshed Mesh Imprint Vertex PCA
Bunny 0.020450 0.044197
Fandisk 0.008237 0.008643
Armadillo 0.003517 0.014637
Blade 0.001020 0.018607
Statuette 0.063070 0.264650
Table 4: Average deviation of principal components (in ra-
dians) when models were simplified.
Simplified Mesh Imprint Vertex PCA
Bunny 0.008457 0.031510
Fandisk 0.024567 0.116733
Armadillo 0.002427 0.007957
Blade 0.005060 0.008093
Statuette 0.017803 0.300917
MeshAlignmentusingGridbasedPCA
177
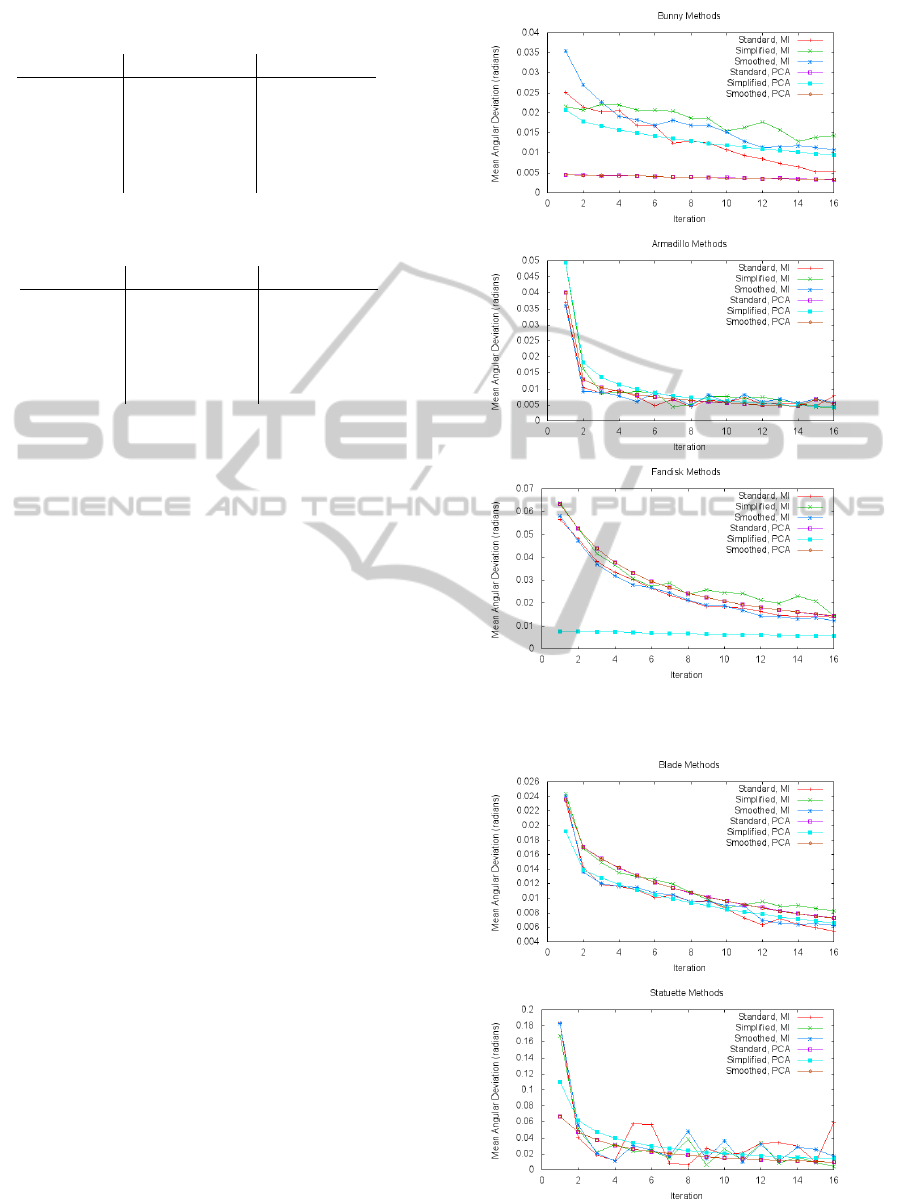
Table 5: Average deviation of principal components (in ra-
dians) when mesh vertices had noise added.
Noisy Mesh Imprint Vertex PCA
Bunny 0.001363 0.000333
Fandisk 0.000047 0.000240
Armadillo 0.000563 0.000757
Blade 0.000753 0.000357
Statuette 0.004997 0.000267
Table 6: Average deviation of principal components (in ra-
dians) when meshes were simplified.
Smoothed Mesh Imprint Vertex PCA
Bunny 0.012873 0.000170
Fandisk 0.006650 0.000080
Armadillo 0.003757 0.000800
Blade 0.000270 0.000107
Statuette 0.001483 0.000000
smoothed variants were better served by vertex PCA.
This is in line with our expectations as remeshing and
simplification are likely to have a larger impact on
vertex distribution than uniformly applied noise and
smoothing.
4.2 Iterative Algorithm
The performance of the iterative algorithm is shown in
Figures 5 and 6. We notice that generally, the itera-
tive algorithm has improved accuracy in each succes-
sive iteration and that most of the improvement mate-
rialises in the first three or four iterations.
Of particular note are the simplified Fandisk re-
sults in Figure 5. Whilst Vertex PCA appears to in-
stantly converge to a highly accurate result, in real-
ity this was a very poor alignment - the simplified
Fandisk had many large, thin triangles. This signif-
icantly altered the distribution of vertices in the mesh
and makes the comparison of the two sets of principal
components invalid. The Mesh Imprint results on the
simplified mesh are a true representation of the align-
ment, as are the Vertex PCA results for the standard
and smoothed Fandisk.
4.3 CAD Meshes
The proposed method is particularly well suited for
CAD meshes that have undergone mesh processing
operations. The Room 215 model shown in Figure 7
is a hand-made replica of an office created using CAD
software, it has 171,711 faces and significant variance
in vertex density. For instance, large areas of walls
are represented by huge triangles, but tiny triangles
are used to pick out the detail and high-curvature of
the radiator grills and chairs. The simplified form has
Figure 5: Mean angular deviation plotted against number of
iterations for the Bunny, Armadillo and Fandisk.
Figure 6: Mean angular deviation plotted against number of
iterations for the Blade and Statuette.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
178

Figure 7: Wireframe view of the Room 215 model. Areas
of high curvature have more triangles and appear as solid
colours.
Figure 8: Wireframe view of the original House model and
its remeshed form.
16,080 faces.
When the principal components of each were
computed and compared, Mesh Imprinting proved
very effective, with a maximum deviation of 0.0086
radians across all principal components, compared to
a minimum deviation of 0.11 radians for vertex PCA.
The same test was run against a simple house
model and a remeshed form thereof shown in Fig-
ure 8. The original mesh had 1,396 faces, the
remeshed model had 98,818. The maximum devi-
ation between the standard house and the remeshed
form thereof was 0.075 radians. Vertex PCA had a
minimum deviation of 0.12.
The model/dressed models in Figure 9 are a pair
of models that both depict a human figure. This fig-
ure is nude in the regular model, but has long hair
and is wearing bulky/baggy clothes in the second.
Both were analysed and had their principal compo-
nents compared. The computation was reasonably
stable for both models, showing only small devia-
tions between the two meshes, but with up to five
times smaller deviations being produced by the mesh
imprint. The maximum deviation between principal
components computed by imprinting was 0.0022 radi-
ans, and the minimum computed by vertex PCA was
0.012.
This is not too surprising, as the two figures have
the same pose and the changes from the regular model
Figure 9: Model/dressed model.
Table 7: Mean angular deviations (in radians) between the
simplified and standard Room215, standard and remeshed
House, and standard and dressed Model.
Mesh Mesh Imprint Vertex PCA
Room 215 0.00647 0.11853
House 0.06064 0.20983
Model 0.00331 0.01230
to the dressed model are relatively rotationally sym-
metric between the two minor principal components.
The largest principal component is along the height
of the model, and the proportions do not change suf-
ficiently to make much difference to this.
4.4 Effect of Resolution
We experimented on grids at 10%, 50%, 100%, and
150% of their original size. The initial size (100%)
of each grid is shown in Table 8. In addition to the
meshes used earlier, the Sphere and Vase models (Fig-
ure 10) were also used.
Predictably, lower-resolution analyses usually
produced alignments that were not so accurate as
higher-resolution analyses. However for the Bunny
and Armadillo models the 150% resolution align-
ments were actually slightly less accurate than the
100% resolution analyses.
The Vase, Sphere and Statuette all highlighted a
limitation of the eigenvector orientation method; they
produced inaccurate results as one principal compo-
Table 8: Initial grid sizes.
Mesh Volume
Bunny 78 × 77 × 60
Armadillo 127 × 151 × 115
Fandisk 121 × 131 × 67
Blade 352 × 598 × 274
Statuette 235 × 396 × 203
Sphere 105 × 108 × 105
Vase 55 × 101 × 55
MeshAlignmentusingGridbasedPCA
179

Figure 10: Sphere and Vase.
nent was incorrectly aligned. This occurs when the
input meshes have high levels of rotational symmetry.
When run at an appropriate resolution the algorithm
correctly orients the principal components, leading to
a successful alignment. However there appears to be
no universally optimal resolution for the lattice in this
regard.
5 DISCUSSION
The implementation of each algorithm was not opti-
mised due to the wide variety of different techniques
and circumstances under which each is possible and
appropriate.
Our implementations took the simple approach of
reading the full file from the hard drive, processing the
data entirely in memory, and writing the output back
to the hard drive in a single execution thread. While
processing large meshes can require large amounts of
memory due to the sheer number of points that must
be processed, our method (by virtue of performing
PCA on fewer points) will naturally have a smaller
memory footprint. Memory could also be saved by
running the proposed algorithm in a layered fashion,
as proposed in (Kaye and Ivrissimtzis, 2011).
Since the proposed method aligned the meshes on
a relatively coarse regular grids, the loss of accuracy
compared to direct vertex PCA was noticeable, but
was inside a range that would be considered tolera-
ble in most applications, that is, around one degree if
there were no problems caused by the rotational sym-
metry of the meshes, or by wrongly oriented eigen-
vectors. Note that these problems are common to both
the proposed method and standard PCA on mesh ver-
tices.
Mesh Imprinting shows its strengths when orig-
inal inputs are poorly meshed, for instance, if they
have many long, thin triangles, or an uneven distribu-
tion thereof. While long thin triangles are very rare
in meshes that are acquired through physical optical
devices such as laser scanners, they often dominate
meshes produced by CAD software. In such cases,
simplification and remeshing significantly affect the
distribution of the vertices, causing Vertex PCA to
produce highly inaccurate alignments.
In the future we plan a systematic analysis of the
error of the standard PCA caused by vertex quantisa-
tion. Indeed, the small alignment error produced by
our method is essentially a vertex coordinate quan-
tisation error, which anyway may be present in the
vertex coordinates, if for example the mesh had un-
dergone lossy compression. By showing, as we con-
jecture, that the alignment error of our method and the
vertex PCA error caused by vertex coordinate quanti-
sation are comparable, we will further justify our ap-
proach.
ACKNOWLEDGEMENTS
The Room215 model is from the Max Planck Insti-
tute. The House mesh was created by user “pabong”
and downloaded from www.tf3dm.com. The model
and dressed model were created using the MakeHu-
man software from www.makehuman.org. The Vase,
Sphere, Statuette, and Blade models were taken from
the AIM@SHAPE repository.
REFERENCES
Ankerst, M., Kastenm
¨
uller, G., Kriegel, H.-P., and Seidl,
T. (1999). 3D shape histograms for similarity search
and classification in spatial databases. In Advances in
Spatial Databases, pages 207–226. Springer.
Besl, P. J. and McKay, N. D. (1992). A method for registra-
tion of 3-d shapes. IEEE Trans. Pattern Anal. Mach.
Intell., 14(2):239–256.
Cantoni, V., Gaggia, A., and Lombardi, L. (2013). Extended
gaussian image. In Encyclopedia of Systems Biology,
pages 724–725. Springer.
Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M.,
Ganovelli, F., and Ranzuglia, G. (2008). Meshlab:
an open-source mesh processing tool. In Sixth Euro-
graphics Italian Chapter Conference, pages 129–136.
Elad, M., Tal, A., and Ar, S. (2002). Content based retrieval
of vrml objects: an iterative and interactive approach.
In Proceedings of the sixth Eurographics workshop on
Multimedia 2001, pages 107–118. Springer-Verlag.
Gelfand, N. and Rusinkiewicz, S. (2003). Geometrically
stable sampling for the icp algorithm. In Proc. Inter-
national Conference on 3D Digital Imaging and Mod-
eling, pages 260–267.
Hyv
¨
arinen, A., Karhunen, J., and Oja, E. (2001). Indepen-
dent Component Analysis. Wiley-Interscience.
Kaye, D. P. and Ivrissimtzis, I. (2011). Memory Effi-
cient Surface Reconstruction Based on Self Organ-
ising Maps. In Theory and Practice of Computer
Graphics, pages 25–32.
Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Poisson
surface reconstruction. In SGP ’06, pages 61–70.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
180

Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2003).
Rotation invariant spherical harmonic representation
of 3D shape descriptors. In SGP ’03.
Maier-Hein, L., Santos, T. R. D., Franz, A. M., and Meinzer,
H.-P. (2010). Iterative closest point algorithm in the
presence of anisotropic noise. In Bildverarbeitung f
¨
ur
die Medizin, pages 231–235.
Papadakis, P., Pratikakis, I., Perantonis, S., and Theoharis,
T. (2007). Efficient 3d shape matching and retrieval
using a concrete radialized spherical projection repre-
sentation. Pattern Recogn., 40(9):2437–2452.
Postelnicu, G., Zllei, L., and Fischl, B. (2009). Combined
volumetric and surface registration. IEEE Trans Med
Imaging, 28(4):508–22.
Roy, M., Foufou, S., and Truchetet, F. (2004). Mesh com-
parison using attribute deviation metric. Journal of
Image and Graphics, 4:1–14.
Rusu, R. B. and Cousins, S. (2011). 3D is here: Point Cloud
Library (PCL). In IEEE International Conference on
Robotics and Automation (ICRA).
Sahambi, H. S. and Khorasani, K. (2003). A neural-
network appearance-based 3-d object recognition us-
ing independent component analysis. IEEE Trans.
Neur. Netw., 14(1):138–149.
Sfikas, K., Theoharis, T., and Pratikakis, I. (2014). Pose
normalization of 3d models via reflective symmetry
on panoramic views. The Visual Computer, pages 1–
14.
Vranic, D., Saupe, D., and Richter, J. (2001). Tools for 3d-
object retrieval: Karhunen-loeve transform and spher-
ical harmonics. In Workshop on Multimedia Signal
Processing.
MeshAlignmentusingGridbasedPCA
181
