Optimization-based Automatic Segmentation

of Organic Objects of Similar Types

Enrico Gutzeit, Martin Radolko, Arjan Kuijper and Uwe von Lukas

Fraunhofer Institute for Computer Research IGD, Joachim-Jungius-Str. 11, 18059 Rostock, Germany

Keywords:

Image Segmentation, Application, Graph Cut, Belief Propagation.

Abstract:

For the segmentation of multiple objects on unknown background in images, some approaches for speciﬁc

objects exist. However, no approach is general enough to segment an arbitrary group of organic objects of

similar type, like wood logs, apples, or tomatoes. Each approach contains restrictions in the object shape,

texture, color or in the image background. Many methods are based on probabilistic inference on Markov

Random Fields – summarized in this work as optimization based segmentation. In this paper, we address the

automatic segmentation of organic objects of similar types by using optimization based methods. Based on

the result of object detection, a fore- and background model is created enabling an automatic segmentation of

images. Our novel and more general approach for organic objects is a ﬁrst and important step in a measuring

or inspection system. We evaluate and compare our approaches on images with different organic objects on

very different backgrounds, which vary in color and texture. We show that the results are very accurate.

1 INTRODUCTION

The segmentation of multiple objects on unknown

background in images is a hard and unresolved prob-

lem in computer vision. There exist some approaches

for speciﬁc objects like wood logs, apples, or toma-

toes. However, no approach is general enough to seg-

ment an arbitrary group of organic objects of similar

type. Each approach contains restrictions in the object

shape, texture, color or in the image background.

To overcome this limitation, we propose to re-

lax the restrictions with a general and novel approach

based on an object detection and optimization based

segmentation. “Optimization based methods” is the

terminology we use to summarize the methods based

on probabilistic inference on Markov Random Fields.

These methods optimize a segmentation by using

probability maps or presegmented images.

In this paper, we address a speciﬁc class of ob-

jects, namely a group of organic objects of similar

type, such as fruits, wood log surfaces, or ﬁshes. We

coin such a group of objects in short “organo-group”

(see section 3 for details). In Figure 1 four different

organo-groups are shown.

The segmentation of an organo-group is an impor-

tant step in inspection, measurement, or recognition

for industrial or research applications. For example,

the volume of a wood stack, the sizes of ﬁshes, or

Figure 1: The picture shows four different groups of organic

objects of similar types (organo-groups), namely wood cut

surfaces, apples, potatoes and ﬂatﬁshes.

the number of apples can be estimated after success-

ful segmentation. The segmentation is most often the

ﬁrst step in a full measuring or inspection system.

In this paper, we introduce our approach, which

is split into the parts organic object detection, veri-

ﬁcation, optimization based segmentation and object

separation.

In the following sections, we analyze related work

and discuss the remaining problems in the subsequent

section. We then introduce our approach and its steps.

Next, we present and compare the results we get by

adapting graph-cut and belief propagation on the seg-

mentation of the four different types of organo-groups

shown in Figure 1, viz. wood log surfaces, ﬁshes,

potatoes, and apples. Finally, we give a conclusion.

591

Gutzeit E., Radolko M., Kuijper A. and von Lukas U..

Optimization-based Automatic Segmentation of Organic Objects of Similar Types.

DOI: 10.5220/0005314905910598

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 591-598

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

There are miscellaneous classiﬁcations of the basic

segmentation methods, depending on the point of

view of the user. From our point of view, there are

four main classes: the pixel-based, contour-based,

region-based and optimization based methods. Pixel-

based methods segment pixel per pixel. Well-known

examples are thresholding techniques (Otsu, 1979;

Sezgin and Sankur, 2004). Contour-based methods

locate, analyze and / or merge contours. An exam-

ple are snakes (Kass et al., 1988; Chan and Vese,

2001). Region-based methods group similar pixels to

regions. Examples are the well-known watershed and

the SLIC approach (Achanta et al., 2012). Another,

but sill similar type is object detection (Zhang et al.,

2013), which mostly use an trained object model to

locate objects in the image.

In this paper, we address optimization based seg-

mentation, which contains the methods based on a

statistical model, especially a Markov Random Field

(MRF) (Li, 1995). Well-known methods of the op-

timization based segmentation class are graph-cut

(Boykov and Kolmogorov, 2004), normalized cut (Shi

and Malik, 2000), belief propagation (Felzenszwalb

and Huttenlocher, 2006) and Fields of Expert (Roth

and Black, 2005). The disadvantage of these meth-

ods is that they normally do not automatically seg-

ment an image and need additional input, like proba-

bility maps or user deﬁned regions. An example for

a semi-automatic graph-cut segmentation is the grab-

cut approach in (Rother et al., 2004). Here, an object

is segmented after a user has drawn a rectangle around

the object.

In contrary to the basic methods, the application-

driven methods are hardly classiﬁed by algorithmic

similarity. The best way for classiﬁcation is the ap-

plication itself. A generic segmentation of an organo-

group does not exist and is thus not state of the art,

but speciﬁc groups are addressed in image processing

literature.

Some approaches exist to segment wood cut sur-

faces. An adaptive local threshold over the image is

used in (Medina Rodriguez et al., 1992). In (Dahl

et al., 2006) a watershed and an automatic scale space

selection is adapted to solve the problem. In (Gutzeit

et al., 2010) the center image is ﬁrst segmented and

the results are then used to create a fore- and back-

ground model. With these models the whole image is

binary segmented (wood / non wood) by the graph-

cut method. This approach needs to have wood logs

in the center of the image. It was extended in (Gutzeit

and Voskamp, 2012) by relaxing these restrictions us-

ing an object detection to estimate the center region

of the stack of wood. Each individual wood log is

segmented in contrast to the complete wood area. In

(Herbon et al., 2014) an iterative detection and seg-

mentation approach for wood-logs by using different

classiﬁers is introduced. The approach lead to very

good results, but need well trained classiﬁers.

The segmentation and detection of fruit objects is

addressed in (Zhao et al., 2005; Wijethunga et al.,

2008; Rui et al., 2010; Akin et al., 2012; Aloisio

et al., 2012) – each addressing a speciﬁc fruit type. A

texture-based object detection by using the gray level

co-occurrence matrix is adapted in (Zhao et al., 2005;

Rui et al., 2010) to detect and segment apples. A spe-

cial and heuristic color range of the RGB color space

is used in (Akin et al., 2012) to detect apples. Another

heuristic color range is applied in (Wijethunga et al.,

2008) to segment kiwis. Especially, cluster of the a

and b channels of the Lab-color space are ﬁrst trained

for kiwis. Then, the distance to the trained cluster is

used to segment the fruits. In (Aloisio et al., 2012)

citrus fruits are pixel-wise segmented with a Bayes

classiﬁer.

The segmentation of ﬁshes is rarely addressed in

research. Existing approaches are mostly designed

for underwater imaging (Lee et al., 2010; Zhu et al.,

2012). In both approaches, the frame to frame coher-

ence is used in videos to segment the moving ﬁshes.

An approach based on single images and individual

ﬁshes is introduced in (White et al., 2006) for the

segmentation of caught ﬁshes lying on a convey belt.

First, the major color range in the RGB color space of

the conveyer belt is calculated in a calibration step. In

the segmentation step, a pixel outside the color space

is segmented as ﬁsh pixel, if 40% of the pixels in a

10 ×10 neighborhood are also outside the threshold.

In summary, many methods to segment organo-

groups exist, but all methods are very specialized.

They only work under speciﬁc conditions and are

mostly designed for a speciﬁc organo-group.

3 ORGANO-GROUPS

In our scenario, a picture of one organo-group is taken

by e.g. a mobile phone. We cannot address all kinds of

organo-groups, but select a subset to validate our ap-

proach. This means, we especially address potatoes,

apples, ﬂatﬁshes and wood cut surfaces. Most objects

of the groups are located on an arbitrary background

(e.g. grass, stone ﬂoor, sand). In the case of wood

cut surfaces, a picture of the front side of a stack of

wood is taken. The objects of the organo-groups we

examine:

• overlap each other not more then 20%

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

592

• are quasi round, which means, that the overlap of

the best ﬁtting circle with the same area is greater

than 60%

• are of the same kind (species) and mostly similar

in texture and color

Figure 2: Pictured is a subset of the organic objects (wood

cut surfaces, ﬂatﬁshes, apples and potatoes) of our scenario.

The objects are different in shape, color and texture. Also

the background is different and unknown.

In one image the objects of one organo-group are

similar, but yet there is a certain variance between

the objects in color, shape and texture. Furthermore,

the characteristics of one organo-group to another

organo-Group are completely different, e.g. wood

logs in compare to ﬂatﬁshes. And last but not least,

the background is unknown and varies in color and

texture. Some objects of each group can be seen in

Figure 2.

4 OUR APPROACH

Our more generalize approach extends the speciﬁc

approach for wood log segmentation in (Gutzeit and

Voskamp, 2012). Similar as in the wood log segmen-

tation case, the objects of a speciﬁc organo-group in

one image are mostly similar in color and texture. For

that reason, we think that an optimization-based seg-

mentation with an appropriate color model is a good

way to solve the problem. In our approach we cre-

ate a color model of the objects (foreground) and non

objects (background) by using an simple object detec-

tion and veriﬁcation method. Based on this model, a

probability map of fore- and background is calculated

with a special sampling approach. The image is then

binary segmented by an optimization-based method

and the objects are ﬁnally separated. The four steps

of our approach are illustrated in Figure 3.

Figure 3: Our principal methodology and the steps of our

organo-group segmentation.

In the ﬁrst step, the organic objects are detected

by a trained detector. We have decided to use haar-

cascades (Viola and Jones, 2001) as a detector, be-

cause they allow the training of a moderate detector

with only a few samples. The detection in our ap-

proach does not have to be very robust, but should

detect approximately 50 % of the objects. Further-

more, the detected objects are veriﬁed by removing

outliers and solving overlaps. The result is a set of

circles C, which is used in the second step to cre-

ate two models. One model contains estimated pix-

els of the foreground and the other one the pixels of

the background. Based on these models and a density

estimation, two probability maps (I

f g

, I

) are cre-

ated. In the third step, the image is binary segmented

with different optimization-based approaches involv-

ing I

f g

and I

. We especially apply graph-cut (GC)

and belief propagation (BP). Finally, the objects are

separated in the fourth step.

In the case of wood logs, the objects (wood cut

surfaces) are grouped in image space, have a high

yellow value and are brighter as the space between

the wood logs. In the general scenario the assump-

tion does not hold, because the organic objects can be

scattered and the color of the objects is unknown. We

thus generalize and improve the following parts (cf.

Figure 3):

• another object veriﬁcation method to optimize the

true positive rate,

• an easier and more general method to estimate

pixels of the fore- and background usable to create

color models for segmentation, and

• an improved object separation method.

Additionally, we apply belief propagation to show the

general aspect and to ﬁnd the best optimization based

method for our purpose. For this, we use probability

maps of the fore- and background as interface to the

optimization based segmentation method.

4.1 Object Detection and Veriﬁcation

In the original wood log segmentation approach, the

wood cut surfaces are detected by well trained haar-

cascades. After that, to optimize the true positive

rate, the detected objects are veriﬁed by eliminating

outliers and overlapping objects. In our scenario the

objects are scattered and not grouped as wood logs.

Hence, an outlier elimination in image space is not

reasonable. Therefore, we also detect the objects,

but verify them by using the color similarity. We

decided us to apply haar-cascades (Viola and Jones,

2001) as detector, because a training set of 100 pos-

itive and 300 negative samples are enough to get a

moderate detector and the creation of some samples

is usually not a hard task. The detection with the

Optimization-basedAutomaticSegmentationofOrganicObjectsofSimilarTypes

593

trained haar-cascades leads to a set of rectangles. To

improve the detection result, we ﬁrst convert the rect-

angles with width w and height h into a set of circles

C. The radius r of one circle is calculated by

w+h

and the center of the circle corresponds to the center

of the rectangle. Next, we apply a special veriﬁca-

tion of the circles in terms of color similarity. For

every circle the mean color of a pixel in RGB color

space px

= (r

)

is calculated. The circles

are therefore scaled down ﬁrst by r = r ·0.75 to get

only pixels of the object. Then, the mean and vari-

ance over all n circle mean colors is calculated:

px =

∑

i=1

; σ

∑

i=1

px − px

;n = |C|

(1)

The circles with the greatest Euclidean distance

to the mean is removed. The process is repeated un-

til the variance σ

is under a certain threshold T .

It experimentally turned out, that T = 20 is a good

threshold for images with r,g,b ∈ [0, 255]. We note

that objects in our scenario only slightly overlap each

other. The overlap from one to another object in C is

normally not greater than 20%. Consequently, we re-

move all smaller objects with an greater overlap. The

two described simple outlier removing methods lead

to fewer false-positive detections (see Figure 4).

Figure 4: The results of the detection (upper row) and ver-

iﬁcation step (lower row) of wood cut surfaces, ﬂatﬁshes,

potatoes and apples.

4.2 Fore- and Background Estimation

The aim of this step is to estimate a foreground

(FG

smp

) and a background pixel set (BG

smp

). With

the pixel sets, the image can be binary segmented with

a kd-tree accelerated density estimation (KD-NN) fol-

lowed by an optimization based segmentation. This

method by using graph-cut applied on wood logs is

called KD-NN-A in (Gutzeit and Voskamp, 2012). In

the KD-NN-A approach, a trimap I

tri

is used to mark

a pixel as unknown, foreground or background. The

foreground pixels are calculated with a heuristic color

segmentation followed by a graph-cut segmentation

on a certain region around the mean of the veriﬁed

objects. In contrast to the foreground pixels, the back-

ground pixels are calculated through a distance trans-

form.

In this approach, we estimate the pixels in an

easier way without color heuristics and a graph-cut

presegmentation. Furthermore, we calculate ﬁrst a

trimap and than a foreground (I

f g

) and background

probability map (I

) by using the KD-NN. A proba-

bility map contains probabilities p ∈[0,1]. Each pixel

of the image I

corresponds to one foreground (p

f g

∈

f g

) and to one background probability (p

∈ I

Both maps are an independent interface to the next

step, the optimization based segmentation. We call

this approach KD-NN-G (KD-NN-generalized).

In our approach, we create the trimap I

tri

by ran-

dom sampling with the set C. One label l in I

tri

cor-

responds to one in I

and can have the value u (un-

known), f g (foreground) or bg (background). Each

circle c ∈ C is represented by a triple c = (x

,r),

whereby (x

)

is the center position and r the ra-

dius. The labels in I

tri

are set for each pixel in I

position (x,y)

by using a threshold a ∈ [0,1]:

f (~p,C,a) =











f g, ∃(~p

,r) ∈C : k~p −~p

< a ·r

u, ∃(~p

,r) ∈C : k~p −~p

∈ [a ·r,r]

bg, otherwise

(2)

It experimentally turned out that a = 0.7 is a good

threshold. All pixels in I

marked with l = f g are put

into the pixel set FG and for l = bg into BG. The pixel

sets are normally not equal in size and can hold falsely

classiﬁed pixels. The usually unwanted case is that

a non-detected object is marked as background. To

weaken the inﬂuence of falsely classiﬁed pixels, we

apply a random sampling over BG and FG. The re-

sults are two subsets of equal size FG

smp

and BG

smp

The size of the subsets is relative to the image width

(w) and height (h) in the following way:

w ·h ·b = |FG

smp

| = |BG

smp

|; b ∈[0,1] (3)

smp

⊆ FG; BG

smp

⊆ BG (4)

A good scaling factor is b = 0.05. All pixels,

which are not in FG

smp

or BG

smp

are set in I

tri

u (unknown) and all pixels in FG

smp

and BG

smp

are

stored in two separate kd-trees. Finally, the probabil-

ity maps I

f g

and I

are created by a density estima-

tion with a sphere environment on the kd-trees.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

594

4.3 Graph-Cut and Belief Propagation

Using the probability maps created in the last step, the

aim of this step is to binary segment the input image

and adapting an optimization based segmentation.

We therefore adapt two different methods, graph-cut

and belief propagation.

A graph-cut (GC) is a cut of a graph G = (V,E)

with the nodes V and weighted edges E. The nodes V

consists of non-terminal (pixel nodes) and two termi-

nal nodes (source s and sink t). A pixel node cor-

responds to an image pixel and is connected to its

four neighbors. A terminal node is connected to all

pixel nodes, whereby s represents foreground and t

background. We directly set the edge weights from a

terminal node to a non-terminal node with the corre-

sponding probabilities in I

f g

and I

. The weights w

between the non-terminal nodes are set with

w = 1 −e

−α·

−px

, (5)

where px = (r,g,b)

denotes a pixel in the RGB color

space, α is a free scaling factor and i, j are adjacent

non-terminal nodes. A suitable value for α is 0.0005.

After the graph weighting, the min-cut/max-ﬂow of

(Boykov and Kolmogorov, 2004) is applied.

For the belief propagation (BP), we adapt the

loopy max-product BP algorithm of (Felzenszwalb

and Huttenlocher, 2006). The algorithms works by

parsing messages around a four connected image

graph. A message from nodes i to the connected node

j is denoted by m

i→j

, whereby k denotes the iteration.

Our message has two dimensions due to the two pos-

sible labels L = {0,1}. 1 labels a object pixel and 0 a

non-object pixel. One message is computed in a sim-

ilar way as in (Felzenszwalb and Huttenlocher, 2006)

at each iteration:

h(l

) = c ·ψ(l

) + c ·φ(l

) +

∑

s∈N( j)\i

k−1

s→j

)

j→i

) = min

(h(l

))

(6)

We extent Eq. (6) by the scaling factor c = 0,9 to

force convergence and to stronger weight the starting

state. l

∈ L are the labels of node i and j. In our

case, the discontinuity cost ψ of two adjacent nodes

and the matching cost φ are computed by:

ψ(l

) =

(

0, l

= l

1, l

6= l

; φ(l

) =

(

1 − p

f g

, l

= 1

1 − p

, l

= 0

(7)

whereby p

denotes the corresponding probability in

f g

or I

of the node i. The ﬁnal belief is calculated

as in (Felzenszwalb and Huttenlocher, 2006).

Figure 5: left: the input image I

, middle: I

, the result

of the GC (left) and BP (right) segmentation, right: I

, the

result of the GMC-G separation on the GC result.

The result of both optimization based methods are

a binary image I

with object pixels (l = 1) and non-

object pixels (l = 0), which is illustrated in Figure 5.

4.4 Object Separation with GMC-G

In this last step, the objects are separated by using

the veriﬁed circles C in the binary image I

(l ∈

{0,1}). We generalized the LSGMC (Log Separa-

tion by Growing Moving Circles) approach described

in (Gutzeit and Voskamp, 2012) and call the extended

one GMC-G (GMC-generalized). The LSGMC is op-

timized for the separation of wood cut surfaces in a

binary image I. The approach ﬁts circles C together

with extracted local maxima into an binary image

. The local maxima are calculated by a distance-

transform and converted into circles. All circles to-

gether simultaneously grow, move and melt until a

certain energy is reached, which means the ratio be-

tween a circle and the underlying segmented pixels

(l = 1). The circle ﬁtting part is called GMC (Grow-

ing Moving Circles).

The major problem of the LSGMC is that non-

round objects will be split into unwanted parts (under-

segmentation). To solve this problem, we additionally

add ﬁrst order statistics of the circle set C and a wa-

tershed segmentation. Especially, we use the mean r

and variance σ

of the circle radii in C.

First, all pixels inside a circle c ∈C in I

are set to

0 and a distance-transform is processed on the result-

ing binary image. Then, the distance image is thresh-

old segmented by T = max (r −3σ

,r/2). The out-

come of the segmentation are those segments S which

are probably non-detected objects. For all S, the mass

center mc = (x

)

and radii r

√

A ÷π are cal-

culated. The symbol A represents the area as well as

the amount of pixels in S. Each S is united as circle

= (x

) with C. The result is an extended set

which is subsequently ﬁt into the image I

by us-

ing the GMC. The ﬁtted circles C

are further used

to determine seed points for a watershed segmenta-

tion. Especially, we determine a marker image I

with |C

|+ 2 labels. Each label in I

inside a circle

(x,y,0.8 ·r) ∈C

is set to the circle index. All other

labels are set to unknown (−1). Furthermore, the la-

Optimization-basedAutomaticSegmentationofOrganicObjectsofSimilarTypes

595

bels in I

, which are background in I

and more than

3·σ

pixels away from the nearest object pixel, are set

to 0. Finally, the image I

is watershed segmented by

using I

. The results on some examples in our data

set can be seen on the right of Figure 5.

5 Results

The detection, veriﬁcation and segmentation results

are evaluated against the ground truth (GT). We all-

together use 71 wood log, 25 potatoes, 25 apples and

25 ﬂatﬁsh images. In all images the background and

objects are different in color, texture, and shape. We

separately evaluate the object veriﬁcation, segmen-

tation, and separation step. For the evaluation we

mainly use the measures precision, recall, and f-score.

Additionally, to evaluate the separation (multi-object-

segmentation) the HD-M (Huang-Dom-measure in

(Huang and Dom, 1995)) is used. In all measures, the

best value is 1 and the worst one is 0. Some results of

our approach in comparison to grab-cut are illustrated

in Figure 6.

5.1 Object Detection and Veriﬁcation

The objects are detected with haar-cascades and are

subsequently veriﬁed. Table 1 shows the average pre-

cision, recall, and f-score we get for the detected (up-

per table) and veriﬁed objects (lower table). The stan-

dard deviation is presented in brackets.

Table 1: Detected (upper table) and veriﬁed (lower table)

organic objects.

object precision recall f-score

wood 0.81 (0.1) 0.69 (0.11) 0.745 (0.1)

apple 0.97 (0.04) 0.95 (0.06) 0.96 (0.05)

potato 0.70 (0.18) 0.59 (0.27) 0.60 (0.21)

ﬂatﬁsh 0.94 (0.11) 0.66 (0.21) 0.76 (0.17)

wood 0.87 (0.07) 0.68 (0.11) 0.76 (0.09)

apple 0.97 (0.04) 0.94 (0.06) 0.95 (0.04)

potato 0.88 (0.2) 0.57 (0.27) 0.65 (0.24)

ﬂatﬁsh 0.96 (0.09) 0.65 (0.21) 0.76 (0.17)

The values related to the detected objects are

mostly between 0,6 and 0,75. The best results are

achieved with apples. The detection of apples is

nearly perfect, because apples have a round shape and

mostly a homogenous color. After the object veriﬁca-

tion step the f-score and the precision is better in all

cases excluding the apples. In the apple case, only

the f-score is a little bit poorer as before. To create

a good foreground model for the segmentation, valid

object samples are needed. For that reason, the preci-

sion of the detection is more important than the recall.

This means regarding to the results the veriﬁcation of

the objects is an useful and appropriate step.

5.2 Binary Object Segmentation

The result of the optimization based segmentation

(BP, GC) is a binary image. To evaluate the binary

segmentation we use again precision, recall, and f-

score. Different to the object veriﬁcation evaluation,

the pixels (object or non object) and not the object

itself are taken into account.

In our approach, the ﬁnal binary segmentation can

be done with graph-cut (GC) or belief propagation

(BP) based on our KD-NN-G. The results of both

methods are illustrated in Table 2.

Table 2: Evaluation of the binary segmentation (classiﬁca-

tion as object or non object pixel). The best values are in

bold print.

object precision recall f-score

KD-NN-A with GC

wood 0.88 (0.08) 0.95 (0.03) 0.91 (0.04)

apple 0.97 (0.03) 0.70 (0.19) 0.80 (0.12)

potato 0.41 (0.47) 0.24 (0.29) 0.29 (0.35)

ﬂatﬁsh 0.19 (0.37) 0.08 (0.2) 0.09 (0.16)

KD-NN-G with BP

wood 0.77 (0.09) 0.94 (0.04) 0.85 (0.07)

apple 0.88 (0.19) 0.71 (0.19) 0.74 (0.13)

potato 0.91 (0.07) 0.76 (0.09) 0.82 (0.05)

ﬂatﬁsh 0.96 (0.07) 0.69 (0.1) 0.8 (0.08)

KD-NN-G with GC

wood 0.92 (0.04) 0.92 (0.05) 0.92 (0.03)

apple 0.98 (0.01) 0.89 (0.08) 0.94 (0.05)

potato 0.93 (0.05) 0.87 (0.06) 0.9 (0.04)

ﬂatﬁsh 0.97 (0.08) 0.82 (0.1) 0.88 (0.08)

The results with the adapted belief propagation

method are in general not as good as the results us-

ing graph-cut, but still suitable with an average f-

score of 0.8. This shows, that different optimization

based methods can be applied to solve the problem,

whereby graph-cut leads to the best results. In com-

parison to the KD-NN-A, our algorithm is even a little

bit better in the segmentation of wood logs and sig-

niﬁcantly better in the segmentation of other organo-

groups. For the segmentation of ﬂatﬁshes and pota-

toes, the KD-NN-A failed. Only for apples, which

are very similar in color like wood cut surfaces, the

KD-NN-A achieves suitable results. This is because

the KD-NN-A is specially designed to segment wood

logs in a stack of wood.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

596

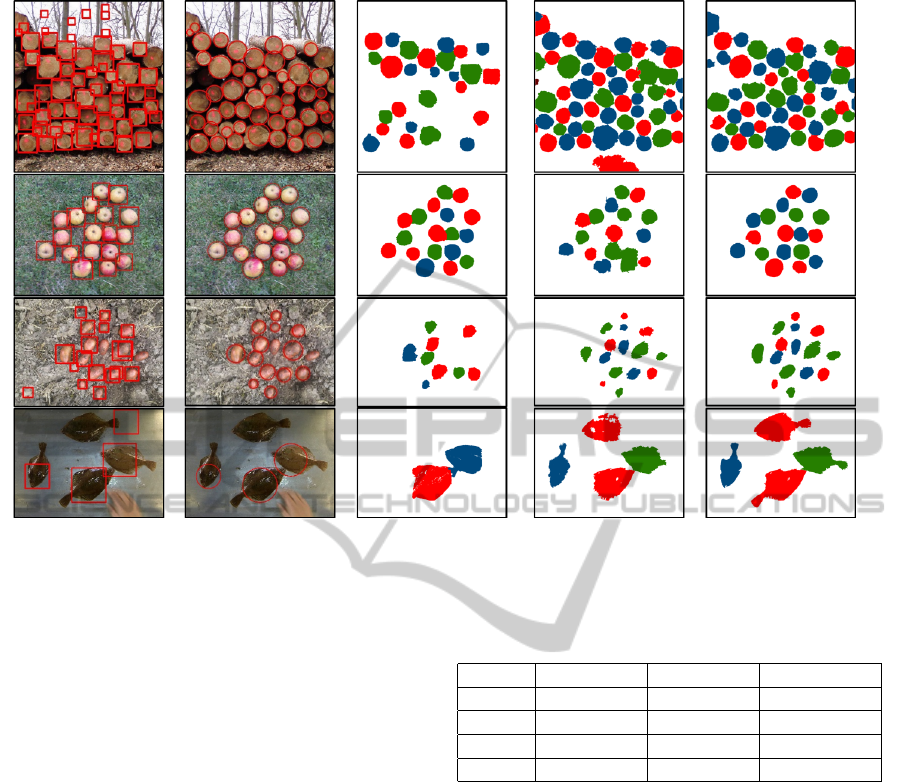
Figure 6: The pictures show some results of our segmentation compared to grab-cut. The ﬁrst column show the detected

objects marked by rectangles and the second one the veriﬁed objects marked by circles. The results of grab-cut are given in

the third column and of our approach with belief-propagation (BP) as well as grab-cut (GC) in the fourth and ﬁfth column.

5.3 Multi-object Segmentation

To evaluate the multi-object segmentation we use the

Huang-Dom-measure (HD-M). The HD-M is based

on the hamming distance from one segmented object

to a corresponding ground truth object and otherwise.

Similar to the f-score, a value of 1 indicates a per-

fect segmentation. Different to the f-score, not seg-

mented objects on a large background can still lead

to a relatively high value, because a not-found corre-

spondence has no penalty in the measure and will be

simply ignored. Consequently, the HD-M is mainly

suitable to compare different methods. The results for

grab-cut, the LSGMC and our GMC-G are presented

in Table 3. The LSGMC separates objects by using

detected objects and a binary image. Our GMC-G im-

proves the LSGMC by combining the separation with

a watershed segmentation. The input binary images

for both methods are generated with graph-cut as de-

scribed before with KD-NN-A or KD-NN-G.

The evaluation results in Table 3 show that our

GMC-G yields for all objects the best results and

Grab-Cut and LSGMC generate in nearly all cases

poorer results. Only in the apple case the grab-cut re-

sults are similar to the GMC-G ones. This is because

the apple detection is nearly perfect. Nevertheless,

grab-cut applied on the veriﬁed objects can also fail,

as shown in Figure 6.

Table 3: Evaluation of the multi-object-segmentation with

the HD-Measure. The best values are in bold print.

object grab-cut LSGMC GMC-G

wood 0.89 (0.04) 0.92 (0.15) 0.93 (0.02)

apple 0.99 (0.01) 0.98 (0.01) 0.99 (0.01)

potato 0.95 (0.36) 0.94 (0.03) 0.97 (0.014)

ﬂatﬁsh 0.90 (0.05) 0.83 (0.07) 0.94 (0.03)

6 CONCLUSION

We presented an automatic segmentation method for

organo-groups in images. Such groups consist of or-

ganic objects of similar types (like wood logs, ap-

ples, or tomatoes) on unknown background. Although

approaches for speciﬁc objects exist, so far no ap-

proach was general enough to segment such an arbi-

trary group. Although this method needs an object

detector in the ﬁrst step, the detector does not have

to be very accurate, because the detection results are

veriﬁed and the approach can compensate these inac-

curacies.

Our approach generalizes and improves existing

work in combining an object veriﬁcation method to

optimize the true positive rate, a fore- and background

probability map creation method usable as input for

an optimization based segmentation method, and an

Optimization-basedAutomaticSegmentationofOrganicObjectsofSimilarTypes

597

improved object separation method.

We compare our approach against grab-cut and a

dedicated wood log segmentation method and outper-

form both methods. In the case of wood log segmen-

tation, our approach is even a little bit better than the

dedicated wood log segmentation method.

REFERENCES

Achanta, R., Shaji, A., Smith, K., Lucchi, A., Fua, P., and

usstrunk, S. (2012). SLIC Superpixels Compared to

State-of-the-Art Superpixel Methods. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

34(11):2274–2282.

Akin, C., Kirci, M., Gunes, E. O., and Cakir, Y. (2012).

Detection of the pomegranate fruits on tree using

image processing. In Agro-Geoinformatics (Agro-

Geoinformatics), 2012 First International Conference

on, pages 1–4.

Aloisio, C., Mishra, R., Chang, C.-Y., and English, J.

(2012). Next generation image guided citrus fruit

picker. In Technologies for Practical Robot Applica-

tions (TePRA), 2012 IEEE International Conference

on, pages 37 –41.

Boykov, Y. and Kolmogorov, V. (2004). An experimental

comparision of min-cut/max-ﬂow algorithms for en-

ergy minimation in vision. In PAMI, pages 1124–

1137.

Chan, T. F. and Vese, L. A. (2001). Active contours with-

out edges. IEEE Transactions on Image Processing,

10(2):266–277.

Dahl, A. B., Guo, M., and Madsen, K. H. (2006). Scale-

space and watershed segmentation for detection of

wood logs. In Vision Day, Informatics and Mathe-

matical Modelling.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2006). Efﬁcient

belief propagation for early vision. Int. J. Comput.

Vision, 70(1):41–54.

Gutzeit, E., Ohl, S., Kuijper, A., Voskamp, J., and Urban,

B. (2010). Setting graph cut weights for automatic

foreground extraction in wood log images. In VISAPP

2010, pages 60–67.

Gutzeit, E. and Voskamp, J. (2012). Automatic segmen-

tation of wood logs by combining detection and seg-

mentation. In ISVC 2012 - 8th International Sympo-

sium on Visual Computing, volume LNCS 7431, pages

252–261.

Herbon, C., Tnnies, K. D., and Stock, B. (2014). Detection

and segmentation of clustered objects by using iter-

ative classiﬁcation, segmentation, and gaussian mix-

ture models and application to wood log detection. In

GCPR, pages 354–364.

Huang, Q. and Dom, B. (1995). Quantitative methods of

evaluating image segmentation. In Image Processing,

1995. Proceedings., International Conference on, vol-

ume 3, pages 53 –56 vol.3.

Kass, M., Witkin, A., and Terzopoulos, D. (1988). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(4):321–331.

Lee, J.-H., Wu, M.-Y., and Guo, Z.-C. (2010). A tank ﬁsh

recognition and tracking system using computer vi-

sion techniques. In Computer Science and Informa-

tion Technology (ICCSIT), volume 4, pages 528–532.

Li, S. Z. (1995). Markov random ﬁeld modeling in computer

vision. Springer-Verlag, London, UK, UK.

Medina Rodriguez, P., Fernandez Garcia, E., and Diaz Ur-

restarazu, A. (1992). Adaptive method for image seg-

mentation based in local feature. Cybernetics and Sys-

tems, 23(3-4):299–312.

Otsu, N. (1979). A threshold selection method from gray-

level histograms. In IEEE Transactions on Systems,

Man and Cybernetics, pages 62–66.

Roth, S. and Black, M. J. (2005). Fields of experts: A

framework for learning image priors. In In CVPR,

pages 860–867.

Rother, C., Kolmogorov, V., and Blake, A. (2004). Grabcut

- interactive forground extraction using iterated graph

cuts. In ACM Transactions on Graphics, pages 309–

314. ACM Press.

Rui, G., Gang, L., and Yongsheng, S. (2010). A recogni-

tion method of apples based on texture features and

em algorithm. In World Automation Congress (WAC),

2010, pages 225 –229.

Sezgin, M. and Sankur, B. (2004). Survey over image

thresholding techniques and quantitative performance

evaluation. Journal of Electronic Imaging, 13(1):146–

168.

Shi, J. and Malik, J. (2000). Normalized cuts and image

segmentation. In IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, pages 888–905.

Viola, P. A. and Jones, M. J. (2001). Rapid object detection

using a boosted cascade of simple features. In CVPR

(1), pages 511–518.

White, D., Svellingen, C., and Strachan, N. (2006). Auto-

mated measurement of species and length of ﬁsh by

computer vision. Fisheries Research, 80(2-3):203–

210.

Wijethunga, P., Samarasinghe, S., Kulasiri, D., and Wood-

head, I. (2008). Digital image analysis based auto-

mated kiwifruit counting technique. In Image and Vi-

sion Computing New Zealand, pages 1 –6.

Zhang, X., Yang, Y.-H., Han, Z., Wang, H., and Gao, C.

(2013). Object class detection: A survey. ACM Com-

put. Surv., 46(1):10:1–10:53.

Zhao, J., Tow, J., and Katupitiya, J. (2005). On-tree fruit

recognition using texture properties and color data. In

Intelligent Robots and Systems, 2005. (IROS 2005).

2005 IEEE/RSJ International Conference on, pages

263 – 268.

Zhu, L.-M., Zhang, Y.-L., Zhang, W., Tao, Z.-C., and Liu,

C.-F. (2012). Fish motion tracking based on rgb color

space and interframe global nerest neighbour. In Auto-

matic Control and Artiﬁcial Intelligence (ACAI 2012),

International Conference on, pages 1061–1064.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

598