Improving the Egomotion Estimation by Correcting the Calibration Bias

Ivan Kre

so and Sini

Segvi

University of Zagreb Faculty of Electrical Engineering and Computing, Unska 3, 10000 Zagreb, Croatia

Keywords:

Stereo Vision, Camera Motion Estimation, Visual Odometry, Feature Tracking, Camera Calibration, Camera

Model Bias, Deformation Field.

Abstract:

We present a novel approach for improving the accuracy of the egomotion recovered from rectiﬁed stereo-

scopic video. The main idea of the proposed approach is to correct the camera calibration by exploiting the

known groundtruth motion. The correction is described by a discrete deformation ﬁeld over a rectangular

superpixel lattice covering the whole image. The deformation ﬁeld is recovered by optimizing the reprojec-

tion error of point feature correspondences in neighboring stereo frames under the groundtruth motion. We

evaluate the proposed approach by performing leave one out evaluation experiments on a collection of KITTI

sequences with common calibration parameters, by comparing the accuracy of stereoscopic visual odometry

with original and corrected calibration parameters. The results suggest a clear and signiﬁcant advantage of the

proposed approach. Our best algorithm outperforms all other approaches based on two-frame correspondences

on the KITTI odometry benchmark.

1 INTRODUCTION

Egomotion estimation is a technique which recov-

ers the camera displacement from image correspon-

dences. The technique is important since it can pro-

vide useful initial solution for more involved struc-

ture and motion (SaM) estimation approaches, which

perform partial or full 3D reconstruction of the scene

(Vogel et al., 2014). These approaches are appeal-

ing due to many potential applications in robotic (e.g.

autonomous navigation (Diosi et al., 2011)) and au-

tomotive systems (e.g. driver assistance (Nedevschi

et al., 2013) and road safety inspection).

Visual odometry (Nist

er et al., 2004) is an interest-

ing special case of egomotion estimation, where we

wish to recover the camera trajectory over extended

navigation essays with predominantly forward mo-

tion. In this special case, complex techniques such

as batch reconstruction (global bundle adjustment) or

recognizing previously visited places (loop closing)

are inapplicable due to huge computational complex-

ity involved and/or real time requirements. Hence,

the only remaining option is to recover partial camera

displacements over short sequences of input frames

and to build the overall trajectory by patching them

one after another. The resulting techniques are neces-

sarily prone to the accumulation of incremental error,

just as the classical wheel odometry, and are hence

collectively denoted as visual odometry.

Due to conceptual simplicity and better stability,

the camera egomotion is usually recovered in cali-

brated camera setups. Camera calibration is the pro-

cess of estimating the parameters of a camera model

which approximates the image formation. When we

have a calibrated camera, we can map every image

pixel to a 3D ray emerging from the focal point of

the camera and spreading out to the physical world.

Most perspective cameras can be calibrated reason-

ably well by parametric models which extend the

pinhole camera with radial and tangential distortion.

However, there is no guarantee that this model has

enough capacity to capture all possible distortions of

real camera systems in enough detail, especially when

high reconstruction accuracy is desired. For exam-

ple, many popular calibration models assume that the

distortion center coincides with the principal point

(Zhang, 2000), while it has been shown that this does

not hold in real cameras (Hartley and Kang, 2005). A

good overview of the camera calibration techniques

and different camera models is given in (Sturm et al.,

2011).

In this paper, we propose a novel approach for cor-

recting the calibration of a stereoscopic camera sys-

tem. In our experiments we come to the conclusion

that the reprojection error is not uniformly distributed

across the stereo image pair and that there exists a reg-

347

Krešo I. and Šegvi

c S..

Improving the Egomotion Estimation by Correcting the Calibration Bias.

DOI: 10.5220/0005316103470356

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 347-356

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

ularity in the reprojection error bias. We hypothesize

that this disturbance in the reprojection error distribu-

tion is caused by inaccurate calibration due to insuf-

ﬁcient capacity of the assumed distortion model. We

propose to alleviate the disturbance by a local cam-

era model (Sturm et al., 2011) formulated as a de-

formation ﬁeld over a rectangular superpixel lattice

in the two images of stereo pair. The proposed cam-

era model has many parameters and hence requires a

large amount of training data. Thus we propose to

learn the parameters of our deformation ﬁeld by ex-

ploiting the groundtruth camera motion and point fea-

ture correspondences in neighboring frames. The two

principal contributions of this paper are as follows:

• a statistical analysis of the reprojection error by

utilizing the groundtruth motion (subsection 4.2);

• a technique for correcting the camera calibration

by exploiting the groundtruth motion for learning

the image deformation ﬁeld (subsection 4.3).

The experimental results presented in Section 5

show that the proposed approach is able to signiﬁ-

cantly improve the accuracy of the recovered camera

motion. Our best algorithm outperforms all other ap-

proaches based on two-frame correspondences on the

KITTI odometry benchmark.

2 RELATED WORK

An increasing number of papers focusing on visual

odometry is an evidence of the problem importance.

A detailed overview of the ﬁeld can be found in

(Scaramuzza and Fraundorfer, 2011; Fraundorfer and

Scaramuzza, 2012). Most recent implementations are

based on the approach that was proposed in (Nist

et al., 2004). The main contribution of their approach

is that they did not deﬁne the cost function as a so-

lution to point alignment problem in 3D space like

earlier researchers (Moravec, 1980; Moravec, 1981).

Instead, they used the 3D-to-2D cost function which

minimizes the alignment error in 2D image space

popularly called the reprojection error. The advantage

of deﬁning the error in image space is that it avoids the

problem of triangulation uncertainty on the depth axis

where the error variance is much larger compared to

other two axes.

Most of the recent work is focused on constraining

the optimization with multi-frame feature correspon-

dences to achieve better global consistency (Badino

et al., 2013; Konolige and Agrawal, 2008), by ex-

perimenting with new feature detectors and descrip-

tors (Konolige et al., 2007) or by doing a further re-

search in feature tracking and outlier rejection tech-

niques (Badino and Kanade, 2011; Howard, 2008).

Despite the vast amount of research on visual odom-

etry done so far, we did not stumble upon any work

addressing the impact of calibration to the accuracy

of the results nor approaches to improve the calibra-

tion by employing the groundtruth motion data. We

have previously shown (Kreso et al., 2013) that the

accuracy of the reconstructed motion signiﬁcantly de-

pends on the quality of the calibration target (A4 pa-

per vs LCD monitor). Now we go a step further by

proposing a method for correcting the calibration bias

due to insufﬁcient capacity of the camera model.

3 STEREOSOPIC VISUAL

ODOMETRY

A typical visual odometry pipeline is illustrated in

Figure 1. Acquired images are given to the feature

tracking process where the features are detected and

descriptors extracted. The descriptors are then used to

ﬁnd the correspondent features in temporal (two adja-

cent frames) and spatial (stereo left and right) domain.

Temporal and stereo matching can be performed inde-

pendently if we do not apply feature detector in right

images, or jointly if we do. After the feature matching

the correspondences typically contain outliers which

are usually rejected by random sampling. Finally we

can optimize an appropriate cost function to recover

the camera motion. Note that the image acquisition

block in Figure 1 also contains the image rectiﬁcation

procedure which depends on camera calibration.

FEATURE

DETECTION

AND

DESCRIPTOR

EXTRACTION

IMAGE

ACQUISITION

TEMPORAL

MATCHING

STEREO

MATCHING

OUTLIER

REJECTION

MOTION

ESTIMATION

Figure 1: A typical visual odometry pipeline.

3.1 Feature Tracking

In order to recover the camera motion we must

ﬁrst ﬁnd enough point correspondences between two

stereo image pairs. It is assumed that the stereo rig

is calibrated and that the images are rectiﬁed (their

acquisition is described by a rectiﬁed stereo cam-

era model). We use a similar tracking technique as

(Nist

er et al., 2004) and (Badino et al., 2013). We de-

tect Harris point features (Harris and Stephens, 1988)

only in left images and perform brute-force matching

of their descriptors inside a search window to obtain

left camera monocular tracks. To extract the descrip-

tors we simply crop plain patches of size 15x15 pix-

els around each detected corner. We establish corre-

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

348

spondences based on the normalized cross-correlation

metric (NCC) between pairs of point features. In or-

der to reduce the localization drift in tracking, we

match all features in the current frame to the oldest

occurrences.

To obtain the full stereo correspondences, we

measure the disparity of every accepted left monoc-

ular track by searching for the best correspondence in

the right image along the same horizontal row. Here

again we compare the plain patch descriptors with

NCC. Compared with matching of independently de-

tected point features, this approach is more robust

to poor repeatability at the price of somewhat larger

computational complexity.

3.2 Cost Function Formulation

Let us denote an image point as q = (u, v)

. Now

we can deﬁne the points q

i,t−1

in the previous frame

(t −1) and q

i,t

in the current frame (t), where i ∈ [1, N]

is the index of the point and k ∈ {l, r} is the value

denoting if the point belongs to the left or right image.

Let us subsequently denote X

i,t

as the i-th 3D point in

the current frame (t):

i,t

= (x, y, z)

= t

t(q

i,t

, q

i,t

) , (1)

where t

t() is the function which triangulates the 3D

point in world coordinate system from measured left

and right image points. The goal of egomotion esti-

mation is to recover the 3x3 rotation matrix R and the

3x1 translation vector t that satisfy the 6DOF rigid

body motion of the tracked points.

In order to formulate the cost function we ﬁrst

need a camera model to describe the image acquisi-

tion process by connecting each image pixel with the

corresponding real world light ray falling on the cam-

era sensor. This can be done using perspective projec-

tion with addition of nonlinear lens distortion model.

For brevity, we skip the modeling of lens distortion

and stereo rectiﬁcation and assume that the images are

already rectiﬁed. The following equation introduces

the pinhole camera model which uses the perspective

projection π to project the world point X = (x, y, z)

to the point q = (u, v)

on the image plane.









= π(X, R, t) =





f 0 c

0 f c

0 0 1





[R|t]













(2)

The ﬁrst part is the camera matrix containing the in-

trinsic camera parameters f , c

and c

. The distance

of the focal point from the image plane f does not cor-

respond directly to the focal length of the lens, since

it also depends on the type and distance of the cam-

era sensor. The principal point (c

, c

) is the image

location where the z-axis intersects the image plane.

Now we can formulate the cost function for the

two-frame egomotion estimation as a least squares

optimization problem with the error deﬁned in the im-

age space:

argmin

R,t

∑

i=1

{l,r}

∑

i,t

− π(X

i,t−1

, R, t

(3)

= t, t

= t

− (b, 0, 0)

(4)

The cost function described by equation (3) is known

as the reprojection error. To minimize the reprojec-

tion error, an iterative non-linear least squares opti-

mization like ﬁrst order Gauss-Newton (Geiger et al.,

2011) or second order Newton method (Badino and

Kanade, 2011) is usually employed. The equation (3)

shows that we are searching for a motion transforma-

tion which will minimize the deviations between im-

age points measured in the current frame and the re-

projections of the transformed 3D points triangulated

in the previous frame. The motion transformation is

represented by the matrix [R|t] which captures the

motion of 3D points with respect to the static cam-

era. We obtain the camera motion with respect to

the world by simply taking the inverse transformation

[R|t]

−1

. One nice property of the transformation ma-

trix emerging from the orthogonality of rotation ma-

trices is that the inverse transformation is fast and easy

to compute as shown in equation (5).

[R|t]

−1



R t



−1



−R



(5)

Note that the optimization is performed with re-

spect to six free parameters, three describing the cam-

era rotation matrix R and three describing the transla-

tion vector t. The equation (4) describes the relation-

ship between translations of the left and right cameras

in the rectiﬁed stereo case. This is because the X

triangulated in coordinate system of the left camera

and we need to shift it along x axis for the baseline

distance b in the case when we are projecting to the

right camera image plane. Note that the rotation ma-

trix is the same for the left and right cameras because

after the rectiﬁcation they are aligned to have coplanar

image planes and they share the same x-axis. Because

the baseline b is estimated in the camera calibration

and rectiﬁcation steps the number of free parameters

for translation remains three.

ImprovingtheEgomotionEstimationbyCorrectingtheCalibrationBias

349

4 LEARNING AND CORRECTING

THE CALIBRATION BIAS

In our previous research we have studied the inﬂu-

ence of subpixel correspondence and online bundle

adjustment to the accuracy of the camera motion esti-

mated from rectiﬁed stereoscopic video. Our prelim-

inary experiments have pointed out a clear advantage

of these techniques in terms of translational and rota-

tional accuracy on the artiﬁcial Tsukuba stereo dataset

(Martull et al., 2012). However, to our surprise, this

impact was signiﬁcantly weaker on the KITTI dataset

(Geiger et al., 2012; Geiger et al., 2013). Therefore,

we have decided to investigate this effect by observ-

ing the reprojection error of two-frame point-feature

correspondences under the KITTI groundtruth cam-

era motion which was measured by an IMU-enabled

GPS device.

4.1 Analysis of the Feature

Correspondences

The analysis pointed out many perfect correspon-

dences with large reprojection errors under the

groundtruth camera motion. Figure 2 shows some

examples of this effect where the points and the im-

age patches describing them are displayed. If we look

closely to any of the four patches, we can conclude

that the localization error between any of the four

frames should be less than 1 pixel. However, the re-

projection errors evaluated for the groundtruth motion

(cf. Table 1) are much larger than the localization er-

rors (7 pixel vs 1 pixel). After observing this we won-

dered whether this is a property of a few outliers or

whether there is a regularity with respect to the image

location.

4.2 Statistical Analysis of the

Reprojection Error

After observing many perfect correspondences with

large reprojection errors we decided to verify whether

this effect depends on image location. We divide the

image space into a lattice of superpixel cells in which

we accumulate the reprojection error vectors. Note

that for every stereo correspondence containing 4 fea-

ture points we have two reprojection errors, one in

the left image and the other in the right image. A sin-

gle left or right reprojection error is deﬁned by three

feature points which can be observed in equation (3).

Now for each reprojection error we share the respon-

sibility between the three points equally, by dividing

the vector by 3 and adding it to the cells containing

Table 1: Reprojection errors of the selected correspon-

dences from Figure 2 evaluated for the groundtruth motion.

The errors have much larger values than the uncertainty of

the point feature locations, as seen in Figure 2.

Color Left error Right error

Red 7.10 7.01

Green 6.68 6.56

Blue 7.4 7.32

Yellow 6.75 6.35

the three points responsible for that error. Figure 3

shows the obtained distribution of the reprojection er-

ror vectors for left camera image in each cell. We

computed the means of the error vector L2 norms and

means and variances on the two image axes spanning

the 2D error vector space. Additionally we used norm

means to draw the heat map of the reprojection error

distribution across the image.

By looking at the heat map and the means in Fig-

ure 3(c) we can conclude that the error minimum is

close to the image center and that the error increases

as we move away from the image center. Even more

importantly, we can observe that the vector means

given in Figure 3(d-e) are biased in certain directions

and that this bias is signiﬁcant considering the error

variances given in Figure 3(f-g). Figure 3 shows that

the minimal error of the camera model appears to be

slightly displaced from the principal point of the im-

age which is very close to the image center. This dis-

placement may be showing us that the center of the ra-

dial distortion is not in the principal point of the cam-

era as assumed by the employed rectiﬁcation model.

This problem was already observed in (Hartley and

Kang, 2005) where the authors proposed a method for

estimating the radial distortion center.

To conﬁrm that these effects are not due to

some strange bias within the tracker, we performed

the same statistical analysis on the Tsukuba stereo

dataset. Figure 4 shows the same heat map as

we showed before. However, we see that here,

on Tsukuba, the reprojection error is uniformly dis-

tributed without any observable pattern. Note that

the contrast between cells is large due to histogram

equalization but the actual values are distributed in

the range from 0.16 to 0.18. Here we didn’t show that

the error vector means on u and v axes are zero, for

brevity.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

350

Figure 2: The image on the top corresponds to the frame #1 of the training KITTI sequence 03. Four point features have been

annotated with different colors. The four bottom images show four 15x15 patches around each feature point in four different

images (current-left, current-right, previous-left, previous-right). The localization error in the four images is less than 1 pixel.

However, the reprojection errors evaluated for groundtruth motion are around 7 pixels as shown in Table 1.

4.3 Learning the Stereoscopic

Deformation Field

We hypothesize that the disturbance in the reprojec-

tion error distribution shown in Figure 3 is caused

by inaccurate image rectiﬁcation arising from the

insufﬁcient capacity of the underlying radial dis-

tortion model. Therefore, we devise a technique

for correcting the camera calibration by exploiting

groundtruth motion. After seeing that mean values of

the vector errors deviate from zero and contain bias

following some speciﬁc patterns we decided to try

to learn the deformation ﬁeld across discrete image

cells. Each element of the deformation ﬁeld contains

two free parameters describing the translational shift

on u and v image axes in the corresponding image

cell. We differentiate between left and right camera

and learn a separate deformation ﬁeld for each of

them. In order to deﬁne the cost function for learning

the deformation ﬁeld we denote D

, D

as the

deformation matrices for u and v axes and left and

right cameras respectively. The motion parameters

and t

in each frame t are taken from groundtruth

data. Now if we deﬁne d

d() to be a simple function

which takes an image point, determines to which cell

of the image it belongs and uses a corresponding

values from deformation matrices to apply the defor-

mation, we can formulate the following optimization:

argmin

∑

t=1

∑

i=1

{l,r}

∑

i,t

− π(X

i,t−1

, R

, t

t,k

(6)

q = d

d(q, D

, D

)

In order to optimize the deformation ﬁeld loss

function, we collect the inlier tracks in all sequences

by ﬁltering them with groundtruth motion using a

ﬁxed error threshold. The collected tracks are seri-

alized, saved to disk and later used by the optimiza-

tion method which learns the stereoscopic deforma-

tion ﬁeld. We minimize the cost function (6) using

the Levenberg-Marquardt method which, in our ex-

periments, converged faster than the line-search gra-

dient descent methods to the same minimum. Note

that the set of point features typically contains many

outliers, since we only ﬁlter them with a permissive

threshold on the reprojection error with respect to the

groundtruth motion. This threshold has to be large

enough in order to capture the impact of larger re-

projection errors as we move further from the image

center (cf. Figure 3). These outliers can exert a sig-

niﬁcant impact to the least-squares optimization. To

take them into account we wrap the square loss into

the robust Cauchy loss function given with the equa-

tion (7).

ρ(s) = a

log(1 +

) (7)

Here the square loss output is denoted with s. By

using the parameter a one can change the scale at

ImprovingtheEgomotionEstimationbyCorrectingtheCalibrationBias

351

(a) Distribution of reprojection error vector norms in the left camera. Darker colors correspond to the lower values. The error

increases in all directions from the minimum which is close to the image center.

16200 43960 60983 88632 159975 219012 167876 144061 171021 150130 100560 62776 39794 22913 8473

24992 79327 109810 141739 204386 315533 406393 384943 292353 216475 139156 98441 73760 45355 17461

27681 85761 122120 155581 216661 317709 424874 429657 290620 202883 141765 108101 86203 57941 22437

10618 46860 81195 115466 154868 174008 156019 131885 184310 155856 112752 80602 62472 44032 16037

1232 9360 18940 27301 38172 42210 38151 35922 40402 46551 41481 31306 26138 16588 5785

(b) Number of observed points in each cell.

0.35 0.367 0.374 0.344 0.301 0.277 0.267 0.272 0.262 0.267 0.292 0.295 0.314 0.334 0.332

0.383 0.369 0.367 0.337 0.293 0.27 0.249 0.245 0.254 0.267 0.292 0.308 0.334 0.367 0.36

0.359 0.369 0.36 0.333 0.297 0.274 0.254 0.249 0.263 0.283 0.305 0.326 0.349 0.373 0.35

0.417 0.439 0.436 0.411 0.386 0.363 0.342 0.343 0.333 0.352 0.381 0.395 0.398 0.398 0.394

0.606 0.587 0.581 0.573 0.538 0.508 0.477 0.474 0.465 0.455 0.462 0.483 0.492 0.494 0.518

-0.129 -0.144 -0.171 -0.159 -0.118 -0.0729 -0.0487 -0.0328 -0.0125 -0.0196 -0.0245 -0.0176 -0.0328 -0.0658 -0.0713

-0.141 -0.124 -0.153 -0.132 -0.0902 -0.0489 -0.0238 -0.022 -0.0277 -0.0394 -0.053 -0.0626 -0.0824 -0.112 -0.125

-0.112 -0.116 -0.138 -0.115 -0.0814 -0.0509 -0.031 -0.0291 -0.0455 -0.0638 -0.0922 -0.0887 -0.109 -0.152 -0.144

-0.182 -0.188 -0.188 -0.168 -0.152 -0.0982 -0.0741 -0.0574 -0.0696 -0.0849 -0.115 -0.121 -0.116 -0.146 -0.134

-0.304 -0.255 -0.243 -0.234 -0.191 -0.131 -0.0874 -0.0892 -0.0945 -0.105 -0.108 -0.122 -0.116 -0.148 -0.18

(d) Reprojection error means on the u axis.

0.0173 0.0252 0.0219 0.0049 -0.00545 -0.00162 0.0048 0.00391 0.00424 0.0178 0.0288 0.0401 0.0601 0.0779 0.0624

0.0169 0.0372 0.0431 0.0345 0.0197 0.0146 0.00939 0.0117 0.0173 0.0265 0.0467 0.0613 0.0726 0.0801 0.0512

0.0255 0.05 0.0545 0.0499 0.0425 0.0345 0.0234 0.0204 0.0325 0.0407 0.0517 0.0581 0.07 0.069 0.0369

0.0641 0.0826 0.0884 0.0924 0.0891 0.0773 0.0769 0.065 0.0779 0.0842 0.0821 0.0921 0.0918 0.0811 0.053

0.144 0.131 0.131 0.148 0.126 0.141 0.128 0.128 0.121 0.133 0.149 0.156 0.166 0.175 0.15

(e) Reprojection error means on the v axis.

0.25 0.238 0.216 0.168 0.117 0.106 0.109 0.119 0.103 0.117 0.155 0.167 0.192 0.209 0.226

0.333 0.267 0.213 0.174 0.131 0.116 0.0947 0.0883 0.104 0.128 0.149 0.181 0.207 0.247 0.235

0.272 0.263 0.224 0.187 0.141 0.12 0.103 0.0968 0.116 0.144 0.169 0.218 0.243 0.243 0.23

0.352 0.347 0.336 0.291 0.228 0.218 0.205 0.237 0.193 0.213 0.27 0.294 0.319 0.296 0.306

0.567 0.543 0.555 0.509 0.452 0.42 0.424 0.437 0.416 0.374 0.386 0.416 0.418 0.382 0.448

(f) Reprojection error variances on the u axis.

0.118 0.131 0.138 0.125 0.123 0.131 0.128 0.13 0.136 0.126 0.135 0.125 0.115 0.11 0.0955

0.134 0.14 0.143 0.131 0.118 0.123 0.116 0.109 0.117 0.113 0.124 0.115 0.117 0.12 0.105

0.119 0.146 0.144 0.133 0.121 0.118 0.11 0.113 0.106 0.108 0.114 0.111 0.114 0.115 0.0932

0.129 0.16 0.167 0.158 0.17 0.169 0.145 0.143 0.14 0.152 0.164 0.151 0.132 0.124 0.116

0.258 0.258 0.25 0.262 0.299 0.289 0.23 0.232 0.243 0.213 0.206 0.227 0.231 0.207 0.193

(g) Reprojection error variances on the v axis.

Figure 3: Distribution of the reprojection error evaluated in groundtruth motion for sequence number 00 in KITTI dataset.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

352

Figure 4: Heat map visualization of the distribution of re-

projection error norms for the left camera image on the

Tsukuba stereo dataset.

which robustiﬁcation takes place.

4.4 Integrating the Deformation Field

in Motion Estimation

We will now integrate the learned stereoscopic defor-

mation ﬁeld into the expression (3) and deﬁne a new

reprojection error cost function which applies the de-

formation ﬁeld to all points before the optimization

step. In order to achieve smooth deformation transi-

tions, we compute the bilinear interpolation between

the four cells of the deformation ﬁeld which surround

the point x

i,t

. In case when the bilinear interpolation

is not possible we use linear interpolation (close to

image edges) or we do not interpolate (close to im-

age corners). Let us denote the interpolation function

with i

i(). Then the proposed cost function for recover-

ing the camera motion can be formulated as follows:

argmin

R,t

∑

i=1

{l,r}

∑

i,t

− π(X

i,t−1

, R, t

(8)

q = i

i(q, D

, D

)

5 EXPERIMENTAL RESULTS

The KITTI odometry benchmark contains 11 training

sequences with available groundtruth motion. These

11 sequences have been acquired with three differ-

ent camera setups each of which has a distinct set

of calibration parameters. We focus on the training

sequences 04-10, which constitute the largest group

of video sequences acquired with the same camera

setup. Our experiments analyze the accuracy of the

recovered camera motion according to the standard

KITTI evaluation criteria (Geiger et al., 2013)

. We

compare the performance of the proposed approach

for correcting the calibration bias by a stereoscopic

deformation ﬁeld with two variants based on the lib-

viso library

. All compared algorithms employ tracks

extracted by our tracker described in Subsection 3.1.

The tracker has been conﬁgured with the same set of

parameters in all experiments.

5.1 Baseline and the Feature Weighting

The two libviso based variants differ in whether the

procedure which we call feature weighting is applied

or not. The simpler of these two variants (the one

without feature weighting) shall be referred to as the

baseline. Feature weighting can also be viewed as

a way to improve the recovered camera motion by

compensating inadequate calibration. This proce-

dure weights the reprojection error residuals kq

i,t

−

π(X

i,t−1

, R, t

and the corresponding Jacobians of

the Gauss-Newton optimization according to the hor-

izontal distance of q

i,t

from the image origin. The

libviso library determined these weights as follows:



− c

+ 0.05



−1

(9)

We did not ﬁnd any explanation in the paper about

libviso for how the equation (9) was chosen.

5.2 Leave One Out Evaluation

We test the impact of the proposed approach for cor-

recting the camera calibration by a stereoscopic defor-

mation ﬁeld by leave-one-out evaluation on the train-

ing sequences 04-10. Therefore, we learn the stereo-

scopic deformation ﬁeld (D

, D

) on six se-

quences and test its performance on the remaining se-

quence. This step is repeated seven times. The ob-

tained results are presented in Tables 2 and 3. Please

note that the columns labeled trans. show the relative

translational error of the recovered motion in percents

of the traveled distance, while the columns labeled

rot. show the relative rotation error in degrees per

meter. The tables show that the proposed approach

signiﬁcantly improves the accuracy of the recovered

camera motion both with respect to the baseline im-

plementation and with respect to the feature weight-

ing. in all of the seven experiments.

A script for evaluating the accuracy is available at:

http://kitti.is.tue.mpg.de/kitti/devkit odometry.zip.

The libviso library can be accessed at:

http://www.cvlibs.net/software/libviso/.

ImprovingtheEgomotionEstimationbyCorrectingtheCalibrationBias

353

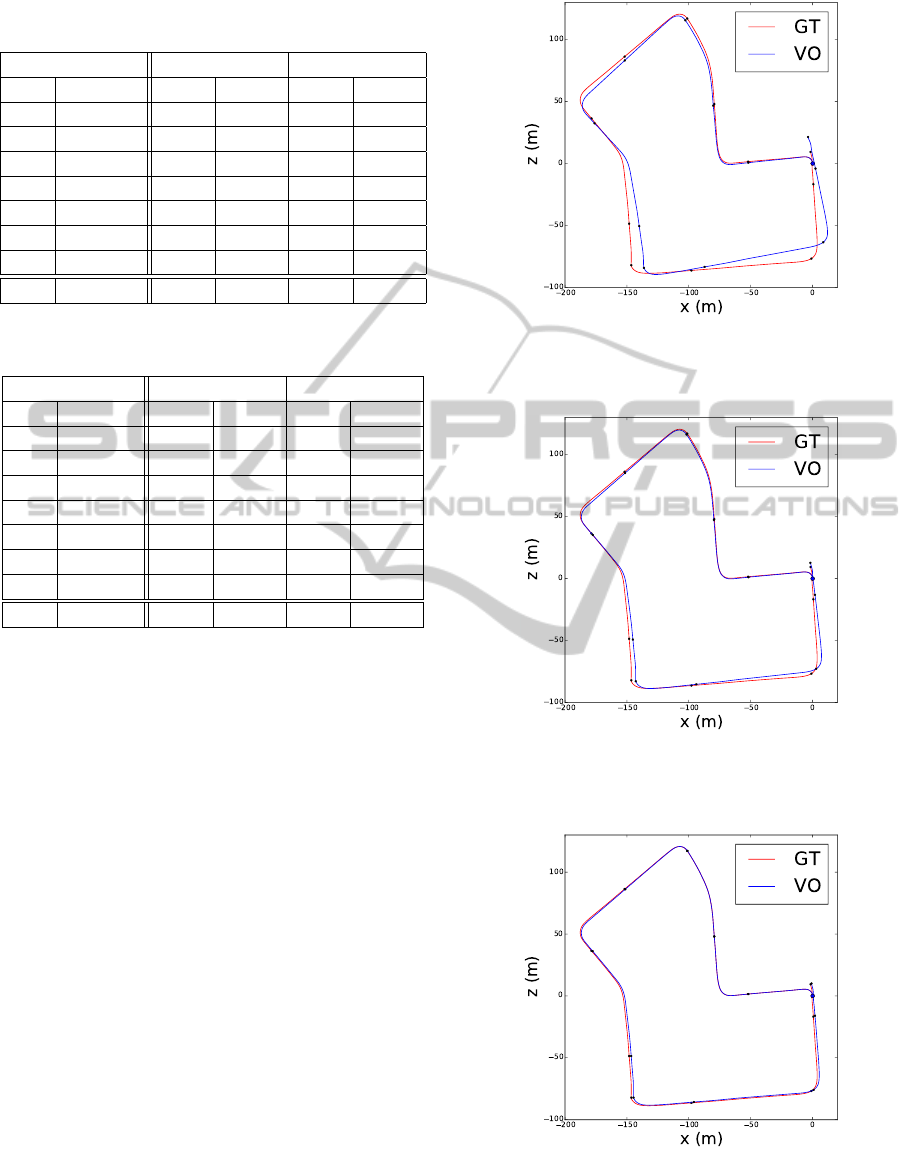
Table 2: Leave one out evaluation: baseline vs stereoscopic

deformation ﬁeld (DF).

KITTI Baseline With DF

Seq. length trans. rot. trans. rot.

04 394 m 1.14 0.0094 0.78 0.0068

05 2206 m 1.29 0.0095 0.43 0.0030

06 1233 m 1.30 0.0069 0.53 0.0047

07 695 m 2.02 0.0221 0.40 0.0034

08 3223 m 1.45 0.0087 1.02 0.0048

09 1705 m 1.51 0.0067 0.97 0.0050

10 920 m 0.80 0.0067 0.70 0.0040

All 10 376 m 1.386 0.0089 0.771 0.0043

Table 3: Leave one out evaluation: baseline vs feature

weighting (FW).

KITTI Baseline With FW

Seq. length trans. rot. trans. rot.

04 394 m 1.14 0.0094 0.63 0.0027

05 2206 m 1.29 0.0095 0.70 0.0047

06 1233 m 1.30 0.0069 0.75 0.0041

07 695 m 2.02 0.0221 0.86 0.0083

08 3223 m 1.45 0.0087 1.10 0.0056

09 1705 m 1.51 0.0067 1.16 0.0041

10 920 m 0.80 0.0067 0.65 0.0042

All 10376 m 1.386 0.0089 0.933 0.0051

5.3 Case Study: The Sequence 07

According to Table 2, the translational accuracy of

the motion recovered by the baseline approach is

2.02%. Feature weighting improves that result to

0.86%. Finally, the stereoscopic deformation ﬁeld

further improves the accuracy to 0.40%. The 2D plots

of the reconstructed three paths are compared to the

groundtruth motion in Figures 5, 6 and 7.

5.4 Implementation

We have implemented all the described methods and

experiments in C++. The OpenMP framework has

been used to parallelize feature tracking and motion

estimation. The implementation is based on the lib-

viso library which was modiﬁed at several places in

order to promote parallel execution and to support the

track correction with the previously calibrated stereo-

scopic deformation ﬁeld.

In all experiments the resolution of the deforma-

tion ﬁeld was set to 21×69 bins in each of the two

stereo images.

We implemented the optimization deﬁned in ex-

pression (6) by using the Ceres Solver (Agarwal et al.,

2014), an open source C++ library for modeling and

Figure 5: The reconstructed camera motion along the se-

quence 07 recovered without the stereoscopic deformation

ﬁeld and without the feature weighting (blue) is compared

to the groundtruth camera motion (red).

Figure 6: The reconstructed camera motion along the se-

quence 07 recovered with the feature weighting and without

the stereoscopic deformation ﬁeld (blue) is compared to the

groundtruth camera motion (red).

Figure 7: The reconstructed camera motion along the se-

quence 07 recovered with the stereoscopic deformation ﬁeld

and without the feature weighting (blue) is compared to the

groundtruth camera motion (red).

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

354

solving large nonlinear least squares problem. One

nice feature of the Ceres Solver is that it supports au-

tomatic differentiation if the cost function is written

in the appropriate form.

6 CONCLUSION

Preliminary experiments in stereoscopic egomotion

estimation had revealed that subpixel accuracy and

multi-frame optimization have a substantially larger

impact when applied to the artiﬁcial Tsukuba dataset

than in the case of the KITTI dataset. We have

decided to more closely investigate the peculiar

KITTI results by observing the reprojection error

of two-frame point-feature correspondences under

groundtruth camera motion. The performed case-

study analyses pointed out many near-to perfect cor-

respondences with large reprojection errors. Addi-

tional experiments have shown that the means and the

variances of the reprojection error signiﬁcantly de-

pend on the image coordinates of the three point fea-

tures involved. In particular, we noticed that the re-

projection error bias tends to be stronger as the point

features become closer to the image borders. We have

hypothesized that this disturbance is caused by inac-

curate image calibration and rectiﬁcation which could

easily arise due to insufﬁcient capacity of the under-

lying radial distortion model.

In order to test our hypothesis, we have designed

a technique to calibrate a discrete stereoscopic de-

formation ﬁeld above the two rectiﬁed image planes,

which would be able to correct deviations of a real

camera system from the radial distortion model. The

devised technique performs a robust optimization of

the reprojection error in validation videos under the

known groundtruth motion. The calibrated deforma-

tion ﬁeld has been employed to correct the feature lo-

cations used to estimate the camera motion in the test

videos. We have compared the accuracy of the es-

timated motion with respect to the two baseline ap-

proaches operating on original point features. The

experimental results conﬁrmed the capability of the

calibrated deformation ﬁeld to improve the accuracy

of the recovered camera motion in independent test

videos, that is in videos which have not been seen dur-

ing the estimation of the deformation ﬁeld.

In our future work we would like to evaluate dif-

ferent regularization approaches in the loss function

used to calibrate the stereoscopic deformation ﬁeld.

We also wish to evaluate the impact of the estimated

correction of the calibration bias to the multi-frame

bundle adjustment optimization.

ACKNOWLEDGEMENTS

This research has been supported in part by the Eu-

ropean Union from the European Regional Develop-

ment Fund by the project IPA2007/HR/16IPO/001-

040514 ”VISTA - Computer Vision Innovations for

Safe Trafﬁc”.

This work has been supported in part by Croatian

Science Foundation under the project I-2433-2014.

REFERENCES

Agarwal, S., Mierle, K., and Others (2014). Ceres solver.

http://ceres-solver.org.

Badino, H. and Kanade, T. (2011). A head-wearable short-

baseline stereo system for the simultaneous estimation

of structure and motion. In IAPR Conference on Ma-

chine Vision Application, pages 185–189.

Badino, H., Yamamoto, A., and Kanade, T. (2013). Visual

odometry by multi-frame feature integration. In First

International Workshop on Computer Vision for Au-

tonomous Driving at ICCV.

Diosi, A., Segvic, S., Remazeilles, A., and Chaumette, F.

(2011). Experimental evaluation of autonomous driv-

ing based on visual memory and image-based visual

servoing. IEEE Transactions on Intelligent Trans-

portation Systems, 12(3):870–883.

Fraundorfer, F. and Scaramuzza, D. (2012). Visual odom-

etry: Part ii: Matching, robustness, optimization,

and applications. Robotics & Automation Magazine,

IEEE, 19(2):78–90.

Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).

Vision meets robotics: The kitti dataset. International

Journal of Robotics Research (IJRR).

Geiger, A., Lenz, P., and Urtasun, R. (2012). Are we ready

for autonomous driving? the kitti vision benchmark

suite. In Conference on Computer Vision and Pattern

Recognition (CVPR).

Geiger, A., Ziegler, J., and Stiller, C. (2011). Stereoscan:

Dense 3d reconstruction in real-time. In IV. Karlsruhe

Institute of Technology.

Harris, C. and Stephens, M. (1988). A combined corner

and edge detector. In Proceedings of the Alvey Vision

Conference, pages 147–152.

Hartley, R. I. and Kang, S. B. (2005). Parameter-free radial

distortion correction with centre of distortion estima-

tion. In ICCV, pages 1834–1841.

Howard, A. (2008). Real-time stereo visual odometry for

autonomous ground vehicles. In IROS, pages 3946–

3952.

Konolige, K. and Agrawal, M. (2008). Frameslam:

From bundle adjustment to real-time visual mapping.

Robotics, IEEE Transactions on, 24(5):1066–1077.

Konolige, K., Agrawal, M., and Sol

a, J. (2007). Large-scale

visual odometry for rough terrain. In ISRR, pages

201–212.

ImprovingtheEgomotionEstimationbyCorrectingtheCalibrationBias

355

Kreso, I., Sevrovic, M., and Segvic, S. (2013). A novel geo-

referenced dataset for stereo visual odometry. CoRR,

abs/1310.0310.

Martull, S., Peris, M., and Fukui, K. (2012). Realistic cg

stereo image dataset with ground truth disparity maps.

Technical report of IEICE. PRMU, 111(430):117–

118.

Moravec, H. P. (1980). Obstacle Avoidance and Naviga-

tion in the Real World by a Seeing Robot Rover. PhD

thesis, Stanford University.

Moravec, H. P. (1981). Rover visual obstacle avoidance. In

IJCAI, pages 785–790.

Nedevschi, S., Popescu, V., Danescu, R., Marita, T., and

Oniga, F. (2013). Accurate ego-vehicle global local-

ization at intersections through alignment of visual

data with digital map. IEEE Transactions on Intel-

ligent Transportation Systems, 14(2):673–687.

Nist

er, D., Naroditsky, O., and Bergen, J. R. (2004). Visual

odometry. In CVPR (1), pages 652–659.

Scaramuzza, D. and Fraundorfer, F. (2011). Visual odome-

try [tutorial]. IEEE Robot. Automat. Mag., 18(4):80–

92.

Sturm, P. F., Ramalingam, S., Tardif, J., Gasparini, S., and

Barreto, J. (2011). Camera models and fundamental

concepts used in geometric computer vision. Foun-

dations and Trends in Computer Graphics and Vision,

6(1-2):1–183.

Vogel, C., Roth, S., and Schindler, K. (2014). View-

consistent 3d scene ﬂow estimation over multiple

frames. In ECCV, pages 263–278.

Zhang, Z. (2000). A ﬂexible new technique for camera

calibration. IEEE Trans. Pattern Anal. Mach. Intell.,

22(11):1330–1334.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

356