Robust Watermarking Algorithm for 3D Multiresolution Meshes
Ikbel Sayahi, Akram Elkefi, Mohamed Koubaa and Chokri Ben Amar
National School of Engineers, Sfax University, Soukra Street, Sfax, Tunisia
Keywords:
3D Watermarking, Multiresolution Mesh, Wavelet Transform, Attacks, Robustness.
Abstract:
Digital watermarking for 3D meshes is a means to copyright protection. In this paper, we propose a robust
watermarking algorithm for 3D Meshes. We work on multiresolution, triangular and semi regular meshes
having various sizes. Our algorithm is able to insert high amount of information in the field of multiresolution .
For this reason, we apply a uniform scalling then a wavelet transform to the host mesh. Embedding step consist
on modifying wavelet coefficients vector according to the bit to be inserted. These techniques do not generate
a quality degradation of the mesh despite the important capacity adopted. Tests applied to various attacks
have shown the robustness of our algorithm against rotation, translation, uniform scaling, Noise addition,
smoothing, simplification and coordinate quantization. A comparison with literature revealed that we have a
remarkable improvement over the published results.
1 INTRODUCTION
3D mesh is a new data type that has emerged from the
2000s. The idea was to use geometric modelization
to build 3D objects presenting real scenes. Since their
birth, 3D meshes have become increasingly used in
several vital areas. Medicine, computer aided design,
games, video and scientific simulations are examples.
This wide range of applications and the birth of the
networks of high speed broadband have encouraged
the sharing and the transmission of this data category
which causes a major security problem. The ques-
tion was how to protect shared 3D meshes against
fraudulent action. Digital watermarking has been one
of the proposed answers. As it was the case for im-
age, sound and video, watermarking 3D meshes con-
sists of inserting indelible data into mesh without de-
teriorating the host object. During the last decade,
many works have been proposed to secure 3D meshes.
Therefore, a diversification in fields using during em-
bedding information into meshes appears. Indeed,
there are approaches that have chosen to work in the
spatial field without transforming the mesh. We cite
the work published in (Sharvari and Ratnadeep, 2012)
and (Chao-Hung and al, 2013) as examples. Other
works aimed to represent host meshes in transformed
areas before embedding information. Among these
used areas, we note the spectral domain as the case
of works published in (Sharvari and Atnadeep, 2012).
The multiresolution domain has also been present in
recent works such as the approaches proposed in (Kai
and al, 2007), (Zhiyong and al, 2013) and (Kai and
al, 2010). Unfortunately, this diversification does not
deny that watermarking 3D meshes is ”still far from
the level of maturity of other watermarking technolo-
gies for audio, video or image (Domenico and al,
2010)”.
In this paper, we propose a robust and multires-
olution domain watermarking algorithm. Our goal is
to maximize the amount of information inserted while
ensuring the preservation of the mesh quality. Treat-
ments applied to watermarked mesh, should never
prevent correct extraction of information.
2 RELATED WORKS
Since the release of the first 3D watermarking algo-
rithm of in the last decade and until our days, 3D wa-
termarking algorithm targeting 3D meshes have con-
tinued to appear. The aim is always to improve the
following criteria: capacity, invisibility and robust-
ness.
Although the goals are the same, the proposed
watermarking algorithms are various. Some work
has chosen to insert the information by modifying ei-
ther the topological information such as the work in
(Chao-Hung and al, 2013) or the geometric one (Xi-
angjiu and Zhanheng, 2012). In this case the mesh
host will be treated in the spatial domain without un-
150
Sayahi I., Elkefi A., Koubaa M. and Ben Amar C..
Robust Watermarking Algorithm for 3D Multiresolution Meshes.
DOI: 10.5220/0005316401500157
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 150-157
ISBN: 978-989-758-091-8
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

dergoing any transformation. Insertion into a trans-
formed domain and in particular the multiresolution
one was an idea adopted in (Sharvari and Atnadeep,
2012) and (Sharvari and Ratnadeep, 2012) to improve
the robustness criterion. These approaches proposed
to modify wavelet coefficients during the insertion of
information. Other approaches proposed like (Xiao
and al, 2012) thought to insert information in the low
frequency coefficients after transforming the mesh
from the spatial domain to the frequency one.
Despite the variety of the proposed 3D water-
marking algorithms and the efforts to innovate in this
area, a perfect solution to the security problem of 3D
meshes has not yet been reached for two reasons. The
first is the complexity of handling 3D meshes com-
pared with other types of data such as sound, image
or video. The second reason was the difficulty of find-
ing a compromise between robustness, visibility and
capacity. These three criteria are closely related to a
watermarking algorithm targeting 3D meshes because
the change of one of these three impulses directly to
the others remaining.
By definition invisibility means Inserting informa-
tion in the mesh should never cause deterioration in
the quality of the later.Capacity is the rate of informa-
tion inserted to the mesh (number of bits in the case of
binary information); As for robustness we can say that
a watermarking Algorithm is said robust if extracting
all inserted information is possible whatever the treat-
ments applied to the watermarked mesh.Indeed, the
increase of the amount of data to be inserted causes
either a serious deterioration of the mesh quality or
reduces the level of robustness.
The work presented in this paper falls into this
context. We propose a new watermarking algorithm
targeting multiresolution triangular meshes. Our goal
is to maximize the rate of information inserted with-
out affecting the quality of the host mesh while en-
suring the robustness criterion. We must be able to
extract all of information correctly regardless of the
attacks that the watermarked mesh can undergo.
3 TECHNIQUES USED
To insert information into multi-resolution triangular
meshes, we used the following techniques: Uniform
scalling, Wavelet transform, Transformation to spher-
ical system.
To prevent the watermark against similar transfor-
mation attacks, the host mesh undergoes a uniform
scaling, said also ”Normalization”, in order to be in-
cluded in a unit sphere (Kai and al, 2010).
To do this, we must first choose a scale having
an arbitrary orientation. Next, we define n (nx, ny,
nz) a unit vector whose direction is parallel to that
of the chosen scale. Let K be the scale factor ap-
plying to plan passes through the origin and which is
perpendicular to n (Zhiyong and al, 2013). For each
vertex V
i
(x
i
, y
i
, z
i
) we calculate the new coordinates
V
s
i
(x
s
i
, y
s
i
, z
s
i
) using formula 1.
V
s
i
= V
i
×S (1)
S is defined in formulas 2, 3, 4 and 5 as follows:
S = [S
1
, S
2
, S
3
] (2)
S
1
=


n
2
x
(K −1) + 1
n
x
n
y
(K −1)
n
x
n
z
(K −1)


(3)
S
2
=


n
x
n
y
(K −1)
n
2
y
(K −1) + 1
n
y
n
z
(K −1)


(4)
S
3
=


n
x
n
z
(K −1)
n
y
n
z
(K −1)
n
2
z
(K −1) + 1


(5)
3.1 Wavelet Transform
Multiresolution analysis has become a center of inter-
est for researchers in our day. To transform the mesh
from spatial domain to multiresolution one, a wavelet
transform should be applied. Only semi-regular mesh
can be used. The main idea is then to decompose a
mesh M
i
in two sets: a low resolution mesh M
i−1
grosser and a set of details D
i−1
(see figure1): the
analysis phase. All these details and meshes of dif-
ferent resolution level are then used to reconstruct the
original mesh: synthesis phase. All details obtained
Figure 1: Wavelet Transform.
during analysis phase are assembled into a single vec-
tor called wavelet coefficient vector (CWV).
CWV =



D
1
.
.
.
D
i



=



d
x
1
d
y
1
d
z
1
.
.
.
.
.
.
.
.
.
d
x
i
d
y
i
d
z
i



(6)
Especially, this vector will be modified during in-
sertion following bits to be inserted. The choice of
RobustWatermarkingAlgorithmfor3DMultiresolutionMeshes
151

multiresolution field is argued by the fact that inser-
tion of information is done at different levels of reso-
lution which eliminates the interaction between them
(Kai and al, 2007).
To apply a wavelet transform to a triangular mesh,
we need the use of 4 butterfly filters (Elkefi and al,
2004): 3 filters for prediction and one filter for update
(Figure 2).
Figure 2: Butterfly filters.
The signal present at the input of the lifting
scheme is divided into four channels. On each chan-
nel, the corresponding filter is applied. The prediction
of a point is a weighted sum of a neighborhood avail-
able at time t.
3.2 Transformation to Spherical System
To embed information into meshes, we choose to
transform the Cartesian coordinates (x, y and z) of
each wavelet coefficient into the spherical coordinate
system (ρ, θ, ψ). This passage is carried out by for-
mulas 7:
ρ =
p
x
2
+ y
2
+ z
2
θ = arccos(
z
ρ
)
ψ =
(
arccos
x
√
x
2
+y
2
2 ×Π −arccos
x
√
x
2
+y
2
(7)
This passage allows obtaining the component ,
which represents the module of the wavelet coeffi-
cient. During insertion, the value of this component
will undergo a modification according to the bit to be
inserted. Therefore, we are changing the module of
coefficients instead of changing the Cartesian compo-
nents of these coefficients. This improves the crite-
rion of invisibility.
To recalculate the wavelet coefficients, the appli-
cation of inverse transformation is necessary after em-
bedding. To ensure this passage, we use formulas 8:
x = ρ ×sinθ ×cos ψ
y = ρ ×sinθ ×sinψ
z = ρ ×cosθ
(8)
4 OVERVIEW OF OUR
APPROACH
Our watermarking algorithm aim is to embed data into
triangular meshes in order to place a copyright protec-
tion or an indexing system.
After a dissemination step, during which many
processing (said also Attacks) may be applied to the
mesh, we carry out an extraction step. Our goal is to
extract data correctly despite all these processing ie,
to confirm the robustness criterion (see Figure 3).
Figure 3: General structure of a watermarking algorithm.
4.1 Embedding Step
During this step, there will be the insertion of infor-
mation in the host mesh. To do it, we should follow
the instructions presented in Figure 5.
Having a 3D mesh, an acquisition step begins then
a uniform scalling will be applied. The next step is
called ”mesh pretreatment”. It aims at transforming
the mesh from the spatial domain to the multiresolu-
tion one. This transformation results from the appli-
cation of a wavelet transform. The present step ends
with the extraction of the wavelet coefficient vector.
Using this vector, embedding watermark can oc-
cur. Watermark is a binary sequence generated us-
ing a pseudo random generator. The present step
includes 3 parts: The first one is Transforming the
wavelet coefficients into spherical system. The sec-
ond is Embedding and recalculating Cartesian repre-
sentation of wavelet coefficients. The last one is In-
versing wavelets transform to rebuild the mesh.
The spherical coordinate transformation allows us
to obtain the component ρ presenting the modulus
of the wavelet coefficient. This component will be
changed every time following bits of information to
insert. This modification follows formula 9:
´
ρ
i
= ρ
i
+ β ×bit
i
(9)
β is called watermarking strength. When the β
value increases, our watermarking treatment becomes
more robust and more visible. β value is determined
experimentally (see the Results section).
After the dissemination step during which the host
mesh can undergo various treatments, the extraction
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
152

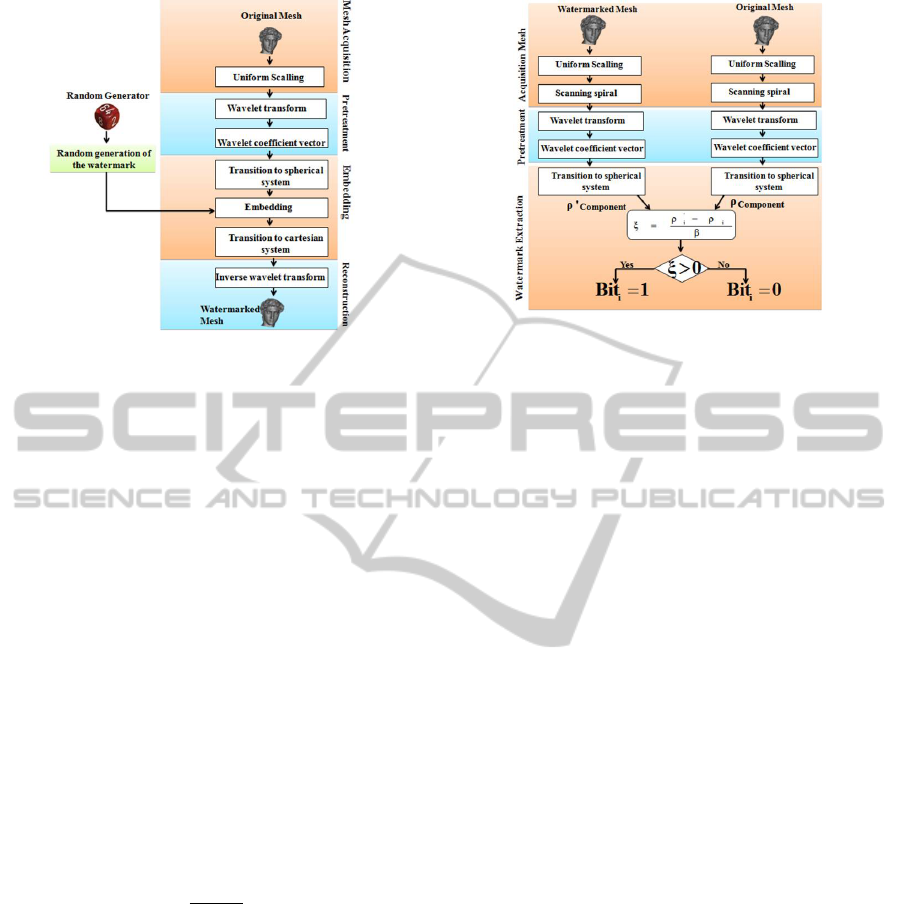
Figure 4: Insertion step.
phase begins. Unfortunately, a correct retrieval of in-
formation in the watermarked mesh is no longer cer-
tain. This is due to the treatments applied to the mesh.
The latters can easily alter and even destroy water-
marked information. To resolve this problem we pro-
pose an extraction scheme shown in figure 5.
4.2 Extraction Step
Extraction has the same steps as insertion. The water-
marked mesh and the original one undergo uniform
scaling then a wavelet transform. At the end of this
step, we will obtain two vectors of wavelet coeffi-
cients. The first contains the watermarked vector and
the other the original one. At this level, the extraction
of embedded bits becomes possible.
To extract information, we have to calculate the
wavelet coefficient vectors corresponding to the orig-
inal and watermarked meshes. A transformation to
the spherical system of these two vectors is necessary
to apply formula 10:
ξ =
´
ρ
i
−ρ
i
β
(10)
To tweak the inserted bit correctly, we need to dis-
cuss according to the value of ξ as follow in formula
11:
bit
i
=

1 i f ξ > 0
0 Otherwise
(11)
5 RESULTS
For evaluating our watermarking algorithm, two cri-
teria must be taken into consideration. The first is
the visibility criterion. Insertion of information in the
host mesh must never cause visual deterioration of the
Figure 5: Extraction step.
latter. The second is the robustness criterion. A wa-
termarking algorithm is said robust if the extraction
of inserted information is correct whatever the treat-
ments applied to the host mesh are.
5.1 Data Used For Tests
To test our approach, we use areal, semi-regular and
multiresolution meshes stored in files. Dat. In this
category of files, 3D object is represented at different
levels of details. It is in fact composed of a coarse
mesh and more information to refine the coarse mesh
to its finest levels version. Very few are the water-
marking works manipulating files with this extension.
This is due to the sensitivity of meshes having this
structure. In this work, we watermarked multiresolu-
tion meshes of various sizes (Feline.dat with 258,046
Vertex, Horse.dat with112642 vertex and venus.dat
with 40962 vertex). These objects are characterized
by containing forms having very sensitive details. The
latters are easily influenced by any treatment which
threatens the invisibility criterion.
5.2 Invisibility Criterion
Inserting a watermark in a host mesh should never
cause detectable visual degradation. This suggests
that the conservation of mesh quality after watermark-
ing is a primary criterion in the evaluation of a water-
marking algorithm.
To conclude on the influence of our algorithm on
the mesh quality, we calculate the difference between
the original mesh and the watermarked one. To find
these differences, we resorted to calculate the Mean
Square Error (MSQE or MSE) (Frederic and Marc,
2006 ). The main idea of this comparison is to cal-
culate the distance between the two meshes. It rep-
resents the distance between a point x from the first
RobustWatermarkingAlgorithmfor3DMultiresolutionMeshes
153

mesh and a surface from the second one (Cline and
Frdric, 2011).
d(M,
ˆ
M) = (
1
area(M)
Z
x∈M
d(x,
ˆ
M)dx)
1
2
(12)
The MSQE is then calculated using formula (13).
MSQE = max(d(M,
ˆ
M), d(
ˆ
M, M)) (13)
Another comparison tool we can also use is the PSNR
(Peak Signal to Noise Ratio) measured in decibels
(dB). This parameter calculates the ratio between the
signal dynamics and the error of the watermarking.
PSNR = 20 ×log
10
(
Bounding Box
MSQE
) (14)
Using these two tools, we have applied many tests in
order to study the influence of our approach on the
visual appearance of processed meshes. First, our
goal is to find the compromise between watermark-
ing strength (i.e β value) and the visibility criterion
(see table 1). Note that when the value of β increases,
the watermarking robustness enhances but the mesh
undergoes more visual degradation. The results pre-
Table 1: MSE and PSNR according to β values.
β values MSQE PSNR
0.1 3 ×10
−2
34.34
0.01 2 ×10
−3
57.76
0.001 4 ×10
−4
71.84
0.0001 2.2 ×10
−5
97
0.00001 4.2 ×10
−6
111.42
sented show that with a β value equal to 0.00001, we
could get good values of MSQE and PSNR. We will
use this value in the remaining tests.
As it is presented in table2, our approach has an
important capacity compared to recently published
work. PSNR and MSQE values prove that our ap-
proach retains almost the same visual appearance of
the original mesh.
5.3 Robustness Criterion
Evaluating the robustness criterion needs the appli-
cation of treatments at the host mesh. We call these
treatments ”attacks”. According to (Kai and al, 2010),
attacks which threaten a perfect extraction of infor-
mation from a watermarked mesh can be classified
into two types. The first one is said ”Geometry at-
tacks”. They are intended to change coordinates of
vertices in the mesh without hitting the topological
data (connectivity). As an example we cite: Similarity
transformation, Noise addition, smoothing and coor-
dinate quantization. The second one is Connectivity
Table 2: Compromise between capacity, visibility and cor-
relation: comparison with literature.
Approach Capacity MSQE PSNR
Our Approach 250000 2.2 ×10
−6
111.4
(Sharvari and
Ratnadeep,
2012)
– – 68.78
(Sharvari and
Atnadeep,
2012)
– – 92
(Kai and al
, 2007)
4000 0 –
(Zhiyong and
al,2013)
38198 – 81,97
(Xiao and
Qing, 2012)
765 0.0001 –
(Kai andal
, 2008)
324 0.006 –
(Cline and
Frdric,
2011)
104551 5 ×10
−6
–
(Jen −T se
and al,
2014)
32 – –
attacks. their goal is to modify the connections be-
tween vertices without changing their positions. Only
the topological information is targeted by this cate-
gory of attacks. Simplification and cropping are ex-
amples. To test our approach we had to program some
attacks treating the multiresolution files based on the
algorithms explained in (Kai and al, 2010). After the
application of each of these attacks, we calculate the
correlation between the information inserted I1 and
that extracted I2 using the formula 15:
C =
(
∑
n
i=1
I1
i
−
¯
I1)×(
∑
n
i=1
I2
i
−
¯
I2)
p
∑
n
i=1
(I1
i
−
¯
I1)
2
×
p
∑
n
i=1
(I2
i
−
¯
I2)
2
(15)
n refer to information size. The extraction of the
information is correct, when the correlation value is
close to 1.
5.3.1 Similarity Transformation Attack
It includes 3 attacks: translation, rotation and uniform
scalling (see figure 6). These types of attacks never
alter the form of the mesh.
Table 3 shows that our algorithm is robust against
translation, rotation and uniform scalling.
Our algorithm is able to extract all the informa-
tion even with the application of similar transforma-
tions attacks. This is justified by the correlation val-
ues shown in table3.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
154

Figure 6: Similarity Transformation Attacks.
Table 3: Robustness against similarity transformation at-
tacks.
Translation Rotation Uniform Scaling
C 1 1 1
5.3.2 Noise Addition Attack
The main idea is to modify the coordinates of the ver-
tices using a pseudo-random generator. This modifi-
cation follows formula 16:
´x
i
= x
i
+ α ×
¯
d
´y
i
= y
i
+ α ×
¯
d
´z
i
= z
i
+ α ×
¯
d
(16)
With d presents the distance from the center of grav-
ity of the mesh and α is a pseudo random number.
This noise can change the coordinates of the vertex
by changing their Cartesian coordinates. This change
will be a multiplication of these coordinates by the
random factor α.
Points of the mesh will be then redistributed ran-
domly in space which threatens inserted information
(see figure 8).
As shown in Table 4, our approach has allowed
us to extract correctly the information inserted even
by applying random noise to the watermarked mesh.
Extraction was acceptable with an intensity noise less
than 10
−3
. P presented in table5 define the propor-
tion of Vertex Affected by Noise. By setting the noise
level and varying the proportion of vertex affected by
noise, we obtained correlation values near to 1. Algo-
rithm published in (Xiao and Qing, 2012) under the
same conditions gave lowest correlation values.
Figure 7: Noise addition Attack.
Table 4: Correlation depending on noise level.
Noise 0,1 10
−3
10
−5
10
−6
C 0,002 0,6 0,88 1
(Roland Hu and
al,2014)
0,12 0.3 0.4 –
Table 5: Correlation depending on Proportion of Vertex Af-
fected by Noise.
P 10% 30% 50% 75% 100%
C 0,92 0,88 0,86 0,83 0,71
(Xiao and
Qing, 2012)
0,84 0,48 0,41 0,30 0,10
Figure 8: Smoothing Attack.
5.3.3 Smoothing Attack
To apply a smoothing attack to a mesh, formulas 17
should be used:
´x
i
= x
i
+ dFactor ×
¯
d
x
´y
i
= y
i
+ dFactor ×
¯
d
y
´z
i
= z
i
+ dFactor ×
¯
d
z
(17)
DFactor is a parameter manually initialized. As for
d
x
, d
y
and d
z
, they should be calculated as it seen in
formula 18.
d
x
=
∑
vertexNumber
i=1
∑
vertexNumber
j=1
x
j
−x
i
VertexNumber
d
y
=
∑
vertexNumber
i=1
∑
vertexNumber
j=1
y
j
−y
i
VertexNumber
d
z
=
∑
vertexNumber
i=1
∑
vertexNumber
j=1
z
j
−z
i
VertexNumber
(18)
Smoothing attack creates a distortion in the mesh.
DFactor parameter measures the degree of this defor-
mation of the mesh. The result of the application of
this attack is a mesh whose surface is smoother than
the original one (see figure 9). Smoothing attack treat-
ment is usually applied to the mesh just after his con-
struction. Table 6 shows that we can extract the infor-
Table 6: Correlation depending on Proportion of deforma-
tion (smoothing level).
dFactor 10
−10
10
−9
10
−8
10
−7
C 1 0,94 0,63 0,15
(Roland Hu
and al,
2014)
0.43 0.31 0.18 –
RobustWatermarkingAlgorithmfor3DMultiresolutionMeshes
155

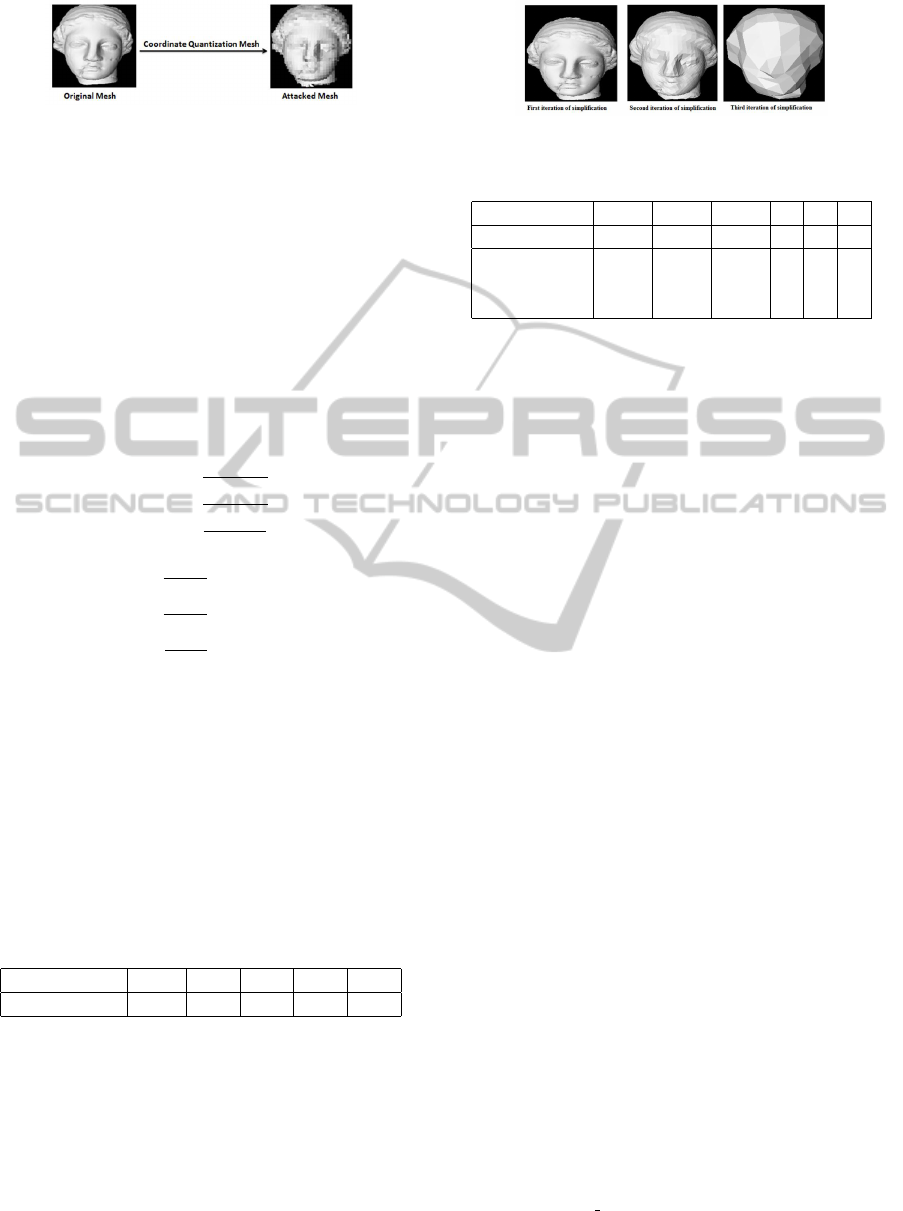
Figure 9: Coordinate Quantization Attack.
mation correctly only for a deformation factor lower
than 10
−8
. Beyond this range, the value of correlation
deteriorates which reflects that a loss of information
took place.
5.3.4 Coordinate Quantization Attack
This attacks aims at quantifying vertex coordination
(see figure 9) using two factors previously calcu-
lated according to the maximum and minimum values
along x, y and z. Let x
max
, x
min
, y
max
, y
min
, z
max
and
z
min
these values. Ql refer to the quantification level
which is initialized manually.
Step
x
=
x
max
−x
min
Ql
Step
y
=
y
max
−y
min
Ql
Step
z
=
z
max
−z
min
Ql
(19)
Factor
x
=
j
x−x
min
Step
x
k
×Step
x
−x
min
Factor
y
=
j
y−y
min
Step
y
k
×Step
y
−y
min
Factor
z
=
j
z−z
min
Step
z
k
×Step
z
−z
min
(20)
Having the two previous factors we can quantify ver-
tex coordinates. For an eventual x
i
, the quantization
occurs following formula 21.
´x
i
=

Factor
x
i f Factor
x
> 0, 5 ×Step
x
Factor
x
+ Step
x
Otherxise
(21)
As it is shown in table 7, correlation values obtained
by testing the approach with different quantization
level show very well the robustness of our approach
against the attack quantization coordinates.
Table 7: Correlation depending on quantizication level.
Quantization 100 196 225 289 361
C 0,01 0,2 0,5 0,9 1
5.3.5 Simplification Attack
The main idea is to present the mesh with a number of
triangles less than the number in the original represen-
tation (see Figure 10). The results we have presented
in Table 8 show very well that our watermarking algo-
rithm is not sensitive to simplification. In fact, what-
ever the simplification degree is operated, the correla-
tion is always 1.
Figure 10: Simplification Attack.
Table 8: Correlation depending on simplification degree.
N.iteration 1 2 3 4 5 6
C 1 1 1 1 1 1
(Roland Hu
and al,
2014)
0.15 0.31 0.46 – – –
6 CONCLUSIONS
In this paper, we present a new watermarking ap-
proach for 3D multiresolution meshes. Our algo-
rithm consists in transforming the host mesh into the
multiresolution area by applying a wavelet transform.
Each wavelet coefficient resulting from this transfor-
mation will be represented in the spherical coordinate
system to be then modified depending on the message
to be inserted. Once all the information is inserted,
the coefficients will be represented again in the Carte-
sian coordinate system to arrive to apply an inverse
wavelet transform. The watermarked mesh is then ob-
tained.
The results presented show clearly that our algo-
rithm protects the mesh quality even with the inser-
tion of a large amount of information compared to
approaches existing in literature. The application of
various attacks (noise addition, coordinate quantiza-
tion, smoothing, simplification, translation, rotation
and uniform scalling) to a watermarked mesh did not
prevent correct retrieval of inserted information. All
the results presented in this paper and the comparative
study with recent works show that our algorithm has
an improvement in terms of visibility, capacity and
robustness.
To extend this work, we aim at minimizing the
amount of memory used during execution, making
this algorithm ”blind” and testing it against the com-
pression attack.
REFERENCES
Cline, R. and Frdric, P. (2011). Remaillage semi-rgulier
pour les mail lages surfaciques triangulaires : un etat
de lart, Revue electronique Francophone dInforma-
tique Graphique.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
156

Chao-Hung, L., Minwen, C., Jyn-Yuan, C., Cheng-Wei,
Y. and Wei-Yen, H. (2013). A high capacity distor-
sion free information hiding algorithm for 3D poly-
gon models, International journal of innovative com-
puting, information and control.
Elkefi, A., Marc, A. and Ben Amar, C. (2004). Transforme
en ondelettes au fil de leau pour les maillages 3D.
First International Congress of signals, circuits and
systems.
Frederic, P,. Marc, A,.(2006). Mean square error approxi-
mation for wavelet based semi-regular mesh compres-
sion, IEEE transaction and computer graphic.
Jen-Tse, W., Yi-Ching, C., Chun-Yuan, Y. and Shyr-Shen,
Y. (2014). Hamming Code Based Watermarking
Scheme for 3D Model Verification, Hindawi Publish-
ing Corporation.
Kai, W., Guillaume, L., Florence, D. and Atilla, B.
(2007). Hierarchical blind watermarking of 3d trian-
gular meshes, COmpression et REprsentation des Sig-
naux Audiovisuels conference.
Kai, W., Guillaume, L., Florence, D. and Atilla, B. (2008).
A Comprehensive Survey on Three-Dimensional
Mesh Watermarking, Multimedia, IEEE Transactions.
Kai, W., Guillaume, L., Florence, D., Atilla, B. and Xiyan,
H. (2010). A Benchmark for 3D Mesh Watermarking,
Shape Modeling International Conference.
Roland H. Li, X., Huimin, Y. and Baocang, D. (2014). Ap-
plying 3D Polygonal Mesh Watermarking for Trans-
mission, Security Protection through Sensor Net-
works.
Sharvari, T. and At nadeep, D. (2012). Blind 3D model wa-
termarking based on multi-resolution representation
and fuzzy logic, International journal of computer sci-
ence and information technology.
Sharvari, C. and Ratnadeep, R. (2012). Watermarking 3D
surface models into 3D surface Models based on AN-
FIS, advances in computing.
Xiangjiu, C. and Zhanheng, G. (2012). Watermarking Al-
gorithm for 3D mesh based on multiscale radial basis
functions, International Journal of Parallel, Emergent
and Distributed Systems.
Xiao, Z. and Qing, Z.(2012). A DCT-Based dual water-
marking algorithm for threedimensional mesh mod-
els, International conference on consumer electronics,
communications and networks.
Zhiyong, s., weiqing, L., Jianshou, K., Yue, D. and Weiqing,
Ta. (2013). Watermarking 3D CAPD models for
topology models for topology verification, Computer-
aided deseign.
RobustWatermarkingAlgorithmfor3DMultiresolutionMeshes
157