The Influence of Gravity-adapted Target Resizing on Direct

Augmented Reality Pointing under Simulated Hypergravity

Daniela Markov-Vetter

1,3

, Vanja Zander

, Joachim Latsch

and Oliver Staadt

Institute Aerospace Medicine, German Aersospace Center, Cologne, Germany

Institute of Cardiology and Sports Medicine, German Sport University Cologne, Cologne, Germany

Institute of Computer Science, University of Rostock, Rostock, Germany

Keywords: Augmented Reality, Interaction, Direct Pointing, Usability.

Abstract: The performance of Augmented Reality direct object selection coded outside of the human egocentric body

frame of reference decreases under short-term altered gravity. Therefore adequate countermeasures are

required. This paper presents the results of a proof-of-concept (POC) study to investigate the impact of

simulated hypergravity on the size and distance of a given target. The POC study is divided in a case study

and a user study, whereby hypergravity was induced by a long-arm human centrifuge and additional arm

weighting. For gravity-dependent resizing and –positioning we used the Hooke’s law that resulted in two

techniques of target deformation (compression, elongation) and compared both methods with normal sized

targets. Besides common metrics to measure the performance, we additionally evaluated the physiological

strain by the heart rate variability and the speed-accuracy tradeoff of the resizing techniques according to

Fitts’ law. The study showed that the online adaption of the present gravity load to targets' size and distance

influences the performance of direct AR direct pointing. The results revealed that the pointing performance

benefits from elongation target deformation by increased target sizes and distances.

1 INTRODUCTION

Advanced concepts of user interfaces are shifting

away from conventional displays and input devices

and claim more integration into our physical world.

Augmented Reality (AR) (Azuma, 1997) keeps the

natural perception and offers a direct interface by

merging 3D-registered virtual information with the

real world in real time. Current research on human

factors of handling AR interfaces presumes the

application under normogravity (1g) condition on

Earth. The application of AR to intra-vehicular

space operations could support astronauts in their

procedural task performance at complex technical

facilities aboard the International Space Station

(ISS) (Agan et al., 1998; Scheid et al., 2010).

In early prototyping and evaluation of an AR-

supported assistance system for standardized space

operations (Markov-Vetter et al., 2013) we could

show the feasibility and acceptance of domain

experts. For ensuring successful user performance

the integration of environmental factors into the

design processes is required. The adaption of

human-computer interaction to weightlessness is a

challenge that strongly affects the level of usability.

Working under altered gravity not only results in an

increased workload of user performance, it also

denotes changes in human sensorimotor

coordination (Bock et al., 1998), especially in aimed

pointing movements (Fisk et al., 1993; Bock et al.,

1992). Previous studies under parabolic flight (PF)

conditions (Markov-Vetter et al., 2012) have shown

that head-mounted AR interfaces for symbolic input

tasks (e.g., AR soft keyboard) under short-term

hyper- and microgravity conditions requires haptic

feedback and should be coded inside of human’s

egocentric body frame of reference (e.g., attached to

limbs). Despite these results, the future main

application of an AR supported guidance system is

predominantly coded outside of the user’s body

frame. Therefore, we are investigating adequate

countermeasures to maintain user performance in

object selection tasks as under those conditions. In

general, the selection performance can be affected

for example by targets’ size and distance. Looser et

al. (2007) evaluated different AR selection

techniques (Direct Touch, Ray-Casting, Magic Lens)

for different predefined target sizes, target density

401

Markov-Vetter D., Zander V., Latsch J. and Staadt O..

The Inﬂuence of Gravity-adapted Target Resizing on Direct Augmented Reality Pointing under Simulated Hypergravity.

DOI: 10.5220/0005316604010411

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 401-411

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

and distance to the users. In contrast to that, we used

a contrary approach for the evaluation of gravity-

adapted targets’ size and position. We used only a

direct touch interface for object selection in a head-

mounted AR environment. We hypothesize that: (1)

increased gravity conditions decrease the pointing

performance towards normal sized targets, and (2)

gravity-adapted target resizing impacts the

performance and workload of direct AR pointing.

Before conducting expensive experiments under

simulated weightlessness conditions (e.g., parabolic

flight), we performed a proof-of-concept (POC)

study under simulated hypergravity (+Gz)

conditions. We predicted variations of the pointing

performance (e.g., response time, speed, etc.)

correlated to the resized and -positioned information

visualisation depends on the adapted gravity force.

In response to visual stimuli the participant should

point towards virtual targets under altered +Gz loads

while wearing an optical see-through head-mounted

display (OST HMD). Until now, there have been no

equivalent studies on gravity-based target resizing

and -positioning conducted under simulated

hypergravity. The POC study was divided into two

parts using different simulations of hypergravity.

Firstly, we performed a case study where +Gz load

was induced by a long-arm human centrifuge and

pointing towards an AR soft keyboard for the

experimentation task. Secondly, we performed an

experiment under normogravity and simulated +Gz

load by additional arm weighting (Guardiera et al.,

2008) as validated method. To evaluate the

performance during the weight study we considered

the international standard for pointing devices

(ISO/DIS 9241-9, 2000) using the Fitts’ multi-

directional tapping task (MacKenzie, 1992). There

have been only few studies applying Fitts’ law on

evaluation of AR interaction (Rohs et al., 2011), or

on head-mounted Mixed Reality pointing (Kohli et

al., 2012).

Measuring the performance of aimed pointing

includes metrics such as the frequency of correct and

incorrect pointing, the accuracy, the response time

and the pointing speed. Since the physiological

factor is essential in sensorimotor coordination, we

recorded and evaluated the physiological strain by

assessing the heart rate variability (HRV) (Tümler et

al., 2008; Oehme et al., 2002) in the weight study.

This is an immanent expression of sympathetic and

parasympathetic influences of the function of the

heart (Task Force, 1996).

In the next section, the gravity adapted sizing

technique that were used for both experiments is

presented. The following sections describe the case

study and weighting experiments. We finally discuss

the results and suggest future research.

2 THE FORCE-BASED SIZING

For improving the performance of aimed pointing

movements towards virtual targets under altered

gravity conditions, we use a force-based approach

for automated transformation of the targets. Force-

based approaches are typically used for automated

positioning of labels and annotations, e.g. in 3D

information visualization (Pick et al., 2010;

Hartmann et al., 2004). Depending on the present

gravity load we calculate a corresponding force

affecting target's size and position. Our approach for

target resizing and -positioning is derived from the

elastic behaviour of soft bodies, which are

proportional deformed to the applied gravity load





, similar to Hooke’s law (Eq. 1). Therefore, we

calculated the axial (Eq. 2) and transversal (Eq. 3)

strain of the target using empirical values for the

modulus of elasticity  and Poisson’s ratio .

Thereby, we distinguished between two techniques

of target sizing – sizing by compression (SC, Eq. 4)

and sizing by elongation (SE, Eq. 5). Their output

was compared with the unmodified sizing technique

(SU) as baseline condition that does not affect the

targets. For first experimentation we limited the

evaluated parameters by automated target resizing

without the transversal strain , but applied the

axial strain  proportionally to target’s height and

width. Figure 1 shows the resulted sizing techniques

that we have investigated. We also applied the

gravity-based changes to the complete interface, i.e.

to targets' position. That resulted in larger target

distance with the SE technique and in smaller

distances with the compressed SC technique. While

the SC sizing technique provides smaller targets and

benefits from smaller target distances, the SE

technique offers larger target size at larger distance.

Therewith, we evaluated the efficiency of

sensorimotor coordination during direct AR pointing

tasks. To our knowledge, gravity-adapted target

sizing was not reported until now.

 with 





 and 





(1)

 

∗

∗

with







and 



(2)

   ∗





(3)





, 





(4)





, 





(5)

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

402

For designing the normal sized targets (SU) we

followed the recommended ergonomic size range for

push buttons (Department of Defense. 1999) and

used a squared target of 15mm width and height for

the unmodified method.

Figure 1: Methods of target sizing being evaluated.

3 CASE STUDY BY LONG-ARM

HUMAN CENTRIFUGE (LAHC)

To proof our concept of the gravity-adapted

approach initially, we were allowed to perform a

case study under +Gz load induced by a long-arm

human centrifuge (LAHC, see Fig. 2). Human

centrifuges enable research in medicine and human

physiology during altered +Gz load and are also

used to train pilots and astronauts. The case study

was performed with one participant. The male

participant (51 years old, space engineer) is very

experienced under altered +Gz load (human

centrifuge, parabolic flight) and familiarized with

the used AR pointing system and task.

3.1 Apparatus

We used a right-sided monocular optical see-through

head mounted display (OST HMD, Shimadzu

dataGlass2/a), which has a semi-transparent LCD

display with a resolution of 800x600 pixels and a

diagonal field of view (FOV) of 30 degrees (see Fig.

3, left). The HMD was connected to the data

processing unit (Lenovo ThinkPad T420s, 2.8 GHz

CPU, NVIDIA Quadro NVS 4200M), which was

installed under the participant’s seat in the centrifuge

cabin. For optical inside-out marker tracking we

equipped the HMD with an optical sensor (Microsoft

HD 5000 webcam with 66 degree diagonal FOV).

To compute the position of participant’s eye relative

to the optical sensor, the participant had to perform a

self-calibration (Kato et al., 1999). To realize

pointing with haptic feedback we used a panel that

was installed in front of the participant and was

equipped with a multi-marker configuration. For the

pointing purpose a single marker was attached to the

participant’s fingertip at the dominant hand. The

pose data were captured with a mean frame rate of

38.74 fps (SD = 10.05) by the optical sensor at

constant artificial light conditions.

Figure 2: Used LAHC (5 m radius) with centrifugal

acceleration a

. The cabin is swinging out during the

rotation with resulted acceleration a in line with subject’s

long body axis.

3.2 Experiment Task

Pointing in response to visual stimuli was done

based on the PF experiment task (Markov-Vetter et

al., 2012) by using a soft AR keyboard with squared

keys of 15mm width and height (Department of

Defense. 1999). The participant was requested to

enter prescribed random pseudo-letters on the virtual

keyboard (see Fig. 3, right). Entering letters onto the

keyboard is determined by collision tests of a virtual

ray ranging from the origin of the fingertip marker to

the top of the index finger. The requested letter was

signalled in green, hitting a correct key was

highlighted in red and then the next key was

signalled. Because the data processing unit was

installed in the cabin of the centrifuge, the

participant needed to start the experiment with a

virtual start button displayed above the keyboard and

hidden afterwards.

Figure 3: Participant sitting in the LAHC cabin, wearing

the OST-HMD and pointing toward the panel (left). The

soft-AR keyboard (right).

3.3 Experiment Procedure

We conducted the experiment during three days. To

perform the tasks, four randomized target pools were

used per sizing technique. We defined a target pool

as a pre-randomized series of keys. Pointing towards

the keys of one target pool should be completed in

25 seconds. Within one centrifugation the participant

performed the task for two sizing techniques (SC,

SE) that resulted in a total pointing time of 200

TheInfluenceofGravity-adaptedTargetResizingonDirectAugmentedRealityPointingunderSimulatedHypergravity

403

seconds for each +Gz load. On the first day we

tested only the feasibility and functionality. Because

it was exhausting for the participant to perform arm

movements for 200 s at one time, we reduced the

operation time of a target pool to 20 s (in total 160 s

per centrifugation) from the second day on. We

distinguished between a fixed operation timer with

20 s runtime and a variable participant timer that

was automatically started after entering the first key.

If the operation timer elapsed, the timer for the

participant was automatically stopped. To avoid

transition effects between pool or method changes

the first and the last signaled key where not

recorded. Within one centrifugation the participant

performed the task under one +Gz load using the

unchanged method (SU) and one of the methods

with force-based target sizing (SC, SE) in an

alternated way. Thereby the sizing technique was

changed after one target pool. We compared the

methods SU with SC (second day) and SU and SE

(third day) under 1.5g, 1.8g and 2.5g in a random

presentation order. For reference purposes we also

measured the pointing performance of the

participant, using the SU method under 1g on the

first day. For physiological regeneration and to

avoid learning effects there was a 10 minutes break

between the changes of the +Gz loads.

3.4 Results

Following we are showing the frequencies of correct

and false target hits, the pointing response time in

millisecond, the percentage error rate and the stroke

rate per second. Thereby a false target hit constitutes

that the participant entered a wrong key. The

response time mirrors the elapsed time between

target’s indication in green and hitting this target.

The stroke rate was calculated by the mean number

of correct targets hits of the four targets pools and

the mean completion time of the target pools. For

analyzing the performance we evaluated a total of

646 correct target hits with a mean of 12.92 (SD =

2.51) as the average number of hits over the target

pools that were collected under the gravity levels 1g,

1.5g, 1.8g and 2.5g. Entering the targets resulted in a

mean stroke rate of 0.675 s

-1

(SD = 0.085) and one

target was hit with an overall mean response time of

1309.00 ms (SD = 204.07). For false target hits we

evaluated a total of 43 (M = 0.86, SD = 1.25) with a

mean percentage error rate of 6.14% (SD = 8.38).

Figure 4 mirrors the distribution of the

frequencies of correct target hits of the three target

sizing techniques (ST) per gravity level. It shows

that pointing towards elongated targets (SE) results

in average most correct target hits under the gravity

levels 1.5g and 1.8g. In contrast, the compressed

sizing technique (SC) led to the lowest number of

correct target hits. Table 1 shows that pointing

towards elongated SE targets also results in the

fastest response time under the +Gz load 1.5g, as

well as in the lowest percentage error rate and the

highest stroke rate under the +Gz loads 1.5g and

1.8g. The pointing performance under 2.5g led to

lowest error rate and the highest stroke rate with the

normal sized technique (SU) and to the fastest

response time with the compressed sizing technique

(SC). Otherwise, the pointing performance with the

SC method was most deteriorated under the +Gz

loads 1.5g and 1.8g.

Figure 4: Distributional characteristics of frequencies of

correct target hits by sizing technique per gravity load.

Table 1: Performance metrics of the LAHC case study.

Response time (ms) Error rate (%) Stroke rate (s

-1

)

mean ± SD mean ± SD mean ± SD

Gz = 1.5g

SU 1367.25 ± 217.33 10.95 ± 5.87 0.649 ± 0.086

SC 1483.18 ± 260.69 10.21 ± 9.05 0.601 ± 0.043

SE 1341.46 ± 81.74 0.00 ± 0.00 0.714 ± 0.048

Gz = 1.8g

SU 1300.01 ± 166.84 2.03 ± 3.79 0.702 ± 0.079

SC 1338.24 ± 181.74 7.28 ± 10.11 0.622 ± 0.027

SE 1312.80 ± 133.50 1.67 ± 3.33 0.710 ± 0.049

Gz = 2.5g

SU 1322.43 ± 256.35 4.49 ± 6.11 0.659 ± 0.053

SC 1239.52 ± 168.98 19.41 ± 3.49 0.585 ± 0.009

SE 1389.13 ± 166.74 14.02 ± 16.23 0.627 ± 0.054

For statistical analysis of the sizing methods over all

and on same Gz load we used proc mixed (SAS®

9.4) with lsmeans/adjust = simulate to keep the

experiment-wise error rate α = 0.05. The test

showed significant differences for correct and false

target hits between the sizing techniques. The

comparison of correct target hits revealed effects on

the sizing method that indicated that scores

compared with the compressed method SC (M =

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

404

11.09, SD = 0.70) were significant higher for the

normal sized method SU (M = 12.65, SD = 1.47, p =

0.0048) and the elongated method SE (M = 12.75,

SD = 1.14, p = 0.0068). The comparison of false

target hits also revealed an effect on the sizing

method that shows that the performance with the

compressed method SC (M = 1.73, SD = 1.35) were

significant decreased (p = 0.0119) compared with

the normal sized method SU (M = 0.57, SD = 0.73).

Overall, the case study showed that gravity-adapted

target resizing and positioning significantly impacts

aimed pointing performance under increased Gz

loads and shows an up-coming trend for the

elongated method SE.

4 USER STUDY BY ARM

WEIGHTINGS

To verify the observed effect of the case study using

the LAHC we performed a subsequent experiment

under normogravity condition. For simulation the

+Gz loads we used corresponding weightings

(Guardiera et al., 2008) that were balanced attached

to the participant’s dominant forearm (see Fig. 5).

The extended arm weights (see Table 2) were

calculated (Eq. 6) for each participant as follows:

















∗







∗.%

(6)

with 



for the simulated gravity force, 



for

the body weight of the participant and 5.38% as

averaged percentage arm weights introduced by

Clauser et al. (1969).

Table 2: Weights of body, arm and the added weight.

Participant





(kg)





(kg)





(kg)

1.5g 2g 2.3g

S1 80.0 4.3 2.2 4.3 5.6

S2 78.0 4.2 2.1 4.2 5.5

S3 75.0 4.0 2.0 4.0 5.3

S4 80.0 4.3 2.2 4.3 5.6

S5 65.0 3.5 1.8 3.5 4.6

S6 69.0 3.7 1.9 3.7 4.8

S7 60.0 3.3 1.7 3.3 4.3

S8 78.0 4.2 2.1 4.2 5.5

4.1 Apparatus

We used the same HMD setup as for the LAHC

study (see section 3.1). Also all participants

performed an eye-sensor calibration (Kato et al.,

1999) immediately before the experiment. To

perform the task of pointing towards outside coded

targets, the participant stood in front of a wall with

Figure 5: Participant sitting in the LAHC cabin, wearing

the OST-HMD and pointing toward the panel (left). The

soft-AR keyboard (right).

50 cm distance. We horizontal aligned the multi-

pattern depending on participant’s body height. The

optical sensor captured the pose data with a mean

frame rate of 38.52 fps (SD = 12.54). In order to

assess the physiological and cognitive workload by

the HRV, the participant was wearing a wireless

eMotion HRV sensor from Mega Electronic (see

Fig. 5, right). The HRV sensor recorded the HRV

and 3-axis acceleration at a sampling frequency of

1000 Hz and an accuracy of 1 ms.

4.2 Experiment Task

To evaluate the speed-accuracy tradeoff related to

Fitts’ law we decided to use an appropriate task and

designed a multi-directional pointing task as

proposed by the ISO/DIS 9241-9 standard (2000).

Therefore eight squared targets with a default size of

15.0 have been used (see Fig. 6). The

targets were arranged in a circle with a default

diameter of 82.5. Like the LAHC task, the

participant should point towards the targets in

response to visual stimuli. For evaluation purposes

by Fitts' law we defined “true” target connections of

0°, 45°, 90° that implied same target distance and

involves horizontal and vertical arm movements.

The remaining target connections were used for

pointing transition only.

Figure 6: Multi-directional task of the weight study.

4.3 Participants

Participants were 6 male and 2 women aged 24 to 51

TheInfluenceofGravity-adaptedTargetResizingonDirectAugmentedRealityPointingunderSimulatedHypergravity

405

years ( 20-31 years: 4 participants, 40-51 years: 4

participants, M = 37.25, SD = 10.55). Seven

participants had experiences with AR interfaces in

terms of participation in previous studies and one

participant was novice. They came from

backgrounds in biology, physiology, aerospace and

medicine. All participants had a right-dominant arm

that was used for the pointing task.

4.4 Procedure and Study Design

The study consists of three independent variables

(SU, SC, SE) on three +Gz loads (1.5g, 2g, 2.3g),

with SU used as baseline condition. In a within-

subject design, each participant performed the test

series for all independent variables under all loads,

resulting in a factorial design of 3 x 3. The repetition

rate for each method amounted to five target pools

per Gz load. Thereby a target pool was specified as

predefined series of randomized target connection of

the multi-directional pointing tasks. Pointing

towards the targets of one target pool should be

completed by the participants in 25 seconds. Overall

each participant performed 50 test series. The multi-

directional task was performed under the following

order of Gz loads: 2.3g, 1.5g and 2g. We used

systematic variations of the presentation order of the

sizing methods per Gz load. Corresponding to the

LAHC study we applied a fixed operation timer with

25 seconds running time and a variable participant

timer that was automatically started after hitting the

first target. To avoid transition effects between pool

changes the first and the last signaled targets

performance were not recorded. Between changes of

the Gz load, the participant had a five minute break

for physiological regeneration and to avoid learning

effects. To be familiar with the pointing task and to

check the integrity of the tracking operation, the

participant undertook a short training session before

starting the first condition.

4.5 Results

The participants performed the pointing task under

all gravity levels using all sizing techniques. Each

participant performed the eye-sensor calibration

directly before starting the experiment. Table 3

presents the resulted target sizes a with its

surrounding radius 







√





and targets’ distance d

to each other calculated by our force-based resizing

approach using the active Gz load. The distance

reflects the pointing range between two "true" target

connections. While pointing towards normal sized

target (SE) always results in same target sizes and

distances at all Gz loads, the elongated sizing

technique (SE) results in increased sizes and

distances on increased Gz loads and contrary for the

compressed technique (SC). The pointing

performance was measured by the number of correct

and incorrect pointing, the Euclidean distance

between the target's center and the final intersection

point, as well as the response time and speed of

hitting a target. We also present the resulted

percentage pointing error rate, the stroke rate per

second and the percentage pointing accuracy. For

statistical analysis the performance of the sizing

techniques over all and on same Gz load, we used

proc mixed (SAS® 9.4) with lsmeans/adjust =

simulate to keep the experiment-wise error rate α =

0.05. For analyzing the pointing response time and

speed we only considered target hits with “true”

target connections that implicated the same pointing

distance per Gz load and sizing technique.

Additionally we evaluated the speed-accuracy

tradeoff of the sizing methods according to Fitts’

law and present the movement time (MT) and

throughput (TP). To evaluate the physiological strain

by HRV, we assessed the R-R distance, which is the

time interval in milliseconds between two

heartbeats. Therefore, the R-R interval shows the

impact to the cardiovascular system on a certain

workload. Larger workload caused a larger impact in

the cardiovascular system and causes therefore a

higher heart frequency and thus a shorter R-R

interval between the heartbeats.

Table 3: Resulted target size a, radius r

and distance d.

 (mm) 



(mm)  (mm)

- 15.00 10.61 082.50

1.5 11.67 08.25 064.17

2.0 10.56 07.45 058.06

2.3 09.89 06.99 054.39

1.5 18.33 12.96 100.83

2.0 19.44 13.75 106.94

2.3 20.11 14.22 110.61

4.5.1 Performance

Pointing Frequencies: The participants performed

the task with 5 repetitions under 10 paired

conditions with a total of 50 trials per participant. A

single task was timed to 25 seconds where the

participant tried to hit signalled targets. Overall, the

participants pointed towards 6708 targets (SU = 30.7

% , SC = 32.3 %, SE = 37.0 %) in a correct way and

towards 102 targets (SU = 33.7 %, SC = 34.7 %, SE

= 31.6 %) in a wrong way. Within 25 seconds (i.e.

one target pool) the average frequency of correct

target hits was 19.39 (SD = 3.37) and of false hits

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

406

0.27 (SD = 0.66). Table 4 splits this into the

interaction effect of the Gz loads on the studied

sizing techniques (SU, SC, SC) and additionally

shows the corresponding average frequency of

incorrect target hits, percentage error rate and hit

rate per second. Examining the three sizing

techniques per increased Gz load (1.5g, 2g, 2.3g)

data reveals that all means of the elongated sizing

technique (SE) are higher (correct hits, stroke rate)

or lower (incorrect hits, error rate) under 2g and 2.3g

than the SU and SC technique. Under 1.5g the

compressed method (SC) resulted in higher mean

values for correct hits and the stroke rate, and the

unchanged technique (SU) in lower means for

incorrect pointing. The distributional characteristics

for correct target hits are featured in Figure 7.

Table 4: Performance metrics of the arm weightings study:

number correct and false hits, error and stroke rate.

ST Correct hits False hits

Error (%) Stroke (s

-1

)

mean ± SD mean ± SD mean ± SD mean ± SD

Gz = 1.5g

SU 20.70 ± 2.63 0.09 ± 0.43 0.53 ± 2.44 0.88 ± 0.11

SC 21.20 ± 2.76 0.13 ± 0.34 0.70 ± 1.92 0.91 ± 0.08

SE 21.07 ± 2.30 0.13 ± 0.34 0.66 ± 1.71 0.89 ± 0.09

Gz = 2.0g

SU 17.56 ± 4.22 0.40 ± 0.82 2.69 ± 5.51 0.75 ± 0.16

SC 18.31 ± 4.37 0.26 ± 0.66 1.85 ± 5.41 0.78 ± 0.18

SE 19.85 ± 2.48 0.18 ± 0.45 1.04 ± 2.58 0.85 ± 0.09

Gz = 2.3g

SU 18.45 ± 3.57 0.46 ± 0.88 2.40 ± 4.67 0.79 ± 0.10

SC 16.88 ± 3.84 0.48 ± 0.85 2.89 ± 5.16 0.73 ± 0.16

SE 18.95 ± 2.36 0.43 ± 0.87 2.23 ± 4.69 0.80 ± 0.10

Figure 7: Distributional characteristics of correct target

hits by sizing technique per gravity load.

In terms of differences between the correct hits of

the sizing techniques over all Gz loads showed an

significant improvement (see Table 5) of the

performance using the elongated sizing technique

SE (M = 20.00, SD = 2.53) compared to the normal

sizing technique SU (M = 19.05, SD = 3.52, p =

0.0373) and to the compressed sizing technique SC

(M = 18.82, SD = 4.09, p = 0.0141 ).

Table 5: Significant differences of correct pointing using

SAS proc mixed with lsmeans/adjust=simulate.

Effect ST Gz ST Gz Estima. StdErr DF Adj P

ST SE - SU - 1.052 0.426 338 0.0373

ST SE - SC - -1.158 0.413 338 0.0141

Accuracy: The pointing accuracy reflects the

precision of target pointing and was measured by the

Euclidean distance





and the surrounding radius 



of the targets (see Table 3). The distance 



is the

distance between the centre of the target and the

intersection point within the target. Table 6 presents

amongst others the means and standard deviations

(SD) of the distance





and the percentage accuracy

of the sizing techniques per Gz load.

Table 6: Euclidean distance, accuracy, response time and

speed of the sizing techniques (ST) per Gz load.





(mm)

Accuracy

(%)

Response time

(ms)

Speed

(mm/ms)

mean ± SD mean ± SD mean ± SD mean ± SD

Gz = 1.5g

SU 4.23 ± 2.49 60.10 ± 23.46 1007.35 ± 173.11 0.085 ± 0.017

SC 3.58 ± 1.96 56.59 ± 23.71 1016.00 ± 173.11 0.065 ± 0.012

SE 5.38 ± 2.99 58.51 ± 23.13 1029.43 ± 164.93 0.101 ± 0.018

Gz = 2.0g

SU 4.78 ± 2.74 54.93 ± 25.79 1012.15 ± 195.92 0.085 ± 0.019

SC 3.80 ± 1.87 49.13 ± 24.99 1039.77 ± 202.71 0.058 ± 0.012

SE 5.85 ± 3.34 57.47 ± 24.30 1031.43 ± 152.39 0.106 ± 0.017

Gz = 2.3g

SU 5.02 ± 2.50 52.72 ± 23.58 1073.56 ± 184.71 0.079 ± 0.015

SC 3.36 ± 1.71 51.94 ± 24.45 1068.76 ± 210.42 0.053 ± 0.012

SE 5.65 ± 3.14 60.24 ± 22.09 1078.08 ± 159.12 0.105 ± 0.016

The graphical distribution of the Euclidean distances

are presented in Figure 8 and shows a proportional

ratio between the distance and target's size, i.e. the

pointing distance is greater with the increment of

target's size and vice versa. The statistical analyzing

of the Euclidean distance confirmed this observation

by significant differences between the sizing

techniques. The test revealed that pointing towards

SC targets (M = 3.56 mm, SD = 1.96) resulted in

significant shorter distances analyzed over all Gz

loads (p < .0001) compared to SU (M = 4.56 mm,

SD = 2.56) and SE (M = 5.61 mm, SD = 3.15). But

it also showed differences (p < .0001) for grouped

effects (ST*Gz) by comparing the sizing techniques

on same Gz stage.

In contrast, the accuracy (see Fig. 9) mirrors the

percentage ratio of the distance





to the target size

expressed by the radius





. The participants pointed

with an overall mean percentage accuracy of 56.39

%. Per sizing technique over all Gz loads data

TheInfluenceofGravity-adaptedTargetResizingonDirectAugmentedRealityPointingunderSimulatedHypergravity

407

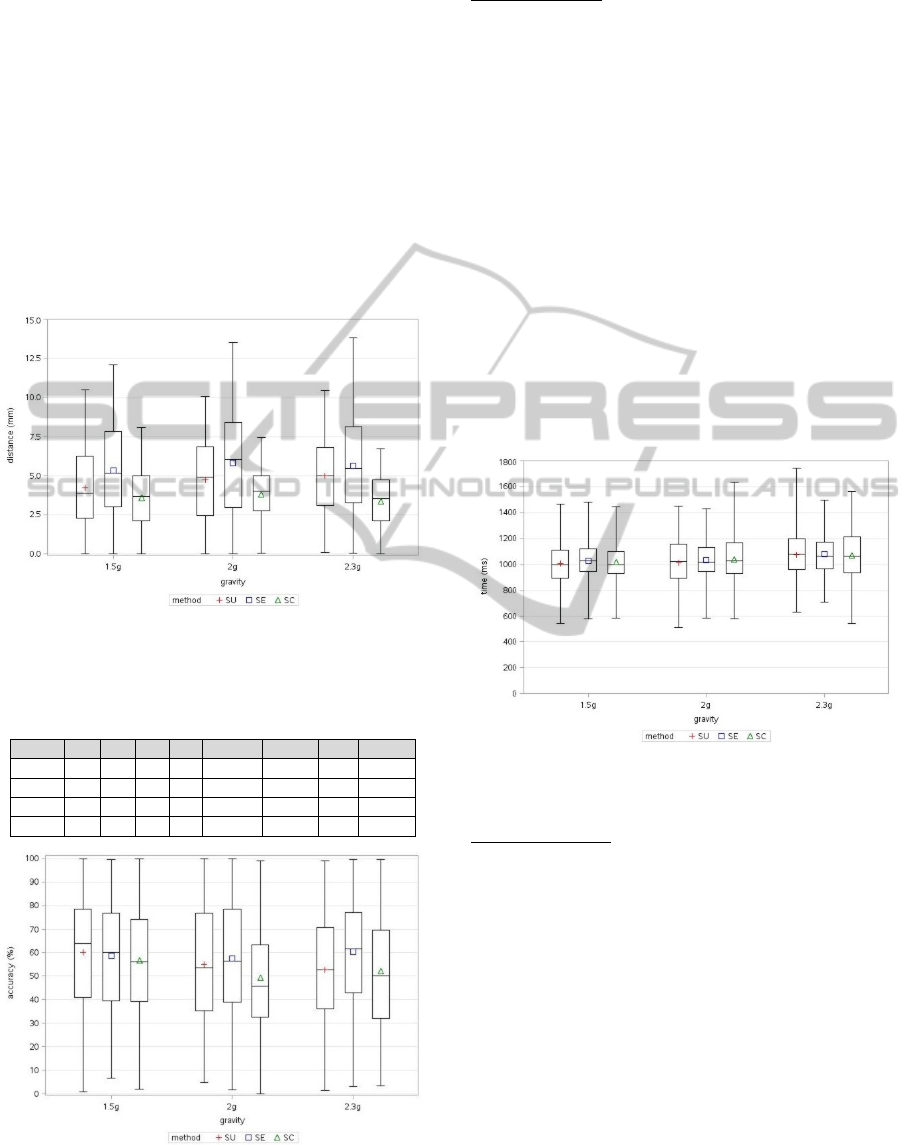
revealed that relative to target's size, participants

more precise pointed using the elongated method

(SE) with 58.72 % accuracy (SU: 56.77 %, SC:

53.19 %). Statistical analyzing (see Table 7)

revealed that pointing towards elongated targets

(SE) enabled a significant improvement (p < .0001)

compared to pointing towards compressed targets

(SC) over all Gz loads and separated by comparison

on same Gz stage, revealed in significant differences

under 2g (p < 0.0178) and 2.3g (p < 0.0072). The

comparison between pointing towards elongated

(SE) and normal sized targets (SU) resulted in

significant improvement under 2.3g (p < 0.0436)

using the SE sizing technique.

Figure 8: Distributional characteristics of Euclidean

distance by sizing technique per gravity load.

Table 7: Significant differences of accuracy using SAS

proc mixed with lsmeans/adjust=simulate.

Effect ST Gz ST Gz Estima. StdErr DF Adj P

ST SE - SC - -6.185 1.292 1951 < .0001

ST*Gz SE 2.0 SC 2.0 -8.341 2.434 1951 0.0178

ST*Gz SE 2.3 SC 2.3 -8.303 2.255 1951 0.0072

ST*Gz SE 2.3 SU 2.3 7.518 2.392 1951 0.0436

Figure 9: Distributional characteristics of accuracy by

sizing technique per gravity load.

Response Time: The response time (in millisecond)

is the time between highlighting a target and

selecting this target by the index finger. The means

and standard deviations (SD) are showed in Table 6.

Overall the participants pointed with a mean

response time of 1038.60 ms (SD = 179.26). Only

considering the sizing techniques at summarized Gz

loads data revealed shorter response times for

pointing towards normal sized target (SU) with a

mean of 1028.62 ms (SD = 183.49) compared to

compressed targets using the SC method (M =

1039.99 ms, SD = 195.32) and elongated targets

using the SE method (M = 1044.75 ms, SD =

160.75). The distribution of the response time for the

sizing techniques per Gz load is presented in Figure

10. Longest response times, but not significant, were

achieved using the elongated method (SE) under

1.5g and 2.3g. This is contrary to our expectation of

significant longer response times at larger target

distances (SE) under all Gz loads

Figure 10: Distributional characteristics of response time

by sizing method per gravity load.

Pointing Speed: The speed (in mm/ms) was

calculated by the distance between the targets (see

Table 3) divided by the response time. The means

and standard deviations (SD) are also presented in

Table 6. Because targets' size and distance varies

with the used sizing technique and the Gz load,

analyzing the speed is more meaningful than the

response time. Overall the participants pointed with

a mean speed of 0.083 mm/ms (SD = 0.024). The

distribution of pointing speed by the sizing

technique per gravity load is presented in Figure 11.

In contrast to the resulted response times, with

significant higher speed was pointed towards

elongated targets (SE) that were placed with greater

distances to each other. In Table 8 we are presenting

significant differences that shows a significant

improvement with p < .0001 for the SE method (M

= 0.104, SD = 0.017) analyzed over all Gz loads at

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

408

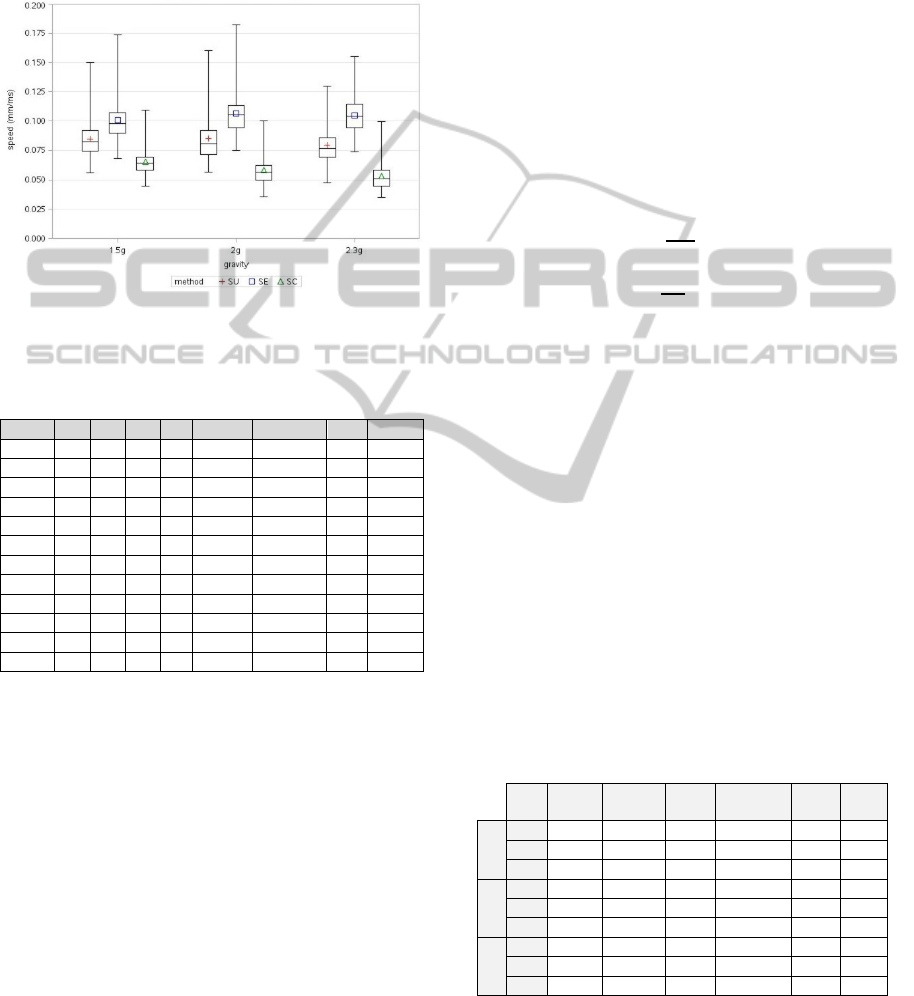
comparing with the other two sizing methods (SU:

M = 0.083, SD = 0.017, SC: M = 0.059, SD =

0.013), and shows significant faster pointing using

the SE methods (p < .0001) for grouped effects

(ST*Gz) by comparing the sizing techniques on

same stage of the Gz load.

Figure 11: Distributional characteristics of pointing speed

by sizing technique per gravity load. (*p < .05).

Table 8: Significant differences of pointing speed using

SAS proc mixed with lsmeans/adjust=simulate.

Effect ST Gz ST Gz Estima. StdErr DF Adj P

ST SE - SC - -0.0451 0.00081 2046 < .0001

ST SE - SU - 0.0209 0.00088 2046 < .0001

ST SC - SU - -0.0242 0.00091 2046 < .0001

ST*Gz SE 1.5 SC 1.5 -0.0355 0.00128 2046 < .0001

ST*Gz SE 2.0 SC 2.0 -0.0480 0.00150 2046 < .0001

ST*Gz SE 2.3 SC 2.3 -0.0518 0.00143 2046 < .0001

ST*Gz SE 1.5 SU 1.5 0.0161 0.00126 2046 < .0001

ST*Gz SE 2.0 SU 2.0 0.0211 0.00175 2046 < .0001

ST*Gz SE 2.3 SU 2.3 0.0256 0.00152 2046 < .0001

ST*Gz SC 1.5 SU 1.5 -0.0195 0.00131 2046 < .0001

ST*Gz SC 2.0 SU 2.0 -0.0269 0.00183 2046 < .0001

ST*Gz SC 2.3 SU 2.3 -0.0262 0.00155 2046 < .0001

4.5.2 Fitts' Law

In designing Human-Computer-Interfaces the

assessment of ergonomics is mainly determined by

Fitts' model of movement time (Eq. 7) (Fitts, 1954)

that a human needs to point at a target of a given

size and distance. Fitts' law predicts longer

movement times at larger distances, as well as at

smaller targets. Our sizing approach interrelates this

characteristics to each other, whereby the elongated

method (SE) provides larger targets at larger

distances, while the compressed method (SC) results

in smaller targets at smaller distances. We used

Fitts’ law to evaluate the speed-accuracy trade-off of

the studied sizing techniques related to direct

pointing affected by added arm weightings. The

metric for comparing the performance is the

Throughput TP (Eq. 8), in bits per second (bps)

calculated by the Index of Difficulty ID and mean

movement time MT (Eq. 8) as time to hit a target in

millisecond with a for the intercept and b for the

slope of measured mean response time by the target

width W. The ID measures the tasks difficulty in bits

using target size and distance. Because we used

squared targets, we calculated the ID only by the

targets' width. For computing the ID (Eq. 9) we used

the Welford formulation (Welford, 1960). To reflect

the observed pointing performance of the

participants, we used the effective target width W

(Eq. 10) (MacKenzie, 1992; Welford, 1960) as the

central 96 % of the spatial distribution with SD

standard deviation of the mean pointing accuracy.

    



(7)

 







(8)





log











0.5

(9)





 4.133 ∗ 



(10)

Table 9 shows the resulting Fitts’ parameter for the

three sizing methods per +Gz load. The SE method

resulted overall in the highest ID

and therefore in

most difficult targets, but also in the highest

throughput (TP). The compressed sizing method

(SC) yielded the highest index of difficulty under

1.5g, but under 2g and 2.3g yielded most simple

targets. Pointing towards normal sized targets (SU)

yielded increased ID

, as well as a growing

throughput with the increment of gravity. Two-Way

analysis of variance did not show significant effects

between the methods' throughputs (F

2,4

= 1.52, p >

.05).

Table 9: Fitts’ resulted parameters: targets' distance (A),

target width (W), effective target width (W

), mean

measured movement time (MT), effective Index of

Difficulty (ID

), and Throughput (TP).

+Gz

(mm)

(ms)

(bits)

(bps)

1.5 82.50 15.00 14.47 1010.61

2.63 2.61

2.0 82.50 15.00 11.04 1052.83

2.99 2.85

2.3 82.50 15.00 11.78 1071.96

2.91 2.71

1.5 64.17 11.67 8.47 1021.53

3.02 2.96

2.0 58.06 10.56 11.12 1032.42

2.52 2.44

2.3 54.39 09.89 9.09 1085.23

2.69 2.49

1.5 100.83 18.33 13.68 1029.36

2.98 2.89

2.0 106.94 19.44 13.39 1035.30

3.09 2.98

2.3 110.61 20.11 13.18 1089.69

3.15 2.89

The resulting Pearson's correlation coefficient r and

the regression equations of Fitts’ movements model

for the sizing conditions are presented in Table 10.

While the movement time and the index of difficulty

TheInfluenceofGravity-adaptedTargetResizingonDirectAugmentedRealityPointingunderSimulatedHypergravity

409

highly linear correlate (r > 8.0) for the SU and SE

conditions, a low correlation was yielded from the

SC condition. The Fitts' model of movement time of

the SU (Eq. 11) and SE (Eq. 13) sizing conditions

provides good descriptions of the observed pointing

behaviour. Contrary to this, the model of the

compressed sizing technique SC (Eq. 12) resulted in

a model with a high intercept at a negative slope,

i.e. that the Movement Time is decreased for an

increased Index of Difficulty and vice versa. The

high intercept implies a movement time of 1.163 s at

ID = 0 bits that is about twice the MT of the SU

condition and about 14-fold of SE's MT.

Table 10: Pearson's correlation coefficient r between MT

and ID

, and linear regression equation of Fitts’ model of

MT per sizing technique over increased Gz loads.

Fitts' model of movement time (ms)

0.856   638142



(11)

-0.321   116343



(12)

0.842   81315



(13)

4.5.3 Physiological Workload

The cardiovascular parameters were assessed during

all phases of the experiment. The 1g SU output was

used as reference measurement and showed the

lowest impact on the cardiovascular system. Since

the physiological workload grows with the

increment of gravity respectively the weight and R-

R distance (see Table 11) decreases during the

experiment under 2g and even more under 2.3g. The

R-R distances are showing the lowest values for the

SU, SC and SE conditions under high Gz load since

the weight attached to the participants’ arm

constituted the major part of the workload. While

pointing towards elongated SE targets (largest target

distances) yielded the lowest values for the R-R

distances under all Gz loads, pointing towards

compressed SC targets (smallest target distances)

resulted in the highest values for the R-R distance

and therefore in the lowest workload. Two-Way

analysis of variance showed a significant effect

between the R-R distance produced by increased Gz

loads (F

2,4

= 27.69, p < .05), but did not show

effects by the sizing methods (F

2,4

= 4.21, p > .05).

Table 11: Assessed HRV parameters: R-R distance in [ms]

median and SD across all participants.

Gz SU SC SE

1.0 723,86 ± 156.88 - -

1.5 674,24 ± 114.76 680,45 ±120.29 665,09 ± 102.56

2.0

642,11 ± 119.43 649,57 ±117.03 625,28 ± 088.07

2.3

641,97 ± 105.77 648,31 ±119.25 645,24 ± 126.40

5 DISCUSSION

While the LAHC study has already shown a small

effect of gravity-based sizing, the weight study has

confirmed that

the performance and workload during AR

selection is influenced by the online adaptation of changed

gravity load to the size and position of the virtual

information. The weight study also confirmed and verified

the observed trend of an improved performance of

pointing towards targets influenced by the present gravity

load in an elongated fashion (greater size, larger distance).

The results showed an overall significant increment of the

pointing frequencies towards elongated targets,

accompanied by a likewise non-significant decrement of

the error rate under 2g and 2.3g. In contrast to elongated

targets, the compressed sizing technique yields the

smallest targets at short distances. This enables significant

closer hits to the targets' centre. Conversely, pointing

towards elongated targets ensures significant most precise

pointing relative to targets sizes. The most important

finding revealed that larger targets at greater distances

between the targets calculated by the active Gz load

significantly accelerates the pointing performance.

Conversely, the results showed that pointing towards

compressed targets (smaller size, shorter distance)

generates the opposite effect resulting in decreased

performance.

Also the analysis of the speed-accuracy

tradeoff related to Fitts’ law yielded in a higher, but not

significantly, throughput by larger target size and distance.

The HRV based parameters showed an effect caused by

changed gravity respectively for attached arm weights and

the alternation of the workload. Therefore, the assessment

of workload during the application of AR, by measuring

cardiovascular parameters such as the HRV, is a

promising method to improve the user performance in

normogravity and altered gravity.

6 CONCLUSION AND FUTURE

WORK

We conducted a proof-of-concept study to

investigate the influence of the online adaption of

the present gravity load to target size and distance on

direct AR pointing. Two experimentations were

performed by simulated hypergravity induced by

long-arm human centrifugation and by added arm

weightings under normogravity. In conclusion, our

results are showing that direct AR pointing under

changed gravity conditions is impacted by adapted

target size, as well as the distance between the

targets. Under increased Gz loads the pointing

performance benefits from increased sizes and

distances depending on the Gz load. This is a

promising direction for further HCI research. Our

next step will be the adaptation of the experiment to

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

410

the corresponding investigation under microgravity

conditions. In further research we will replace direct

fingertip pointing by gaze-based selection for more

adequate fitting the AR view management of our

future AR supported assistant system for space

operation procedures. Related to the HRV, for the

next step we will consider separating physical and

cognitive workload by assessing the muscular

activity and applying electromyogram (EMG) to the

participant’s weighted arm. By doing that we could

even more precisely assess the workload during

pointing and targeting.

REFERENCES

Agan, M., Voisinet, L. A., Devereaux, A.. 1998. NASA’s

Wireless Augmented Reality Prototype (WARP). In

Proc. of AIP’98, pp. 236-242, 1998.

Azuma, R.T. 1997. A survey of augmented reality. In

Presence, Teleopera-tors and Virtual Environments,

vol. 6, no. 4, pp. 355–385.

Bock, O., Howard, I. P., Money, K. E., Arnold, K. E.

1992. Accuracy of aimed arm movements in changed

gravity. In Aviation, Space, and Environmental

Medicine, vol. 63, pp. 994-998.

Bock, O. 1998. Problems of sensorimotor coordination in

weightlessness. In Brain Research Reviews, vol. 28,

pp. 155-160.

Clauser, C. E., McConville, J. T., Young, J. W. 1969.

Weight, volume, and center of mass of segments of the

human body. AMRL Technical Report 69-70. Wright-

Patterson Air Force Base.

Department of Defense. 1999. Design criteria standard,

human engineering. Technical Report MIL-STD-

1472F.

Fisk, J., Lackne, J. R., DiZio, P. 1993. Gravitoinertial

force level influences arm movement control. In

Journal of Neurophysiology, vol. 69, pp. 504-511.

Fitts, P.M. 1954. The Information Capacity of the Human

Motor System in Controlling the Amplitude of

Movement. In Journal of Experimental Psychology,

47 pp. 381-391.

Guardiera, S., Schneider, S., Noppe, A., Strüder, H. K.

2008. Motor performance and motor learning in

sustained +3Gz acceleration. In Aviation Space and

Environmental Medicine, vol. 79(9), pp. 852-9.

Hartmann, K., Ali, K., Strothotte, T. 2004. Floating

Labels. Applying Dynamic Potential Fields for Label

Layout. In Smart Graphics, vol. 3031, Springer, pp.

101–113.

ISO/DIS 9241-9. 2000. Ergonomic requirements for office

work with visual display terminals (VDTs) - Part 9:

Requirements for non-keyboard input devices.

International Standard, International Organization for

Standardization.

Kato, H., Billinghurst, M. 1999. Marker Tracking and

HMD calibration for a video-based augmented reality

conferencing system. In Proc. IWAR‘99, vol. 0, pp.

85-94.

Kohli, L., Whitton, M. C., Brooks, F. P. 2012. Redirected

touching: The effect of warping space on task

performance. In Proc of 3DUI’12, pp. 105-112.

Looser, J., Billinghurst, M., Grasset, R., Cockburn, A.

2007. An evaluation of virtual lenses for object

selection in augmented reality. In Proc of.

GRAPHITE’07, pp. 203-210.

MacKenzie, I. S. 1992. Fitts’ law as a research and design

tool in human-computer interaction. In Journal of

Human-Computer Interaction, vol. 7, pp. 91–139.

Markov-Vetter, D., Moll, E., Staadt O. 2012. Evaluation

of 3D Selection Tasks in Parabolic Flight Conditions:

Pointing Task in Augmented Reality User Interfaces.

In Proc. of VRCAI‘12, pp.287-293.

Markov-Vetter, D., Zander, V., Latsch, J. Staadt, O. 2013.

The Impact of Altered Gravitation on Performance and

Workload of Augmented Reality Hand-Eye-

Coordination: Inside vs. Outside of Human Body

Frame of Reference. In Proc. of JVRC’13, pp. 65-72.

Oehme, O., Schmidt, L., Luczak, H. 2002. Comparison

between the strain indicator hrv of a head based virtual

retinal display and lc-mounted displays for augmented

reality. In Proc. of WWDU ‘02, pp. 387-389.

Pick, S., Hentschel, B., Tedjo-Palczynski, I., Wolter, M.,

Kuhlen, T. 2010. Automated positioning of

annotations in immersive virtual environments. In

Proc. of JVRC’10, pp. 1-8.

Rohs, M., Oulasvirta, A., Suomalainen, T. 2011.

Interaction with magic lenses: real-world validation of

a Fitts' Law model. In Proc. of CHI’11, pp. 2725-

2728.

Scheid, F., Nitsch, A., König, H., Arguello, L., De Weerdt,

D., Arndt, D., Rakers, S. 2010. Operation of European

SDTO at Col-CC. SpaceOps 2010 Conference.

Task Force of the European Society of Cardiology and the

North American Society of Pacing and

Electrophysiology. Heart Rate Variability: standards

of measurement, physiological interpretation and

clinical use. 1996. Circulation 1996 (93) 1043-1065 /

Eur Heart J, 17(3):354-81.

Tümler, J., Mecke, R., Schenk, M., Huckauf, A., Doil, F.,

Paul, G., Pfister, E., Böckelmann, I., Roggentin, A.

2008. Mobile Augmented Reality in Industrial

Applications: Approaches for Solution of User-

Related Issues. In Proc. of ISMAR’08, pp. 87-90.

Welford, A. T. 1960. The measurement of sensory-motor

performance: Survey and reappraisal of twelve years'

progress. In Ergonomics, 3, 189-230.

TheInfluenceofGravity-adaptedTargetResizingonDirectAugmentedRealityPointingunderSimulatedHypergravity

411