Low Complexity Multi-object Tracking System Dealing with Occlusions

Aziz Dziri

, Marc Duranton

and Roland Chapuis

Embedded Computing Lab, CEA, LIST, F-91191 Gif-sur-Yvette, France

Institut PASCAL, Pascal Blaise University, 63171 Aubiere, France

Keywords:

GMPHD, Occlusion, Overlapping, Multi-object Tracking, Background Subtraction.

Abstract:

In this paper, we propose a vision tracking system primarily targeted for systems with low computing re-

sources. It is based on GMPHD ﬁlter and can deal with occlusion between objects. The proposed algorithm

is supposed to work in a node of camera network where the cost of the computer processing the information

is critical. To achieve a low computing complexity, a basic background subtraction algorithm combined with

a connected component analysis method are used to detect the objects of interest. GMPHD was improved

to detect occlusions between objects and to handle their identities once the occlusion ends. The occlusion

is detected using a low complexity distance criterion that takes into consideration the object’s bounding box.

When an occlusion is noticed, the features of the overlapped objects are saved. At the end of the overlapping,

the extracted features are compared to the current features of the objects to perform the object reidentiﬁcation.

In our experiments two different features are tested: color histogram features and motion features. The exper-

iments are performed on two datasets: PETS2009 and CAVIAR. The obtained results show that our approach

ensures a high improvement of GMPHD ﬁlter and has a low computing complexity.

1 INTRODUCTION

Multi-object tracking is an important step for several

vision applications. It is often used in surveillance

applications for action recognition, behavior analy-

sis (Vezzani et al., 2013; Wang et al., 2003) and au-

tomatic trafﬁc monitoring (Roller et al., 1993). The

multi-object tracking is also used in Advanced Driver

Assistance Systems (ADAS) (Lamard et al., 2012;

Geronimo et al., 2010). Multi-object tracking is a

challenging problem because of the varying number

of objects over time, illumination change, overlap-

ping between objects and varying appearance of ob-

jects (color, dynamic shape, ...). To solve this chal-

lenge several methods were developed and a detailed

survey can be found in (Yilmaz et al., 2006; Vezzani

et al., 2013).

Recently, the development of visual camera net-

work for surveillance applications is increasing and

the challenge to reduce the energy consumption of

these systems is becoming critical. The solution to

this problem is the reduction of the communication

cost between the nodes of the network and the use

of embedded calculators for information processing.

Embedded calculators consume less energy than PCs

but they are limited by their computing resources and

memory. For this reason, developing low complexity

algorithms is highly required. In this case, the best al-

gorithm is the one ensuring the best trade-off between

the tracking quality and the computing complexity.

Objects tracking algorithms can be classiﬁed into

three main categories (Yilmaz et al., 2006): point

tracking, kernel tracking and silhouette tracking.

Both, kernel tracking and silhouette tracking algo-

rithms use visual features (appearance model, con-

tour,...) to achieve the correspondence between the

object instances across frames. These methods are

efﬁcient and can handle partial or/and full occlu-

sions. However, their complexity is high, because

it is related to the number of objects and the num-

ber of pixels processed to extract the visual feature

and to match them. In the other hand, in point

tracking algorithms, the object is represented by one

point and, often, is tracked based only on its motion

(Joint Probability Data Association (JPDA) (Black-

man and Popoli, 1999), Multi-Hypothesis tracking

(MHT) (Blackman, 2004), Gaussian Mixture Prob-

ability Hypothesis Density (GMPHD) (Vo and Ma,

2006)...). The point representation of the objects

causes a less efﬁcient tracking for a visual system

where there is a lot of occlusions between objects.

However, it allows low complexity algorithms.

194

Dziri A., Duranton M. and Chapuis R..

Low Complexity Multi-object Tracking System Dealing with Occlusions.

DOI: 10.5220/0005316701940201

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 194-201

ISBN: 978-989-758-089-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper, we propose a low complexity multi-

object tracking system that can handle occlusions be-

tween objects. To detect the objects of interest we

use a basic background subtraction (BGS) algorithm

and a connected component analysis method to en-

sure a low complexity detection. The detected ob-

jects are then tracked with GMPHD tracker. The

original GMPHD ﬁlter is a point tracker that can-

not handle occlusions. To deal with this problem,

GMPHD were improved to detect and deal with oc-

clusions. This approach is developed to be used in

a node of global surveillance system where several

nodes are connected to each other and where the cost

of each node and its energy consumption should be

minimized.

The section-2 of the paper presents the detection

method. The section-3 reviews the original GMPHD

tracker. In section-4, the related work for occlusion

handling based on GMPHD tracker are discussed.

The section-5 explains our approach dealing with oc-

clusions between objects. Finally, the whole tracking

system is tested with PETS2009 (pets2009, 2009) and

CAVIAR (caviar, 2004) datasets and the results are

compared to the original GMPHD tracker.

2 DETECTION

Detection is the step allowing to localize the objects

of interest in the image plan. It is the part requiring a

lot of computing resources in a vision tracking system

that uses a point tracker. Indeed, to have a low com-

plexity multi-target tracking system, a low complex-

ity detection method is required. A basic background

subtraction method, deﬁned by equations (1) and (2),

is used. The noise is reduced by a morphological ﬁl-

tering. A connected component analysis is performed

on the ﬁltered image and the bounding box, the cen-

troids coordinates and the area of each blob are ex-

tracted. The blobs with an area lower than a deﬁned

threshold are eliminated. The other blobs form the ob-

jects of interest. The centroids coordinates, the height

and the width of the objects constitute the observa-

tions used by GMPHD tracker.

(x, y) = (1−α)BG

k−1

(x, y) +αI

(x, y)

(1)

(x, y) =



1 if |I

(x, y) −BG

k−1

(x, y)| ≥ th

0 if |I

(x, y) −BG

k−1

(x, y)| < th

(2)

and FG

are respectively the background model

and the foreground binary image at time k, I

is the

input image at time k and α is the learning rate of the

background model.

This detection method requires only one gray-

level frame to buildthe backgroundmodel. Compared

to a complex modeling of the background like Gaus-

sian Mixture Model (GMM) where each pixel of the

model is represented by a mixture of Gaussian, the

complexity of the used method is lower. For the con-

nected component analysis efﬁcient implementations

already exist (Ma et al., 2008). The detection quality

of this method remains acceptable for slow illumina-

tion change of the scene.

3 GAUSSIAN MIXTURE

PROBABILITY HYPOTHESIS

DENSITY

GMPHD is an implementation of the Probabil-

ity Hypothesis Density (PHD) ﬁlter developed by

Mahler (Mahler, 2003), for multi-target tracking

(MTT). The PHD ﬁlter is used, in computer vision,

for multi-object tracking (Wang et al., 2006), (Ed-

man et al., 2013) or to improve the objects detection

in videos (Hoseinezhad et al., 2009), (Wu and Hu,

2010).

GMPHD is the implementation of PHD where the

multi-target state is modeled by a Gaussian mixture.

Each track is represented by a Gaussian distribution

that is deﬁned by a weight used to conﬁrm the track,

a mean that describes the state vector of the target,

a covariance matrix and an unique ID that represents

the target’s identity. The advantage of this ﬁlter com-

pared to other methods, is that it allows to track a time

varying number of targets. Furthermore, it manages

the initialization, the maintenance and the termination

of tracks. The track initialization can be caused by a

birth of new targets or by targets spawned from exist-

ing targets. It also takes into account the clutter den-

sity in the surveillance region. The clutter in a vision

tracking system is generally caused by the imperfec-

tion of the detection method (miss detectionsand false

alarms).

The ﬁrst step of GMPHD consists in predicting the

multi-target state based on the previous multi-target

state, i.e, it initializes the new tracks using an initial-

ization model and propagates the existing tracks using

a state model. This step is described by equations (3)

to (7). In the prediction step, new IDs are assigned to

the new tracks and the existing tracks will keep their

IDs. The weight, mean and covariance of the Gaus-

sian components representing new tracks are deﬁned

by the initialization model. The mean and the covari-

ance of Gaussian components representing the exist-

ing tracks are predicted as in Kalman ﬁlter.

LowComplexityMulti-objectTrackingSystemDealingwithOcclusions

195

k|k−1

) =

γ,k

∑

i=1

(i)

γ,k

N (x

k|k−1

(i)

γ,k

, P

(i)

γ,k

)

k−1|k−1

∑

i=1

β,k

∑

j=1

(i)

k−1|k−1

( j)

β,k

N (x

k|k−1

(i, j)

, P

(i, j)

)

+ p

s,k

k−1|k−1

∑

i=1

(i)

k−1|k−1

N (x

k|k−1

(i)

, P

(i)

)

(3)

(i, j)

= F

( j)

β,k

(i)

k−1|k−1

+ d

( j)

β,k

(4)

(i, j)

= Q

( j)

β,k

+ F

( j)

β,k

(i)

k−1|k−1

( j)

β,k

)

(5)

(i)

= F

(i)

k−1|k−1

(6)

(i)

= Q

+ F

(i)

k−1|k−1

(7)

The form GM(x) =

∑

i=1

N (x;m

, P

) represents a

Gaussian mixture. J is the number of Gaussian com-

ponents in the mixture. ω

and P

are respectively

the weight, the mean and the covariance matrix of the

Gaussian component. V

k|k−1

) is the Gaus-

sian mixture modeling the predicted multi-target state

at time k. J

γ,k

, ω

γ,k

, m

γ,k

, P

γ,k

deﬁne the Gaussian mix-

ture modeling the birth of new targets. J

β,k

, ω

β,k

, m

S,k

deﬁne the Gaussian mixture modeling spawned

targets from existing targets. J

k−1|k−1

, ω

k−1|k−1

, P

k−1|k−1

deﬁne the Gaussian mixture mod-

eling the multi-target state at time k. p

s,k

k−1

) is the

probability of the target whose state is x

k−1

at time

k − 1 to survive at time k. F

and Q

describe the dy-

namic model of the targets at time k, and F

(i)

β,k

, d

(i)

β,k

and

(i)

β,k

describe the spawning model at time k. A

is the

transpose of a matrix A.

The second step of GMPHD consists in updat-

ing the multi-target state by using the current obser-

vations. This step is described by equations (8) to

(15). Each Gaussian component representing a pre-

dicted track is expanded to M

+ 1 Gaussian compo-

nents where M

represents the number of observations

at time k. M

of these Gaussian components are the

result of updating the state with the observations. The

other Gaussian component is the result of updating

the track without any observation. This allows to take

into account the miss detection of the target that can

be caused by the detection method. The M

+1 Gaus-

sian components have the same ID as the predicted

track from where they were expanded.

k|k

) =

∑

z∈Z

k|k−1

∑

i=1

(z)

(i)

N (x

(z)

(i)

, P

(i)

)

+ (1− p

D,k

)

k|k−1

∑

i=1

(i)

k|k−1

N (x

(i)

k|k−1

, P

(i)

k|k−1

)

(8)

where

(z)

(i)

D,k

(i)

k|k−1

N (z;m

(i)

, S

(i)

)

(z) + L(z)

(9)

(i)

= H

(i)

k|k−1

(10)

(i)

= R

+ H

(i)

k|k−1

(11)

L(z) = p

D,k

k|k−1

∑

j=1

( j)

k|k−1

N (z;m

( j)

, S

( j)

)

(12)

(z)

(i)

= m

(i)

k|k−1

+ K

(i)

(z− m

(i)

)

(13)

(i)

= [I − K

(i)

k|k−1

(14)

(i)

= P

(i)

k|k−1

(i)

−1

(15)

k|k

) is the Gaussian mixture modeling the up-

dated multi-target state at time k. J

k|k−1

, ω

k|k−1

, P

k|k−1

deﬁne the predicted Gaussian mixture

at time k. Z

is the set of observations at time k.

D,k

) is the probability to detect a target having

the state x

at time k. κ

(.) is the parameter model-

ing clutter density at time k. H

and R

describe the

observation model at time k.

Equations (3) and (8) show that the number of

Gaussian components in the mixture increases from

k−1|k−1

at time k − 1 to J

k|k

= (J

k−1|k−1

(1 + J

β,k

) +

γ,k

)(M

+ 1) at time k. To limit the number of com-

ponents to J

max

, a pruning and merging method was

developed by Vo (Vo and Ma, 2006). This step in-

volves to delete the Gaussian components with low

weights and merge the Gaussian components close to

each other. Mahalanobis distance is used to detect

if two Gaussian components are close to each other.

When several Gaussian components are merged, the

ID of the result will be the ID of the Gaussian compo-

nent with the highest weight. Finally, after the prun-

ing and the merging, only the J

max

Gaussian compo-

nents with highest weights are kept.

In the ﬁnal Gaussian mixture, several Gaussian

components can have the same ID. This happens

when a target splits. The Gaussian component with

the highest weight keeps the ID and all the others will

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

196

receive new IDs (Clark et al., 2006). The Gaussian

components with weights above a deﬁned threshold

(th

estimation

) constitute the conﬁrmed tracks.

GMPHD is a point tracker offering the best trade-

off between the computing complexity and the track-

ing quality (Dziri et al., 2014). However, in a video

tracking scenario, the objects are not points and oc-

clusions between objects can occur. In this case, the

detection method detects only one object and only one

observation is generated. This observation will be

associated to only one of the occluded objects. The

weights of the Gaussian components representing the

other objects decrease very fast and become lower

than the pruning threshold. The tracks of these objects

are, then, pruned and the objects’ IDs are lost. When

the occlusion ends, these objects receive new IDs be-

cause of the splitting, detected in GMPHD. This is

a big limitation for consistent targets labeling. To

solve this problem, several approach were developed.

These approaches are reviewed in the next section.

4 RELATED WORK

To solve the occlusion problem, the authors of (Vi-

jverberg et al., 2009) improved the tracking by ex-

tending the state vector (position and velocity) with

the width and the height of the extracted bounding

box. The second contribution is the use of Fisher cri-

terion instead of Mahalanobis distance in the merging

step of GMPHD. Finally, to handle the occlusion be-

tween targets, occlusion detection is performed after

the prediction step. If the distance between two pre-

dicted Gaussian components is smaller than a deﬁned

threshold, there is a high probability that the observa-

tions of the targets associated to these Gaussian com-

ponents will overlap. In this case, a composed tar-

get is initialized. The composed target contains refer-

ences to the overlapped targets. Both composed target

and overlapped targets are updated in GMPHD. After

the pruning and merging step, an overlapped target

is removed from the composed target if it is too far

from all the other overlapped targets belonging to the

composed target. In the same way, the composed tar-

get is removed if it contains less than two overlapped

targets. Finally, the overlapped targets are merged ir-

reversibly when the weight of the composed target is

higher than the sum of the weights of the overlapped

targets. This approach does not introduce a big over-

head in the complexity of the algorithm. However,

the drawback of this approach is that the weights of

overlapped targets will decrease very fast when there

is no observations generated for them. This leads to

perform an irreversible merging after some frames of

overlapping and to lose the overlapped targets.

The occlusion problem in (Eiselein et al., 2012) is

addressed by using the approach of hypothesis propa-

gation described in (Panta et al., 2009). The approach

of (Panta et al., 2009) uses label trees to ensure a con-

sistent target labeling. Each label represents a unique

physical target. Each branch of a label tree is a possi-

ble state trajectory of the target. The hypothesis prop-

agation is managed as in Track Oriented Multiple Hy-

pothesis Tracking (TOMHT) ﬁlter (Blackman, 2004).

Each label tree is classiﬁed as conﬁrmed or tentative

and the N-scan pruning procedure is used to limit the

number of hypothesis. The score used in hypothesis

propagation is based on the weight of tracks. In each

branch, the track with the highest score is selected to

form the target trajectory. When an occlusion occurs

between two targets, both states will exist in both la-

bel trees. The score computed with Log-Likelihood

Ratio (LLR) is propagated from time k − 1 to time k

to rank the tracks. When the occlusion ends, the track

with the highest score is selected in each label tree.

The authorsof (Eiselein et al., 2012) adopted the same

approach for a vision system. They contributed by

using an appearance feature (color histogram) to rank

the tracks when an overlapping occurs. Indeed, if two

targets are close to each other, they will be considered

overlapped and the N-scan pruning procedure is dis-

abled. At that time, both states will exist in both label

trees and histogram matching will be used to compute

the score. When the targets get far from each other,

the track with highest score is selected in each label

tree. The method is interesting for vision tracking

since it allows the use of image features (color, tex-

ture, ...) to handle objects overlapping in GMPHD.

However, it has the same drawbacks as the TOMHT

approach where the complexity increases rapidly with

the occlusion time and the number of hypothesis.

The authors of (Lamard et al., 2012) perform ob-

jects tracking in real world coordinate using Gaussian

Mixture Cardinalized PHD (GMCPHD) ﬁlter. They

use the image information to detect occlusions. After

prediction, targets are projected from the real world

to the image plan. If an overlapping between targets

is noticed in the image, the detection probability is

modeled in GMCPHD to take that into consideration.

This allows to have both targets when occlusion oc-

curs and to reidentify the targets when the occlusion

ends, if they did not change their directions. How-

ever, this method requires camera calibration which is

not always possible. Additionally, the image features

cannot be exploited in the reidentiﬁcation process.

LowComplexityMulti-objectTrackingSystemDealingwithOcclusions

197

5 OUR APPROACH

To deal with occlusion between objects we extend the

original GMPHD tracker, presented in section-3, by

occlusion detection module and objects reidentiﬁca-

tion module, as shown in the ﬁgure 1. The occlusion

Figure 1: Schematic diagram of the improved GMPHD

tracker.

detection module consists in computing a distance be-

tween the predicted Gaussian components represent-

ing active targets. We consider a target as active if the

weight of its Gaussian component is above the esti-

mation threshold th

estimation

, for more than N succes-

sive frames. If the distance between the predictions

of active targets is lower than a deﬁned threshold,

the active targets are considered overlapping. In this

case, the weights, means and covariance matrices of

the Gaussian components are merged using the merg-

ing method described in section-3 to form a composed

target. All the targets’ IDs are kept in the composed

target. Furthermore, features from each target are ex-

tracted and saved in the composed target to allow a

correct reidentiﬁcation when the occlusion ends, i.e.

assign the right ID to the right target. Several features

can be extracted from the objects, to choose the ap-

propriate features the reader is invited to see (Vezzani

et al., 2013). Finally, in the image plan, an occluded

target is represented by one rectangle containing sev-

eral IDs and is deﬁned by its centroid coordinates,

width and height. To incite the split of the composed

target, the standard deviation of the coordinates x and

y of the state vector are increased. This allows to en-

large the area where the observations, generated by

the objects resulting from the split, appear.

The distance used to detect objects overlapping is

the distance between two rectangles, described in ﬁg-

ure 2. When an overlapping occurs between two rect-

angles the distance is equal to zero. In cases where

rectangles do not overlap the distance is equal to the

minimum Euclidean distance between the points of

the rectangles. The choice of this distance is due to

the model of objects represented by rectangles. Fur-

thermore, this distance has more physical meaning, in

this case, than Mahalanobis distance or Fisher crite-

rion used in (Vijverberg et al., 2009). It also uses sim-

ple operations which makes it a low complexity dis-

tance. The composed targets and all the other tracks

undergo the update and pruning steps of the original

GMPHD ﬁlter. To avoid losing targets because of the

merging step, i.e merge two active targets and keep

Figure 2: Distance between two rectangles.

only one ID, we only merge the non-active targets.

GMPHD tracker (section-3) allowsthe association

of one track to several observations when an object

splits. The objects corresponding to these observa-

tions will have the same ID. When this happens, the

object represented by the Gaussian component with

the highest weight keeps its ID and the other objects

receive new IDs. In our approach, this is true only

when the split target is not a composed target, i.e.

the split target have only one ID. Indeed, if two or

more objects have the same set of IDs and the num-

ber of IDs in each track is greater than one, it means

that a composed target is split into several targets and

that the occlusion ended. In this case, the reidenti-

ﬁcation module compares the saved features to the

new features, in order to assign the right ID to the

right object. For example, assume that a color his-

togram is used as features and can be extracted by

the detection method for each detected object. When

an occlusion is detected between several objects, the

histogram of the objects are extracted. These objects

are merged in global object and their histograms are

saved. When the occlusion ends, several composed

objects will have the same set of IDs. The histogram

given by the detection method for each objects is com-

pared to the features saved in the composed object

using Euclidean distance. The ID associated to the

feature allowing the smallest distance is assigned to

the object, and this ID is deleted from all the other

composed objects.

If a composed object contains more than two oc-

cluded objects, when the occlusion ends, the object

with the big bounding box will contain the largest

number of IDs. For example, if three objects over-

lap and if the global object split into two objects, the

one with the big bounding box keeps two IDs and the

other takes the ID given by the re-identiﬁcation mod-

ule.

Our approach can be used independently on the

detection method and it is not constrained by the type

of features. The image features and the matching dis-

tance in the object reidentiﬁcation module can be se-

lected by the user depending on the reidentiﬁcation

rate and the computing resources allowed for a given

tracking scenario. Our approach uses the image fea-

tures only when it is required. Indeed, as the use of

image features requires considerable computing re-

sources, our approach optimizes the use of these fea-

tures to allow a low complexity multi-object tracking,

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

198

200 300 400 500 600 700 800

Number of objects

frame

detection

GMPHD tracker

our approach

ground truth

Figure 3: Number of objects estimated over time for PETS2009 dataset. The markers are shifted for the different approaches

for readability purpose.

i.e, the image features are only used when there is oc-

clusion between objects.

6 RESULTS

In this section, our approach is compared to GMPHD

tracker presented in section-3 and the improvements

obtained are evaluated. The state vector, in both ap-

proaches, contains the position and the velocity coor-

dinates of the object. The width and the height of the

objects are deﬁned by the detection method.

Tracking systems are evaluated based on the fol-

lowing functionalities:

1. The ability of estimating the correct position of

objects

2. The ability of estimating the correct number of

objects in each frame

3. The ability of ensuring consistent labeling of ob-

jects over time, i.e. assign a unique ID for each

object and keep this assignement over the track-

ing.

The functionalities (1) and (2) depend on both detec-

tion and tracking methods. However, functionality (3)

is only related to the tracking method. Indeed, our im-

provement will affect the functionalities (2) and (3)

when objects overlapping occurs. Our approach does

not change the way that the position of objects is es-

timated, the estimation is the same as the one of GM-

PHD tracker. Because of that, the functionality (1) is

not discussed.

Our approach is evaluated using the sequence

S2L1-view1 of PETS2009 dataset (pets2009, 2009)

where several humans (the maximum at the same

time is 9) walk in the scene and several occlu-

sions happen between them. The second sequence

is Meet

WalkTogether1 of CAVIAR dataset (caviar,

2004) where two humans meet and walk together.

The tracking is performed from frame 201 to 700 in

PETS2009 dataset. The 200 ﬁrst frames were used

to initialize the background model. For CAVIAR

dataset, the tracking is performed on the frames 1250

to 1450. The frame 1000 to 1250 are used to initialize

the background model.

240 260280 300 320 340360 380 400 420 440460

Number of objects

frame

detection

GMPHD tracker

our approach

ground truth

Figure 4: Number of objects estimated over time for

CAVIAR dataset. The markers are shifted for the different

approaches for readability purpose.

Firstly, the accuracy of our method in estimating

the number of objects in the ﬁeld of view (FoV) of the

camera is evaluated and compared to the ground truth.

The ground truth is manually evaluated by counting

the number of humans in each frame. As the num-

ber of estimated objects is directly related to the de-

tector quality, both number of detected objects and

estimated objects are given in ﬁgures 3 and 4. The

number of objects in each frame is estimated on both

datasets with both methods.

Figures 3 and 4 show that our method estimates

LowComplexityMulti-objectTrackingSystemDealingwithOcclusions

199

well the number of objects in FoV of the camera and

outperforms GMPHD tracker. Indeed, even if the de-

tector does not return the correct number of objects

in the frame because of the occlusion, our method

can handle that and gives the right number of ob-

jects. This is due to the occlusion detection module.

The error in estimating the number of objects in the

frames 506 to 540 of the PETS2009 dataset is because

two objects entered the FoV already occluded. When

the occlusion ends, the corrected number of object is

estimated. The number of object estimated by both

methods is not correct in the frames 690 to 790 of

PETS2009 dataset. This is because the human open-

ing the trunk of the car present in the scene is very

small to be detected.

The performance of ﬁnding the correct ID of each

object, after an occlusion, is evaluated by counting

the number of times that the object’s ID changes for

each real object over the tracking. When an object

leaves the scene and enters again, it is considered as a

new object. As each object is represented by a unique

ID, the less the object’s ID changes, the most efﬁcient

the tracking algorithm is. This is evaluated on both

datasets and two different features are tested: color

histogram and motion feature. The results obtained

are compared to GMPHD tracker. There are seven-

teen objects, in PETS2009 sequence and two objects

in CAVIAR sequence.

The color histogram feature is used as explained

in the example of section-5. The use of motion fea-

ture involves to save in the composed target the state

vectors of occluded objects. At each time iteration,

these features undergo the prediction step of GM-

PHD. When the composed target splits, the motion

direction is used to reidentify the objects. The direc-

tion can be deduced from the sign of velocity coordi-

nates of the state vector. Indeed, if two objects cross

each other, their velocity coordinates will have differ-

ent sign. In this case, the split object will get the ID

corresponding to the feature having the same velocity

sign. When the overlapped objects have the same di-

rection, the velocity sign is not enough to reidentify

them correctly. In this case, the Euclidean distance

between their positions is used. The ID corresponding

to the feature with the smallest distance is assigned to

the object.

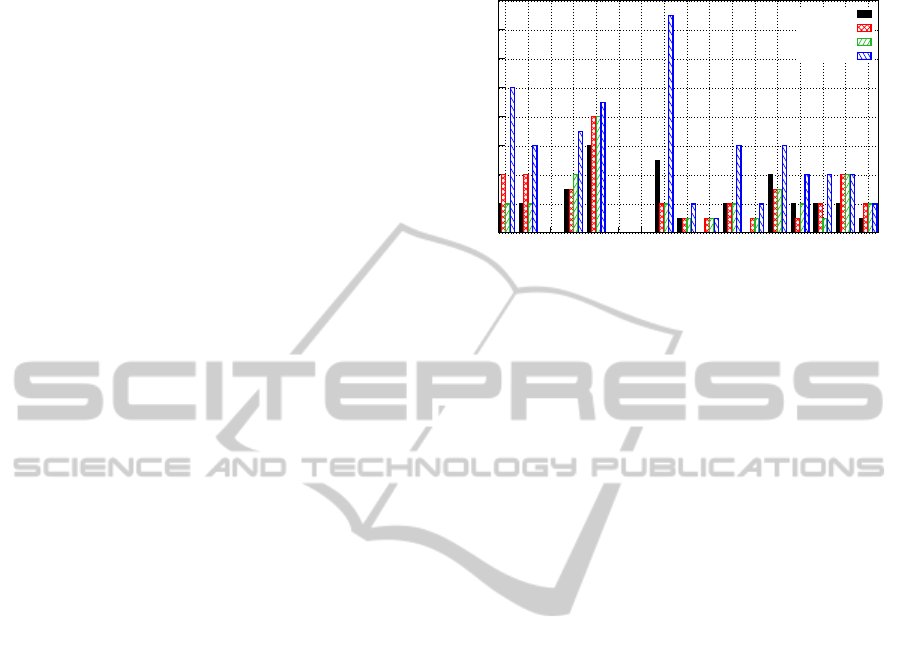
Figure 5 shows the number of times that the ob-

ject’s ID change in the PETS2009 dataset. The num-

ber of change per object is high in GMPHD tracker.

This number is reduced, using our approach. The mo-

tion feature performs better than the color histogram

because, in this dataset, the color of the cloths is not

very different from one human to another. Using 256

bins per channel, in the color histogram, allows more

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Number of times that the ID changed

Real object

motion feature

color 8 bins

color 256 bins

GMPHD tracker

Figure 5: Object’s ID change in PETS2009 dataset. Color

8 bins: the RGB histogram with 8 bins per channel. Color

256 bins: the RGB histogram with 256 bins per channel

robust reidentiﬁcation than the case where only 8 bins

are used per channel. Even with our approach, the

number of the objects’ ID change is not zero. Indeed,

a lot of changes are caused by miss detection, when

the objects are occluded by the environment, typically

the light pole in the middle of the scene. GMPHD

tracker has an average of 4.58 change of ID per ob-

ject. However, our method achieve an average of 1.89

with the motion feature and 2 with the color histogram

256 bins.

The same experiment is performed on CAVIAR

dataset. Using GMPHD tracker, the ﬁrst object

changes its ID 2 times and the second 4 times. With

our approach, this change is reduced to zero for both

objects independently on the used features.

Several examples of images are presented in ﬁg-

ure 6. In each example, the states: before occlusion,

during occlusion and at the end of the occlusion are

showed for our approach and for GMPHD tracker.

Concerning the complexity of the algorithm, our

tracking system is implemented using C language.

Using the motion feature on PETS2009 dataset with

an image resolution of 768 × 576, the whole multi-

object tracking system (detection + tracking + occlu-

sion handling) exceeds 60 fps on a core 2 duo PC run-

ning at 3 GHz. These results are very promising for

an embedded implementation on low cost computer

architecture.

7 CONCLUSION

In this paper, we presented a low complexity multi-

object tracking algorithm that can be used in a node

of a global tracking system to ensure a low cost sys-

tem. Our approach is based on GMPHD ﬁlter and can

handle the occlusion between objects. The obtained

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

200

Figure 6: Examples of tracking.

results on PETS2009 and CAVIAR datasets show that

our approach offers a high improvement in estimat-

ing the number of objects and in ensuring a consistent

targets labeling over time, compared the original GM-

PHD. Furthermore, our approach exceeds 60 fps on a

PC. This makes it a good candidate for an embedded

implementation.

The future work consists in implementing our

method on an embedded processor with low comput-

ing resources connected to an image sensor in order

to form a smart camera. The idea is to extend our

approach to a network of smart cameras.

REFERENCES

Blackman, S. (2004). Multiple hypothesis tracking for mul-

tiple target tracking. Aerospace and Electronic Sys-

tems Magazine, IEEE, 19(1):5–18.

Blackman, S. and Popoli, R. (1999). Design and Analysis of

Modern Tracking Systems. Artech House, Norwood,

MA.

caviar(2004). http://homepages.inf.ed.ac.uk/rbf/caviardata1.

Clark, D., Panta, K., and Vo, B.-N. (2006). The gm-phd

ﬁlter multiple target tracker. In Information Fusion,

2006 9th International Conference on, pages 1–8.

Dziri, A., Duranton, M., and Chapuis, R. (2014). Low com-

plexity multi-target tracking for embedded systems.

In Information Fusion (FUSION), 2014 17th Interna-

tional Conference on, pages 1–8.

Edman, V., Maria, A., Granstr¨om, K., and Gustafsson, F.

(2013). Pedestrian group tracking using the gm-phd

ﬁlter. In Proceedings of the 21st European Signal Pro-

cessing Conference :.

Eiselein, V., Arp, D., Patzold, M., and Sikora, T. (2012).

Real-time multi-human tracking using a probability

hypothesis density ﬁlter and multiple detectors. In Ad-

vanced Video and Signal-Based Surveillance (AVSS),

2012 IEEE Ninth International Conference on, pages

325–330.

Geronimo, D., Lopez, A., Sappa, A., and Graf, T. (2010).

Survey of pedestrian detection for advanced driver as-

sistance systems. Pattern Analysis and Machine Intel-

ligence, IEEE Transactions on, 32(7):1239–1258.

Hoseinezhad, R., Vo, B.-N., and Suter, D. (2009). Fast

single-view people tracking. In Cognitive Systems

with Interactive Sensors (COGIS2009).

Lamard, L., Chapuis, R., and Boyer, J.-P. (2012). Dealing

with occlusions with multi targets tracking algorithms

for the real road context. In Intelligent Vehicles Sym-

posium (IV), 2012 IEEE, pages 371–376.

Ma, N., Bailey, D., and Johnston, C. (2008). Optimised sin-

gle pass connected components analysis. In ICECE

Technology, 2008. FPT 2008. International Confer-

ence on, pages 185–192.

Mahler, R. (2003). Multitarget bayes ﬁltering via ﬁrst-order

multitarget moments. Aerospace and Electronic Sys-

tems, IEEE Transactions on, 39(4):1152–1178.

Panta, K., Clark, D., and Vo, B.-N. (2009). Data association

and track management for the gaussian mixture prob-

ability hypothesis density ﬁlter. Aerospace and Elec-

tronic Systems, IEEE Transactions on, 45(3):1003–

1016.

pets2009 (2009). http://cs.binghamton.edu/ mrl-

data/pets2009.html.

Roller, D., Daniilidis, K., and Nagel, H. (1993). Model-

based object tracking in monocular image sequences

of road trafﬁc scenes. International Journal of Com-

puter Vision, 10(3):257–281.

Vezzani, R., Baltieri, D., and Cucchiara, R. (2013). People

reidentiﬁcation in surveillance and forensics: A sur-

vey. ACM Comput. Surv., 46(2):29:1–29:37.

Vijverberg, J. A., Koeleman, C. J., and With, P. H. N. d.

(2009). Tracking rectangular targets in surveillance

videos with the gm-phd ﬁlter. In Proceedings of

the 30-th Symposium on Information Theory in the

Benelux, pages 177–184.

Vo, B.-N. and Ma, W.-K. (2006). The gaussian mixture

probability hypothesis density ﬁlter. Signal Process-

ing, IEEE Transactions on, 54(11):4091–4104.

Wang, L., Hu, W., and Tan, T. (2003). Recent develop-

ments in human motion analysis. Pattern Recognition,

36(3):585 – 601.

Wang, Y.-D., Wu, J.-K., Kassim, A., and Huang, W.-M.

(2006). Tracking a variable number of human groups

in video using probability hypothesis density. In Pat-

tern Recognition, 2006. ICPR 2006. 18th Interna-

tional Conference on, volume 3, pages 1127–1130.

Wu, J. and Hu, S. (2010). Phd ﬁlter for multi-target visual

tracking with trajectory recognition. In Information

Fusion (FUSION), 2010 13th Conference on, pages

1–6.

Yilmaz, A., Javed, O., and Shah, M. (2006). Object track-

ing: A survey. ACM Comput. Surv., 38(4).

LowComplexityMulti-objectTrackingSystemDealingwithOcclusions

201