A New Kernel for Outlier Detection in WSNs Minimizing MISE

Rohit Jain, C. P. Gupta and Seema Sharma

Department of Computer Science and Engineering, Rajasthan Technical University, Kota, India

Keywords: Kernel, Kernel Density Estimation, Mean Integrated Squared Error, Outlier Detection.

Abstract: In sensor network, data generated by various sensors deployed at different locations need to be analyzed in

order to identify interesting events correspond to outliers. The presence of outliers may distort contained

information. To ensure that the information is correctly extracted, it is necessary to identify the outliers and

isolate them during knowledge extraction phase. In this paper, we propose a novel unsupervised algorithm

for detecting outliers based on density by coupling two principles: first, kernel density estimation and

second assigning an outlier score to each object. A new kernel function building a smoother version of

density estimate is proposed. An outlier score is assigned to each object by comparing local density estimate

of each object to its neighbors. The two steps provide a framework for outlier detection that can be easily

applied to discover new or unusual types of outliers. Experiments performed on synthetic and real datasets

suggest that the proposed approach can detect outliers precisely and achieve high recall rates which in turn

demonstrate the potency of the proposed approach.

1 INTRODUCTION

Tremendous growths in wireless sensor network

technology have enabled the decentralized processing

of enormous data generated in network, scientific and

environmental sensing applications at low

communication and computational cost. Generated

sensor data may pertain to physical phenomenon

(like temperature, humidity, and ambient light),

network traffic, spatiotemporal data about weather

pattern, climate change or land cover pattern etc.

Availability of vast amount of sensor data and

imminent need for transforming such data into true

knowledge or into useful information require

continuous monitoring and analysis as they are

highly sensitive to various error sources. True

knowledge provides useful application-specific

insight and gives access to interesting patterns in

data; the discovered pattern can be used for

applications such as fraud detection, intrusion

detection, earth science etc. Sudden changes in the

underlying pattern may represent rare events of

interest or may be because of errors in the data.

Outlier detection refers to detecting such abnormal

patterns in the data.

Several definitions have been proposed, but none

of them is universally accepted because, the

measures and definition of outliers vary widely.

Barnett et al. (Barnett and Lewis 1994) defined

outliers as “an observation or subset of observations

which appears to be inconsistent with the remainder

of that set of data”.

Outliers may arise due to fraudulent behavior,

human error, malfunctioning or injection in sensing

devices, faults in computing system and uncontrolled

environment. Outlier shows deviation from normal

behavior. Declaration of outlier based on observed

deviation in the values is a subjective judgement and

may vary depending upon application.

Several approaches for detecting outliers have been

proposed (Chandola, Bannerjee and Kumar 2009;

Hodge and Austin 2004; Gupta, Aggarwal and Han

2013). Techniques for outlier detection can be

classified as either statistical approach (Knorr and

Raymond 1997), distance based approaches, density

based approaches, profiling methods, or model based

approaches. In statistical approach, data points are

first modeled using stochastic distribution, and then

are labeled as outliers based on their fitness with the

distribution model. An outlier score is assigned to

each object based on their nearest neighbor distances

by distance based outlier detection technique. In

density based approach, an outlier score is computed

by comparing the local density estimate of each

object to the local density estimate of its neighbors,

and the objects are flagged as outliers based on their

169

Jain R., Gupta C. and Sharma S..

A New Kernel for Outlier Detection in WSNs Minimizing MISE.

DOI: 10.5220/0005318401690175

In Proceedings of the 4th International Conference on Sensor Networks (SENSORNETS-2015), pages 169-175

ISBN: 978-989-758-086-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

outlier score. In profiling methods, different

techniques of data mining are used to build profiles

of normal behavior, and deviations from these

underlying profiles are flagged as outliers. In model-

based approaches, first, by using some predictive

models, the normal behavior is characterized, and

then the deviations from the normal behavior are

flagged as outliers.

In this paper, we propose an outlier detection

algorithm combining statistical and the density based

approaches. Our proposed approach uses kernel

density estimators to approximate the data

distribution and then computes the local density

estimate of each data point, and thus detects potential

outliers. Experiments performed on both synthetic

and real data sets shows that the proposed approach

can detect outliers precisely and achieve high recall

rates, which in turn demonstrate the potency of the

proposed approach.

Rest of the paper is organized as follows: Section

II describe the literature review of the work. Section

III explains the kernel density estimators. Section IV

presents the proposed work. Section V provides the

discussion on results. Section VI concludes the work.

2 RELATED WORK

Breunig et al. (Breunig, Kriehel, Raymond and

Sander 2000) introduced Local Outlier Factor (LOF)

for detecting outliers in a multidimensional dataset.

In the proposed scheme, local density estimate of

each object were compared with average density

estimate for MinPts-nearest neighbors. The resulted

density ratio was referred as local outlier factor.

Local outlier factor was computed in order to

determine the physical location of each object in

feature space. An object lied deep inside a cluster

when its local outlier factor was approximately 1

whereas an object that got higher value of local

outlier factor corresponds to low neighborhood

density. An object with higher local outlier factor

was flagged as an outlier. The proposed method was

free from local density problem but dependent on the

choice of MinPts.

Local Outlier Correlation Integral (LOCI)

(Papadimitriou, Kitagawa, Gibbons and Faloutsos

2003) was based on the concept of multi-granularity

deviation factor (MDEF) and dealt with both local

density and multi-granularity successfully. The

scheme had lower sensitivity to chosen parameters.

The proposed scheme strictly relied on counts and

needed to test arbitrary

radii

−

. An automatic,

data-dedicated cut-off was provided to determine

whether a point is an outlier. In the proposed scheme,

MDEF was computed for each data point in feature

space. A data point with MDEF of 0 signified that it

got neighborhood density equal to average local

neighborhood density whereas a data point with large

MDEF was flagged as an outlier.

A variant of LOF was proposed by Latecki et al.

(Latecki, Lazarevic, Pokrajac 2007) combining the

LOF and kernel density estimation in order to utilize

the strength of both in density based outlier detection,

which was referred as outlier detection with kernel

density function. In this approach, first, a robust local

density estimate was generated with kernel density

estimator and then by comparing the local density

estimate of each data point to the local density

estimate of all of its neighbors, the outliers were

detected. Local density factor (LDF) is computed for

each data point in feature space and the data points

with higher LDF values were flagged as outliers.

Kriegel et al. (Kriegel, Kröger, Schubert Zimek

2009) proposed a method for local density based

outlier detection referred as Local Outlier Probability

(LoOP) which was more robust to the choice of

MinPts. The proposed method combined the local

density based outlier scoring with probability and

statistics based methods. An outlier probability in the

range of (0, 1) was assigned to each data point as

outlier score signifying severity of outlierness. More

specifically, higher the outlier score meant more

severe a point to be declared as outlier.

Most of the density based outlier detection

methods were bounded to detect specific type of

outliers. Schubert et al. (Schubert, Zimek, Kriegel

2014) proposed a general framework for density

based outlier detection referred as KDEOS and could

be adjusted to detect any specified types of density-

based outliers. In KDEOS, the density estimation and

the outlier detection steps were decoupled in order to

maintain the strength of both.

Several Non-parametric estimators were

presented in (Zucchini, Berzel, Nenadic 2005).

Histogram was the simplest non-parametric estimator

used for density estimation but generated density

estimates were highly dependent on the starting point

of bins. Kernel Density Estimators (Aggarwal 2013;

Silverman 1986) were used as an alternative to

histograms. KDE were superior in terms of accuracy

and hence, had attracted a great deal of attention. A

smoother version of density profile was constructed

by kernel density estimator.

Sheng et al. (Sheng, Li, Mao and Jin 2007)

introduced Outlier Detection in Wireless Sensor

Network based on histogram method to detect

distance based outliers. In the proposed method, to

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

170

filter out unnecessary observations correspond to

potential outlier the collected hints about data

distribution are modeled as histogram.

The problem associated with unsupervised outlier

detection in WSN was addressed by Branch et al.

(Branch, Giannella, Szymanski, Wolf and Kargupta

2013). The proposed algorithm for outlier detection

was generic evidenced by its suitability to various

outlier detection heuristics and it does not require, for

a data source, any prior assumption about global

model.

Kernel density estimation was coupled with the

various outlier detection methods in order to build a

framework for detecting density based outliers and

the resulted quality of density based outlier detection

was improved. Outlier score is dependent on the

choice of approach used to detect outliers. Several

approaches are used for detecting outliers using

kernel density estimation. In all these schemes, the

density estimate is constructed with previously

available kernel functions (Zucchini, Berzel, Nenadic

2005). Most of these works considered performance

measure for outlier detection while ignoring accuracy

of density estimate. We propose a kernel function

that can improve the accuracy of the density estimate

quantified by Mean Integrated Squared Error

(MISE), and then incorporate these density estimates

in the computation of outlier score in order to

improve the efficiency of outlier detection method.

3 KERNEL DENSITY

ESTIMATOR

Kernel density estimators belong to non-parametric

(Zucchini, Berzel, Nenadic 2005) class of density

estimators. The non-parametric estimators

incorporate all data points to reach an estimate.

Contribution of each data point in an estimate is

smoothed out by kernel estimator. Kernel density

estimators place a kernel K on each data point

the sample. Let, x

, x

,…,x

be the sample of size

and dimensionality

dim which are identically and

independently distributed according to some

unknown density

()

x . Expected density

estimate

()

is the convolution of true unknown

density

()

x with kernel

is computed as follows:

()

dim

fx K

nhx

−

∑

⎛⎞

⎜⎟

⎝⎠

(1)

where,

is a non-negative, real-valued kernel

function of order-

(degree of polynomial), and

()hx

is the bandwidth applied at each data point

A univariate kernel function

of order-2 must

satisfy the requirements of (i) unit area under the

curve, 9ii) symmetry, (iii) zero odd moments, and

(iv) finite even moments.

Quality of estimated density is determined by the

choice of both the smoothing parameter and the

kernel. A kernel may exhibit either finite or infinite

support. A kernel with finite support is considered as

optimal. The accuracy of the kernel is quantified by

Mean Integrated Squared Error (MISE) (Marron and

Wand 1992). The MISE between the estimated

density

()

x and the actual density ()

x is

computed using:

1/5

24 4/5

(, ) ( ) ( )( '')

MISE f f K R K R f n

−

⎡⎤

⎣⎦

(2)

In other words,

1/5

() ()

MISE K R K

αμ

⎡

⎤

⎣

⎦

where,

(K) K (u)Rdu=

∫

is the roughness,

(K) (u)

u du

∫

is second moment of

K(u) and

is second derivative of f.

4 PROPOSED WORK

1. Kernel Function

We propose a kernel function of order-2 as follows:

()

32 3/2

1.56

forKuu

proposed h

=− <

(3)

It satisfies all the requirements of being a kernel

function which are described below:

(i)

Area under Curve

()

3/2

.32

1.56

3/2

duKudu u

=−

∫∫

−

3/2

1.56 3

=− =

⎡⎤

⎢⎥

⎣⎦

(ii)

Symmetry

() ( )

uKu=−

(iii)

Odd Moment

()

3/2

1.56

3/2

uK u du u u du

=−

∫∫

−

ANewKernelforOutlierDetectioninWSNsMinimizingMISE

171

3/2

13 2

1.56 2 4

3/2

=−=

−

⎡⎤

⎢⎥

⎣⎦

(iv)

Even Moment

()

uKudu

∫

()

3/2

1.56

3/2

uudu

=−

∫

−

3/2

13 2

1.56 3 5

3/2

=−

−

⎡⎤

⎢⎥

⎣⎦

0.2999=

(v)

Roughness

()

udu

∫

()

3/2

1.56

3/2

32 duu

∫

−

⎛⎞

−

⎜⎟

⎝⎠

23/2

1412

1.56 5 3

uu u

=+−

⎛⎞⎡ ⎤

⎜⎟

⎢⎥

⎝⎠⎣ ⎦

0.4899=

2. Outlier Detection

Outlier detection using kernel density estimation

involves two principled and clear steps, which are

described as follows:

Step 1: Density Estimation- In this step, the density

estimate is constructed with a non-parametric

estimator which is superior in terms of accuracy is

the kernel. The kernel function is taken as an input

parameter to the algorithm. We will use our

proposed kernel function of bandwidth

and

dimensionality

for density estimation:

1.56

proposed h

=−

⎛⎞

⎜⎟

⎝⎠

(4)

The balloon estimator (Branch, Giannella,

Szymanski, Wolf and Kargupta 2013) is:

() ( ).

,()

DE o K o p

balloon h h o

=−

∑

(5)

In our approach, we will use balloon estimator

for constructing the density estimates because it

optimizes

ISE

pointwise (Terell and Scott 1992).

The smoothing parameter applied to the data

controls the smoothness of the constructed density

estimate. A nearest-neighbor distance (Loftsgaarden

and Quesenberry 1965) is a classic approach to

calculate local kernel bandwidth. Sheather and Jones

(Sheather and Jones 1991) proposed a data-driven

procedure for selecting the kernel bandwidths

known as “plug-in bandwidth estimator”. To prevent

from division by 0 we

use

() min{ ( , ),}ho mean d po

pkNN

∈

Selection of parameter

is non-trivial. In our

proposed scheme, instead of choosing a single value

a range of

......

max

min

kk k=

is employed that

produces a series of density estimate, one for each

The proposed scheme is elegant, computationally

efficient, and produces stable and reliable results.

Step 2: Density Comparison- In this step, the local

density estimate of each object

is compared to the

local density estimate of all of its nearest

neighbors

()pkNNo∈ . Let,

be the local density

estimate and

(, )Nok be the number of objects in

the

-neighborhood of object

. The resulted

density ratio which is referred as Local Outlier

Factor (LOF) is computed using:

()

(, )

pkNNo

LOF o

Nok

∑

∈

(6)

An LOF value corresponding to each value of

min max

...kk

is computed and then mean of LOFs is

taken over the range in order to produce more

stabilized LOF value for each object

score−

Transformation is utilized to standardize the outlier

scores and objects with

3Zscore−≥

are declared

outliers.

5 RESULTS

1. Kernel Density Estimator

Table 1 shows statistics and comparison of our

proposed kernel against various previously available

kernel functions. Our proposed kernel function has

minimum

ISE . The value of efficiency is relative

efficiency computed using

() ()

{

}

ˆˆ

using using

ISE f K MISE f K

opt proposed opt

For example, the efficiency of Gaussian kernel is

approximately 96%. That is the

()

ISE f

opt

obtained using proposed kernel function with

96n =

is approximately equal to the

()

ISE f

opt

obtained using a Gaussian kernel function

with 100

n = .

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

172

Table 1: statistics and comparison of various kernel

functions.

Kernels

()

MISE Efficiency

Proposed

0.4899 0.2999 0.34904

Epanechnikov

35 15

0.34908

0.9998

Biweight

57 17

0.35079

0.9950

Triangular

23 16

0.35307

0.9885

Gaussian

0.36341 0.9604

Box

12 13

0.37010

0.9430

Figure 1: Analysis of statistical properties.

Figure 1 shows the variation of statistical properties

of the proposed KDE with bandwidth. Bias and

variance, the two subcomponents of prediction

errors are unable to give appropriate understanding

about prediction model behavior as there is always a

tradeoff between bias and variance. So, instead of

relying on specific decomposition (viz. bias and

variance) we relied on overall error that takes into

account both the sources of error i.e. error due to

bias and variance (Zucchini, Berzel, Nenadic 2005).

The optimal point drew in figure 1 refers to the

optimal bandwidth

opt

at which the overall error is

minimized.

Figure 2 reflects the bias effects for a kernel

density estimate.

Figure 2: Visualization of bias effects.

2. Kernel Density Estimation and Outlier Detection

Datasets:

To evaluate the proposed kernel and

outlier detection method, experiments were carried

out on real as well as synthetic datasets. In our

experiments, we used two real datasets.

Figure 3: Density estimate constructed from old faithful

geyser data

0.25h =

Figure 4: Density estimate constructed from Intel Lab

data

0.5h =

The first dataset contains the data about

eruptions of old faithful geyser taken from

Weisberg (1980) and the second datasets

contains the data about temperature, humidity,

light, and voltage collected between February

28th and April 5th, 2004 from 54 Mica2Dot

motes deployed in the Intel Berkeley Research

Lab (Intel Lab Data).

(i) Evaluation of Outlier Detection Technique: We

have applied the kernel density estimation step

to approximate the density at various kernel

points. Figures 3 and 4 shows the density

estimate constructed from the observations of

eruptions of old faithful geyser and Intel lab

data.

These density estimates are incorporated in

outlier detection method to calculate Local Outlier

Factor (LOF) of each data point present in the

particular dataset. Computed LOF values will

expose the indices of potential outliers. We have

ANewKernelforOutlierDetectioninWSNsMinimizingMISE

173

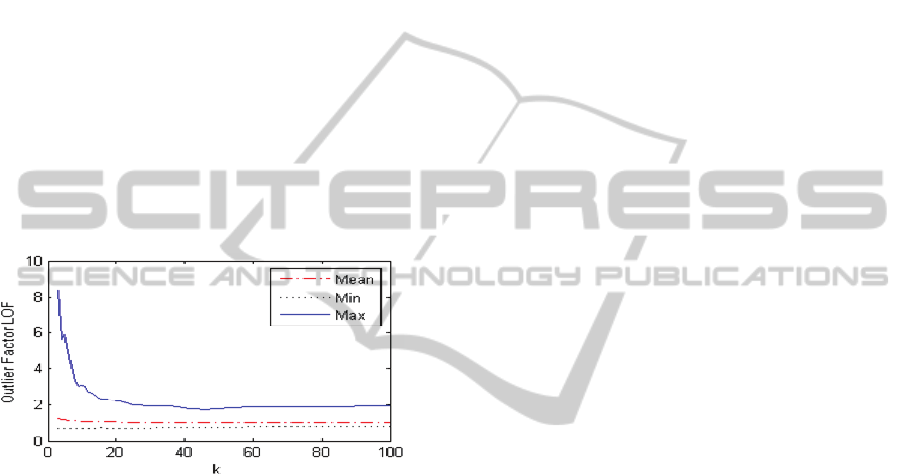
also applied both of these steps to the synthetic

datasets and have evaluated the impact of

kvalues−

on LOF. Figure 5 shows the impact of

k value−

on Local Outlier Factor (LOF). It

demonstrates a simple scenario where the data

objects belong to a Gaussian cluster i.e. all the data

objects within a cluster follows a Gaussian

distribution. For each

k value−

ranging from 3 to

100, the mean, minimum and maximum LOF values

are drawn. It can be observed that, with

increasing

k value−

, the LOF neither increases nor

decreases monotonically. For example, as shown in

Figure 5, the maximum LOF value is fluctuating as

k value−

increases continuously and eventually

stabilizes to some value showing that a single value

is inefficient to produce a more accurate LOF

value. So, mean of LOFs is taken over the range of

......

max

min

kk k=

in order to produce more

stabilized LOF values. These are shown in Figure 5.

Figure 5: Fluctuation of outlier factors within a Gaussian

cluster.

6 CONCLUSIONS

In this paper, we have proposed a symmetric and

computationally efficient kernel of order-2. Our

proposed kernel obtained lower MISE than the

previously available kernels and hence, produced a

more accurate density estimate. We have also

proposed an outlier detection method that uses our

proposed kernel function in order to construct density

estimates. We have decoupled the density estimation

and the local density based outlier detection steps in

order to preserve the strength of both. As a

consequence, the resulted framework can be easily

adjusted to any application-specific environment.

Experiments performed on both real and synthetic

datasets indicate that the proposed techniques can

detect outliers efficiently. As future work, we will be

focusing on classification of transient faults in

wireless sensor networks using outlier scores.

REFERENCES

Aggarwal C. C., 2013. Outlier analysis, Springer,

doi:10.1007/978-1-4614-6396-2.

Barnett, V. and Lewis, T., 1994. Outliers in statistical

data, Wiley, vol. 3, New York.

Branch J. W., Giannella C., Szymanski B., Wolf R. and

Kargupta H., 2013. “In-Network Outlier Detection in

Wireless Sensor Networks,” Knowledge and

Information System, vol. 34 no. 1, pp. 23-54.

Breunig M. M.,. Kriegel H. P., Raymond T. Ng. and

Sander J., 2000. “LOF: identifying density-based local

outliers,” ACM Sigmod Record, vol. 29 no. 2, pp. 93-

104, doi:10.1145/335191.335388.

Chandola V., Banerjee A. and Kumar V., 2009. “Anomaly

detection: A survey”, ACM Computing Surveys

(CSUR), vol. 41 no. 3: 15, pp. 1-58,

doi:10.1145/1541880.1541882.

Gupta M., Gao J., Aggarwal C.C. and Han J., 2013.

“Outlier detection for temporal data: A survey”, IEEE

Transaction on Knowledge and Data Engineering, vol.

25 no. 1, doi:10.1109/TKDE.2013.184.

Hodge V. J., Austin J., 2004. “A survey of outlier

detection methodologies,” Artificial Intelligence

Review, vol. 22 no. 2, pp. 85-126, doi:10.1007/

s10462-004-4304-y.

Intel Lab Data downloaded from http://db.csail.mit.edu/

labdata/labdata.html.

Jin W., Tung A. KH, Han J. and Wang W., 2006.

“Ranking outliers using symmetric neighborhood

relationship,” Advances in Knowledge Discovery and

Data Mining, Springer Berlin Heidelberg, pp. 577-

593, doi:10.1007/11731139_68.

Knorr E. M. and Raymond T. Ng., 1997. “A Unified

Notion of Outliers: Properties and Computation,”

Proc. KDD. Available at: http://www.aaai.org/Papers/

KDD/1997/ KDD97-044.pdf.

Kriegel H. P., Kröger P., Schubert E., Zimek A., 2009.

“LoOP: local outlier probabilities,” Proc. of the 18th

ACM conference on Information and knowledge

management (CIKM 09), ACM, pp. 1649-1652,

doi:10.1145/1645953.1646195.

Latecki L. J., Lazarevic A. and Pokrajac D., 2007. “Outlier

detection with kernel density functions,” Machine

Learning and Data Mining in Pattern Recognition,

Springer Berlin Heidelberg, pp. 61-75,

doi:10.1007/978-3-540-73499-4_6.

Loftsgaarden D. O. and Quesenberry C. P., 1965. “A

nonparametric estimate of a multivariate density

functions,” The Annals of Mathematical Statistics, vol.

36 no. 3, pp. 1049-1051. Available at:

http://projecteuclid.org/euclid.aoms/1177700079.

Marron J. S. and Wand M. P., 1992. “Exact mean

integrated squared error,” The Annals of Statistics,

vol. 20 no. 2, pp. 712-736. Available at:

http://projecteuclid.org/download/pdf_1/euclid.aos/11

76348653.

Papadimitriou S., Kitagawa H., Gibbons P. B. and

Faloutsos C.,2003. “Loci: Fast outlier detection using

the local correlation integral,” Proc. of the 19th

SENSORNETS2015-4thInternationalConferenceonSensorNetworks

174

International Conference on Data Engineering (ICDE

03), IEEE, Bangalore, India, pp. 315-326,

doi:10.1109/ICDE.2003.1260802.

Schubert E., Zimek A. and Kriegel H.P., 2014.

“Generalized Outlier Detection with Flexible Kernel

Density Estimates”, Proc. of the 14

SIAM

Conference on Data Mining (SDM 14), 2014.

Available at: http://www.dbs.ifi.lmu.de/~zimek/

publications/SDM2014 /KDEOS.pdf.

Sheather S. J. and Jones M. C., 1991. “A reliable data-

based bandwidth selection method for kernel density

estimation,” Journal of the Royal Statistical Society,

series B vol. 53 no. 3, pp. 683-690. Available at:

http://www.researchgate.net/publication/ 224817413.

Sheng B., Li Q., Mao W. and Jin W., 2007. “Outlier

Detection in Sensor Network”, MobiHoc 07, ACM,

pp. 219-228.

Silverman B.W., 1986. Density estimation for statistics

and data analysis, Vol. 26, CRC press, ISBN 0-412-

24620-1.

Terrell G. R. and Scott D. W., 1992. “Variable kernel

density estimation,” The Annals of Statistics, pp.

1236-1265. Available at: http://www.jstor.org/stable/

2242011.

Zucchini W., Berzel A. and Nenadic O., 2005. Applied

smoothing techniques.

ANewKernelforOutlierDetectioninWSNsMinimizingMISE

175