
Distributed Graph Matching and Graph Indexing Approaches
Applications to Pattern Recognition
Zeina Abu-Aisheh, Romain Raveaux and Jean-Yves Ramel
Laboratoire d’Informatique (LI), Universit
´
e Franc¸ois Rabelais, 37200, Tours, France
Keywords:
Graph Matching, Graph Edit Distance, Pattern Recognition, Classification, Distributed Systems, Scalability.
Abstract:
Attributed graphs are powerful data structures for the representation of complex objects. In a graph-based
representation, vertices and their attributes describe objects (or part of objects) while edges represent interre-
lationships between the objects. Due to the inherent genericity of graph-based representations, and thanks to
the improvement of computer capacities, structural representations have become more and more popular in the
field of Pattern Recognition (PR). In this thesis, we tackle two important graph-based problems for PR: Graph
Matching and Graph Indexing. The comparison between two objects is a crucial operation in PR. Represent-
ing objects by graphs turns the problem of object comparison into graph matching where correspondences
between nodes and edges of two graphs have to be found. Moreover, graph-based indices are important so that
a graph query can be retrieved from a large database via such indices, such a problem is referred to as graph in-
dexing. The complexity of both graph matching and graph indexing is generally stated to be NP-COMPLETE
or NP-hard. Coming up with a graph matching algorithm that can scale up to match graphs involved in PR
tasks is a great challenge. Among the graph matching methods dedicated to PR problems, the Graph Edit
Distance (GED) is of great interest. Over the last decade, GED has been applied to a wide range of specific
applications from molecule recognition to image classification. In this report, we present the first part of the
thesis. We tackle GED, shed light on the importance of having exact solutions rather than approximate ones
and come up with a distributed GED where the search tree is decomposed into smaller trees which are solved
independently and in a complete distributed manner. In the second part of the thesis, we aim at proposing new
distributed graph-indexing approaches that aim at retrieving a graph from a large graph-based index as fast as
possible. Graph indexing will be reported as a perspective of this work.
1 INTRODUCTION
Graphs are an efficient data structure for structural ob-
jects representation. Over the last decades, much at-
tention has been shed on using graphs as a structural
representation of objects in Pattern Recognition (PR).
In PR, the attributes of both nodes and edges play
an important role for representing graphs. Combin-
ing both symbolic and numeric attributes on nodes
and edges makes the extracted nodes and edges more
meaningful and highly representative. Unlike the
other graphs used in other fields (e.g., shortest path)
where the combination of symbolic and numeric at-
tributes is not necessarily needed. Representing ob-
jects by graphs easily transforms the problem of ob-
ject detection or objects comparison into a graph
matching one.
Graph matching is the process of finding a corre-
spondence between the nodes and the edges of two
graphs g
1
and g
2
that satisfies some (more or less
stringent) constraints ensuring that similar substruc-
tures of the source graph are mapped to similar sub-
structures of the target graph. Recently, graph match-
ing has been considered as a fundamental problem in
PR. Such a problem is known to be NP-complete, ex-
cept for graph isomorphism, for which it has not yet
been demonstrated whether it belongs to NP or not
(Conte et al., 2004).
Exact graph matching addresses the problem of
detecting identical (sub)structures of two graphs g
1
and g
2
and their corresponding labels. This category
assumes the existence of only noise-free objects while
in reality objects are usually affected by noise and
distortion. Consequently, researchers often shed light
on the other category, i.e., inexact or so-called error-
tolerant graph matching, where some degree of er-
ror tolerance can be easily integrated into the graph
matching process.
In the context of attributed graphs, the problem
of error tolerant graph matching presents a higher
3
Abu-Aisheh Z., Raveaux R. and Ramel J..
Distributed Graph Matching and Graph Indexing Approaches - Applications to Pattern Recognition.
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

complexity than exact graph matching as it takes dis-
tortion and noise into account during the matching
process. Indeed, the exact algorithms dedicated to
solving error-tolerant graph matching are computa-
tionally complex (Vento, 2014); and (M. Neuhaus
and Bunke., 2006)). Consequently, lots of works
have been employed to approximately solve the error-
tolerant graph matching problem. Such methods are
often called heuristics or approximate methods. Ap-
proximate methods for the error-tolerant graph match-
ing problem have been investigated based on genetic
algrithm (A.D.J. Cross and Hancock, 1997), proba-
bilistic relaxation (W. Christmas and Petrou., 1995),
EM algorithm (Andrew D. J. Cross, 1998); (Finch,
1998) and neural networks (Kuner and Ueberreiter,
1988). The aforementioned techniques are expected
to present a polynomial run-time. However, they can-
not ensure the quality of their solutions and are likely
to output suboptimal solutions.
Graph Edit Distance, referred to as GED, is an
error-tolerant technique that has been widely studied
and largely applied to PR (Tsai and Fu, 1979). Its
flexibility comes from its generality as it is applicable
on unconstrained attributed graphs. GED is a general-
ization of the graph isomorphism problem where the
goal is to minimize the cost of graph transformation.
In GED, graph g
1
is transformed into graph g
2
by
means of series of transformations. The allowed edit
operations are: deletion, insertion and substitution of
nodes and their corresponding edges. GED is compu-
tationally complex or expensive, it is said to be an NP-
COMPLETE problem where the complexity is expo-
nential in the number of nodes of the involved graphs.
Such a fact limits GED algorithms to work on rela-
tively small graphs. To overcome this problem three
main directions have been adopted in the literature.
First, optimal methods based on admissible heuristics
to prune the search space (e.g., (Riesen et al., 2007)).
Second, sub-optimal methods simplifying the prob-
lem (e.g., (M. Neuhaus and Bunke., 2006)). Third,
sub-optimal methods by means of approximate op-
timization algorithm (e.g., (Riesen, 2009); and (An-
dreas Fischer, 2013)). However, sub-optimal meth-
ods does not guarantee to find the best matching and
the error rate gets higher as the involved graphs get
larger. Accordingly, in this thesis a focus is given to
optimal methods. To prevent the combinatorial ex-
plosion, many works have been focused on efficiently
pruning the search space. The computation of ad-
missible lower bounds have been deeply studied to
reduce memory and CPU complexity (Bunke, 1983);
and (Zeng et al., 2009).
Most of the current techniques are optimized for
centralized graph processing. A distributed approach
providing horizontal scalability is required in order to
handle the analysis workload. Thus, besides provid-
ing lower and upper bounds for the problem, we have
adopted the idea of decomposing GED into smaller
problems, or sub-problems, via a divide and conquer
strategy. The sub-problems are then solved in a dis-
tributed manner.
The rest of this report is organized as follows. In
Section 2, a focus on the related works is given. In
Section 3 the notations and the definitions used in the
paper are presented and our approach is positioned
up in the literature. Section 4 reports our proposed
sequential algorithm used to solve GED. In Section
5, the chosen parallel computing model and the pro-
posed distributed GED are presented, respectively. In
Section 6 the databases and the experimental protocol
used to point out the performance of the proposed ap-
proaches are represented. Section 7 demonstrates the
results achieved so far. Finally, conclusions are drawn
and future perspectives are discussed in Section 8.
2 RELATED WORKS
The distributed and parallel graph matching methods,
presented in the literature, can be divided into two cat-
egories: Data-Parallelism and Search-Parallelism. In
Data-Parallelism, the graphs g
1
and g
2
can be parti-
tioned into sub-graphs. These small sub-graphs can
be matched independently in a sequential or in a par-
allel manner. The results of all the sub-problems
are reassembled producing a global answer of the
main graph matching problem ((Qiu and Hancock,
2006); (Patwary et al., 2010); and (Kollias, 2012)). In
Search-Parallelism, matching g
1
and g
2
is considered
as a single problem. However, the search space of g
1
and g
2
is partitioned and then processed in a com-
pletely parallel manner ((Allen and Yasuda, 1997);
(Wan, 1998); and (Plantenga, 2013)).
We focus on two distributed works, belonging to
the Search-Parallelism category and are dedicated to
solving graph matching problems:
2.1 Maspar-SIMD
A parallel inexact graph matching algorithm is pro-
posed in [22]. This algorithm, referred to as MasPar-
SIMD, is depth-first branch-and-bound for determin-
ing a minimum-distance correspondence between two
unlabeled graphs. The heuristic, called forward
checking, used to prune the search space, examines
the possible sources of edges mismatches and thus
forward checking keeps track of constraints (edges)
that are not satisfied. The degree of mismatch of a
ICPRAM2015-DoctoralConsortium
4

permutation π is defined of as the number of edges
in g
1
that are not mapped by π to edges in g
1
plus
the number of edges in g
2
not mapped to edges in
g
1
. At each iteration, the edge errors are accumu-
lated. Results show that MasPar-SIMD consistently
outperforms the sequential version when the involved
graphs have more than 16 vertices. This algorithm is
inexact for two reasons. First, the mismatch of edges
are taken into account whereas mismatch of nodes are
ignored. Second, the heuristic is not a lower bound
and cannot ensure the optimal solution to be found.
Also, the graphs involved in the algorithm are unla-
beled and thus numeric and attributed graphs are not
included. As for the exploration of the search space,
the best permutation and the best degree of match are
only updated at the end of each iteration, such a fact
does not allow pruning the search space as fast as pos-
sible.
2.2 SGIA-MR
Recently, a Hadoop MapReduce implementation for
subgraph type isomorphism, called SGIA-MR, has
been implemented in (Plantenga, 2013). This algo-
rithm makes use of an implicit multi-partite graph
which finds sub-graphs in a single large graph (i.e.,
given a pattern G
p
, find all the walks in the graph G
that correspond to the pattern G
p
).
In (Plantenga, 2013), the type-isomorphism match
is inexact in the sense that matched subgraphs do
not necessarily have isomorphic structures. SGIA-MR
only considers symbolic or unlabeled graphs and thus
it cannot be easily extended to work on numeric at-
tributed graphs. Moreover, this algorithm is a noise-
free one as neither nodes nor edges distortion is in-
cluded in the matching process.
2.3 Conclusion on Parallel and
Distributed Graph Matching
Methods
To our best of knowledge, none of the parallel and
distributed graph matching methods has included nu-
meric attributed graphs, besides that all of them fall
within the suboptimal graph matching category and so
they cannot ensure the optimal solution to be found.
Moreover, neither bounds on the optimal solution nor
quality measure or confidence on the solution are pro-
vided. In the literature, there is also no effort devoted
to solving GED problems in a distributed manner. In-
deed, MasPar-SIMD and SGIA-MR cannot be easily
extended to solve GED. We believe that there is a need
for a distributed and optimal GED method that can be
used to match symbolic and numeric attributed graphs
in a way that outperforms the sequential GED algo-
rithms.
3 GRAPH EDIT DISTANCE
Graph edit distance (GED) is a graph matching ap-
proach whose concept was first reported in (Sanfeliu
and Fu, 1983). The basic idea of GED is to find the
best set of transformations that can transform graph g
1
into graph g
2
by means of edit operations on graph g
1
.
The allowed operations are inserting, deleting and/or
substituting vertices and their corresponding edges.
Definition 1. Graph Edit Distance
Let g
1
= (V
1
, E
1
, µ
1
, ζ
1
) and g
2
= (V
2
, E
2
, µ
2
, ζ
2
) be
two graphs, the graph edit distance between g
1
and g
2
is defined as:
GED(g
1
, g
2
) = min
e
1
,···,e
k
∈γ(g
1
,g
2
)
k
∑
i=1
c(e
i
) (1)
Where c denotes the cost function measuring the
strength c(e
i
) of an edit operation e
i
and γ(g
1
, g
2
) de-
notes the set of edit paths transforming g
1
into g
2
.
A standard set of edit operations is given by inser-
tions, deletions and substitutions of both vertices and
edges. We denote the substitution of two vertices u
and v by (u → v), the deletion of node u by (u → ε)
and the insertion of node v by (ε → v). For edges (e.g.,
w and z), we use the same notations used for vertices.
A complete edit path (EP) refers to an edit path
that fully transforms g
1
into g
2
(i.e., complete solu-
tion). Mathematically, EP = {e
i
}
k
i=1
. An example of
an edit path between two graphs g
1
and g
2
is shown in
Figure 1, the following operations have been applied
in order to transform g
1
into g
2
: three edge deletions,
one node deletion, one node insertion, one edge inser-
tions and three node substitutions.
Figure 1: Transforming g
1
into g
2
by means of edit opera-
tions. Note that vertices attributes are represented in differ-
ent gray scales.
Many fast heuristic methods have been proposed
in the literature such as (W. Christmas and Petrou.,
1995); (Zeng et al., 2009); (Fankhauser et al., 2012);
(Combier et al., 2013); and (Andreas Fischer, 2013).
However, these heuristic algorithms can only find un-
bounded suboptimal values. On the other hand, only
few exact approaches have been proposed to postpone
the graph size restriction (Tsai and Fu, 1979); (Justice
DistributedGraphMatchingandGraphIndexingApproaches-ApplicationstoPatternRecognition
5

and Hero, 2006); and (Riesen et al., 2007). Lots of
exact branch and bound graph matching algorithms
have been proposed in the literature. However, to
the best knowledge of the authors these works have
not addressed the GED problem and cannot be eas-
ily extended to solve such a problem. For instance,
a branch and bound algorithm dedicated to solving
GED was proposed in (Tsai and Fu, 1979) but it was
restricted to graphs that are structurally isomorphic.
Afterwards, this work has been extended in (Tsai and
Fu, 1983) that has taken into account insertion and
deletion of nodes and edges. However, the proposed
algorithm was devoted to error-correcting subgraph
isomorphism.
3.1 Exact Graph Edit Distance
Computation
A widely used method for exact GED computation
is based on the A* algorithm (Riesen et al., 2007),
this algorithm, referred to as A*GED, is considered
as a foundation work for solving GED. A*GED ex-
plores the space of all possible mappings between two
graphs by means of an ordered tree. Such a search
tree is constructed dynamically at run time by itera-
tively creating successor nodes linked by edges to the
currently considered node in the search tree. In the
worst case, the space complexity can be expressed as
O(|σ|) (Cormen et al., 2009) where |σ| is the cardi-
nality of the set of all possible edit paths. Since |σ|
is exponentional in the number of vertices involved in
the graphs, the memory usage is still an issue.
Algorithm 1 depicts the A*GED computation. In
order to determine the node which will be used for
further expansion of the actual mapping in the next
iteration, a heuristic function added to the actual edit
path cost is usually used. Formally, for a node p in
the search tree, g(p) represents the cost of the edit
path accumulated so far, h(p) denotes the estimated
costs from p to a leaf node, h(p) must not underes-
timate the remaining cost in order to guarantee the
optimality of the final solution. Also, it should be
done in a faster way than the exact computation and
return a good approximation of the true future cost.
The sum g(p) +h(p), referred to as lb(p), depicts the
total cost assigned to an open node in the search tree.
Obviously, the edit path p that minimizes g(p) +h(p)
is chosen next for further expansion. Note that the
smaller the difference between lb and the real future
cost, the fewer the expanded nodes. The choice of lb
is a crucial parameter and many lower bounds have
been proposed in the literature. To the best of the
authors’ knowledge, the best lower bound has been
presented in (Riesen, 2009). In A*GED, h(p) is com-
Algorithm 1 : Astar Graph Edit Distance algorithm
(A*GED).
Input: Non-empty attributed graphs g
1
=
(V
1
, E
1
, µ
1
, v
1
) and g
2
= (V
2
, E
2
, µ
2
, v
2
) where V
1
= {u
1
, ..., u
|v
1
|
} and V
2
= {u
2
, ..., u
|v
2
|
}
Output: A minimum cost edit path from g
1
to g
2
e.g.,
p
min
={u
1
→ v
3
, u
2
→ ε , ε → v
2
}
1: Initialize OPEN to the empty set
2: For each node w ∈ V
2
, insert the substitution in-
sert the substitution {u
1
→ w} into OPEN
3: Insert the deletion {u
1
→ ε} into OPEN
4: while true do
5: Find p
min
= argmin{g(p) + h(p)} s.t. p ∈
OPEN
6: Remove p
min
from OPEN
7: if p
min
is a complete edit path then
8: Return p
min
as the solution (i.e., a mini-
mum cost edit distance from g
1
to g
2
)
9: else
10: Let p
min
= {u
1
→ v
i1
, ..., u
k
→ v
ik
}
11: if k < |V
1
| then
12: For each w ∈ V
2
\ {v
i1
, ..., v
ik
}, insert
p
min
∪ {u
k+1
→ w} into OPEN
13: p
new
= {p
min
, u
k+1
→ ε}
14: Insert p
new
into OPEN
15: else
16: Insert p
min
∪
S
w∈V 2\{v
i1
,...,v
ik
}
{ε → w}
into OPEN
17: end if
18: end if
19: end while
puted using an assignment algorithm on un-
mapped vertices and edges yet to estimate the
future costs. This is performed by an assign-
ment algorithm (Riesen, 2009) whose complexity is
O(max{n
1
, n
2
}
3
). The unprocessed edges of both
graphs are handled analogously. Obviously, this pro-
cedure allows multiple substitutions involving the
same vertex or edge and, therefore, it possibly rep-
resents an invalid way to edit the remaining part of g
1
into the remaining part of g
2
. However, the estimated
cost certainly constitutes a lower bound of the optimal
cost.
3.2 Conclusion on A*-GED
A*GED is a best-first search algorithm and so the list
of candidate solutions, called OPEN, grows quickly.
Such a fact leads to high memory consumption and
thus is considered as a bottleneck of A*GED. In this
paper, we outperform A*GED by getting rid of high
memory consumption and the re-computation of ver-
tices and nodes matching costs. We propose a new al-
ICPRAM2015-DoctoralConsortium
6

gorithm that reduces the used memory space using a
different exploration strategy (i.e., depth-first instead
of best-first). This approach also reduces the com-
putation time as the unfruitful nodes are pruned by
the lower and upper bounds strategy. A preprocessing
strategy is included. First, edges and vertices costs
matrices are constructed to get rid of re-computation
when exploring nodes in the search tree. Second, the
list V
1
is sorted to speed up the search for the best edit
path to be explored.
4 OUR SEQUENTIAL PROPOSAL
In this section, we introduce our proposal and we
mention its advantages over A*GED.
4.1 Depth-first Graph Edit Distance
As mentioned before, A*, with all its different lower
bounds, suffers from a high memory consumption
while searching for the best edit path. A*, which
is a best-first search algorithm, constructs the search
tree dynamically at run time. The construction of the
search tree is achieved iteratively by creating succes-
sor nodes linked by edges to the currently considered
node in the search tree.
In order to get rid of the high memory consump-
tion and to converge faster to the optimal solution,
we propose a depth-first GED (DF). This strategy has
O(|V
1
.V
2
|) space complexity in the worst case for stor-
ing the pending edit paths in the set OPEN (Cormen
et al., 2009). That is, at any time t the number of
pending nodes is relatively small and thus there is no
high memory consumption as in A*.
The elements of the algorithm are described in
Sections 4.2 to 4.7. Moreover, a pseudo-code for the
method is presented in Section 4.8.
4.2 Structure of Search-tree Nodes
From now on, we will refer to the search-subtree
rooted in node p as Partial Edit Path (p). Figure 2
illustrates an example of a partial edit path.
Each p is then identified by the following ele-
ments:
• matched-vertices(p) and matched-edges(p): the
elements contained in these sets are vertices and
edges that have been matched so far in both g
1
and g
2
. These sets can contain substitution (u →
v), deletion (u → ε) and/or insertion (ε → v) of
vertices and edges, correspondingly.
a
b c d
e
f
g(a)=0
lb(a)=4
f(a)=4
g(d)=4
lb(d)=4
f(d)=8
g(c)=2
lb(c)=1
f(c)=3
g(b)=2
lb(b)=2
f(b)=4
g(e)=5
lb(e)=1
F(e)=6
g(f)=4
lb(f)=1
f(f)=5
Figure 2: An example of a partial edit path p whose ex-
plored nodes so far are a, c and f . f (∗) = g(∗) + h(∗).
• pending-vertices
i
(p) and pending-edges
i
(p):
these sets represent vertices and edges of both
g
1
and g
2
(i.e., V
1
, V
2
, E
1
and E
2
) that are
not substituted, deleted or inserted yet where
pending-vertices
1
(p) and pending-vertices
2
(p)
represent pending V
1
and pending V
2
, respectively
whereas pending-edges
1
(p) and pending-
edges
2
(p) represent pending E
1
and pending E
2
,
respectively.
• parent(p): the parent of p.
• siblings(p): for any node p, the exploration is
achieved by choosing the next most promising
vertex u
i
of pending-vertices
1
(p) and matching it
with all the elements of pending-vertices
2
(p) in
addition to the deletion of this node (i.e., u
i
→ ε).
All these matchings are referred to as siblings(p).
• h(p): is the estimated future cost from node p.
h(p) does not underestimate the complete solu-
tion. The calculation of h(p) is described in Sec-
tion 4.6.
• g(p): the cost of matched-vertices(p) and
matched-edges(p). Both h and g depend on the
attributes as well as the structure of the involved
sub-trees. The cost functions involved with each
PR dataset permit to calculate insertions, dele-
tions and substitutions of vertices and/or edges.
4.3 Preprocessing
Preprocessing is applied before the branch and bound
procedure starts in order to speed up the tree search
exploration. First, vertices and edges cost matri-
ces are constructed. Second, vertices-sorting is con-
ducted.
4.3.1 Cost Matrices
The vertices and edges cost matrices (C
v
and C
e
) are
constructed, respectively. This step aims at speeding
up branch and bound by getting rid of re-calculating
the assigned costs when matching vertices and edges
of g
1
and g
2
.
DistributedGraphMatchingandGraphIndexingApproaches-ApplicationstoPatternRecognition
7

Let g
1
= (V
1
, E
1
, µ
1
, ξ
1
) and g
2
= (V
2
, E
2
, µ
2
, ξ
2
)
be two graphs with V
1
= (u
1
, ..., u
n
) and V 2 =
(v
1
, ..., v
m
). A vertices cost matrix C
v
, whose dimen-
sion is (n + 2) X (m + 2), is constructed as follows:
C
v
=
c
1,1
... ... c
1,m
c
1←ε
c
1→ε
... ... ... ... ... ...
... ... ... ... ... ...
c
n,1
... ... c
n,m
c
n←ε
c
n→ε
c
ε→1
... ... c
ε→m
∞ ∞
c
ε←1
... ... c
ε←m
∞ ∞
where n is the number of vertices of g
1
and m is
the number of vertices of g
2
.
Each element c
i, j
in the matrix C
v
corresponds to
the cost of assigning the i
th
vertex of the graph g
1
to
the j
th
vertex of the graph g
2
. The left upper corner
of the matrix contains all possible node substitutions
while the right upper corner represents the cost of all
possible vertices insertions and deletions of vertices
of g
1
, respectively. The left bottom corner contains
all possible vertices insertions and deletions of ver-
tices of g
2
, respectively whereas the bottom right cor-
ner elements cost is set to infinity which concerns the
substitution of ε − ε.
Similarly, C
e
contains all the possible substitu-
tions, deletions and insertions of edges of g
1
and g
2
.
C
e
is constructed in the very same way as C
v
.
4.3.2 Vertices-Sorting Strategy
As GED aims at transforming g
1
into g
2
so it is impor-
tant to sort V
1
in order to start with the most promis-
ing vertices that will speed up the exploration of the
search tree while searching for the optimal solution.
The aforementioned C
v
is used as an input of the
vertices-sorting phase. To sort V
1
, Munkres’ algo-
rithm is applied (Riesen, 2009). From now on, we
will refer to the set of sorted vertices as sorted-V
1
.
4.4 Branching Strategy
A systematic evaluation of all possible solutions is
performed without explicitly evaluating all of them.
The solution space is organized as an ordered tree
which is explored in a depth-first way. In depth-first
search, each node is visited just before its siblings.
In other words, when traversing the search tree, one
should travel as deep as possible from node i to node
j before backtracking.
The root r of the search-tree is the node with
matched-vertices(r) = φ, matched-edges(r) = φ,
pending-vertices
1,2
(r) = V
1
∪V
2
, pending-edges
1,2
(r)
= E
1
∪ E
2
, g(r) = ∞ and lb(r) = ∞. Initially r is the
only node in the set OPEN; the set of the edit paths,
found so far. The exploration starts with the first most
promising vertex u
1
in sorted-V
1
in order to gener-
ate the root’s siblings siblings(r). Then, siblings(r) is
added to OPEN. Consequently, a minimum edit path
(p
min
) is chosen to be explored by selecting the min-
imum cost node (i.e., min(lb(p)) among siblings(r)
and so on. We backtrack to continue the search for a
good edit path by revoking p
min
(if p
min
equals null)
and trying out the next child in the set of siblings(r)
and so on.
4.5 Reduction Strategy
As in A*, pruning, or bounding, is achieved thanks to
h(p), g(p) and a global upper bound UB obtained at
node leaves. Formally, for a node p in the search tree,
the sum g(p) + h(p) is taken into account and com-
pared with UB. That is, if g(p) + h(p) is less than U B
then p can be explored. Otherwise, the encountered
p will be pruned from OPEN and a backtracking is
done looking for the next promising node and so on
until finding the best UB that represents the optimal
solution of DF-GED. This algorithms differs from
A* as at any time t, in the worst case, OPEN con-
tains approximately |V
1
|.|V
2
| elements and hence the
memory consumption is not exhausted.
4.6 Lower Bound
The lower bound lb(p), adapted to DF-GED, is the
one used in section A*GED, see Section 3.1.
4.7 Upper Bound
The very first upper bound is computed by Munkres’
algorithm as it provides fast preliminary results on the
GED problem, see (Riesen, 2009) for more details.
Afterwards and while traversing the search tree, the
upper bound UBCOST is replaced by the best UB-
COST found so far (i.e., a complete path whose cost
is less than the current UBCOST). After finishing the
traversal of the search tree (i.e., when p
min
is empty
and its parent is r), the best UBCOST is outputted
as an optimal solution of DF. Encountering upper
bounds when performing a depth-first traversal effi-
ciently prunes the search space and thus helps at find-
ing the optimal solution faster than A*.
4.8 Pseudo Code
As depicted in Algorithm 2, DF-GED starts by a pre-
processing step (line 2), then an upper bound UB-
COST is calculated by BP (line 3). The traversal of
ICPRAM2015-DoctoralConsortium
8

Algorithm 2: Depth-first GED algorithm (DF-GED).
Input: Non-empty attributed graphs g
1
=
(V
1
, E
1
, µ
1
, v
1
) and g
2
= (V
2
, E
2
, µ
2
, v
2
) where V
1
= {u
1
, ..., u
|v
1
|
} and V
2
= {u
2
, ..., u
|v
2
|
}
Output: A distance UBCOST and a minimum cost
edit path (UB) from g
1
to g
2
e.g., {u
1
→ v
3
, u
2
→ ε
, ε → v
2
}
1: OPEN ← {φ}, p
min
← φ
2: Generate C
v
, C
e
and sorted-V
1
3: (U B , UBCOST) ←BP(g
1
,g
2
)
4: for w ∈ V
2
do
5: OPEN ← OPEN ∪{u
1
→ w} s.t. u
1
∈ sorted-
V
1
6: end for
7: OPEN ← OPEN ∪ {u
1
→ ε}
8: r ← parent(u
1
), parent
tmp
← r
9: while true do
10: p
min
← bestSibling(parent
tmp
)
11: while p
min
is not empty and parent
tmp
does
not equal to r do
12: parent
tmp
← backtrack(parent
tmp
)
13: p
min
← bestSibling(parent
tmp
)
14: end while
15: if p
min
is empty and parent
tmp
equals to r then
16: Return UB and UBCOST
17: end if
18: OPEN ← OPEN \ p
min
19: if g(p
min
) + h(p
min
) < UB then
20: if pending-vertices
1
(p
min
) is not empty
then
21: for w ∈ pending-vertices
2
(p
min
) do
22: p ← p
min
∪ {u
k+1
→ w}
23: if g(p) + h(p) <UBCOST then
24: OPEN ← OPEN ∪ {p}
25: end if
26: end for
27: p ← p
min
∪ {u
k+1
→ ε}
28: if g(p) + h(p) <UBCOST then
29: OPEN ← OPEN ∪ {p}
30: end if
31: else
32: Generate a complete solution p ←
p
min
∪
S
w∈pending−vertices
2
(p)
{ε → w}
33: if g(p) + h(p) <UBCOST then
34: UBCOST ← g(p)
35: UB ← p
36: end if
37: end if
38: end if
39: parent
tmp
← p
min
40: end while
the search tree starts by selecting a first vertex
u
1
∈ sorted-V
1
where u
1
substituted with all vertex
w in graph g
2
as well as the deletion case (u
1
→ ε)
are inserted into OPEN (lines 4 to 7). A branching
step is performed in line 10 where the best sibling
p
min
is selected, the backtracking is done when there
is no more siblings to explore in the selected branch
and the parent node (parent
tmp
) is not the root (lines
11 to 14). p
min
is explored by substituting the next
promising node u
k+1
with pending-vertices
2
(p
min
)
and also deleting u
k+1
, respectively (lines 20 to 30).
Similar to A*GED, if pending-vertices
1
(p
min
) is
empty, pending-vertices
2
(p
min
) will be inserted (line
32). UB and UBCOST are updated whenever a better
UBCOST is encountered (lines 34 and 35). Each
time the next parent to be explored will be replaced
by p
min
(line39). This algorithm guarantees to find
the optimal solution of GED(g
1
, g
2
). Note that edges
operations are taken into account in the matching
process when substituting, deleting or inserting their
corresponding vertices.
4.9 Deadlocks to be Released
DF-GED ends up finding the optimal edit path be-
tween two graphs. However, its bottleneck comes
from its CPU consumption. Indeed, DF-GED is com-
putationally complex as the size of the search space
increases exponentially with the number of nodes of
the involved graph. Such facts restrict it to work on
small graphs only. On the other hand, approximate
methods often have a polynomial running time in the
size of the input graphs which is much faster, but are
not guaranteed to find the optimal solution. We, au-
thors, believe that the more complex the graphs, the
larger the error committed by the approximate meth-
ods. The graphs are more complex when they have
more vertices and a well-connected structure. For
all these reasons we shed light on the necessity of
having a distributed DF-GED in order to work on
larger graphs that cannot be matched using DF-GED.
Scaling-out is essential and flexible as one can add M
machines for enhancing the execution time.
5 OUR DISTRIBUTED
PROPOSAL
Recently, people have been increasingly flooding onto
deploying their applications on servers which respond
to more complicated requirements: scalability, pro-
ductivity and performance. To respond to this de-
mand, an application server is proposed in this re-
search. We present a distributed DF-GED algorithm,
denoted by D-DF. This proposed algorithm is built
DistributedGraphMatchingandGraphIndexingApproaches-ApplicationstoPatternRecognition
9
on top of Hadoop-MapReduce. The search tree is de-
composed into smaller trees, or sub-trees and the ex-
ploration of the partial edit paths is done in parallel.
Definition 2. Scalability
The capability of a system or a process to handle a
growing amount of work, e.g., larger graphs, or to be
easily expanded or upgraded, when required, to ac-
commodate that amount of work. This is done by
adding more machines to the distributed system.
For the sake of programming ease, we have cho-
sen MapReduce as a model on which we build our dis-
tributed approach. MapReduce is easier to program,
even for programmers who have no much background
about parallel computing as it hides the details of par-
allelization, fault-tolerance, data distribution and load
balancing from them.
5.1 MapReduce Framework
MapReduce is a GOOGLE parallel computing frame-
work (Dean, 2004) used to process vast amounts of
data in-parallel. In the MapReduce model, the work
is divided into two phases: a Map phase and a Re-
duce phase. Both of these phases work on key-value
pairs. These pairs are defined by the MapReduce pro-
grammers depending on the problems they are han-
dling (e.g., words in a text paired by their number of
occurrences).
DF-GED is a data-intensive task where lots of edit
paths are extracted searching for a best complete edit
path to transform g
1
into g
2
. MapReduce is a Single
Program Multiple data (SPMD) model, dedicated to
data-intensive tasks. As a consequence, such a par-
allel computing model suits DF-GED, thanks to its
scalability and its ability to be run on a large cluster
of machines.
Definition 3. Job
A MapReduce job contains a Map procedure and a
Reduce procedure. Each procedure has one or more
workers (i.e., Map or Reduce workers that are as-
signed to Map or Reduce tasks, respectively). Map
and Reduce tasks are run by their workers in parallel.
MapReduce uses file-systems as a communication
way between Map and Reduce functions. In other
words, MapReduce programs read and write theirs re-
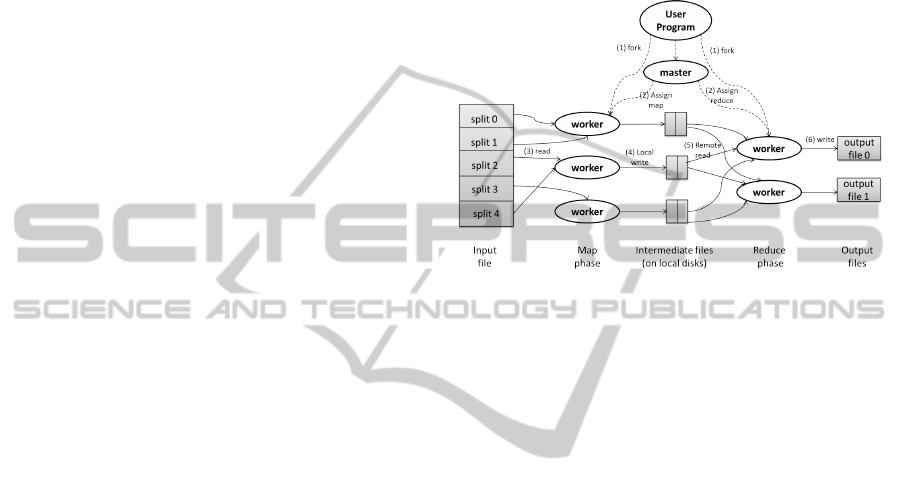
sults to disks. Figure 3 represents a MapReduce job.
In MapReduce, the input files are split into N pieces,
or splits, by the MapReduce library in the user pro-
gram. Then the master, which has a special copy of
the program, assigns Map and Reduce tasks to Map
workers and Reduce workers, respectively. Each Map
worker is assigned one or more file splits (i.e., one or
more map tasks), depending on its idleness. When
a Map worker finishes its associated task, it saves its
buffered key-value pairs to the local disk. The local
locations of these buffers are sent back to the master
which will inform Reduce workers about them when
all the Map workers finish their assigned tasks. Re-
duce workers read these buffers from their locations,
group data by their keys and start to execute the Re-
duce function.
Figure 3: MapReduce Job (Dean, 2004).
5.2 Architecture
The time complexity of DF-GED is exponential in the
number of vertices of the involved graphs (i.e., g
1
and
g
2
), in order to decrease the execution time of DF-
GED, a search tree decomposition is proposed here
to fragment the graph matching problem into smaller
problems that are solved in a parallel manner. We re-
fer to this distributed approach as D-DF. D-DF has
a single job that has a Map phase without a Reduce
one. It starts with two graphs g
1
and g
2
and ends up
finding the optimum distance (d).
Figure 4 demonstrates D-DF’s architecture. D-DF
is divided into two phases:
• Initialization phase: a certain number of edit paths
is generated using A*-GED. Moreover, a first up-
per bound (UB-best) is computed using a bipartite
graph matching (BP). The interested reader is re-
ferred to (Riesen, 2009) for more details.
• Distributed phase: each worker on the map side
takes an edit path to be solved using DF-GED.
When a map worker m
i
succeeds in finding a bet-
ter upper bound, it updates the value of UB-best
and notifies the other map workers so that they
get the new value. Also, when a worker is done
with one edit path, it communicates with the mas-
ter program in order to get another edit path that
has not been explored yet. This job finishes when
there is no more edipath to explore. The value
UB-best represents the optimal solution (i.e., dis-
tance) between g
1
and g
2
.
ICPRAM2015-DoctoralConsortium
10

Initialization:
Generate X edit paths using A*-GED
Compute a first upper bound UB-best
DF-GED with
UB-best
g2 g1
𝑃𝐸𝑃
1
𝑃𝐸𝑃
2
𝑃𝐸𝑃
𝑋
PEP
UB-best
Partial Edit Path
Global upper bound
Save to hadoophard disk
DF-GED with
UB-best
DF-GED with
UB-best
UB-best
• Update UB-best if a better value is found
• Notifiy other workers so that they can get
the new value
Update &
notify ?
Update &
notify ?
Update &
notify ?
Figure 4: The architecture of DF-F.
6 EXPERIMENTS
6.1 Environment
Evaluations are conducted on a 4-core Intel i7 proces-
sor 3.07GHz and 8 GB of memory.
6.2 Protocol and Quality Measures
In this section, we explain the protocol used to
evaluate the two sequential and optimal approaches
(A*GED and DF-GED). This Protocol is three-fold:
• Calculating the distance matrix under a small time
constraint.
• Calculating the distance matrix under a big time
constraint.
• Classification test under a reasonable time con-
straint.
Let S be a graph dataset consisting of m graphs,
S = {g
1
, g
2
, ..., g
m
}. Let P = {A*GED, DF-GED}
be the set the compared methods. Given a method
p ∈ P , we computed the square distance matrix
M
p
∈ M
m
(R
+
), that holds every pairwise compar-
ison M
p
i, j
= d
p
(g
i
, g
j
), where the distance d
p
(g
i
, g
j
)
is the value returned by the method p on the graph
pair (g
i
, g
j
) within a certain time and memory limits.
Hence, M
A*GED
and M
DF-GED
denote distance matri-
ces of A*GED and DF-GED methods, respectively.
Let GT ∈ M
m
(R
+
) be the reference matrix that
holds the best found distance for each pair of graphs.
We aim at comparing the errors committed by the dif-
ferent methods as well as their speed under a time
constraint C
T
and a memory constraint C
M
when
graphs sizes increase (i.e., on GRECk) and also on
GREC-mix. To this objective, we test the accuracy of
P when C
T
is small (C
T
= 350ms) and when C
T
is big
(C
T
= 5 minutes). C
M
is set to 1GB during all the ex-
periments. We expect A*GED to violate C
M
specially
when graphs get larger.
In the following, we define the measurements used
for evaluating our protocol:
Deviation. we evaluate the error committed by a
method p over the reference distances. To this end,
we measure an indicator called deviation and defined
by the following equation:
deviation(i, j)
p
=
|M
p
i, j
− GT
i, j
|
GT
i, j
, ∀(i, j) ∈ J1, mK
2
, ∀p ∈ P
(2)
Where GT
i, j
is the smallest distance among all dis-
tances generated by P when matching g
i
and g
j
.
Running Time. we measure the running time
in millisecond for each comparison d(g
i
;g
j
). This
value reflects the overall time for GED computation
including all the inherits costs computations (i.e.,
g(p); h(p); and U B)
For the classification test, we are interested in the
average computation time (t) which corresponds to
the average time elapsed when classifying all the test
graphs of GREC and the classification accuracy (AC)
which defines the error made when classifying the test
graphs of GREC. Both measurements are achieved
when C
T
= 500ms and C
M
= 1GB. The classification
stage is performed by a 1-NN classifier. Each test
graph g
t
is compared to the entire training set. The
nearest neighbor’s label is assigned to g
t
.
7 RESULTS AND DISCUSSION
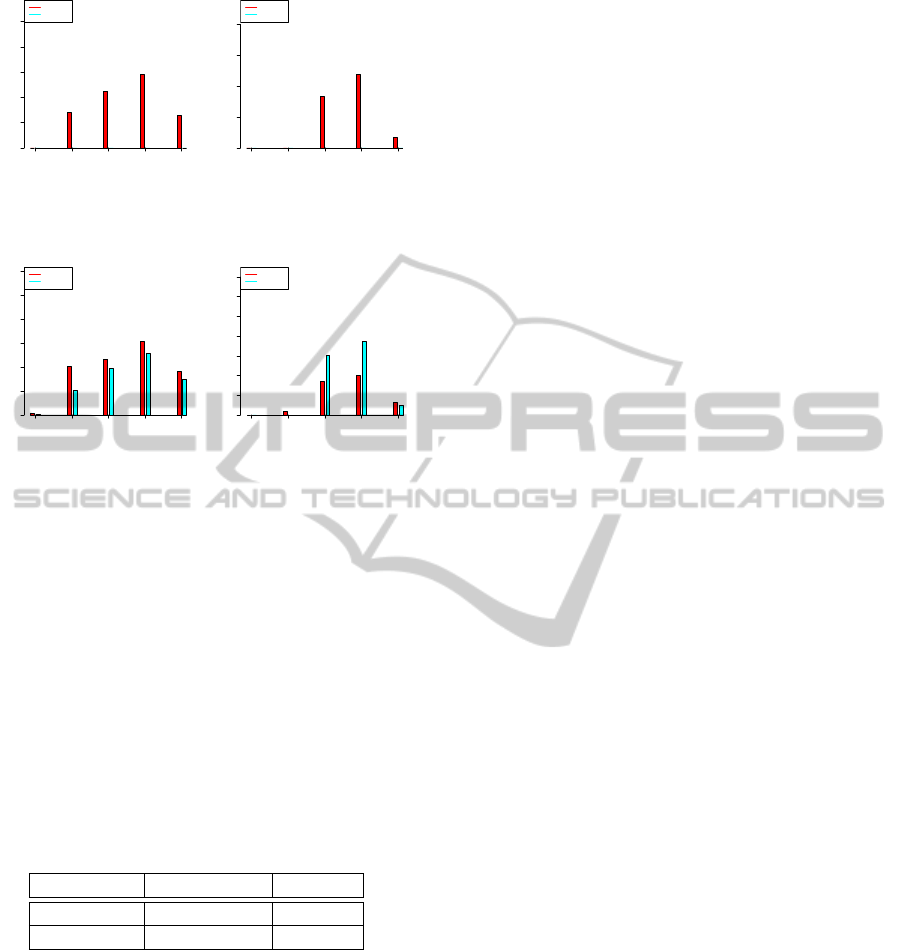
Figure 5 shows the deviation results under 350 mil-
liseconds and 5 minutes respectively. We observe that
DF-GED always outperforms A*GED under the same
time constraint. For all GED computations, DF-GED
gives the best distance (i.e., GT
i, j
) and so its deviation
is always 0%. In contrast with DF-GED, the deviation
of A*GED decreases when C
T
= 5 minutes. How-
ever, when the size of graphs increase (e.g., GREC15
and GREC20), the deviation starts to converge due to
memory saturation where the best recently known so-
lution is outputted before halting.
Figure 6 demonstrates the running time of both
A*GED and DF-GED. When C
T
= 350 milliseconds
both running times are relatively equal on GREC15
and GREC20 and that is because non of them is
able to find an optimal solution before exceeding C
T
.
When C
T
increases, DF-GED becomes faster as it ex-
plores the search tree in a depth-first way (i.e., not
stopped by C
M
) while pruning the search tree thanks
to its upper and lower bounds as well as the prepro-
cessing step, see Section 4.3. On the other hand,
DistributedGraphMatchingandGraphIndexingApproaches-ApplicationstoPatternRecognition
11
GREC5 GREC10 GREC15 GREC20 GREC−mix
Number of vertices
Mean deviation in (%)
0 20 40 60 80 100
A*GED
DF−GED
GREC5 GREC10 GREC15 GREC20 GREC−mix
Number of vertices
Mean deviation in (%)
0 20 40 60 80
A*GED
DF−GED
Figure 5: Deviation. Left:(350 milliseconds), Right:(5 min-
utes).
GREC5 GREC10 GREC15 GREC20 GREC−mix
Number of vertices
Mean running time in milliseconds
0 100 200 300 400 500 600
A*GED
DF−GED
GREC5 GREC10 GREC15 GREC20 GREC−mix
Number of vertices
Mean running time in milliseconds
0 50000 150000 250000 350000
A*GED
DF−GED
Figure 6: Running Time. Left:(350 milliseconds), Right:(5
minutes).
A*GED does not continue for further exploration on
GREC15 and GREC20 because of the size of the in-
volved graphs where available memory is exhausted
and so the best recently known solution is given be-
fore halting.
For the classification experiment, 151008 compar-
isons are performed on 286 training graphs and 528
test graphs of the GREC dataset. As depicted in Ta-
ble 1, results show that the classification accuracy AC
of DF-GED is 2.3 times higher under the same C
T
where C
T
=500 milliseconds. Moreover, DF-GED is
1.7 times faster as the average time t is smaller.
Table 1: Classifying graphs of GREC (C
T
= 500 millisec-
onds).
Algorithms t AC
A*GED 119491.5 ms 42.23%
DF-GED 69006.3 ms 98.48 %
8 CONCLUSION AND
PERSPECTIVES
As presented in this report, we have discussed the first
part of the thesis, we have considered the problem
of GED computation for PR. Graph edit distance is
a powerful and flexible paradigm that has been used
in different applications in PR. The exact algorithm,
A*GED, presented in the literature suffers from high
memory consumption and thus cannot match large
graphs due to the exponential complexity of GED
computation. In this report, we proposed another ex-
act GED algorithm, DF-GED, which is based on a
depth-first tree search. This algorithm speeds up the
computations of graph edit distance thanks to its up-
per and lower bounds pruning strategy and its prepro-
cessing step. Moreover, this algorithm does not ex-
haust memory as the number of pending edit paths
that are stored in the set OPEN is relatively small
thanks to the depth-first search where the number of
pending nodes is |V 1|.|V 2| in the worst case.
In the experimental section, we have proposed to
evaluate sub-optimally both exact methods: A*GED
and DF-GED under some memory and time con-
straints. Experiments on the GREC database em-
pirically demonstrated that DF-GED outperforms
A*GED in terms of accuracy, speed and classification
rate. For future work, we aim at measuring the qual-
ity of solutions found by our distributed approach (D-
DF) as well as the aforementioned approximate meth-
ods. All these different graph edit distance computa-
tions will be evaluated on different PR databases. We
expect D-DF to outperform other methods in terms of
accuracy. We also want to conduct a scalability study
to show the importance of such a flexible distributed
approach for solving PR problems.
In the next phase of the thesis, we also aim
at proposing a distributed graph-indexing approach
where a graph g is fragmented and indexed in a fully
distributed manner.
REFERENCES
(1998). A genetic algorithm and its parallelization for graph
matching with similarity measures. 2(2):68–73.
A.D.J. Cross, R. W. and Hancock, E. (1997). Inexact graph
matching using genetic search. Pattern Recognition,
pages 953–970.
Allen, R., C. L. M. S. T. S. S. L. and Yasuda, D. (1997). A
parallel algorithm for graph matching and its maspar
implementation. Pattern Recognition, page 490501.
Andreas Fischer, Ching Y. Suen, V. F. K. R. H. B. (2013). A
fast matching algorithm for graph-based handwriting
recognition. GbRPR 2013, pages 194–203.
Andrew D. J. Cross, E. R. H. (1998). Graph matching with
a dual-step em algorithm. IEEE Trans. Pattern Anal.
Mach. Intell., 20:1236–1253.
Bunke, H. (1983). Inexact graph matching for struc-
tural pattern recognition. Pattern Recognition Letters,
1(4):245–253.
Combier, C., Damiand, G., and C., S. (2013). Map edit
distance vs graph edit distance for matching images.
In Proc. of 9th Workshop on Graph-Based Represen-
tation in Pattern Recognition (GBR), volume 7877,
pages 152–161.
ICPRAM2015-DoctoralConsortium
12

Conte, D., Foggia, P., Sansone, C., and Vento, M. (2004).
Thirty Years of Graph Matching. 18(3):265–298.
Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,
C. (2009). Introduction to Algorithms, Third Edition.
The MIT Press, 3rd edition.
Dean, J., G. S. (2004). Mapreduce : Simplified data pro-
cessing on large clusters. Symposium on Operating
Systems Design and Implementation., 28:137149.
Fankhauser, S., Riesen, K., Bunke, H., and Dickinson, P. J.
(2012). Suboptimal graph isomorphism using bipar-
tite matching. IJPRAI, 26.
Finch, Wilson, e. a. (1998). An energy function and contin-
uous edit process for graph matching. Neural Compu-
tat, 10.
Justice, D. and Hero, A. (2006). A binary linear program-
ming formulation of the graph edit distance. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 28(8):1200–1214.
Kollias, G. (2012). Fast parallel algorithms for graph simi-
larity and matching.
Kuner, P. and Ueberreiter, B. (1988). Pattern recognition
by graph matching: Combinatorial versus continuous
optimization. International Journal in Pattern Recog-
nition and Artificial Intelligence, 2:527542.
M. Neuhaus, K. R. and Bunke., H. (2006). Fast suboptimal
algorithms for the computation of graph edit distance.
Proceedings of 11th International Workshop on Struc-
tural and Syntactic Pattern Recognition., 28:163172.
Patwary, M. M. A., Bisseling, R. H., and Manne, F. (2010).
Parallel greedy graph matching using an edge parti-
tioning approach. Proceedings of the fourth interna-
tional workshop on High-level parallel programming
and applications - HLPP ’10, page 45.
Plantenga, T. (2013). Inexact subgraph isomorphism in
mapreduce. Journal of Parallel and Distributed Com-
puting, page 164175.
Qiu, H. and Hancock, E. R. (2006). Graph matching and
clustering using spectral partitions. Pattern Recogni-
tion, 39(1):22–34.
Riesen, K., B. H. (2009). Approximate graph edit distance
computation by means of bipartite graph matching.
Image and Vision Computing., 28:950959.
Riesen, K., Fankhauser, S., and Bunke, H. (2007). Speed-
ing up graph edit distance computation with a bipartite
heuristic. In MLG.
Sanfeliu, A. and Fu, K. (1983). A distance measure be-
tween attributed relational graphs for pattern recogni-
tion. IEEE Transactions on Systems, Man, and Cyber-
netics, 13:353–362.
Tsai, W.-H. and Fu, K.-S. (1979). Error-correcting isomor-
phisms of attributed relational graphs for pattern anal-
ysis. Systems, Man and Cybernetics, IEEE Transac-
tions on, 9(12):757–768.
Tsai, W. H. and Fu, K. S. (1983). IEEE Transactions on
Systems, Man and Cybernetics, pages 48–62.
Vento, M. (2014). A long trip in the charming world of
graphs for pattern recognition. Pattern Recognition.
W. Christmas, J. K. and Petrou., M. (1995). Structural
matching in computer vision using probabilistic relax-
ation. IEEE Trans. PAMI,, 2:749764.
Zeng, Z., Tung, A. K. H., Wang, J., Feng, J., and Zhou,
L. (2009). Comparing stars: On approximating graph
edit distance.
DistributedGraphMatchingandGraphIndexingApproaches-ApplicationstoPatternRecognition
13
