The Effect of Concurrent Programming Idioms on Veriﬁcation

A Position Paper

David Harel

, Guy Katz

, Assaf Marron

and Gera Weiss

Dept. of Computer Science and Applied Mathematics, The Weizmann Institute of Science, Rehovot, Israel

Dept. of Computer Science, Ben Gurion University, Beer-Sheva, Israel

Keywords:

Concurrency, Veriﬁcation, Design for Veriﬁcation, Behavioral Programming.

Abstract:

In recent years formal veriﬁcation techniques have become an important part of the development cycle of

concurrent software. In order to tackle the state explosion problem and verify larger systems, a great deal

of work has been put into improving the scalability of veriﬁcation tools. In this work, we seek to draw

attention to an alternative/complementary approach to improving scalability, which sometimes receives less

notice: the effect the concurrent programming model itself has on one’s ability to verify programs encoded

within it. Recent work suggests that a suitable choice of model, tailored to the problem at hand, may render

the produced software more amenable to veriﬁcation techniques. We recapitulate some recent and new results

demonstrating this effect in programming models for discrete, synchronous reactive systems, and outline some

directions for future work. We hope that the paper will trigger additional research on this important topic.

1 INTRODUCTION

Concurrent reactive systems are typically character-

ized by a myriad of threads and services running in

parallel, continuously interacting with each other and

with their environment. Errors in these systems often

do not originate from single threads or components,

but are the result of unexpected interleaving of sets

thereof. Hence, they tend to be hard to predict, under-

stand and prevent.

In recent decades, a prominent approach for tack-

ling this issue has been that of formal veriﬁcation.

There, one relies on automatic tools that methodi-

cally explore the state space of the system, looking

for bugs. The main hindrance to the applicability of

formal veriﬁcation to large systems is the state explo-

sion phenomenon: the size of the state space of a sys-

tem can be exponential in the size of its constituent

components. This makes it difﬁcult to impossible for

veriﬁcation techniques to scale up to real-world sys-

tems.

In its ongoing attempts to improve the scalability

of veriﬁcation tools, the research community has di-

rected a great deal of effort into ﬁnding more efﬁcient

ways to detect bugs, which do not entail explicitly

enumerating and visiting every state of the system. A

few notable examples include the efﬁcient traversal of

state graphs using BDDs (Bryant, 1986; Burch et al.,

1990), ignoring redundant thread interleaving via par-

tial order reductions (Alur et al., 1997), compositional

veriﬁcation (Grumberg and Long, 1994), abstraction-

reﬁnement based techniques (Clarke et al., 2000), and

also the use of theorem provers and SMT solvers for

veriﬁcation (De Moura and Bjørner, 2011; Ghilardi

and Ranise, 2012).

In this position paper we seek to draw attention

to an aspect of the veriﬁcation problem which, we

feel, has received less attention: the effect the se-

lected computational model (e.g., the programming

language idioms) has on the complexity of software

veriﬁcation. It is now widely accepted that a great

many bugs result from the “unconstrained” concur-

rency that characterizes modern programming lan-

guages (Lu et al., 2008), and also that some advanced

programming language features (e.g., pointers, alias-

ing) are very difﬁcult for veriﬁcation tools to handle.

The approach that we advocate in this work is a de-

sign for veriﬁcation approach: by carefully choos-

ing the programming idioms to use in the develop-

ment of a particular system, one can program in a

rich and expressive environment, but at the same time

reduce concurrency in the program, making it more

amenable to formal analysis. This direction is or-

thogonal to the advanced veriﬁcation techniques men-

tioned in the previous paragraph, and, as we later

demonstrate, a combination of both may result in im-

363

Harel D., Katz G., Marron A. and Weiss G..

The Effect of Concurrent Programming Idioms on Veriﬁcation - A Position Paper.

DOI: 10.5220/0005324203630369

In Proceedings of the 3rd International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2015), pages 363-369

ISBN: 978-989-758-083-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

proved performance of the analysis tools.

This approach naturally raises the question of

which computational model to use. From a veriﬁ-

cation point of view, the simpler the model, the bet-

ter, but from a software engineering point of view ad-

vanced features are needed to make the model attrac-

tive to programmers. Indeed, this is a trade-off that

needs to be addressed intelligently. As part of our at-

tempts to answer this question, we have been studying

idioms for concurrent programming, attempting to

measure the veriﬁcation-wise cost of including them

in a programming model on one hand, and their use-

fulness as programming idioms on the other. Some of

our recent results appear in later sections. Our ulti-

mate goal is to offer engineers a pool of programming

idioms, with a detailed analysis of the beneﬁts and

costs of each, thus helping them tailor the program-

ming framework to their needs.

In the following sections we demonstrate the

principles of our approach by focusing on the re-

cently proposed behavioral programming paradigm

for scenario-based programming (Harel et al., 2012),

and its main concurrency idioms: the requesting,

waiting-for and blocking of events. Recent work

shows that this relatively simple model may be ap-

pealing to programmers, but may also facilitate ver-

iﬁcation. Our main goal is not to claim that behav-

ioral programming is necessarily the best program-

ming model for veriﬁcation — but rather to encourage

additional discussion and research on this topic, by

demonstrating the connection between the program-

ming model and veriﬁcation complexity.

The rest of this paper is organized as follows. Sec-

tion 2 introduces behavioral programming. In Sec-

tion 3 we discuss the compositional veriﬁcation of this

model, and in particular the effect that its program-

ming idioms have on the veriﬁcation complexity. In

Section 4 we discuss the advantageous effect certain

programming idioms may have on another aspect of

the veriﬁcation problem — program repair. Related

work appears in Section 5, and we conclude in Sec-

tion 6.

2 BEHAVIORAL

PROGRAMMING

Behavioral programming (BP) (Harel et al., 2012) is a

programming approach, aimed particularly at design-

ing and incrementally developing reactive systems.

BP emerged from the live sequence charts (LSCs)

programming language (Damm and Harel, 2001) and,

like LSCs, it is a scenario-based paradigm. Intu-

itively, a behavioral program is a collection of scenar-

ios, each corresponding to one desired or undesired

system behavior. During execution these scenarios

are woven together, producing cohesive system be-

havior.

More formally, a behavioral program consists of

independent threads of behavior (each encoding a sin-

gle scenario) that are interwoven at run time. Each be-

havior thread (abbr. b-thread) speciﬁes events which,

from its own point of view must, may, or must not oc-

cur. These threads are then run simultaneously, and

are synchronized by an execution infrastructure re-

sponsible for selecting events that constitute the in-

tegrated system behavior.

A key principle in the BP model is that b-threads

do not communicate with each other directly; in-

stead, at every execution cycle, they each declare

events that they want to be considered for trigger-

ing (called requested events), events that they do not

actively request but simply “listen out” for (waited-

for events), and events whose triggering they forbid

(blocked events). Once this information has been col-

lected from all participating threads, the execution in-

frastructure triggers one event that is requested and

is not blocked, and resumes all b-threads that re-

quested or waited for that event. Figure 1 (borrowed

from (Harel et al., 2014)) demonstrates a simple be-

havioral application. In practice, behavioral programs

are implemented using various high level languages,

such as Java, C++, Erlang, Javascript and, of course,

LSCs (see the BP website at http://www.b-prog.org/).

wait for

WaterLow

request

AddHot

request

AddHot

request

AddHot

wait for

WaterLow

request

AddCold

request

AddCold

request

AddCold

wait for

AddHot

while

blocking

AddCold

wait for

AddCold

while

blocking

AddHot

Stability

···

WaterLow

AddHot

AddCold

AddHot

AddCold

AddHot

AddCold

···

Event Log

Figure 1: (From (Harel et al., 2014)) Incremental develop-

ment of a system for controlling water level in a tank with

hot and cold water sources. The b-thread AddHot repeat-

edly waits for WaterLow events and requests three times

the event AddHot. AddCold performs a similar action with

the event AddCold, capturing a separate requirement, which

was introduced when adding three water quantities for every

sensor reading proved to be insufﬁcient. When AddHot and

AddCold run simultaneously, with the ﬁrst at a higher pri-

ority, the runs will include three consecutive AddHot events

followed by three AddCold events. When a new require-

ment is introduced, to the effect that that water temperature

be kept stable, the b-thread Stability is added, enforcing

the interleaving of AddHot and AddCold events by using

event blocking.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

364

The software-engineering motivation for using BP

is its strict and simple synchronization mechanism.

By having all threads repeatedly synchronize, and

interact only indirectly — through requested and

blocked events — BP facilitates incremental, non-

intrusive development, and the resulting systems of-

ten have threads that are aligned with the speciﬁca-

tion (Harel et al., 2012). Additional studies also indi-

cate that BP is natural, in the sense that it is easy to

learn and fosters abstract programming (Gordon et al.,

2012; Alexandron et al., 2014).

We recap the formal deﬁnitions of BP, as they ap-

pear in (Harel et al., 2010; Katz, 2013). A b-thread

BT over event set E is a tuple BT = hQ, δ, q

, R, Bi,

where Q is a set of states (one for each synchro-

nization point), q

is the initial state, R : Q → 2

and B : Q → 2

map states to the sets of events re-

quested and blocked at these states (respectively), and

δ : Q × E → 2

is a transition function.

Behavioral programs are created by composing

b-threads. The parallel composition of threads BT

, δ

, q

, R

, B

i and BT

= hQ

, δ

, q

, R

, B

i over

the common event set E yields the b-thread deﬁned by

k BT

= hQ

× Q

, δ, hq

, q

i, R

∪ R

, B

∪ B

where h ˜q

, ˜q

i ∈ δ(hq

, q

i, e) if and only if ˜q

∈

, e) and ˜q

∈ δ

, e). The union of the label-

ing functions is deﬁned in the natural way; i.e. e ∈

∪ R

)(hq

, q

i) if and only if e ∈ R

) ∪ R

A behavioral program P comprised of b-threads

, BT

, . . . , BT

is the composite thread P = BT

. . . k BT

Let P = hQ, δ, q

, R, Bi. An execution of P starts

from q

, and in each state q along the run an enabled

event is chosen for triggering, if one exists (i.e., an

event e ∈ R(q) − B(q)). Then, the execution moves to

state ˜q ∈ δ(q, e), and so on. An execution can be in-

ﬁnite, or ﬁnite if it ends in a state with no successors

(a deadlock state); and it can be formally recorded

as a (possibly inﬁnite) sequence of states and trig-

gered events, ε = q

→ q

→ ·· ·. The matching set

of events, without states, is called a run. The set of all

runs of the program is denoted by L(P).

In (Harel et al., 2011; Harel et al., 2013a), it is

demonstrated how the transition systems underlying

b-threads can be automatically extracted from high

level code, composed, and then traversed in order to

verify safety and liveness properties. In (Katz, 2013),

this model checking technique is enhanced with ab-

straction capabilities: b-threads are replaced with ab-

stract versions thereof, in which multiple states are

symbolically represented by a single state, with ad-

justed requested and blocked events.

3 SUCCINCTNESS AND

COMPOSITIONAL

VERIFICATION

A key technique in combating state explosion, which

has been studied extensively, is compositional veriﬁ-

cation (Grumberg and Long, 1994): instead of span-

ning the entire composite state graph in order to ver-

ify the program (effectively transforming a concurrent

program into an equivalent, sequential program), the

idea is to ﬁrst prove sub-properties on individual mod-

ules/threads, and then show, by some sort of reason-

ing, that the sub-properties entail the desired global

property. By verifying each module separately, the

exploration of composite states is avoided.

Compositional veriﬁcation is easy to grasp but dif-

ﬁcult to perform: breaking the system down into mod-

ules, and especially coming up with the “right” mod-

ule properties, can prove tricky (and sometimes even

impossible (Cobleigh et al., 2006)). In modern pro-

gramming languages, concurrent threads may affect

each other in many subtle ways, and hence it is dif-

ﬁcult to capture and formulate the properties of just

one module, in isolation. Given these facts, we ar-

gue that a computational model is “compatible” with

compositional veriﬁcation if two conditions hold:

1. Programs in the model may be broken down into

modules, such that verifying properties of the

modules is substantially cheaper than verifying

the composite program.

2. The modules are such that it is possible (prefer-

ably straightforward) to formulate meaningful

module properties, which may later imply the de-

sired global property.

The trade-off we discussed earlier, between the

need to have a model that is easy to verify and adding

more advanced features to make the model usable, ex-

ists here too: the more advanced features we add, the

smaller the modules we can have — but the modules’

ability to inﬂuence each other in a variety of ways

makes it harder to formulate the properties of just a

single one. Thus, we argue, it is desirable to have

a computational model that has just enough concur-

rency in it to make the modules small, but not too

much concurrency, so that reasoning about them re-

mains easy. Clearly, the program in question plays a

role in determining what “just enough concurrency”

means, depending on the tasks at hand. In the remain-

der of the section, we discuss the beneﬁts of using a

simple concurrency model — in this case, BP — in

compositional veriﬁcation.

The topic of compositionally verifying behavioral

programs was discussed in (Harel et al., 2013b).

TheEffectofConcurrentProgrammingIdiomsonVerification-APositionPaper

365

a, b

R = {a}

B = {b}

R = {a, b}

B =

Thread 1

a a

a, b

R = {a}

B = {b}

R = {a}

B = {b}

R = {a, b}

B =

Thread 2

R =

B =

R =

B = {a, b}

Thread 3

Figure 2: (From (Harel et al., 2013b)) Compositional veriﬁcation of a behavioral application. In the depicted program, Thread

1 counts modulo two: on odd steps it requests event a and blocks event b, and on even steps it requests both events. Thread 2

is similar, but counts modulo three, and only requests both events every third step. Together, these two threads count modulo

6, producing the language (a

(a + b))

. The ﬁnal thread, Thread 3, encodes the property to be checked: that event b is never

triggered (and thus, the program is unsafe). If b is triggered, this thread moves to its “bad” state (marked in red).

Verifying this program directly would entail spanning the composite state graph (2 ·3 ·2 = 12 states). In (Harel et al., 2013b),

we demonstrate a compositional approach, by ﬁrst expressing thread properties as logical lemmas. For Thread 1, this lemma

is: triggered(b, i) =⇒ i ≡ 0(mod 2), where triggered(b, i) means that the i’th event triggered was b; and for Thread 2, the

lemma is triggered(b, i) =⇒ i ≡ 0(mod 3). Using these lemmas, an SMT solver can deduce that if a violation occurs, it

occurs in the 6th step; and then, the intermediate composite states can be ignored. Intuitively, the number of states explored in

this process is the sum of the threads’ sizes, instead of the product thereof. That paper demonstrates a signiﬁcant improvement

in veriﬁcation run time when compositional veriﬁcation is applied to this example, and others.

There, thread properties are summarized as logical

formulas, which are then given to an SMT solver

that proves the global property. An example (adopted

from that paper) appears in Figure 2. The key ob-

servation is that in a simple and strict computational

model it is possible to reason about modules without

resorting to more complex assume-guarantee proofs

(e.g., (Henzinger et al., 1998; Flanagan et al., 2002))

or the circular reasoning sometimes required in less

constrained paradigms. In our opinion, such exam-

ples serve as evidence that condition 2 above may be

satisﬁed by using this kind of simple model.

The other requirement we mentioned (condition 1)

was that verifying module properties, such as those in

Figure 2, be cheaper than verifying the global prop-

erty on the composite system. In practice, since

model-checking is linear in the size of the program,

this can be translated into having modules that are

exponentially smaller than the composite program in

terms of the number of states. Clearly, concurrency

allows one to write smaller modules; but will the lim-

ited kind of concurrency afforded by the BP synchro-

nization method and its request, wait-for and block

idioms sufﬁce?

New results that we have obtained (to appear sepa-

rately) indicate that each of the three requesting, wait-

ing and blocking idioms affords an exponential in-

crease in succinctness; that is, each of the idioms

enables the writing of programs in an exponentially

more compact manner than the best possible with-

out it (see Figure 3). More speciﬁcally, we show

that the request idiom allows one to succinctly encode

programs that contain a disjunction of constraints;

the blocking idiom does the same for conjunctions;

and the wait-for idiom allows the creation of succinct

threads that cooperate in achieving a shared goal. In

fact, the example of Figure 2 includes a conjunction of

constraints (that event b be allowed only in indices di-

visible by both 2 and 3), and hence the blocking idiom

is suitable there. Further, our results show that when

these idioms afford an exponential improvement in

succinctness, even a far more liberal model (e.g., the

Statecharts model (Harel, 1987), in which each mod-

ule is completely aware of the internal state of other

modules) cannot improve this succinctness further.

R W B

W B

R W

R B

Figure 3: The succinctness afforded by programming mod-

els comprised of combinations of the request (R ), wait-for

(W ) and block (B) idioms. Each arrow indicates a tight

exponential gap in succinctness: some programs, when

“moved” from the source model to the target model, must

increase exponentially in size. The ﬁgure shows that the

omission of any of the three idioms results in a blowup for

some classes of programs. A precise mathematical formu-

lation of these properties and their proofs will be published

separately.

4 PROGRAM REPAIR

In this section we discuss another aspect of formal

veriﬁcation, which deals also with the correction of

bugs, separately from their detection. In program re-

pair, one takes as input a program with a bug, and at-

tempts to turn it into a correct program. Common ap-

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

366

proaches to the repair of general programs include re-

placing faulty modules with synthesized ones (Staber

et al., 2005; Jobstmann et al., 2005), and genetic and

co-evolution based techniques (Arcuri and Yao, 2008;

Weimer et al., 2010).

In (Harel et al., 2014; Katz, 2013) we show that

using a simple concurrency model can have beneﬁcial

effects on program repair as well. Speciﬁcally, we

demonstrate repair algorithms for BP which widely

leverage the blocking idiom. This form of repair has

the important advantage that it is non-intrusive; i.e., it

is performed strictly by adding new modules.

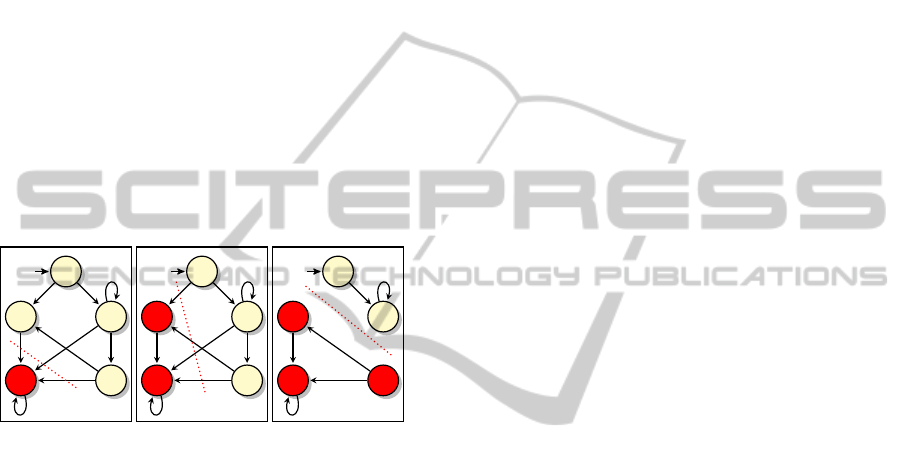
Figure 4 demonstrates the repair of a safety viola-

tion (i.e., an error of the form “something bad hap-

pens”) in a behavioral program. Intuitively, when-

ever a violating run is found, a new “patch” thread

designed to prevent the error is added to the program.

This new thread utilizes the event blocking idiom in

order to prevent the sequence of events leading to the

bad state from occurring.

III

Figure 4: (From (Katz, 2013)) Automatically repairing a

safety violation in a behavioral program. The safety vio-

lation occurs when a red state is reached. The violation is

ﬁxed using event blocking, which effectively trims edges

from the graph. Graph I depicts the initial conﬁguration,

with only one bad state: q

. The edges leading to q

cross

the dotted red line, and are candidates for blocking. In the

ﬁrst iteration, blocking these edges would cause a deadlock

in state q

. Thus, in graph II state q

is also marked as bad.

Unfortunately, blocking the edges that now cross the dotted

line would create a deadlock in state q

, and so we iterate

again. Only then, in graph III, can edges crossing the dotted

line be safely removed without causing deadlocks. The red

states are thus rendered unreachable, ﬁxing the safety vio-

lation. This form of repair is made possible because of the

blocking idiom, and because of the simple and strict syn-

chronization mechanism between b-threads.

The second type of error covered in (Harel et al.,

2014) is that of liveness violations; i.e. that “some-

thing good that should happen, does not”. This type

of bug is likewise repaired using the blocking idiom:

whenever it is detected that the system is traversing a

cycle in which no good events occur, a repair thread

occasionally blocks all the events that do not lead the

system towards a good event. Thus, with only min-

imal interference, the system is “steered back” to-

wards the correct course. As is the case with safety

violations, repairing liveness violations is performed

strictly by adding new modules to the program.

These examples indicate that it may be worthwhile

to study the beneﬁts of various concurrency idioms,

from BP and from other computational models, for

additional formal and semi-formal methods: static

analysis, design-by-contract approaches, combinato-

rial test designs, etc.

5 RELATED WORK

The design for veriﬁcation approach has appeared in

several studies over the years. In (Austin, 2001), the

author challenges engineers to design systems that are

easier to verify, focusing on separation of concerns, so

that modules may be veriﬁed in isolation. A similar

approach appears in (Kharmeh et al., 2011), where the

authors discuss implementing communication proto-

cols from pre-veriﬁed blocks, in order to more easily

guarantee their correctness. Our work offers a dif-

ferent/complementary perspective on this topic: in-

stead of focusing on design patterns and pre-veriﬁed

modules, we seek to adjust the entire computational

model, removing some features while retaining oth-

ers, in order to assist veriﬁcation tools. Naturally,

what all these approaches have in common is that they

are more likely to succeed if the programmer coop-

erates; i.e., if he/she attempts to write code that is

amenable to veriﬁcation.

In (Klein et al., 2010), the authors present the de-

sign for veriﬁcation of a complete microkernel (nearly

10,000 lines of code). They discuss design patterns

that they favored and those that they avoided in order

to facilitate veriﬁcation. Another set of design pat-

terns that facilitates veriﬁcation, this time aimed at de-

signing air trafﬁc control software, appears in (Betin-

Can et al., 2005), and additional rules, evaluated on

a robot control software system, appear in (Sharygina

et al., 2001). These studies and similar ones can hope-

fully serve to identify programming idioms that are

more amenable to veriﬁcation than others.

6 CONCLUSION AND FUTURE

WORK

The formal veriﬁcation of software is a tremendously

important task given today’s large systems, but is still

very difﬁcult. The development of more efﬁcient ver-

iﬁcation algorithms and tools is thus a worthy en-

deavor, and has already born much fruit. However,

there seems to be untapped potential in designing

TheEffectofConcurrentProgrammingIdiomsonVerification-APositionPaper

367

software in a way that makes it more veriﬁcation com-

patible: by carefully choosing a computational model

that is on one hand expressive and convenient, and on

the other hand amenable to formal veriﬁcation tools,

one can often achieve improved scalability.

We have demonstrated these principles on three

idioms for concurrent programming — the request-

ing, waiting-for and blocking of events, which to-

gether make up the BP model. We recapitulated work

showing that, because of its strict synchronization

protocol, the BP model produces programs that may

be more amenable to compositional reasoning and re-

pair than less restricted concurrent models, and yet

that a behavioral program may be signiﬁcantly more

succinct than an equivalent sequential program.

Our work focused on BP, which is but one

paradigm among many for discrete event reactive sys-

tems. As discussed earlier, a key ingredient in our

proposed approach is an appropriate mapping of pro-

gramming idioms to problems they can solve, and

their respective costs, veriﬁcation-wise. In order to

fully harness this synergy in practice, extensive study

of additional idioms is required. For instance, it

would be interesting to compare results for BP with

other models for reactivity such as BIP (Basu et al.,

2006), Signal (Le Guernic et al., 1991) and Lus-

tre (Halbwachs et al., 1991).

In the longer run, we envision an extensive catalog

of idioms for programmers to choose form, according

to the problem at hand. Perhaps in the further away

future these decisions could even be performed by an

automated recommender system.

ACKNOWLEDGEMENTS

The work of all the authors was supported by an Israel

Science Foundation grant. The research of G. Weiss

was also supported by the Lynn and William Frankel

Center for CS at Ben-Gurion University, and by a

reintegration (IRG) grant under the European Com-

munity’s FP7 Programme.

REFERENCES

Alexandron, G., Armoni, M., Gordon, M., and Harel, D.

(2014). Scenario-Based Programming: Reducing the

Cognitive Load, Fostering Abstract Thinking. In Proc.

36th Int. Conf. on Software Engineering (ICSE), pages

311–320.

Alur, R., Brayton, R. K., Henzinger, T. A., Qadeer, S., and

Rajamani, S. K. (1997). Partial-Order Reduction in

Symbolic State Space Exploration. In Proc. 9th. Int.

Conf. on Computer Aided Veriﬁcation (CAV), pages

340–351.

Arcuri, A. and Yao, X. (2008). A Novel Co-evolutionary

Approach to Automatic Software Bug Fixing. In Proc.

10th IEEE Congress on Evolutionary Computation

(CEC), pages 162–168.

Austin, T. (2001). Design for veriﬁcation? IEEE Design &

Test of Computers, 18(4):80–80.

Basu, A., Bozga, M., and Sifakis, J. (2006). Modeling Het-

erogeneous Real-time Systems in BIP. In Proc. 4th

IEEE Int. Conf. on Software Engineering and Formal

Methods (SEFM), pages 3–12.

Betin-Can, A., Bultan, T., Lindvall, M., Lux, B., and Topp,

S. (2005). Application of Design for Veriﬁcation with

Concurrency Controllers to Air Trafﬁc Control Soft-

ware. In Proc. 20th. Int. Conf. on Automated Software

Engineering (ASE), pages 14–23.

Bryant, R. E. (1986). Graph-Based Algorithms for Boolean

Function Manipulation. IEEE Trans. on Computers,

100(8):677–691.

Burch, J., Clarke, E., McMillan, K., Dill, D., and Hwang,

L. (1990). Symbolic Model Checking: 10

States

and Beyond. In Proc. 5th IEEE Annual Symposium on

Logic in Computer Science (LICS), pages 428–439.

Clarke, E., Grumberg, O., Jha, S., Lu, Y., and Veith, H.

(2000). Counterexample-Guided Abstraction Reﬁne-

ment. In Proc. 12th Int. Conf. on Computer Aided

Veriﬁcation (CAV), pages 154–169.

Cobleigh, J., Avrunin, G., and Clarke, L. (2006). Breaking

Up is Hard to do: an Investigation of Decomposition

for Assume-Guarantee Reasoning. In Proc. Int. Symp.

on Software Testing and Analysis (ISSTA), pages 97–

108.

Damm, W. and Harel, D. (2001). LSCs: Breathing Life into

Message Sequence Charts. J. on Formal Methods in

System Design, 19(1):45–80.

De Moura, L. and Bjørner, N. (2011). Satisﬁability Modulo

Theories: Introduction and Applications. Communi-

cations of the ACM, 54(9):69–77.

Flanagan, C., Freund, N. S., and Qadeer, S. (2002). Thread-

Modular Veriﬁcation for Shared-Memory Programs.

In Proc. 11th. European Symp. on Programming Lan-

guages and Systems (ESOP), pages 262–277.

Ghilardi, S. and Ranise, S. (2012). MCMT: A Model

Checker Modulo Theories. In Proc. 5th Int. Joint

Conf. on Automated Reasoning (IJCAR), pages 22–29.

Gordon, M., Marron, A., and Meerbaum-Salant, O. (2012).

Spaghetti for the Main Course? Observations on

the Naturalness of Scenario-Based Programming. In

Proc. 17th Conf. on Innovation and Technology in

Computer Science Education (ITICSE), pages 198–

203.

Grumberg, O. and Long, D. (1994). Model Checking and

Modular Veriﬁcation. ACM Trans. Program. Lang.

Syst., 16(3):843–871.

Halbwachs, N., Caspi, P., Raymond, P., and Pilaud, D.

(1991). The Synchronous Data-Flow Programming

Language LUSTRE. Proc. of the IEEE, 79(9):1305–

1320.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

368

Harel, D. (1987). Statecharts: A visual formalism for com-

plex systems. Science of Computer Programming,

8(3):231–274.

Harel, D., Kantor, A., and Katz, G. (2013a). Relaxing Syn-

chronization Constraints in Behavioral Programs. In

Proc. 19th Int. Conf. on Logic for Programming, Arti-

ﬁcial Intelligence and Reasoning (LPAR), pages 355–

372.

Harel, D., Kantor, A., Katz, G., Marron, A., Mizrahi, L.,

and Weiss, G. (2013b). On Composing and Proving

the Correctness of Reactive Behavior. In Proc. 13th

Int. Conf. on Embedded Software (EMSOFT), pages

1–10.

Harel, D., Katz, G., Marron, A., and Weiss, G. (2014). Non-

Intrusive Repair of Safety and Liveness Violations in

Reactive Programs. Transactions on Computational

Collective Intelligence (TCCI), 16:1–33.

Harel, D., Lampert, R., Marron, A., and Weiss, G. (2011).

Model-Checking Behavioral Programs. In Proc. 11th

Int. Conf. on Embedded Software (EMSOFT), pages

279–288.

Harel, D., Marron, A., and Weiss, G. (2010). Program-

ming Coordinated Scenarios in Java. In Proc. 24th

European Conf. on Object-Oriented Programming

(ECOOP), pages 250–274.

Harel, D., Marron, A., and Weiss, G. (2012). Behav-

ioral Programming. Communications of the ACM,

55(7):90–100.

Henzinger, T. A., Qadeer, S., and Rajamani, S. K. (1998).

You Assume, We Guarantee: Methodology and Case

Studies. In Proc. 10th Int. Conf. on Computer Aided

Veriﬁcation (CAV), pages 440–451.

Jobstmann, B., Griesmayer, A., and Bloem, R. (2005). Pro-

gram Repair as a Game. In Proc. 17th Int. Conf. on

Computer Aided Veriﬁcation (CAV), pages 226–238.

Katz, G. (2013). On Module-Based Abstraction and Re-

pair of Behavioral Programs. In Proc. 19th Int. Conf.

on Logic for Programming, Artiﬁcial Intelligence and

Reasoning (LPAR), pages 518–535.

Kharmeh, S. A., Eder, K., and May, D. (2011). A

Design-For-Veriﬁcation Framework for a Conﬁg-

urable Performance-Critical Communication Inter-

face. In Proc. 9th. Int. Conf. on Formal Modeling and

Analysis of Timed Systems (FORMATS), pages 335–

351.

Klein, G., Andronick, J., Elphinstone, K., Heiser, G., Cock,

D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolan-

ski, R., Norrish, M., et al. (2010). seL4: Formal Veri-

ﬁcation of an Operating-System Kernel. Communica-

tions of the ACM, 53(6):107–115.

Le Guernic, P., Gautier, T., Le Borgne, M., and Le Maire,

C. (1991). Programming Real-Time Applications with

Signal. Proceedings of the IEEE, 79(9):1321–1336.

Lu, S., Park, S., Seo, E., and Zhou, Y. (2008). Learn-

ing from Mistakes: a Comprehensive Study on Real

World Concurrency Bug Characteristics. In Proc.

13th. Int. Conf. on Architectural Support for Program-

ming Languages and Operating Systems (ASPLOS),

pages 329–339.

Sharygina, N., Browne, J. C., and Kurshan, R. P. (2001). A

Formal Object-Oriented Analysis for Software Relia-

bility: Design for Veriﬁcation. In Proc. 4th. Int. Conf.

on Fundamental Approach to Software Engingeering

(FASE), pages 318–332.

Staber, S., Jobstmann, B., and Bloem, R. (2005). Diagnosis

is Repair. In Proc. 16th Int. Workshop on Principles

of Diagnosis (DX), pages 169–174.

Weimer, W., Forrest, S., Le Goues, C., and Nguyen, T.

(2010). Automatic Program Repair with Evolutionary

Computation. Communications of the ACM, 53:109–

116.

TheEffectofConcurrentProgrammingIdiomsonVerification-APositionPaper

369