
A Real-Time Feedback Scheduler based on Control Error for
Environmental Energy Harvesting Systems
Akli Abbas
1,3
, Emmanuel Grolleau
2
, Malik Loudini
3
and Walid-Khaled Hidouci
3
1
Universit´e Akli Mohand Oulhadj de Bouira, Algiers, Algeria
2
Universit´e de Poitiers, ISAE-ENSMA, LIAS lab., Poitiers, France
3
´
Ecole Nationale Sup´erieure d´Informatique (ESI), LCSI lab., Algiers, Algeria
Keywords:
Embedded Systems, Feedback Scheduling, Dynamic Voltage and Frequency Selection (DVFS), Energy
Harvesting, Control Cost.
Abstract:
This paper addresses a real-time scheduling problem inherent to energy harvesting real-time systems. Tradi-
tionally, the energy saving problem is solved mainly by taking into account the tasks scheduling parameters
such as worst-case execution time and period. In this work, we construct a feedback control scheduling
scheme in which a discrete processor speed is assigned according to the control error and available energy.
The real-time control tasks would get high processor speeds when their control errors increase. The experi-
mental evaluation of this solution verifies that the feedback scheduling system based on control error gives a
good compromise between available energy and systems performance.
1 INTRODUCTION
Energy consumption is today an important design
issue of embedded control systems and becomes a
crucial optimization metric. New innovative sys-
tems are designed (e.g. wireless sensors, Internet of
Things) which are aimed to be autonomous energeti-
cally. These systems see the availability of their ser-
vices limited by the amount of energy available in the
batteries over time. Several methods are proposed
for reducing the system energy dissipation, however
any embedded system will eventually exhaust the bat-
tery. In this case and before the device can continue
functioning, replacing or recharging the battery is re-
quired. However, in some applications, replacing bat-
tery is either costly or impractical. Hence, ideally
such a system should be designed to achieveperpetual
functioning without replacing or recharging batteries.
To overcome limitations due to the batteries life, the
alternative energy sources present in our environment
could be exploited to achieve a perpetual operating of
these systems : this is energy harvesting. This ap-
proach extends the batteries life or eliminates them
entirely.
The problem of minimizing energy consumption
while guaranteeing real-time constraints in energy
harvesting systems has been widely addressed in real-
time literature. However, those solutions are all based
on a the Worst-Case Execution Time (WCET) which
is the upper bound of a highly volatile parameter
(Axer et al., 2014), and do not consider the control
performance (control error) and the available energy
in the battery. Our contribution and singularity of our
work lie on this new central working hypothesis.
In this paper, we present a new approach, an en-
vironmental energy-aware feedback scheduler for en-
ergy harvesting real-time systems. Our solution aims
to establish compromise between energy available
and control performance. The objective is to optimiz-
ing the Quality of Control (QoC) and preventing any
energy shortage that would result in the destabiliza-
tion of the controlled process.
The rest of the paper is organized as follows.
We give background materials in section 2. Related
works are described in section 3. In section 4, we
present the computing model, then we give the en-
ergy consumption models. We also present energy
source model which is used to supplement the battery.
Our contribution is presented in section 5. We discuss
our contribution concerning the feedback scheduling
under energy harvesting. Performance results are in-
cluded and discussed in section 6. The main conclu-
sions and some future directions are highlighted in
section 7.
349
Abbas A., Grolleau E., Loudini M. and Hidouci W..
A Real-Time Feedback Scheduler based on Control Error for Environmental Energy Harvesting Systems.
DOI: 10.5220/0005325503490357
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (ESAE-2015), pages 349-357
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 BACKGROUND MATERIAL
2.1 Real-Time Systems and Scheduling
Policy
Real-Time Systems (RTS) are defined as these sys-
tems in which correctness depends not only on the
correct result, but they must also consider time con-
straints, mainly deadlines, to deliver this result. Our
work focuses on soft real-time control tasks i.e. tasks
that may miss deadlines from time to time (in contrast
to the so called hard real-time tasks). As a conse-
quence the objective of our scheduling algorithm is to
optimize the QoC. We use the scheduling theory in or-
der to check temporal constraints. The EDF algorithm
(Liu and Layland, 1973) is probably the most known
fixed-job priority assignment scheduler in real-time
systems. It is optimal regarding schedulability in the
context of independent tasks and preemptive unipro-
cessor scheduling. Our aim in using EDF is to im-
prove the QoC which does not require, as shown later
in this paper, to meet all the deadlines.
2.2 Power Management Techniques
The conventional power management techniques are
classified into two categories based on the nature of
energy dissipation reduction. One of them is Dy-
namic Power Management (DPM). It aims to reduce
the static energy dissipation by switching the active
component to the low power state or shutting down
the idle components. The other technique is Dynamic
Voltage and Frequency Selection (DVFS) which aims
to reduce the dynamic energy dissipation by lowering
the operating frequency of the processor. In our work,
we consider the DVFS capabilities.
3 RELATED WORKS
Traditional real-time scheduling algorithms, after the
seminal works of (Liu and Layland, 1973), that in-
troduced Rate Monotonic (RM) and Earliest Dead-
line First (EDF), are built on precisely known and
fixed timing constraints and depend on workload to
provide performance guarantees in predictable envi-
ronments. However, the Worst-Case Execution Time
(WCET) taken into account in task models is the up-
per bound of a highly volatile parameter (Axer et al.,
2014). In addition, these classical algorithms may
perform poorly in dynamic environments. The feed-
back scheduling (FBS) (Cervin, 2003; Xia, 2006;
˚
Arz´en et al., 2006) offers a promising approach to
overcome these limitations where actual execution
times are not fixed and unknown until the task com-
pletes. Several authors treated the problems of min-
imizing power by combining feedback control meth-
ods and DVFS strategy in order to take the effective
task duration into account. For instance, the popu-
lar PID (Proportional-Integral-Derivative)control has
been integrated into several DVFS algorithms (Soria-
Lopez et al., 2005). A feedback fuzzy-DVFS schedul-
ing method has been developed in (Jin et al., 2007). In
(Xia et al., 2008), a solution is proposed to achieve
further reduction in energy consumption over pure
DVFS while not jeopardizing the quality of control,
the sampling period of each control loop is adapted
to its actual control performance, thus exploring flex-
ible timing constraints on control tasks. However,
these algorithms do not consider energy harvesting
capabilities. For ambient energy harvesting, a variant
of EDF, called Lazy Scheduling Algorithm (LSA) is
proposed in (Moser et al., 2007) to optimally sched-
ule tasks with deadlines, periodic or not. However,
the task slack is not exploited for energy savings and
DVFS was not considered (Liu et al., 2012). Some
heuristics have been compared to LSA in (Chetto and
Zhang, 2010) with no DVFS capabilities. Recently,
in (Chetto, 2014) a novel energy-aware scheduling al-
gorithm, namely ED-H, is presented. This algorithm,
based on WCET, proved to be optimal and appropri-
ate for the scheduling of real time jobs.
In our work, we are concerned with the DVFS
technique that we apply in the so-called real-time en-
ergy harvesting systems. Closely related to our work,
Liu et al. (Liu et al., 2008) proposed a DVFS algo-
rithm (called EA-DVFS) to enhance the performance
of LSA. EA-DVFS adjusts the processor behavior ac-
cording to the stored energy and the energy prediction
(harvested energy in future). Particularly, if the sys-
tem has a sufficient amount of energy, tasks are ex-
ecuted at full speed; otherwise, the processor slows
down to save energy. However, EA-DVFS is based
on WCET and considers one task at a time instead
of considering all tasks together. In addition, since
the EA-DVFS algorithm uses the energy prediction,
it schedules the task at full speed if there may be just
as little as 1% energy left in the energy storage while
the system can operate at full speed for a task without
depleting the energy. That is not the desired behavior.
More recent works can be found in (Liu et al., 2009;
Liu et al., 2012), which also present extensions of
LSA with DVFS technical and permit to improve the
deadline miss rate and energy saving. The proposed
algorithms compute both the start time and finishing
time of every task from timing and energy constraints
such as WCET. As mentioned above, this will lead
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
350

to compute approximate start time and finishing time
and to declare unschedulable task sets that are actu-
ally feasible. Let us mention that in (Liu et al., 2008;
Liu et al., 2009; Liu et al., 2012), tasks are assumed
to execute at full speed if the system has sufficient en-
ergy which causes rapid discharge of the battery and
induces changes in processor frequency. Also, such
approach needs to be provided with a highly predic-
tive model which necessarily has high computation
complexity and memory requirement. This may be
a serious problem for embedded systems with small
memory space. In addition, the solutions proposed
assume negligible overhead due to processor voltage
and frequency switching.
In a previous work (Abbas et al., 2013), we
have proposed a real-time feedback scheduler algo-
rithm for environmental energy harvesting systems,
in which the processor speed can be adjusted continu-
ously. The presented solution accounts for the energy
harvesting capabilities under the variability of tasks
execution times. However, the proposed algorithm
does not account for the available energy. It changes
rapidly and frequently the processor speed (see Fig-
ure 7 and provokes deadline miss. Quality of control
appears to be finally unacceptable. Recently, in (Ab-
bas et al., 2014), we have addressed the same problem
under discrete processor frequency modes. The pro-
posed solution returns, when available energy level
is below the threshold (set offline), the lowest discrete
processor speed proportionally to the available energy
and to the CPU load. However, this solution behaves
like the one proposed (Abbas et al., 2013) when the
portion of the available energy is below the CPU load.
In this paper, we present a new approach, an en-
vironmental energy-aware feedback scheduler for en-
ergy harvesting systems, that dynamically adjusts the
discrete processor frequency according to the control
performance and the available energy. The objective
is to set experimentally a technique for optimizing the
QoC while preventing any energy shortage that would
result in the destabilization of the controlled process.
4 SYSTEM MODELS
In this section, we describe the computing model and
the energy model.
4.1 Computing Model
A typical embedded real-time control system is com-
posed (as illustrated in Figure 1) of plants to be con-
trolled, actuators, sensors and a set of N control tasks
Γ = {τ
i
| 1 ≤ i ≤ N} which are independent and
fully preemptible. Each task is responsible for con-
trolling an independent physical process (plant). The
tasks run concurrently over the same shared proces-
sor.
Figure 1: Embedded real-time control system.
Assume that the processor has M
discrete operating frequencies f
m
:
{ f
m
|1 ≤ m ≤ M, f
min
= f
1
< ... < f
m
= f
max
}.
We define a scaling factor or processor speed S
m
as
the normalized frequency of f
m
with respect to the
maximum frequency f
max
, that is :
S
m
=
f
m
f
max
(1)
We use EDF scheduling policy (Liu and Layland,
1973) where the task priority is proportional to its ur-
gency. A task τ
i
is characterized by the following in-
dependent parameters :
• r
i
, the first release time of the task τ
i
; a task in-
stance is named a job τ
i,k
, k > 0. The job τ
i,0
is
released at the date r
i,0
= r
i
= 0;
• T
i
the release period of the task τ
i
: ev-
ery subsequent job τ
i,k
is released at the date
r
i,k
= (k − 1) × T
i
, k > 0. By default, we
consider the relative deadline of a control task to
be equal to its period;
• e
i
, the absolute error of the task τ
i
: is defined
as the absolute difference between the reference
input x
i
and the plant output y
i
, i.e., e
i
=| x
i
− y
i
|.
In order to compare the solution givenin this work
to other ones based on tasks parameters, we define the
following additional parameter :
• U
inst
(t) =
∑
n
i=1
C
i,1
(t)
T
i
, as the instantaneous proces-
sor utilization. The term C
i,1
(t) is equal to the lat-
est estimated execution time of task τ
i
at time t ac-
cording to the low-passfilter proposed by (Cervin,
2003).
4.2 Energy Consumption Model
We are concerned with the DVFS technique which
is able to reduce the dynamic power dissipation of a
CMOS integrated circuit, such as a modern computer
AReal-TimeFeedbackSchedulerbasedonControlErrorfor
EnvironmentalEnergyHarvestingSystems
351

processor, by reducing the frequency at which it op-
erates. The dynamic power dissipation is given by :
P = C × v
2
× f, where C denotes the effective switch
capacitance related to the type of processor, f is the
frequency and v is the voltage.
In this work, we based our study on the commer-
cial processor XScale (XScale, 2007). Its main char-
acteristics are given in Table 1 (Xu et al., 2007).
Table 1: XScale Parameters.
V(V) 0.75 1.0 1.3 1.6 1.8
F(MHz) 150 400 600 800 1000
S
m
0.15 0.4 0.6 0.8 1
P(mW) 80 170 400 900 1600
Energy switch (1.2 µJ)
Switch time (12 µs)
Idle Power (mW) (63.85 )
We want to compare an algorithm that assumes
continuous change with others assume discrete fre-
quency changes so we need a model of continuous
consumption. According to the relation derived in
(Xu et al., 2007), several power models of this proces-
sor are cited in the literature. Those models describe
the power consumption as a polynomial function of
the processor speed S. We selected the model pre-
sented in (Chen et al., 2013) where the active power
function is written as :
P = 1543.28× S
2.87
+ 63.85 (2)
Figure 2 shows that the continuous approximation
of the power consumed depending on the frequency,
is fitting with the constructor discrete power over fre-
quency values. Therefore, the function shown in Fig-
ure 2 appears to be as realistic as possible, if we were
to assume the existence of a XScale processor able to
change its frequency continuously.
0.15 0.4 0.6 0.8 1
80
170
400
900
1600
Normalized Frequency
Power [mW]
Actual power
63.58+1543.28*S
2.87
Figure 2: Power Consumption function.
For a time interval [t
1
,t
2
], the energy consumption
is given by Ec(t
1
,t
2
) =
R
t
2
t
1
P(S(t))dt.
4.3 Energy Source Model
We assume that the environmental energy, such as so-
lar energy, is harvested and converted into electrical
energy to supplement the battery of an embedded sys-
tem. The solar energy source behavior is modelized
as follows (Moser et al., 2007) :
Ps(t) = |0.9R(t) × cos(
t
0.7π
) × cos(
t
0.1π
)| (3)
where R(t) denotes a uniform distributed random
variable between 0 and 1. The values of Ps have been
cutted off at the value Ps,max = 0.9.
1 2 3 4 5 6 7
0
0.1
0.3
0.5
0.7
0.9
Time
Ps(t)
Figure 3: Power trace Ps(t).
As shown in Figure 3, the obtained power trace
Ps(t) is simulating periods similar to those experi-
enced by solar cells in an outdoor environment.
The input power Ps(t) has excluded the loss in-
curred by auxiliary circuitry. In other words, Ps(t) is
the net power to feed the storage unit. The total en-
ergy, Es(t
1
,t
2
), that is harvested in the time interval
[t
1
,t
2
] is given by Es(t
1
,t
2
) =
R
t
2
t
1
Ps(t)dt.
The system uses an energy storage unit with nom-
inal capacity, (E, expressed in Joules or Watts-hour).
The energy level, denoted as El(t) at a given time t,
has to remain between two boundaries E
min
and E
max
.
If the storage is fully discharged, no task can be ex-
ecuted, and the processor has to be stopped. In con-
trast, if the storage is fully charged, and we continue
to charge it, energy is wasted. To reduce waste and
to ensure QoC, it would be useful to perform tasks at
the maximum CPU speed when the battery is ”almost
full”.
5 FEEDBACK SCHEDULING
BASED ON CONTROL ERROR
5.1 Control Cost Model
Assume that the reference signal x
i
is a square signal
whose period is 2h. The reference signal is run during
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
352

N
r
periods. From a control standpoint, the error be-
tween the reference signal x
i
and the measured signal
y
i
should mirror how good is the control strategy (see
Figure 4 (a)). If we include a decay constraint on the
error we impose by the same way a relative degree of
stability. It is more appropriate to impose (see Figure
4 (b)), at each half signal period, an exponential decay
on the error by forcing the absolute value of the error
to lie inside an envelope limited by a function of the
form: f(t) = k
0
e
− α t
, where the parameters k
0
and
α have to be chosen appropriately by the designer. k
0
and α define the desired relative stability degree.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
−2
0
2
4
(a)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
3
4
(b)
X
i
Y
i
f(t)=k
0
e
− α t
e
i, k
(t)
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
1
2
(c)
I
i
(t)
Figure 4: Parameters illustration of the control cost model.
To appropriately measure the QoC at the execution of
the job τ
i,k
at time t, we define the control cost as :
I
i,k
(t) =sup
0 ; e
i
(t) − k
0
e
−α(t−(q−1)h)
with 1 ≤ q ≤ 2N
r
(4)
where h is the duration of the half period of the refer-
ence signal, N
r
is the running periods, k
0
e
−α(t−(q−1)h)
is the exponential decay function imposed at the q
th
-
half period of the reference signal, e
i
(t) is the abso-
lute error of the task τ
i
at time t. The idea is to con-
sider at each execution of the job τ
i,k
only the positive
value of the difference between the absolute error and
exponential decay function (see Figure 4 (b)).
We assume the FBS task to be executed periodi-
cally with a period T
Fs
. We define the control cost of
the control task τ
i
at the j
th
(j > 0) execution of the
FBS task as :
I
i
=
Z
jT
Fs
( j−1)T
Fs
I
i,k
(t)dt (5)
The idea is to compute the control cost of the control
task τ
i
between two consecutive executions of FBS
task. Note that I
i
allows to measure how far is the i
th
plant from an acceptable behavior. It provides enough
information about plant stability (see Figure 4 (c)).
We assume that if the value I
i
is not null, the corre-
sponding plant is unstable.
For N control tasks, we define the maximum con-
trol cost of the control system as :
I
sys
=
Max
1≤i≤N
I
i
(6)
The use of the Max function is motivated by the
will to give greater attention to the unstable plant.
5.2 Feedback Scheduling Framework
The framework of the proposed scheme is shown in
Figure 5. Aside from the control loops, an outer
feedback loop is introduced to implement feedback
scheduling. The basic role of the feedback scheduler
is to use the amount of available energy and the con-
trol cost given by Eq.6 of each control task as the
feedback information in order to compute a discrete
frequency for the processor.
Plant N
Plant 1
CPU
.
.
.
.
.
.
Feedback
scheduling
y
n
y
1
x
1
x
n
Energy
Source
B a tte ry
Task 1
Scaling factor
Control cost
Energy available
and
Task N
Figure 5: Scheme of the feedback scheduler.
5.3 Presentation of the Algorithm
The objective of our work is to propose a heuristic
(see Algorithm 1) called FSCE-EH (Feedback Sched-
uler based on Control Error for Energy Harvesting)
enabling the execution of tasks with a speed just
above current speed if maximum control cost of the
system I
sys
(see Eq. 6) is greater than 0. Otherwise,
the FSCE-EH returns current speed as a new speed
if the amount of available energy is greater than
a threshold set off-line. The FSCE-EH algorithm
returns a speed just below current speed when I
sys
is null and the available energy level is below this
threshold.
AReal-TimeFeedbackSchedulerbasedonControlErrorfor
EnvironmentalEnergyHarvestingSystems
353

Assuming El(t) the amount of available energy in
the battery at time t, I
sys
the maximum control cost of
the system (see Eq. 6), L the energy threshold and
the current speed (scaling factor) S(k). The new speed
S is given by the algorithm below :
Algorithm 1: FSEC-EH.
Input:
El(t), the amount of energy available;
I
sys
, the maximum control cost of the system
(see Eq.6);
L, the threshold ;
S(k), the current speed (see Eq.1);
Output:
S, the scaling factor required
1 if I
sys
> 0 then
2 S ← S(k+ 1)
3 else
4 if El(t) > L then
5 S ← S(k)
6 else
7 S ← S(k− 1)
8 return S;
6 PERFORMANCE RESULTS
This section presents the simulation experiments us-
ing TrueTime (Cervin et al., 2010). Simulations aim
to evaluate the QoC of the proposed scheme.
6.1 Environment and Simulation
Context
For our experiments, a power generator source which
supplies a battery according to the model given in
Eq.(3) is implemented in TrueTime (Cervin et al.,
2010). We consider an embedded control system that
consists of three independent control loops. Each
plant is controlled using a PID algorithm whose
parameters are similar to those given in (Cervin
et al., 2010). The transfer function of each plant is
G(s) = 1000/(s
2
+ s). For this, we consider the set
of three tasks Γ = {τ
i
| 1 ≤ i ≤ 3}. In our experiments,
the nominal sampling periods of three loops are set to
be T
1
= 15 ms, T
2
= 16 ms, and T
3
= 17 ms, respec-
tively. The power consumption of the task τ
i
under
the processor speed S is given in Eq. (2), with the
processor idle power equal to 63.58 mW. We assume
that the energy storage capacity is E
max
= 2.5 Joules
at t = 0. The FBS task period is equal to T
Fs
= 80 ms.
We assume that at t = 0 the processor speed is S = 1.
In our simulation, the reference signal was run dur-
ing Nr = 55 periods. The parameters of the stability
degree are k
0
= 3 and α = 5
Based on the above description, we compare the
proposedfeedback scheduling method (FSCE-EH) to
the three following methods :
1. EDFnoDVFS: The processor operates at its full
speed (S = 1) under the classical EDF policy,
i.e., there is no DVFS scheme and no feedback
scheduling;
2. EDFbs-EgC: Earliest Deadline Feedback
Scheduling with Energy guarantee under Con-
tinuous voltage/frequency modes algorithm,
proposed in (Abbas et al., 2013) in which the
scaling factor S takes a value S = U
inst
(t) at each
execution of the FBS task;
3. FS-EH (Feedback Scheduler with Energy Har-
vesting): heuristic proposed in (Abbas et al.,
2014) in which the scaling factor S takes
a value S = 1 at each execution of the
FBS task if the amount of available energy is
greater than a threshold (set offline), otherwise
S = min{ S
m
| S
m
≥ max(U
inst
(t),El(t)/L)}.
6.2 Results and Discussions
In this section we present results of the simulations for
the four methods previously listed. Each simulation
has been performed during 55 s. With the aim to show
the effect of the choice of the threshold, we chose 25
different values for the threshold L from 0.1 to 2.5
(battery nominal capacity).
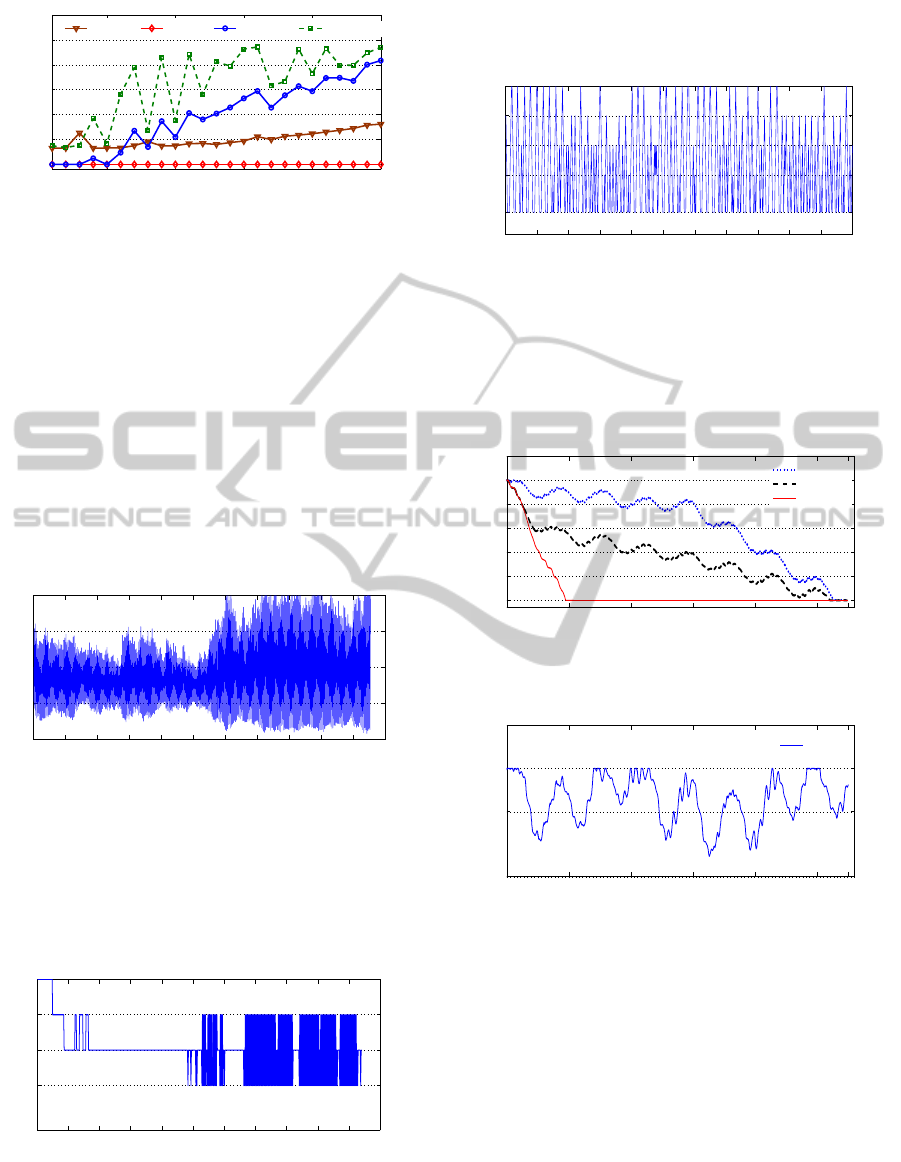
6.2.1 Average and Minimum Energy Available
We show here, for each threshold value, the average
and minimum energy available during the experiment.
When FSCE-EH and FS-EH are used, Figure 6
shows that the increases of the average energy avail-
able with the increase of threshold values. Accord-
ing to experiments, we found that when the thresh-
old value is spread over the entire battery capacity
(equal to 2.5) provides a high average energy avail-
able. We can see also that the minimum energy avail-
able is equal to 0 with FS-EH for all threshold values
caused by the total discharge of the battery which in-
duces the experiment stop. We note that the average
energy available with EDFnoDVFS and EDFbs-EgC
are equal to 0.36 J and 1.53 J, respectively. The min-
imum energy available with the two last algorithms is
equal to 0.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
354
0,1 0,5 1 1,5 2 2,5
0
0,5
1
1,5
2
2,5
Average and Minimum
Energy available
Threshold values
Aver FS−EH Min FS−EH Min FSCE−EH Aver FSCE−EH
Figure 6: Average and Minimum Energy available vs
Threshold with FSCE-EH and FS-EH.
6.2.2 Processor Speed Comparison
In this section, we present results showing the proces-
sor frequency variation with each method presented
previously. We note that there is an overhead in time
and energy for every frequency change (see Table.
2). We note also that when FSCE-EH and FS-EH are
used, the threshold take value equal to 2.5
From Figure 7, we can see that under EDFbs-
EgC algorithm the processor frequency is changing
rapidly. The frequent change in processor frequency
from low values to high values induces less reduction
in energy consumption (see Figure 10).
0 5 10 15 20 25 30 35 40 45 50 55
0.2
0.4
0.6
0.8
1
Times [s]
Scaling Factor
Figure 7: Scaling Factor with EDfbs-EgC.
Figure 8 shows that when FS-EH algorithm is
used, a frequent change in processor frequency occur.
We note that with EDFbs-EgC (resp. with FS-EH)
algorithm the execution stop due to the battery dis-
charge at t = 52.7 s (resp. t = 54.4 s) which causes
the destabilization of controlled plant.
0 5 10 15 20 25 30 35 40 45 50 55
0.15
0.4
0.6
0.8
1
Times [s]
Scaling Factor
Figure 8: Scaling Factor with FS-EH.
Figure 9 shows that when FSCE-EH algorithm is
used, the execution does not stop. We can see also
that FSCE-EH algorithm returns a lower speed (0.15)
to favor the charge of the battery and return also a the
high speed (1) to improve control performance.
0 5 10 15 20 25 30 35 40 45 50 55
0
0.15
0.4
0.6
0.8
1
Times [s]
Scaling Factor
Figure 9: Scaling Factor with FSCE-EH.
6.2.3 Energy Consumption Comparison
Figures 10 and 11 show the energy available with the
four methods. We can see that FSCE-EH protects
against a total discharge of the battery.
0 10 20 30 40 50 55
0
0.5
1
1.5
2
2.5
3
Times [s]
Energy available
EDFbs−EgC
FS−EH
EDFnoDVFS
Figure 10: Energy available with EDFnoDVFS, EDfbs-EgC
and FS-EH.
0 10 20 30 40 50 55
2
2,3
2,5
Times [s]
Energy available
FSCE−EH
Figure 11: Energy available with FSCE-EH.
6.2.4 Rate of Missed Deadlines Comparison
We present results concerning the rate of missed dead-
lines that is the number of deadlines missing divided
by the total number of jobs.
Figure 12 shows that under FSCE-EH a small rate
of deadlines are missed. The maximum (resp. mean)
rate of missed deadlines is 10.74% (resp. 4.96%)
comparatively to the rate under FS-EH which equals
to 0. With EDFbs-EgC algorithm the rate of missed
deadlines is 0.37%.
AReal-TimeFeedbackSchedulerbasedonControlErrorfor
EnvironmentalEnergyHarvestingSystems
355

0,1 0,5 1 1,5 2 2,5
0
2
4
6
8
10
12
Rate of missed deadlines(%)
Threshold values
with FS−EH with FSCE−EH
Figure 12: Rate of missed deadlines under FSCE-EH and
FS-EH.
6.2.5 Quality of Control Comparison
The Integral of Absolute Error (IAE) for each closed
loop system i, i.e J(i) =
R
t
sim
0
e
i
(t)dt measures the
QoC (Quality of Control), where e
i
is the absolute
control error. For an experiment, we define the maxi-
mum error cost as : J
Max
=
Max
1≤i≤3
J(i).
Figure 13 shows the maximum error cost J
Max
with FSCE-EH and FS-EH for each threshold value.
We can see that FSCE-EH algorithm induce less cost
comparatively to the cost induced bay FS-EH algo-
rithm. We note that the minimum J
Max
under FS-
EH is equal to 375330 obtained with threshold value
equal to 2.5. Under FSCE-EH, the minimum J
Max
is
equal to 63393 (which is 16.9% less) obtained with
threshold value equal to 0.7. We note also that under
EDfbs-EgC the maximum error cost J
Max
is equal to
906100. These results show that the FSCE-EH algo-
rithm optimizes the QoC even if it induces small rate
of missed deadlines (see Figure 12).
0,1 0,2 0,5 1 1,5 2 2,5
0
2
4
6
8
10
12
x 10
8
Error cost
Threshold values
FSCE−EH FS−EH
Figure 13: Maximum error cost J
Max
with FSCE-EH and
FS-EH.
7 CONCLUSIONS
This paper has addressed the problem of real-time
scheduling in ambient energy harvesting systems with
discrete voltage/frequency modes through the use of a
feedback scheduler. The proposed solution computes
the processor speed with taking into accountthe avail-
able energy and the control performance. The eval-
uation of this solution shows experimentally a good
compromise between the available energy and the
quality of control and we can say that our approach
is promising.
In the near future, we plan to study the problem of
scheduling hybrid tasks (hard and soft real-time task)
under harvesting energy constraints. The objective is
to guarantee, with energy saving, the hard real-time
constraints and at the same time reduce the rate of
missed deadlines for the soft real-time tasks. We plan
also to improve and test our work on a real hardware.
REFERENCES
Abbas, A., Grolleau, E., Loudini, M., and Mehdi, D. (2013).
A real-time feedback scheduler for environmental en-
ergy harvesting. In Systems and Control (ICSC), 2013
3rd International Conference on, pages 1013–1019.
Abbas, A., Grolleau, E., Mehdi, D., Loudini, M., and Hi-
douci, W.-K. (2014). A real-time feedback sched-
uler for environmental energy with discrete volt-
age/frequency modes. In The 2nd International Con-
ference on Future Internet of Things and Cloud. IEEE.
˚
Arz´en, K.-E., Robertsson, A., Henriksson, D., Johansson,
M., Hjalmarsson, H., and Johansson, K. H. (2006).
Conclusions of the artist2 roadmap on control of com-
puting systems. SIGBED Review, 3(3):11–20.
Axer, P., Ernst, R., Falk, H., Girault, A., Grund, D., Guan,
N., Jonsson, B., Marwedel, P., Reineke, J., Rochange,
C., Sebastian, M., Hanxleden, R. V., Wilhelm, R., and
Yi, W. (2014). Building timing predictable embedded
systems. ACM Transactions on Embedded Computing
Systems, 13(4).
Cervin, A. (2003). Integrated Control and Real-Time
Scheduling. Phd thesis, Lund University.
Cervin, A., Henriksson, D., and Ohlin, M. (2010). True-
time: Reference manual.
Chen, G., Huang, K., Huang, J., Buckl, C., and Knoll,
A. (2013). Effective online power management with
adaptive interplay of dvs and dpm for embedded real-
time system. In DSD, pages 881–889.
Chetto, M. (2014). Optimal scheduling for real-time jobs
in energy harvesting computing systems. IEEE Trans-
actions on Emerging Topics in Computing, 2(2):122–
133.
Chetto, M. and Zhang, H. (2010). Performance evaluation
of real-time scheduling heuristics for energy harvest-
ing systems. In Green Computing and Communica-
tions (GreenCom), 2010 IEEE/ACM Int’l Conference
on Int’l Conference on Cyber, Physical and Social
Computing (CPSCom), pages 398–403. IEEE Com-
puter Society.
Jin, H., Wang, D., Wang, H., and Wang, H. (2007). Feed-
back fuzzy-dvs scheduling of control tasks. The Jour-
nal of Supercomputing, 41(2):147–162.
Liu, C. L. and Layland, J. W. (1973). Scheduling algo-
rithms for multiprogramming in a hard-real-time en-
vironment. Journal of the ACM (JACM), 20(1):46–61.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
356

Liu, S., Lu, J., Wu, Q., and Qiu, Q. (2012). Harvesting-
aware power management for real-time systems with
renewable energy. IEEE Transactions on Very Large
Scale Integration (VLSI) Systems, 20(8):1473–1486.
Liu, S., Qiu, Q., and Wu, Q. (2008). Energy aware dynamic
voltage and frequency selection for real-time systems
with energy harvesting. In Proceedings of the Con-
ference on Design, Automation and Test in Europe,
DATE ’08, pages 236–241.
Liu, S., Wu, Q., and Qiu, Q. (2009). An adaptive schedul-
ing and voltage/frequency selection algorithm for real-
time energy harvesting systems. In Design Automa-
tion Conference, 2009. DAC’09. 46th ACM/IEEE,
pages 782–787. IEEE.
Moser, C., Brunelli, D., Thiele, L., and Benini, L. (2007).
Real-time scheduling for energy harvesting sensor
nodes. Real-Time Systems, 37(3):233–260.
Soria-Lopez, A., Mej´ıa-Alvarez, P., and Cornejo, J. (2005).
Feedback scheduling of power-aware soft real-time
tasks. In ENC, pages 266–273.
Xia, F. (2006). Feedback scheduling of real-time control
systems with resource constraints. Phd thesis, Zhe-
jiang University.
Xia, F., Ma, L., Zhao, W., Sun, Y., and Dong, J. (2008). En-
hanced energy-aware feedback scheduling of embed-
ded control systems. arXiv preprint arXiv:0809.4917.
XScale (2007). Intel xscale microarchitecture.
Xu, R., Moss´e, D., and Melhem, R. (2007). Minimiz-
ing expected energy consumption in real-time systems
through dynamic voltage scaling. ACM Trans. Com-
put. Syst., 25(4).
AReal-TimeFeedbackSchedulerbasedonControlErrorfor
EnvironmentalEnergyHarvestingSystems
357
