
Crack Growth Monitoring by Embedded Optical Fibre
Bragg Grating Sensors
Fibre Reinforced Plastic Crack Growing Detection
G. Pereira, L. Mikkelsen and M. McGugan
Technical University of Denmark, Department of Wind Energy, Frederiksborgvej 399, 4000 Roskilde, Denmark
Keywords:
Fibre Bragg Grating Sensors, Crack Growth Monitoring, Fibre Reinforced Plastic Crack Monitoring, Digital
Image Correlation.
Abstract:
This article presents a novel method to asses a crack growing/damage event in fibre reinforced plastic, or ad-
hesive using Fibre Bragg Grating (FBG) sensors embedded in a host material. Different features of the crack
mechanism that induce a change in the FBG response were identified. Double Cantilever Beams specimens
made with glass fibre glued with structural adhesive, were instrumented with an array of FBG sensors embed-
ded in the material and tested using an experimental fracture procedure. A digital image correlation technique
was used to determine the presence of the specific phenomena caused by the crack, and to correlate with the
FBG sensor. A Material-Sensor model was developed in order to predict the sensor output response under a
crack/delamination situation, which can be used as an analysis tool for future application of this measurement
technology in more complex structures.
1 INTRODUCTION
1.1 Fibre Reinforced Plastic Materials
Fibre reinforced plastic (FRP) materials (composite
materials) have been extensively used in aerospace,
automotive, naval, civil engineering and wind energy
applications. These fibre reinforced materials consist
of two macroscopic phases, a stiff fibre phase (usually
glass or carbon fibre) and a polymer matrix (usually
polyester or epoxy). The main advantage of this mate-
rial is its capability to be tailored for a specific appli-
cation, this enables an enhancement, and a high level
of customization of mechanical properties, such as
light-weight, thermal expansion, chemical/corrosion
resistance, fatigue behaviour, etc (Jones, 1999).
The increased used of fibre reinforced plastic ma-
terials requires a proper understanding of the failure
mechanisms. Delamination is one of the most impor-
tant failure mechanisms and is considered the most
widespread mode of life reduction.
1.2 Delamination/Damage Mechanism
Often in fibre reinforced polymers, delamination is
accompanied by the formation of a crack bridging
zone, where intact fibres connect the crack faces be-
hind the crack tip, thus the energy required for the
crack to propagate is higher that required to initiate.
The relationships between the crack bridging stresses
and the crack opening displacement (bridging laws)
are used to describe the effect of fibres on the crack
propagation (B.F. Sørensen, 2010). The cracking in
homogeneous isotropic materials usually occurs un-
der pure Mode I (opening loading) but in weak planes
or along interfaces, like in composite materials crack-
ing, occurs under a combination of Modes (Shear and
opening loading). Figure 1 shows the fibre bridging
phenomenon in a fibre reinforced polymer specimen.
Figure 1: Fibre bridging phenomenon in a fibre reinforced
polymer specimen.
Another important feature of the fibre bridging
phenomena for our study case, is the formation of a
compression field ahead the crack tip, and traction be-
fore the crack tip. The fibres connecting the crack
133
Pereira G., Mikkelsen L. and McGugan M..
Crack Growth Monitoring by Embedded Optical Fibre Bragg Grating Sensors - Fibre Reinforced Plastic Crack Growing Detection.
DOI: 10.5220/0005325901330139
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (OSENS-2015), pages 133-139
ISBN: 978-989-758-092-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

faces behind the crack tip will act like cables, forc-
ing the faces to close, creating a traction stress in that
area. However, to maintain a force equilibrium, a
compression field is formed ahead the crack tip. The
compression-traction fields move as the crack grows.
1.3 Crack/Delamination Detection in
Fibre Reinforced Plastic Materials
Sensing technology has been implemented in order to
track delamination in FRP materials. Acoustic emis-
sion (Silversides et al., 2013) that measures the stress
waves generated by the crack front growing, vibration
(Kyriazoglou and Guild, 2004) that detects changes in
the specific damping capacity of the structure, model
analysis (Hu et al., 2006) by monitoring the material
natural frequencies and mode shapes, piezo-electric
actuators/sensors and wavelet analysis (Yan and Yam,
2002) based on the energy variation of the structural
dynamic. However, these measurement systems have
several limitations, among these the need for quali-
fied operators, expensive hardware and impractical to
use under operation. Also, to detect delamination in
FRP materials the sensor must be embedded in the
laminate layers or in the interface of the FRP and a
structural adhesive.
Fibre Bragg Gratings (FBG) have the capability to
be embedded in the FRP material, even in an opera-
tional structure, without compromising its structural
resistance. This is due to the FBG reduced size, with
a diameter of 125µm, it is virtual non-intrusive to the
material. Also, FBG sensors present other interesting
features, such high resolution, multiplexing capabil-
ity, immunity to electromagnetic fields, chemical in-
ertness and long term stability (fatigue behaviour).
1.4 Crack/Delamination Detection by
Embedded Fibre Bragg Gratings
During a crack/delamination event different fracture
features will be present near the crack tip. Being able
to identify and measure this specific phenomena with
a FBG sensor is a key factor to correctly determine
the presence of damage and it growth.
In figure 2, the different stages of the FBG re-
sponses under a crack growth event are presented.
First, before the crack reach the proximity of the grat-
ing, figure 2a), the material will build up uniform
strain (considering structure loading or geometric sin-
gularities distant enough from the grating), that will
make a uniform wavelength shift in the FBG reflected
peak. Next, a compression field is formed ahead of
the crack tip due to the formation of a crack bridging
zone, witch was discussed in section 1.2, will reach
the grating area creating a peak splitting of the FGB
response, figure 2b). This peak split phenomena will
be discussed later, but briefly is due a birefringent ef-
fect. Then, when the grating is near the influence of
the crack singularity (region dominated by stress con-
centration) a non-uniform strain field will also create
a change in the shape of the reflected peak, as showed
in figure 2c). Finally, after the crack passes the FBG
sensor, the shape of the reflected peak will go back
to the original shape, and the sensor response will
again be a simple wavelength shift, because at this
stage only uniform strains will be present in the FBG
proximity, figure 2d).
2 FIBRE BRAGG GRATING
WORKING PRINCIPLE
A Fibre Bragg Grating (FBG) is formed by a perma-
nent periodic modulation of the refractive index along
a section of an optical fibre, by exposing the optical
fibre to an interference pattern of intense ultra-violet
light (Hill and Meltz, 1997). The photosensitivity of
the silica exposed to the ultra-violet light is increased,
so when the optical fibre is illuminated by a broad-
band light source a very narrow wavelength band is
reflected back. The spectral response of a homoge-
neous FBG is a single peak centred at the wavelength
λ
b
. The wavelength λ
b
is described by the Bragg con-
dition ,
λ
B
= 2n
e f f ,0
Λ
,0
(1)
where n
0
is the mean effective refractive index at the
location of the grating, the index 0 denotes unstrained
conditions (initial state). n
e f f
is the effective refrac-
tive index and Λ is the constant nominal period of the
refractive index modulation (Morey et al., 1990).
2.1 Fibre Bragg Grating Response to a
Uniform Variation of Strain and/or
Temperature
The wavelength shift ∆λ
b
of an embedded FBG under
a uniform variation of strain ε
zz
, and temperature ∆T
is given by the equation 2 (Zhang et al., 2008),
∆λ
b
λ
b
= (1 − p
e
)ε
zz
+ [(1 − p
e
)(α
s
− α
f
) + ξ]∆T (2)
where p
e
is a photoelastic coefficients, α
s
and α
f
are
the thermal expansion coefficients of the host material
and the optical fibre, respectively, and ξ is the thermo-
optic coefficient.
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
134

Reflectivity
Wavelength
Simple wavelength shift
a)
FBG
High
x
FBG
x
x
y
IW
y
x
Wavelength shift under transversal force
Reflectivity
Wavelength
b)
Reflectivity
Wavelength
Simple wavelength shift
d)
c)
Wavelength shift under non-uniform strain
Reflectivity
Wavelength
Figure 2: Different stages of the FBG responses under a crack growth event.
2.2 Fibre Bragg Grating Response
Under a Transverse Force:
Birefringent Effect
An optical fibre can present a birefringent behaviour,
defined by the change of the refractive index n
e f f
in
the two directions n
e f f x
and n
e f f y
, when the grating
is subjected to a transverse force. The variation of the
refractive index in the two directions n
e f f x
and n
e f f y
is given by the equation (3) and (4) (Sørensen et al.,
2007; Zhang et al., 2014; J
¨
ulich and Roths, 2010;
Bosia et al., 2003).
∆n
x
= −
n
3
0
2E
f
{(p
11
− 2ν
f
p
12
)σ
x
+ [(1 − ν
f
)p
12
− ν
f
p
11
](σ
y
+ σ
z
)} (3)
∆n
y
= −
n
3
0
2E
f
{(p
11
− 2ν
f
p
12
)σ
y
+ [(1 − ν
f
)p
12
− ν
f
p
11
](σ
x
+ σ
z
)} (4)
σ
y,x
is the transverse stress, E
f
is the elastic modulus
of the optical fibre,ν
f
is the Poisson’s ration, n
0
is the initial refractive index, p
11
and p
12
are the
photo-elastic coefficients of the optical fibre.
Rewriting the equation (3) and (4) it is possible
to determine the increase in the width of the reflected
peak, ∆λ
IW
= kλ
x
− λ
y
k, caused only by a transverse
stress.
∆λ
IW
= 2Λk∆n
e f f x
− ∆n
e f f x
k
=
Λn
3
o
E
f
[(1 + ν
f
)p
12
− (1 + ν
f
)p
11
]kσ
y
k
(5)
2.3 Fibre Bragg Grating Response
Under a Non-uniform Strain
When an FBG sensor is near a defect, a crack, a ma-
terial change or a geometric variation, this can create
a stress concentration that will lead to an abrupt vari-
ation of strain. This non-uniform strain will change
CrackGrowthMonitoringbyEmbeddedOpticalFibreBraggGratingSensors-FibreReinforcedPlasticCrackGrowing
Detection
135

the periodicity of the grating pattern along the sensor
length, modifying the grating pattern configuration
from ”uniform” to ”chirped” (Yashiro et al., 2007;
Zhang et al., 2007).
As demonstrated by Peters (Peters et al., ), in
a uniform grating the applied strain will induce a
change in both grating period and the mean index.
These two effects can be superimposed by applying
an effective strain of ”(1 − p
e
)ε
zz
(z)”, similar the first
part of equation (2) but taking into account the strain
variation along the z direction. Then it is possible to
rewrite the grating period as:
Λ(z) = Λ
0
[1 + (1 − pe) ×ε
zz
(z)] (6)
Where Λ
0
is the grating period with zero strain. The
non-uniform strain effect can be approximated by us-
ing the maximum and minimum strain values along
the grating. So, the maximum grating period Λ
max
and minimum Λ
min
can be calculated using the equa-
tion (6). Thus, an approximated increase of the width
of the reflected peak due to a non-uniform strain ∆λ
IW
is given by combining equations (6) and (1),
∆λ
IW
= 2n
e f f
Λ
max
− 2n
e f f
Λ
min
(7)
3 MATERIAL AND
EXPERIMENTAL PROCEDURE
In order to measure the different features of the
fracture mechanism, experiments were conducted on
Double Cantilever Beams (DCB) with embedded
FBG sensors, subjected to a fracture testing proce-
dure.
3.1 Material and Testing Procedure
Eight (8) DCB specimens were tested in a loading de-
vice commonly used to determine material fracture
properties, developed by (Sørensen et al., 2006). The
DCB specimens were loaded in different conditions
at 1 mm/min, ranging pure Mode I to pure Mode II,
in order to simulate the different crack/delamination
situations. Using this testing technique allows stable
crack growth and makes it possible to correctly eval-
uate the FBG response at different stages.
The DCB specimens were manufactured using
two composite material arms, made of a mix of uni-
directional and triaxial glass layers (SAERTEX UD
and TRIAX), that were glued by a commercial epoxy
structural adhesive (Epikote MGS BPR 135G/Epikote
MGS BPH137G). The geometry of the DCB speci-
men is presented in figure 3.
UD
TRIAX
Adhesive
FBG
300
30
7
7
7
Figure 3: Sketch of the specimen geometry.
3.2 Sensors and Measurement
Technology
An array of 5 uncoated single mode (SM) FBG sen-
sors, witch with a length of 10 mm, were embedded in
the interface of the composite material with the struc-
tural adhesive. The gratings array were spaced by 10
mm from each other, and the first grating was posi-
tioned 10 mm from the edge of the adhesive. The
sensors were connected to a Optical Spectral Anal-
yser (OSA) FS2200 - Industrial BraggMETER from
FiberSensing
TM
.
A digital image correlation technique was applied
to the specimens, in order to determine the pres-
ence of specific phenomenon caused by the crack
(ex:non-uniform strain) and to correlate it with the
FBG output. Digital image correlation is an optical
method that by tracking changes in a random pat-
tern in the specimen, can correlate this information
with deformation/strain in the material. A pattern
was painted on the side surface of the DCB specimen
and ARAMIS
TM
software was used to calculated the
strains from each measurement.
All the measurements from the Braggmeter and
Aramis were synchronized with the crack growth.
4 DISCUSSION OF RESULTS
Figure 4 shows some measurements from a five (5)
FBG array embedded in a DCB under a Mode II
fracture testing (the full test was more measurement
points, but is not possible to show it all in this arti-
cle). The reflected peak at 1580 nm (furthest to the
right) corresponds to the grating closest to the crack
tip, and consequently the peak at 1530 nm (furthest
to the left)is the most distant. It is possible to observe
changes in the reflected peaks as the crack propagates.
This change in the shape of the reflected peaks is due
the proximity of the crack, as described in section 1.4.
Evaluating and tracking this change will permit a de-
termination of the presence and position of the crack.
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
136
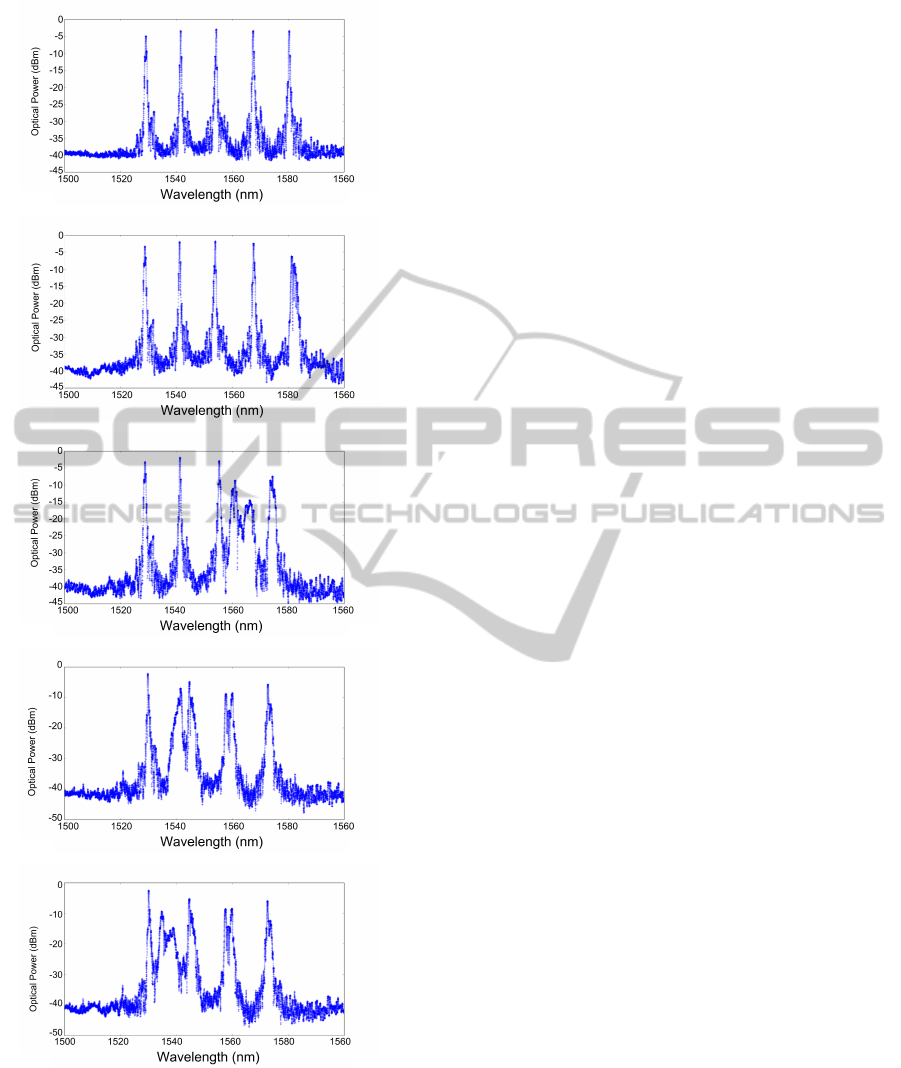
Figure 4: FBG array output under Mode II crack growing.
Figure 5 presents the shape of the reflected peak
(FBG 5- 1580nm) during a crack growth under Mode
II. Digital image correlation technique was used in or-
der to determine the strain/stress shape distribution
during the measurement.It shows the different crack
features that can change the shape of the reflected
peak, as described in section 1.4 and figure 2. The
measurement pictures in the left column (ε
y
com-
pression) presents the specimen areas with compres-
sion stress (blue area). These compression areas can
cause the birefringent effect in the FBG sensor, as de-
scribed in 2.2. The measurement pictures in the cen-
ter column (ε
x
- Non-uniform), present the longitudi-
nal strain in the specimen, where a gradient of colors
represent variation of strain. This non-uniformity of
strain can also create a change in the shape of the re-
flected peak, as described in 2.3.
As described in section 1.4, it is possible to iden-
tify the different stages of the crack growth from the
sensor response. Before the crack reach the proximity
of the grating, the material builds up uniform strain,
that induces a uniform wavelength shift in the sen-
sor response. Next, the compression field that was
formed ahead of the crack tip reaches the grating area
creating a peak splitting/increase of the width. Then,
when the grating is near the influence of the crack sin-
gularity (region dominated by stress concentration),
the non-uniform strain field creates a change in the
shape of the reflected peak. Finally, after the crack
passes the FBG sensor the shape of the reflected peak
is gradually recovered to the original shape.
5 CONCLUSIONS
In this article the capability of Fibre Bragg Gratings
embedded in composite material to detect and track
cracks/delamination was demonstrated. The use of
digital image correlation technique proved that spe-
cific fracture features near the crack can create a
change in the shape of the reflected peak. Thus, it
is possible to extract information from sensor that is
independent of the loading type, geometry and bound-
ary conditions, and depends only on the proximity of
the crack. This fact allow the application of this tech-
nique in general composite material structures.
In figures 6,7 and 8, the wavelength shift and
peak width at -30dBm, computed from the output of
the FBG array in tree different loading conditions, is
presented. Each different color plotted corresponds
to each Bragg grating in the sensor array, being the
FBG5 (Orange color line) the grating located closest
to adhesive edge and the FBG1 (Black color line) the
grating more distant. The crack growth in the order:
FBG 5 → 4 → 3 → 2→ 1.
The wavelength shift is dependent on the loading
type, but the increase in the width of the peak is re-
lated to the presence of the crack (Birefringent effect
and non-uniform strain). Using this information it is
possible to track the crack by an abrupt variation of
CrackGrowthMonitoringbyEmbeddedOpticalFibreBraggGratingSensors-FibreReinforcedPlasticCrackGrowing
Detection
137
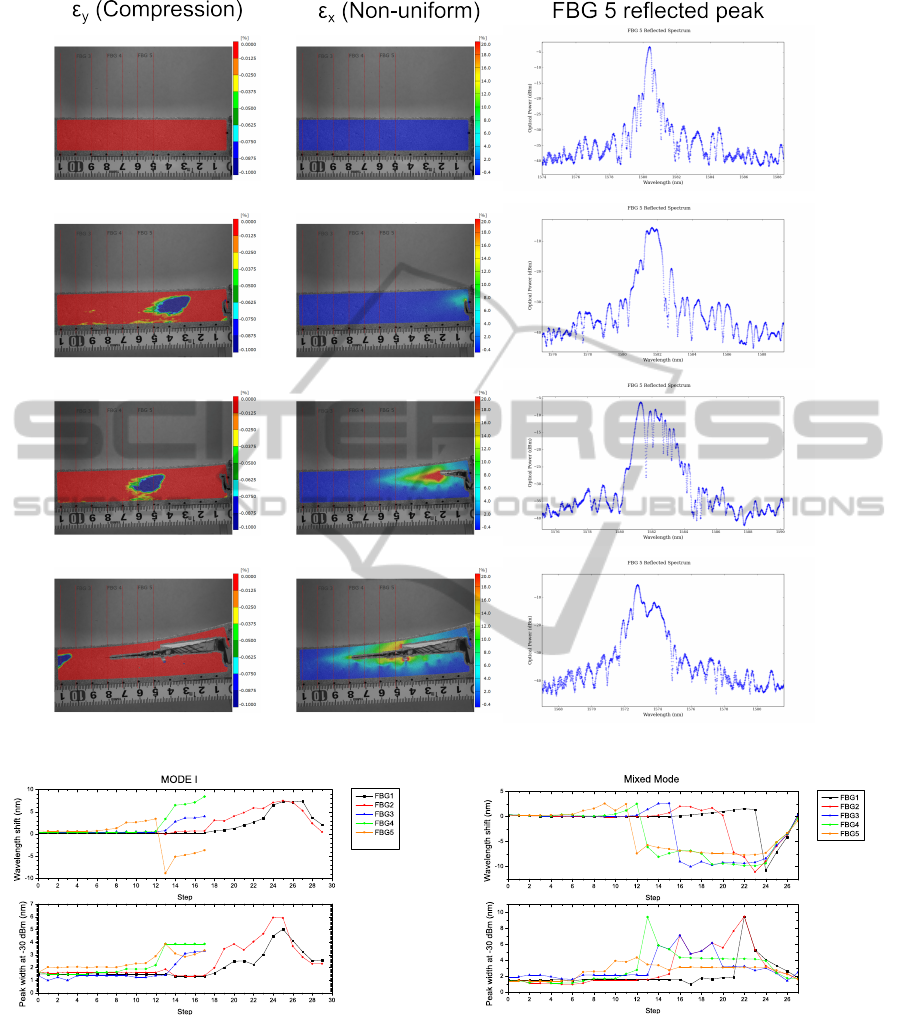
Figure 5: Different stages of the sensor output during a crack growth.
Figure 6: Sensor array output for Mode I crack growing.
the wavelength and/or increase in the width of the re-
flected peak. This monitoring method can be imple-
mented in a structural model using the equations de-
veloped in section 2. This makes it possible to study
the application of this monitoring technique in other
locations, predict the sensor output and determine the
optimized sensor-structure configuration.
Figure 7: Sensor array output for Mixed Mode crack grow-
ing.
ACKNOWLEDGEMENTS
The authors acknowledges the Seventh Framework
Programme (FP7) for funding the project MareWint
(Project reference: 309395) as Marie-Curie Initial
Training Network, Fibersensing for providing the
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
138
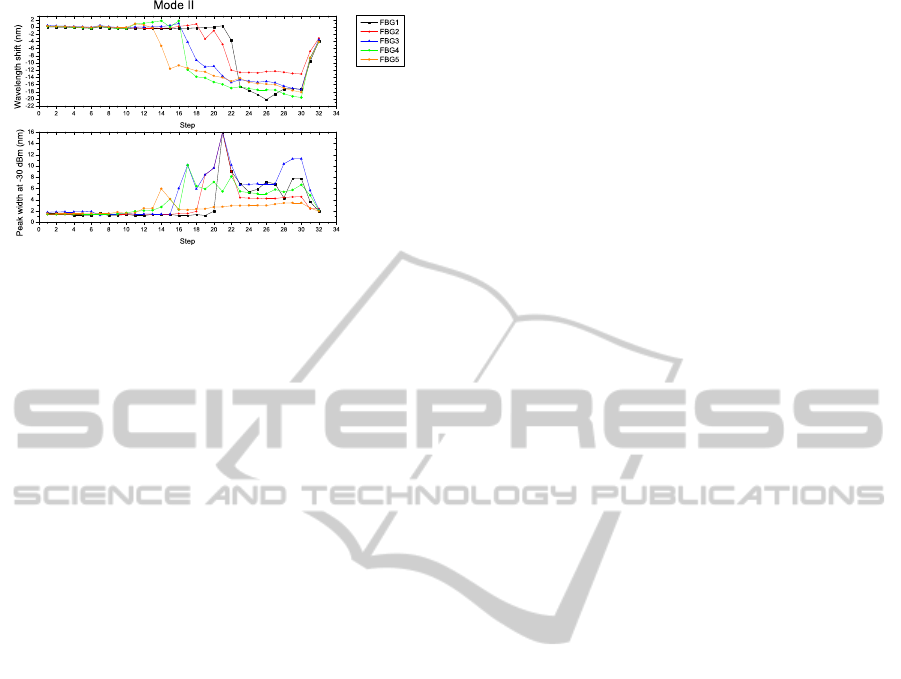
Figure 8: Sensor array output for Mode II crack growing.
FBG sensors and hardware, and SSP-Technology for
providing the material tested.
REFERENCES
B.F. Sørensen, Technical Univ. of Denmark, R. N. L. f. S.
E. M. R. D. (2010). Cohesive laws for assessment of
materials failure: Theory, experimental methods and
application. Risø DTU.
Bosia, F., Giaccari, P., Botsis, J., Facchini, M., and Lim-
berger, H. (2003). Characterization of the response
of fibre Bragg grating sensors subjected to a two-
dimensional strain field. Smart Materials and Struc-
tures, 925(12):925–934.
Hill, K. and Meltz, G. (1997). Fiber Bragg grating technol-
ogy fundamentals and overview. Journal of lightwave
technology, 15(8):1263–1276.
Hu, H., B. Wang, C. L., and Su, J. (2006). Damage de-
tection of surface cracks in composite laminates using
modal analysis and strain energy method. Composite
Structures, 74(4):399–405.
Jones, R. (1999). Mechanics of composite materials. Taylor
& Francis.
J
¨
ulich, F. and Roths, J. (2010). Comparison of transverse
load sensitivities of fibre Bragg gratings in different
types of optical fibres. 7726(0):77261N–77261N–9.
Kyriazoglou, C. and Guild, F. (2004). Vibration damping
for crack detection in composite laminates. Compos-
ites Part A: Applied Science and Manufacturing, 35(7-
8):945–953.
Morey, W., Meltz, G., and Glenn, W. (1990). Fiber optic
Bragg grating sensors. OE/FIBERS’89.
Peters, K., Studer, M., Botsis, J., Iocco, A., Limberger, H.,
and Salath, R. Embedded Optical Fiber Bragg Grating
Sensor in a Nonuniform Strain Field : Measurements
and Simulations. pages 19–28.
Silversides, I., Maslouhi, A., and Laplante, G. (2013). Inter-
laminar fracture characterization in composite materi-
als by using acoustic emission 2 . Experimental pro-
cedures and FEM Modeling. (November):13–15.
Sørensen, B., Jørgensen, K., Jacobsen, T., and Østergaard,
R. C. (2006). DCB-specimen loaded with uneven
bending moments. International Journal of Fracture,
141(1-2):163–176.
Sørensen, L., Botsis, J., Gm
¨
ur, T., and Cugnoni, J. (2007).
Delamination detection and characterisation of bridg-
ing tractions using long FBG optical sensors. Com-
posites Part A: Applied Science and Manufacturing,
38(10):2087–2096.
Yan, Y. and Yam, L. (2002). Online detection of crack dam-
age in composite plates using embedded piezoelec-
tric actuators/sensors and wavelet analysis. Composite
Structures, 58(1):29–38.
Yashiro, S., Okabe, T., Toyama, N., and Takeda, N. (2007).
Monitoring damage in holed CFRP laminates using
embedded chirped FBG sensors. International Jour-
nal of Solids and Structures, 44(2):603–613.
Zhang, L., Zhang, W., and Bennion, I. (2008). In-Fiber
Grating Optic Sensor, Fiber Optic Sensors, Second
Edition. CRC Press.
Zhang, W., Chen, W., Shu, Y., Lei, X., and Liu, X. (2014).
Effects of bonding layer on the available strain mea-
suring range of fiber Bragg gratings. Applied Optics,
53(5):885.
Zhang, X., Max, J., and Jiang, X. (2007). Experimental
investigation on optical spectral deformation of em-
bedded FBG sensors. SPIE, Photonics Packaging, In-
tegration, and Interconnects VII, 6478.
CrackGrowthMonitoringbyEmbeddedOpticalFibreBraggGratingSensors-FibreReinforcedPlasticCrackGrowing
Detection
139
