Automatic Detection of High-voltage Spindles for Parkinson’s Disease

V. Vigneron

, T. Syed

and Hsin Chen

Electrical Department, Universit

e d’Evry, 91020 Evry, France

Informatics Department, National University of Computer and Emerging Sciences, Karachi, Pakistan

Electrical Department, National Tsing Hua University, Hsinchu, Taiwan

Keywords:

Parkinson, Animal Experiment, HVS, Eigen Decomposition, Detection, Sensor Grid.

Abstract:

Parkinson’s disease is a progressive neurodegenerative disorder which can be characterized by several symp-

toms such as tremor, slowness of movements, bradykinesia/akinesia and absence of postural reﬂexes . . . and

affects 10 million people worldwide. This paper develops a novel strategy for treating patients with PD: si-

lence High-Voltage-Spindle that resemble the pathophysiological β-waves and contribute to the development

of β-waves. Silencing HVSs is expected to delay or even prevent the development of β-waves and thus the

progression of PD motor symptoms. High-voltage spindles (HVSs) are observed during waking immobility of

patients. In this study, the local ﬁeld potentials collected from the lesioned and control rats on multiple chan-

nels were analyzed with an online detection algorithm to identify the characteristic oscillations of HVSs from

the second-order statistical properties of the signals and the detection performance is investigated to obtain the

optimal choices. These results provide further motivation for the real−time implementation of the automatic

HVS detection systems with improved performance for pathophysiological and therapeutic applications to the

thalamocortical network dysfunctions.

1 INTRODUCTION

This paper develops a novel strategy for treating pa-

tients with Parkinson’s disease (PD). Hemi-PD rats

will be used as a model here. We will focus on

implementing a closed-loop Deep-Brain-Stimulation

(DBS) system that will delay the development of

the excessive beta oscillations (called β-waves hence-

forth). Their are found to be associated with spa-

tial memory impairments (Radek et al., 1994), sud-

den arrest of ongoing behaviour and PD and to the

movement abnormalities found in PD model rats. The

HVSs are different from the epileptic spike-wave dis-

charges whose dominant frequency lies in the 30−50

Hz band (Sitnikova et al., 2009) and from normal

sleep spindles in both physiology aspects and signal

dynamics. Indeed HVSs (i) are synchronous spike-

and-wave patterns of local ﬁeld potentials (LFPs) (ii)

are oscillating in the 5−13 Hz frequency band (iii)

are initiated in cortex whereas the sleep spindles are

Corresponding author.

This project was funded by a PhD grant from universit

d’

Evry number 4552013 and PHC ORCHID. The authors

express their sincere thanks to the French embassy collabo-

rators for their interest and kind permission to publish.

prevalent in sleep states (iv) can occur frequently dur-

ing passive wakefulness. More, the onset and end

of HVSs episodes could occasionally vary across the

cortical-basal ganglia structures and thus leads to dif-

ferent morphological features.

Such uniqueness of HVSs demands an appropriate

spindle detection algorithm with a suitable threshold-

ing mechanism.

Although HVSs exhibit larger amplitudes than

normal LFPs, the motion artifacts of an awake rat also

induce large transients in LFPs. In addition, LFPs are

non-stationary and coupled with non-negligible noise.

These properties make it difﬁcult to detect HVSs

by simple threshold or envelope detection. More-

over, although the prominent frequency components

of HVSs are around 5−13Hz, the duration of each

HVS episode is only 1−4 s. Such a short duration

makes it challenging to detect HVS episode at the on-

set by conventional frequency analysis (e.g. the Fast-

Fourier Transform), which suffers from the trade-off

between time and frequency resolutions. Based on

our pilot studies, time-frequency (TF) analysis pre-

serving the energy distribution over both time and fre-

quency spaces is useful to extract the distinctive fea-

tures of HVSs, see e.g. (Perumal and Chen, 2014)

372

Vigneron V., Syed T. and Chen H..

Automatic Detection of High-voltage Spindles for Parkinson’s Disease.

DOI: 10.5220/0005328503720378

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (MPBS-2015), pages 372-378

ISBN: 978-989-758-069-7

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

who use a continuous wavelet transform (CWT) to

detect the characteristic oscillations of HVSs. But the

detection performance are related to a suitable choice

of the wavelet parameters and the thresholding mech-

anism that are critical to determine the detection per-

formance. Therefore, we will compare the features

extracted by TF analysis and our proposed algorithm

for detecting the distinctive features of HVSs auto-

matically and reliably.

Finally, as this algorithm is based mainly on

second-order statistics the proposed algorithm can be

extended further to the FPGA-based real time systems

for pathophysiological and therapeutic applications.

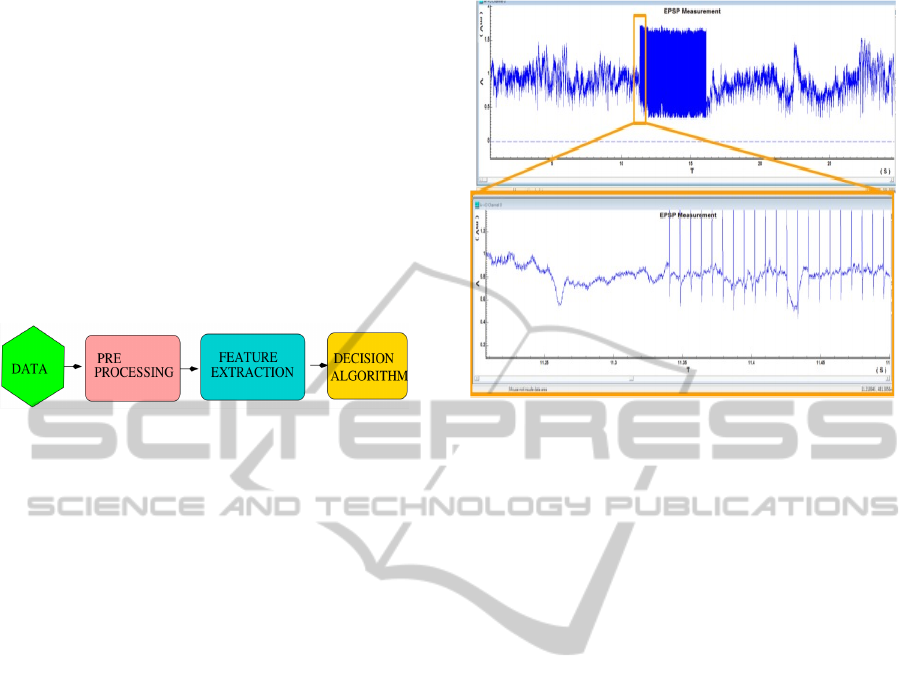
Figure 1: An overview of the HVSs detection process.

A simpliﬁed scheme in Fig. 1 gives an overview

of the work.

2 DATA ACQUISITION

The PD rat models were induced in 3-4 months old

Sprague-Dawley rats by unilateral injection (coordi-

nates: AP -4.4 mm, ML +1.2 mm, V -7.8 mm rel-

atively to bregma) of 6-OHDA in the medial fore-

brain bundle (MFB) at the rate of µl/min using an

integrated electrophysiology instrument suitable for

deep brain stimulation (DBS) procedure. Four weeks

following the unilateral injection of 6-OHDA, the le-

sioned group of rats were determined as successful

PD models through amphetamine-induced rotational

behaviour (Amp, 3mg/kg, ip) by measuring the rota-

tional speed of the lesioned rats as 6 turns per minute.

The rats were unilaterally implanted bipolar stimula-

tion electrode into the ipsilateral STN with their initial

coordinates at AP -3.6 mm and L +2.5 mm. The elec-

trode was lowered slowly along the dorsal ventral axis

of brain and then advanced ventrally to the STN to ob-

tain the electrophysiological signal with a strikingly

silent structure. The EEG recordings were collected

from a group of 34 lesioned rats and 20 control rats.

The LFPs of the lesioned rats were recorded in both

sleeping and waking immobile states in order to study

the behaviour of spindling and non-spindling charac-

teristics. The EEG patterns without artifacts and with

the duration of sixty seconds were considered in the

following sections to evaluate the performance of the

spindle detection algorithm (see Fig. 2).

Figure 2: The LFP recorded by the micro-system during

electrical stimulation (130Hz, 100 µA). The lower panel is

the magniﬁed view of the region shown in the top trace dur-

ing the period when stimulation is just turned on.

3 ELIMINATION OF THE

BACKGROUND NOISE

The raw artifact-free EEG recordings from lesioned

(PD) and control rats (CR) are used as direct inputs to

the HVS detection algorithm with a noise cancellation

stage.

In the case of HVSs, there are several different

causes for the noise. We can mention the defects in

the sensors, the environment in which the recording

is done or also the decay of the recording medium.

Among all the type of noises encountered in practice,

the following 2 types occur in practice:

• the background noise which can be represented

by a stationary process, often originated from the

electronic circuits of the ampliﬁcation devices.

• the impulse noise represented as a sequence of

very brief impulses, with random amplitudes and

locations.

To reduce these noises and restore the signal as best as

possible, we are considering them and deal with them

separately. The elimination of background noise is a

particular difﬁcult problem since we have to ﬁnd what

characterizes the difference between the useful part

of the signal and the unwanted part. We can mention

(DeFreitas et al., 2012; Miyano et al., 1980; Clancy

and Farry, 2000) among the different denoising meth-

ods in a stationary background noise for which the

methods gives satisfactory results. They usually re-

quire for the spectral properties of the noise to be

AutomaticDetectionofHigh-voltageSpindlesforParkinson'sDisease

373

known. They can do this by using a portion of the

signal that contains nothing but noise. This portion is

selected either by a direct observation of the signal or

by automatically detecting the active areas of the use-

ful signal.

We suggest here a simple spectral substraction lead-

ing to an acceptable result that we implemented. If we

assume that the noise is white with a power σ

esti-

mated from a portion of the signal containing nothing

but noise, the short term amplitude spectrum of the

denoised signal σ

is estimated by the expression:

X(k) = G(k)X(k) (1)

where

X(k) =

N−1

∑

n=0

x(n)e

−2 jπnk/N

, (2)

refers to the Discrete Fourier Transform of a length N

window of the noisy signal x(n) and where

G(k) =

(



1 −λ

√

|X(k)|



if λ

√

|X(k)|

< 1

µ otherwise.

(3)

where the parameters λ and µ are adjusted experimen-

tally so as to obtain the best result. The results show

that the background noise is rather well eliminated but

the method introduces HF noises that get louder as µ

decreases. In particular, µ = 0 leads to the plain and

simple elimination of the spectral components below

the threshold, causing certain components of the noise

to behave as isolated “peaks”. HF noise can be re-

duced by decreasing λ and increasing µ but at the cost

of a lower noise reduction.

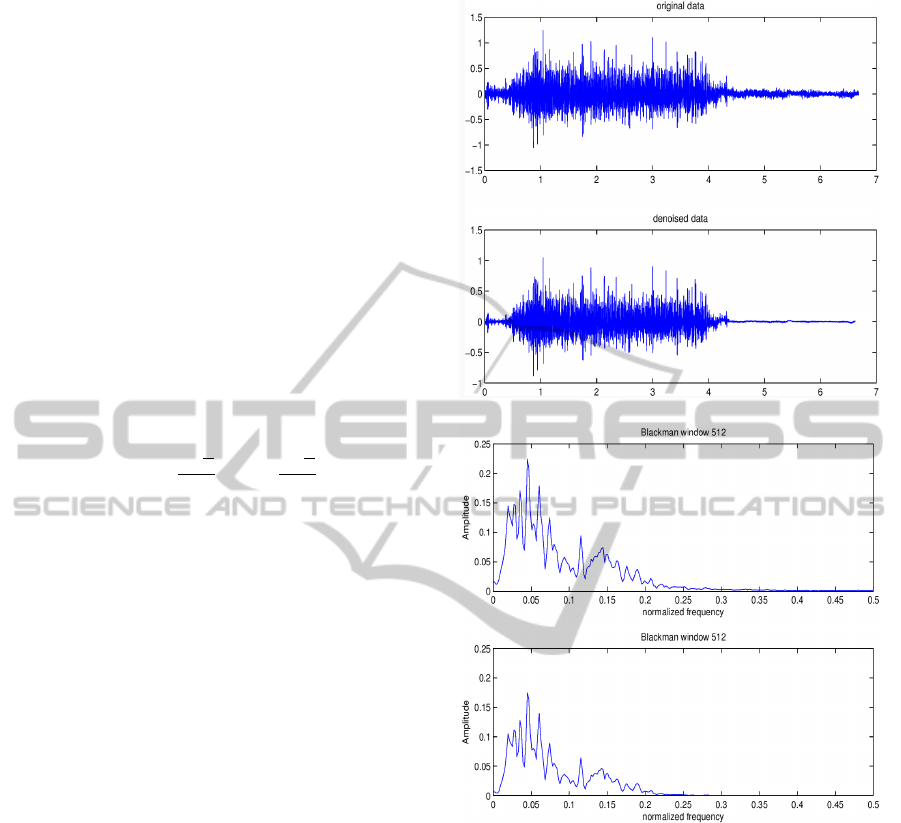
The ﬁgure 3 shows the effect of the frequency do-

main denoising operation. λ and µ have been adjusted

experimentally so as to archive the best result. This

method can effectively be applied to processes that do

have to be conducted in real-time. Detecting a “silent”

segment automatically is not an easy task, not to say

impossible to solve.

4 ALGORITHMS

Collaborative signal and information processing over

a network is a new area of research and is related

to distributed information fusion. Processing data

from many sensors generally results in better per-

formance e.g. in distributed robotics (Denzler and

Brown, 2002), environment monitoring, medical as-

sistance (Vrins et al., 2004; Vigneron and Jutten,

2004), etc. but it also requires more communication

resources (and thus, more energy); the reasons for this

are that (i) 2 sensors don’t record exactly the same

(a) Signals before and after the denoising operation

(b) Spectra of the corresponding signals

Figure 3: Noise removal demo. The frequency is expressed

in normalized frequency.

signal, (ii) all sources must be involved in the record-

ing with a non-zero variance, (iii) electrodes provid-

ing irrelevant signals can be rejected, (vi) the low

power of the signal of interest can be improved, (v)

there doesn’t exist an optimal location of the sensors,

constant in time as the “target” moves. These con-

siderations in mind, in addition to the low power of

the signal, may explain why the locations of the elec-

trodes can improve the signal extraction, while others

can decrease its efﬁciency. Therefore, one needs to

consider the trade-offs between performance and re-

source utilization in using networked sensors. Numer-

ous articles have dealt with this topic, but usually in

the area of digital communications (Yao et al., 1998).

BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

374

4.1 The Karhunen-loeve Expansion for

Random Processes

We consider the situation in which n sensors are ran-

domly distributed in a spatial region, which is 3 di-

mensional (the cortex) but could be less. The sen-

sors relative positions are unknown. The sources may

be narrow-band or broadband and they may be in

the far or near ﬁeld with respect to the sensor ar-

ray. The sources do not have speciﬁc characteristics

that can be used to our advantages. Due to these

limitations, our initial goal is limited to the detec-

tion. We assume the existence of n source signals

(t), 1 ≤ i ≤ q} (with n < q), statistically indepen-

dent and zero-mean and the observation of at most as

many mixtures {x

(t), 1 ≤i ≤ n}, formed by (suppos-

edly) linear combinations of the unknown sources, i.e.

(t) =

∑

j=1

i j

(t) + n

(t), (4)

for each i = 1,...,n. This is compactly represented

by the mixing equation x(t) = As(t), where the ma-

trix A

(n×q)

collects the mixing coefﬁcients, s(t) =

(t), ...,s

(t))

is a column vector collecting the

unobserved source signals

, x(t) collects the n ob-

served signals. n

(t) is a spatially white noise with

zero mean and variance σ

. Denote the n ×1 sensor

data vector by

= (x

(t), ...,x

(t))

denotes a random process.

T +1











Figure 4: Augmented table.

Let X

be the table collecting the samples x

,t =

1,..., T (see ﬁgure 4) and C

be the covariance ma-

trix of x estimated by

∑

t=1

and

,i =

1,..., n the eigenvectors and eigenvalues of

. Note

that

and

are estimates of λ

and φ

, and that they

denotes usually the transpose operator.

are resp. random variables and vectors. In section 4.2,

we shall show approximate formulas for the expected

values and variances of these estimates. The array

covariance matrix C = E[x(t)x

(t)] = ASA

+ σ

where S = E[s(t)s

(t)], I

is the n ×n identity matrix.

Consistent estimates of eigenvectors and eigenvalues

of C are given by the eigen decomposition of the sam-

ple covariance matrix (Cover and Thomas, 1991)

C =

T +1

∑

i=t

, (5)

where the ˆq × ˆq and (n − ˆq) ×(n − ˆq) diagonal matri-

ces

and

contain the ˆq and n− ˆq signal and noise

subspace eigenvalues respectively. The columns of

the n ×q and n ×(n − ˆq) matrices

and

contain

the signal and noise subspace eigenvectors, and ˆq is

any consistent estimate of q.

We wish to obtain a ﬁrst-order approximation of the

eigenvectors and eigenvalues of C in terms of the φ

’s

and λ

’s, where C = C

+ ∆C. Suppose that X is aug-

mented by a bloc of values x

T +1

(see ﬁgure 4), then

C = X

X =



T +1





T +1



T +1

(6)

where ∆C = x

T +1

can be seen as a (real sym-

metric) perturbation matrix. Suppose that the λ

’s are

distinct. These may be obtained by retaining the terms

of ﬁrst order of the equation:

+ ∆C)(φ

+ ∆φ

) = (λ

+ ∆λ

)(φ

+ ∆φ

), (7)

where C

= λ

. The resulting equation is:

∆φ

+ ∆Cφ

u λ

∆φ

+ ∆λ

. (8)

To calculate ∆λ

, we premultiply (8) by φ

and, since

= λ

, we have:

∆λ

u φ

∆Cφ

. (9)

The {φ

,..., φ

} form a complete set of basis vectors

i.e. φ

= δ

i j

,∀i, j, where δ

i j

is the Kronecker oper-

ator (δ

i j

= 1 iff i = j). Hence ∆φ

can be expanded as

a linear combination of the φ

’s as follows

∆φ

∑

j=1

i j

, (10)

where b

are vectors of unknown parameters. From

(10), b

i j

= φ

∆φ

If we premultiply (8) by φ

and rearrange, we have

for i , j:

i j

∆Cφ

−λ

(i , j) (11)

To determine b

, we impose a ﬁrst-order normaliza-

tion condition on φ

+ ∆φ

, that is, we require

kφ

+ ∆φ

≈ kφ

+ 2φ

∆φ

, (12)

AutomaticDetectionofHigh-voltageSpindlesforParkinson'sDisease

375

and it follows that φ

∆φ

= b

≈ 0.

Noting that φ

= λ

and φ

= 0 for i , j, we

summarize this section as follows:

+ ∆λ

u φ

Cφ

(13)

i j







Cφ

−λ

, for i , j,

0, for i = j.

(14)

Notice that most of the approach is implicitly based

on a model where the sequence x

is i.i.d., i.e. noth-

ing is assumed concerning temporal evolution. The

algorithm detailed in (13) and (14) examine the non-

stationary case, i.e. falling the ’id’ in i.i.d.

4.2 Estimation of Eigenvalues and

Eigenvectors

Our next task is to estimate the eigenvalues and eigen-

vectors λ

and φ

(i = 1, . ..,n) of the autocorrelation

matrix C. For this, we calculate the sample autocorre-

lation matrix

C =

∑

t=1

and calculate the eigen-

values and eigenvectors

and

C. We can deter-

mine a value of T such that the estimates are sufﬁ-

ciently accurate. Since

C u C for T sufﬁciently large,

we may use the approximations (13) and (14) to ex-

press

and

(i = 1,..., n):

u φ

Cφ

(15)

u φ

∑

j=1

j,i

Cφ

−

. (16)

Consider the expected value of the estimate: since the

expected value of

C E[

C] = C, therefore E[φ

Cφ

] =

C]φ

= φ

Cφ

= λ

i j

. It follows from (15) and

(16) that

] u φ

, E[

] = λ

. (17)

The estimates are unbiased only when the ﬁrst or-

der approximation are used, i.e. the bias come usu-

ally from the second order term of the approximation

(Cover and Thomas, 1991) and the the variance comes

from the ﬁrst order, thus

] u φ

, E[

] = λ

(18)

where f

and g

are functions of C, with a functional

form too complex to determine.

The variances can be obtained from the ﬁrst order ap-

proximation and their approximated values may be

computed as follows:

var(

) = E[(

−λ

)

] = E[

] −λ

u E[φ

Cφ

] −λ

(19)

and

cov(

) = E[(

−φ

)(

−φ

)

]

∑

j=1

j,i

∑

k=1

k,i

E[φ

Cφ

]

(λ

−λ

)(λ

−

)

(20)

∑

k=1

k,i

E[(φ

Cφ

)

]

(λ

−λ

)

(21)

Note that both equations (19) and (21) are expressed

as function of E[(φ

Cφ

)

Suppose now that the X is normally distributed,

E[(φ

Cφ

)

] can be computed as follows. Let

Cφ

∑

k=1

where y

= φ

(22)

and

E[(φ

Cφ

)

] =

∑

k=1

∑

`=1

E[y

] (23)

T −1

i j

E[(y

)

]. (24)

The second subscript on y is dropped since the x

’s

are identically distributed. When X is normally dis-

tributed with zero mean, the y

’s are also normal with

E[y

] = 0. Therefore

E[y

] =

(

3λ

for i = j

for i , j

. (25)

Finally

E[(φ

Cφ

)

] = λ

i j

(λ

i j

+ λ

). (26)

and var(

) ≈

and cov(

) ≈

∑

`=1

j,i

(λ

−λ

)

4.3 HVSs Detection

The HVS detection problem can be modeled as an hy-

pothesis testing problem (Vigneron et al., 2010) and

formulated into a maximum likelihood test we de-

scribe in the following (Johnson et al., 2011).

The observations provided by the sample process are

supposed independent. The input to the detector is de-

noted by z = (z

,..., z

)

where z

, (1 ≤ i ≤ n) will

consist of either noise alone, z

= v

either signal plus

noise z

computed with (15). The noise alone

possibility is called the null hypothesis and is denoted

by H

. The signal plus noise possibility is called the

alternative and is denoted by H

. The detection prob-

lem may be written as testing H

versus H

(

: z

∼ N(0,σ

= σ

)

: z

∼ N(

,σ

= σ

)

, (i = 1, . ..,n) (27)

BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

376

Two assumptions are made on the noise probability

distributions (i) the noise components are indepen-

dent, (ii) their distributions are Gaussian. The inde-

pendence assumption is solely a practical requirement

for the purpose of solving the equations involved.

The gaussianity assumption comes from signal-space

analysis of considering n-dimensional space. The

choice of the Gaussian probability density function

(pdf) is more interesting when computing the likeli-

hood ratio and lead to interesting graphical interpreta-

tion. The conditional probability density of the obser-

vations p(z|H

) and p(z|H

) are unknown. Hence we

shall rewrite the conditional density as p(z|H

,θ

where θ

is a vector of unknown parameter values for

which the we have no prior on the pdf and which are

selected from a set Ω

. We shall select θ

so as to

maximize p(z|H

,θ

). Then our likelihood ratio test

takes the following form:

Λ(z) =

max

∈Ω

p(z|H

,θ

)

max

∈Ω

p(z|H

,θ

)

≶

η. (28)

Suppose that we take a set of n independent identi-

cally distributed observations of the preceding form.

Then we must select θ

= (s; Σ) which maximizes the

joint distribution

p({z

}|H

,θ

) =

∏

i=1

p(z

,θ

) (29)

= (2π)

−nT /2

|Σ|

−n/2

exp

−

trΣ

−1

(30)

where Σ = diag(var(

)) computed with (15) and (16)

is the covariance matrix of z, S is the scatter matrix

S =

∑

i=1

−s)(z

−s)

. The value of θ

which

maximizes p(z|H

,θ

) is s =

∑

i=1

/n.

We suppose that the noise variance estimate is the

same for both hypothesis. Substituting these values

back into the conditional probabilities of the likeli-

hood ratio in Eq. (28) yields

(2π)

−nT /2

|Σ|

−n/2

exp



−

trΣ

−1



(2π)

−T p/2

|S|

−n/2

exp



−

−1



≶

η (31)

Taking the logarithm of both side and recombining

yields

`(z) = z

−1

≶

2lnη + n(log|Σ|+ trΣ

−1

S −|S|).

(32)

The statistic that has been identiﬁed as `(z) is obvi-

ously a sufﬁcient statistic for this problem: it will

tell in which decision region z lies. We need the

means and the variance of `(z) to ﬁnd the densities

p(`|H

) and p(`|H

). z

−1

z is a stochastic quadratic

form. If we assume that all coordinates n

are inde-

pendent, have the same central moments σ

,µ

and

denote a = diag(S

−1

), then

E[`(z)|H

] = n + s

−1

var[`(z)|H

] = 2σ

tr(S

−1

)+(µ

−3σ

a+4s

−1

and

E[`(z)|H

] = E[n

−1

n] = tr(S

−1

Σ) = n

var[`(z)|H

] = var(n

−1

n) = 2σ

tr(S

−1

)+(µ

−3σ

The probability density p(`|H

) is therefore given by:

p(`|H

) = K exp



−

(` −n)

2σ

tr(S

−1

) + (µ

−3σ



(33)

so that p(d

) becomes p(d

) =

∞

p(`|H

)d`

and β = 2 lnλ + n(log|Σ|+ trΣ

−1

S −|S|)

5 RESULTS AND DISCUSSION

We can deﬁne by Z

= {z|`(z) < β} and Z

{z|`(z) ≥ β} two subsets of the n-dimensional space.

Therefore the conditional probability that z ∈ Z

(resp. Z

) is just the conditional probability that `(z)

is less (resp. greater) than β, i.e. HVS burst vs only

noise. Detected HVS patterns are shown in Fig. 5,

with η = 1 (no prior).

Figure 5: Illustration of the detection of PD of HVS burst.

Table 1: Main results number of burst detected with respect

to signal on noise ratio (SNR).

# sensors Signal on noise ratio

3 7 21 20

5 12 24 41

6 21 29 65

8 39 50 88

For short, the performances, as expected, increase

with the number of sensors and a high SNR.

AutomaticDetectionofHigh-voltageSpindlesforParkinson'sDisease

377

6 CONCLUSION

The proposed plan enable us to detect most HVS

episodes at its onset from the local ﬁeld potentials

recorded from awake, freely moving rats and to trig-

ger the delivery of stimulations with arbitrary wave-

forms onto particular brain regions upon detecting

HVSs automatically. More generally, it could help to

improve the existing biometrics methods through bet-

ter event detection and apparently it is well adapted

for multidimensional signal. Previous results show

that the proposed ﬁlter detects about 90% of the

events and commits few errors, ensuring that most

HVS episodes identiﬁed are in agreement with real-

ity.

This corpus of methods relies on a running time

window whose window length (0.5−1s) is too long

to efﬁciently stop individual HVSs episodes (1−4 s).

Under this concern we will investigate in the future

the feasibility of using dynamical models to predict

the occurrence of a HVS before its onset and study if

β-waves can be induced by artiﬁcially evoked HVSs

REFERENCES

Clancy, E. and Farry, K. (2000). Adaptive whitening of

the electromyogram to improve amplitude estimation.

IEEE Trans Biomed Eng., 47(6).

Cover, T. and Thomas, J. (1991). Elements of Information

Theory. John Wiley and Sons.

DeFreitas, J., Beck, T., and Stock, M. (2012). Compar-

ison of methods for removing electromagnetic noise

from electromyographic signals. Physiological Mea-

surement, 33(2):147.

Denzler, J. and Brown, C. (2002). Information theoretic

sensor data selection for active object recognition and

state estimation. IEEE trans. on Pat. Anal. and Mach.

Intel., 24(2):145–156.

Johnson, B. A., Abramovich, Y. I., and Scharf, L. L. (2011).

Detectionestimation of multi-rank gaussian sources

using expected likelihood. Digital Signal Processing,

21(5):568 – 575.

Miyano, H., Masuda, T., and Sadoyama, T. (1980). A note

on the time constant in low-pass ﬁltering of rectiﬁed

surface emg. IEEE Trans Biomed Eng., 27(5):274–8.

Perumal, R. and Chen, H. (2014). Performance analysis in

a wavelet-based algorithm for automatic detection of

high-voltage spindles in parkinson’s disease rat mod-

els. In 9th Asian-Paciﬁc Conference on Medical and

Biological Engineering, Tainan, Taiwan.

Radek, R. J., Curzon, P., and Decker, M. W. (1994). Charac-

terization of high voltage spindles and spatial memory

in young, mature and aged rats. Brain Research Bul-

letin, 33:183188.

Sitnikova, E., Hramov, A. E., Koronovsky, A. A., and van

Luijtelaar, G. (2009). Sleep spindles and spike-wave

discharges in eeg: their generic features, similarities

and distinctions disclosed with fourier transform and

continuous wavelet analysis. J. Neurosci. Methods,

180:304316.

Vigneron, V. and Jutten, C. (2004). Independent Component

Analysis and Blind Signal Separation, volume LNCS

3195 of Lectures Notes in Computer Science, chap-

ter Fisher Information in Source Separation Problems,

pages 168–176. Springer.

Vigneron, V., Syed, T., Montagne, C., Barlovatz-Me imon,

G., and Lelandais, S. (2010). Template matching and

test detection. Application to cell l ocalization in cells

imagery. Pattern Recognition Letters, 31(14):2214–

2224.

Vrins, F., Jutten, C., and Verleysen, M. (2004). Fifth Inter-

national Conference, ICA 2004, volume LNCS 3195,

proceedings Sensor array and electrode selection for

non invasive fetal electrocardiogram extraction by In-

dependent Component Ananlysis. Springer-Verlag,

Granada, Spain.

Yao, K., Hudson, R., D., C., and Lorenzelli, F. (1998). Blind

beamforming on a randomly distributed sensor array

system. IEEE Journal on selected areas in communi-

cation, 16(8):1555–1566.

BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

378