
Slow Trends
A Problem in Analysing Pupil Dynamics
Christoph Strauch, Juliane Georgi, Anke Huckauf and Jan Ehlers
General Psychology, Ulm University, 89069, Ulm, Germany
Keywords: Pupillometry, Trend, Filter-Algorithm, Signal-Analysis, Trend Removal, Long Term Recording.
Abstract: As of recently, research efforts are intensified to operationalize pupil dynamics for cognitive and affective
classification in human-machine interaction. However, signal analysis of pupil diameter changes is
problematic since the respective dynamics consist of three essential components that have to be
disentangled: Very slow diameter changes, slow and high frequencies. The current paper discusses the
amount of slow trends in pupillary signal courses and the effects on functional parameters of pupil dilations.
Thereby we confront our data with linear detrending approaches and reveal various forms of trend
progressions that differ over time and cannot be fixed with conventional linear procedures.
1 INTRODUCTION
The recognition of pupil sizes underlies interest in
human-computer interaction and in research contexts
since the 1960’s (Schwalm, 2009). However, despite
its popularity, the signal analysis remains
problematic. The pupillary signal can be split into
three components: Fast moving changes over
milliseconds (often referred to as signal noise), slow
frequencies and trends, defined as very slow changes
in the signal over many seconds or minutes (Lee et
al., 2007). Those three signal components are
superimposed. Therefore, it is questionable to define
which signal parts are of interest and which parts
belong to noise. High frequencies, if not of interest,
are usually removed using a low pass filter (Siegle et
al., 2003). However filtering mechanisms with
regard to various pupillary signal trends are not
properly investigated yet. The cut off frequency has
still to be tied to a certain frequency.
A common approach in pupil size analysis is the
calculation and comparison of absolute parameters:
maximum, minimum or average values. Those
parameters are calculated during certain time
intervals to draw conclusions, e.g. about the
intensity of a stimulus which appeared at a certain
point of time. However, for other physiological
parameters (e.g. skin conductance) very slow
frequencies are assumed to underlie relevant signal
components and to bias their characteristics (Lehr &
Bergum, 1966; Schandler & Grings, 1976; Siegle et
al., 2003; Szabo & Gauvin, 1992). In all probability,
similar problems arise in pupil dynamics. As a
consequence, comparisons derived from pupil size
amplitudes between stimuli are invalid.
This paper addresses pupillary trends in
laboratory contexts as observed before (e.g. Siegle et
al., 2003). However, a standardized approach to
handle the resulting biases has not been introduced
yet. Closing this methodological gap for the analysis
of pupillary signals seems crucial for the validity of
research efforts in this field.
2 PUPIL DIAMETER IN
RESEARCH
Pupillary size can be measured with eyetrackers.
(Klingner, 2010). Apart from light intensity (Tryon,
1975), different psychological correlates can be
derived from pupil dynamics as a physiological
indicator. This is possible, since size and
responsiveness of the human pupil are determined
by the interplay of two antagonistic muscle groups,
governed by the parasympathetic and sympathetic
system (Beatty & Lucero-Wagoner, 2000).
Increasing sympathetic activity is accompanied by
inhibition of parasympathetic activity and leads to an
enlargement of pupil diameter. Against this, lower
arousal correlates with smaller pupil sizes. Well-
examined psychological correlates of pupil
61
Strauch C., Georgi J., Huckauf A. and Ehlers J..
Slow Trends - A Problem in Analysing Pupil Dynamics.
DOI: 10.5220/0005329400610066
In Proceedings of the 2nd International Conference on Physiological Computing Systems (PhyCS-2015), pages 61-66
ISBN: 978-989-758-085-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

dynamics are cognitive load (tracing back to Hess &
Polt, 1964) as well as emotional activation (Partala
& Surakka, 2003), fatigue and daytime (Wilhelm et
al., 2001) or habituation (Lehr & Bergum, 1966).
3 SIGNAL COMPONENTS
Dismantling the signal results in three definable
components: Trends as very slow frequencies, slow
frequencies and high frequencies, depicted in Figure
1 along their respective frequencies (Lee et al.,
2007).
Figure 1: Pupillary signal components.
High frequent parts are clearly visible in the raw
pupillary signal. High frequencies can be filtered;
however, sometimes they make up the main focus of
interest: A prominent methodological access to high
frequent dynamics in pupil diameter is depicted in
the Index of Cognitive Activity (Marshall, 2002). If
those signal components are not relevant, moving
average smoothing functions or other low pass filters
can be applied. Siegle et al. (2003) used a five point
average filter, which was applied twice for pupil
diameter. The fitting smoothing window size
depends on pupil tracking speed, as high speed
measurements capture more higher frequencies in
the signal, a bigger moving window is necessary for
high speed measured data (Klingner et al., 2008).
The isolation of high frequencies was already
demonstrated (Lee et al., 2007).
For comparisons of mean or maximum pupil
sizes, reactions to stimuli are assumed to be found in
low-frequencies and usually depict the decisive
parameter for researchers. Dilations are defined as
an expansion of pupil-diameter. With regard to
cognitive dynamics, they display a clear onset and a
latency of about 0.2-0.5 seconds (Bergamin &
Kardon, 2003). Thereby, a maximum dilation is
usually reached after about 1-2 seconds (Partala &
Surakka, 2003). The depicted parameters are
consulted in a variety of studies (e.g.: Bradley et al.,
2008; Ekman et al., 2008; Hyönä et al., 1995;).
The origins of very low frequencies remain
unclear. Three explanations are imaginable: First,
the habituation to tasks or stimuli can lead to
decreasing pupil diameters (Lehr & Bergum, 1966).
Secondly, habituation to the laboratory setting could
be decisive for smaller pupils; and third, an overall
process due to the general decline of sympathetic
activation over time could apply. Presumably, all
three factors play a certain role.
If measurements are longer than just few
seconds, it is crucial to control for trends, because
low-frequency movements lie upon very slow
frequencies. Therefore the comparison between
values measured at different times is biased if very
slow frequencies are not controlled. Trends pose a
strong threat regarding the interpretability of
measurements. Long term trends in pupil size have
possibly a bigger influence on pupil diameter than
the low frequency changes elicited by experimental
conditions which apply.
It is important to note that very low frequencies
have been observed for other physiological
parameters like heart rate or skin conductance as
well as for pupil diameter (Lehr & Bergum, 1966;
Schandler & Grings, 1976; Siegle et al., 2003; Szabo
& Gauvin, 1992).
4 WAYS TO DEAL WITH TRENDS
4.1 Linear Detrending Pupil Sizes
The observed very low frequencies in pupillometric
research, where addressed, have often been
subjected to post-hoc mathematical correction by
linear detrending functions (e.g.: Siegle et al., 2003).
Those functions calculate a best fit trend line by
application of least squares methods. After this, each
value on the trendline gets subtracted from the raw
signal. The zero line then represents the overall
average pupil size, and the trend is thus removed.
This procedure has been in use for short
measurement periods (e.g. Siegle, 2003).
Figure 2: Pupil size and linear detrended pupil size of one
subject over 270 seconds.
PhyCS2015-2ndInternationalConferenceonPhysiologicalComputingSystems
62
Measurements for this paper with eight subjects,
who were students at Ulm University have shown an
average decline in pupil size within four and a half
minutes of about 0.4 mm. (MStart = 5.15 mm, MEnd
= 4.72 mm; T (8) = -1.12 p = .13 n.s.). Participants
were asked to go silently through the alphabet to
induce mild cognitive load. This mild cognitive load
increases the comparability of measurements
producing a vanilla-baseline condition, which is less
sensitive to carry overs or trends than other baselines
(Jennings et al., 1992). In between, different tasks
that induce pupil size dilations were completed by
the participants. Participants imagined situations
where they were in fear as first, second and third
task. The fourth task was to calculate; tasks five to
seven asked the participants to relax. All those tasks
were performed while a biofeedback signal showing
the current pupil size was present. A measurement
was conducted every 36 seconds. The average
observed trend showed a non-linear decline in pupil
size, a quicker decline in the first two minutes of
about 0.28 mm was followed by a slower decline of
about 0.16 mm in the remaining two minutes.
However, trends showed a considerable variance
between participants: close to linear declines,
asymptotical declines, but also almost constant and
wavelike signals were observed. Although the
subject number is low, trends posed a problem in the
analysis of each subject’s data. Individual trends
could not be cleared through averaging; furthermore
retesting the same subjects reveals similar trends. As
usually values are compared within persons, a
methodological solution is needed. Longer
measurements show even larger declines, see also
Davidson and Hiebert (1971) for similar
observations.
Figure 2 shows the pupillary signal of a single
subject who took part in this study. The blue line
depicts the averaged pupil size during the
measurements. The red line marks the linear
calculated trend. The dashed line connects the
average pupil size values. Between the first and third
measurement, pupil size declined about 0.9 mm,
between fifth and seventh measurement the decline
was about 0.17 mm. Linear detrending removes the
linear trend (red), this removal results in the zero
line (black). The linear detrending of raw values
(blue) results in the green depicted values. Figure 2
also illustrates the different trends occurring within
each of the seven measurements.
One of the main problems using linear
detrending is the selection of the interval for the
trend. As can be seen in Figure 2, a decrease is
observed within the interval of 270s. When using
intermediate intervals of 60s, fluctuations are
evident. As is illustrated in Figure 3, intervals
approaching the lengths of reactions to a stimulus
can drastically change the compiled effect sizes in
pupil dilations.
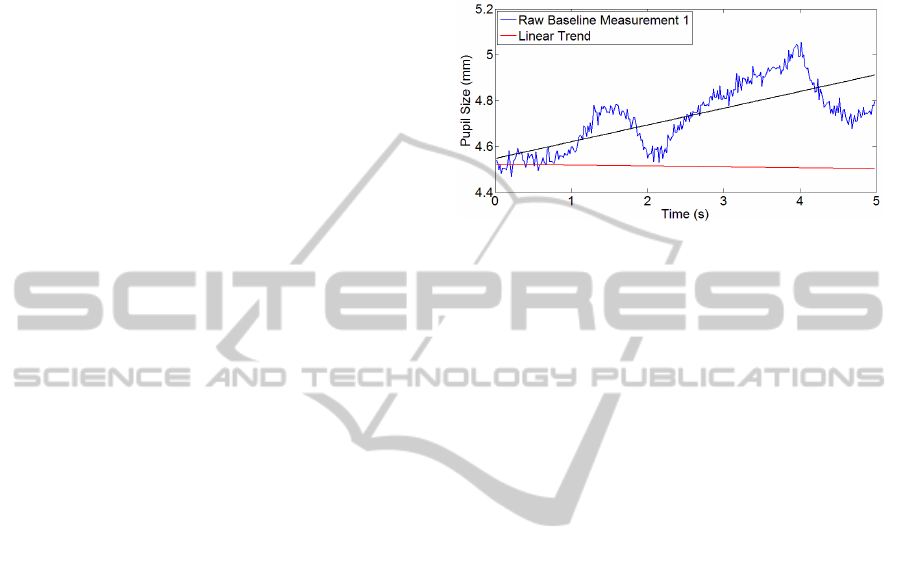
Figure 3: Comparison of the overall linear trend (red) and
the trend in the first measurement (black).
Figure 3 depicts the first of seven measurements
in the original raw signal. The red line displays the
linear trend for the complete signal (overall trend).
To emphasize the problem of overall trending, the
black line illustrates the linear trend of the five
second interval.
It appears that the slope of the five second
measurement is clearly contrary to the overall linear
trend. This indicates that linearly detrending cannot
diminish the trend, as it is completely different for
the displayed period of time. As a consequence, the
trend-caused bias may even get enlarged and would
contradict the intended idea of a linear detrend.
There is no “gold standard” which can serve as a
reference for the appropriateness of a filter yet.
Biases affect both, raw signal and the linear
detrended course: The raw signal is biased by very
slow frequencies and the detrended signal by the
application of linear detrend. Amplitudes in reaction
to stimuli are often the desired parameters in slow
frequencies; these amplitudes take place in
comparably short time intervals of few seconds,
which is why very slow frequencies should not have
a big influence when one amplitude is compared
with the following one. Therefore a close to similar
ratio between amplitudes within few seconds before
and after detrending might serve as a reference for
detrending methods.
The two data plots in Figure 4 depict the raw and
the detrended signal of the first measurement. The
biasing effects of linear detrending are clearly
evident if amplitudes of pupillary events are
compared before and after detrending procedure. If
linear detrending was an appropriate method, the
relations between amplitudes should be the same
before and after linear trend removal. The following
SlowTrends-AProbleminAnalysingPupilDynamics
63
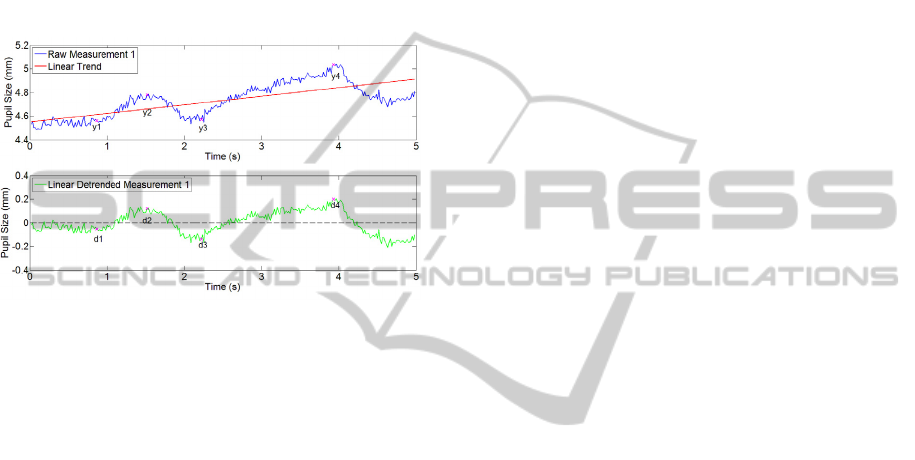
example illustrates the problem: The amplitude of
the first signal peak in the raw data is given by the
difference of y2 and y1. The amplitude of the second
peak is the difference of y4 and y3. In the detrended
signal, the amplitude of the first dilation is given by
the difference of d2 and d1 whereas the amplitude of
the second dilation is the difference of d4 and d3.
The ratio of the two dilations in the raw data is 0.50
while it amounts to 0.54 in the detrended data. This
implicates that linear detrending biases the
amplitudes, in this case by nearly eight percent.
Figure 4: Raw and Detrended Signal with Marked
Amplitudes.
The bias is unequal for every data point
according to its distance to the trendline. As a
consequence, the comparison between different
points within the detrended signal produces invalid
results. Additionally, overall linear detrend
approaches are incapable of correcting wavelike
very slow changes in pupil size. Moreover, linear
detrending does not only affect very slowly
changing parts of the signal but also slow and high
frequencies which leads necessarily to biases
(Moncrieff et al., 2005).
As the autonomous nervous system underlies a
non-linear control mechanism, pupil size as one of
its peripheral correlates changes most probably non-
linear as well (Zhong et al., 2006). Taken together,
linear detrending is probably not suitable for longer
pupil measurements.
4.2 Changing the Protocol
Specific experimental designs can be used to control
for overall trends. The use of several baselines is one
possibility to reduce the impact of trends or carry-
over effects. Vanilla conditions can be used to make
baselines comparable (Jennings et al., 1992). Before
each experimental condition, a corresponding
baseline measurement is conducted. Using this
approach implicitly relies on the assumption that the
trends between baselines and the subsequent
conditions are close to similar. The trend-caused
bias would therefore emerge of comparable size.
The current data oppose this possibility as trends
differ in their dynamic over time. As a consequence
the biases differ and the implicit assumption is
violated.
Another possibility is the usage of a randomized
control group, for which the implicit assumption is
that trends are comparable in experimental and
control group. However, this is only feasible when
all participants and conditions are associated with a
comparable amount of arousal.
4.3 Possible Future Approaches
Trends in pupil size data occur, these appear to be
non-linear – linear removal of trends seems to be
inappropriate. Fitting approaches for removal of
trend should therefore be adaptive.
Even though this problem has been addressed for
electrodermal activity (Benedek & Kaernbach,
2010), a detailed solution does not exist for pupillary
dynamics. However, both parameters are reported to
be highly correlated (Bradley et al., 2008;
Kahneman et al., 1969). Benedek and Kaernbach
(2010) present a filter for the analysis of EDA
signals. The filter enables the division of the signal
into phasic and tonic components. Phasic signal
parts are defined as reactions to stimuli, while tonic
components are defined as a basic level of
electrodermal activity in the absence of stimulation.
This division results in a more valid interpretation of
phasic responses while tonic changes can be
ignored. Decisive for this approach is the
deconvolution of the EDA signal. Deconvolution
comprises the convolution of the raw signal with an
estimated impulse response for phasic EDA
reactions. In the resulting signal, periods of phasic
reactions are made visible. Since tonic components
are defined as the absence of phasic activity, a tonic
signal course can be estimated via interpolation over
the phasic reactions. The subtraction of the
estimated tonic signal from the raw data leads to a
clearer interpretability of phasic activity. Benedek
and Kernbach’s filter approach (2010) allows the
reconstruction of the separated signal parts, which
serves as a validation of the procedure. The
methodological know-how in EDA signal analysis
seems to be a good basis for pupil diameter, since
deconvolution approaches have recently been used
for the detection of dilations (Wierda et al., 2012).
Another possibility to remove trends properly
lies in the division of the pupillary signal along
PhyCS2015-2ndInternationalConferenceonPhysiologicalComputingSystems
64

temporal frequencies according to very slow and
high frequencies as well as slow frequencies.
Relevant frequencies might be recognized and
separated from the overall signal using both low-
and high pass filters.
5 PERSPECTIVES OF TREND
REMOVAL
Especially long and trend sensitive measurements
could profit from an appropriate trend removal.
Long baseline measurements would pose a smaller
problem if corrected, as trends within baselines
could be eliminated. Moncrieff et al. (2005) provides
various detrending approaches for different time
series. This comparison includes linear detrending,
mean removal and running mean filters. As
Moncrieff et al. (2005) dealt with weather data, a
similar strategy could help to identify suitable ways
to handle trends in pupil dynamics. Additional
possibilities with promising results in other areas are
wavelet analysis and detrending approaches applied
in HRV analysis (Homborg et al., 2012; Lee et al.,
2007; Tarvainen et al., 2002). The best method may
be used as a basis for evaluating a new standardized
approach in pupil-trend removal. This standard
would help increasing the quality of results and
enable comparability between results of pupil based
research.
REFERENCES
Beatty, J., & Lucero-Wagoner, B. (2000). The Pupillary
System. In J. T. Cacioppo, L. G. Tassinary & G. G.
Berntson (Eds.), Handbook of Psychophysiology (pp.
142–162). New York: Cambridge University Press.
Benedek, M., & Kaernbach, C. (2010). Decomposition of
Skin Conductance Data by Means of Nonnegative
Deconvolution. Psychophysiology, 47(4), 647-658.
Bergamin, O., & Kardon, R. H. (2003). Latency of the
Pupil Light Reflex: Sample Rate, Stimulus Intensity,
and Variation in Normal Subjects. Investigative
Ophthalmology & Visual Science, 44(4), 1546-1554.
Bradley, M. M., Miccoli, L., Escrig, M. A., & Lang, P. J.
(2008). The Pupil as a Measure of Emotional Arousal
and Autonomic Activation. Psychophysiology, 45(4),
602-607.
Davidson, P. O., & Hiebert, S. F. (1971). Relaxation
Training, Relaxation Instruction, and Repeated
Exposure to a Stressor Film. Journal of Abnormal
Psychology, 78(2), 154.
Ekman, I., Poikola, A., Mäkäräinen, M., Takala, T., &
Hämäläinen, P. (2008). Voluntary Pupil Size Change
as Control in Eyes Only Interaction. In Proceedings of
the 2008 Symposium on Eye Tracking Research &
Applications, (pp. 115-118).
Hess, E. H., & Polt, J. M. (1964). Pupil Size in Relation to
Mental Activity During Simple Problem-
Solving. Science, 143(3611), 1190-1192.
Homborg, A. M., Tinga, T., Zhang, X., van Westing, E. P.
M., Oonincx, P. J., de Wit, J. H. W., & Mol, J. M. C.
(2012). Time–Frequency Methods for Trend Removal
in Electrochemical Noise Data. Electrochimica Acta,
70, 199-209.
Hyönä, J., Tommola, J., & Alaja, A. M. (1995). Pupil
Dilation as a Measure of Processing Load in
Simultaneous Interpretation and Other Language
Tasks. The Quarterly Journal of Experimental
Psychology, 48(3), 598-612.
Jennings, J. R., Kamarck, T., Stewart, C., Eddy, M., &
Johnson, P. (1992). Alternate Cardiovascular Baseline
Assessment Techniques: Vanilla or Resting Baseline.
Psychophysiology, 29(6), 742-750.
Kahneman, D., Tursky, B., Shapiro, D., & Crider, A.
(1969). Pupillary, Heart Rate, and Skin Resistance
Changes During a Mental Task. Journal of
Experimental Psychology, 79(1), 164.
Klingner, J., Kumar, R., & Hanrahan, P. (2008).
Measuring the Task-Evoked Pupillary Response with
a Remote Eye Tracker. In Proceedings of the 2008
Symposium on Eye Tracking Research & Applications,
(pp. 69-72).
Klingner, J. M. (2010). Measuring Cognitive Load During
Visual Tasks by Combining Pupillometry and Eye
Tracking. Dissertation, Stanford University. Stanford:
University Press.
Lee, J. C., Kim, J. E., & Park, K. M. (2007). Posture
Change Affects Indices of Pupil Size-Korean Males in
Their Twenties. Journal Biomedical Engineering
Research, 28, 1-7.
Lehr, D. J., & Bergum, B. O. (1966). Note on Pupillary
Adaptation. Perceptual and Motor Skills, 23(3), 917-
918.
Marshall, S. P. (2002). The Index of Cognitive Activity:
Measuring Cognitive Workload. In Human factors and
Power Plants, 2002. Proceedings of the 2002 IEEE
7th Conference on Human Factors, (pp. 5-9).
Moncrieff, J., Clement, R., Finnigan, J., & Meyers, T.
(2005). Averaging, Detrending, and Filtering of Eddy
Covariance Time Series. In X. Lee et al. (Eds.)
Handbook of Micrometeorology (pp. 7-31). Dordrecht:
Springer Netherlands.
Partala, T., & Surakka, V. (2003). Pupil Size Variation as
an Indication of Affective Processing. International
Journal of Human-Computer Studies, 59(1), 185-198.
Schandler, S. L., & Grings, W. W. (1976). An
Examination of Methods for Producing Relaxation
During Short-Term Laboratory Sessions. Behaviour
Research and Therapy, 14(6), 419-426.
Schwalm, M. (2009). Pupillometrie als Methode zur
Erfassung mentaler Beanspruchungen im automotiven
Kontext. Dissertation. Saarbrücken: Universität
Saarbrücken.
SlowTrends-AProbleminAnalysingPupilDynamics
65

Siegle, G. J., Steinhauer, S. R., Stenger, V. A., Konecky,
R., & Carter, C. S. (2003). Use of Concurrent Pupil
Dilation Assessment to Inform Interpretation and
Analysis of fMRI Data. Neuroimage, 20(1), 114-124.
Szabo, A., & Gauvin, L. (1992). Reactivity to Written
Mental Arithmetic: Effects of Exercise lay-off and
Habituation. Physiology & Behavior, 51(3), 501-506.
Tarvainen, M. P., Ranta-aho, P. O., & Karjalainen, P. A.
(2002). An Advanced Detrending Method with
Application to HRV Analysis. IEEE Transactions on
Biomedical Engineering, 49(2), 172-175.
Tryon, W. W. (1975). Pupillometry: A Survey of Sources
of Variation. Psychophysiology, 12(1), 90-93.
Wierda, S. M., van Rijn, H., Taatgen, N. A., & Martens, S.
(2012). Pupil Dilation Deconvolution Reveals the
Dynamics of Attention at High Temporal Resolution.
Proceedings of the National Academy of Sciences,
109(22), 8456-8460.
Wilhelm, B., Giedke, H., Lüdtke, H., Bittner, E.,
Hofmann, A., & Wilhelm, H. (2001). Daytime
Variations in Central Nervous System Activation
Measured by a Pupillographic Sleepiness Test.
Journal of Sleep Research, 10(1), 1-7.
Zhong, Y., Jan, K. M., Ju, K. H., & Chon, K. H. (2006).
Quantifying Cardiac Sympathetic and Parasympathetic
Nervous Activities Using Principal Dynamic Modes
Analysis of Heart Rate Variability. American Journal
of Physiology - Heart and Circulatory Physiology,
291(3), 1475-1483.
PhyCS2015-2ndInternationalConferenceonPhysiologicalComputingSystems
66
