
Time-variant Adaptive Passive Time Reversal Equaliser and a
Perspective for Environmental Focusing Method
Lussac P. Maia, Ant
´
onio Silva and S
´
ergio M. Jesus
SiPLAB-DEEI-FCT, University of Algarve, Campus de Gambelas, PT-8005-139, Faro, Portugal
Keywords:
Digital Underwater Acoustics Communications, Passive Time Reversal, Coherent Signalling, Environmental-
based Equalisation, Matched Field Processing, Time-variant Channel Modelling.
Abstract:
High digital data throughput in Underwater Acoustic Communications (UAComm) is a challenging sub-
ject, specially in shallow water where the channel is a wave-guide causing multipath propagation and where
Doppler effect usually occurs due to relative source-receiver motion jointly to ocean dynamics. The source
and receiver sensors can be used for telemetry in point-to-point underwater communications or as nodes of an
underwater acoustic network within the scope of oceanic research observatory or offshore activities. However,
channel tracking is required for reliable digital underwater communications between the sensors, which is a
hard task due to the complicated propagation of acoustic waves in the ocean. Equalisation is often required
to perform a compensation method aiming to overcome the inter-symbol interference (ISI) caused by multi-
path propagation. The motivation of this work is to propose a compensation method deploying the adaptive
passive time-reversal (ApTR) equaliser, aiming to perform ISI mitigation jointly to Doppler compensation
in time-variant channels. The benefit given by ApTR processing would be the performance improvement in
underwater communications between an active sensor and a vertical line array of receiver sensors, relying in
well-succeed time-variant channel impulse response estimation. Furthermore, this position paper discusses the
perspective of use an environmental focusing method for channel estimation within the ApTR equaliser, based
on the idea that a set of oceanic acoustic physical parameters – which are generally estimated in low-frequency
matched field processing problems like geoacoustic assessment, ocean tomography and source localization –
could be conveniently used for channel compensation in high frequency underwater communications using
a carefully chosen search space of replicas. The results are two fold: in one hand the equalisation shall im-
prove the UAComm system, and in the other hand, the best match of channel parameters consequently yields
a refined local environmental assessment.
1 INTRODUCTION
The use of high data rate signalling for UAComm
is a challenging subject studied by the scientific
community, finding applications in point-to-point
(P2P) communications and underwater acoustic net-
works (UAN) used for, e.g., offshore activities
and oceanic reasearch observatories (Vilaipornsawai
et al., 2014). The complicated acoustic propagation
in ocean waveguide channels makes hard the task
of establish high rate data troughput between two
node sensors, maily because of multipath propagation
and Doppler distortion, often requiring equalisation.
The equaliser can use channel estimates in the signal
processing to reach compensation for time-frequency
distortion imposed by the variable channel, aiming
to mitigate ISI and improve communications perfor-
mance.
Any channel estimation technique must deal with
frequency selective attenuation, time dispersion from
multipath propagation and frequency dispersion due
to Doppler effect. Further, the use of coherent sig-
nalling is desirable for high data throughput because
of its improved bandwidth efficiency, a desired char-
acteristic in the UAComm system design consider-
ing the bandwidth limitation imposed by the ocean
channel. Additionally, one can note that conventional
equalisers do not use acoustic physical parameters of
the ocean channel, at least in a direct form. This is
not specifically a design requirement, but at first look
one could expect to explore more incisively those pa-
rameters, because they rule the physics of propaga-
tion in the channel. This work proposes to deploy
the adaptive passive time reversal (here after named
ApTR) for achieve channel equalisation in P2P wire-
less underwater communication, using single-input-
103
P. Maia L., Silva A. and M. Jesus S..
Time-variant Adaptive Passive Time Reversal Equaliser and a Perspective for Environmental Focusing Method.
DOI: 10.5220/0005330901030108
In Proceedings of the 4th International Conference on Sensor Networks (SENSORNETS-2015), pages 103-108
ISBN: 978-989-758-086-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

multiple-output (SIMO) structure as required by pas-
sive time reversal technique.
Passive time-reversal (pTR) – and its frequency
domain version named passive phase conjugation
(PPC) (Gomes et al., 2008) – is inspired in active
time-reversal (TR) which compensates the channel
exploring the retro-focusing propagation property of
the wave equation in wave-guide. The TR concept
was first demonstrated in underwater acoustics by
(Parvulescu, 1961). In its passive version the process-
ing can be performed synthetically, exploring spa-
tial and temporal diversity of the acoustic channel by
software setup. Nonetheless, the conventional pTR
equaliser requires to estimate the channel impulse re-
sponse (CIR) which is usually obtained by an ini-
tial channel probe, being unable to track for channel
variability along the data transmission. The ApTR
equaliser is designed to overcome this problem. Fur-
ther, it is proposed for investigation the environmental
focusing method aiming to estimate the time-variant
channel during the data transmission, performing cor-
relation between the observed channel and carefully
chosen replicas in a data bank which is pre-computed
for a restrict area using time-variant high-frequency
acoustic propagation model.
Section II describes the theoretical background for
time-variant UAComm channel modelling. Section
III presents the ApTR, including a preliminary test
in simulated ocean waveguide channel, and discuss
the environmental focusing method. The conclusion
is presented in the Section IV.
2 THEORETICAL BACKGROUND
2.1 CIR Modelling for UAComm
Acoustic propagation in shallow water performs mul-
tiple paths, causing ISI that contributes to errors in
demodulation. Additionally, ocean dynamics and
relative motion between source and receiver cause
time-frequency dispersion, requiring compensation
for Doppler distortion. Under the time-invariant chan-
nel assumption, the ray tracing acoustic propagation
model is suitable for UAComm, because it allows to
range-dependency, have fast computation and use the
infinite-frequency approximation from the ray theory
in the solution of the Helmholtz equation. However,
there are naturally temporal variations in the ocean
channel that make the time-variant approach neces-
sary for more realistic CIR modelling.
The work of (Rodriguez and Silva, 2012)
presented the Time-Variable Acoustic Propagation
Figure 1: Bi-static scattering geometry (full line and dash-
dot line) and mono-static geometry (fine dot line).
Model (TVAPM) that can simulate underwater acous-
tic propagation in time-variant channel using sequen-
tial runs of the Bellhop model (Porter, 2011). The
set of sequential runs of the ray model aims to build
a matrix that provides information about the time-
variant CIR and implements Doppler distortion to
simulate the received signal. The fundamental as-
sumptions to the dynamic propagation simulations
with TVAPM are: source and array can be placed any-
where in a three-dimensional box limited by specified
bathymetry and by a pressure release surface which
can include a wind-driven surface model (JONSWAP
spectrum model was used in this work); a transmitted
signal is specified as input; linear velocities can be at-
tributed to both source and array and the correspond-
ing positions are updated progressively along trans-
missions. This model was used in the present work to
perform time-variant CIR simulations and link them
to a coherent UAComm model containing the ApTR
equaliser.
2.2 Doppler Distortion in Wave-guide
The Doppler distorted signal can be computed for
each path of the multipath propagation through the in-
sertion of a compression factor (β
p
). This factor per-
forms compression/expansion in time and frequency
shift (with compression/expansion in the correspond-
ing spectrum) in the signal.
Figure 1 shows the bi-static scattering geometry
scenario (Ziomek, 1995), where the signal transmitted
by a moving source (T) is reflected in a moving point
scatterer (S) and received in a moving receptor (R).
The velocity vectors for the transmitter, receiver and
point scatterer are
~
V
t
,
~
V
r
and
~
V
s
respectively; ˆn
t,p
and
ˆn
r,p
are the unity vectors in direction of propagation of
the transmitted and received waves, respectively, for
each path.
The time compression factor β
p
for a single path
in the bi-static scattering geometry (paths 1 and 2) is
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
104

(Ziomek, 1995; Gomes et al., 2008)
β
p
=
(1 −
~
V
s
• ˆn
t,p
/c)(1 −
~
V
r
• ˆn
r,p
/c)
(1 −
~
V
s
• ˆn
r,p
/c)(1 −
~
V
t
• ˆn
t,p
/c)
− 1 (1)
where c is the sound speed in the medium, the sym-
bol • denotes dot product and
~
V
x
• ˆn
x,p
represents the
projection of a given velocity vector (
~
V
t
,
~
V
r
or
~
V
s
) in
the ray path direction. The same expression is valid to
compute the mono-static geometry (path 0), just con-
sidering that
~
V
s
is null and ˆn
r,0
is equal to ˆn
t,0
.
The compression factors (β
0
for the direct path,
β
1
for the free surface reflected path and β
2
for the
bottom reflected path) represent the compression (or
dilation) suffered by the signal when travelling to the
receiver through each path.
Consider a transmitted bandpass signal ˜s(t) with
carrier angular frequency ω
c
and low-pass equivalent
signal s(t) containing the information bit sequence
a(n) shaped by the pulse shape p(t) sampled at the
symbol interval T
s
, as follows:
˜s(t) = Re{s(t)e
jω
c
t
}; s(t) = a(n)p(t − nT
s
) (2)
The Doppler distorted bandpass signal ˜s
D
(t) is the
sum of the distorted path signals, which consider the
Doppler compressional factor β
p
in each path p to
perform time compression/expansion and frequency
shift:
˜s
D
(t) =
∑
p
Re{s((1 + β
p
)t)e
jω
c
(1+β
p
)t
} (3)
Using baseband equivalent notation, the received
noiseless signal for a single path can be represented
as the convolution of the path distorted signal s
D
p
(t)
with the single path impulse response g
p
(ν). Perform-
ing algebra manipulation, the time-variant channel
impulse response in the p-th path is given by (Gomes
et al., 2008):
h
p
(t, µ) =
1
1 + β
p
g
p
(
µ + β
p
t
1 + β
p
)e
jω
c
β
p
1+β
p
(t−µ)
(4)
with
y
p
(t) =
Z
s(t − µ)h
p
(t, µ)dµ (5)
In the i-th hydrophone, the time-variant CIR is:
h
i
(t, µ) =
∑
p
h
p,i
(t, µ)δ(t − µ
p,i
) (6)
3 APTR EQUALISER
The passive time-reversal technique performs for
each channel the correlation between the reverse-
conjugated estimated CIR and the observed CIR. The
sum over the channels will yield a function that allows
for a straightforward analysis of the performance of
passive time-reversal based equalisers.
Considering a time-variant channel impulse re-
sponse h
i
(t, µ) and its estimate
ˆ
h
i
(t, µ), where i is the
hydrophone index of a vertical line array, t denotes
time and µ denotes delay, the Q(t,µ)-function is the
summation along the array of the cross-correlation
function between the CIR and the corresponding esti-
mate, as follows
Q(t, µ) =
∑
i
Z
ˆ
h
∗
i
(t, −ν)h
i
(t, µ − ν)dν (7)
For the time-invariant case, since the CIR do not vary
along time, the variable t can be suppressed. Consid-
ering the usual assumptions of pTR, that the sensor
array spans the most energetic area of the water col-
umn for the normal mode orthogonality to hold,
Q(t = 0, µ) ' δ(t = 0, µ) (8)
The pTR output signal is given by
z(t) =
L
∑
i=1
z
i
(t) =
Z
Q(µ)I(t − µ)dµ (9)
where I(t) contains the information data signal a(t)
and the auto-correlation of the pulse shape p(t) used
in the transmitted signal and the receiver, as follows
I(t) =
Z
a(µ)R(t − µ)dµ (10)
and
R(t) =
Z
p
∗
(−µ)p(t − µ)dµ (11)
Since the ApTR adaptive processing is completely
done in the Q-function, equation (9) represents (as
well for the pTR case) the ApTR output signal.
3.0.1 Static CIR and Conventional pTR
Usually the conventional pTR equaliser obtains the
estimated CIR by an initial probe. In static channel
case, considering the usual assumptions of pTR, the
equation (7) have impulse-like shape and it is valid
the relation (8).
3.0.2 Time-variant CIR and Conventional pTR
For the time-variant case with pTR using initial chan-
nel estimate, the function Q(t, µ) becomes
Q(t, µ) =
∑
i
Z
ˆ
h
∗
i
(0,−ν)h
i
(t, µ − ν)dν (12)
and due to the h
i
(t, µ) variability there will be mis-
match between the CIR and the corresponding esti-
mate. It results that, as time goes by, the impulse-like
shape is lost and the ISI increases.
Time-variantAdaptivePassiveTimeReversalEqualiserandaPerspectiveforEnvironmentalFocusingMethod
105

Figure 2: Time-variant ApTR equalizer block diagram.
3.0.3 Time-variant CIR and ApTR
The ApTR, instead of estimating the CIR only at the
time of a initial probe, estimates the time-variant CIR
along the data frame, making possible to maintain the
impulse-like shape of the Q(t,µ)-function. In such
conditions, the validity of relation (8) is kept and ISI
is mitigated. Under the ideal case, it is assumed that
the estimated (simulated) time-variant CIR matches
perfectly with the observed CIR. However, more re-
alistic approach requires to estimate the time-variant
channel using a suitable method. This question is di-
cussed in subsection 3.1.
Figure 2 shows the ApTR equaliser block dia-
gram. The signal s(t) containing the information se-
quence is transmitted through the time-variant chan-
nel and the received signals are processed in the
ApTR equalizer, such that the sum of the processed
channels generates the ApTR output signal z(t), over
which the coherent demodulation yields the estimated
message.
3.1 Environmental Focusing
A well-known technique that employs acoustic prop-
agation modelling is matched field processing (MFP).
It performs correlations between replicas of acoustic
pressure field from a propagation model with the ob-
served field in a receiver array, aiming to estimate an
specific set of physical parameters. It was firstly pro-
posed by (Hinich, 1973). Generally the searched pa-
rameters aims to solve three classes of problems: pas-
sive source localization, matched field inversion for
geoacoustic parameters and ocean acoustic tomog-
raphy to perform estimation of water column sound
speed profile (or the closely related ocean temperature
field). Important benchmarking in MFP are found in
(Bucker, 1976; Tolstoy et al., 1991; Jesus, 1993; Bag-
geroer et al., 1993).
The environmental focusing method for ApTR
equalisation proposed in this work is inspired in the
focalization technique (Collins and Kuperman, 1991),
used in MFP for source localization. Focalization,
which simultaneously focuses and localizes, elimi-
nates the stringent requirement of accurate knowledge
of the ocean-acoustic environment by including the
environment in the parameter search space. The idea
of environmental focusing in UAComm is to create a
data bank of carefully chosen channel replicas (search
space) that reaches the CIR with best acoustic fitness,
which should update the ApTR filters. Generally, it is
quite difficult to accurately model the ocean channel.
Therefore, to make it a less rigid requirement, it is
used this focusing method aiming to reach the replica
that best matches the observed channel, instead of use
an outdated initial probe. In fact, this method does
not use the initial probe to be performed during the
signal transmission. The method is based in careful
pre-computation (and at large number) of time-variant
channel replicas for a specific restrict area, acting
as a probe-independent process (just as it happens
in MFP). The success in channel tracking using the
replicas data bank strongly depends of how well the
channel variability was inserted in the search space.
For example, it is known that even small changes
in the source/receiver positions cause corresponding
changes in acoustic field that severely affect the de-
modulation of coherent UAComm signals, then the
pre-computed search space must contain replicas that
track such geometrical variability in a fine scale. It
can be expected considerable high computational cost
in this procedure and for that reason it is need at least
a coarse knowledge of the environmental/geometric
physical parameters of the local where the system
is employed. The influence of acoustic propagation
physical parameters must be investigated, because its
understanding strongly contributes to build a suitable
search space of replicas. It should not be deliberately
performed a brute force method for choosing the a
priori sets of parameters aiming to avoid the corre-
sponding huge computational cost. The area where
the UAComm system will be employed must be anal-
ysed, being another basis for reasonable selection of
a priori candidates.
This environmental focusing method proposed for
ApTR equalisation is intended to be investigated and
extensively tested by the author in future work. It
is expected that the well-succeed experience of low-
frequency MFP technique could be advantageously
used in model-based adaptive passive time-reversal
equalisation for high-frequency (i.e., 3–50 kHz band)
underwater communications. An evidence that the
cases are similar also resides in the fact that in both
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
106
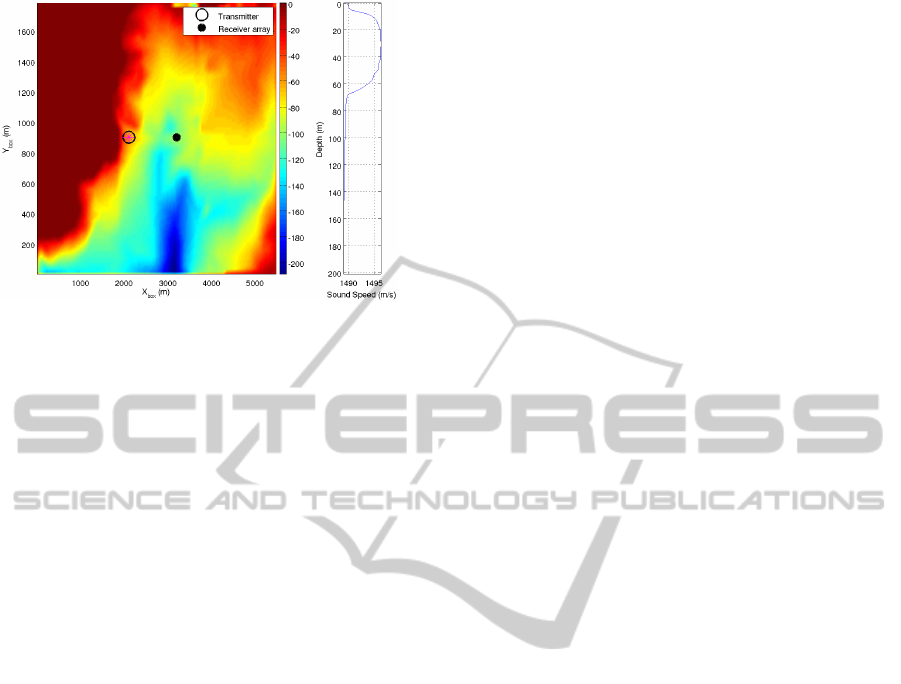
Figure 3: Scenario used in the preliminary test with
TVAPM integrated to the UAComm model.
problems the same wave equation with boundary con-
ditions must be solved. The results would yield the
set of acoustic physical parameters that comes from
the best fit between replicas and the observed CIR,
being the process performed for each channel corre-
sponding to each receiver sensor of the vertical line
array. Such replicas with best fitness should be used
to feed the respective ApTR filters and the sum over
the channels yields the equalised output signal.
3.2 Simulated CIR Test
The following test shows the results from UAComm
simulation using TVAPM to model time-variant CIR.
The test uses simulated channels for feeding the
corresponding ApTR filters, so that the ideal case
is achieved (i.e., best possible match between esti-
mated CIR and observed CIR). Even though no up-
date through focusing method is done yet, the simula-
tion results will show the Doppler compensation and
equalisation being performed by the ApTR.
Figure 3 shows the scenario considered in this test.
The moving source (the star with big circle marks
the initial position) and the static array (small circle)
are positioned inside a 3-D environmental-based box
with range-dependent bottom bathymetry. The upper
surface is computed inside the TVAPM with wind-
driven model using spectrum JONSWAP (Rodriguez
and Silva, 2012), direction 090 degrees, intensity 10
m/s . The runs were done with the sound source ac-
tive sensor developing the velocities of 0 m/s, 0.4 m/s
and 1 m/s. BPSK signals were transmitted with a
carrier frequency 10 kHz. The data frame contained
1024 symbols with bit rate 1000 bit/s. The results
show that the ApTR filters achieved the compensa-
tion for Doppler effect and the equalisation. Figure 4
shows the received constellations after be processed
by conventional pTR (plottings in the first column),
after be processed by ApTR (plottings in the second
column) and after be processed by ApTR with rota-
tion lock (plottings in the third column). Each line of
plottings, from top to bottom, corresponds to the runs
with source velocities 0, 0.4 and 1 m/s, respectively.
In the case of received signal constellation for the
pTR equaliser, the clouds expand themselves rotat-
ing, in ring-like form. This strong distortion is caused
by the Doppler effect from the source motion along
the transmission. In the case of the received con-
stellation after the ApTR equaliser the dense clouds
clearly indicate the Doppler compensation and equal-
isation. Column 2 still shows that constellation ro-
tation still occurs (for the clouds as a whole) after
the ApTR processing. It is an effect from the cross-
correlation between Doppler distorted CIR. Substitut-
ing the time-variant CIR of equation (4) and (6) into
the Q-function of the equation (7) and performing the
integral, one can note that the result contain a remain
phase factor (not showed), which causes the constel-
lation clouds rotation. This was solved performing
the tracking of the constellation rotation angle using
the short m-sequence probe which was previously in-
serted in the frames for time synchronization. The
estimated constellation angle is then used to correct
the rotation, yielding the results showed in column 3.
4 CONCLUSION
The ApTR processor was proposed to perform equal-
isation jointly to Doppler compensation, aiming to
mitigate ISI and improve performance in coherent un-
derwater acoustic communications links whose sen-
sors are in SIMO configuration. The adaptive proce-
dure requires a method to update the equaliser filters
with the time-variant CIR estimates. In this sense,
the environmental focusing method was suggested for
investigation, inspired in the low-frequency matched
field technique, exploring the understanding about the
influence of acoustic propagation physical parameters
for channel modelling, since they rule the physics of
the acoustic propagation in the ocean channel.
Using suitable replicas of realistic environment,
reached from well-tuned modelling that considers
some a priori coarse information relative to the spe-
cific area where the system is used, the estimates of
time-variant CIR feed the ApTR filters. As results are
expected to achieve environmental-based equalisation
of communications signalling and refined local envi-
ronmental assessment. The corresponding UAComm
performance improvement could benefit P2P commu-
nications or the link between two UAN nodes.
Time-variantAdaptivePassiveTimeReversalEqualiserandaPerspectiveforEnvironmentalFocusingMethod
107
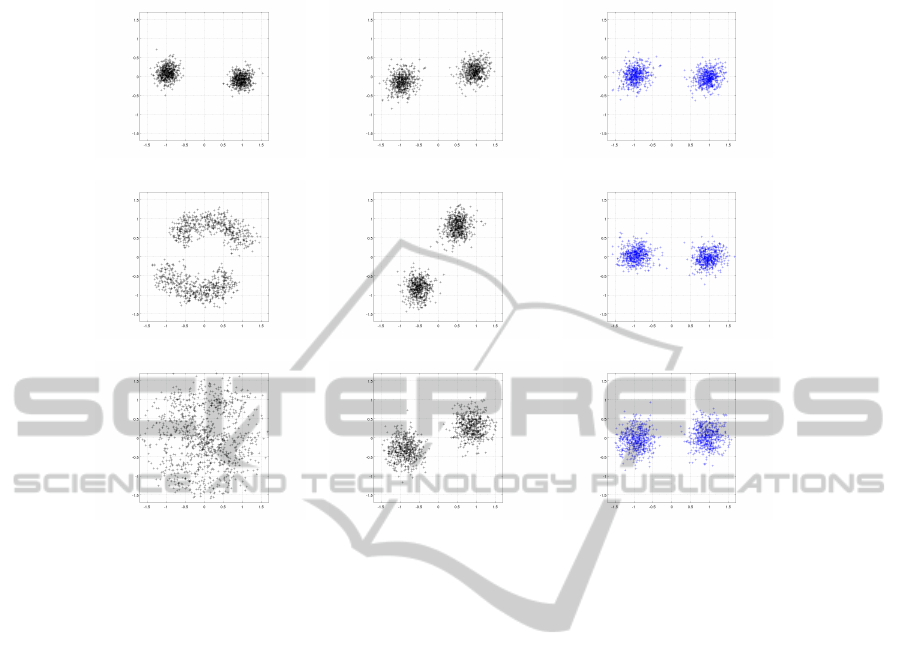
(a) pTR (b) ApTR (c) ApTR + rotation lock
Source-velocity = 0 m/s
Source-velocity = 0.4 m/s
Source-velocity = 1 m/s
Figure 4: Constellations for moving source and wind-driven modelled surface. Column (a): pTR; Column (b): ApTR without
constellation angle correction. Column (c): ApTR with constellation angle correction.
ACKNOWLEDGEMENTS
This work was funded under the Foreign Courses
Program of MB, PCExt-Port219/EMA. The authors
would like to thank the valuable research support
from SiPLAB-FCT team, University of Algarve.
REFERENCES
Baggeroer, A. B., Kuperman, W. A., and Mikhalevsky, P. N.
(1993). An overview of matched field methods in
ocean acoustics. IEEE Journal of Oceanic Engineer-
ing, 18(4):401–424.
Bucker, H. P. (1976). Use of calculated sound fields and
matched-detection to locate sound source in shallow
water. Journal of Acoustical Society of America,
59:368–373.
Collins, M. D. and Kuperman, W. A. (1991). Focaliza-
tion: environmental focusing and source localization.
Journal of Acoustical Society of America, 90(3):1410–
1422.
Gomes, J., Silva, A., and Jesus, S. (2008). Adaptive spatial
combining for passive time-reversed communications.
Journal of Acoustical Society of America, (124):1038–
1053.
Hinich, M. J. (1973). Maximum-likelihood signal process-
ing for a vertical array. Journal of Acoustical Society
of America, 54:499–503.
Jesus, S. (1993). Broadband matched-field processing of
transient signals in shallow water. Journal of Acousti-
cal Society of America.
Parvulescu, A. (1961). Signal detection in a multipath
medium by m.e.s.s. processing. Journal of Acousti-
cal Society of America, 33:1674.
Porter, M. B. (2011). The BELLHOP Manual and User’s
Guide. Heat, Light, and Sound Research, Inc., La
Jolla, CA, USA.
Rodriguez, O. C. and Silva, A. J. (2012). The Time Variable
Acoustic Propagation Model (TV-APM). Signal Pro-
cessing Laboratory, FCT, Universidade do Algarve,
http://www.siplab.fct.ualg.pt/tvapm.shtml.
Tolstoy, A., Diachok, O., and Frazer, L. (1991). Acoustic
tomography via matched-field processing. Journal of
Acoustical Society of America, 89:1119–1127.
Vilaipornsawai, U., Silva, A., and Jesus, S. M. (2014). Ex-
perimental testing of asymmetric underwater acoustic
networks. In IEEE Fifth International Conference on
Communications and Eletronics (ICEE), pages 118–
123, Danang, Vietnam. IEEE.
Ziomek, L. J. (1995). Fundamentals of Acoustic Field The-
ory and Space-Time Signal Processing. CRC.
SENSORNETS2015-4thInternationalConferenceonSensorNetworks
108
