
Automatic Generation of Suitable DWT Sub-band
An Application to Brain MRI Classification
Mohamed Mokhtar Bendib
1
, Hayet Farida Merouani
1
and Fatma Diaba
2
1
LRI Laboratory, Badji-Mokhtar University, Annaba, Algeria
2
LMA Laboratory, Badji-Mokhtar University, Annaba, Algeria
Keywords: Magnetic Resonance Imaging, Brain MRI Classification, Discrete Wavelet Transform, Undecimated
Wavelet Transform, Genetic Programming.
Abstract: This paper addresses the Brain MRI (Magnetic Resonance Imaging) classification problem from a new
point of view. Indeed, most of the works reported in the literature follow the subsequent methodology: 1)
Discrete Wavelet Transform (DWT) application, 2) sub-band selection, 3) feature extraction, and 4)
learning. Consequently, those methods are limited by the information contained on the selected DWT
outputs (sub-bands). This paper addresses the possibility of creating new suitable DWT sub-bands (by
combining the classical DWT sub-bands) using Genetic Programming (GP) and a Random Forest (RF)
classifier. These could be employed to efficiently address different classification scenarios (normal versus
pathological, one versus all, and even multiclassification) as well as other automatic tasks.
1 INTRODUCTION
The MRI is a powerful acquisition technology that
allows to efficiently explore the human brain
through different views (Axial, Coronal, and
Sagittal) and modalities (T1, T2, Flair). Many
important clinical tasks are highly dependent on the
MRI: brain pathologies detection, treatment
validation, surgical planning, etc.
Up to now, brain MRI analysis is mostly
performed in a supervised way. Nevertheless, the
human expertise is tiring, subjective, and greatly
impacted by the immediate environment. For all
these reasons, it is necessary to conceive automated
and reliable tools for diagnostic support.
Recognizing abnormal brains and identifying the
pathology type, are two central tasks assured by the
physicians. Thus, several works have tried to
automatically address them (Chaplot et al., 2006)
(El-Dahshan et al., 2010) (Zhang et al., 2011)
(Lahmiri and Boukadoum, 2011) (Saritha et al.,
2013) (Kalbkhani et al., 2013). All these methods
repeats the same reasoning: 1) DWT application, 2)
empirical selection of sub-bands, 3) feature
extraction, 4) learning and testing. By doing so, the
final performances are inevitably limited by the
information contained on the selected DWT outputs.
The present work proposes a method to
automatically search for (discover) new appropriate
sub-bands, in order to efficiently address different
classification tasks. It applies UWT (a special
variant of the DWT), combines the resulting sub-
bands through GP, and evaluates the pertinence of
the resulting representations by means of a RF
classifier.
The rest of the paper is organized as follows:
Section 2 presents the employed methodology.
Section 3 explains the validation phase. Section 4
concludes the paper by evoking some future
directions.
2 METHODOLOGY
The flowchart of the proposed method is illustrated
in Figure 1. Note that this scheme can address
different classification scenarios:
-Normal versus pathological.
-Each pathology against the rest (one versus all).
-Multiclassification.
In what follows, each step of system is explained in
more details.
166
Bendib M., Merouani H. and Diaba F..
Automatic Generation of Suitable DWT Sub-band - An Application to Brain MRI Classification.
DOI: 10.5220/0005333001660170
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 166-170
ISBN: 978-989-758-091-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Overview of the proposed system for creating
new appropriate sub-bands.
2.1 DWT
The DWT (Mallat, 1989) of a signal
can be
written as:
,
∗
2
(1)
,
∗
2
(2)
,
and
,
are the approximation (low
frequency content) and detail (high frequency
content) coefficients of the signal
, respectively.
is the low pass filter whereas is the high pass
filter. and designate the wavelet scale and
translation factor, respectively.
When applied to a two-dimensional signal, the
DWT produces four sub-bands LL (approximate
coefficients), LH (Horizontal Details), HL (Vertical
Details), and HH (Diagonal Details) at each scale.
The DWT employs a subsampling process that
reduces the size of the data (by half) at every scale.
That means that the resulting sub-bands have
different sizes and cannot be intuitively combined.
Therefore, to address this problem, we make use of a
special variant of the DWT, which is the
Undecimated Wavelet Transform (UWT) (Nason
and Silverman, 1995). Whatever the scale, this
signal analysis technique produces sub-bands that
have exactly the same size as the original signal.
2.2 Random Forests (RF)
RF (Breiman, 2001) is an ensemble-learning
paradigm that grows and combines multiple decision
trees in order to make prediction (classification or
regression). When compared to other learning
methods, RF has a fewer input parameters and runs
quickly on vast databases. It can handle a huge
amount of variables (without any normalization) as
well as incomplete data. Moreover, cross-validation
is not necessary because RF generates an unbiased
estimation of the generalization error during the
training phase (out-of-bag classification error). The
RF learning process is an iterative scheme that
includes for every tree to:
-Select a subset from the training set by picking
n times with replacement.
-Grow the tree on the selected subset.
-At each node of the tree, randomly choose m
variables and compute the best split based only
on those ones.
Note that after the training phase, it is not necessary
to prune the resulting trees. Furthermore, the
response of the model to a new data instance is often
taken as the mode of the responses returned by all
the units.
2.3 Genetic Programming (GP)
GP (Koza, 1992) is an evolutionary computation
technique, which can be considered as a systematic
and domain independent method, for getting
computers to automatically resolve problems,
without the need of clearly telling them how to do
(Langdon et al, 2008). It consists of applying the
Darwinian evolution theory (Darwin, 1864) on a
population of programs (which are generally tree
shaped) through several iterations, by applying
different operators. The GP formalism used in the
present work is described below:
2.3.1 Terminals and Nonterminals
The terminals used in the proposed method consist
of the sub-bands that are produced by the UWT;
these are matrices of 256*256 size. Nonterminals are
taken from usual mathematical functions; +, -, *, /,
ABS, SQRT, LOG, POW2, POW3, SIN, COS, MIN,
MAX. These are applied at the matrix level (so as to
avoid undefined outputs). Besides these functions,
some other operations that are specifically related to
the matrix formalism could also be employed
(inverse, transpose, etc.).
2.3.2 Individuals
Each individual is composed of a single tree; a
combination of several sub-bands.
AutomaticGenerationofSuitableDWTSub-band-AnApplicationtoBrainMRIClassification
167
2.3.3 Initialisation
Initializing an individual implies initializing its tree.
This task is tackled by the Ramped half-and-half
method (Koza, 1992), which produces trees of
different sizes and shapes.
2.3.4 Selection
This operation allows to select the individuals that
will contribute to form the next generation. It
consists of performing a stochastic binary
tournament.
2.3.5 Crossover
This operator permits to combine the genetic
material. It consists of randomly picking two
positions on two individuals and aggregating two
parts of them in order to form a new individual.
2.3.6 Mutation
This operation enables to prevent early convergence.
It includes randomly selecting a sub-tree and
replacing it by another randomly generated tree.
2.3.7 Fitness
In the proposed method, computing the fitness of a
given individual involves the execution of its
corresponding tree, the use of the resulting values to
train and test a RF classifier (employing two distinct
datasets), the computation of the number of correct
classifications in the testing set, and the deduction of
the accuracy. To avoid a rapid growth of the
individuals, the accuracy is combined with the
individual size (number of nodes in the tree), which
results in:
∗
(3)
serves to control the influence of the size on the
fitness.
The evaluation of the fitness function may
involve a relatively high complexity. However, we
think that using an appropriate programming
language (e.g. C++) and a multithreaded
implementation would greatly ease that issue.
3 VALIDATION
The data used in this study consists of T2 weighed
256 × 256 axial brain images, which were collected
from the Whole Brain Atlas database
(http://www.med.harvard.edu/aanlib/home.html).
Six categories are considered: Alzheimer, Chronic
Subdural Hematoma, Fatal Stroke, Glioma,
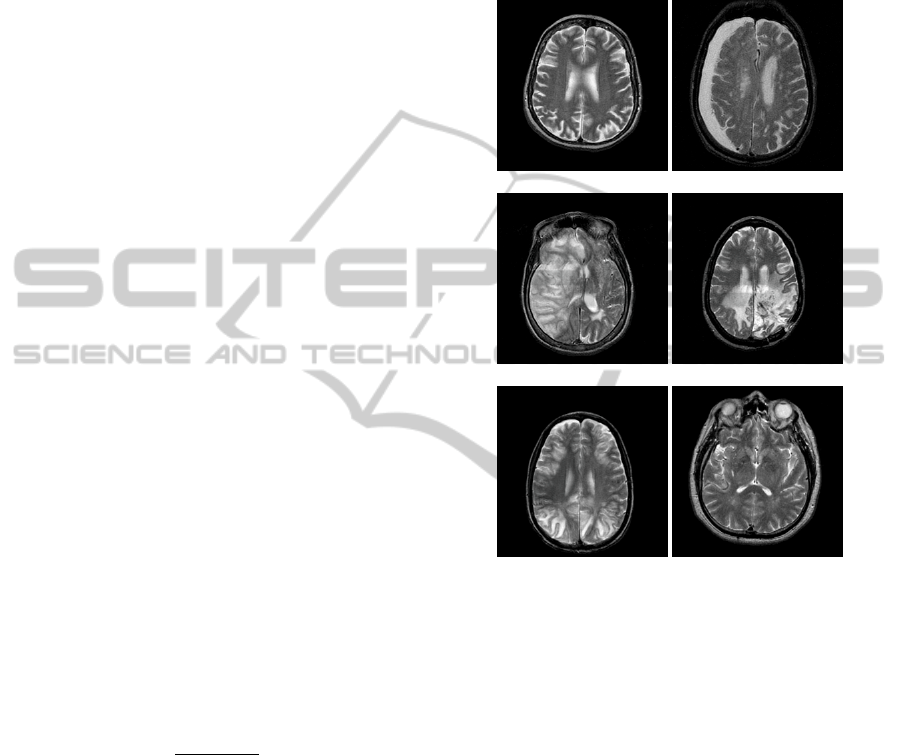
Hypertensive Encephalopathy, and Normal. Figure 2
gives an overview of each category.
(a) (b)
(c) (d)
(e) (f)
Figure 2: Instances from the different categories that are
considered in the proposed Method: Alzheimer (a),
Chronic Subdural Hematoma (b), Fatal Stroke (c), Glioma
(d), Hypertensive Encephalopathy (e), Normal (f).
Twelve samples are randomly selected from each
category and three subsets P1, P2, and P3 are created
by randomly dividing each category. P1 and P2 are
used to train and tune the system whereas P3 is
employed to evaluate the performance.
Figure 3 gives an overview of the UWT outputs
(each sub-band repents a specific view of the
original signal). Figure 4 depicts what is expected
from the proposed system (highlighting a given
aspect of the image).
4 CONCLUSIONS
In this paper, the brain MRI classification problem
was tackled by a new strategy. This latter can
address different classification scenarios by creating
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
168
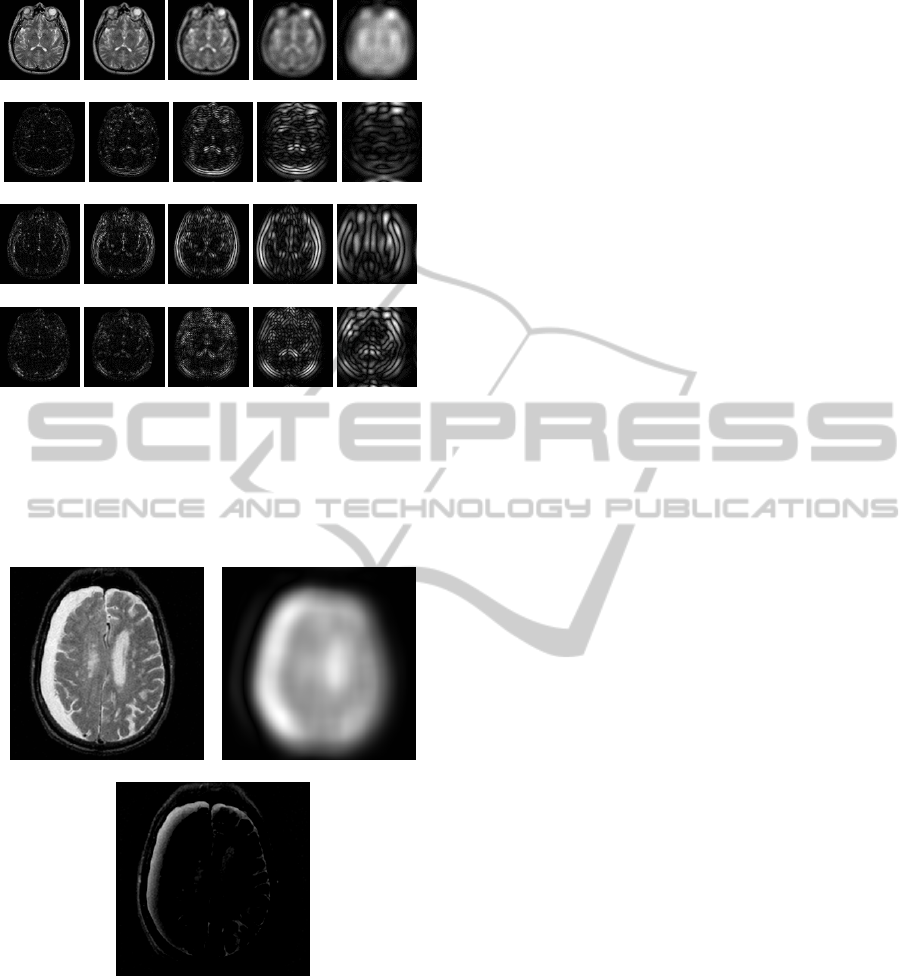
Figure 3: UWT outputs (5 levels using the Daubechies 2
(db2) wavelet): application to Figure 2(f). From left to
right, the five levels (15). From top to down, the LL,
LH, HL, and HH components, respectively. This work
assumes that it is possible to discover more pertinent sub-
bands (to address different classification scenarios) by
combining the base UWT sub-bands.
(a) (b)
(c)
Figure 4: an example of a pertinent handcrafted
combination using the db2 wavelet: (a) the approximation
coefficients of the first UWT decomposition level of
Figure 2(b), (b) the approximation coefficients of the fifth
UWT decomposition level of Figure 2(b), and (c) result of
(a) minus (b). From (c), one can note that a large part of
the hematoma is highlighted (next to some other small
non-pertinent regions).
new useful sub-bands (from the base UWT sub-
bands) using GP. The newly created representations
can be used as they are, or they can serve as a base
for an efficient feature extraction or reduction phase.
We are currently testing the proposed method
according to the different scenarios defined earlier.
Note that the fallout out of the proposed scheme
goes far beyond the problem treated in this paper,
since it could allow the creation of sub-bands that
can efficiently highlight a given structure (thalamus,
caudate nucleus, etc.) or a given cerebral matter
(White Matter, Gray Matter, or Cerebrospinal Fluid).
Thereby, some important tasks like segmentation or
quantification could be greatly enhanced.
The current state the of the system enables to
exploit the sub-bands that are produced by only one
wavelet at a time. However, one can envisage to use
the outputs of different wavelets simultaneously.
REFERENCES
Breiman, L., 2001. Random forests, Machine Learning.
45(1), 5-32.
Chaplot, S., Patnaik, L. M., Jagannathan, N. R., 2006.
Classification of magnetic resonance brain images
using wavelets as input to support vector machine and
neural network. Biomedical Signal Processing and
Control 1(1), 86-92 (2006).
Darwin, C., 1864. On the origin of species by means of
natural selection or the preservation of favoured races
in the struggle for life. Cambridge University Press.
Cambridge, UK.
El-Dahshan, E. S. A., Hosny. T., Salem, A. B. M., 2010.
Hybrid intelligent techniques for MRI brain images
classification. Digital Signal Processing 20(2), 433-
441.
Kalbkhani, H., Shayesteh, M. G., Zali-Vargahan, B., 2013.
Robust algorithm for brain magnetic resonance image
(MRI) classification based on GARCH variances
series. Biomedical Signal Processing and Control 8(6),
909-919.
Koza, J., 1992. Genetic programming: On the
programming of computers by means of natural
selection. MIT Press. Cambridge, MA, USA.
Lahmiri, S., Boukadoum, M., 2011. Classification of brain
MRI using the LH and HL wavelet transform sub-
bands. In IEEE International Symposium on Circuits
and Systems 1025-1028 (Rio de Janeiro).
Langdon, W. B., Poli, R., MacPhee, N. F., Koza, J. R.,
2008. Genetic Programming: An Introduction and
Tutorial, with a Survey of Techniques and
Applications, in Computational Intelligence: A
Compendium, Studies in Computational Intelligence
115, 927-1028, Springer Heidelberg. Berlin,
Deutschland.
Mallat, S. G., 1989. A theory for multiresolution signal
decomposition: the wavelet representation. In IEEE
Transactions on Pattern Analysis and Machine
Intelligence 11(7), 674-693.
AutomaticGenerationofSuitableDWTSub-band-AnApplicationtoBrainMRIClassification
169

Nason, G. P., Silverman, B. W., 1995. The stationary
wavelet transform and some statistical applications.
Wavelets and Statistics, Lecture Notes in Statistics
103, 281-299.
Saritha, M., Joseph, K. P., Mathew, A. T., 2013
Classification of MRI brain images using combined
wavelet entropy based spider web plots and
probabilistic neural network. Pattern Recognition
Letters 34(16), 2151-2156.
Zhang, Y., Dong, Z., Wu, L., Wang, S., 2011. A hybrid
method for MRI brain image classification. Expert
Systems with Applications 38(8), 10049-10053.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
170
