
Optical Properties of Coated Nanospheres in Visible Wavelength
Range
A. Rostami
1,2
, M. Dolatyari
2
, G. Rostami
2
, S. Khosravi
1
and M. Keshavarz
2
1
Photonics and Nanocrystal research Lab. (PNRL), Faculty of Electrical and Computer Engineering,
University of Tabriz, Tabriz, 5166614761, Iran
2
OIC Research Group, School of Engineering-Emerging Technologies, University of Tabriz, Tabriz, 5166614761, Iran
Keywords: Negative Permittivity, Core-Shell Nanoparticles, Effective Medium and Resonance Wavelength.
Abstract: In this paper we have studied polymeric structures which possess coated spherical nanoparticles in visible
wavelength range. Medium with metallic cores and silicon (Si) shells and structures composed by Si cores
and metallic shells have been studied. Since, the size of particles is very small related to the incident
wavelength, semi-static approximation and Clausius-Mossotti formula have been used in order to calculate
the effective permittivity. Resonance wavelength of the structure depends on size and filling fraction of the
guest nanoparticles. Resonance wavelength has been obtained by the mathematical relations and simulation
results. Studied structures are applicable in invisibility.
1 INTRODUCTION
Mediums composed by core-shell nanoparticles in
terms of application in photovoltaic cells,
nanoantenna, optical switches and building blocks of
metamaterial are important (Tang, Huo, Brittman,
Gao, and Yang, 2011, Li, Engheta, 2007, Li,
Salandrino, and Engheta, 2007, Rostami, Shahabadi,
AfzaliKusha, and Rostami, 2012, Paniagua-
Dominguez, Lopez-Tejeira, Marques, and Sanchez-
Gil, 2011).
Also, sensors composed by coated spherical particles
which possess the metal (Ag) cores and dielectric
shells (SiO
2
) or crystalline core-shell particles are of
interest to the researches (Aslan, Wu, Lakowicz, and
Geddes, 2007, Choi, Park, and Kim, 2009).
Biosensors based on Localised Surface Plasmon
Resonance (LSPR) constructed by core-shell
nanoparticles have been studied in (Hao, Sonnefraud,
Dorpe, Maier, Halas, and Nordlander, 2008, Endo,
Kerman, Nagatani, Hiepa, Kim, Yonezawa, Nakano,
and Tamiya, 2006) .
Moreover, medium with random distribution of core-
shell nanoparticles in terms of simplicity in
construction are particularly important. These
polymeric mediums have electric resonances
managed by filling fraction and size of particles,
therefore these structures can be applicable in optical
cloaking.
In this paper first we have studied a polymeric media
with random distribution of spherical coated
nanoparticles in visible wavelength range. First a
polymeric medium possesses spherical nanoparticles
with a metallic cores (Ag) and Si shells has been
studied. Since metallic cores are surrounded only by
Si, the effective medium has only one resonance
wavelength in the visible range. For cylindrical
cloaking excited by a transverse magnetic (TM) plane
wave polarization state permittivity from 0 to 1 is
required, so design of a cloak based on these
investigated structures is possible in visible
wavelength range (Cai, and Shalaev, 2010).
Polymeric medium which possesses core-shell
nanoparticles with Si cores and metallic shells (Ag)
has been studied in the next step. In this structure
metals are surrounded by two medias (Si cores and
polymeric host) therefore the structure has two
resonance wavelengths. The resonances have been
occurred in the visible and ultraviolet bands.
Therefore as has been noted for first structure, cloak
operated at two wavelengths in visible and ultraviolet
bands can be designed by desired filling factor and
size of particles. Resonance conditions of both
effective medium have been obtained by
mathematical relations and simulation results. It has
been shown that the resonance condition strongly
depends on the size and filling fraction of guest
nanoparticles.
90
Rostami A., Dolatyari M., Rostami G., Khosravi S. and Keshavarz M..
Optical Properties of Coated Nanospheres in Visible Wavelength Range.
DOI: 10.5220/0005334800900095
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 90-95
ISBN: 978-989-758-093-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Since the size of nanoparticals is very small related to
the incident wavelength, semi-static approximation
and Clausius-Mossotti formula in order to calculate
the effective permittivity have been used.
2 THEORETICAL AND
SIMULATION RESULTS
A polymeric media with random distribution of
spherical nanoparticles containing metallic cores
(Ag) with radius
1
and Si shells with radius
2
has
been studied. Dielectric constants of silver cores and
Si shells are
1
and
2
respectively. Effective
permittivity of media has been obtained by Clausius-
Mossotti formula as (Paniagua-Dominguez, Lopez-
Tejeira, Marques, and Sanchez-Gil, 2011) :
3
2
E
h
h
a42
-
π
α
εε
ε
ε
f
eff
eff
=
+
(1)
Where,
, and
are electric polarizability,
filling fraction of the spherical nanoparticles and
permittivity of host media respectively. A schematic
of the structure has been shown in Figure 1:
Figure 1: First structure has nanoparticles with metallic
cores and Si shells.
Resonance wavelength of effective medium depends
on size and filling fraction of the spherical particles
as has been discussed in the following.
Since, the size of the particle is very small related to
the incident wavelength, the electric polarizability of
a core-shell can be expressed by semi-static
approximation as equation (2) (Bohren, and Huffman,
1983):
))(22()2)(2(
)2)(()2)((
4
212212
221212
3
2
εεεετεεεε
ε
ε
ε
ε
τ
ε
ε
ε
ε
πα
−−+++
+−++−
=
hh
hh
a
(2)
Where, = (
1
/
2
)
3
. The resonance condition for a
particle can be obtained by setting the denominator of
equation (2) to zero, but for the effective medium the
resonance condition is different, because we are
dealing with a set of particles. The effective
permittivity can be expressed versus electric
polarizability as:
)
4
1(
)
4
2
1(
3
2
3
2
a
f
a
f
h
eff
π
α
ε
π
α
ε
−
+
=
(3)
By inserting (2) in (3) the effective permittivity can
be discussed as:
h
hhhh
hhhh
eff
ff
ff
ε
εεεετεεεεεεεετεεεε
ε
ε
ε
ε
τ
ε
ε
ε
ε
ε
ε
ε
ε
τ
ε
ε
ε
ε
ε
)2)(()2)(())(22()2)(2(
)2)((2)2)((2))(22()2)(2(
221212212212
221212212212
+−−+−−−−+++
+−++−+−−+++
=
(4)
By setting the denominator of (4) to zero and solving
the equation versus
1
, resonance conditions will be
expressed as:
2222
22222
1
2222
)2222242(
τετεεετετεεε
τ
ε
τ
ε
ε
ε
τ
ε
τ
ε
ε
ε
ε
ε
ffff
ffff
hhhh
hhhh
res
++−++−−−
+++−+−+
=
(5)
By setting, dielectric constants of shells and host as
2
=12.1 and
h
=2.1904 equation (5) can be discussed
by:
ττ
τ
τ
ε
ff
ff
res
3.269.98.194.16
)3.268.198.199.32(1.12
1
++−−
+−−
=
(6)
Dielectric constant of the metallic core has been
assumed as Drude model (Cai, and Shalaev, 2010) :
()
ωγω
ω
ωε
i
p
+
−=
2
2
1
1
(7)
Where,
p
=14*10
15
and =0.032*10
15
are the plasma
frequency and collision frequency of silver
respectively (Cai, and Shalaev, 2010). Therefore the
resonance frequency is obtained as equation (8):
0
3.269.98.194.16
)3.268.198.199.32(1.12
*10*032.0*
)10*14(
1
152
215
=
++−−
+−−
−
+
−
ττ
ττ
ωω
ff
ff
i
resres
(8)
The roots of the above equation are complex; the
frequency which has the positive real part is the
desired answer. Real part of this value is resonant
frequency of the effective media.
The roots depend on
and . The effective
permittivity of the polymeric medium by fixing the
inner radius and changing the outer radius of the guest
particles has been shown in Figure 2.
As can be seen in Figure 2 the real part of the effective
permittivity is negative in visible wavelength range,
so these structures can be useful in construction of
building blocks for metamaterials. The wavelength
band with negative permittivity becomes wider by
OpticalPropertiesofCoatedNanospheresinVisibleWavelengthRange
91

(a)
(b)
(c)
Figure 2: Real part of effective permittivity with different
fill factors in visible region for (a) R
in
=15nm, R=25nm, (b)
Rin=15nm, R=30nm, (c) R
in
=15nm, R=35nm, the host
medium is polymeric with refractive index of 1.48.
increasing the filling fraction of nanoparticles,
because the number of the guest particles increases.
The particle can be assumed as a cavity, so by
increasing the outer radius of the cavity resonance
wavelength shifts to higher values. The effective
permittivity by fixing the outer radial and changing
the inner radial of the particles has been shown in
Figure 3.
By increasing the inner radius of the particles the
resonance wavelength is shifted to the lower
wavelength values. Because by increasing the inner
radial of the particles and decreasing the thickness of
the shells, the particles can be assumed in the
polymeric medium without any shells. Therefore the
resonance conditions for the particles (
particles
=-2
h
)
shifts to lower wavelength.
(a)
(b)
(c)
Figure 3: Real part of effective permittivity with different
fill factors in visible region for (a) R
in
=20nm, R=35nm, (b)
R
in
=25nm, R=35nm, (c) R
in
=30nm, R=35nm, the host
medium is polymeric with refractive index of 1.48.
As has been shown in Figure 2 and 3 the resonance
wavelength depends on the filling fraction. The
resonance wavelength which has been obtained by
mathematical relations and diagrams has been given
in the Table 1.
Table 1: Resonance wavelength obtained by mathematical
relations and diagrams for different size and filling fraction
of guest particles.
(nm)by Diagrams(nm)by (8)
f
574.1 574.7 (15/25)
3
0.1
619.3 620 (15/30)
3
0.2
643.5 644.5 (15/35)
3
0.3
603.3 603.9 (20/35)
3
0.3
529.9 530.1 (25/35)30.2
431.6 431.4 (30/35)30.1
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
92
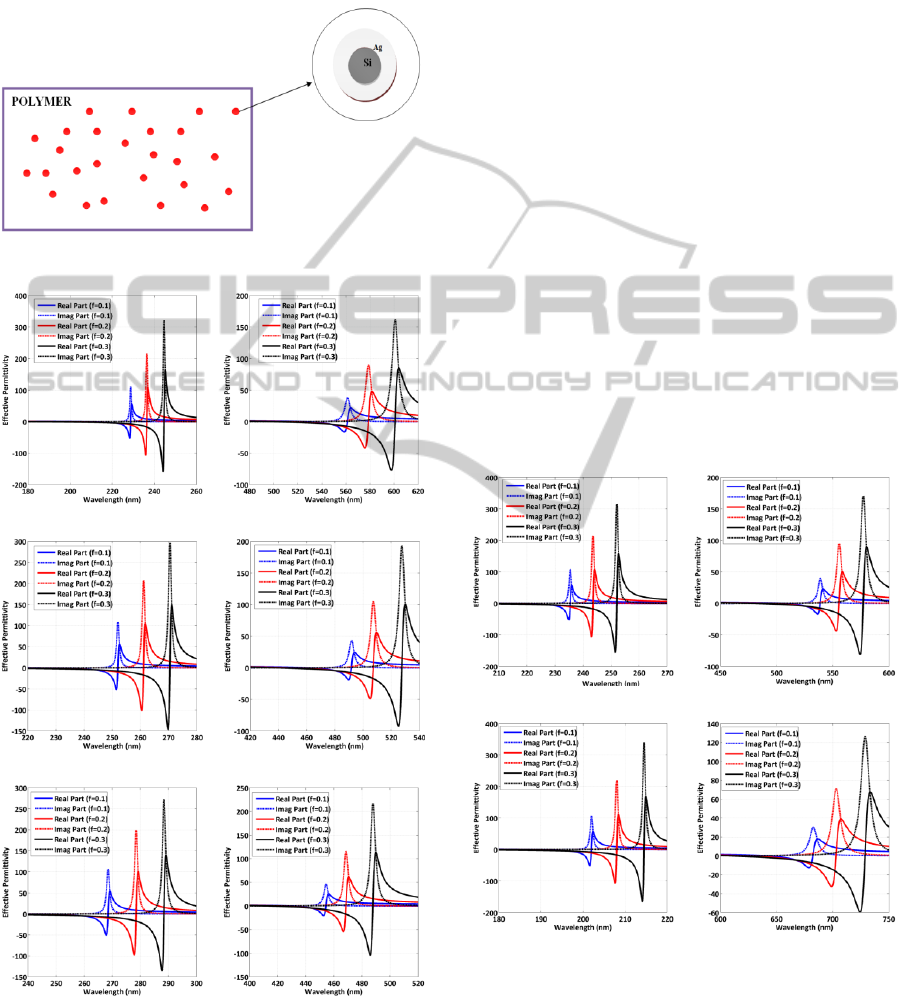
Also a polymeric medium with random distribution
of spherical nanoparticles compose by Si cores with
radius
1
and metallic shells (Ag) with radius
2
has
been studied. The structure which has been
considered has been shown in Figure 4:
Figure 4: nanoparticles with Si core and metallic shell.
(a)
(b)
(c)
Figure 5: Real part of effective permittivity with different
fill factors in visible region for (a) Rin=15nm, R=25nm, (b)
R
in
=15nm, R=30nm, (c) R
in
=15nm, R=35nm, the host
medium is polymeric with refractive index of 1.48.
By similar analysis which have been accomplished
for the first polymeric media, the resonance
wavelength can be obtained as the following.
The resonance conditions is achieved by setting the
denominator of (4) to zero and solving it for
2
.
As has been obtained in (9), the equation is a
binominal equation versus
2
. In this polymeric media
there are two resonance wavelengths.
One of the wavelengths is in ultraviolet wavelength
range and the other one is in visible band. Two
resonances are due to existence of the silvers
surrounded by two mediums, shells and host
polymeric media. Each mediums causes to resonance
separately. The resonance in visible range is due to
the Si cores and another one in ultraviolet band is due
to the polymeric host media.
0)2)(()2)((
))(22()2)(2(
221212
212212
=+−−+−−
−−+++
εεεετεεεε
ε
ε
ε
ε
τ
ε
ε
ε
ε
hh
hh
ff
(9)
The effective permittivity of the polymeric medium
by fixing the inner radius and changing the outer
radius of the guest particles has been shown in Figure
5.
Also effective permittivity by fixing the outer radius
and changing the inner radius has been indicated in
Figure 6.
(a)
(b)
Figure 6: Real part of effective permittivity with different
fill factors in visible region for (a) R
in
=20nm, R=35nm (b)
R
in
=25nm, R=35nm, the host is polymeric medium with
refractive index of 1.48.
The resonance which has been obtained by
mathematical relations and diagrams has been given
OpticalPropertiesofCoatedNanospheresinVisibleWavelengthRange
93

in the Table 2 and Table 3 for the visible and
ultraviolet band respectively. Since the effective
medium is studied, the resonance wavelength
depends on the filling fraction as has been discussed
previously. This polymeric structure can be useful in
construction of building blocks for metamaterials in
two wavelength bands.
Table 2: Resonance wavelength in the visible range has
been obtained by mathematical relations and diagrams for
different size and filling fraction of guest particles.
by Diagrams
(nm)
by Equation
(nm)
f
561.4 561.39 (15/25)
3
0.1
507.4 507.26 (15/30)
3
0.2
487.9 487.86 (15/35)
3
0.3
577.2 577.22 (20/35)
3
0.3
703.2 703.12 (25/35)
3
0.2
Table 3: Resonance wavelength in the ultraviolet range has
been obtained by mathematical relations and diagrams for
different size and filling fraction of guest particles.
by Diagrams
(nm)
by Equation
(nm)
f
228.8 228.76 (15/25)
3
0.1
261.1 261.13 (15/30)
3
0.2
288.4 288.43 (15/35)
3
0.3
252.1 252.06 (20/35)
3
0.3
208 208.01 (25/35)
3
0.2
As has been observed in Table 3 in visible wavelength
range, by increasing the thickness of the metal the
resonance wavelength shifts to lower amounts of
wavelength. This effect can be related to the plasmon
resonance energy. Since the electric charge increases
the plasmon resonance energy is greater, therefore the
resonance wavelength shifts to the smaller amounts
of the wavelength.
In the ultraviolet band according to the Table 4, the
noted argument can be used for fixed outer radius too.
In ultraviolet wavelength range by increasing the size
of particles the resonance wavelength shifts to the
higher amounts of wavelength. Similar to the
argument which has been expressed for the first
structure which the particles can be considered as a
cavity.
4 CONCLUSIONS
We studied two polymeric structures with random
distribution of core-shell nanoparticles. In the first
structure the coated spheres with metallic cores (Ag)
and Si shells was studied. Resonance wavelength was
obtained by mathematical relations and simulation
results. In this structure, the medium possess only one
resonance wavelength because the metallic particles
are surrounded by one shell (Si). The similar analysis
were accomplished in a polymeric media with Si
cores and metallic shells. Since the metals are
surrounded by two medias (Si cores and polymeric
host) effective medium has two resonance
wavelengths. The resonance conditions were studied
by mathematical relations and simulation results. It
was shown that the resonance wavelength in both
structures depends on size and filling fraction of
spherical nanoparticles. In order to calculate the
effective permittivity semi-static approximation and
Clausius-Mossotti formula used. Both studied
structures are applicable in optical cloaking with
metamaterials.
ACKNOWLEDGEMENTS
This work is supported by Photonics and Nanocrystal
research Lab. (PNRL), Faculty of Electrical and
Computer Engineering and School of Engineering-
Emerging Technologies of Tabriz University.
REFERENCES
Tang, J., Huo, Z., Brittman, S., Gao, S., and Yang, P., 2011.
Solution-processed core–shell nanowires for efficient
photovoltaic cells. Nature Nanotechnology 6, 568–572.
Li, J., Engheta, N., 2007, Core-Shell Nanowire Optical
Antennas Fed by Slab Waveguides, IEEE
TRANSACTIONS ON ANTENNAS AND
PROPAGATION, VOL. 55, NO. 11, 3018-3026.
Li, J., Salandrino, A., and Engheta, N., 2007, Shaping light
beams in the nanometer scale: A Yagi-Uda
nanoantenna in the optical domain. Phys. Rev. B 76,
245403.
Rostami, G., Shahabadi, M., AfzaliKusha, A., and Rostami,
A., 2012. Nanoscale all-optical plasmonic switching
using electromagnetically induced transparency.
Applied Optics, Vol. 51, Issue 21, pp. 5019-5027.
Paniagua-Dominguez, R., Lopez-Tejeira, F., Marques, R.,
and Sanchez-Gil, J.A., 2011. Metallo-Si core–shell
nanospheres as building blocks for optical three-
dimensional isotropic negative-index metamaterials.
New Journal of Physics 13, pp. 1-15.
Aslan, K., Wu, M., Lakowicz, J.R., and Geddes, C.D.,
2007. Fluorescent Core-Shell Ag@SiO2
Nanocomposites for Metal-Enhanced Fluorescence
and Single Nanoparticle Sensing Platforms. J. AM.
CHEM. SOC. 129, 1524-1525.
Choi, W. Park, J.Y., and Kim, S.S., 2009. Synthesis of
SnO
2
–ZnO core–shell nanofibers via a novel two-step
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
94

process and their gas sensing properties.
Nanotechnology 20 465603.
Hao, F.,Sonnefraud, Y., Dorpe, P.V., Maier, S.A., Halas
N.J., and Nordlander, P., 2008. Symmetry Breaking in
Plasmonic Nanocavities: Subradiant LSPR Sensing and
a Tunable Fano Resonance. Nano Lett., 8 (11), pp
3983–3988.
Endo, T., Kerman. K.,,Nagatani, N.,Hiepa, H.M., Kim,
D.K., Yonezawa, Y., Nakano, K., andTamiya, E., 2006.
Multiple Label-Free Detection of Antigen−Antibody
Reaction Using Localized Surface Plasmon Resonance-
Based Core−Shell Structured Nanoparticle Layer
Nanochip. Anal. Chem.78 (18), pp 6465–6475.
Cai, W., and Shalaev, V., 2010. Optical Metamaterials
Fundamentals and Applications. Springer New York
Dordrecht Heidelberg London.
Bohren, G.F., and Huffman, D.R., 1983. Absorption and
Scattering of Light by Small Particles. JOHN WILEY
& SONS.
OpticalPropertiesofCoatedNanospheresinVisibleWavelengthRange
95
