3-D Analysis of Terahertz Frequency Multiplier Excited Due to

Interaction of Convection Electron Beam and Surface Waves

(Smith-Purcell Effect)

Alireza Tavousi

, Ali Rostami

1,2

, Ghassem Rostami

and Mahboubeh Dolatyari

Photonic and Nanocrystal Research Lab. (PNRL), Faculty of Electrical and Computer Engineering,

University of Tabriz, Tabriz 5166614761, Iran

OIC Research Group, School of Engineering-Emerging Technologies, University of Tabriz, Tabriz 5166614761, Iran

Keywords: Convection Electron Beam, Terahertz Wave Generation, Smith-Purcell Effect, Surface Wave, Frequency

Multiplier.

Abstract: In this paper, we present a three dimensional numerical study on a terahertz frequency multiplier. The

process of frequency multiplication is proposed via study of spontaneous Smith-Purcell (SP) radiation.

Through introducing a single electron bunch perturbation which is passing over above a metallic grating,

and due to interaction of electron bunch with surface wave, the evanescent wave radiates from the ends of

the grating and the SP radiation is generated in the span of 0.466~1.1 THz. We found that the maximum of

SP radiation amplitude is distributed around 90° with the centre frequency 0f ~0.65 THz. Simulations on the

generation of SP radiation at THz frequencies have been performed with the help of the 3D particle-in-cell

(PIC) finite integral method and results agree very well with analytic ones.

1 INTRODUCTION

The ‘terahertz’ term has been applied in diverse

electromagnetic spectra such as for frequency

coverage of point contact diode detectors

(Kerecman, 1973), frequency of a Michelson

interferometer (Fleming, 1974), frequencies below

the far infrared, the resonant frequency of a water

laser, and now terahertz is applied to sub-millimetre

wavelengths span between 100 and 1000 μm (0.3

THz to 3 THz) (Siegel, 2002). Until recently there

were no appropriate sources and detectors for THz

and thus this portion of the EM spectrum has been

used just about. Among the most advanced terahertz

applications which the scientific research is

concerned about, we bring up the followings:

medical imaging, security, communications,

industrial applications, chemistry and biochemistry

measurements, molecular recognition and protein

folding, and sub-millimetre astronomy (Rostami et

al., 2010).

Smith–Purcell (SP) radiation (Smith & Purcell,

1953) which works based on excitation of “surface

Eigen wave” (Bratman et al., 2009; Cao et al., 2014)

in metallic gratings, is one of the most interesting

methods for generating sub-millimetre waves

especially in THz domain (Bratman et al., 1979;

Bratman et al., 2007; Gover & Sprangle, 1981; Liu

& Xu, 2014; Mizuno et al., 1973; Price et al., 1991;

Rusin & Bogomolov, 1966; Schächter & Ron,

1988). At the frequency harmonics of the surface

wave, electron bunches arise and produce

spontaneous Smith–Purcell radiation. Due to

spontaneous nature of SP radiation as discussed in

the most of theoretical works (Andrews & Brau,

2004) and in experiment (Urata et al., 1998) the

radiated power is low. But by using an additional

cavity, higher power and better selectivity can be

obtained (Bratman et al., 2007). This mechanism

which is conceptually shown in Figure 1 is

frequently studied for electron-beam driven

frequency multiplication and undoubtedly it is a

promising candidate for producing radiation in the

terahertz domain (Andrews & Brau, 2004; Bratman

et al., 2009; Li et al., 2006; Shin et al., 2007).

The grating is assumed to be a perfect conductor

and unlike the experiment (Urata et al., 1998) with

pencil-like electron beams, in the proposed design a

sheet electron beam is used which through

enhancing the interaction of electron beam and

surface wave, increases the operating current and

output power. It is known that single-mode

Tavousi A., Rostami A., Rostami G. and Dolatyari M..

3-D Analysis of Terahertz Frequency Multiplier Excited Due to Interaction of Convection Electron Beam and Surface Waves - (Smith-Purcell Effect).

DOI: 10.5220/0005335100340039

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 34-39

ISBN: 978-989-758-093-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

operation of the surface wave in the case of a fairly

narrow beam is possible (Li et al., 2007). However

when the beam width becomes much larger than the

wavelength of the surface mode, different transverse

parts of the beam would be able to excite different

transverse surface modes which their frequencies

and phases are slightly different (Bratman et al.,

2009). This is already mentioned for SP backward

wave oscillators (BWOs) that they will not operate

with an infinitely wide grating because the optical

beam diffuse (Li et al., 2007).

Figure 1: Scheme of an electron-beam driven THz range

frequency multiplier which is self-excited due to surface

waves of open grating (Bratman et al., 2009).

In this paper, we perform a three-dimensional finite

integral based particle-in-cell simulation for the

evaluating the incoherent spontaneous SP radiation

using CST studio suite, a code which simulates the

situations in which the space charge and

electromagnetic fields are concurrently interacting.

2 SIMULATION MODEL

Here in this paper, we consider a metallic grating

slab having a period L and thus a wave number of K

= 2π/L (the length of the grating is set differently for

each particular simulation case). Generally, an

evanescent wave can travel above the surface of

such grating in the direction in which the slab is

periodic (perpendicular to the grooves). The phase

velocity is v

= ω/k = cβ

, and the group velocity is

= dω/dk = β

c where c is the speed of light, ω is

the frequency of the traveling evanescent wave and k

is the wave number. It is known that (Andrews et al.,

2006) the dispersion relation is periodic in k space

and for each Brillion zone the dispersion curve is

symmetric about k/K = 0.5 (π-type surface mode).

Depending on the position of the synchronous point

which may be located on the right-hand or left-hand

side of the Bragg point k/K=0.5 (for which the group

velocity vanishes), the operating characteristics of

the device changes fundamentally. For k/K > 0.5, the

group velocity is negative and for k/K < 0.5 the

group velocity is positive. Here we are interested in

the former case in which the operating point lies in

the negative group velocity regions. If we assume

that there is no gain or losses in the grating due to an

electron beam then we may use Floquet’s theorem in

order of solving Maxwell equations on top of the

grating and the dispersion relation D

(ω, k) = 0 is

obtained for the evanescent waves.

With respect to the operating point, our Smith-

Purcell based THz source is a backward wave

oscillator in which, if a certain beam current

threshold known as start current is reached, the

optical intensity grows to saturation even if no

feedback mirrors are employed. In this device, the

moving electron beam must interact significantly

with the fundamental surface mode which is

confined very close to the grating. To describe the

interaction between the surface mode and the

moving electron beam, we need to numerically solve

the coupled Maxwell-Lorentz equations. For this

purpose, we used the CST studio suite software

which solves these coupled equations via finite

integral method. The radiation wavelength

observed at the angle

measured from the direction

of moving electron beam is given by:

(cos),

||Ln











(1)

where n is the diffraction order. In order to compare

our 3-D simulation results with experiment results

and 2-D simulations, we chose to use grating

parameters of Urata et al (Urata et al., 1998)

summarized in Table 1. Since we have performed

our simulations in a 3-D scheme, a width of 800 µm

is used for grating. The grating length is arranged to

be 20, 40, 60, 80, and 100 periods. The main

simulations are performed using a grating with

length Ng=100 periods and then the results are

extended and compared width grating lengths of

Ng=20, 40, 60, and 80 periods.

Table 1: Grating profile used in the experiments of Urata

et al (Urata et al., 1998).

Grating period 173µm

Groove width 62µm

Groove depth 100µm

2 SIMULATION RESULTS

The dispersion diagram of the first three modes of a

grating with parameters from Table 1 is shown in

Figure 2. The 40 Kev beam line intersect with the

first mode in negative group velocity region i.e.

k/K>0.5, thus the synchronous point frequency

3-DAnalysisofTerahertzFrequencyMultiplierExcitedDuetoInteractionofConvectionElectronBeamandSurface

Waves-(Smith-PurcellEffect)

would be calculated as 0.466 THz. For a device

operating in positive group velocities, higher beam

energies is required. For example in this figure we

have shown the 250 Kev beam line which is

intersecting the evanescent mode in k/K<0.5 region.

To study the incoherent (spontaneous) SP

radiation, first we let the length of the grating to be

=100L and then we perform the simulation with a

single electron bunch which last for 0.1 ps length

and carry a charge equal to q=0.048 pC. Since this

bunch is short enough compared to the longest

radiation wavelength, we can assume that the

radiation is coherent. Our focus is on the first order

SP radiation (|n|=1). As shown in Figure 3a-f, by

recording the temporal behaviour of the radiated

signal which we have detected them at different

detection points of

=70º, 90º, 125º, 135º, 150º, and

170º

(and 5.5 mm distance from the centre of the

grating) and taking fast Fourier transform, we find

out that two clear radiation peaks exists in the

spectrum. Figure 4a shows that the one which

peaked at 525 GHz is the SP radiation, while the

other peak at 466 GHz is the evanescent wave (for

ease of visualization, only FFT of Figure 3c at

=135º is shown in Figure 4a).

Figure 4b compares the analytic expression for

wavelength of SP radiation with the centre

frequencies recorded by sweeping

with 6º step for

all detection angles between 0º<θ<180º. From this

figure we find out that indeed

the longest radiation

wavelength (lowest radiation frequency) is equal to

the wavelength of the evanescent wave. The results

obtained from CST are in good agreement with

those obtained via equation (1). Recording the FFT

amplitude for all swept angles (Figure 5),

we find

out that unlike the evanescent wave frequency

which is angle independent, both SP radiation centre

frequency and amplitude are changing with

detection angle. As shown in this figure the

maximum SP amplitude occurs in angle θ=90º. The

short come of this equation is that it says nothing

about the SP radiation amplitude.

Given the detection angle, period, diffraction

order, and the phase velocity of the electron beam to

the analytic equation (1), one can predict the

Figure 2: Dispersion diagrams of the first three surface

modes of the metallic grating with parameters given in

Table 1. The 40 Kev and 250 Kev beam lines intersect

with the fundamental mode in k/K<0.5 and k/K>0.5

regions respectively.

Figure 3: The temporal behaviour of the radiated signal detected at the angle θ=135º and 5.5 mm distance from the centre of

the grating for Ng=100L.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

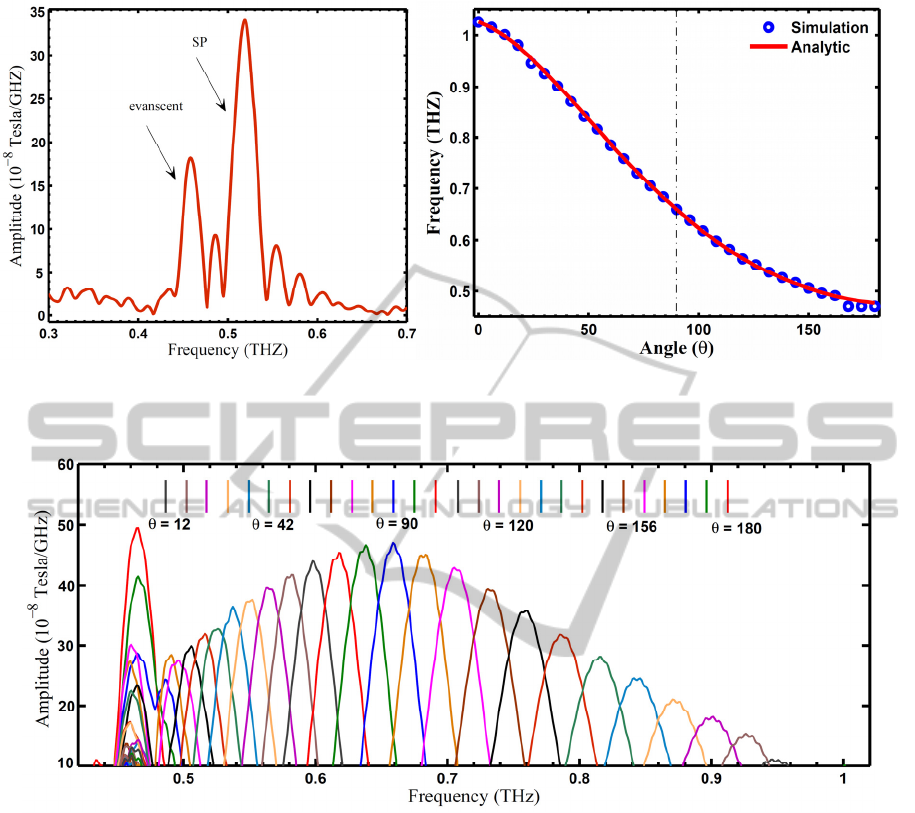
Figure 4: (a) FFT taken from temporal behaviour of the radiated signal detected at the point θ=135º for Ng=100L. (b)

Comparison of analytic expression for wavelength of SP radiation with the center of SP frequencies swept from θ=0º to

θ=180º.

Figure 5: FFT taken from temporal behaviour of the radiated signal detected at the different points varying from

12º<θ<180º with step of



θ =6º for Ng=100L.

wavelength in which the SP radiation occurs. Figure

6 shows the normalized far field polar plot for the H-

field at different θ angels. These plots show that the

main radiation lobe of each specific frequency is

located in the angle which was predicted by equation

(1). In the 0.466 THz, our result show that radiation

occur near 180º, and as we know from previous, this

frequency belongs to the evanescent wave so

radiates from the upper grating end (near gun). The

0.55 THz, 0.65 THz, and 0.85 THz cases are also

radiating at 120º, 90º, and 40º, respectively.

Figure 7a, and Figure 7b both show the FFT

amplitudes of time signals for different grating

lengths. In Figure 7a, we swept the detection angle

from 0º to 180º and recorded the maximum of FFT

amplitude for gratings with Ng=20, 40, 60, 80, and

100L. We can see that, as the length of grating

increase from 20 to 100 periods, the amplitude

grows nonlinearly. Given this, we are able to

calculate the growth-rate of the produced signal. In

Figure 7b, focusing only on one detection angle in

which the radiation is maximum (i.e.

=90º), we

find out that by increasing the grating length, not

only the FFT amplitude increases but the spectral

resolution of the signal increases too.

3-DAnalysisofTerahertzFrequencyMultiplierExcitedDuetoInteractionofConvectionElectronBeamandSurface

Waves-(Smith-PurcellEffect)

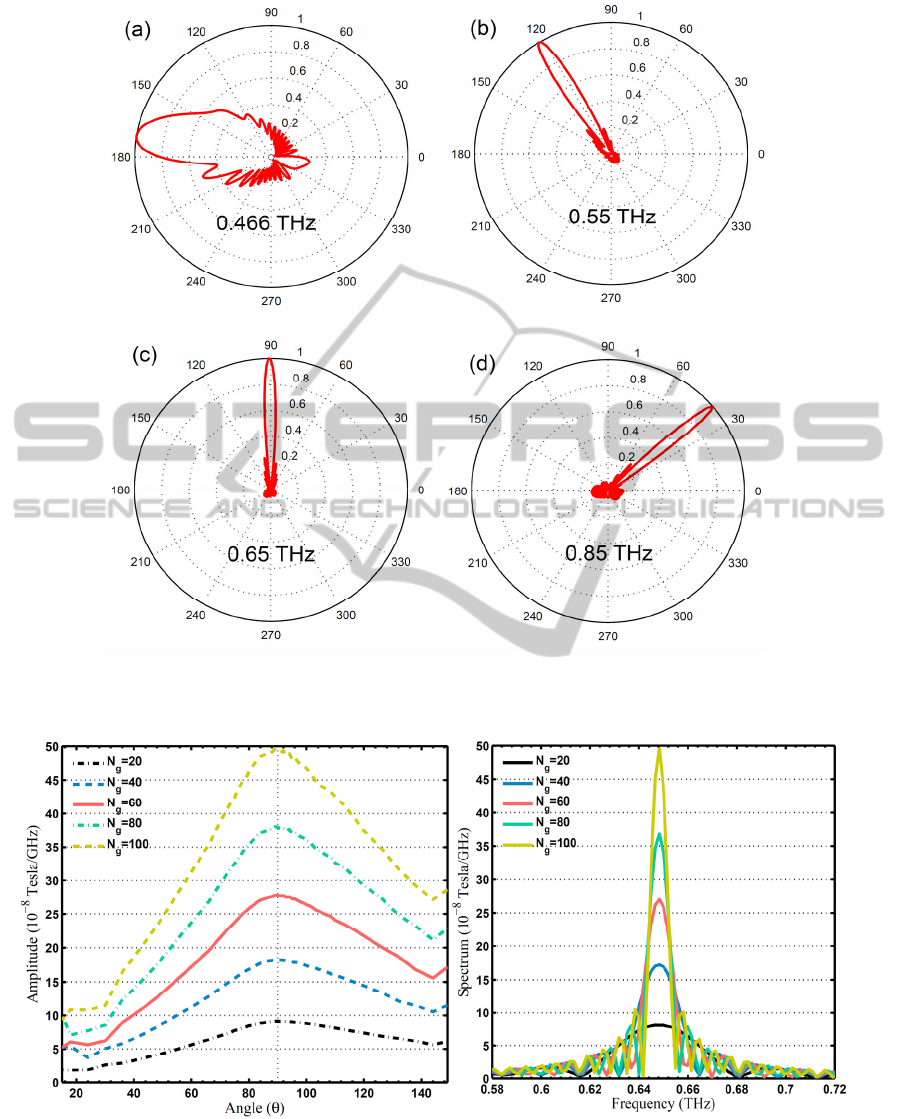
Figure 6: Far field polar plots for H-field at different frequencies of a) 0.466 THz, b) 0.55 THz, c) 0.65 THz, and d) 0.85

THz. The plots are normalized.

Figure 7: (a) The max FFT amplitude of time signals versus detection angel for different grating widths of Ng=20L, 40L,

60L, 80L, and 100L (b) The max FFT amplitude of time signals versus detection angel of

=90º for different grating

widths of Ng=20L, 40L, 60L, 80L, and 100L.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

3 CONCLUSIONS

In this paper, we presented a three dimensional

numerical study on a terahertz frequency multiplier.

This SP based frequency multiplier can provide

terahertz radiation with a comparatively high level

of output power. The process for frequency

multiplication was proposed by studying the

spontaneous SP radiation. This non-relativistic

device neither requires a high operating voltage nor

a high external magnetic field. It can fill up the need

for convenient compact THz radiation source for

diverse range of applications such as spectroscopy

and diagnostics of different media. Simulations on

the generation of SP radiation at THz frequencies

have been performed with the help of the 3D

particle-in-cell (PIC) finite integral method and

results agree very well with analytic ones.

ACKNOWLEDGEMENTS

The authors would like to thank University of

Tabriz.

REFERENCES

Andrews, H. L., Boulware, C., Brau, C., Donohue, J.,

Gardelle, J., & Jarvis, J. (2006). Effect of reflections

and losses in Smith–Purcell free-electron lasers. New

Journal of Physics, 8(11), 289.

Andrews, H. L., & Brau, C. A. (2004). Gain of a Smith-

Purcell free-electron laser. Physical Review Special

Topics - Accelerators and Beams, 7(7), 070701.

Bratman, V. L., Fedotov, A. E., Makhalov, P. B., & Rusin,

F. S. (2009). Smith–Purcell frequency multiplier with

synchronization of radiation from a wide electron

beam. Applied Physics Letters, 94(6), 061501.

Bratman, V. L., Ginzburg, N., & Petelin, M. (1979).

Common properties of free electron lasers. Optics

Communications, 30(3), 409-412.

Bratman, V. L., Makhalov, P., Fedotov, A., &

Khaimovich, I. (2007). Excitation of orotron

oscillations at the doubled frequency of a surface

wave. Radiophysics and Quantum Electronics, 50(10-

11), 780-785.

Cao, M., Liu, W., Wang, Y., & Li, K. (2014). Three-

dimensional theory of Smith-Purcell free-electron

laser with dielectric loaded grating. Journal of Applied

Physics, 116(10), 103104.

Fleming, J. (1974). High-resolution submillimeter-wave

Fourier-transform spectrometry of gases. IEEE

Transactions on Microwave Theory Techniques, 22,

1023-1025.

Gover, A., & Sprangle, P. (1981). A unified theory of

magnetic bremsstrahlung, electrostatic

bremsstrahlung, Compton-Raman scattering, and

Cerenkov-Smith-Purcell free-electron lasers. Quantum

Electronics, IEEE Journal of, 17(7), 1196-1215.

Kerecman, A. J. (1973). The Tungsten-P Type Silicon

Point Contact Diode. Paper presented at the

Microwave Symposium, 1973 IEEE G-MTT

International.

Li, D., Imasaki, K., Gao, X., Yang, Z., & Park, G.-S.

(2007). Reduce the start current of Smith-Purcell

backward wave oscillator by sidewall grating. Applied

Physics Letters, 91(22), 221506.

Li, D., Imasaki, K., Yang, Z., & Park, G.-S. (2006). Three-

dimensional simulation of super-radiant Smith-Purcell

radiation. Applied physics letters, 88(20), 201501.

Liu, W., & Xu, Z. (2014). Simulations of table-top watt-

class 1 THz radiation sources with two-section

periodic structure. Journal of Applied Physics, 115(1),

014503.

Mizuno, K., Ono, S., & Shibata, Y. (1973). Two different

mode interactions in an electron tube with a Fabry-

Perot resonator-The Ledatron. Electron Devices, IEEE

Transactions on, 20(8), 749-752.

Price, E., Walsh, J., & Kimmitt, M. (1991). Short

submillimeter operation of the Planar Orotron.

Nuclear Instruments and Methods in Physics Research

Section A: Accelerators, Spectrometers, Detectors and

Associated Equipment, 304(1), 133-136.

Rostami, A., Rasooli, H., & Baghban, H. (2010).

Terahertz technology: fundamentals and applications

(Vol. 77): Springer.

Rusin, F., & Bogomolov, G. (1966). Generation of

electromagnetic oscillations in an open resonator.

JETP Letters, 4, 160-162.

Schächter, L., & Ron, A. (1988). Exponential gain in a

Smith–Purcell amplifier. Applied physics letters,

53(10), 828-830.

Shin, Y.-M., So, J.-K., Jang, K.-H., Won, J.-H.,

Srivastava, A., & Park, G.-S. (2007). Superradiant

terahertz Smith-Purcell radiation from surface

plasmon excited by counterstreaming electron beams.

Applied Physics Letters, 90(3), 031502.

Siegel, P. H. (2002). Terahertz technology. IEEE

Transactions on microwave theory and techniques,

50(3), 910-928.

Smith, S. J., & Purcell, E. M. (1953). Visible Light from

Localized Surface Charges Moving across a Grating.

Physical Review, 92(4), 1069-1069.

Urata, J., Goldstein, M., Kimmitt, M. F., Naumov, A.,

Platt, C., & Walsh, J. E. (1998). Superradiant Smith-

Purcell Emission. Physical Review Letters, 80(3), 516-

519.

3-DAnalysisofTerahertzFrequencyMultiplierExcitedDuetoInteractionofConvectionElectronBeamandSurface

Waves-(Smith-PurcellEffect)