Temperature Effect on Intermediate Band Solar Cells (IBSCs)

M. Esgandari, H. Heydarzadeh, A. Rostami, M. Dolatyari and G. Rostami

OIC Research Group, School of Engineering-Emerging Technologies, University of Tabriz, Tabriz 5166614761, Iran

Keywords: Efficiency, IBSCs, Temperature Effects, Detailed Balance Model, Varshni Model.

Abstract: Temperature has profound effect on the performance of solar cells. Most of the electrical processes in the

semiconductor devices depend on the temperature and revealed in dramatically variations in their

characteristics such as open circuit voltage, short circuit current, power conversion efficiency and the band

gap of semiconductor. The aim of this paper is investigation of temperature effects on the Intermediate Band

Solar Cells (IBSCs). The theoretical results indicate that performance of this type of the solar cells is low at

high temperatures. Increasing in temperature from 300K to 600K decreases the efficiency of solar cell from

63% to 59 % and this decrement continues with temperature increment. This is while temperature can decrease

the open circuit voltage and increase the short circuit current.

INTRODUCTION

Photovoltaic phenomenon is the most interesting field

that converts the solar radiation to the electrical

energy. In order to studying this filed of science some

parameters should be considered and influence of the

power conversion efficiency such as temperature

effect is one of the important parameters. Generally,

solar cells operate under terrestrial temperature

conditions below than 350K (Sze and Ng, 1981) and

in the temperatures higher than room temperature, we

obvious different behaviours. For increasing the

intensity of solar irradiance the concentrators and

mirrors on the solar cell have been used that increases

the power conversion efficiency. However, these

methods have negative effects on solar cell. For

example they have thermalization effects on the cell.

Thermalization of cell can be created by photons

with energy higher than the band gap (

akeda and

Motohiro ,2013 , Singh, Lal and Husain, 2008)

and it

can effect on the performance of solar cells and

optoelectronic characteristics such as carrier mobility

and the optical band gap (Landis, Raffaelle, and

Merritt, 2004). For overcoming this effect the

materials with broad band gap can operate as best

candidates. The Silicon Carbide (SiC) can be used for

this aim due to its wider band gap, which harvests

high energy photons. Another advantage of SiC is the

high stability of the material (Rostami, Heidarzadeh,

Baghban, Dolatyari, and Rasooli, 2013).

In a single junction solar cell the limiting efficiency

calculated by detailed balance model is 40.7% which

is achievable by a material with the band gap of 1.12

eV (Shockley and Queisser, 1961

With existing an

Intermediate band between the valance band and

conduction band (Luque and Marti, 1997), the

limiting efficiency obtains as 63.2% for a host

material with the band gap of 1.95 eV (Henry, 1980).

However, in the higher temperatures these values

change. The important parameters that can be defined

for a solar cell are the open circuit voltage, short

circuit current and efficiency and their temperature

dependency can be studied. This paper investigates

the temperature dependency of intermediate band

solar cells based on 3C-SiC.

THEORETICAL BASIS

Effect of temperature on the band gap has been

studied by Varshni model (Varshni, 1967,

Sarswat

and

Free, 2012).

() (0)

CV CV











(1)

Where ε

(T) is the band gap of semiconductor at

temperature T, ε

(0) is the band gap at 0K and , 

are constants and their values for 3C-SiC are 6×10

-4

eVK

-1

and 1200K respectively (Levinshtein,

Rumyantsev and Shur , 2001).

Esgandari M., Heydarzadeh H., Rostami A., Dolatyari M. and Rostami G..

Temperature Effect on Intermediate Band Solar Cells (IBSCs).

DOI: 10.5220/0005335300960100

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 96-100

ISBN: 978-989-758-093-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

For analysing the cell, the detailed balance model has

been used. In calculation, we use blackbody

modelling of the sun. Therefore, the photon and

emitted energy ﬂux density respectively is derived

from Planck’s law over the energy range



and



(Shockley and Queisser, 1961).

(, ,,)

exp(( ) / ) 1





 









(2)

where µ is the chemical potential, h is the Plank

constant, K is the Boltzmann constant, c is the speed

of light and



and



are lowest and highest energy,

respectively. The schematic diagram for an IBSC is

shown in Figure 1.

Figure 1: Schematic band diagram of an IBSC.

To develop the limiting efficiency of the IBSC we use

detailed balance model and try to model the output

current that extracted from contacts as:







 



.,,0, .,,0,

.,,0, .,,,

SlhSSlhC

ClhCClhC

out

qf N T f N T

fN T fN T

 

  











 





.,,0,

.,,,

SlhS

CS lh C

ClhC

qf N T

ffN T

fN T



 







(3)

Where q is the charge of electron, f

and f

geometrical factors that depends on the angle of the

cell that subtended by the sun (Mruczkiewicz, Kłos,

and Krawczyk, 2008, Shockley and Queisser, 1961).

In one sun concentration, values of f

and f

are

2.18×10

-5

and in maximum concentration that implies

for 46050 suns their values is 1. (Quan, Zhi-Hua,

Chun-Lai, Yu-Hua and Qi-Min, 2011, Green, 2001).

Now with considering maximum concentration and

applying to the last equation, we have the output

current density as:











 



,,0, ,,,

,,0, ,, ,

CI CV S CI CV CI C

CV S CV CV C

JqN TN T

NTN T

out

  







(4)

Where 



and µ

are the difference between

quasi Fermi levels and we have:

= qV (5)

V is the output voltage that takes account from Carnot

factor (Green, 2001):

(1 )

out





(6)

Where T

and

is the cell and the sun temperature

that equals to 300K and 6000K respectively and in

final the efficiency can be calculated from this:

out out







(7)

Where σ is the Stephan-Boltzmann constant and

equals to 5.67×10

-8

W.m

-2

-4

(Quinn and Martin,

1985, Blevin and Brown, 1971).

SIMULATION RESULTS AND

DISCUSSION

In this work, we evaluate the IBSC based on SiC at

different temperatures. At first we simulate the

current-voltage characteristics in temperature of

300K and 600K and the results are shown in Figure 2 .

As shown in Figure 2, in the temperature of 600K,

voltage and current are changed. In this temperature

the band gap decreases and consequentially the

voltage due to its dependency on the band gap

decreases, while the current increases. However, an

important point that can be revealed is the output

power that these decrement and increment can change

it. In this way increasing in temperature results

decreasing in efficiency.

Figure 3 shows this phenomenon that in

temperature 300 K, the efficiency is about 63% and

in temperature 1500K it drops to 33%.

The position of IB is an important case to

achieving the optimal and maximum efficiency in an

IBSC. Efficiency variations versus sub band gaps

have been shown in Figure 4 in 300K.

TemperatureEffectonIntermediateBandSolarCells(IBSCs)

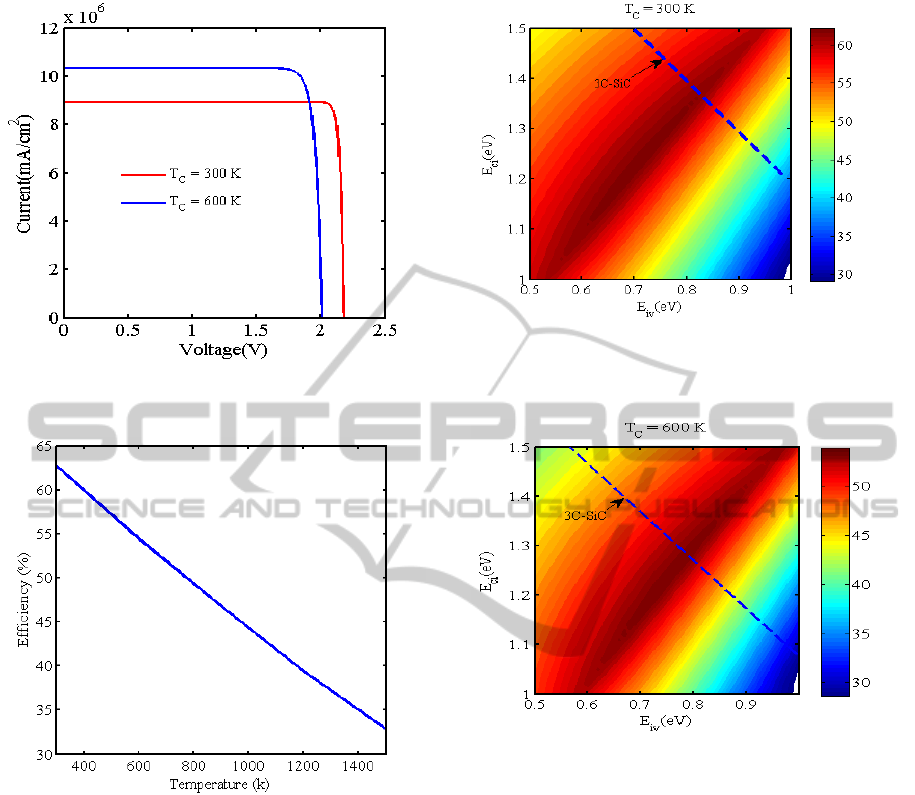
Figure 2: I-V characteristics of an IBSC in two different

temperatures; 300K and 600 K.

Figure 3: Efficiency versus temperature variation.

As seen in this figure, for the darker region contains

from 0.6 eV to 0.8 eV for E

and from 1 eV to 1.5 eV

for E

ci,

the maximum efficiency is about 63%. In this

case we have larger region for choosing the IB

position. Here the introduced material is the 3C-SiC

with band gap of 2.2 eV and location of this band gap

is traced with dashed line. Using these information we

can choose the best sub band gaps (E

and E

) to have

the maximum efficiency. In this case when, the value

of E

and E

is about 0.84 eV and 1.36 eV, we

achieve the maximum efficiency that is about 60%.

Figure 4: The influence of the position of IB on the

efficiency in the temperature of 300K and location of the

3C-SiC band gap in dashed line.

Figure 5: The influence of the position of IB on the

efficiency in the temperature of 600k location of the 3C-

SiC band gap in dashed line.

If the temperature increases, the total band gap

changes. So the sub band gaps and position of IB

change too.In the temperature of 600K (that has been

shown in

Figure

5) the values of E

and E

has been changed

and the maximum efficiency is about 59% that occur

in the ranges between 0.65 eV to 0.85 eV for E

and

between 1.1 eV to 1.35 eV for E

. In this case the

ranges of E

and E

become smaller compared to

Figure 4 and the band gap of 3C-SiC is reduced and

is equals to 2.08 eV (dashed line shows the location

and value of it). If we choose the IB position at 0.8

eV upper than the valance and 1.28eV lower than the

conduction band

the efficiency is

maximized which is

equals to 54 %.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

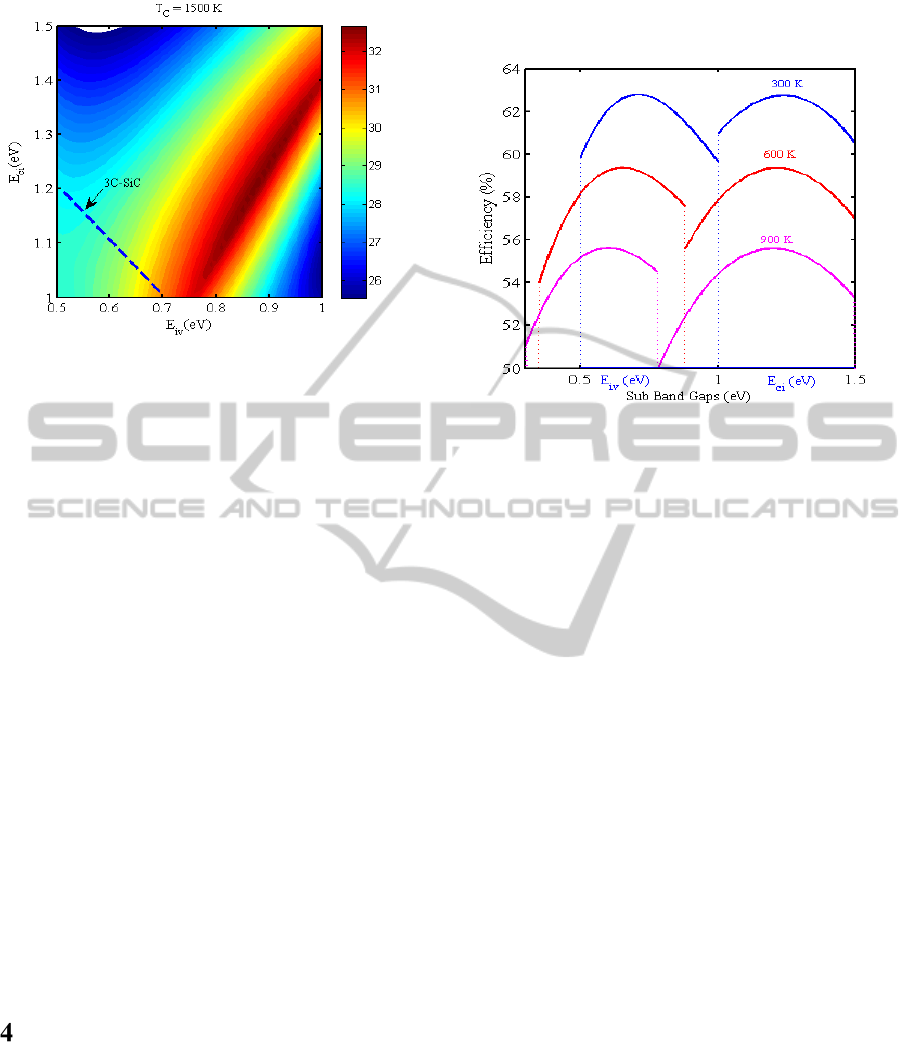
Figure 6: The influence of the position of IB on the

efficiency in the temperature of 1500K.

In the temperatures of 1500K that is shown in the

Figure 6, the maximum efficiency decreases to about

33% and the location of the IB has been changed. The

darker region is limited in this condition and it means

that we have a limit to choosing the best IB position.

Another occurred event is reducing of the band gap of

3C-SiC and its value is 1.7 eV (the dashed line). The

best position of IB for achieving the maximum

efficiency is 0.7 eV upper than the valance band or 1

eV lower than the conduction band.

Efficiency variation with temperature for the sub

band gaps, E

and E

, are shown in the Figure 7. The

efficiency decreases with increasing the temperature.

So at 300K, we have the maximum efficiency that has

been occurred in the 0.71 eV for E

and 1.24 eV for

while in 900K it’s drops to 55% and the value of

and E

is about 0.6 eV and 1.2 eV respectively.

These are due to the variations in the output current

and voltage that results in the variation of the output

power. If the temperature increases the band gap of

semiconductor decreases and the voltage decreases

due to its dependency to band gap but the current has

increases and finally the voltage decrement plays an

effective role in the efficiency decrement.

CONCLUSIONS

In this paper, we evaluate the IBSCs based on 3C-

SiC. Our simulation shows that the open circuit

voltage, short circuit current and efficiency vary with

temperature increment. So in the temperature 300K

the efficiency is about 63% and for example in the

temperature 600K the efficiency drops to 59% and

this decrement continues with temperature increment.

In this regard, the open circuit voltage decreases and

short circuit current increases and results in changing

of the output power.

Figure 7: Efficiency versus sub band gaps (E

and E

)in

three different temperatures (blue curve in 300K, red curve

in 600K and cyan curve in 900K).

REFERENCES

Blevin, W. R., & Brown, W. J., 1971. A precise

measurement of the Stefan-Boltzmann constant.

Metrologia, 7(1), 15.

Green, M. A., 2001. Third generation photovoltaics: Ultra

high conversion efficiency at low cost. Progress in

Photovoltaics: Research and Applications, 9(2), 123-

135.

Henry, C. H. ,1980. Limiting efficiencies of ideal single and

multiple energy gap terrestrial solar cells. Journal of

applied physics, 51(8), 4494-4500.

Landis, G. A., Raffaelle, R. P., & Merritt, D., 2004. High-

temperature solar cell development, 19th European

Photovoltaic Science and Engineering Conference,

June7–11, 2004, Paris, France.

Levinshtein, M. E., Rumyantsev, S. L., & Shur, M. S.

(Eds.). 2001. Properties of Advanced Semiconductor

Materials: GaN, AIN, InN, BN, SiC, SiGe. John Wiley

& Sons.

Luque, A., & Martí, A.,1997. Increasing the efficiency of

ideal solar cells by photon induced transitions at

intermediate levels. Physical Review Letters, 78(26),

5014.

Mruczkiewicz, M., Kłos, J. W., & Krawczyk, M., 2008.

Semiconductor Super lattice-Based Intermediate-Band

Solar Cells.

Quan, C., Zhi-Hua, M., Chun-Lai, X., Yu-Hua, Z., & Qi-

Ming, W., 2011. Detailed balance limit efficiency of

silicon intermediate band solar cells. Chinese Physics

B, 20(9), 097103.

Rostami, A., Heidarzadeh, H., Baghban, H., Dolatyari, M.,

& Rasooli, H., 2013. Thermal stability analysis of

TemperatureEffectonIntermediateBandSolarCells(IBSCs)

concentrating single-junction silicon and SiC-based

solar cells. J. Optoelectron. Adv. Mater, 15(1-2), 1-3.

Sarswat, P. K., & Free, M. L., 2011. A Study of Energy

Band Gap Temperature Relationships for Cu2ZnSnS4

Thin Films. ArXiv preprint arXiv: 1107.3890.

Shockley, W., & Queisser, H. J., 1961. Detailed balance

limit of efficiency of p-n junction solar cells. Journal of

applied physics, 32(3), 510-519.

Singh, P., Singh, S. N., Lal, M., & Husain, M., 2008.

Temperature dependence of< i> I</i>–< i> V</i>

characteristics and performance parameters of silicon

solar cell. Solar Energy Materials and Solar Cells,

92(12), 1611-1616.

Sze, S. M., & Ng, K. K., 1981. Physics of semiconductor

devices. Creator/Author, Sze, sm. Publication Date,

1981 Jan 01. OSTI Identifier, OSTI ID: 5381484...

Takeda, Y., & Motohiro, T., 2013. Intermediate band

assisted hot carrier solar cells using indirect band gap

absorbers. Progress in Photovoltaics: Research and

Applications, 21(6), 1308-1318.

Varshni, Y. P., 1967. Temperature dependence of the

energy gap in semiconductors. Physica, 34(1), 149-154.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

100