Stochastic Resonances in Photon Number Resolving Detectors

Shree Krishnamoorthy

, Harish Ravishankar

, Pradeep K. Kumar

and Anil Prabhakar

Indian Institute of Technology, Madras, Chennai, India

Indian Institute of Science, Bangalore, India

Indian Institute of Technology, Kanpur, India

Keywords:

Avalanche Photodiodes (APDs), Low Light Level, Photodetectors, Fiber Optics Sources and Detectors.

Abstract:

The photon number statistics of a coherent optical pulse will typically follow a Poissonian distribution. At

low photon numbers, a gated avalanche photo-detector (GAPD) is used to detect the presence of photons in

each optical pulse. GAPDs use a thresholding logic, but suffer from after-pulsing effects. The efﬁciency of

a GAPD was characterized and its after-pulses were analyzed by looking at the detection patterns obtained.

The GAPD was found to show evidence of stochastic resonance which affected the dark noise of the detector.

We post-process the detected bit patterns to eliminate the resonances and estimate the true dark count of the

detector. The GAPD was then used with a recirculating optical loop to build a multi-photon resolving detector

(MPRD). In the MPRD, the probability of detection at consecutive loop round trip times were used to estimate

the mean photon number. We quantify these statistics and establish a reliable measure of photon number at

an optical power of -94 dBm. The digital electronics was able to store data for 2

optical pulses, making the

statistical analysis meaningful.

1 INTRODUCTION

Quantum cryptography holds the promise of uncon-

ditional security (Bennett et al., 1984; Lo and Chau,

1999). However, practical implementations of quan-

tum key distribution, such as DPS-QKD or FC-QKD,

use coherent optical states that are susceptible to pho-

ton number splitting attacks (Norbert and Mika, 2002;

Inoue et al., 2003; Bloch et al., 2007; Valerio et al.,

2009). In the absence of purely single photon sources,

development of QKD systems need photon number

resolution (Hadﬁeld, 2009). While, optical ﬁbers

are easily adapted for quantum communication, the

detectors needed for photon number resolution are

not easily available and the development of photon

counting detectors continues to be of current inter-

est (Blasej et al., 2014). In the telecommunication

band, around 1.55 µm, PMTs have very low efﬁcien-

cies of about 2% where as InGaAs avalanche pho-

todiodes (APDs) provide an efﬁciency of 20% with

lower dark counts (Hadﬁeld, 2009). APDs operated

in Geiger mode indicate only the presence of or ab-

sence of photons and cannot resolve the number of

incident photons, making their output binary in na-

ture. The Geiger mode enhances the sensitivity, but is

accompanied by a degradation in the signal to noise

ratio (Kolb, 2014). For photon number resolution,

the incoming photons are redistributed to multiple de-

tection slots, using spatial or temporal multiplexing

methods (Fitch et al., 2003; Mogilevtsev, 2010). Tem-

poral multiplexing can be achieved by an optical ﬁber

loop connected to the coupler (Haderka et al., 2004;

Ravi and Prabhakar, 2011), and the timing informa-

tion can be used to gate the APD.

APDs are based on the avalanche process which

dictates the noise characteristics in them (McIntyre,

1966). Gated APD (GAPD) systems suffer from dark

counts and after-pulsing (Cova et al., 2004; Tosi et al.,

2009). Other than the known noises, our implemen-

tation of the GAPD shows evidence of stochastic res-

onance at low photon numbers. In this article we an-

alyze the probabilities of occurrence of different bit

patterns to extract the photon number statistics in the

presence of stochastic resonance. We ﬁrst character-

ize the GAPD, and estimate the efﬁciency of detec-

tion. We then measure the photon arrival statistics and

compare them to theoretical predictions for a GAPD

in the presence of noise and underlying stochastic res-

onance.

We implement a MPRD with a recirculating op-

tical loop followed by the GAPD. When a coherent

state is input to the MPRD, the bit pattern that ensues

should follow a statistical distribution. The roundtrip

time of the circulating loop was less than one-eighth

Krishnamoorthy S., Ravishankar H., K. Kumar P. and Prabhakar A..

Stochastic Resonances in Photon Number Resolving Detectors.

DOI: 10.5220/0005335800400046

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 40-46

ISBN: 978-989-758-093-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

of the time between coherent optical pulses input to

the loop. This allowed us to use digital electronics to

store and analyze the 8-bit pattern of 1’s and 0’s fol-

lowing each input pulse, and to repeat the exercise for

N = 2

input pulses. Our experiments validate the

Poissonian statistics of the coherent state down to an

average photon number of 0.024.

2 DETECTOR

CHARACTERIZATION

When counting photons, we often assume that the

sources of noise (typically shot and thermal noise)

are independent of the photon counts. In cases where

there are other low amplitude stationary processes

that look like noise, the assumption of independent

noise statistics breaks down. Stochastic resonance is

one such phenomenon that can cause higher null de-

tections at periodic intervals in a system using gated

detection, like in our system. We ﬁnd a suitable op-

erating point for the GAPD and extract actual photon

detection probabilities with proper data analysis in the

presence of stochastic resonances.

2.1 Efﬁciency

Dark counts are a result of thermally triggered elec-

tron currents. We describe how to ﬁnd the optimal op-

erating point for the detector and ﬁnd average contri-

bution of the underlying noise. A null detection must

occur in the absence of any electron currents, trig-

gered either thermally or by incident photons. We as-

sume that dark counts occur, with a probability p

(1)

and an efﬁciency η for the detector. When a pulse

with mean photon number n is incident on the detec-

tor from a coherent laser source, we could register a

’1’ either due to a photo-generated avalanche process,

or due to the dark noise of the detector. The probabil-

ity of no detection, p(0), occurs when there are no

photons and there is also no dark count, i.e.,

p(0) = e

−ηn

(1 − p

(1)). (1)

To arrive at the probability of a positive detection,

p(1), we recognize that a detection occurs either

due to the presence of a photons, with a probability

(1 − e

−ηn

), or due to the dark count, with a probabil-

ity p

(1). However, since the two events are indepen-

dent, we must subtract the probability of both events

occurring together, i.e., p

(1)(1 − e

−ηn

). Thus,

p(1) = (1 − e

−ηn

) + p

(1) − p

(1)(1 − e

−ηn

)

= 1 − p(0). (2)

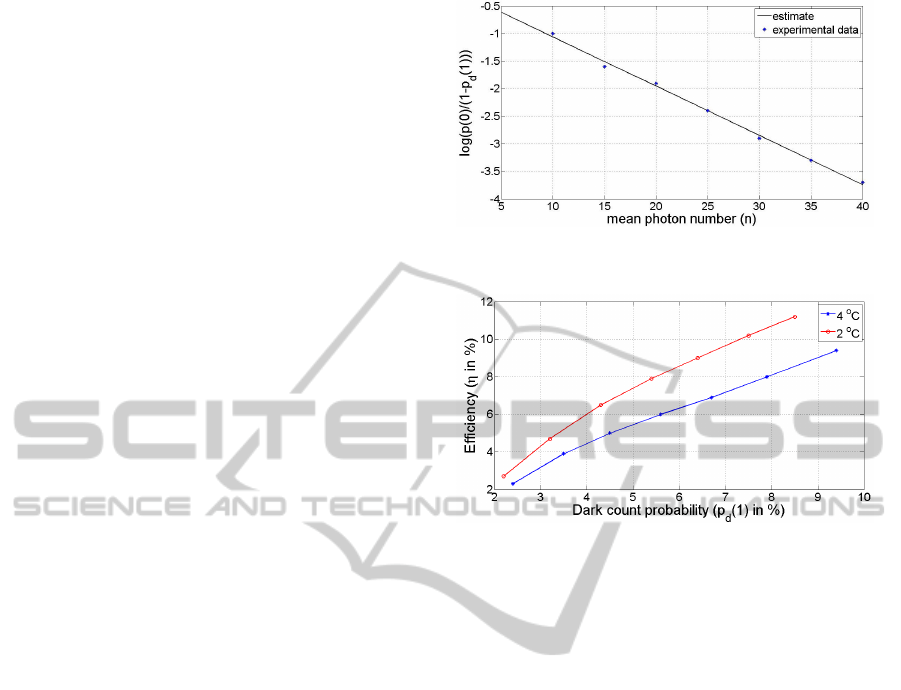
Figure 1: Null detections with increasing mean photon

numbers, used to ﬁnd detector efﬁciency η.

Figure 2: Detection efﬁciency for different case tempera-

tures and dark counts at constant bias. The APD was cooled

by an internal Peltier, to about 20

◦

C below the case temper-

ature.

For our experiments, we have used an InGaAs APD

(model NR8300FP from NEC) with an internal Peltier

cooler. The detector case was further cooled by an

external Peltier stage. The breakdown voltage of the

APD was about 71 V at a case temperature of 4

◦

C. To

operate the APD in Geiger mode, we bias the APD

below 71 V and apply a gating voltage of 3.3 V for

5.2 ns. The GAPD followed by digital counting elec-

tronics (FPGA based), acted as one photon counter.

The digital electronics had 2 GB RAM, or 16 Gbits,

to easily collect and store obtained statistics.

Fig. 1 shows the dependence of p(0)/(1 − p

(1))

on n, from which we extract the efﬁciency η of the

detector. At a bias of 69.7 V and a detector case

temperature of 4

◦

C, we found that the efﬁciency η

was 0.0893±0.006. We also conﬁrm that a change

in temperature and bias conditions change the dark

count and the efﬁciency of the detector, as shown in

Fig. 2.Thus, we ﬁnd the optimal operating point for

the GAPD at a case temperature of 2

◦

C with a bias

voltage of 69.7 V, where η = 0.11 , and the dark

count p

(1) = 0.085. For a 10% higher detection

rate than the dark count the null detection probability

is p(0) = 0.9065. Substituting p(0) in (1) and using

η = 0.11, we estimate the average photons per pulse

to be n = 0.0848, or one true detection for every 12

gate pulses at the GAPD. The average photon number

StochasticResonancesinPhotonNumberResolvingDetectors

Figure 3: Effect of bias voltage and optical input, on the

time between consecutive detections. Each 0 bit corre-

sponds to a delay of 1µs.

resolution can be further improved by using this de-

tector after a recirculating loop as described in Sec.3.

2.2 Detection Probabilities and

Stochastic Resonance

In the previous section, we obtained the optimal op-

erating point for the GAPD by studying the average

noise statistics. However, we are in a position to look

at the statistics of how the detector responds in Geiger

mode, both with and without an incident optical pulse.

Consider a coherent optical pulse train, with an

average of n photons in each pulse, incident on the

detector. For the experimental setup in the inset of

Fig. 3, we send N such pulses, and collect statistics

on the number of times the detector is triggered. For

each received pulse, if a null detection occurs then a

“0” is recorded and when a positive detection occurs

a “1” is recorded. We thus obtain binary statistics of

(0,1) for each received pulse.

For N incident optical pulses, positive detections

will follow a binomial distribution with a mean µ =

N p and a variance of N(1 − p)p, p , p(1) is the prob-

ability of detection for each incident pulse. Averaging

over the number of detection events, we get an esti-

mate ¯p = µ/N = p , with the standard deviation

p(1 − p)

decreasing with increasing N.

There is a 1 µs gap between successive gate pulses.

Analyzing the digital bit pattern at the output of the

GAPD is akin to obtaining a digital frequency spec-

trum, with a resolution of 1 MHz. In Fig. 3, we

plot the frequency of occurrence of the m consecu-

tive 0-bits for N = 2

bits collected in each exper-

iment.We observe an increased occurrence of some

patterns when compared to others, as indicated by the

arrows. These “resonances” are quenched when op-

tical pulses of power of -72 dBm are provided. The

Figure 4: GAPD behavior in terms of bit pattern occu-

rances, with change in bias and temperature. The arrows

mark anomalous increases in event detections, and are at-

tributed to a stochastic resonance.

Figure 5: Frequency of stochastic resonance of the GAPD,

with inset showing the experimental setup used.

occurrence of patterns at periodic intervals and its re-

duction due to the incidence of a few photons is sug-

gestive of a stochastic resonance in the system (Gam-

maitoni, 1995).

In Fig. 4, we see that these resonances persist,

and are even magniﬁed, as we change the bias and

increase the temperature. Both bias voltage and the

temperature signal change the noise in the system and

affect the intensity of the resonance. To further con-

ﬁrm the stochastic resonance behavior, we perform

a separate experiment with the same detection sys-

tem. We used a laser modulated by a sinusoidal sig-

nal, as shown in the inset of Fig. 5. We found that the

GAPD shows a four fold increase in signal to noise ra-

tio (SNR) close to 66 kHz. This enhancement in SNR

is related to the Kramer’s rate of switching between

the 0 and 1 bit for the binary output detector system

(McDonnell et al., 2008).

Previous experiments on the GAPD at a lower bias

of 67 V, had established that a 1 µs gap between gate

pulses would be sufﬁcient to release any trapped en-

ergy (Kumar et al., 2009). With increasing ON time

of the laser pulses (20 ns), longer dead times of up to

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

Figure 6: After pulsing statistics in the presence of stochas-

tic resonances. The APD was gated every 1 µs.

10 µs in the GAPD has been reported in other studies

(Ben-Michael et al., 2006; Tosi et al., 2009).

Longer dead times are attributed to after-pulsing

effects in the avalanche photodetector. We take a

closer look at one of the data sets in Fig. 4, with optics

off, and estimate the probability of dark count detec-

tion in the presence of stochastic resonances. Since

< 0.1, the probability of detecting more than two

after-pulses becomes negligible. Hence, we restrict

our analysis to understanding the probability of ob-

serving two 1s separated by m 0s. This is equivalent

to the probability of obtaining m 0s followed by a 1

in the state diagram model for the gated Geiger mode

APD, developed by Kolb, for obtaining SNR with af-

terpulsing (Kolb, 2014). Assuming that our ﬁrst bit is

detected with a probability p

, followed by m 0s, the

next bit is detected with a probability p

(1 − p

)

Repeating this experiment N times, we obtain

P(m) = N p

(1 − p

)

. (3)

To estimate the probability p from the data we ignore

the regions affected by the resonance and ﬁt the re-

maining data using (3). In all the collected data-sets,

we found that resonance peaks occur every m = 16

pulses, consistent with one of the stochastic resonance

peaks in Fig. 5. The width of each resonance is 4 con-

sistently for all bias and temperature conditions. With

this information we exclude the data around the local

maxima, ﬁt the rest of the data to a semilog function,

ﬁnd the slope and extract p

= 0.024. Since the data

was obtained in the absence of any optical signal, we

found that removing the resonance peak in the col-

lected data, while post-processing, decreased the ef-

fective dark counts by a factor of four. In Fig. 6, the

residuals were scaled with respect to the number of

events found experimentally for each point. Fig. 6

also shows that we can observe stochastic resonances

till approximately 0.2 ms, corresponding to m = 200,

beyond which the residual error in our ﬁt builds up.

Figure 7: The MPRD setup showing timing information

),coupler splitting ratio (ε),and transmittances (θ

3 RESOLVING PHOTON

NUMBERS

The MPRD setup consists of a coherent, pulsed laser

source, a variable optical attenuator (VOA) followed

by an optical recirculating loop and GAPD as shown

in Fig. 7. The laser pulses, attenuation of the VOA

and the gating of GAPD are computer controlled. To

analyze the working of the MPRD, we use the GAPD

characteristics obtained in Sec. 2, and estimate the

decrease in detection probability for each recircula-

tion of the optical pulse. Finally, we analyze the bit

patterns obtained at the detector for consecutive de-

tections and compare them to theoretical probability

estimates. With 2 GB RAM, we were able to collect

over a million instances of the experiment.

3.1 Experimental Setup

The MPRD experiment was ﬁrst reported in (Ravi and

Prabhakar, 2011). A laser pulse of 5.2 ns pulse width

is sent through the MPRD. We chose a delay ﬁber

length of 2 km, which gave the detector 10 µs to re-

cover between successive measurements. The recir-

culation repeats until the pulses are sufﬁciently atten-

uated in the system. We used a 3 dB splitter, connec-

tors with about 0.5 dB loss and a 2 km long spool with

0.4 dB loss. The optical path lengths were adjusted so

that the return pulses arrived in synchronization with

the system clock. For this purpose, we used an optical

ﬁber array with length increasing in steps of 20 cms

(1 ns delay) in series with our ﬁber spool until our

pulses were correctly synchronized and the detection

probability was maximized.

All the elements in the MPRD were controlled

electronically, by a XILINX (SPARTAN XC3S400)

ﬁeld programmable gate array (FPGA). The FPGA

was clocked at 24 MHz and two digital clock man-

agers (DCMs) available on the FPGA were used to

StochasticResonancesinPhotonNumberResolvingDetectors

Figure 8: Pulse travel time from the laser to the detector

after multiple round trips in the MPRD (Number of gating

pulses, N=8).

multiply the clock frequency to 48 MHz and to pro-

vide a 90 degree phase shifted signal. These were

used to generate laser pulses of width 5.2 ns and gat-

ing pulses of width 10.4 ns. The FPGA was used for

pulsing the laser, gating the APD, setting of bias and

threshold. The variable optical attenuator was used to

change the incident power or photon number in the

optical pulse. At the output of the comparator in the

GAPD, eight detections are recorded for each laser

pulse transmitted through the MPRD, giving us a byte

of data for each laser pulse, with each bit synchro-

nized to the round trip time of the recirculating loop.

3.2 Timing Synchronization in MPRD

To synchronize the detector gates to the incoming op-

tical pulses from the recirculating loop, we look at the

pulse arrival times in Fig. 8. The pulses arrive at the

GAPD with a ﬁxed delay T

delay

from the laser. The

detector has a gating period of 10.4 ns twice that of

the optical pulse. The off time (T

off

) of the detec-

tor needs to be precisely matched to the subsequent

pulse arrival. If the pulse takes time T

to travel up

to the coupler, time T

to travel from the edge of

the coupler to the GAPD, time T

to loop once in

the ﬁber and time T

to travel through the coupler.

Thus, the arrival time for the k

pulse at the detec-

tor is found to be T

+ T

+ (T

+ T

)k + T

. We set

delay

= T

+ T

using multiple sections of opti-

cal ﬁber, while T

off

= T

+ T

is set electronically.

3.3 Photon Redistribution Statistics

The coupler has a division ratio of ε : 1 − ε, the op-

tical delay ﬁber has a transmittance t

, the connec-

tors have a transmittance of θ

=θ and the detector has

an efﬁciency of detection η as shown in Fig. 8. We

calculate the transmission of the k

pulse (Ravi and

Prabhakar, 2011)

eff

= θ

k−1

(1 − ε)

)

η. (4)

Figure 9: Average detection probability of successive return

pulse in MPRD.

Figure 10: Measured versus predicted bit pattern probabil-

ities of detection patterns obtained in MPRD at -63 dBm.

Modiﬁed from (Ravi and Prabhakar, 2011).

For a coherent input with an average photon number

n, the k

detection pulse corresponds to an average

photon number of nT

eff

Starting from an average photon number n, the

theoretical prediction for the probability of detection

(1) for the k

pulse is,

(1) = 1 − e

−ηnT

eff

| {z }

no photon

(1 − p

)

| {z }

no noise

. (5)

For n = 30, η = 0.15, T

eff

= 0.398 (corresponding to

4dB loss), and p

(1) = 0.014, Fig. 9 shows the de-

creasing probability of a detection for each round trip

and we observe a good match between our theoretical

estimates and our experimental observations.

For each byte recorded, we analyzed bit patterns

for 3, 4 and 5 bits as shown in Fig. 10. An input pulse

with average power of −63 dBm at the input of the

3dB splitter in the MPRD, goes through seven round

trips through the optical loop, with a loss of 4 dB per

recirculation, to produce the last detection bit. The

last bit out of the recirculating loop will, now, have an

average power of −94dBm, assuming a 5.2ns pulse

of optical wavelength 1.55 µm, corresponding to an

average photon number of 0.024. Even so, the Poisso-

nian statistics of a coherent pulse are well preserved

and the occurrence of a bit pattern follows the pre-

dicted probabilities.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

4 SUMMARY

This article describes the characterization of a gated

avalanche photo-detector, used subsequently in a

multi-photon resolving detector. We ﬁrst experimen-

tally characterize the GAPD and ﬁnd its efﬁciency.

We found that the GAPD was susceptible to stochas-

tic resonance, which was affected by temperature and

bias. The stochastic resonance was further investi-

gated, and we saw that it had characteristic frequency

around 66 kHz. When we used gated detection, with

a delay of 1 µs between gate pulses, we were in ef-

fect digitally sampling the stochastic resonance. Dis-

counting these resonances in our experimentally mea-

sured probabilities, we were able to characterize the

GAPD for very low average photon numbers.

A recirculating loop is a simple way of splitting

a Poissonian state into a series of temporal pulses.

We described the statistical properties of such a multi-

photon resolving detector. In our experiments, the re-

circulating loop was set up to achieve a delay of 10µs

between successive optical pulses, while we gated the

avalanche photodiode every 1µs. After each input co-

herent optical pulse we recorded the output for 8 gate

pulses as one byte, and did this for N = 2

optical

pulses. We then searched for correlations between

successive gate pulses in the data bytes by looking

at the bit patterns for 3, 4 and 5 bits. The probability

of occurrence of a bit pattern followed the predicted

probabilities, within the noise bounds of the system.

Thus, we conclude that the MPRD could be used for

photon number resolution, for average photon num-

bers as low as n = 0.024 per pulse.

We observed that the stochastic resonance de-

pends on both APD bias and temperature. Conse-

quently, we were able to adjust these parameters and

avoid the resonance, as we set up our photon number

resolving experiments. We believe that we are the ﬁrst

authors to report on stochastic resonances in a GAPD

system. Further investigations about the origins of the

resonace, along with an appropriate statistical noise

model, will help improve the performance of single

photon detectors.

ACKNOWLEDGEMENTS

This work was partly funded by the Department

of Science and Technology, India under Grant No.

SR/S3/EECE/21/2005. HR and PK were at IIT-

Madras during the course of their studies. HR is also

grateful to IIT-Madras for supporting his work as an

Innovative Student Project.

REFERENCES

Ben-Michael, R., Itzler, M. A., Nyman, B., and Entwistle,

M. (2006). Afterpulsing in InGaAs/InP single photon

avalanche photodetectors. In Dig. LEOS Summer Top.

Meet., pages 15–16, Quebec City. IEEE.

Bennett, C. H., Brassard, G., et al. (1984). Quantum cryp-

tography: Public key distribution and coin tossing. In

Proc. IEEE Int. Conf. Computers, Systems and Signal

Processing, Bangalore, volume 175-179, Bangalore.

New York, IEEE.

Blasej, K., Prochazka, I., and Kodet, J. (2014). Photon

counting detector for high-repetition-rate optical time

transfer providing extremely high data yield. Optical

Engineering, 53:081903.

Bloch, M., McLaughlin, S. W., Merolla, J. M., and Patois,

F. (2007). Frequency-coded quantum key distribution.

Opt. Lett., 32:301–303.

Cova, S., Ghioni, M., Lotito, A., Rech, I., and Zappa, F.

(2004). Evolution and prospects for single-photon

avalanche diodes and quenching circuits. J. Mod. Op-

tic, 51(9-10):1267–1288.

Fitch, M., Jacobs, B., Pittman, T., and Franson, J. (2003).

Photon-number resolution using time-multiplexed

single-photon detectors. Phys. Rev. A, 68(4):043814.

Gammaitoni, L. (1995). Stochastic resonance and the

dithering effect in threshold physical systems. Phys.

Rev. E, 52(5):4691.

Haderka, O., Hamar, M., and Peˇrina Jr, J. (2004). Exper-

imental multi-photon-resolving detector using a sin-

gle avalanche photodiode. Eur. Phys. J. D - Atomic,

Molecular, Optical and Plasma Physics, 28:149–154.

Hadﬁeld, R. H. (2009). Single-photon detectors for opti-

cal quantum information applications. Nat. photonics,

3(12):696–705.

Inoue, K., Waks, E., and Yamamoto, Y. (2003). Differential-

phase-shift quantum key distribution using coherent

light. Phy. Rev. A, 68:022317.

Kolb, K. (2014). Signal-to-noise ratio of geiger-mode

avalanche photodiode single-photon counting detec-

tors. Optical Engineering, 53(8):081904–081904.

Kumar, P., Thevan, S., and Prabhakar, A. (2009). Optimiza-

tion of gated photodetection for quantum key distri-

bution. In SPIE Europe Optics and Optoelec. Conf.,

Prague. SPIE.

Lo, H.-K. and Chau, H. F. (1999). Unconditional security

of quantum key distribution over arbitrarily long dis-

tances. Science, 283(5410):2050–2056.

McDonnell, M. D., Stocks, N. G., Pearce, C. E. M.,

and Abbott, D. (2008). Stochastic resonance: from

suprathreshold stochastic resonance to stochastic sig-

nal quantization. Cambridge University Press, Cam-

bridge.

McIntyre, R. (1966). Multiplication noise in uniform

avalanche diodes. IEEE Trans. Electron Devices, ED-

13(1):164–168.

StochasticResonancesinPhotonNumberResolvingDetectors

Mogilevtsev, D. (2010). Calibration of single-photon

detectors using quantum statistics. Phys. Rev. A,

82(2):021807.

Norbert, L. and Mika, J. (2002). Quantum key distribu-

tion with realistic states: photon-number statistics in

the photon-number splitting attack. New J. of Phys.,

4(1):44.

Ravi, H. and Prabhakar, A. (2011). Coherent state statistics

from time-resolved photon counting. In SPIE OPTO,

pages 79600S–79600S, San Francisco. SPIE.

Tosi, A., Mora, A. D., Zappa, F., and Cova, S. (2009).

Single-photon avalanche diodes for the near-infrared

range: detector and circuit issues. J. Mod. Optic, 56(2-

3):299–308.

Valerio, S., Helle, B. P., Nicolas, C., Miloslav, D., Norbert,

L., and Momtchil, P. (2009). The security of prac-

tical quantum key distribution. Rev. of Mod. Phys.,

81(3):1301.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology