Simulation and Implementation of a Poly Methyl Methacrylate based

Whispering Gallery Mode Ring Resonator in Microwave Range

A. Malekpour, A. Rostami, M. Sarmadi, M. Dolatyari and G. Rostami

OIC Research Group, School of Engineering-Emerging Technologies, University of Tabriz, Tabriz 5166614761, Iran

Keywords: Ring Resonator, Poly Methyl Methacrylate (PMMA), Whispering Gallery Mode, Microwave Frequency.

Abstract: This article introduces the ring resonator sensing principle and presents the simulation and fabrication of a

ring resonator structure. The material Poly methyl methacrylate (PMMA) with refractive index of 1.5 has

been used for fabricating it. It has low loss and thereby is a good material for constructing low loss ring

resonators and generating high Q-factors. 3-D finite element numerical method (FEM) simulation results

show the path of light through ring resonator and the transmission parameter of a waveguide in close proximity

of a ring resonator. After coupling electromagnetic wave from the waveguide into the ring resonator, the

standing waves are formed as resonant optical modes. Subsequently resonance peaks are formed in

periodically repetitive frequencies in the transmission parameter of the waveguide. Transmission spectrum of

waveguide has been studied in the frequency range 8-8.3 GHz. Ring resonator parameters like free spectral

range and quality factor have been calculated by 0.1245 GHz and 200 respectively. Agreement and differences

between simulation and experiment have been discussed.

1 INTRODUCTION

Whispering gallery modes (WGMs) are specific

resonances of a wave field, inside a given resonator

or a cavity with smooth edges. The resonators have

axially symmetric geometry such as sphere, disk or

ring. WGMs can be described as propagating modes

circling around the resonator, supported by

continuous total internal reflection of the resonator or

cavity surface, that meet the resonance condition.

This means that after one round trip they return to the

same point with the same phase shift of integer

multiples of 2π. Hence the waves interfere

constructively with themselves, and form standing

waves.

The operating principle in ring resonator based

sensors is mainely based on resonance perturbation

method, where a sample under test perturbed the

effective refractive index of the resonator (Zhu,

Hongying, 2007, Delâg, 2009). Resonance field

perturbes by the refractive index changes and causes

a change in the resonance frequency and Q-factor.

Other perturbation in resonance frequency is caused

by the attachment of a desirable particle (Ahmadi,

2014). These changes can be calibrated to represent

the sensing parameters of interest. This is an example

of RI sensors that involves detecting the spectral shift

of a resonance feature as the RI varied. The other

approaches of such RI sensors are valid and have a

wide range of applications in areas such as life

science (Yu. Zongfu, 2011). Yet the most interesting

from a practical viewpoint about electromagnetic

WGMs, is that they posses many unique properties,

such as ultra-high Q-factors, having low mode

volumes and operating at optical and

telecommunication frequencies of light. So WGM is

one of the most accurate and sensitive techniques

proposed to date for sensing applications due to its

sensitivity and selectivity.

High unloaded Q-factor is mainely limited by the

loss tangent of the resonator material for highly

confined modes. Hence chossing very low loss

materials such as poly methyl methacrylate (PMMA)

is of paramount importance. Depending on where the

sensing signal originates, there are two types of

sensing that a ring resonator can accomplish. The

sample under test in close proximity to the ring

resonator surface (much closer that the evanescent

field decays length) performs the surface sensing

signal. Whereas bulk sensing signals comes from the

optical change induced by the presence of the sample

in the whole region of the evanescent field. Placing

and removing the sample at predetermined location

108

Malekpour A., Rostami A., Sarmadi M., Dolatyari M. and Rostami G..

Simulation and Implementation of a Poly Methyl Methacrylate based Whispering Gallery Mode Ring Resonator in Microwave Range.

DOI: 10.5220/0005335901080112

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 108-112

ISBN: 978-989-758-093-2

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

close to the resonator, is very easy due to open

structure of a WGM structure, unlike metallic cavity.

In addition, at microwave range of the

electromagnetic spectrum, whispering gallery

resonators have relatively large dimensions and

therefore, they are easy to handle and manipulate. By

this idea, the structure becomes suitable fore mass

production, because the time consuming part of

manual adjustment is eliminated.

In this paper we have presented the simulation

results and the fabricated ring resonator structure

using PMMA that creates peak resonances in

microwave range. PMMA is considered one of the

best materials to exhibits the lowest loss. Hence high

unloaded Q-factor can be achieved. The gap between

waveguide and resonator is an important factor for the

ring resonator. Since the field distribution is weak in

the middle hole at microwave range, it is not sensitive

sensor if the sample filled the core of the ring

resonator. Placing the sample in the vicinity of the

outer rim of the resonator is not possible, because

there is no limitation for the liquid to remain in the

vicinity. For having got a good perforemance sensor,

it's a good idea to implement a groove at the ring's

surface and near the outer rim of the resonator. This

idea is practical and in the future we will have done

it.

2 THEORY AND FORMULATION

It is known from the waveguide-based optics that

occurring total internal reflection on the border of

core and clad is the basically condition for generating

waveguide structures (Taya. Sofyan, 2014). The

reflected waves interfere constructively with each

other and the modes are formed and propagated in the

waveguide. So the larger RI of the core than the RI of

the clad is an essential condition for confinement of

the wave in the core and formation of the propagating

modes in waveguides.

Waveguide cut-off frequency depends on the

effective RI and the dimensions of the waveguide.

Unlike the slab waveguides, in the rectangular

waveguides, there is no precise formula for wave

propagation in the waveguide. After a simple and

meaningful approximation, has been performed on

the solving Maxwell's equations in rectangular

waveguides, formulas have been obtained and tables

have been presented for a rectangular waveguide

(Marcatili, Enrique, 1969). So the correct dimensions

for a waveguide with predetermined RI are obtained.

It is seen that, by keeping the effective refractive

index constant, as the dimensions become larger, the

cut-off frequency of the waveguide shift to lower

frequencies. The dimensions of the waveguide are

about the wavelength of the propagating mode in that.

So for getting a waveguide at frequency 8GHz the

waveguide dimensions are in the range of centimetre

(cm), because wavelength at this range is about 3 cm.

This is also the case for ring resonator. If the ring

resonator is considered as the curved waveguide,

wave propagation in it, is the same as for the straight

waveguide. The difference between them is that there

are losses due to curved boundaries in ring resonator.

The resonance modes are in the wavelength λ, which

is given by (Sun, Yuze, 2011):

reff

rn m







(1)

Where r is the resonator rim,

eff

is the effective RI

experienced by the optical resonant mode, and m is

an integer number. One important parameter is the

distance between resonance peaks, which is called the

free spectral range (FSR). The relation between the

FSR and the radius of the ring resonator and effective

RI is given by (Rabus. Dominik G, 2007):

eff

FS R







(2)

It can be seen that the FSR have a direct relationship

with square of the wavenumber and an inverse

relationship with the effective RI and the radius of the

ring resonator. So it is expected that if the structure is

at microwave range the FSR would decrease by

decreasing the wavelength.

Achieving a narrowness of the resonance dip in

figure 1 is an important issue in the sensor

applications of ring resonator. The parameter of

importance is the resonance width at half maximum

or 3 dB bandwidth





of the resonance lineshape.

The narrowness of linewidth





is characterized by

the resonator's quality factor. This parameter is a

measure of the sharpness of the resonance. It is

defined as the ratio of the operation wavelength and

the resonance width:







(3)

Not too surprisingly, Q can be shown to be

proportional to the number of round trips that

circulating resonant light can make along the ring

resonator. The quality factor can also be regarded as

the stored energy divided by the power lost per optical

cycle. As the detection of the ring resonator based

sensors limit is set by how well one can locate

resonance frequency, the sharpness is important and

SimulationandImplementationofaPolyMethylMethacrylatebasedWhisperingGalleryModeRingResonatorin

MicrowaveRange

109

a high Q is essential.

Figure 1: Exhibition of the linewidth in a resonance

frequency for calculating the quality factor. .

3 DESIGN AND SIMULATION OF

THE STRUCTURE

The top view of the structure that consists of a PMMA

waveguide and a PMMA resonator is shown in Figure

2. The ring and the waveguide have the same height

1.5 cm. The cross sectional dimensions of the

waveguide are chosen to be 1.5 cm by 3.2 cm to excite

the fundamental mode

The inner and outer radiuses of the ring are 15 cm

and 24 cm respectively. The gap is chosen to be zero

in simulation and also in the experimental test to have

a good coupling at 8-8.3 GHz. In addition here a

groove is implemented in the surface of the ring for

sensing applications of the structure that we will have

in the future works. It is considerable that this groove

has effects on the resonance frequency. So resonance

frequencies are different from the situation that there

is no groove on the ring's surface. In order to keeping

up the agreement between simulation and fabrication

a groove has been added to the ring's surface in the

simulation. Having accurate measurement and

characterization, we need standard ports. So the two

ends of the PMMA waveguide are tapered and

inserted in WR-112, standard rectangular metallic

waveguide at 7.05-10.0 GHz band.

The entire structure is simulated in CST

MICROWAVE Studio 12.0, a finite element solver,

to solve for the electric field distribution and the

transmission parameter of the ring resonator

structure. The simulated distribution of electric field

in the waveguide and resonator are shown in Figure

The transmission parameter of the structure which

is shown in figure 4 shows that the transmission from

one side to another of the waveguide is good, except

for the frequencies that are the resonance frequency

of ring resonator. It shows that the FSR of the ring

Figure 2: The top view of waveguide and ring resonator

structure.

resonator is about 0.13 GHz and the Q-factors are

about 1100 for resonance peaks and they are a bit

different for each resonance peak.

Figure 3: Distribution of absolute electric field over the

PMMA ring resonator beside the PMMA waveguide at

resonance frequency 8.017.

Figure 4: Transmission parameter of the PMMA structure

in the simulation.

4 FABRICATION

Despite of the previous ring resonator structures

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

110

dimensions, the present case here, have centimetre

dimensions. So fabricating of it, is easy, practical and

affordable, and has no time consuming. There is no

need for complicated technologies like the dark room

or photolithography for fabrication. A PMMA slab

with 1.5 cm height has been cut by laser such that a

waveguide and a ring have been created. The vertical

and horizontal cuttings of the two tapered ends of the

waveguide are done by the former way and computer

numerical control (CNC) milling machine

respectively. Since both the waveguide and the ring

has not the precise above mentioned dimensions (in

section 3), they machined by CNC milling machine

to have accurate dimensions in the implemented

structure exactly equal to that dimensions presented

by the simulation. The groove on the surface of the

ring is cut by machinery mechanic too. The next

problem when implementing such kind of structures

was fixing them to have a correct gap between the

ring and the waveguide. Connecting the waveguide

ends to the ports needs fixing too. Having centimetre

dimensions this problems have been solved by

themselves. The PMMA ring resonator is placed

close to the PMMA waveguide by manual

adjustment. Centimetre geometries both in the ports

and in the tapered ends as a coupler, we connect them

to each other by manual adjustment too. Figure 5

shows the final device after fabricating it.

Figure 5: The fabricated PMMA waveguide and PMMA

ring resonator.

5 EXPERIMENTAL SETUP

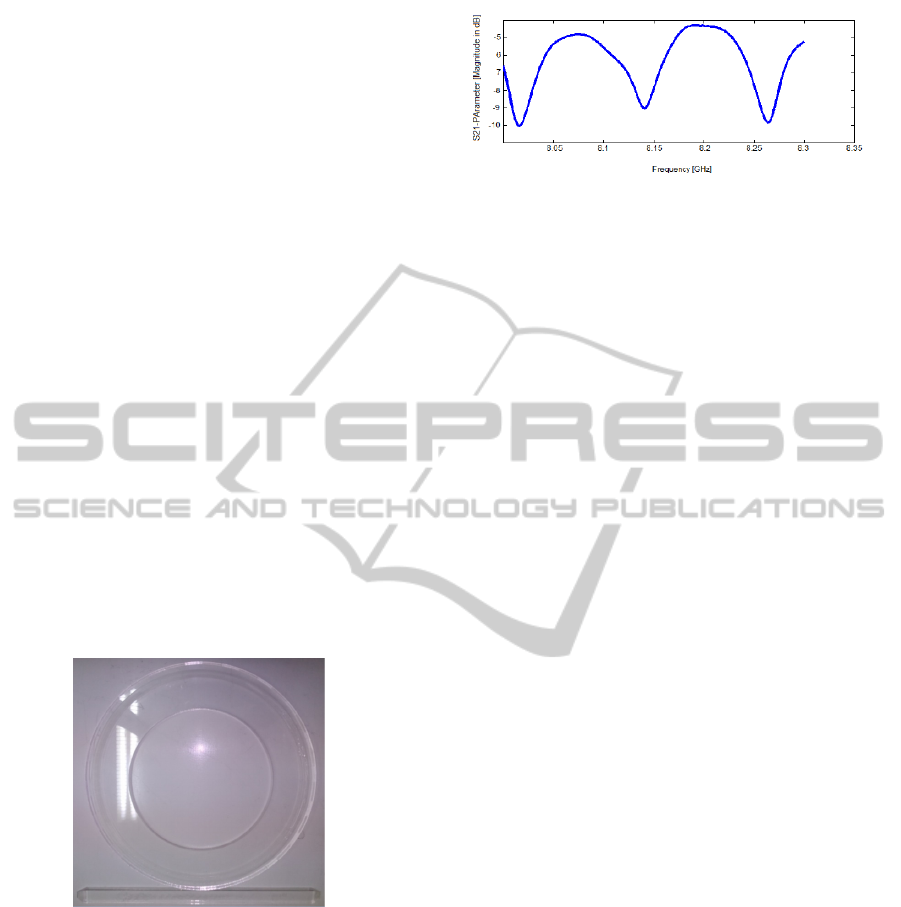
The source wave at 8-8.3 GHz is provided by 85107A

network analyzer. It has plotted the transmission

parameter which is shown in figure 6 in order to

calculating the ring resonator parameters, FSR and Q.

It should be mentioned that the FSR can be attributed

to the refractive index and loss of the PMMA. The

matching between simulation and experimental

transmission parameter is achieved.

Figure 6: The plotted transmission Parameter of the ring

resonator structure in the implementation.

It shows that the FSR of the ring resonator in the

experiment is about 0.12 GHz and the Q-factors are

about 200 and they are a bit different for each

resonance peak.

The resonance frequencies are approximately the

same as for the simulation. As it is visible from the

comparison between simulation and fabrication there

is a drop in the resonator response between

resonances of the implemented structure. This is

because of the attenuation that occurred by the two

tapered ends, and it is unavoidable. The tapered ends

are essential to have a good impedance matching

between the waveguide and the ports. This impedance

matching is frequency dependence of course, but the

dependency could be ignored in a small frequency

band such as 8-8.3 GHz. If this frequency band

became larger, the variant impedance matching

respect to the frequency would be visible. The other

reason for the attenuation in the fabricated structure

is the trivial PMMA electrical conductivity that has

been assumed zero in simulation and here creates an

offset in the waveguide's transmission.

The other difference which is visible in the

experimental results in comparison with the

simulation is lower quality factor and is due to the

attenuation caused by the PMMA electrical

conductivity in the ring resonator. Since we expect

that Q decrease by the attenuation enhancement in the

ring resonator, it is more likely that the groove

geometry affects that resonator transmission function.

This could be seen more obviously in figure 7. By

punctuality it is seen that electromagnetic wave has

some breaks in the border of PMMA and groove, but

they are tolerable for the wave and the propagation

don't perturbed by them. These breaks are the other

reason which is beneficial for explaining the

decreasing of the quality factor. The electromagnetic

waves tolerate the RI differences between the groove

(free space RI) and PMMA. The photon recirculation

limits by this groove and this means a slaked quality

factor. In implemented structure these breaks are

accompanied by the electrical conductivity of the

PMMA which is assumed to be zero in simulation.

SimulationandImplementationofaPolyMethylMethacrylatebasedWhisperingGalleryModeRingResonatorin

MicrowaveRange

111

Because of that the quality factors are more slaked in

the fabrication.

Figure 7: simulated 3D electric field (x component)

distribution of the ring resonator with a groove on the

surface. The electromagnetic waves break when they meet

the groove.

As it can be seen from the comparison, the FSR in the

experiment is lower than the simulation. This rises

from a trivial difference that we have in the PMMA

refractive index. Also the RI of the air in the reality is

more than 1 (the assumed RI for the air in simulation).

This causes that the effective RI that resonant mode

in the ring experience become larger. Since FSR have

an inverse relationship with the effective RI, it is

predictable that FSR become lower in the experiment.

6 CONCLUSIONS

In this paper, the experimental setup and simulation

results of a PMMA ring resonator and a PMMA

waveguide was presented. The set of polymer based

ring resonator and waveguide were designed and

optimized to excite the WGM modes of the ring

resonator. The centimetre range dimensions facilitate

the accurate fabrication process of WGM resonator

by CNC milling machine and not further manual

assembly is required, which is suitable for mass

production. The differences of the simulation and

fabrication that are an offset in the transmission

parameter and a decreasing in the quality factor rises

from the attenuation that caused by the PMMA and

the air electrical conductivity. The lower FSR in the

experiment is the other difference that can be seen. It

is because of the larger refractive indices that PMMA

and air have and cause a bigger effective RI for

resonance light.

REFERENCES

Zhu, Hongying, Ian M. White, Jonathan D. Suter,

Mohammad Zourob, and Xudong Fan., 2007.

Analytical chemistry 79, no. 3, 930-937.

Delag, Andre, Dan-Xia Xu, Ross W. McKinnon, Edith

Post, Philip Waldron, Jean Lapointe, Craig Storey et al.,

2009. Journal of light wave Technology 27, no. 9: 1172-

1180.

Ahmadi, H., H. Heidarzadeh, A. Taghipour, A. Rostami, H.

Baghban, M. Dolatyari, and G. Rostami., 2014. Optik-

International Journal for light and electron Optics.

Yu, Zongfu, and Shanhui Fan. 2011. Optics express 19, no.

11:10029-10040.

Taya, Sofyan, and Taher El-Agez. 2011, Turk. J. Phys 35:

31-36.

Marcatili, Enrique AJ, 1969, Bell System Technical Journal

48, no. 7: 2071-2102.

Sun, Yuze, and Xudong Fan., 2011, Analytical and

bioanalytical chemistry 399, no 1: 205-211.

Rabus, Dominik G., 2007. Integrated ring resonators,

Springer.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

112