
Overhead Considerations in Real-time Energy Harvesting Systems
Hussein El Ghor
1
and Maryline Chetto
2
1
Lebanese University, University Institute of Technology, B.P. 813, Saida, Lebanon
2
IRCCyN Research Institute, University of Nantes 1, Rue de la Noe, F-44321 Nantes, France
Keywords:
Overhead, Real-time systems, EDF, Renewable energy, Time complexity.
Abstract:
The effectiveness of a real-time scheduling algorithm depends on both its ability to schedule feasible task
sets and its runtime overhead. In this paper, we investigate overheads incurred by a scheduler dedicated to
embedded systems that are powered by renewable energy. We specifically focus on the overhead cost of an
EDF-based scheduler known as ED-H. We analyze the number of tasks factor that can possibly affect the
resulting performance of ED-H. The simulation experiments demonstrate that the implementation costs of
ED-H remain acceptable so as to make it a practicable scheduler.
1 INTRODUCTION
The overhead of an operating system represents the
time lost in handling all kernel mechanisms such as
context-switching and task scheduling management.
Context-switching overhead is the time needed to
preempt a task, save its context, load the context of
another task and resume that task. This overhead is
only incurred in a preemptive environment. A context
switch is forced only when the active task ceases
to be the highest priority one. For any scheduling
algorithm, the overhead incurred by its implementa-
tion results from the computational complexity of the
algorithm that is used to select the future active task.
In most of papers found in the literature, it is assumed
that the overhead cost is negligible. This hypothesis
is realistic for most of traditional schedulers that
do not perform on-line computations. They just
amount to order lists of tasks according to a given
priority rule and dispatch the highest priority task at
scheduling points. Whatever the priority assignment
rule, the overhead is limited. Most of priority driven
schedulers are work-conserving in that sense they
never let the processor idle whenever at least one task
is pending for execution (liu, 2000). Consequently,
no computation is involved in determining when the
processor should be active.
Recently (Chetto, 2014), we addressed the
scheduling problem that arises in a uniprocessor plat-
form that is powered by a renewable energy storage
unit and uses a recharging device such as photovoltaic
cells (Kansal and Hsu, 2006). We proposed a dynamic
priority scheduling algorithm called ED-H. ED-H is
based on the EDF (Earliest Deadline First) dynamic
priority assignment rule (Liu and Layland, 1973).
ED-H is a generalization of a scheduling heuristic
called EDeg that we intoduced in 2011 (Ghor et al.,
2011). ED-H considers a set of deadline constrained
tasks including periodic tasks whose characteristics
are well known at design time. ED-H is a clairvoyant
scheduler that requires to know in advance both the
energy source profile and characteristics of the tasks
(arrival time, computation time and energy require-
ment).
The ED-H scheduler involves overhead due to
specific on-line computations which are absent in the
classical EDF scheduler that greedily consumes en-
ergy. ED-H requires the online computation of two
data respectively called slack time and slack energy
in order to build the schedule at run time. The over-
head of the ED-H scheduler clearly depends on both
the computational complexity for slack time and slack
energy and the frequency of these computations.
In (Chetto, 2014), we proved that ED-H is op-
timal. But gaining in performance generally means
losing in cost. Consequently, this paper aims to show
that the gain in performance in comparison with clas-
sical EDF scheduler turns out to be higher than the
actual overhead cost.
The rest of the paper is organized as follows: We
first introduce the model and terminology in Section
2. Section 3 describes the necessary background for
ED-H including slack time and slack energy concepts.
358
El Ghor H. and Chetto M..
Overhead Considerations in Real-time Energy Harvesting Systems.
DOI: 10.5220/0005341103580362
In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (ESAE-2015), pages 358-362
ISBN: 978-989-758-084-0
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Overhead evaluation is described in Section 4. Sec-
tion 5 is concerned with experimental results. Finally,
we conclude the paper in Section 6.
2 MODEL AND TERMINOLOGY
2.1 Task Set
We consider a real-time system that is composed of
n periodic tasks. A task τ
i
is described by a Worst
Case Execution Time (WCET) of C
i
time units and
relative deadline D
i
. We assume that 0 ≤ C
i
≤ D
i
≤
T
i
for each 1 ≤ i ≤ n. Timing values are generally
expressed in seconds. A periodic task τ
i
makes its
initial request at time 0 and its subsequent requests
at times k.T
i
, k = 1, 2,... called release times. The
least common multiple of {T
1
,T
2
,...,T
n
} (called the
hyperperiod) is denoted by T
LCM
. Each request of τ
i
requires a Worst Case Energy Consumption (WCEC)
of E
i
energy units. We define the processor utilization
as U
p
=
∑
n
i=1
C
i
T
i
and the energy utilization as U
e
=
∑
n
i=1
E
i
T
i
.
2.2 Energy Model
We concentrate on the harvested energy since it can
incorporate all losses caused by power conversion and
charging process. We assume that the energy source
is uncontrolled but predictable: we cannot control it
but its behavior may be modeled to predict the ex-
pected availability at a given time within some error
margin. The energy source module harvests the en-
ergy from its ambient environment and then converts
it into electrical energy at power P
r
(t) where P
r
(t) is
called the WCCR (Worst Case Charging Rate).
The harvested energy is stored in an energy stor-
age unit with capacity E. The energy level has to
remain between two boundaries E
min
and E
max
with
E = E
max
− E
min
. The stored energy may be used
at any time later and does not leak any energy over
time. If the storage is fully charged, and we continue
to charge it, energy is wasted. In contrast, if the stor-
age is fully discharged, no job can be executed.
3 BACKGROUND MATERIALS
In this section we describe the ED-H scheduling algo-
rithm that has been proposed in (Chetto, 2014). The
idea behind ED-H is to order the jobs according to the
EDF rule since the jobs issued from the periodic tasks
have hard deadlines. Executing them in accordance
with their relative urgency appears to be the best ap-
proach even if they are not systematically executed as
soon as possible due to possible energy shortage.
The difference between ED-H and classical EDF
is to decide when to execute a job and when to let
the processor idle. Before authorizing any job to exe-
cute, the energy level of the storage must be sufficient
so that all future occurring jobs execute timely with
no energy starvation, considering their timing and en-
ergy requirements and the replenishment rate of the
storage unit. In our model, any job consumes energy
with instantaneous power that fluctuates along its ex-
ecution.
Before starting the execution of any job, it must
be verified that the energy will be available to execute
it until completion with no energy starvation.
If this condition does not hold, the processor has
to idle during a certain time interval. The recharging
process terminates when either the energy storage unit
has fully replenished or one job absolutely needs to
start execution so that all deadlines can be met.
The ED-H algorithm uses three major data re-
spectively denoted by E(t), Slack
energy(t) and
Slack time(t) where t is the current time. E(t) refers
to the amount of energy that is currently stored at time
t. Slack energy(t) and Slack time(t) are respectively
the slack energy and the slack time of the system at
time t (as defined later in this article). Let PEND-
ING(t) be a boolean which equals true whenever there
is at least one job in the ready list queue at time t.
Function wait() puts the processor in the sleep mode.
Function execute() puts the processor in the active
mode and starts executing the highest priority job in
the ready list.
ED-H checks the ready list queue at every current
time t since it is a preemptive scheduler. The pro-
cessor idles if the ready list is empty. Else ED-H se-
lects the highest priority job for execution. Nonethe-
less, ED-H authorizes the execution of the job only if
the slack energy has a positive value. Otherwise, the
processor idles. The question is: for how long time?
ED-H answers this question by computing the slack
time of the system. And the processor will be let inac-
tive until the next time instant where either the energy
storage unit fully replenishes or there is no more slack
time. Let us note that whenever the processor does
not execute any job, the slack time linearly decreases
with time. ED-H also tests whether E(t) > E
min
where
E
min
refers to the threshold for the level of the energy
storage unit.
OverheadConsiderationsinReal-timeEnergyHarvestingSystems
359

Output: The ED-H schedule.
1: while (1) do
2: while PENDING(t)=true do
3: while (E(t) > E
min
and Slack energy(t) >
0) do
4: execute()
5: end while
6: while (E(t) < E
max
and Slack time(t) > 0)
do
7: wait()
8: end while
9: end while
10: while PENDING=false do
11: wait()
12: end while
13: end while
3.1 Slack Time Computation
Slack time is a well known concept used in the
conventional literature about real-time scheduling.
By definition, the slack time of a hard deadline task
set at current time t is the length of the longest
interval starting at t during which the processor may
be idle continuously while still satisfying all the
timing constraints. The slack time of a periodic task
set at a given time instant can be obtained on-line by
computing the dynamic EDL schedule. Details of
computation are given in (Silly-Chetto, 1999).
Proposition 1. The time complexity for computing
the slack time at run time is O(K.n) with n the number
of periodic tasks, K equal to dR/pe, R and p respec-
tively the longest deadline and the shortest period of
tasks.
3.2 Slack Energy Computation
The slack energy of the periodic task set at current
time t, is defined as the maximum amount of energy
that can be consumed from t continuously while still
satisfying all the timing constraints. The slack energy
at time t is computed only when there is at least one
job, say J
j
which will be released after t and has a
deadline d
j
that is less than or equal to that of the
highest priority job, ready at t. The slack energy of the
system is determined by the minimum slack energy of
all the jobs.
Then the slack energy of job J
j
at time t will be given
by:
Slack energy(J
j
,t) = E(t) +
Z
d
j
t
P
r
(k)dk − A
j
(1)
Where A
j
is the energy demand within [t,d
j
) required
by the periodic jobs ready to be processed between t
and d
j
.
A
j
=
∑
d
k
≤d
j
E
k
(2)
Consequently, the slack energy of the system at time
t is determined by:
Slack energy(t) = min(Slack energy(J
j
,t)) (3)
Proposition 2. The time complexity for computing
the slack energy is O(K.n) with n the number of pe-
riodic tasks, K equal to dR/pe, R and p respectively
the longest deadline and the shortest period of tasks.
4 OVERHEAD EVALUATION
The overhead of ED-H depends on the complexity
for computing slack time and slack energy and the
number of times we are obliged to compute these two
quantities. In order to compute the total overhead in-
curred by slack time and slack energy computations,
we have to evaluate:
• the overhead for one slack time computation,
• the overhead for one slack energy computation,
• the number of slack time computations in a refer-
ence interval,
• the number of slack energy computations in a ref-
erence interval.
The global overhead refers to the total overhead
due to slack time computations plus the total overhead
due to slack energy computations.
4.1 Illustrative Example
Let us illustrate the overhead measurement for slack
time computation, one slack energy computation
and finally the global overhead. We consider a
periodic task set Γ composed of three periodic tasks
τ
i
with τ
i
= (C
i
,D
i
,T
i
,E
i
). Let τ
1
= (1, 5,6, 12),
τ
2
= (2,8, 10,15) and τ
3
= (4,11, 15,22). We
assume that the level in the storage unit at time 0
is E(0) = 25. It equals the capacity of the energy
storage unit. The environmental power varies over
time as described in table 1. Tasks in Γ are first
scheduled according to the EDS rule (i.e. executed
as soon as possible) until t = 10 where E(10) = 13.
At t = 10, τ
2
is the highest priority task. The slack
energy of the system is then computed from all jobs
released after t = 10 with absolute deadline less than
or equal to the absolute deadline of τ
2
equal to 18.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
360

Table 1: Values of P
r
(t).
Interval of time [0, 1] [1,2] [2, 3] [3,4] [4, 5] [5,6] [6, 7] [7,8] [8, 9] [9,10]
P
r
(t) 5 3 4 6 2 4 7 8 4 6
Interval of time [10,11] [11,12] [12,13] [13,14] [14,15] [15,16] [16, 17] [17, 18] [18,19] [19,20]
P
r
(t) 3 7 8 4 2 5 4 7 3 5
Interval of time [20,21] [21,22] [22,23] [23,24] [24,25] [25,26] [26, 27] [27, 28] [28,29] [29,30]
P
r
(t) 4 6 7 3 7 8 3 4 5 6
Slack energy(J
1
,10) = E(10) +
Z
17
10
P
r
dt −E
1
= 34
(4)
The overhead incurred by the slack energy com-
putation is 7 defined as the number of arithmetic op-
erations implemented in that computation.
Slack energy(J
2
,10) = E(10) +
Z
18
10
P
r
dt −(E
1
+ E
2
)
= 26 (5)
Thus, the overhead for one computation of the
slack energy is 8. At time t = 15, the slack energy
needs to be computed again. This generates an over-
head equal to 19 operations. At t = 18, τ
1
is the high-
est priority task ready for execution and E(18) = 4.
Nevertheless, there is no sufficient energy in the en-
ergy storage for starting execution of τ
1
. The proces-
sor stays inactive as long as the energy storage has
not filled completely and the latest start time has not
been attained. This presupposes to compute the slack
time of the system. The static idle time vector and the
static deadline vector are assumed to be available with
no computation since these values are computed off-
line. We have K = (0,5, 8,11, 17,18, 23,26, 28,29)
and D = (3,0, 0,4, 0,2,0,0,1,1).
The dynamic EDL schedule for the interval
[18,30] is obtained from the dynamic deadline vec-
tor K (18) = (18,23,26, 28,29) and the dynamic idle
time vector D(18) = (4,2, 0,1, 1). Three on-line
computations are performed for obtaining D(18).
Consequently, the overhead generated by this slack
time evaluation amounts to 3 operations. The slack
time at t = 18 equals 4 time units. At t = 22, the en-
ergy level is E(22) = 22 energy units. Instances are
executed according to EDS until t = 24 where the bat-
tery storage unit becomes empty, needs to recharge
thus involving computation of the slack time with
overhead equal to 3. Scheduling continues until the
end of the hyperperiod where E(30) = 10.
From the observation of ED-H along one hyper-
period, we conclude that:
• The number of slack time computations equals 2,
• The number of slack energy computations equals
2,
• The total overhead due to slack energy computa-
tion equals 34,
• The total overhead due to slack time computation
equals 6,
• Global overhead given by the total overhead in-
curred by slack time computations and slack en-
ergy computations equals 40, exactly 34 + 6.
Consequently, the overhead cost per job amounts to
4 basic operations since 10 jobs occur within every
hyperperiod.
5 EXPERIMENTAL RESULTS
In this section, we evaluate the overhead of the ED-
H scheduler. We assume an energy source with con-
stant power P
r
. We have developed a discrete event-
driven simulator in C. We report here an experiment to
compare the overhead by varying the number of tasks.
For a specific processor utilization setting, we repeat
experiments for 50 periodic task sets. We report the
experiments for task sets with high energy utilization
and low energy utilization successively.
5.1 Task Sets with Low Energy
Utilization
Let us assume that the normalized energy utilization
U
e
/P
r
= 0.3. Consequently, the average consump-
tion power of the tasks is about 30% of the harvested
power. In this experiment, the time overhead is eval-
uated by varying the number of periodic tasks. Time
overhead is defined as the number of times where we
compute either the slack time or the slack energy rel-
ative to the total number of instances.
The number of slack time and slack energy com-
putations is clearly not dependent on the number of
tasks. However, the the number of overhead compu-
tations incurred by every computation of either the
slack time or the slack energy linearly increases as
the number of tasks increases. But when computing
the time overhead, we have to divide the number of
overhead computations by total number of instances.
OverheadConsiderationsinReal-timeEnergyHarvestingSystems
361
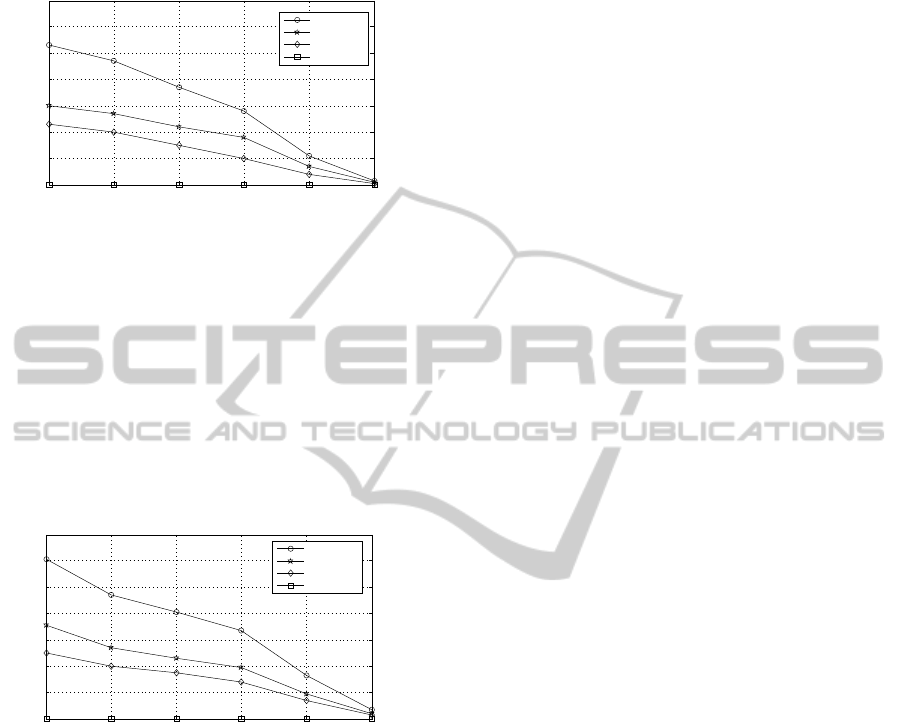
Consequently, time overhead decreases upon increas-
ing the number of tasks.
5 10 15 20 25 30
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Number of Tasks
Time Overhead
ED−H
Slack Time
Slack Energy
EDS
Figure 1: Time overhead by varying the number of tasks for
low energy utilization.
Figure 1 shows that the time overhead decreases
as n increases. Thus the overhead cost (about 0.15) is
still in the acceptable margin and consequently it will
not affect the performance gain of ED-H.
5.2 Task Sets with High Energy
Utilization
We consider periodic task sets with normalized en-
ergy utilization U
e
/P
r
= 0.9.
5 10 15 20 25 30
0
0.2
0.4
0.6
0.8
1
1.2
1.4
Number of Tasks
Time Overhead
ED−H
Slack Time
Slack Energy
EDS
Figure 2: Time overhead by varying the number of tasks for
high energy utilization.
Figure 2 shows that the overhead cost decreases
as the number of tasks increases. If n increases with
U
e
/P
r
keeping constant, the overall overhead cost
due to slack energy computations decreases while the
number of these computations remains constant.
In summary, the overhead increases by about 29%
from low energy utilization to high energy utilization.
Hence, the maximum overall overhead cost will be
about 0.22, which is also still in the acceptable mar-
gin.
6 CONCLUSION
Traditional real-time schedulers behave poorly be-
cause they greedily consume the energy by execut-
ing systematically the tasks as soon as possible. Very
recently, we presented the framework of a new mono-
processor preemptive scheduling algorithm, namely
ED-H. ED-H jointly handles constraints from both
energy and time domain. For this purpose, we intro-
duced the concept of slack energy that guarantees the
absence of energy starvation for every task as long as
the application is feasible.
In this paper, we presented the overhead cost of
ED-H through a detailed simulation by varying the
number of tasks. We explored specifically the time
lost to compute at run time two key data, namely slack
time and slack energy. Our interrogation has con-
cerned the number of such computations on a refer-
ence interval given by the hyperperiod of the periodic
tasks as well as the complexity of such computations.
The simulation study evaluated the impact of
overheads on the relative performance of different
scheduling strategies including EDF, the classical
real-time scheduler which does not involve specific
computations at run time. So in a hard real-time sys-
tem where all the tasks must imperatively meet their
timing requirements, it is of practical interest to prove
that the gain in performance is higher than the in-
curred cost. To investigate the time overhead incurred
by the schedulers under different application profiles,
we made vary the number of tasks. The highest over-
head cost is obtained under high energy utilization.
Still, this value is acceptable and will not affect the
performance of ED-H.
REFERENCES
J. W. S. Liu. Real-Time Systems, Prentice Hall, 592 pages,
2000.
M. Chetto. Optimal Scheduling for Real-Time Jobs in En-
ergy Harvesting Computing Systems. IEEE Transac-
tions on Emerging Topics in Computing, 2(2), pp.122-
133, 2014.
A. Kansal, J. Hsu. Harvesting aware Power Management
for Sensor Networks. Proc. of ACM/IEEE Design Au-
tomation Conference, pp. 651-656, 2006.
H. El Ghor, M. Chetto and R. Hage Chehade. A real-time
scheduling framework for embedded systems with en-
vironmental energy harvesting. Computer and Electri-
cal Engineering Journal, 2011.
M. Silly-Chetto. The EDL Server for scheduling periodic
and soft aperiodic tasks with resource constraints,
Real-Time Systems, 17(1), pp.1-25, 1999.
C-L Liu and J-W Layland. Scheduling algorithms for
multiprogramming in a hard real-time environment. J
ACM, 46-61, 1973.
PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems
362
