Performance Evaluation of the Clustering Based Sequence Equalizer in

Direct Detection Optical Communication Links

Kristina Georgoulakis and George-Othon Glentis

University of Peloponnese, Department of Informatics and Telecommunications, Tripoli, Greece

Keywords:

Optical Communication, Direct Detection, Electronic Equalization, Maximum Likelihood Sequence Estima-

tion, Cluster based Equalizer.

Abstract:

In this paper the performance of the Clustering Based Sequence Equalizer is investigated in the context of

Intensity Modulated Direct Detection optical communications links operating at 10Gb/s, when non-return to

zero on-off keyed and optical differential encoded phase shift keyed transmission is employed. The afore-

mentioned equalizer provides an attractive implementation of the Maximum Likelihood Sequence Estimation,

comprising of two successive steps, namely a) nonparametric estimation of the channel response using a clus-

ter based approach and b) sequence estimation using the Viterbi algorithm. The performance of the cluster

based equalizer in ﬁber links is investigated my means of computer simulation.

1 INTRODUCTION

The Intensity Modulated Direct Detection set up

(IM/DD) has been extensively used for 10Gb/s up

to 40Gb/s commercial optical communication links

(Stavdas, 2010). In the IM/DD systems the opti-

cal to electrical conversion is directly realized via a

nonlinear device, the photodetector, which acts as a

square-law function (Agrawal, 2012). Chromatic dis-

persion (CD) is perhaps the dominant linear impair-

ment which is liable of electronic equalization. When

a train of pulses is transmitted, excessive dispersion

can force successive pulses to overlap resulting in In-

tersymbol Interference (ISI). Electronic equalization,

applied in the receiver part, is used to mitigate ei-

ther the residual CD resulting from the incomplete

optical compensation or the accumulated CD result-

ing from uncompensated optical transmission (Singer

et al., 2008).

Equalization methods based on the Maximum

Likelihood Sequence Estimation (MLSE) have been

proposed as a powerful tool for mitigating the effect

of the ISI in wireless as well as in wireline com-

munication systems (Proakis, 2001). The MLSE ap-

proach has been successfully applied in the context

of electronic equalization of optical communication

links (Agazzi et al., 2005; Foggi et al., 2006a; Foggi

et al., 2006b; Bosco and Poggiolini, 2006; Hueda

et al., 2007; Poggiolini et al., 2008; Bosco et al.,

2009; Alﬁad et al., 2009; Bosco et al., 2010; Mag-

gio et al., 2014), for IM/DD non-return to zero on-

off keyed (NRZ-OOK) and for optical differential en-

coded phase shift keyed (NRZ-DPSK) transmission

set up. The MLSE electronic equalizer has been im-

plemented using the Viterbi algorithm (VA) (Proakis,

2001). The histogram method, as well as, paramet-

ric closed form approximations of the received signal

probability density function (PDF) have been utilized

for the computation of the branch metrics associated

to the VA implementation (Agazzi et al., 2005; Hueda

et al., 2007), requiring however a huge amount of data

in order to obtain reliable results. Alternatively, the

VA branch metrics can be computed at a much lower

cost, adopting a Gaussian approximation for the per-

tinent PDFs, either directly from the received data

(Alﬁad et al., 2009), or by means of channel identi-

ﬁcation using a second order Volterra model (Chung,

2010).

The Clustering Based Sequence Equalizer

(CBSE) provides an attractive alternative to the

implementation of the MLSE method (Theodor-

idis et al., 1995; Georgoulakis and Theodoridis,

1997; Georgoulakis and Theodoridis, 2000). The

implementation of the MLSE equalizer requires

the estimation of the response of the transmission

channel. According to the CBSE appoach, the

design of the equalizer is treated as a classiﬁcation

task (Theodoridis and Koutroumbas, 2008), thus

freeing itself from the need of an explicit adoption

of speciﬁc models for the channel as well as for the

113

Georgoulakis K. and Glentis G..

Performance Evaluation of the Clustering Based Sequence Equalizer in Direct Detection Optical Communication Links.

DOI: 10.5220/0005342601130120

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 113-120

ISBN: 978-989-758-092-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

interference. The CBSE approach comprises of two

successive steps, namely a) estimation of the channel

response to the transmitted data using a cluster based

approach and b) the estimation of the transmitted

sequence using the Viterbi algorithm. The main

advantage of the cluster based approach that speciﬁc

modeling of the channel or the interference is no

longer required. Moreover, the CBSE is able to cope

with either one-dimensional (1D) or two-dimensional

(2D) formulations of the received data, providing in

the later case, the advantage of using, apart from the

Euclidean, the Mahalanobis distance. One dimen-

sional CBSE implementations of the MLSE have

been proposed in the context electronic equalization

of IM/DD optical links, either implicitly (Foggi et al.,

2006b), or explicitly (Lisnanski and Weiss, 2006;

Yang et al., 2008). The application of the 2D CBSE

approach in the case of IM/DD NRZ-OOK signaling

has been discussed in (Georgoulakis et al., 2010).

In this paper, the performance of the CBSE equal-

izers is evaluated in the context of IM/DD opti-

cal communication links, when NRZ-OOK or NRZ-

DPSK transmission is employed. The performance

of the CBSE equalizers is investigated by means of

computer simulation, both for 1D as well as for 2D

formulation of the received data. In the later case,

both the Euclidean and the Mahalanobis distance are

considered for the computation of the branch metrics

of the VA. The required Optical Signal to Noise Ratio

(OSNR) for an achieved Bit Error Rate (BER) lower

that 10

−3

is used as a performance index. Moreover,

the performance of each method in a typical metro op-

tical link that consists of short or medium long haul

optical transmission system hence comprising multi-

ple ﬁber spans, each of length equal to 100 Km, is

investigated in terms of the achieved BER. The com-

putational complexity of each approach is also dis-

cussed. Finally, design guidelines for the selection

of the appropriate modulation format and the elec-

tronic equalization method are drawn, based on the

overall performance of each approach, in terms of the

achieved BER and the complexity of each method.

2 MLSE AND CBSE CONCEPTS

Consider the discrete time system described by the

following equation

y(n) = c(n) + w(n) (1)

where

c(n) = f (I(n),I(n− 1),...,I(n− M+ 1)) (2)

is the noiseless channel output sequence, f(.) is the

function representing the channel action, I(n) is an

equiprobable sequence of the transmitted data taken

from a binary alphabet, i.e. I(n) ∈ {0,1}, and w(n)

is the disturbance or the noise signal. The channel

memory is represented by M while the channel length

is given by L = M + 1. The MLSE selects, among

all possible transmitted sequences, the one that mini-

mizes the cost

min

}



∑

(e(n))



(3)

where

e(n) = y(n) − c(n) (4)

The minimization of (4) is performed efﬁciently using

the Viterbi algorithm (Proakis, 2001).

The implementation of the MLSE equalizer re-

quires the estimation of the channel response, c(n) in

(2), for a given input sequence I(n),I(n− 1),...,I(n−

M+ 1). This in turn requires either the a priori knowl-

edge of the channel, or the identiﬁcation of the chan-

nel, usually employing a parametric model, based on

the available data set. Alternatively, the channel re-

sponse to the input sequence can be estimated using

a non parametric technique known as clustering, due

to the fact the input is taken from a ﬁnite alphabet

(binary in our case) (Georgoulakis and Theodoridis,

1997). The clustering based concept focuses on the

clusters, which the received data form. The received

data y(n) form a set of B = 2

M+1

clusters in the 1D

space. Each cluster is represented by a suitably cho-

sen representative which corresponds to an estimate

of the noiseless channel response, i.e. ˆc(n) ∈ {c

,m =

0,1, ...,B− 1} . The clusters are usually estimated us-

ing a training sequence, although blind cluster estima-

tion may be applied (Georgoulakis and Theodoridis,

2000). Subsequently, the transmitted sequence is es-

timated using (3), by means of the VA. The resulting

MLSE implementation is known as the 1D CBSE ap-

proach.

The number of the states of the VA, in the 1D

CBSE case, is given by S = 2

. The number of the

branches associated to the states of the VA coincides

to the number of clusters. Given a set of training data

{I(n),y(n)}, n = 1,2,...,N, the cluster representa-

tives are estimated by averagingthose values of the re-

ceived data that belong to a certain cluster. Let I(n) =

[I(n),I(n− 1),...,I(n− M+ 1)]

be a vector that car-

ries the transmitted bits upon which the output signals

y(n) are constructed. Clearly, I(n) ∈ {I

,.. .I

B−1

where I

denotes the binary representation of the in-

teger m, with m = 0, 1,. .., B − 1. The cluster repre-

sentatives are computed as

∑

(y(n)|I(n) = I

) (5)

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

114

with N

denoting the cardinality of the set {I(n) =

}, n = 1,2, ...,N. During the decision mode, the

branch metrics associated to each cluster of the VA

are estimated as

= (y(n) − c

)

, m = 0,1, ... ,B− 1. (6)

The branch metrics are subsequently utilized to up-

date of the metrics associated to each state of the VA

using a compare add select unit. The detection of the

transmitted symbol

I(n− D) is performed by means

of the trace back search unit, with D ≈ 5M represent-

ing the depth of the search (Proakis, 2001).

The 2D CBSE is formulated in a similar way; the

new input is the pair of data at consequent time in-

stances n and n− 1, Thus a received signal of a higher

dimension is constructed as

y(n) =



y(n)

y(n− 1)



. (7)

The advantages of this approach over the 1D counter-

part are a) better cluster classiﬁcation, and b) the abil-

ity to cope with nonwhite interference. (Georgoulakis

and Theodoridis, 1997).

The 2D CBSE minimizes the cost function

min

}



∑



(n)We(n)





(8)

where

e(n) = y(n) −



f (I(n),.. .,I(n− M + 1))

f (I(n− 1),...,I(n− M)))



(9)

is the error between the received 2D data and the cor-

responding channel response. W is an appropriately

chosen weighting matrix of dimensions equal to 2×2.

The number of the states of the 2D VA is given by

= 2

M+1

and the number of the associated branches

is given by B

= 2

M+2

Let I

(n) = [I(n),I(n− 1),.. .,I(n− M+ 1)I(n−

M)]

be a vector that carries the transmitted bits upon

which the output signal vector y(n) depends upon at

the time instant n. It holds I

(n) ∈ {I

,.. .I

−1

where I

denotes the binary representation of the in-

teger m, with m = 0,1, ... ,B

. During the training

mode the cluster representatives are computed as

∑



y(n)|I

(n) = I



(10)

with N

denoting the cardinality of the set {I

(n) =

}, n = 1,2, ... ,N. The choice of W =



1 0

0 1



re-

sults to the standard Euclidean distance. In this case,

the branch metrics associated to the 2D VA are esti-

mated as

= (y(n) − c

)

(y(n) − c

) (11)

A/D

OOK CBSE

OBPF

ELPF

I(n)

y (n)

y(t)

Figure 1: The NRZ-OOK receiver.

with m = 0,1,.. .,B

− 1. Alternatively, the weight-

ing matrix in (8) may be set equal to the inverse of

the estimated error covariance matrix corresponding

to each one 2D data cluster, i.e.,

= Σ

−1

, m = 0,1,.. .,B

− 1, (12)

where

= (13)

∑



(y(n) − c

)(y(n) − c

)

(n) = I



This particular choice of the weighting matrix results

to the so called Mahalanobis metric, where the branch

metrics of the 2D VA are computed as

= (y(n) − c

)Σ

−1

(y(n) − c

)

. (14)

3 CBSE IN OOK SIGNALING

The schematic diagram of the NRZ-OOK receiver is

depicted in Figure 1. After optical band pass ﬁlter-

ing, the optical signal is converted to an electrical sig-

nal by means of a photodetector. The electrical signal

is subsequently passed through an electrical low pass

ﬁlter and sampled by an Analog to Digital (A/D) de-

vice. Fractionally spaced sampling is employed, as in

this case the performance of the electronic equalizers

becomes less sensitive to the sampling phase of the

receiver (Singer et al., 2008).

Let T

being the symbol period and let y(t) be the

electrical signal that is produced at the receiver. Let

(n) ∈ ℜ and y

(n) ∈ ℜ denote the received signal

sampled at time instances nT

and nT

+ T

/2 respec-

tively (fractionally spaced at T

/2 is assumed). The

receiver diversity, due to the fractionally spaced sam-

pling, is incorporated into the MLSE cost as

min

}

∑

i=1

(y(n) − c

(n))

. (15)

Here, c

(n) , f

(I(n),I(n− 1),...,I(n− M+ 1)), i =

1,2 denote the channel response to the input sequence

I(n),I(n− 1),.. .,I(n− M+ 1).

When the 1D CBSE is considered, two set of clus-

ters c

m,1

and c

m,2

, m = 0,1,. .., B − 1, are estimated

PerformanceEvaluationoftheClusteringBasedSequenceEqualizerinDirectDetectionOpticalCommunicationLinks

115

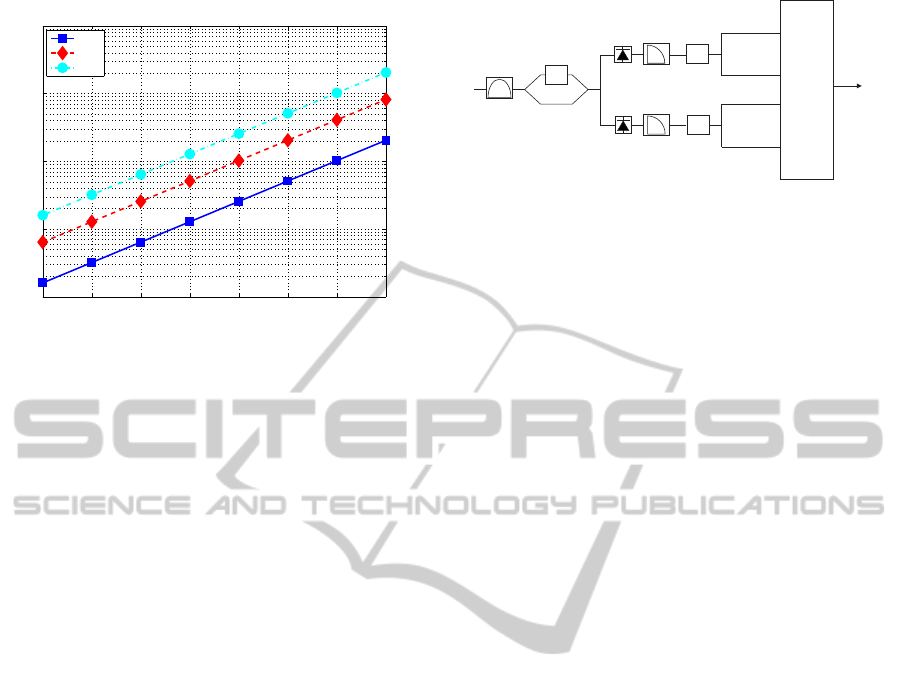
2 3 4 5 6 7 8 9

Complexity

Channel Memory

CBSE OOK

V2E

V2M

Figure 2: Computational complexity of the CBSE equal-

izer in the case of NRZ-OOK signaling, for the 1D imple-

mentation (V1), the 2D implementation using the Euclidean

metric (V2E) and for the 2D implementation using the Ma-

halanobis metric (V2M).

during the training mode using (5). Each one of them

corresponds to the fractionally spaced received sig-

nals y

(n) and y

(n). During the decision mode, the

computation of the branch metrics associated to the

1D VA are computed using (6) as

∑

i=1

(n) − c

m,i

)

, m = 0,...,B− 1. (16)

In the case of the 2D CBSE, the cluster representa-

tives c

m,1

and c

m,2

, m = 0,1, ... ,B

− 1 are estimated

using (10). When the Euclidean metric is considered,

the branch metrics of the 2D VA are computed as

∑

i=1

(n) − c

m,i

)

(y(n) − c

) (17)

with m = 0,1,.. .,B

− 1. In the case when the Ma-

halanobis metric is adopted, the branch metrics are

∑

i=1

(n) − c

m,i

)Σ

−1

m,i

(n) − c

m,i

)

. (18)

m,1

and Σ

m,2

are the covariance matrices computed

using (13) for each one of the received signals y

(n)

and y

(n).

The computational complexity of the CBSE

equalizer in the case of NRZ-OOK signaling, mea-

sured in terms of the required multiplications, is given

by C

OOK

= 2

M+2

, C

2DE

OOK

= 2

M+4

and C

2DM

OOK

= 5 ×

M+3

, for the 1D implementation, the 2D implemen-

tation using the Euclidean metric and for the 2D im-

plementation using the Mahalanobis metric, respec-

tively. The computational complexity of the NRZ-

OOK CBSE equalizers is illustrated in Figure 2, for

various values of the assumed channel memory M.

A/D

DPSK CBSE

MZDI

ELPF

OBPF

I(n)

y (n)

1,c

y (n)

1,d

y (n)

2,c

y (n)

2,d

y(t)

Constructive Branch

Destructive Branch

Figure 3: The NRZ-DPSK receiver.

4 CBSE IN DPSK SIGNALING

The NRZ-DPSK transmission has received increased

attention as, compared to the NRZ-OOK counterpart,

a 3dB improvement is achieved at the back-to-back

operation, (Wang and Kahn, 2004; Alﬁad et al., 2009;

Bosco et al., 2010). The electronic equalization of

optical NRZ-DPSK transmission is treated in a simi-

lar way, noting however that in this case the equalizer

is designed using jointly the constructive and the de-

structive signals available at the receiver, at the output

of a pair of balanced photo-detectors used for the de-

modulation of the optical DPSK signal (Alﬁad et al.,

2009). The schematic diagram of the NRZ-DPSK re-

ceiver when joint MLSE equalization is employed is

depicted in Figure 3. At the receiver side the sig-

nal is processed by a Mach-Zahnder delay interfer-

ometer which extracts the information from the op-

tical phase between two adjacent symbols, produc-

ing the constructive (upper branch) and the destruc-

tive (lower branch) output signals. These signals are

subsequently fed into two photodetectors and after

being ﬁltered by the corresponding electrical ﬁlters

and fractionally sampled, are both used as input to

the MLSE equalizer (Alﬁad et al., 2009; Bosco et al.,

2010).

As in the case of OOK signaling, fractionally

spaced sampling is considered. Thus, at each time

instant, four signals are available at the receiver. Let

1,c

(n) ∈ ℜ and y

2,c

(n) ∈ ℜ denote the received sig-

nals at the constructive branch of the DPSK receiver

sampled at time instances nT

and nT

+ T

/2. More-

over, let y

1,d

(n) ∈ ℜ and y

2,d

(n) ∈ ℜ be the corre-

sponding received signals at the destructive branch of

the DPSK receiver. The DPSK receiver diversity im-

plies the following MLSE cost

min

}

∑

i=1

i,c

(n) − c

i,c

(n))

∑

i=1

i,d

(n) − c

i,d

(n))

(19)

where c

1,c

(n), c

2,c

, c

1,d

and c

2,d

denote the channel re-

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

116

2 3 4 5 6 7 8 9

Complexity

Channel Memory

CBSE DPSK

V2E

V2M

Figure 4: Computational complexity of the CBSE equal-

izer in the case of NRZ-DPSK signaling, for the 1D imple-

mentation (V1), the 2D implementation using the Euclidean

metric (V2E) and for the 2D implementation using the Ma-

halanobis metric (V2M).

sponse to the input sequence I(n),I(n− 1),.. .,I(n −

M + 1).

The 1D CBSE in the case of DPSK signaling

involves the computation of four sets of clusters,

namely the c

m,1,c

and c

m,2,c

that correspond to the

constructive branch of the receiver, as well as the

m,1,d

and c

m,2,d

which correspond to the destructive

branch of the receiver, m = 0, 1,. .., B, using (5) ap-

plied on the received signals y

1,c

(n), y

2,c

(n), y

1,d

(n)

and y

2,d

(n). During the decision mode, the computa-

tion of the branch metrics associated to the 1D VA, are

computed using (6), tailored to the DPSK diversity as

V =

∑

i=1

i,c

(n) − c

m,i,c

)

∑

i=1

i,d

(n) − c

m,i,d

)

The 2D CBSE can be derived following the approach

applied in the OOK case, noting however that the re-

ceiver diversity includes apart from the fractionally

spaced signaling, the diversity due to the constructive

and the destructive branches of the DPSK receiver.

The computational complexity of the CBSE

equalizer in the case of NRZ-DPSK signaling, is

given byC

DPSK

= 2

M+3

, C

2DE

DPSK

= 2

M+5

and C

2DM

DPSK

5 × 2

M+4

, for the 1D implementation, the 2D im-

plementation using the Euclidean metric and for the

2D implementation using the Mahalanobis metric,

respectively. The computational complexity of the

NRZ-DPSK CBSE equalizers is illustrated in Figure

4, for various values of the assumed channel mem-

ory M. Clearly, the computational complexity of the

CBSE equalization methods in the case of DPSK sig-

naling is twice of that required in the case of OOK

signaling.

0 1 2 3 4

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

Without Equalization

OOK

DPSK

Figure 5: Required OSNR for BER=10

−3

without elec-

tronic equalization, for OOK as well as for DPSK signaling

at 10Gb/s.

5 PERFORMANCE EVALUATION

The electronic equalization schemes are used to mit-

igate either the residual dispersion resulting from in-

complete optical compensation or the total dispersion

resulting from uncompensated optical transmission.

Here we focus on the later case, when uncompensated

optical transmission is considered. The performance

of the MLSE electronic equalizers has been investi-

gated in the past, for the IM/DD NRZ-OOK as well as

for the NRZ-DPSK signaling at 10Gb/s, using the 1D

VA method (Bosco and Poggiolini, 2006; Rosenkranz

and Xia, 2007; Chen et al., 2007; Poggiolini et al.,

2008; ?; Bosco et al., 2009). We extend the perfor-

mance analysis of the aforementioned methods, con-

sidering the 1D CBSE as well as the 2D CBSE ap-

proach described in the preceding Section. The re-

quired OSNR for an achieved BER < 10

−3

is used as

a performance index. Moreover, the performance of

each method in a typical metro optical link compris-

ing multiple ﬁber spans, each of length equal to 100

Km, is investigated in terms of the achieved BER.

The numerically simulated optical link operating

at 10Gb/s consists of a transmitter comprising a 1mW

CW laser at 1550 nm with an external modulator hav-

ing extinction ratio of 25 dB and a Standard Single

Mode Fiber with dispersion coefﬁcient 17 ps/nm/km.

When NRZ-OOK transmission is considered, on the

receiver side, there is an optical ﬁlter with 20GHz

bandwidth with a 3rd order Gaussian frequency re-

sponse representing the corresponding demultiplexer

output. The photodetector is a PIN diode with a sen-

sitivity of 0.83 A/W and the receiver includes an elec-

trical ﬁlter with 4th order Bessel frequency response

with a cut-off frequency of 7GHz. The output is frac-

tionally sampled and is fed as input to the CBSE

PerformanceEvaluationoftheClusteringBasedSequenceEqualizerinDirectDetectionOpticalCommunicationLinks

117

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

OOK−V1

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(a)

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

OOK−V2E

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(b)

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

OOK−V2M

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(c)

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

DPSK−V1

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(d)

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

DPSK−V2E

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(e)

2 4 6 8 10

Required OSNR @ BER<10

−3

CD x 1700 ps/nm

DPSK−V2M

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

BB+3dB

(f)

Figure 6: Required OSNR for OOK and DPSK signaling with CBSE equalization, for the the 1D implementation (V1), the

2D implementation using the Euclidean metric (V2E) and for the 2D implementation using the Mahalanobis metric (V2M),

for various sizes of the assumed channel memory M, 10Gb/s.

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

OOK−V1D

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(a)

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

OOK−V2DE

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(b)

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

OOK−V2DM

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(c)

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

DPSK−V1D

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(d)

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

DPSK−V2DE

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(e)

0 2 4 6 8 10

−6

−5

−4

−3

−2

−1

Length x 100Km

BER

DPSK−V2DM

M=2

M=3

M=4

M=5

M=6

M=7

M=8

M=9

FEC−LIMIT

(f)

Figure 7: Achieve BER for electronically equalized transmission over a typical optical communication link, comprising of

multiple spans, of length equal to L = 100Km, 10Gb/s.

equalizers. In the case of NRZ-DPSK transmission,

the DPSK modulator is implemented using a standard

Mach-Zehnder modulator. At the receiver side the

signal is processed by a Mach-Zahnder delay interfer-

ometer. These signals are subsequently fed into two

photodetectors and after being ﬁltered by the corre-

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

118

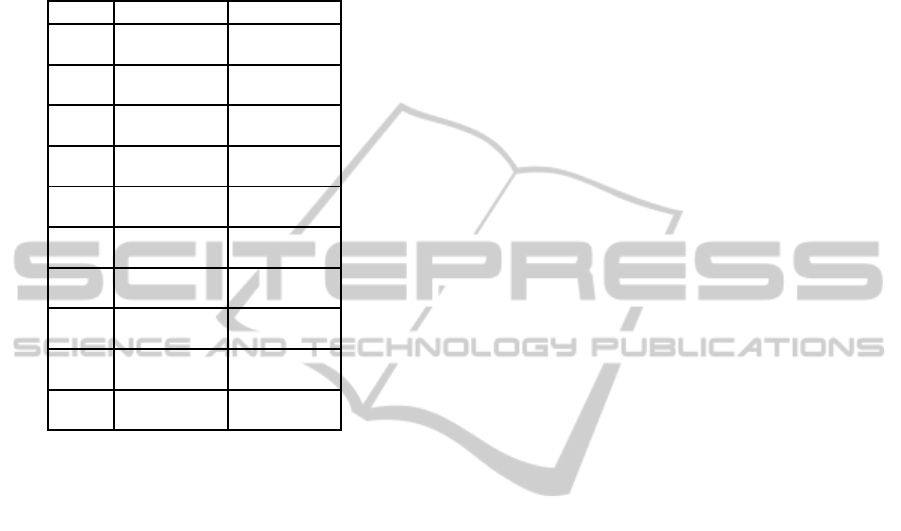
Table 1: Selected signaling and CBSE approach for particu-

lar values of the target BER. Notation V1, V2E and V2M is

used to indicate the CBSE approach, i.e. the 1D implemen-

tation, the 2D implementation using the Euclidean metric

and the 2D implementation using the Mahalanobis metric,

respectively. The assumed channel length and the required

computational complexity of each method are indicated as

[M/C].

L Km BER< 10

−3

BER< 10

−5

100 OOK V1 OOK V1

[2/16] [2/16]

200 OOK V1 OOK V1

[2/16] [2/16]

300 OOK V1 OOK V1

[2/16] [3/32]

400 OOK V2E OOK V2E

[2/32] [3/64]

500 OOK V2E OOK V2E

[4/128] [4/128]

600 OOK V2E OOK V1

[4/128] [6/256]

700 OOK V2E OOK V2E

[6/256] [8/2048]

800 OOK V2E OOK V2E

[7/1024] [9/4096]

900 OOK V2E DPSK V2M

[8/2048] [7/10240]

1000 DPSK V2E DPSK V2M

[9/8192] [8/20480]

sponding electrical ﬁlters and being fractionally sam-

pled. In both cases, the system is optically ampliﬁed

using a single polarization Erbium Doped Fibre Am-

pliﬁer such that the powerat the receiverinput is equal

to the transmitted power, which is set equal to 0dBm.

The input signal I(n) is a binary sequence of

length equal to N = 2

. In all cases, the given results

are obtained by averaging the output of ten indepen-

dent computer experiments. The experimental con-

ditions impose a lower bound on the estimated BER,

given by BER > 10

−6

. The required OSNR versus

the accumulated CD for uncompensated NRZ-OOK

as well as for NRZ-DPSK transmission is depicted in

Figure 5. The performance of the CBSE equalizers

is illustrated in Figure 6, where it is shown the re-

quired OSNR versus the accumulated CD for the 1D

and the 2D CBSE approaches, for various values of

the assumed channel memory, varying from M = 2

and going up to M = 9. The attained performance is

compared against the the back-to-back performance

corresponding to the OOK and to the DPSK signal-

ing. For both modulation formats, the 2D CBSE us-

ing the Mahalanobis metric demonstrates the better

performance within the margin of the 3dB penalty,

followed by the 2D CBSE using the Euclidean met-

ric. The 1D CBSE has the worst performance, noting

however that it requires the least amount of computa-

tion. In all cases, the DPSK signaling performs better

than the OOK counterpart, at the expense of an in-

crease in the complexity of the transponder circuitry

and the amount of computations required by the elec-

tronic equalization modules.

The achieved BER for each modulation format,

when the CBSE approach is used for the implemen-

tation of the MLSE, is illustrated in Figure 7, for

uncompensated optical transmission over a distance

of up to 1000 Km, with the optical link compris-

ing of multiple ﬁber spans, each of length equal to

100 Km. Once again, the DPSK signaling outper-

forms the OOK counterpart, however at an expense

of complexity. Subsequently, the performance of each

method in terms of the required computational com-

plexity is investigated, for two different target BER,

speciﬁcaly for BER < 10

−3

and for BER < 10

−5

. The

results are tabulated in Table 1, where the selected

method, as well as the computational complexity of

each CBSE approach is presented. In the case when

the target BER is achieved by more than one meth-

ods, that which corresponds to the minimum assumed

channel lenght M is selected.

6 CONCLUSIONS

The performance of the electronic equalization using

the CBSE approach has been investigated by means of

computer simulation, in the context of IM/DD optical

communications links operating at 10Gb/s, for NRZ-

OOK as well as for NRZ-DPSK signaling. The 1D

CBSE, as well as the 2D CBSE using the Euclidean

or the Mahalanobis distance for the computation of

the branch metrics of the VA, provide an attractive ap-

proach for the implementation of the MLSE, bypass-

ing the need of explicit estimation of the optical chan-

nel response. In principle, the electronically equal-

ized DPSK signaling outperforms the OOK counter-

part. Finally, the application of the CBSE method is

considered in a simulated typical metro optical trans-

mission link. For a given value of the target BER,

the required computational complexity is investigated

for different modulation formats and for the various

discussed CBSE approaches.

ACKNOWLEDGEMENTS

This work was funded through a grant (THALES

PROTOMI, MIS 377322) in the framework of the

O.P. Education and Lifelong Learning from Commu-

nity (ESF) and national funds.

The authors would like to thank Dr. Christos Ma-

trakidis for providing the code for the simulation of

PerformanceEvaluationoftheClusteringBasedSequenceEqualizerinDirectDetectionOpticalCommunicationLinks

119

the optical communications link.

REFERENCES

Agazzi, O., Hueda, M., Carrer, H., and Crivelli, D. (2005).

Maximum likelihood sequence estimation in disper-

sive optical channels. J. Lightwave Tech., 23(2):479–

762.

Agrawal, G. (2012). Fiber Optic Communication Systems.

Wiley.

Alﬁad, M. S., Borrne, V. D., Hauske, Fand Napoli, A., and

Koonen, A. M. J. (2009). Maximum-Likelihood se-

quence estimation for optical Phase-Shift Keyed mod-

ulation formats. 27(20):4583–4594.

Bosco, G., Cano, I., Poggiolini, P., Li, L., and Chen, M.

(2010). MLSE-based DQPSK transmission in 43 Gb/s

DWDM long-haul dispersion-managed optical sys-

tems. Journal of Lightwave Technology, 28(10):1573–

1581.

Bosco, G., Fonseca, D., Klonidis, D., Poggiolini, P.,

Rosenkranz, W., Teixeira, A., Tomkos, I., and Xia, C.

(2009). Electronic channel equalization techniques.

pages 23–47.

Bosco, G. and Poggiolini, P. (2006). Long-distance effec-

tiveness of MLSE IMDD receivers. IEEE Photonics

Technology Letters, 18(9):1037–1039.

Chen, W., Buchali, F., Yi, X., Shieh, W., Evans, J. S., and

Tucker, R. S. (2007). Chromatic dspersion and PMD

mitigation at 10 Gb/s using Viterbi equalization for

DPSK and DQPSK modulation formats. Optics ex-

press, 15(9):5271–6.

Chung, W. (2010). Channel estimation methods based

on Volterra kernels for MLSD in optical communi-

cation systems. IEEE Photonics Technology Letters,

22(4):2009–2011.

Foggi, T., Colavolpe, G., Forestieri, E., and Prati, G.

(2006a). Channel estimation algorithms for MLSD

in optical communication systems. IEEE Photonics

Technology Letters, 18(19):1984–1986.

Foggi, T., Forestieri, E., Colavolpe, G., and Prati, G.

(2006b). Maximum-likelihood sequence detection

with closed-form metrics in OOK optical systems im-

paired by GVD and PMD. Journal of Lightwave Tech-

nology, 24(8):3073–3087.

Georgoulakis, K., Matrakidis, C., Glentis, G. O., and

Stavdas, A. (2010). Fractionally spaced clustering

based equalizer for optical channels. In OSA SPPCom

Conference, Karlsruhe Germany.

Georgoulakis, K. and Theodoridis, S. (1997). Efﬁcient clus-

tering techniques for channel equalization in hostile

environments. Signal Processing, 58(2):153–164.

Georgoulakis, K. and Theodoridis, S. (2000). Blind and

semi-blind equalization using hidden markov mod-

els and clustering techniques. Signal Processing,

80(9):1795 – 1805.

Hueda, M. R., Crivelli, D. E., Carrer, H. S., and Agazzi,

O. E. (2007). Parametric estimation of IM/DD op-

tical channels using new closed-form approximations

of the signal PDF. Journal of Lightwave Technology,

25(3):957–975.

Lisnanski, R. and Weiss, A. J. (2006). Low complexity gen-

eralized EM algorithm for blind channel estimation

and data detection in optical communication systems.

Signal Processing, 86(11):3393–3403.

Maggio, G. N., Hueda, M. R., and Agazzi, O. E. (2014). Re-

duced complexity MLSD receivers for nonlinear op-

tical channels. IEEE Photonics Technology Letters,

26(4):398–401.

Poggiolini, P., Bosco, G., Benlachtar, Y., Savory, S. J.,

Bayvel, P., Killey, R. I., and Prat, J. (2008). Long-haul

10 Gbit/s linear and non-linear IMDD transmission

over uncompensated standard ﬁber using a SQRT-

metric MLSE receiver. Optics express, 16(17):12919–

36.

Proakis, J. G. (2001). Digital Communications. McGRaw -

Hill, 4th edition edition.

Rosenkranz, W. and Xia, C. (2007). Electrical equalization

for advanced optical communication systems. AEU -

International Journal of Electronics and Communica-

tions, 61(3):153–157.

Singer, A., Shanbag, N., and Bae, H. (2008). Electronic dis-

persion compensation. IEEE Signal Proc. Magazine,

pages 110–130.

Stavdas, A., editor (2010). Core and Metro Networks. Wi-

ley.

Theodoridis, S., Cowan, C., and See, C. (1995). Schemes

for equalization of communication channels with non-

linear impairments. IEE Proceedings on Communica-

tions, 142(3):165–171.

Theodoridis, S., and Koutroumbas, K.(2001). Pattern

Recognition . Academic Press, 4th edition.

Wang, J. and Kahn, J. (2004). Impact of cromatic and

polarization-mode dispersions on DPSK systems us-

ing interferometric demodulation and direct detection.

J. Lightwave Tech., 22(2):362–371.

Yang, C., Yang, F., and Wang, Z. (2008). Clustering based

adaptive channel estimator for optical ﬁber communi-

cation systems. IEEE Photonics Technology Letters,

20(20):1670 – 1672.

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

120