
Constrained Agglomerative Hierarchical Software Clustering with
Hard and Soft Constraints
Chun Yong Chong and Sai Peck Lee
Department of Software Engineering, Faculty of Computer Science and IT, University of Malaya, Kuala Lumpur, Malaysia
Keywords: Agglomerative Hierarchical Clustering, Constrained Clustering, Reverse Engineering.
Abstract: Although agglomerative hierarchical software clustering technique has been widely used in reverse
engineering to recover a high-level abstraction of the software in the case of limited resources, there is a
lack of work in this research context to integrate the concept of pair-wise constraints, such as must-link and
cannot-link constraints, to further improve the quality of clustering. Pair-wise constraints that are derived
from experts or software developers, provide a means to indicate whether a pair of software components
belongs to the same functional group. In this paper, a constrained agglomerative hierarchical clustering
algorithm is proposed to maximize the fulfilment of must-link and cannot-link constraints in a unique
manner. Two experiments using real-world software systems are performed to evaluate the effectiveness of
the proposed algorithm. The result of evaluation shows that the proposed algorithm is capable of handling
constraints to improve the quality of clustering, and ultimately provide a better understanding of the
analyzed software system.
1 INTRODUCTION
Software requires continuous change and
enhancement to satisfy new business rules and
technologies. This is a human intensive task that
requires deep understanding and comprehension of a
software before any decision to modify it. Therefore,
software maintainers must first gain a complete
understanding of the structure and behavior of the
software to be maintained before making any major
changes. However, most software that had undergone
instant changes does not have up-to-date
documentation. Thus, software maintainers may need
to reverse engineer the source code to gain a high-
level abstraction view of the software. Software
clustering is one of the techniques used to recover a
semantic representation of the software design and
documentation. It has received a substantial attention
in recent years because of its capability to help in
improving the modularity of poorly designed
software systems.
However, in certain scenarios, software
maintainers may have access to additional
information or domain knowledge about the software
to be maintained. For instance, the core business
rules and functionalities of a software remain
unchanged after undergoing several major updates,
or stakeholders have additional knowledge about the
software because they were involved in the early
stage of software development. Thus, even if the
software documentation is not up-to-date,
maintainers are able to salvage some useful
information about the structure of the software.
However, such information are worthless unless
there is a proper way to synthesis them.
An improvement to conventional clustering
techniques was proposed in (Basu et al., 2004) by
incorporating side information to further improve the
accuracy of clustering results. The side information is
commonly referred as “constraints” which reveal the
similarity between pairs of clustering entities, or user
preferences about how those entities should be
grouped during clustering.
It has been proven in several fields of research
that constrained clustering can significantly improve
the reliability and accuracy of clustering results
(Davidson and Ravi, 2009). However, there is still a
lack of studies on integrating constrained clustering
to effectively improve the modularity of poorly
designed software. In cases where end-users or
developers have side information regarding the
software to be maintained, the relevant knowledge
177
Chong C. and Lee S..
Constrained Agglomerative Hierarchical Software Clustering with Hard and Soft Constraints.
DOI: 10.5220/0005344001770188
In Proceedings of the 10th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2015), pages 177-188
ISBN: 978-989-758-100-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

can help improve the results of clustering by the
means of constraints.
In this study, we focus on fulfilling different
types of constraints using agglomerative hierarchical
clustering. Agglomerative hierarchical clustering is a
bottom-up approach that iteratively merge pair of
clusters until all clusters are merged into a big
cluster. Unlike the work by (Davidson and Ravi,
2009) which solely imposed absolute constraints
(must be fulfilled regardless of any situation), the
constrained clustering technique to be presented in
this paper involves several types of constraints which
differ according to their importance, i.e. must be
fulfilled, or good to have. As such, a constrained
clustering algorithm is introduced in this study to
help ease the software maintenance problem when
the system documentation is non-existent or
inconsistent with real implementation.
2 RELATED WORK
Software maintenance and verification is crucial to
discover and validate the relationship between
technology and business models. How well a certain
software fulfills stakeholders’ requirements often
depicts the effectiveness of the software.
A major fraction of software life cycle’s
expenditure is contributed by software maintenance
and support. The authors estimated that over 50% of
software development budget is spent on maintaining
and supporting the software itself. This shows that
maintenance indeed plays a very important role in the
software life cycle. Before performing any relevant
maintenance work, the person in charge must first
gain a complete understanding of the particular
software. This is to ensure that when there are
requests to update a particular functionality,
maintainers can recognise in advance, the interrelated
components. Eventually, the threats of introducing
faults and bugs during maintenance can be
minimized. Therefore, maintainers often need to
spend a significant amount of time in comprehending
the structure and design of the software.
Accomplishment of maintenance is highly dependent
on how much information can be extracted by
maintainers.
However, maintainers are typically not involved
in early stages of software design and development.
Furthermore, the documentation of the software is
usually not up-to-date, especially for projects that
follow agile software development where software
requirements and solutions evolve rapidly. Thus,
maintainers require additional options. One way to
alleviate these problems is through remodularization
of software, which is one of the reverse engineering
techniques used to help recover a semantic
representation of the design and documentation.
Software clustering is one of the techniques used
to perform remodularization of software. The goal of
clustering is to form multiple groups of clusters, such
that components within the same group are similar to
each other, and dissimilar from components in other
groups. The measurement of similarities between
components is based on inter-relationships between
components or common features shared by them
(Maqbool and Babri, 2007). Mutual exclusive groups
of components can be identified to provide more
insight toward the analyzed software. The results of
clustering can also help maintainers to understand the
behavior and dependencies of programs, identify
orphaned source code, and allow adding of new
software modules without interfering with the
general workflow of the software system (Antonellis
et al., 2009).
2.1 Software Clustering
Clustering can be based on either a supervised or
unsupervised approach to pick from a collection of
entities, then form multiple groups of entities such
that entities within the same group are similar to each
other, while dissimilar from entities in other groups.
In the context of software clustering, entities are
normally source code or classes. Similarity measures
are normally common global variables used by an
entity or function calls made by an entity. The
identification of similarity is often depending on
what kind of reliable information is available.
Generally, clustering can be categorized into
partitional and hierarchical clustering. Given a
collection of data, partitional clustering works by
directly decomposing it into a set of disjoint clusters.
On the other hand, hierarchical clustering iteratively
merge smaller clusters into larger ones or divide
large clusters into smaller ones, depending on either
it is a bottom-up or top-down approach. Merging or
dividing operations are usually depend on the
clustering algorithm used in the existing studies. The
result of partitional clustering are usually presented
in several disjoint set of clusters, with each cluster
contains at least one entity and each entity belongs to
only one cluster. Meanwhile, the final result of
hierarchical clustering is a tree diagram, called
dendrogram. A dendrogram shows taxonomic
relationships of clusters produced by hierarchical
clustering. Cutting the dendrogram at a certain height
produces a set of disjoint clusters.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
178

In the domain of software clustering, partitional
clustering is less viable because it is almost
impossible to know the initial number of clusters
before performing software clustering (Chong et al.,
2013). According to the work by (Wiggerts, 1997),
the working principle of agglomerative clustering
(bottom-up hierarchical clustering) is actually similar
to reverse engineering where the abstractions of
software designs are recovered in a bottom-up
manner. Thus, in this research, agglomerative
clustering will be used to recover high-level
abstraction of a poorly documented or poorly
designed software system.
Agglomerative hierarchical clustering starts by
forming all entities as initial clusters. At each step, a
pair of entities is merged and the algorithm ends with
one big cluster. The following steps show a standard
agglomerative hierarchical clustering algorithm.
Input: Set
,
,⋯,
of entities.
Output: Dendrogram
1. Each entity
forms an initial cluster
. The
total number of clusters K = n. For each pair of
clusters
and
, , the distance between
and
is denoted by
,
.
2. Find a pair of clusters with minimum distance,
,
:
Let
,
,
Merge
∪
and
reduce the number of clusters K= K-1
3. If K = 1, stop the iteration; else update
distance
,
, for all other clusters
.
(Follow step 2)
Although some clustering algorithms produce a
single clustering result for any given dataset, a
dataset may have more than one natural and optimum
clustering. For instance, source code can only tell
very limited information about the architectural
design of a software system since it is a very low-
level software artifact. The work by Deursen and
Kuipers (1999) adopted a greedy search method by
using mathematical concept analysis to analyze the
structure of cluster entities and identify the features
that are shared by them. The proposed approach finds
all of the possible combination of clusters and
evaluates the quality of each combination.
Agglomerative clustering is used in this work. The
authors discovered that it is hard to analyze all
possible combination and useful information might
be missing if no attention is given to analyze the
results of different dendrogram cutting points.
In contrast to the greedy search method proposed
by Deursen and Kuipers, the work by (Fokaefs et al.,
2009; Fokaefs et al., 2012) proposed an approach that
results in multiple solutions from which software
designers can select their best solution. Their goal is
to decompose large classes by identifying Extract
Class refactoring opportunities. The authors used
agglomerative clustering to generate the dendrogram
that demonstrated how the clusters are formed.
On other hand, our previous work (Chong et al.,
2013) proposed a technique to enhance existing
agglomerative clustering algorithms by minimizing
redundant effort and penalizing for the formation of
singleton clusters during software clustering. By
utilizing a least-squares polynomial regression
analysis, the algorithm finds the optimum result that
produces sets of clusters with high cohesion and low
coupling. The proposed technique is based on a
bottom-up approach, which starts by transforming
source code into a flat sequence of class diagrams,
and finally restructures them into a package diagram
to provide a high-level semantic view of the whole
system design. Figure 1 shows the overall workflow
of the work presented in (Chong et al., 2013). The
clustering process are summarized as follow.
1. Identification of entities and features - UML
classes are represented as cluster entities, while
relationships between classes are used to
calculate the distance between a pair of entities.
2. Calculation of similarity measure - Sorensen-
Dice coefficient (Sørensen, 1948) is used to
calculate the similarity between pairs of cluster
entities because it is more suitable to be applied
to asymmetric binary features, which is similar to
the behavior of functional dependencies and
method calling.
3. Application of clustering algorithm - Un-
weighted Pair-Group Method using Arithmetic
Average (UPGMA) is used to merge pairs of
entities and form the dendrogram.
Figure 1: Architecture recovery process proposed in
(Chong et al., 2013).
Our previous work does not differentiate between
aggregation, association, cardinality and
ConstrainedAgglomerativeHierarchicalSoftwareClusteringwithHardandSoftConstraints
179

generalization through different weightage. The
presence of any type of correlation will be
represented as a direct relationship between two
entities. The technique does not have the ability to
integrate domain knowledge or other sources of
information which can further improve the quality of
clustering result. Such way of incorporating domain
knowledge is also known as semi-supervised
software clustering.
If one has the ability to exploit high-level
information to guide and improve clustering, this will
further improve the quality of the results.
Constrained clustering, for instance, is one of the
semi-supervised clustering techniques that combine
external information in order to improve clustering
results.
2.2 Constrained Software Clustering
Recent works (Basu et al., 2004; Davidson and Ravi,
2009; Wagstaff and Cardie, 2000) have attempted to
discover the benefits of instance-level constraints in
both hierarchical and non-hierarchical clustering. The
must-link (ML) and cannot-link (CL) constraints
specify that two entities must both be part of or not
part of the same cluster respectively. These
constraints are useful when the information of cluster
entities is vague, allowing domain experts to guide
the clustering process. The information is normally
given as a set of pairwise constraints which involve
two entities and impose restriction such as
determining whether the involved entities should be
clustered into the same group or not. Constrained
clustering method is contrary to traditional
unsupervised clustering method where users have no
influence toward the clustering results.
Work by (Wagstaff and Cardie, 2000) has found
that side information such as constraints can improve
the quality of clustering when compared against
those without constraints. Meanwhile, the work by
(Davidson and Ravi, 2009) examined the complexity
of traditional clustering algorithms and investigated
methods to improve the efficiency of constrained
agglomerative hierarchical clustering. The authors
introduced new constraints apart from the traditional
ML and CL constraints to further improve the run-
time of agglomerative hierarchical clustering. They
discovered that small amounts of constraints not only
improve the accuracy of agglomerative hierarchical
clustering but also the overall run-time. However,
clustering under all types of constraints is NP-
complete, which means that creating a feasible
cluster hierarchy under all types of constraints is
intractable.
We found that there is a lack of research that
focuses on applying constrained clustering in the
field of software reverse engineering to remodularize
poorly designed software systems. The NP-complete
problem stated in the work by (Davidson and Ravi,
2009) can be minimized if each constraint is assigned
with a certain degree of importance, i.e. constraints
that must be fulfilled, or optional constraints that are
good to have. Therefore, different from the work by
(Davidson and Ravi, 2009), this study aims to
maximize the fulfillment of software constraints
according to the degree of importance derived from
stakeholders.
Generally, current works involving constrained
clustering methods can be divided into three
categories, namely distance based, constrained based,
or hybrid of both. In distance based constrained
clustering, a distance metric is trained to satisfy the
constraints before the clustering process. The
distance metric represents the dissimilarity strength
between pairs of entities. Merging or splitting of
clusters is based on the distance metric. Thus,
training the distance metric allows one to manipulate
the process of clustering to allow certain pairs of
entities to be clustered into the same group, or
separated if otherwise. Examples of methods to train
distance metrics include shortest path (Klein et al.,
2002), expectation maximization (Bilenko and
Mooney, 2003), and convex optimization (Shental
and Weinshall, 2003).
On the other hand, constrained based methods
work by modifying the cluster assignments, i.e.
manually assign entities to designated clusters. For
instance, must-link constraints can be used to
initialize the baseline of cluster hierarchy so that the
must-link constraints can be satisfied
indefinitely(Kestler et al., 2006). Constrained based
approaches ensure that all the constraints are fulfilled
because the clustering assignments are manipulated
by users based on the given constraints. However,
experiments performed by (Davidson and Ravi,
2009) discovered that manipulating with the
clustering assignments might lead to “dead-end”
situation where no pair of clusters can be merged to
obtain a feasible clustering result. Thus, a proper way
to ensure the fulfillment of constraints must be
formulated before enforcing any kind of clustering
constraints.
Fulfillment of constraints can be classified as
either hard or soft constraints associated with some
cost of violation if those constraints cannot be
fulfilled (Basu et al., 2004). Hard constraints are
constraints that cannot be violated during the
clustering process regardless of any condition. These
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
180

sets of constraints are usually highly reliable
knowledge or information given by domain experts.
In general, the cost of violating hard constraints
supersedes the objective function of constrained
clustering. Constrained based clustering method is
one of the most reliable approaches to make sure that
all hard constraints are fulfilled as much as possible.
Meanwhile, soft constraints are usually associated
with uncertainties and ambiguous information (Basu
etal., 2004). The cost of violating soft constraints
varies depending on the level of confidence provided
by the stakeholders. Clustering results will still be
acceptable if some of the soft constraints are not
fulfilled, with a condition that it falls within an
acceptable threshold (Ares et al., 2012). Soft
constraints are more robust against “noisy” or
incorrect. As a general rule, most of the objective
functions attempt to maximize the fulfillment of hard
and soft constraints. However, it is to be noted that
constrained clustering can fall into a NP-Complete
problem if the must-link and cannot-link constraints
are contradicting with each other, for instance,
(Must-Link ∪ Cannot-Link) > 0. Thus, potential
conflicts among hard constraints must be identified
in advance.
All in all, we found that it is feasible to
incorporate the notion of constrained clustering with
remodularization of software system. For instance,
experienced software developers can provide
opinions with a certain degree of confidence to
suggest if two entities should be clustered into the
same group. Furthermore, relationships among
software entities such as inheritance and dependency
suggest that two entities have strong affiliation and
they must be grouped together. There are plenty of
methods to derive constraints from the software itself
or side information from stakeholders. However,
there are certain cases where the stakeholder is not
assertive enough to judge whether the given
constraints are absolute, especially in the domain of
software engineering. For instance, as mentioned in
Section 1, the stakeholder who was involved in the
early stage of software design might provide some
constraints about the software to be maintained.
However, such constraints might not be valid
anymore after several phases of software updates and
changes. Thus, the constraints given by the
aforementioned stakeholder might be ambiguous or
contains erroneous information. A proper method is
needed to distinguish between absolute constraints
and optional constraints, and subsequently fulfill
those constraints according to their level of
importance. Therefore, in this study, a constrained
software clustering algorithm is proposed to alleviate
the problem mentioned above for aiding in reverse
engineering.
3 PROPOSED APPROACH
Constraints can be derived easily from stakeholders,
who are not necessary experts in a particular domain,
by asking them to make judgment whether two items
are similar or not (Hong and Yiu-ming, 2012). The
stakeholders can evaluate their judgments based on
their level of confidence or based on background
knowledge to support their decisions. In this
proposed approach, if the stakeholder is highly
confident that the provided constraints are reliable,
they will be categorized as hard constraints. These
sets of constraints must be fulfilled under any kind of
conditions. On the other hand, if the stakeholder is
doubtful about the given constraints, it will be
categorized as soft constraints.
3.1 Constraints with High Level of
Confidence
If a stakeholder has a high degree of confidence that
a pair of entities must be grouped together or
separated, these sets of constraints will be
categorized as the Must-Link Hard (MLH) or
Cannot-Link Hard (CLH) constraints. MLH and
CLH constraints are relatively easier to fulfill using
k-mean clustering because clustering assignment can
be manipulated during the process of clustering.
However, it is more difficult to achieve the same
results for agglomerative hierarchical clustering
because all entities in the dataset are linked together
at some level of the cluster hierarchy (Bair, 2013).
MLH and CLH constraints must always be fulfilled
at all levels of the hierarchy. The work by
(Miyamoto, 2012) introduced a distance based
approach to impose MLH constraints by requiring
entities linked by MLH constraints to be clustered
together at the lowest level of cluster hierarchy. This
is done by reducing the dissimilarities between pairs
of MLH constraints to zero.
Given a
,
,⋯,
with entities
,
,⋯,
. For (
,
∈, the distance
between
and
is modified to
,
0.
This will eventually form a baseline model for the
clustering hierarchy. Since the MLH constraints are
unconditionally fulfilled at the lowest level of the
hierarchy, one can ensure that the same can be
achieved all the way through the top of hierarchy.
Thus in this study, we will adopt the same technique
ConstrainedAgglomerativeHierarchicalSoftwareClusteringwithHardandSoftConstraints
181
proposed by (Miyamoto, 2012) to ensure the
fulfillment of MLH constraints.
For CLH constraints, there are typically two ways
to enforce using either constrained based or distance
based method. Constrained based methods modify
the cluster assignments by inspecting the merger of
two entities. If the chosen entities belong to the CLH
pairs, one will need to look for the next pair of
entities with the second highest similarity score.
However, the work by (Davidson and Ravi, 2009)
found that the formation of dendrogram may stop
prematurely in a certain scenario. The authors called
this scenario as the “dead-end” situation where
unless CLH constraints are violated, there will be no
more merging possible to form the final dendrogram.
Thus, constrained based approach to fulfill CLH
constraints is a less viable option in our case.
Distance based approaches, on the other hand,
modify the dissimilarities between pairs of CLH
constraints to be a value high enough to prevent them
from merging.
Given a set
,
,⋯,
with entities
,
,⋯,
. For
,
∈,
,
,
where is a constant large
enough to prevent linkage in between entities
,
.
By enforcing this rule, the pairs of CLH
constraints will not be chosen to merge unless there
is no more entities pair with distance more
than
,
. Entities which belong to
CLH constraints will then be merged at the top of the
hierarchy to form the complete dendrogram. By
looking into another perspective, the CLH constraints
are violated at the top of the hierarchy since without
violating them, “dead-end” situation will occur.
However, we argue that violating CLH constraints at
the top of the hierarchy is negligible because it is
almost impossible to cut the dendrogram at that
location. In a typical scenario, cutting the
dendrogram at the top of hierarchy will yield very
small number of clusters because this decision is at
the trade-off of relaxing the constraint of cohesion in
the cluster membership. Clusters formed under this
cutting point are usually made up of entities with
very fragile cohesion strength.
However, changing the distance measure of MLH
and CLH pairs will most likely result in violating the
triangle inequality of resemblance matrix (Klein et
al., 2002). This means that for some entities
,
∉,
,
∉ which were distance
,
apart before imposing MLH or CLH
constraints may now be ′
,
,
along some path which skip through the MLH or
CLH pairs. As pointed out by (Klein et al., 2002),
this problem can be solved by finding a new distance
value with respect to the modified constraints pairs
using all-pairs-shortest-path algorithm.
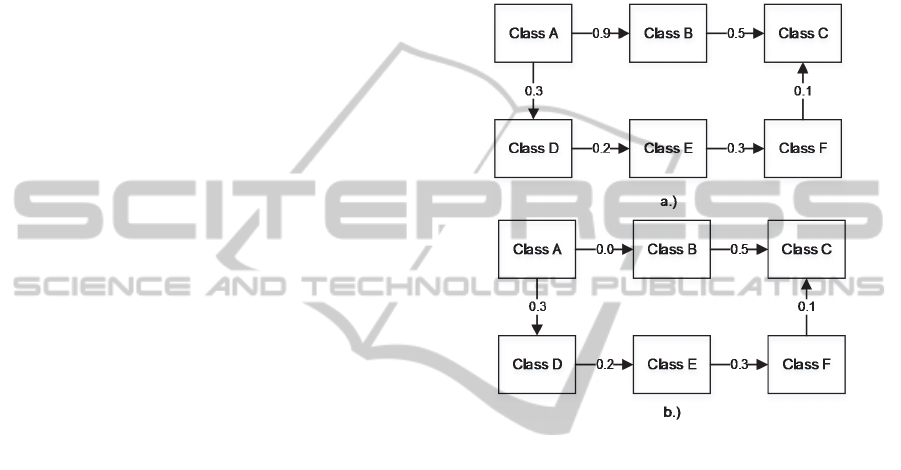
For instance, Figure 2a shows a simple example
of 6 entities, Classes A,B,C,D,E, and F. The number
on the edges indicate the distance between two
entities. In Figure 2a, the shortest distance between
Class A and Class C is 0.9 with the following order:
A-D-E-F-C.
Figure 2: Example of problem when imposing MLH and
CLH constraints.
After several discussions, the original developers
discovered that Class A and Class B in fact are very
closely related and impose a MLH constraint onto the
cluster. Thus, the distance between A and B is now
0.0 to reflect the MLH constraint, as illustrated in
Figure 2b. Therefore, the shortest path between Class
A and Class C after the imposition of MLH
constraint is now 0.5, with the following order: A-B-
C. If we do not update the distance matrix
accordingly, the final clustering results might contain
erroneous outcome. The overall algorithm to fulfill
both MLH and CLH constraints is shown below.
Input: A set of entities S = {
,
,⋯,
, a set of
MLH (must-link hard constraints) and a set of CLH
(cannot-link hard constraints)
Output: A modified distance matrix
1. Calculate the distance between each pair of
entities and store it in a distance matrix D where
,
,
2. Initialize: Let D’ = D (create a clone distance
matrix to modify the original one)
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
182

3. while ∀
,
∈∩
∀
,
∈
0
i. for (
,
∈, ′
,
0
run all-pair-shortest-path algorithm to prevent
violation of triangular inequality
ii. for (
,
∈, ′
,
′
,
where is a constant large enough
to prevent linkage in between entities
,
run all-pair-shortest-path algorithm to prevent
violation of triangular inequality
3.2 Constraints with Low Level of
Confidence
In cases where users are not confident enough to
judge whether the given constraints are absolute,
these sets of constraints will be categorized as soft
constraints. Since soft constraints are not definite,
clustering results with partial fulfillment of soft
constraints are still acceptable in most cases.
However, soft constraints might be derived with a
different level of importance and ranking, subject to
the information provided by users. Fulfilling a
handful of higher importance soft constraints might
overshadow the fulfillment of several less important
ones. Soft constraints are typically assigned with a
penalty score. The penalty score is used to evaluate
the quality of clustering results where minimization
of the penalty score is preferred. Thus, a
prioritization and ranking mechanism of soft
constraints is introduced in this study.
The nature of prioritizing a given set of
constraints is a multi-criteria decision-making
(MCDM) problem. MCDM is a research of methods
and procedures by which it concerns about
evaluating multiple conflicting criteria and derive a
way to come to a compromise. This set of criteria
often differs in the degree of importance. Examples
of methods to handle MCDM problems are analytic
hierarchical process (AHP), fuzzy AHP, goal
programming, scoring methods, and multi-attribute
value functions.
In this study, ranking and prioritizing the
importance of soft constraints are achieved using the
fuzzy AHP technique. Fuzzy AHP is capable of
handling the fuzziness of users’ opinions with respect
to the importance of soft constraints (Chong et al.,
2014). The results gathered from fuzzy AHP will be
represented in a table which shows a list of candidate
criteria (soft constraints) associated with weightage
(importance toward the analyzed software), where a
higher weightage value represents higher priority.
The result will act as a baseline to evaluate the
penalty score of each soft constraint. MLS and CLS
will be evaluated separately because the notion of
ML and CL is opposing to each other. The objective
function of MLS and CLS constraints is shown
below:
Given a set S = {
,
,⋯,
with entities
,
,⋯,
, a set of MLS (must-link soft
constraints) and a set of CLS (cannot-link soft
constraints). The objective function is to maximize
the number of satisfied MLS and CLS constraints:
1
1
2
Subject to
0,1,⋯
0
1, 1,⋯
Where
is the total number of available soft
constraints (including MLS and CLS) and
is
the number of satisfied soft constraints involving
pairs of entities with
as one of the entities. The
left side of the equation is the ratio of fulfilled soft
constraints over the total number of soft constraints.
Meanwhile,
is the penalty score for violated
constraints involving pairs of entities with
as one
of the entities. The penalty score is based on its
importance toward the overall software system using
fuzzy AHP technique. The cumulative weightage
(penalty score) of either MLS or CLS constraints is
equal to 1. Thus, a scaling constant of 1/2 is used to
normalize the second part of the equation when
adding both the MLS and CLS constraints.
Maximization of function is the goal of this
objective function. The evaluation of soft constraints
fulfillment is performed after the formation of
dendrogram. The dendrogram needs to be cut at a
certain height to produce a set of disjoint clusters.
Evaluation of soft constraints can then be done by
inspecting the set of disjoint clusters, to check
whether or not the soft constraints are violated. A
few cutting points can be executed to compare and
contrast the quality of each cut with respect to the
minimization of soft constraints penalty.
3.3 Constrained Agglomerative
Hierarchical Clustering Algorithm
All in all, the complete algorithm of the proposed
constrained agglomerative hierarchical software
clustering is shown below.
Given a set of entities S, the distance for each pair
of entities x and y in S is 1
,
0 and a set
of constraints ,,,.
1. Construct the baseline clusters from MLH
ConstrainedAgglomerativeHierarchicalSoftwareClusteringwithHardandSoftConstraints
183

constraints resulting in n number of initial
clusters
,
,⋯
.
2. If there is a pair of entities
,
in
,
,⋯
and CLH
,
∈, then this is a
NP-Complete problem with no solution.
3. Construct an initial clustering with
clusters
consisting of the n clusters
,
,⋯
and a
singleton cluster for each entity.
is the
maximum number of clusters for the set of
entities S.
4. while 1
a. Find the pair of entities
,
with
minimum distance.
b. Merge
∪
at the level of
dissimilarity.
c. Remove
,
.
d. 1.
e. repeat step 4.
5. Generate a dendrogram tree based on the
clustering results.
6. Cut dendrogram at several points.
7. Evaluate the fulfillment of MLS and CLS with
respect to the penalty score.
The overall workflow of the proposed technique
work in the following manner:
Software maintainers provide the UML class
diagrams of the software to be analyzed. If class
diagrams are not available, source codes are
converted into class diagrams using an off-the-shelf
round-trip engineering tool. The formation of
clustering entities, identification of features,
construction of dissimilarity matrix, and formation of
dendrogram are executed based on our previous work
(Chong et al., 2013) as discussed in Section 2.1.
After the dendrogram is formed, software
maintainers and/or the original developers can then
provide domain knowledge to aid in the software
clustering process. Based on the confidence level of
the maintainers and/or developers, each input is
categorized into hard or soft constraints.
Dendrograms are cut based on the available
constraints. Each cutting point is evaluated using the
objective function proposed in Section 3.2. Cutting
points that can fulfill the most constraints are
prioritized.
4 EVALUATION
The work by Anquetil and Lethbridge (Anquetil and
Lethbridge, 1999) discussed that instead of
recovering a software system’s architecture,
clustering techniques actually create a new one based
on the parameters and settings used by the clustering
algorithm. Thus, a way to evaluate the effectiveness
of the produced result is needed. MoJoFM is a well-
established technique used to compare the similarity
between clustering result and gold standard. High
similarity between two partitions is more desirable as
it indicates that the produced result resemble the gold
standard.
However, Mitchell and Mancoridis (2001)
discussed that often time, gold standard does not
Figure 3: Overview of the original package diagram and the constrained software clustering results.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
184

exist. The author suggested another approach by
clustering the analyzed software using different
clustering algorithms. Then, the similarity between
the results of different algorithms are compared with
each other. This will allow one to identify not only
the quality of the clustering results, but also the
stability of the clustering algorithm.
Thus, in this paper, we perform the evaluation of
the proposed technique in the following manner.
1. Perform normal software clustering (without any
constraints) based on our previous work (Chong
et al., 2013).
2. Perform constrained software clustering using our
proposed technique by incorporating hard and
soft constraints.
3. Retrieve the original package diagram of the
analyzed software. The original package diagram
is by no means the gold standard since we could
not verify the quality of the decomposition.
However, it can be treated as a guideline to
evaluate and compare between the results
produced by the proposed technique and the
documented artifact.
4. Use MoJoFM to calculate the similarity between
all three results (normal clustering, constrained
clustering, and package diagram).
Two evaluations were carried to assess the feasibility
of the proposed method. First, we choose a university
research project, MathArc ("MathArc - Ensuring
Access to Mathematics Over Time," August 2009),
as the input for our experiment. This project is aimed
at creating a system that is capable of the long-term
preservation and dissemination of digital journals in
mathematics and statistics. This system is a joint
project by Cornell University Library and Göttingen
State University Library, which took two years to
develop. The system contains 33 classes with an
average of 8 attributes and 4 methods per class.
The system’s functional modules are presented in
Figure 3. Dotted black boxes represent the original
UML packages. There are a total of six subsystems in
this software. Since the software design of the
MathArc system is documented properly, we can test
the feasibility of our proposed algorithm in the
following manner:
1. Prior to the experiment, we assume that all the
entities are scattered around and not grouped in
their respective packages.
2. Based on the original UML package diagram, we
extract a few MLH, CLH, MLS, and CLS
constraints. For instance, based on Figure 3, we
understand that class “Monitor” and
“Preservation” must be grouped into the same
cluster because they are from the same
subsystem. Thus, a MLH constraint “Monitor-
Preservation” is generated in Table 1.
3. For MLS and CLS constraints, penalty score for
violating the soft constraints are generated
randomly. Besides that, we intentionally generate
an erroneous constraint, but assign a very low
penalty score to see how the proposed algorithm
handles the constraint. For instance, although the
original package diagram indicates that “Media”
and “Standards” classes belong to different
packages, we create a MLS constraint with
penalty score of 0.1. This MLS constraint
simulates the situation where stakeholders are not
very confident about the given constraint.
4. Apply the proposed constrained clustering
algorithm to restructure the class diagram, so that
similar classes are grouped into the same
package, while dissimilar ones are separated from
each other.
5. Use MoJoFM to compare the result of the
proposed constrained clustering technique with
the original packages to identify its effectiveness.
Table 1 shows some of the constraints generated for
this experiment. Note that the bracketed value in
MLS and CLS represents the cost of violating a
constraint. Davies-Bouldin index (Davies & Bouldin,
1979) is used in this experiment to evaluate the
quality of cluster cohesion and separation.
Table 1: Generated constraints for MathArc system.
Constraints
MLH CLH MLS(penalty)
CLS
(penalty)
Submission-
QualityAssu
AccessControl-
Submission
Report-SysD(0.3)
Monitor-
Negotiator
(0.5)
Monitor-
Preservation
Report-
Services
Standards-
AccessControl(0.3)
Submission-
Services(0.5)
ErrorCheck-
Media
Updates-
APGeneration(0.3)
ReplaceMedia-
Media
Media-
Standards(0.1)
Figure 3 shows the clustering results using the
proposed algorithm. The blue and red boxes
represent the experimental results, with each box
representing one subsystem. The blue boxes indicate
the clustering results that match the original package
diagram, while the red boxes indicate the mixture of
results that match and do not match the original
package diagram. The diagram was redrawn to
normalize all of the association, aggregation, and
generalization into the form of normal association
notation.
ConstrainedAgglomerativeHierarchicalSoftwareClusteringwithHardandSoftConstraints
185
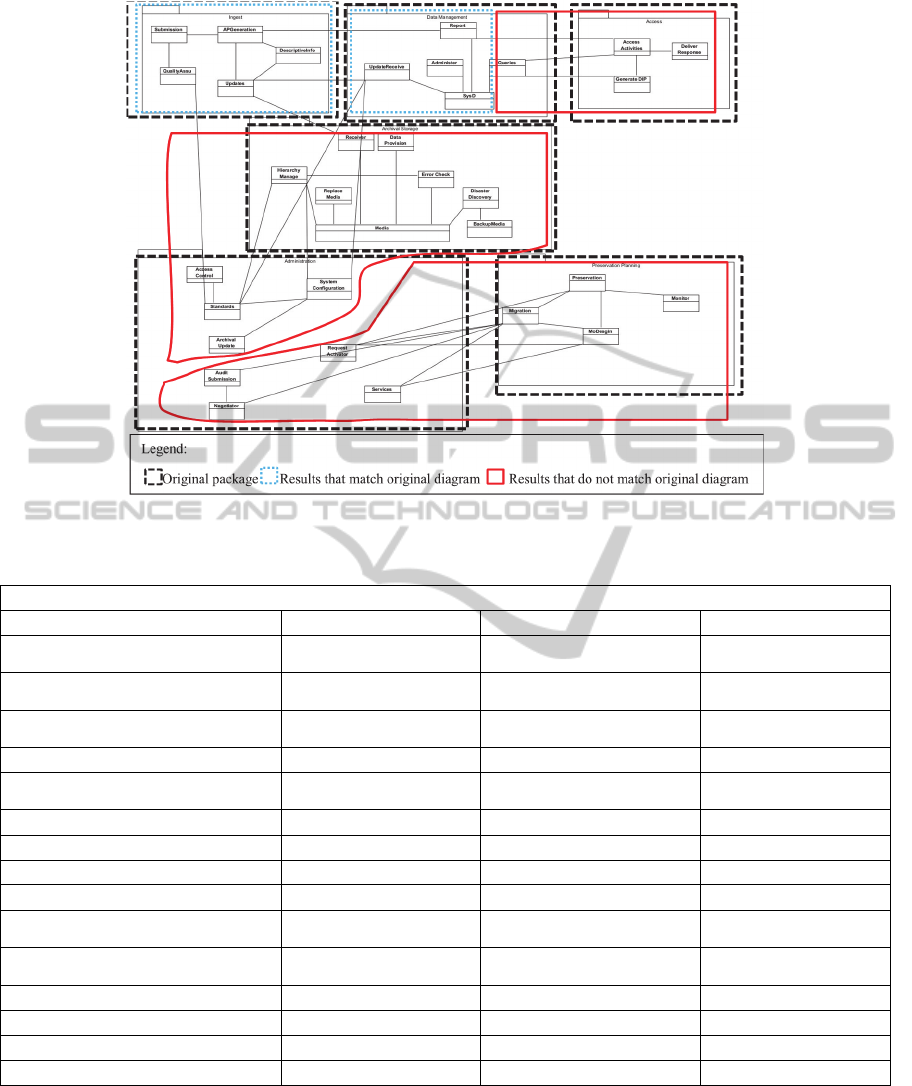
Figure 4: Overview of the original package diagram and the clustering results without pairwise constraints.
Table 2: Generated Constraints for JSPWiki system.
Constraints
MLH CLH MLS(penalty) CLS(penalty)
GroupCommand-AbstractCommand Workflow-TemplateDirTag Tast-Outcome (0.3)
Command-
WikiEventUtil(0.2)
AbstractCommand-WikiCommand MailUtil-Entry WatchDog-RSSThread(0.3)
WikiPrinciple-
WikiPage(0.3)
UserCheckTag-WikiServletFilter
Workflow-
CommandResolver
PageManager-
EditorManager(0.2)
Step-ParseException(0.3)
AdminBeanManager-WikiEngineEvent PageRenamer-Entry Feed-RSS20Feed(0.1) UserBean-Editor(0.1)
UserDatabase-WikiSession
Workflow-
WikiRPCHandler
Editor-RSSGenerator(0.1) BlogUtil-FileUtil(0.1)
Entry-AclImpl MessageTag-Denounce
WikiSession-UserProfile MessageTag-Entry
FormClose-FormSelect FileUtil-RPCCallable
FormElement-FormSet Heading-MarkupParser
FormOutput-FormOpen
Heading-
ProviderException
FormInput-FormTestArea
SecurityVerifier-
WikiException
InsertPage-TableofContents FileUtil-ClassUtil
Entry-FileSystemProvider BasicPageFilter-CoreBean
InitializablePlugin-Plugin Util.PageSorter-Outcome
TemplateDirTag-WikiRPCHandler Outcome-Feed
Note that all the MLH and CLH constraints are
fulfilled in the result. However, the MLS constraint
of "Media-Standards was violated. This is because
based on Davies-Bouldin index, fulfilling the MLS
constraint of “Media-Standards” will result in low
cohesion strength among the associated clusters.
Since the cost of violation is relatively smaller,
selecting another cutting point that violates this MLS
constraint is a better option. The objective function of
soft constraints in this experiment is
5/60.05 0.7833. The left side of the
equation signifies that 5 out of 6 soft constraints are
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
186

fulfilled. The value of 0.05 is calculated based on the
penalty score of violating the constraint “Media-
Standards” and multiplying it with scaling constant
of 1/2.
By using the MoJoFM tool provided by (Zhihua
and Tzerpos, 2004), we manage to achieve MoJoFM
metric of 92.59%. This shows a very high
resemblance between the result of our proposed
constraint clustering technique and the original
package diagram. However, as mentioned earlier, the
original package diagram is by no mean the ‘gold
standard’ because we are unable to verify if it is the
best abstraction to represent the software design of
MathArc system. Thus, we perform another
evaluation by comparing the results without
imposing the pairwise constraints. The result is
shown in Figure 4.
In Figure 4, we can observe that the
‘Administrator’ package (lower left hand side)
contains classes from two other packages. The reason
is that these classes behave similarly to utility
classes, for which the association strengths within the
same package are relatively weak compared to the
other packages. When compared with the original
package diagram, the MoJoFM achieves value of
88.89%. Although there are slight improvement
when using the proposed constrained clustering
technique, it is not significant enough. Thus, we
decided to perform another experiment using a larger
software.
We chose another open-source project, the
JSPWiki which is a Wiki engine written in J2EE
component. Wiki engines are used to host and
manage Wiki web pages. JSPWiki contains 42560
lines of code and 425 classes with an average of 5.5
methods per class.
We extracted 15 MLH and CLH constrains, and 5
MLS and CLS constraints from the original package
diagram of JSPWiki. The constraints are listed in
Table 2. However, due to the number of classes exist
in the project, the size of the class diagram is too
large to be displayed. We decided to report the
MoJoFM metric instead.
MoJoFM Metric: Constrained clustering compared to
original package = 76.25%
MoJoFM Metric: Normal clustering (without
constraints) compared to original package = 62.45%
The improvement by imposing pairwise constraints,
observing from the perspective of MoJoFM metric, is
more significant in larger software systems. The
same observation was also found in the work by
(Davidson and Ravi, 2009), where the author claimed
that when performing on large datasets, a small
number of constraints can significantly improve the
results of agglomerative hierarchical clustering.
5 CONCLUSION AND FUTURE
WORK
This paper presents a technique to integrate the
concept of constrained clustering with agglomerative
hierarchical software clustering to remodularize
poorly designed and documented software systems.
The proposed algorithm is capable of handling four
types of constraints, namely MLH, CLH, MLS, and
CLS constraints. Hard constraints are fulfilled
throughout the whole clustering process while soft
constraints are optional constraints associated with
some validation of penalty if they are violated.
The proposed algorithm has been successfully
implemented on two projects, the MathArc and
JSPWiki system. Several MLH, MLS, CLH, and
CLS constraints were generated to test the proposed
technique. We managed to restructure the software
and present it in the form of package diagram. When
compared against clustering without any constraints,
our proposed approach managed to achieve better
results measured using MoJoFM metric.
Finally, we believe that there is potential research
that can further improve the effectiveness of the
proposed technique. For example, one can attempt to
adapt the technique to be applied on partitional
clustering algorithms such as k-mean clustering.
ACKNOWLEDGEMENTS
This work is carried out within the framework of a
research project supported by eScienceFund with
reference 01-01-03-SF0851, funded by Ministry of
Science, Technology and Innovation (MOSTI),
Malaysia.
REFERENCES
Anquetil, N., & Lethbridge, T. C. (1999). Recovering
software architecture from the names of source files.
Journal of Software Maintenance, 11(3), 201-221. doi:
10.1002/(sici)1096-908x(199905/06)11:3<201::aid-
smr192>3.0.co;2-1
Antonellis, P., Antoniou, D., Kanellopoulos, Y., Makris,
C., Theodoridis, E., Tjortjis, C., & Tsirakis, N. (2009).
Clustering for Monitoring Software Systems
Maintainability Evolution. Electron. Notes Theor.
ConstrainedAgglomerativeHierarchicalSoftwareClusteringwithHardandSoftConstraints
187

Comput. Sci., 233, 43-57. doi:
10.1016/j.entcs.2009.02.060
Ares, M. E., Parapar, J., & Barreiro, Á. (2012). An
experimental study of constrained clustering
effectiveness in presence of erroneous constraints.
Information Processing & Management, 48(3), 537-
551.
Bair, E. (2013). Semi-supervised clustering methods.
Wiley Interdisciplinary Reviews: Computational
Statistics, 5(5), 349-361. doi: 10.1002/wics.1270
Basu, S., Banerjee, A., & Mooney, R. (2004). Active
Semi-Supervision for Pairwise Constrained Clustering
Proceedings of the 2004 SIAM International
Conference on Data Mining (pp. 333-344).
Bilenko, M., & Mooney, R. J. (2003). Adaptive duplicate
detection using learnable string similarity measures.
Paper presented at the Proceedings of the ninth ACM
SIGKDD international conference on Knowledge
discovery and data mining, Washington, D.C.
Chong, C. Y., Lee, S. P., & Ling, T. C. (2013). Efficient
software clustering technique using an adaptive and
preventive dendrogram cutting approach. Information
and Software Technology, 55(11), 1994-2012.
Chong, C. Y., Lee, S. P., & Ling, T. C. (2014). Prioritizing
and Fulfilling Quality Attributes For Virtual Lab
Development Through Application of Fuzzy Analytic
Hierarchy Process and Software Development
Guidelines. Malaysian Journal of Computer Science,
27(1).
Davidson, I., & Ravi, S. S. (2009). Using instance-level
constraints in agglomerative hierarchical clustering:
theoretical and empirical results. Data Mining and
Knowledge Discovery, 18(2), 257-282. doi:
10.1007/s10618-008-0103-4
Davies, D. L., & Bouldin, D. W. (1979). A Cluster
Separation Measure. Pattern Analysis and Machine
Intelligence, IEEE Transactions on, PAMI-1(2), 224-
227. doi: 10.1109/TPAMI.1979.4766909
Deursen, A. v., & Kuipers, T. (1999). Identifying objects
using cluster and concept analysis. Paper presented at
the Proceedings of the 21st international conference on
Software engineering, Los Angeles, California, USA.
Fokaefs, M., Tsantalis, N., Chatzigeorgiou, A., & Sander,
J. (2009). Decomposing Object-Oriented Class
Modules Using an Agglomerative Clustering
Technique. IEEE International Conference on
Software Maintenance, 93-101.
Fokaefs, M., Tsantalis, N., Stroulia, E., & Chatzigeorgiou,
A. (2012). Identification and application of Extract
Class refactorings in object-oriented systems. Journal
of Systems and Software, 85(10), 2241-2260. doi:
10.1016/j.jss.2012.04.013
Hong, Z., & Yiu-ming, C. (2012). Semi-Supervised
Maximum Margin Clustering with Pairwise
Constraints. Knowledge and Data Engineering, IEEE
Transactions on, 24(5), 926-939. doi:
10.1109/TKDE.2011.68
Kestler, H., Kraus, J., Palm, G., & Schwenker, F. (2006).
On the Effects of Constraints in Semi-supervised
Hierarchical Clustering. In F. Schwenker & S. Marinai
(Eds.), Artificial Neural Networks in Pattern
Recognition (Vol. 4087, pp. 57-66): Springer Berlin
Heidelberg.
Klein, D., Kamvar, S. D., & Manning, C. D. (2002). From
Instance-level Constraints to Space-Level Constraints:
Making the Most of Prior Knowledge in Data
Clustering. Paper presented at the Proceedings of the
Nineteenth International Conference on Machine
Learning.
Maqbool, O., & Babri, H. A. (2007). Hierarchical
Clustering for Software Architecture Recovery.
Software Engineering, IEEE Transactions on, 33(11),
759-780. doi: 10.1109/TSE.2007.70732
MathArc - Ensuring Access to Mathematics Over Time.
(August 2009).
Mitchell, B. S., & Mancoridis, S. (2001, 2001).
Comparing the decompositions produced by software
clustering algorithms using similarity measurements.
Paper presented at the Software Maintenance, 2001.
Proceedings. IEEE International Conference on.
Miyamoto, S. (2012). An Overview of Hierarchical and
Non-hierarchical Algorithms of Clustering for Semi-
supervised Classification. In V. Torra, Y. Narukawa,
B. López, & M. Villaret (Eds.), Modeling Decisions
for Artificial Intelligence (Vol. 7647, pp. 1-10):
Springer Berlin Heidelberg.
Shental, N., & Weinshall, D. (2003). Learning Distance
Functions using Equivalence Relations. Paper
presented at the In Proceedings of the Twentieth
International Conference on Machine Learning.
Sørensen, T. (1948). A Method of Establishing Groups of
Equal Amplitude in Plant Sociology Based on
Similarity of Species Content and Its Application to
Analyses of the Vegetation on Danish Commons: I
kommission hos E. Munksgaard.
Wagstaff, K., & Cardie, C. (2000). Clustering with
Instance-level Constraints. Paper presented at the
Proceedings of the Seventeenth International
Conference on Machine Learning.
Wiggerts, T. A. (1997, 6-8 Oct 1997). Using clustering
algorithms in legacy systems remodularization. Paper
presented at the Reverse Engineering, 1997.
Proceedings of the Fourth Working Conference on.
Zhihua, W., & Tzerpos, V. (2004, 24-26 June 2004). An
effectiveness measure for software clustering
algorithms. Paper presented at the Program
Comprehension, 2004. Proceedings. 12th IEEE
International Workshop on.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
188
