
Computing Attributes of Software Architectures
A Static Method and Its Validation
Imen Derbel
1
, Lamia Labed Jilani
1
and Ali Mili
2
1
Institut Superieur de Gestion, Bardo, Tunisia
2
New Jersey Institute of Technology, Newark, NJ, 07102-1982, U.S.A.
Keywords:
Software Architecture, Architecture Description Language, Analysis, Quality Attributes, Acme, Response
Time, Throughput, Reliability.
Abstract:
During the last two past decades, software architecture has been a rising subject of software engineering.
Since, researchers and practitioners have recognized that analyzing the architecture of a software system is
an important part of the software development process. Architectural evaluation not only reduces software
development efforts and costs but it also enhances the quality of the software by verifying the addressability
of quality requirements and identifying potential risks. To this aim, several approaches have been recently
proposed to analyze system non-functional attributes from its software architecture specification.
In this paper, we propose an ADL based formal method for representing and reasoning about system non-
functional attributes at the architectural level. We are especially interested in analyzing performance and
reliability quality attributes. We also propose to analyze the sensitivity of the system by identifying compo-
nents that have the greatest impact on the system quality. The automation of our model was followed by a
series of experiments that allowed us to validate our inductive reasoning to prove the capabilities of our model
to represent and analyze software architectures.
1 INTRODUCTION
Software Architecture is a rising subject of software
engineering that helps people to oversee a system in
high level. It is defined as the system structure(s),
which comprise software elements, the externally vis-
ible properties of those elements, and the relation-
ships between them (Bass et al., 1998).
The architecture of a software product is tradition-
ally modeled from the requirements specification, ac-
cording to the needs expressed by one or more clients.
The specification expresses customer needs in terms
of service functions, constraints, quality, etc. From
the specifications, the designers propose one or more
solutions that meet the customer needs. At this stage,
we must ensure that these proposed alternatives meet
all requirements specification to pass the later stages
of the life cycle (eg. implementation, integration,
etc.). It is therefore recommended to develop methods
and tools to analyze non-functional properties of soft-
ware architectures to provide designers with a sup-
port in their activities. Analysis of the product early
in the software life cycle, helps not only to discover
the problems of the architecture but also to make de-
cisions refinements of software products upstream.
This reduces software development efforts and costs,
and enhances the quality of the software by verifying
the addressability of quality requirements and identi-
fying potential risks.
In this context, several approaches have been pro-
posed in order to analyze systems quality attributes
at the architectural level. However, despite capacities
of architecture description languages (ADLs) in for-
mal description of software architectures, there is a
notable lack of support for non-functional attributes
in existing ADLs. Acme, Aesop, Weaves and others
allow the specification of arbitrary component proper-
ties, but none of them interprets such properties nor do
they make direct use of them (Medvidovic and Taylor,
2000).
In this paper, we propose an ADL based formal
method for representing and reasoning about system
non-functional attributes at the architectural level. We
are interested in analyzing performance attributes (re-
sponse time and throughput) and reliability (failure
probability). We aim to compile an architectural de-
scription and obtain a set of equations that charac-
terize non-functional attributes of software architec-
55
Derbel I., Labed Jilani L. and Mili A..
Computing Attributes of Software Architectures - A Static Method and Its Validation.
DOI: 10.5220/0005347300550066
In Proceedings of the 10th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE-2015), pages 55-66
ISBN: 978-989-758-100-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

tures, using an inductive reasoning. These equations
are then solved using Mathematica (
c
Wolfram Re-
search) in order to obtain system properties as func-
tion of components and connectors properties. We
also propose to analyze the system performance sen-
sitivity and the system reliability sensitivity by iden-
tifying architectural components and connectors that
limit the system quality and that need an urgent at-
tention to be improved. In this paper, we report on
our experimentation of our approach on Aegis system
(Allen and Garlan, 1996). The goal here is to val-
idate the inductive reasoning and the model we have
proposed. First, we analyzed the non-functionalprop-
erties of Aegis using our ADL based approach. Then,
we simulate the performance of the Aegis system to
determine and calculate its response time, its through-
put and its reliability.
This paper is organized as follows. Section 2
presents the background and the related work. Section
3 introducesACME+ ADL and presents the main syn-
tactic features that we have added to Acme. Section
4, describes the compiler that we propose for analyz-
ing ACME+ descriptions. Section 5, discusses per-
formance and reliability sensitivity analysis. Section
6, presents the generation of an automated tool for
the proposed analysis model. Section 7 outlines ex-
periments that we have conducted to validate our in-
ductive reasoning and analysis model. Section 8 con-
cludes this paper.
2 RELATED WORK
Several methods have been proposed for evaluating
software architectures quality attributes. These meth-
ods can be categorized as either being informal meth-
ods (including experience-based, simulation-based,
scenario-based approaches) or being formal ones (in-
cluding mathematical modeling based approaches)
(Bosch, 1999).
Some approaches are interested to the qualitative
analysis (Giannakopoulou et al., 1999), (wr2, 2005),
they verify structural and behavioral properties of the
software product such properties are: vivacity, live-
ness, coherence, blocking free, etc. While some other
approaches focus on quantitative analysis, they calcu-
late the values of software product measurable prop-
erties such as performance, reliability, availability,
maintainability, etc. Our approach falls into formal
analysis of quantitative quality attributes. In this con-
text, a number of mathematical modeling-based soft-
ware architecture evaluation methods have been de-
veloped. These methods model software architectures
using well-known formalisms and models. Then,
these models are used to estimate operational qual-
ity attributes. However, each approach analyzes only
one attribute, either reliability or performance.
In the following, we first discuss different ap-
proaches for assessing performance of a software ar-
chitecture. Then, we discuss the approaches for pre-
dicting reliability at the architectural level.
Several studies address the performance assess-
ment from a software architecture description. Each
approach is based on a certain type of performance
model and specification language. The latter includes
specification formalisms such as ADL descriptions,
Chemical abstract machine, and UML based specifi-
cation. Performance models include Stochastic Pro-
cess Algebras, queueing networks (QN) and their ex-
tensions called Extended Queueing Networks (EQN)
and Layered Queueing Networks (LQN), etc.
QN is one of the best known performance models.
Aquilani et al., in (Aquilani et al., 2001), proposed
the derivation of QN models from Labeled Transi-
tion Systems (LTS) describing the dynamic behavior
of SAs. Spitznagel and Garlan, in (Spitznagel and
Garlan, 1998), proposed the transformation of Acme
descriptions to QN models using ”distributed message
passing” style defined in Aesop ADL. However, they
propose only performance analysis of client/server
systems. Bernardo et al. in (Balsamo et al., 2002) pro-
posed Æmilia, an architectural description language
based on stochastic Process Algebra that allows to
solve performance indices using Timed Markov Mod-
els.
Several studies address the reliability assessment
from a software architecture description. Goseva-
Popstojanova and Trivedi (Goseva-Popstojanova and
Trivedi, 2001) classify these approaches into three
categories: state-based, path-based and additive. We
discuss the path-based and the state-based approaches
while ignoring the additive approach as it is not di-
rectly related to software architecture.
Path-based approaches (Shooman, 1976), (Krish-
namurthy and Mathur, 1997) assess the reliability of
the system according to the possible execution paths
of the program, which can be obtained experimen-
tally, by testing or algorithmically. In other words,
the reliability of each path is obtained as a product
of the reliabilities of the components along that path.
Then, the system reliability is calculated by averag-
ing the reliability of all the paths. One of the major
problems with the path-based approaches is that they
provide only an approximate estimate of application
reliability (Franco et al., 2012).
State-based approaches (Cheung, 1980), (Franco
et al., 2012), (Gokhale, 2007) assume that the transi-
tions between states havea Markov property, meaning
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
56

that at any time the future behaviour of components
or transitions between them is conditionally indepen-
dent of the past behaviour. These models consider
software architectures as a discrete Markov chain
(DTMC) or a continuous time Markov chain (CTMC)
or a semi-Markovprocess (SMP) which are solved us-
ing probabilistic model checking tools such as Prism
(Kwiatkowska et al., 2009). However, Markov mod-
els face a common problem, the combinatorial growth
of the statespace. This occurs when the model has a
large number of states and a great number of tran-
sitions between those states exceeding the memory
available.
3 ACME+: AN ARCHITECTURAL
DESCRIPTION LANGAGE
In order to support the automated derivation of syn-
thesized attributes from the attributes of building
components and connectors, an ADL needs to have
two important features: constructs to represent rele-
vant attributes and constructs to represent functional
dependencies between components and connectors.
These two constructs are needed to reason about how
attributes are synthesized throughout the architecture.
For the purposes of our study, we define an ADL
called ACME+ as an extension of Acme ADL.
Acme was selected for extension because it is an
interchange language offering benefits from the com-
plementary capabilities of ADLs. Also, it is supported
by AcmeStudio tool which enables users to edit archi-
tectures via a graphical user interface. In addition, it
offers a complete ontology to describe software ar-
chitectures, distinguishing between various architec-
tural elements: components, connectors, and config-
uration. The construct of
functional dependency
arises from the observation that the topological infor-
mation represented by Acme is not sufficient to de-
rive synthesis rules for the various attributes, and con-
sists primarily in defining relationships between the
various ports of an Acme component and the various
roles of an Acme connector. To fix our ideas, we fo-
cus on functional dependencies within a component,
which represent the relationships between the ports
of a component. At a minimum, the
functional
dependency
must specify which ports are used for
input
and which ports are used for
output
. In ad-
dition, for input ports, we must specify whether the
component may proceed with data from any one of
the ports (
AllOf
) or the component needs data from
all ports before it proceeds (
AnyOf
); also, there are
cases where we may need a majority of input ports to
proceed (
MostOf
), such as in a modular redundancy
scheme (for example, we have three input ports pro-
viding duplicate information, and we proceed as soon
as two out of the three produce the same input data).
As an example, let a component C has, say five
ports, P1, P2, P3, P4, P5 and we wish to record that
P1, P2, P3 are the input ports, then, depending on
which configuration we want to represent, we write:
input(AllOf(P1,P2,P3)),
input(AnyOf(P1,P2,P3)),
input(MostOf(P1,P2,P3)).
In the latter two cases, we must also specify
whether the input ports must deliver their inputs
synchronously
or
asynchronously
. Hence we
could say, for example:
input(AllOf(asynch(P1,P2,P3)),
input(MostOf(synchro(P1,P2,P3)).
As for output ports, in case we have more than one
for a given component, we may represent two as-
pects: the degree of overlap between the data on
the various ports (
duplicate
,
exclusive
,
overlap
),
and the synchronization between the output ports
(
simultaneous
,
asavailable
). Pursuing the exam-
ple discussed above, if P4 and P5 are output ports,
then we can write, depending on the situation:
output(overlap(asavailable(P4,P5)),
output(exclusive(simultaneous(P4,P5)),
output(exclusive(asavailable(P4,P5)).
In ACME+, a functional dependency is written at the
end of a component description, after the declaration
of all the ports, or at the end of a connector descrip-
tion, after the declaration of all the roles. A declara-
tion of a
functional dependency
has the following
fields:
• a name, to identify the dependency,
• a declaration of the input relation (how input ports
are coordinated),
• a declaration of the output relation (how output
ports are coordinated),
• a declaration of relevant properties (e.g. process-
ing time for components, transmission time for
connectors, etc).
As an example, we may write:
FunDep { Name_of_functional_dependency
input (MostOf(synchro(P1,P2,P3))),
output(exclusive(asavailable(P4,P5))),
properties(processingTime=0.02,
throughput = 45,failureProbability = 0.03)}
ComputingAttributesofSoftwareArchitectures-AStaticMethodandItsValidation
57

4 A COMPILER FOR ACME+
ARCHITECTURE
We have developed a compiler for ACME+; while
programming language compilers map source code
onto executable code, our compiler maps ACME+
source code onto a set of Mathematica equations that
characterize the non functional attributes of the ar-
chitecture of interest. To this effect, we assume that:
all ports of components are labeled for
input
or for
output
(
input
ports feed data or control information
to the component, and
output
ports receive data or
control information from the component); all roles of
connectors are labeled as
origin
or as
destination
(connectors carry data or control information from
their
origin
roles to their
destination
roles); there
is a single component without input port and with a
single output port, called the
source
; there is a single
componentwithout output port and with a single input
port, called the
sink
; we assume that the
source
and
sink
components are both dummy components, that
are used solely for the purposes of our model (if the
architecture happens to have a real component with-
out input port and with a single output port, we pro-
vide it an input port and we attach a dummy source
component and a dummy connector upstream of it;
likewise for the sink component). We define an at-
tribute grammar on such architectures, as follows:
• Each port of each component has an attribute for
each property of interest (response time, through-
put, failure probability); hence each port has
three attributes, labeled RT (response time), TP
(throughput), FP (failure probability).
• Likewise, each role of each connector has an at-
tribute for each property of interest, labeled the
same way.
• The output port of the source component has triv-
ial values for all the attributes, namely:
source.inpPort.RT = 0,
source.inpPort.TP = infinity,
source.inpPort.FP = 0.
• The system inherits the attributes associated to the
input port of the sink component, namely:
System.ResponseTime = sink.outPort.RT,
System.Throughput = sink.outPort.TP,
System.FailureProbability = sink.outPort.FP.
The question that we must address now is, of course,
how do we compute the attributes of the sink from the
properties of components and connectors. We do so
by propagating attributes from the
source
to the
sink
in a stepwise manner, by considering the following
information:
• The functional dependency of each component, as
a relation between its input ports and output ports.
• The functional dependencyof each connector,as a
relation between its origin roles and its destination
roles.
• The relevant properties of each component. For
example, each component has a property called
Processing Time, that may come in handy when
we want to compute the value of the RT (response
time) attribute of its output ports as a function of
the value of the RT attribute of its input ports.
• The relevant properties of each connector. For
example, each connector has a property called
Transmission Time, that may come in handy when
we want to compute the value of the RT (response
time) attribute of its destination roles as a function
of the value of the RT attribute of its origin roles.
• Whenever a port is attached to a role, the attribute
values are passed forward from the output port to
the source role. For each attachment of the form:
C.outPort to N.originRole.
We write:
C.outPort.RT = N.originRole.RT,
C.outPort.TP = N.originRole.TP,
C.outPort.FP = N.originRole.FP.
What remains to explain now is how the attributes
are propagated from input ports to output ports
within a component and from origin roles to des-
tination roles within a connector.
Let C designates a component, whose input ports
are called inPort
1
;...;inPort
n
and output ports are
called outPort
1
;...;outPort
k
. We suppose that these
input and output ports are related with a
functional
dependency
relation R expressed as follows:
R(
Input(InSelection(InSynchronisation
(inPort1; ..; inPortn)));
Output(OutSelection(OutSynchronisation
(outPort1; ..; outPortk)));
Properties(procTime=0.7;thruPut=0.2;failProb=0.2)
)
We review in turn the three attributes of interest.
4.1 Response Time
For each output port outputP
i
expressed in the rela-
tion R, we write:
C.outPort
i
.RT = function(C.inPort1.RT;
...;C.inPort
n
.RT) +C.R. procTime.
(1)
where function depends on the construct
InSelection
, expressing the nature of the rela-
tion between input ports.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
58

If InSelection is AllOf, then function is the maxi-
mum, we write:
C.outPort
i
.RT = Max(C.inPort
1
.RT;...;C.inPort
n
.RT)
+C.R. procTime.
(2)
If InSelection is AnyOf, then function is the mini-
mum, we write:
C.outPort
i
.RT = Min(C.inPort
1
.RT;...;C.inPort
n
.RT)
+C.R. procTime.
(3)
If InSelection is MostOf, then function is the median,
we write:
C.outPort
i
.RT = Med(C.inPort
1
.RT;...;C.inPort
n
.RT)
+C.R. procTime.
(4)
4.2 Throughput
For each output port outPort
i
of the component C ex-
pressed in the relation R, we write an equation relating
the component’s throughput and inPort
i
.TP. This rule
depends on whether all of inputs are needed, or any
one of them. Consequently if InSelection is AllOf,
and since the slowest channel will impose its through-
put, keeping all others waiting, we write:
C.outPort
i
.TP = Min(C.R.thruPut;
(C.inPort
1
.TP+ ... +C.inPort
n
.TP)).
(5)
Alternatively, if InSelection is AnyOf, since the
fastest channel will impose its throughput, we write:
C.outPort
i
.TP = Max(Min[C.R.thruPut;C.inPort
1
.TP];
...;Min[C.R.thruPut;C.inPort
n
.TP]).
(6)
If InSelection is MostOf, then we write:
C.outPort
i
.TP = Min(C.R.thruPut;
(C.inPort
1
.TP+ ... +C.inPort
n
.TP) ÷ n).
(7)
4.3 Failure Probability
For each output port outPort
i
of the component C ex-
pressed in the relation R, we write an equation relating
component’s failure probability and failure probabil-
ities of its input ports. This rule depends on whether
all of inputs are needed, or any one of them. We first
consider that inPort
i
, i = 0..n, provides complemen-
tary information (InSelection is AllOf). A compu-
tation initiated at C.outPort
i
will succeed if the com-
ponent C succeeds, and all the computations initiated
at the input ports of C succeed. Assuming statistical
independence, the probability of these simultaneous
events is the product of probabilities. Hence we write:
C.outPort
i
.FP = 1−
(1− C.inPort
1
.FP× ... ×C.inPort
n
.FP)
(1− C.R.FailProb).
(8)
Second we consider that inPort
i
provide interchange-
able information (InSelection is AnyOf). A compu-
tation initiated at C.outputP
i
will succeed if compo-
nentC succeeds, and one of the computations initiated
at input ports C.inPort
i
succeeds. Whence we write:
C.outPort
i
.FP = 1− (1−C.inPort
1
.FP) × ...
×(1− C.inPort
n
.FP)(1−C.R.FailProb).
(9)
If InSelection is MostOf,then we write:
C.outPort
i
.FP = 1− (1−C.R.FailProb)×
(1− (C.inPort
1
.FP+ ... +C.inPort
n
.FP) ÷ n).
The ACME+ compiler generates all the equations that
we have discussed in this section in Mathematica for-
mat, to enable us to reason about the non functional
attributes of the overall system, as a function of the
relevant properties of its components and connectors,
its functional dependencies, and its topology.
5 SENSITIVITY ANALYSIS
Sensitivity analysis informs architects about what are
the architectural constituents that need an urgent at-
tention to be improved. So they can improve a soft-
ware architecture, test and validate it based on its
components and connectors properties, architectural
style, etc. Therefore, we developed a performance
and reliability sensitivity analysis able to help archi-
tects identify architectural components that require
changes.
5.1 Performance Sensitivity Analysis
Performance sensitivity analysis consists in identify-
ing component bottleneck that limits the system per-
formance. Hence, we have used queueing networks
laws. We present below the most important two laws
(equations 10 and 11) that we have used. A more
detailed explanation can be found in (Denning and
Buzen, 1978). Let D
i
be the total service demand on
the constituent i (component or connector). D
i
is de-
fined by :
D
i
=
X
i
X
× S
i
(10)
where X
i
and S
i
are respectively the processing time
and the throughput of constituent i. The system
ComputingAttributesofSoftwareArchitectures-AStaticMethodandItsValidation
59

throughput X verifies the following inequality:
X ≤
1
D
i
(11)
Therefore, the constituent with largest D
i
limits the
system throughput and is the bottleneck. Since in our
model, each constituentC is described by one or more
functional dependency
relations and each relation
R is characterized by a processing time, we propose
to calculate service demand D
C
R
i
of constituent C rel-
ative to each relation R
i
. D
C
R
i
is defined by:
D
C
R
i
=
(C.R
i
.thruPut×C.R
i
. procTime)
System.Throughput
(12)
The constituent having the largest value of D
C
R
i
, is the
bottleneck of the system.
5.2 Reliability Sensitivity Analysis
Reliability sensitivity analysis consists in identifying
component bottleneck that limits the system reliabil-
ity. Let’s recall that the equations generated by our
compiler will be resolved by Mathematica numeri-
cally and symbolically. The symbolic resolution is to
keep components and connectors properties unspeci-
fied and use Mathematica to produce a system prop-
erty expression based on components and connectors
properties. This form of resolution helps in analyz-
ing the sensitivity with respect to reliability. Note
that our model allows the analysis of system fail-
ure probability according to components and connec-
tors failure probabilities. To determine which compo-
nent/connector that most affects system reliability, we
calculate the derivative of the system failure probabil-
ity with respect to its components/connectors failure
probabilities. The derivative of the formula is defined
by the equation 13:
∂System.FailProb
∂C
i
.FailProb
;i = 1, 2, ..., n (13)
where C
i
is the component/connector i. The compo-
nent/connector having the highest value of the deriva-
tive is the reliability bottleneck.
6 AN AUTOMATED TOOL FOR
ARCHITECTURE ANALYSIS
We have developed an automated tool that analyzes
architectures according to the pattern discussed in this
paper. This tool uses a compiler to map the architec-
ture written in ACME+ onto Mathematica equations,
then it invokes Mathematica to analyze and solve the
resulting system of equations. The analysis process
is illustrated by figure 1. It can be observed that
our analysis tool takes as input a file containing a
given system architecture description written in our
enriched ACME+ ADL. The compiler then translates
this file into mathematical equations that characterize
the system’s non-functional attributes. Then, the tool
invokes Mathematica to compute actual values of the
system’s attributes or to highlight functional depen-
dencies between the attributes of the system and the
attributes of the system’s components and connectors.
Figure 1: Analysis process workflow.
7 EXPERIMENTS
Our work consists in analyzing quantitative non-
functional requirements that can inductively be de-
rived such as response time, throughput, failure prob-
ability, etc. In order to validate our inductive ap-
proach, we propose to analyze the Aegis system
(Allen and Garlan, 1996) using our ACME+ based
method and verify the obtained results by simulating
the system architecture.
7.1 ACME+ Analysis of Aegis System
Aegis Weapons System (Allen and Garlan, 1996) is
designed to defend a battle group against air, sur-
face and subsurface threats. These weapons are
controlled through a large number of control con-
soles, which provide a wide variety of tactical de-
cision aids to the crew. Figure 2 depicts the ba-
sic architecture of Aegis represented in AcmeStudio
(Kompanek, 1998). The system consists of seven
components: Geo
Server, Doctrine Reasoning, Doc-
trine Authoring, Track Server, Doctrine Validation,
Display
Server and Experiment Control. To this con-
figuration, we add, for the sake of illustration, two
dummy components Sink and Source and their asso-
ciated connectors.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
60

Figure 2: Aegis system architecture represented in ACME
Studio.
• ACME+ Description
Using our proposed constructs of functional
dependency, we give below examples of ACME+
descriptions. For the sake of brevity, we content
ourselves with giving ACME+ descriptions of only
two components of Aegis system. The overall
architecture description of the Aegis Weapon System
in ACME+ is available online at:
http://web.njit.edu/∼mili/AegisArch.txt.
We present ACME+ descriptions of the two compo-
nents Display
Server and Doctrine Authoring.
1. Display
Server operates in a single process (R) re-
quiring all data from its input ports to display the
results on its output port.
Component Display_Server {
Port inPort0; Port inPort1;
Port inPort2;Port inPort3;
FunDep = {R(
Input(AllOf(Synchronous(inPort0; inPort1;
inPort2; inPort3)));
Output(outPort);
Properties(procTime=1;thruPut=0.4;failProb=0.3)
)}};
2. The second example concerns the component
Doctrine Authoring which operates in a single
task (R). Its output ports send simultaneously du-
plicate information.
Component Doctrine_Authoring {
Port inPort; Port outPort0;
Port outPort1; Port outPort2; Port outPort3;
FunDep= {R(
Input(inPort);
Output(Duplicate(Simultaneous(outPort1;
outPort0;outPort2; outPort3)));
Properties(procTime= 0.7;thruPut=0.2;
failProb=0.2))}};
• Inductive Rules
The compiler generates the following Mathematica
equations for Display Server:
Within Component Display
Server. Dis-
play Server input ports are related with AllOf
relation. Then, if we refer to equation 2, we can
write:
DisplayServer.outPort.RT = Max(
DisplayServer.inPort0.RT;
DisplayServer.inPort1.RT;
DisplayServer.inPort2.RT;
DisplayServer.inPort.RT)+
DisplayServer.R1. procTime
(14)
With reference to equation 5, we can write:
DisplayServer.outPort.TP = Min(
DisplayServer.R.thruPut;
3
∑
i=0
(C.inPort
i
.TP))
(15)
With reference to equation 8, we can write:
DisplayServer.outPort.FP = 1−
(1− DisplayServer.R. failProb)×
(1−
3
∏
i=0
DisplayServer.inPort
i
.FP)
(16)
Between Display
Server and Connectors. When-
ever a component port is attached to a connector role,
the attribute values are passed forward from the out-
put port to the source role. Hence, we write:
DisplayServer.inPort0.RT = Pipe13.toRole.RT
(17)
ComputingAttributesofSoftwareArchitectures-AStaticMethodandItsValidation
61

DisplayServer.inPort1.RT = Pipe10.toRole.RT
(18)
DisplayServer.inPort2.RT = Pipe12.toRole.RT
(19)
DisplayServer.inPort3.RT = Pipe11.toRole.RT
(20)
DisplayServer.outPort.RT = Pipe14. fromRole.RT
(21)
The compiler generates the following Mathematica
equations for Doctrine Authoring :
Within Component Doctrine
Authoring. Doc-
trine
Authoring has only one input port, then the re-
sponse time of each outPort
i
, i = 0..3, is equal to the
sum of its processing time and the response time of
its input port. We write:
DoctrineAuthoring.outPort
i
.RT =
(DoctrineAuthoring.R1. procTime+
DoctrineAuthoring.inPort.RT);i = 0..3
(22)
The throughput of each outPort
i
, i = 0..3, is
equal to the minimum between its throughput and the
throughput of its input port. We write:
DoctrineAuthoring.outPort
i
.TP =
Min(DoctrineAuthoring.R.thruPut;
C.inPort.TP);i = 0..3
(23)
In order for a computation that is initiated at
DoctrineAuthoring.outPort
i
i = 0..3, to succeed,
component Doctrine Authoring has to succeed, and
the computation initiated at its input port has to suc-
ceed. Assuming statistical independence, the proba-
bility of these simultaneous events is the product of
probabilities. Hence, we write:
DoctrineAuthoring.outPort
i
.FP =
1− (1− DoctrineAuthoring.R. failProb)×
(1− DoctrineAuthoring.inPort.FP);i = 0..3
(24)
Between Doctrine
Authoring and Connectors.
Whenever a component port is attached to a connec-
tor role, the attribute values are passed forward from
the output port to the source role. Hence, we write:
DoctrineAuthoring.inPort.RT = Pipe0.toRole.RT
(25)
DoctrineAuthoring.outPort0.RT = Pipe5. fromRole.RT
(26)
DoctrineAuthoring.outPort1.RT = Pipe3. fromRole.RT
(27)
DoctrineAuthoring.outPort2.RT = Pipe6. fromRole.RT
(28)
DoctrineAuthoring.outPort3.RT = Pipe11. fromRole.RT
(29)
• System Properties
To determine the response time, the throughput and
the failure probability of the system, we use Math-
ematica to solve the system of equations derived by
the compiler taking as unknown Datasink.input.RT,
Datasink.input.TP and Datasink.input.FP respec-
tively. Figure 3 depicts the system response time, fig-
ure 4 depicts the system throughput and figure 5 de-
picts the system failure probability.
Figure 3: Aegis response time as function of its components
and connectors response time.
Figure 4: Aegis throughput as function of its components
and connectors throughput.
• Reliability Sensitivity Analysis
We propose to analyze the sensitivity of the Aegis
system relatively to the reliability. Thus, we propose
to use Mathematica to calculate the derivative of the
system failure probability with respect to the failure
probability of each one its components / connectors.
The derivative of the formula is defined by the equa-
tion 30, where C
i
represents component i.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
62
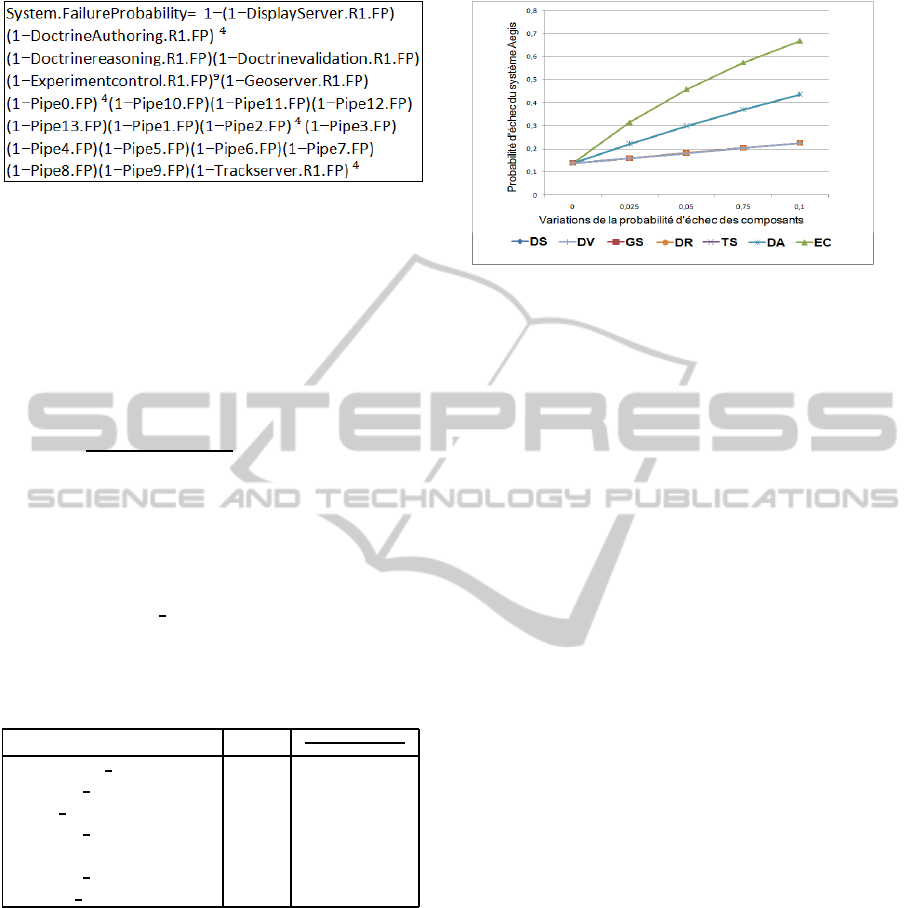
Figure 5: Aegis failure probability as function of its com-
ponents and connectors failure probability.
In this example, we assume that all connectors
have a low probability of failure equal to 0.001 and
we propose to determine the component representing
the reliability bottleneck. So, for each component of
Aegis, we calculate the derivative defined in equation
30.
∂System.FailProb
∂C
i
.FailProb
;i = 1, 2, ..., n (30)
In table 1, the components are ordered by decreas-
ing order of their derivatives values. The component
having the largest value of the derivative is the one
that most affects the reliability of the system, it is the
bottleneck of the system. More specifically, the com-
ponent Experiment
control is on the top of the list,
showing that it has an impact on the overall system
reliability.
Table 1: Reliability sensitivity analysis.
Composant C C.FP
∂System.FailProb
∂C.FP
Experiment Control(EC) 0.007 7.813
Doctrine Authoring(DA) 0.004 3.462
Track Server(TS) 0.006 3.469
Doctrine Reasoning(DR) 0.008 0.869
Geoserver(GS) 0.009 0.869
Doctrine Validation(DV) 0.005 0.866
Display Server(DS) 0.003 0.864
To check on our approach of sensitivity analysis
of Aegis system, we study the effect of variations of
components reliabilities to identify points in the ar-
chitecture where the variation has a higher impact on
the property of the whole system. Thus, we vary the
probability of failure of each component of the Aegis
system (variation of 0.025) and calculate the failure
probability of the system by keeping fixed the val-
ues of failure probability of other components. The
same variations of failure probabilities values are per-
formed for all components.
The graph in figure 6 depicts the failure proba-
bility of the overall system according to variations of
0.025 on components failure probabilities.
Figure 6: Reliability sensitivity analysis.
For the readability of the results, in the graphic’s
caption, from the left to the right, components are
ordered from the lower to the higher increase of the
impact on the overall system reliability. The graph
clearly shows that the component Experimentcontrol
has the highest impact, representing then, the bottle-
neck of the system. Hence, we note the compliance of
conclusions drawn from the graph compared to those
found by our approach.
7.2 Analysis of Aegis System by
Simulation
In order to simulate Aegis system, we have first cod-
ified the architecture of the whole system using an
(M × N) matrix which we denote by arch. M rep-
resents the number of system connectors and N is re-
ferred to the number of system components. This ma-
trix describes the links between components and con-
nectors. The intersection of a line i with a column
j in arch matrix indicates whether the connector i is
connected by its source role to the component j, is
connected by its destination role to the component j
or is not connected to this component.
Functional dependency relations (AllOf, AnyOf,
MostOf), expressing links between input ports of the
component, are also codified using relation matrix.
Each column j of the relation matrix describes which
connectors have to complete their transmissions in or-
der to let component j proceed.
In order to compare the results found by our analy-
sis tool ACME+ and those found by the simulation
method, we proceed as follows:
1. we generate random values of components and
connectors non-functional properties,
2. we use the formula found by our ACME+ analysis
tool to calculate the property of the whole system.
Let’s recall that this formula expresses the prop-
erty of the overall system based on the properties
ComputingAttributesofSoftwareArchitectures-AStaticMethodandItsValidation
63

of components and connectors,
3. we execute the simulation using the values of
components and connectors properties which are
generated in step 1,
4. we store the results found by ACME+ tool and by
simulation method,
5. Finally, we compare the obtained results.
The whole process is applied to each one of the qual-
ity attributes: response time, throughput and reliabil-
ity. It is repeated a hundred times in order to validate
our inductive reasoning.
• Response Time Simulation
To calculate the system response time by the simu-
lation method, we have used an array of structure,
which we denote by Exec. It stores for each compo-
nent and each connector respectively his ”execution
time” and his ”transmission time”, its ”state” de-
scribing the state of the component or the connec-
tor: ”waiting”, ”finished” or in ”execution”, ”time”
expressing the remaining time for the component or
connector to terminate and go to the state ”finished”.
Initially, for every element of Exec (corresponding to
a component or connector), fields ”execution time”
and ”transmission time” are initialized to correspond-
ing values randomly generated, the field ”state” is set
to ”waiting”, the value of the field ”time” is set to the
value of the execution time / transmission time of the
component / connector.
In order to simulate the performance of the Aegis
system, we start by assuming that the component
Datasource starts execution and all other components
are pending. We initialize the value of a clock to 0.
We iterate over the array of structure Exec. In each
iteration, the value of clock is incremented by 1 and
at the same time:
• the field ”time” of components and connectors in
execution are decremented by 1,
• components and connectors that have finished,
have their states changed to ”finished” ,
• check which components or connectors must be
triggered and change their states to ”execution”.
This requires consulting matrices arch and
relation to verify the links between components
and connectors.
The system response time is the value of the clock
when the states of all components and connectors are
changed to ”finished”.
• Throughput Simulation
To calculate the throughput of the system by the
method of simulation, we have used an array of
structure Exec that stores for each component / con-
nector their throughput values randomly generated,
their ”state” describing the state of the component /
connector: ”waiting”, ”finished” or in ”execution”,
”time” representing the time remaining to complete
and pass the state ”finished”, ”amount”, the amount
of information processed or communicated by the
component or the connector. The amount of an archi-
tectural element depends on the amount of informa-
tion received and on its throughput. In order to sim-
ulate the execution of the Aegis system, we start by
assuming that the component Datasource starts ex-
ecution and all other components are pending. Ini-
tially the ”amount” of each component and connector
is set to 0, the ”time” of each component is set to its
execution time and that of each connector is initial-
ized to its transmission time. Except the first compo-
nent who starts its execution, its ”amount” is set to its
throughput.
We iterate over the array of structure Exec. In each
iteration:
• ”time” of components and connectors in execu-
tion are decremented by 1,
• components and connectors that have finished,
have their states changed to ”finished”,
• check which components or connectors must be
triggered and change their states to ”execution”
and change their fields ”amount” to the amount
of data that they can treat or emit. This requires
consulting matrices arch and relation to verify the
links between components and connectors. The
”amount” of an architectural element is equal to
the minimum between the ”amount” received and
its throughput.
The system throughput will be the value of ”amount”
emitted by the last component of the architecture that
was executed.
• Failure Probability Simulation
To determine the reliability of the system by the
method of simulation, we used an array of struc-
ture that stores for each component / connector
his ”probabilityof failure”, its ”state” (”waiting”,
”finished”, ”execution”), the ”time” remaining to fin-
ish and move on to the state ”finished” and ”run”
which indicates whether the component / connector
succeeds or fails. We generate random values of com-
ponents and connectors probabilities of failure. We
also randomly determine if the architectural element
fails or succeeds the current execution, according to
its probability of failure. The overall system succeeds
or fails based on the failure or the success of its com-
ponents and connectors. We iterate over the array of
structure Exec. In each iteration:
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
64
• the field ”time” of components and connectors in
execution are decremented by 1,
• components and connectors that have finished,
have their states changed to ”finished”,
• check which components or connectors must be
triggered and change their states to ”execution”.
This requires consulting matrices arch and
relation to verify the links between components
and connectors.
• verify which components and which connectors
have succeeded or have failed and update their
corresponding values of ”run”.
The success or the failure of the overall system is de-
termined by the success or the failure of the last ex-
ecuted component. The steps already described are
repeated several times (100 or 200 times) and each
time, we determine whether the system succeeds or
fails. We then calculate the probability of failure of
the system as the quotient of the number of failures
by the total number of tests.
7.3 Comparison of Analysis Results
We have analyzed Aegis system using two ap-
proaches: simulation and ACME+ tool. We have run
many tests, in each test we generate random values
of components and connectors properties. Then, we
run our analysis tool ACME+ on these values in order
to calculate properties of the whole system. We also
run the simulation and finally, we compare the results
found by the two methods.
To visualize the difference between the obtained
results, we propose to represent the analysis results in
bar charts graphics which plot Aegis properties com-
puted by ACME+ tool and by simulation in each test.
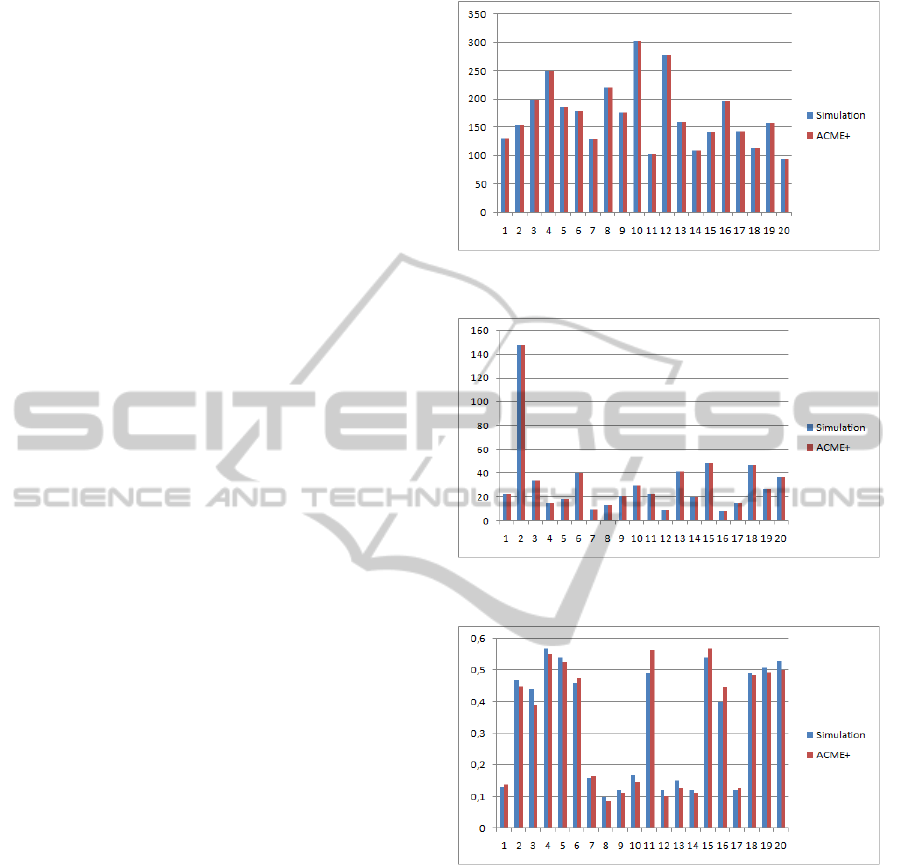
Graphics shown by figures 7, 8, 9 depicts an exam-
ple of 20 tests done to compare respectively response
time, throughput and failure probability values found
by simulation approach and by our ACME+ tool.
Figures 7, 8 show that the analysis of the Aegis
system by simulation and ACME+ tool generates
equal values of response time and throughput prop-
erties. However, figure 9, relative to failure probabil-
ity property, shows close results. Hence, these results
claim the validity of our inductive reasoning.
8 CONCLUSION
In this paper, we propose an ADL based formal
method for representing and reasoning about system
non-functional attributes at the architectural level. We
Figure 7: Aegis response time values found by simulation
and ACME+.
Figure 8: Aegis throughput values found by simulation and
ACME+.
Figure 9: Aegis failure probability values found by simula-
tion and ACME+.
aim to automatically analyze performance and reli-
ability of system architecture from performance and
reliability of its components and connectors. For
these reasons, we propose ACME+ as an extension of
Acme ADL, and discuss the development and opera-
tion of a compiler that compiles architectures written
in ACME+ ADL to generate equations that character-
ize non functional attributes of software architectures.
We then conduct a sensitivity analysis on the results,
to determine existent bottlenecks that most affect the
performance and the reliability of the system. This
will help architects to identify components and con-
nectors that need urgent attention to be improved in
order to ameliorate system quality.
ComputingAttributesofSoftwareArchitectures-AStaticMethodandItsValidation
65

Our work can be characterized by the following
attributes, which set it apart from other work on ar-
chitectural analysis.
• from a software architectural specification it is
quite simple to derive an ACME+ textual descrip-
tion thanks to its expressiveness.
• we propose to estimate the non-functional prop-
erties directly from an architectural description to
avoid problems occurred when using a mathemat-
ical models. In fact, the transformation of soft-
ware architecture to a mathematical model, im-
posed by the analytical approaches, limits their
capacities of analysis which depends on the used
model.
• our analysis approach can be applied to any sys-
tem that can be described by components and con-
nectors for any architectural style (client/server,
pipes and filters, etc.) unlike Acme-based ap-
proach, presented in (Spitznagel and Garlan,
1998), which is limited to client/server systems
analysis.
• system analysis must deal with various quality at-
tributes to enable a better understanding of the
strengths and weaknesses of complex systems
(Dobrica and Niemelae, 2002). Thus, unlike ap-
proaches found in the literature, which analyze ei-
ther performance or reliability quality attributes,
it is possible with the same ACME+ specification
of a software system to analyze both performance
and reliability. It is also possible to extend anal-
ysis to other quality attributes that can be induc-
tively derived such as availability, maintainability,
etc.
• our approach is supported by an automated tool.
The user can perform many different experi-
ments by analyzing the software architecture and
modifying the components and connectors non-
functional properties values or changing the soft-
ware topology to get better performances before
iterating the process again. It is then very easy
to perform many ”what-if” experiments, changing
parameters or structure of the model to see what
the result is.
Among the extensions we envision for this work, we
cite: the analysis of other quantitative non functional
attributes and to investigate more profoundly archi-
tecture styles and dynamic architectures.
REFERENCES
(December 2005). Wr2fdr. http://www.cs.cmu.edu/∼able/
wright/wr2fdr
bin.tar.gz.
Allen, R. and Garlan, D. (1996). A case study in architec-
tural modeling: The aegis system. In In Proceedings
of the 8th International Workshop on Software Speci-
fication and Design, pages 6–15.
Aquilani, F., Balsamo, S., and Inverardi, P. (2001). Per-
formance analysis at the software architectural design
level. Perform. Eval., 45(2-3):147–178.
Balsamo, S., Bernardo, M., and Simeoni, M. (2002). Com-
bining stochastic process algebras and queueing net-
works for software architecture analysis. In Workshop
on Software and Performance, pages 190–202.
Bass, L., Clements, P., and Kazman, R. (1998). Software
Architecture in Practice. Addison Wesley Longman
Publishing Co., Inc., Boston, MA, USA.
Bosch, J. (1999). Design and use of industrial software ar-
chitectures. In Proceedings of Technology of Object-
Oriented Languages and Systems.
Cheung, R. (1980). A user-oriented software reliability
model. IEEE Trans. on Software Engineering, 6:118–
125.
Denning, P. and Buzen, J. (1978). The operational analysis
of queueing network models. ACM Computing Sur-
veys, 10:225–261.
Dobrica, L. and Niemelae, E. (2002). A survey on software
architecture analysis methods. IEEE Transactions on
Software Engineering, 28:638–653.
Franco, J., Barbosa, R., and Rela, M. (2012). Automated re-
liability prediction from formal architectural descrip-
tions. In WICSA/ECSA, pages 302–309.
Giannakopoulou, D., Kramer, J., and Cheung, S. (1999).
Behaviour analysis of distributed systems using the
tracta approach. Journal of Automated Software Engi-
neering, 6(1):7–35.
Gokhale, S. S. (2007). Architecture-based software reliabil-
ity analysis: Overview and limitations. IEEE Trans.
Dependable Sec. Comput., 4(1):32–40.
Goseva-Popstojanova, K. and Trivedi, K. (2001).
Architecture-based approach to reliability assess-
ment of software systems. Journal of Performance
Evaluation, 45(2-3):179–204.
Kompanek, A. (1998). Acmestudio user’s manual.
Krishnamurthy, S. and Mathur, A. P. (1997). On the estima-
tion of reliability of a software system using reliabil-
ities of its components. In Proceedings of the Eighth
International Symposium on Software Reliability En-
gineering, ISSRE ’97, pages 146–155.
Kwiatkowska, M., Norman, G., and Parker, D. (2009).
Prism: Probabilistic model checking for performance
and reliability analysis. ACM SIGMETRICS Perfor-
mance Evaluation Review, 36(4):40–45.
Medvidovic, N. and Taylor, R. (2000). A classification and
comparison framework for software architecture de-
scription languages. IEEE Transactions on Software
Engineering, 11(1):70–93.
Shooman, M. (1976). Structural models for software reli-
ability prediction. In Proceedings of the 2Nd Inter-
national Conference on Software Engineering, ICSE
’76, pages 268–280.
Spitznagel, B. and Garlan, D. (1998). Architecture-based
performance analysis. In Proceedings of the 1998
Conference on Software Engineering and Knowledge
Engineering, pages 146–151.
ENASE2015-10thInternationalConferenceonEvaluationofNovelSoftwareApproachestoSoftwareEngineering
66
