Inferring Geo-spatial Neutral Similarity from Earthquake Data using

Mixture and State Clustering Models

Avi Bleiweiss

Platform Engineering Group, Intel Corporation, Santa Clara, U.S.A.

avi.bleiweiss@intel.com

Keywords:

Earthquake, Seismic, Mixture Model, Expectation-maximization, Hidden Markov Model, Clustering.

Abstract:

Traditionally, earthquake events are identiﬁed by prescribed and well formed geographical region boundaries.

However, ﬁxed regional schemes are subject to overlook seismic patterns typiﬁed by cross boundary relations

that deem essential to seismological research. Rather, we investigate a statistically driven system that clus-

ters earthquake bound places by similarity in seismic feature space, and is impartial to geo-spatial proximity

constraints. To facilitate our study, we acquired hundreds of thousands recordings of earthquake episodes that

span an extended time period of forty years, and split them into groups singled out by their corresponding

geographical places. From each collection of place afﬁliated event data, we have extracted objective seismic

features expressed in both a compact term frequency of scales format, and as a discrete signal representation

that captures magnitude samples in regular time intervals. The distribution and temporal typed feature vectors

are further applied towards our mixture model and Markov chain frameworks, respectively, to conduct cluster-

ing of shake affected locations. We performed extensive cluster analysis and classiﬁcation experiments, and

report robust results that support the intuition of geo-spatial neutral similarity.

1 INTRODUCTION

Modern seismological exploration of disseminating

earthquake sites and magnitudes rests on both the

advancement in instrumental seismometry and the

analysis of macroseismic effects, including geologi-

cal structures, population, and the landscape (Hough,

2014). To describe the severity of shaking, seismic ef-

fects are commonly assigned an intensity scale set by

different yet fairly correlated standards, traditionally

in the range of one to ten. In recent years, the develop-

ment of methods to quantitatively and objectively an-

alyze scale data, coupled with the emerging of online

systems to generate unprecedented volumes of both

real-time and archival earthquake data, had sparked

renewed interest in research to assess global seismic

intensity distribution. One indispensable resource for

practitioners in the ﬁeld is the United States Geolog-

ical Survey (USGS, 2004) science organization, fully

devoted to furnish impartial information on the health

of our ecosystem. Amongst the many services, USGS

provides a large web based repository of geo-spatially

rich data for expressing earthquake events that are dy-

namically collected as they occur, and furthermore al-

lows for this knowledge base to be programmatically

accessible for software development. Figure 1 shows

a high level, distributed earthquake scale around the

globe, based on USGS data we acquired that repro-

duces an extent of four decades, from 1975 till 2014.

In our work, we investigate a discovery (Rajara-

man and Ullman, 2011) method that extracts a statisti-

cal relation model of earthquake bound geographical

locations from a large data set of hundreds of thou-

sands of recorded seismic events, and incorporates

both information retrieval (Manning et al., 2008) and

unsupervised machine learning (Duda et al., 2001)

techniques. Information retrieval (IR) is rapidly be-

coming the dominant form of data source access.

Amongst multitude disciplines, IR encompasses the

ﬁeld of grouping a set of documents that enclose non

structured content, to behave similarly with respect

to relevance to information needs. Our work closely

leverages IR practices by realizing a seismic bound

place after a text document, composed of a collection

of intensity scales and represented in a compact his-

togram of term frequencies format. For a broader con-

text, we contrast this distribution feature form with a

classic, discrete seismic signal constructed of a series

of shake magnitudes over time that spans a course

of several tens of years. Furthermore, we are inter-

ested in uncovering objectively the underlying cluster

nature of hundreds of geographical sites, without re-

Bleiweiss A..

Inferring Geo-spatial Neutral Similarity from Earthquake Data using Mixture and State Clustering Models.

DOI: 10.5220/0005347500050016

In Proceedings of the 1st International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM-2015), pages

5-16

ISBN: 978-989-758-099-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Earthquake events: showing magnitude scale as a function of time, tracking forty years from 1975 till 2014.

sorting to any prior knowledge of the erupting phys-

ical location, nor to constraining geo-spatial proxim-

ity as prescribed by the Flinn-Engdahl regionalization

scheme (Young et al., 1995). To this extent, we use

both ﬁnite mixture (Mclachlan and Peel, 2000) and

Markov chain (Rabiner, 1989) models, recognized for

providing effective and formal statistical framework

to cluster high dimensional data of continuous nature.

Finite mixture models are widely used in the ﬁeld

of cluster analysis (Fraley and Raftery, 2002) (Fra-

ley and Raftery, 2007), and apply to a growing ap-

plication space including web content search, gene

expression linking, and image segmentation. They

form an expressive set of classes for multivariate den-

sity estimation, and the entire observed data set of

scale histograms is represented by a mixture of ei-

ther continuous or discrete, parametric distribution

functions. An individual distribution, often referred

to as a component distribution, constitutes thereof a

cluster. Traditionally, the likelihood paradigm pro-

vides a mechanism for estimating the unknown pa-

rameters of the mixture model, by deploying a method

that iterates over the maximum likelihood. One of

the more broadly used and well behaved technique

to guarantee process convergence is the Expectation-

Maximization (EM) algorithm (Dempster et al., 1977)

that scales well with increased data set size. Upon

completion, the likelihood function reﬂects the con-

formity of the model to the incomplete observed data.

While not immediately applicable to our work, note-

worthy is the research that further extends the empiri-

cal likelihood paradigm to a model, whose component

dimension is unknown. Hence, both model ﬁtting and

selection must be determined from the data simultane-

ously, by using an approximation based on any of the

Akaike Information Criterion (AIC) (Akaike, 1973),

the Bayesian Information Criterion (BIC) (Schwarz,

1978), or the sum of AIC and BIC plus an entropy

term (Ngatchou-Wandji and Bulla, 2013).

The discrete Hidden Markov Model (HMM)

(Baum and Petrie, 1966) (Rabiner, 1989) is a prob-

abilistic framework that formalizes a reasoning about

a series of observations over time, to recover a set of

states. The model is extensively used in many appli-

cation domains including speech recognition, biolog-

ical sequence analysis, and stochastic natured ﬁnan-

cial economics. HMM is described by a set of param-

eters that are estimated to maximize the probability

of an observation. Much like the mixture model, it

employs the maximum likelihood estimation princi-

pal and commonly uses the Baum-Welch algorithm

(Baum, 1972), an analog to the EM method. In our

work, we characterize a time progression of earth-

quake events, occurring in a prescribed geographi-

cal location, as a discrete seismic signal comprised of

shake scale samples. A seismic signal thus forms an

observation vector, and a collection of these temporal

feature vectors are applied to HMM, deriving for each

a log-likelihood measure. Unlike the mixture model,

the grouping of observation vectors in HMM is not

implicit, hence we follow HMM to perform hierarchi-

cal agglomerative clustering (Manning and Schutze,

2000) (Johnson, 1967) on log-likelihood values.

The main contribution of our work is a novel, sta-

tistically drivensystem that combines IR and unsuper-

vised learning techniques to discover instinctive clus-

ter patterns from presumed unlabeled seismic data,

and best match earthquake bound geographical loca-

tions by objective similarity in feature space. In con-

trast to a more constraining approach that prescribes

physical regionalization boundaries. The remainder

of this paper is organized as follows. We overview

the motivation for selecting seismic feature represen-

tations, leading to our compact formats of intensity

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement

scale distribution and a time series signal, in section

2. Section 3 reviews algorithms and provides the-

ory to multivariate cluster analysis, discussing both

the normal mixture model and Markov chain foun-

dations, and the role of their respective EM method

in estimating model parameters. Whereas in section

4, we present our evaluation methodology of seismic

cluster analysis and classiﬁcation, and report quanti-

tative results of our experiments. We conclude with a

discussion and future prospect remarks, in section 5.

2 SEISMIC FEATURES

We acquired seismic data from the USGS (USGS,

2004) science organization. USGS provides real-time

earthquake data in a well-structured format, GeoJ-

SON (GeoJSON, 2007), readily parsed by most pro-

gramming languages. GeoJSON uses the popular

JavaScript Object Notation (JSON) to encode a di-

verse set of geographic data structures. A GeoJSON

object may represent any of a geometry, a feature or a

collection of features. Typically, an earthquake event

is characterized by a geometrical bounding box and

a set of seismic features (Table 1). The three dimen-

sional volume of eruption is deﬁned by the minimum

and maximum extent of each of the longitude, lati-

tude, and depth attributes. An event speciﬁes a rather

extensive set of seismic properties, although many of

them appear either unavailable or partially missing in

the data frames we gathered. Most relevant features

to our work include the magnitude, magnitude type,

place, and time. The magnitude value is measured

and recorded by a seismograph that responds to dis-

tinct seismic waves traveling through the ground, who

are excited by relative motion of the earth. Whereas

magnitude type identiﬁes the method or algorithm to

calculate the scale of the event. Most commonly used

scales comprise of local (M

), also referred to the

Richter scale, surface-wave (M

), body-wave (M

and moment (M

) metrics. Moment scale is directly

related to the faulting process and is considered a

more consistent measure of earthquake size, unlike

the rest that are accuracy limited by an upper bound.

Nonetheless, all magnitude types yield approximately

the same value for a given earthquake event. The

place property is a named geographic location closest

to the event, either a city or a region enumerated in the

Flinn-Engdahl seismic and geographical, globe parti-

tioning scheme (Flinn-Engdahl, 2000), along with the

time of a shake occurrence, reported in milliseconds.

Our seismic dataset comprises several hundreds of

thousands earthquake events that track an extended

time period of several tens of years. The process of

extracting features from this large seismic collection

proceeds in several stages. First, we split the dataset

into groups, each embedding all event occurrences

in an identical place or region, chronologically. Our

transformed dataset represents now a compilation of

distinct places drawn out from our raw data, and totals

several thousands data points. Let P = {p

, p

, ..., p

}

be our observed, place subjected seismic data, with

each place data point, p

, retaining a different event

count. Next, we derive from each data sample, p

, two

domain feature vectors to provide for uniﬁed dimen-

sionality. An unnormalized, scale distribution vector

D ∈ N

|V|

, with |V| the number of possible magnitude

values, and a time series vector S ∈ R

of a sampling

dimensionality d.

Table 1: Features extracted from a GeoJSON object that

describes geometry and selected seismic properties of an

earthquake event. Showing for each value range and units.

(a) Bounding Box.

Dimension Range Units

longitude [−180.0

◦

, +180.0

◦

] degrees

latitude [−90.0

◦

, +90.0

◦

] degrees

depth [0, 1000] kilometer

(b) Seismic Properties.

Feature Range Units

mag [−1.0, 10.0] scale

mag type M

, M

string

place Flinn-Engdahl region string

time date-time milliseconds

D formalizes a term frequency description that as-

signs each vector element a count of unique mag-

nitude occurrences, accumulated in the events pre-

scribed to a place data point, p

. This is modeled af-

ter the bag of words (Baeza-Yates and Ribeiro-Neto,

1999) representation, a simple and one of the more ef-

fective text retrieval methods, founded on the premise

that the respective order of events to emerge in a loca-

tion, is ignored. In our work, we tend to events who

record a scale in the [4.0, 9.9] range and sampled in

0.1 increments, hence |V|, the dimensionality of D,

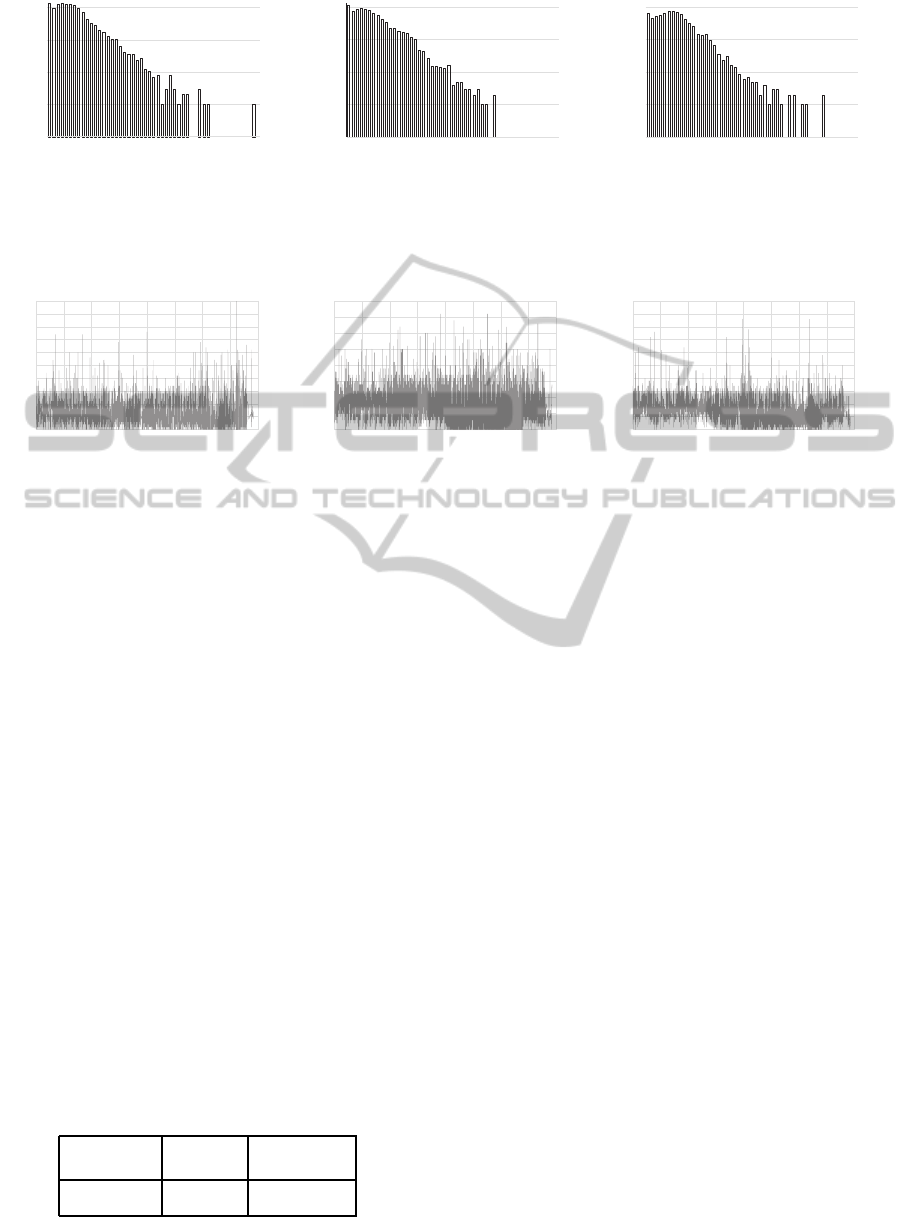
amounts to 60 elements. Figure 2 outlines scale dis-

tribution feature vectors extracted from three distinct,

place data points. The location compact format of

bag of scale words is passed on to our mixture model

to perform seismic place clustering, and follows ef-

ﬁcient similarity calculations, directly from the well

known Vector Space Model (Salton et al., 1975).

The raw, time series vector we extract is an irreg-

ular periodicity formulation of magnitudes, dispersed

InferringGeo-spatialNeutralSimilarityfromEarthquakeDatausingMixtureandStateClusteringModels

0.1

100

1000

4 4.5 5 5.5 6 6.5 7 7.5 8 8.5

Frequency

Magnitude

(a) Honshu, Japan.

0.1

100

1000

4 4.5 5 5.5 6 6.5 7 7.5 8 8.5

Frequency

Magnitude

(b) Fiji region.

0.1

100

1000

4 4.5 5 5.5 6 6.5 7 7.5 8 8.5

Frequency

Magnitude

Figure 2: Scale distribution feature vector: showing in log scale the number of magnitude occurrences extracted from events

associated with a place data point, for three geographical locations.

4.5

5.5

6.5

7.5

8.5

1975 1980 1985 1990 1995 2000 2005 2010

2015

Magnitude

Time

(a) Honshu, Japan.

4.5

5.5

6.5

7.5

1975 1980 1985 1990 1995 2000 2005 2010

2015

Magnitude

Time

(b) Fiji region.

4.5

5.5

6.5

7.5

8.5

1975 1980 1985 1990 1995 2000 2005 2010

2015

Magnitude

Time

Figure 3: Time series feature vector: resampled irregular raw signal using the year-week sampling mode, for three geograph-

ical locations. A sample of no event is assigned a zero magnitude.

sequentially along the course of our event capturing

time frame of forty years. S is then further resampled

with regular time intervals consisting of year-week,

monthly and bi-monthly formats, thus leading to a

time series feature vector of dimensionality depicted

in Table 2. Our year-week sample index, [0, 53], fol-

lows the US rule, and for a place of multiple events,

excited in the same week, we compute a weekly mean

of all magnitudes to ensure a single scale is identiﬁed

with a week. Whereas a week of no event defaults

to the value of zero intensity. The monthly and bi-

monthly sampling modes arise from a direct decima-

tion of the year-week signal by a factor of four and

eight, respectively. Time series vectors, resampled in

the year-week mode for three geographical places are

further illustrated in Figure 3. Subsequently, we use a

hidden Markov chain (HMM) to model the durational

and spectral variability of our generated seismic sig-

nal, S, that constitutes an observation vector.

Table 2: Time series vector: listing uniform resampling

modes and corresponding dimensionality.

Year-Week Monthly Bi-Monthly

2120 530 265

3 PLACE CLUSTERING

Clustering procedures based on ﬁnite mixture mod-

els provide a ﬂexible approach to multivariate statis-

tics. They become increasingly preferred over heuris-

tic methods, owing to their robust mathematical ba-

sis. Mixture models standout in admitting clus-

ters to directly identify with the components of the

model. To model our system probability distribu-

tion of scale count features, we deploy the well es-

tablished, Normal (Gaussian) Mixture Model (GMM)

(Mclachlan and Basford, 1988) (Mclachlan and Peel,

2000), known for its parametric, probability density

function that is represented as a weighted sum of

Gaussian component densities. GMM parameters are

estimated from our incomplete training data, com-

posed of bags of intensity scale words, using the

iterative Expectation-Maximization (EM) (Dempster

et al., 1977) algorithm. Correspondingly, for our

place bound, seismic signal features we exploit the

Hidden Markov Model (HMM) (Baum and Petrie,

1966) (Rabiner, 1989), using the Baum-Welch algo-

rithm (Baum, 1972) to repeatedly recalibrate model

parameters, and follow this process to construct an ag-

glomerative hierarchy of seismic aware clusters, em-

ploying an efﬁcient dynamic tree cutting technique.

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement

3.1 Normal Mixture Model

Let X = {x

, x

, ..., x

} be our observed collection of

seismic bound places, each represented as an intensity

scale, term frequency vector I ∈ N

. An additive mix-

ture model, deﬁnes a weighted sum of k components,

whose density function is formulated by equation 1:

p(x|Θ) =

∑

j=1

(x|θ

), (1)

where w

is a mixing proportion, signifying the prior

probability that an observed place x, belongs to the

mixture component, or cluster. Mixing weights,

satisfy the constraints

∑

j=1

= 1, and w

≥ 0. The

component probability density function, p

(x|θ

), is

a d-variate distribution, parameterized by θ

. Most

commonly, and throughout this work, p

(x|θ

) is the

multivariate normal (Gaussian) density (equation 2),

characterized by its mean vector µ

∈ R

and a co-

variance matrix Σ

∈ R

dxd

. Hence, θ

= (µ

, Σ

), and

the mixture parameter vector Θ = {θ

, θ

, ...., θ

(2π)

|Σ

exp(−

(x− µ

)

−1

(x− µ

)) (2)

Seismic places, distributed by mixtures of multi-

variate normal densities, are members of clusters that

are centered at their means, µ

, whereas the cluster ge-

ometric feature is determined by the covariance ma-

trix, Σ

. For efﬁcient processing, our covariance ma-

trix is diagonal, Σ

= diag(σ

, σ

, ..., σ

), and thus

clusters are of an ellipsoid shape, each nonetheless of

a distinct dimension. To ﬁt the normal mixture pa-

rameters onto a set of training feature vectors, we use

the maximum likelihood estimation (MLE) principal.

Furthermore, in regarding the set of seismic places as

forming a sequence of n independent and identically

distributed data samples, the likelihood correspond-

ing to a k-component mixture, becomes the product

of their individual probabilities:

L(Ψ|X) = Π

i=1

∑

j=1

|θ

), (3)

where Ψ = {Θ, w

, w

, ..., w

}. However, the multi-

plication of possibly thousands of fractional probabil-

ity terms, incurs an undesired numerical instability.

Therefore, by a practical convention, MLE operates

on the log-likelihood basis. As a closed form solu-

tion to the problem of maximizing the log-likelihood,

the task of deriving Ψ analytically, based on the ob-

served data X, is in many cases computationally in-

tractable. Rather, it is common to resort to the stan-

dard, expectation-maximization(EM) algorithm, con-

sidered the primary tool for model based clustering.

To add more ﬂexibility in describing the dis-

tribution P(X), the EM algorithm introduces new

independences via k-variate hidden variables Z =

, z

, ..., z

}. They mainly capture uncertainty in

cluster assignments, and are estimated in conjunction

with the rest of the parameters. The combined ob-

served and hidden portions form the complete data

set Y = (X, Z), where z

= {z

, z

, ...z

} is an unob-

served vector, with indicator elements

(

1, if x

belongs to cluster c

0, otherwise.

(4)

EM is an iterative procedure, alternating between the

expectation (E) and maximization (M) steps. For the

hidden variables z

, the E step estimates the posterior

probabilities w

that a place object x

belongs to a

mixture cluster c, given the observed data and the cur-

rent state of the model parameters

|µ

, Σ

)

∑

j=1

|µ

, Σ

)

. (5)

Then the M step maximizes the joint distribution of

both the observed and hidden data, and parameters are

ﬁtted to maximize the expected log-likelihood, based

on the conditional probabilities, w

, computed in the

E step. The E step and M step are iterated until con-

vergence or up to a set limit of iterations, after which

a scale distribution feature vector, x

, is assigned to

a cluster, corresponding to the highest conditional or

posterior probability of its membership. EM typically

performs well once the observed data reasonably con-

forms to the mixture model, and by ensuring robust

selection of random values assigned to starting pa-

rameters, the algorithm warrants convergence to ei-

ther a local maximum or a stationary value.

3.2 Hidden Markov Model

The Hidden Markov Model (HMM) (Baum and

Petrie, 1966) (Rabiner, 1989) formulates an effective

statistical framework to describe time varying pro-

cesses of physical systems. HMM is a stochastic

model of a signal that at regularly spaced time sam-

ples undergoes state transitions conforming to a set

of probabilities identiﬁed for each state. HMM mod-

els the joint probability of a collection of the random

variables O = {o

, o

, ..., o

} and Q = {q

, q

, ..., q

overtime T. O comprisesa set of discrete eventobser-

vations in a time series feature vector. An observation

takes one of M possible symbols ∈ {v

, v

, ..., v

expressed by the magnitudes ∈ {4.0, 4.1, ..., 9.9}

along with the value zero to mark a no-event element,

InferringGeo-spatialNeutralSimilarityfromEarthquakeDatausingMixtureandStateClusteringModels

thus making the vocabulary size M = 61. Q is hid-

den, with each its elements set to one of N admissi-

ble states ∈ {1, 2, ..., N}. Under the discrete Markov

chain, there are two conditional independence as-

sumptions about these random variables that make

related algorithms tractable. Namely, the t

hidden

variable only depends on the (t−1)

hidden variable,

and the t

observation solely rests on the t

state.

These hypotheses resonate well with our seismic sig-

nal, constructed of loosely coupled and independent

place events. We further assume that the underlying

hidden Markov chain, deﬁned by P(Q

t−1

), is time

homogeneous and represented as a stochastic transi-

tion matrix A = {a

} ∈ R

NxN

, where a

= P(Q

j|Q

t−1

= i). Time t = 1 is deemed a special case spec-

iﬁed by the initial state distribution π

= P(Q

= i).

Respectively, the probability of an observation sym-

bol at time t for state j is expressed by the emission

matrix B = {b

)} ∈ R

MxN

, where b

) = {P(O

= j)}. Parametrically, an HMM is compactly

represented as λ = (A, B, π), and our goal is to solve

the HMM learning problem for each of our observed,

place constructed seismic signals, by maximizing the

probability of an observation vector O, P(O|λ), and

iteratively estimating the model parameters.

Akin to the EM algorithm used for mixture

models, we adopted the Baum-Welch (BW) method

(Baum, 1972) to ﬁnd the maximum likelihood esti-

mation of the HMM parameters, for each of our gen-

erated, shake signal vectors. The method starts by

choosing arbitrary values for the model parameters.

It then proceeds to compute the forward probability,

(t), for the partial observation {o

, ..., o

} ending in

state i at time t, and the backward probability, β

(t),

for the complementary sequence {o

t+1

, ..., o

} that

started on state i, at time (t + 1). Time T is bound

to the resampling mode set for the time series vectors,

matching the sizes depicted in Table 2. Both α

(t) and

(t) are calculated efﬁciently using recursion. The

algorithm then creates two auxiliary variables: γ

(t)

(equation 6) as the probability of being in state i at

time t, normalized over the entire observed symbols

(t) =

(t)β

(t)

∑

j=1

(t)β

(t)

, (6)

and ξ

(t) (equation 7) representing the joint proba-

bility of being successively in state i at time t and in

state j at time (t + 1), normalized for the integrated

feature vector

(t) =

(t)a

(t + 1)b

t+1

)

∑

i=1

∑

j=1

(t)a

(t + 1)b

t+1

)

. (7)

From γ and ξ, the deﬁnition of intuitive update rules to

the model parameters ensues, as shown in equations

8, 9, and 10, respectively

= γ

(1), (8)

T−1

∑

t=1

(t)

T−1

∑

t=1

(t)

, (9)

(k) =

∑

t=1

(t)

∑

t=1

(t)

. (10)

In the BW algorithm, the steps of computing forward

and backward probabilities, calculating γ and ξ, and

updating model parameters, repeat ﬁnite times or until

convergenceis reached. For each of the seismic signal

vectors, the procedure returns the log-likelihood value

that we further use for hierarchical clustering.

3.3 Agglomerative Merge

Unlike a mixture model, there is no implicit clus-

tering directly derived from HMM. Therefore, the

log-likelihood values we computed for each of our

observed seismic vectors, serve as input for further

feature matching grouping. We opted for hierarchi-

cal clustering (Manning and Schutze, 2000) (John-

son, 1967) over ﬂat data structures, with the former

intended for more detailed data analysis, and found

agglomerative grouping more intuitive in our design

compared to the divisive approach. The clustering al-

gorithm starts with each individual geographicalplace

as its own cluster, and successively combines clusters

that are most similar. This process builds a tree topol-

ogy from bottom-up and is repeated until it reaches

the root node that merges all of our seismic places.

For n geographical places we compute an nxn matrix

of similarity coefﬁcients, and update the matrix as the

hierarchy is constructed. We chose the Euclidean dis-

tance as the similarity metric, and applied a subset of

the most commonly used linkage methods (Kaufman

and Rousseeuw, 1990) that determine how clusters are

merged. Similarity functions must obey monotonic-

ity to warrant the operation of merging does not in-

crease similarity, and furthermore are agnostic to the

merge order. Linking procedures along with their cor-

responding formulas are further listed in Table 3. The

single linkage measures the distance between near-

est neighbors of the combined clusters, whereas the

complete procedure evaluates the two farthest mem-

ber points. In average mode, the mean distance of all

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement

inter-group pairs is computed, and for the Ward min-

imum variance method (Ward, 1963), notably is its

tendency to join clusters with a small number of ob-

servations, and be strongly biased towards producing

clusters of roughly the same size.

Table 3: Dissimilarity formulas in merging clusters A and

B, for selected linkage methods (d - distance, c - centroid).

Linkage Method Cluster Dissimilarity

Single min

a∈A,b∈B

d[a, b]

Complete max

a∈A,b∈B

d[a, b]

Average

|A||B|

∑

a∈A

∑

b∈B

d[a, b]

Ward

2|A||B|

|A|+|B|

||c

− c

Our hierarchical clustering implementation ex-

ploits a dynamic tree cut method that expands on the

work by Langfelder et al. (Langfelder et al., 2007),

and detects a set of coherent groups, each with its cor-

related seismic features of shake affected places. We

use an adaptive branch height approach to generate

a user deﬁned, number of clusters. The algorithm re-

spects the order of merges encountered in building our

tree, and for each similarity measure it traverses the

tree in a top-down manner, until the number of clus-

ters desired becomes stable. Starting at the root node

that represents a single cluster, the search descends

the tree nodes comparing for each its similarity mea-

sure to a provided adaptive threshold. The subtrees

of a successful horizontal cut are then explored down

to their leaf nodes to extract their corresponding geo-

graphical seismic places. Agglomerative clustering is

typically visualized as a dendrogram, shown in Figure

4 for our top one hundred seismic places of the high-

est event count. The dendrogram depicted resulted

from employing the Ward linkage method, known to

form more evenly distributed clusters. Graphically,

each merge is represented by a horizontal line, and

the y coordinate of the horizontal line is the similarity

measure of the two clusters that were merged.

4 EMPIRICAL EVALUATION

To validate our system in practice, we have imple-

mented a software library that realizes the cluster

analysis of seismic places in several stages. After col-

lecting and cleaning the archived earthquake data, our

library commences with extracting both static and dy-

namic, location based feature vectors. They take the

formulationof scale distribution and temporal signals,

successively fed into our mixture and Markov chain

models, respectively. Our features are regarded as un-

labeled, and follow either an implicit or explicit clus-

tering. Constructed groups of places are then contex-

tually contrasted against a standardized, seismic re-

gionalization scheme (Flinn-Engdahl, 2000).

4.1 Experimental Setup

Our work exploits the R programming language (R,

1997) to acquire the raw earthquake data and further

clean it to serve useful in our software environment.

We have managed to retrieve from USGS a total of

326,267 recorded events occurred in a forty years

interval that started on the ﬁrst year-week of 1975

till the fourteenth year-week in 2014. Shake events

are spread across 3,247 geographical places, however

1,300 of those are affected by a single incident, and

additional 1,579 sites enumerate under 100 episodes.

To reason statistically for conducting cluster analysis,

this leaves out then 368 places of sustainable feature

vectors. Tables 4 and 5 lists top ﬁve places of highest

event count and of largest magnitudes, respectively.

Table 4: Top ﬁve places of highest seismic event count.

Place Event Count

Honshu, Japan 12293

Fiji Islands Region 8887

Kuril Islands 7584

Vanuatu Islands 6750

Tonga Islands 6064

Table 5: Top ﬁve places of highest magnitude, showing for

each statistical summarization of scale distribution.

Place Min Max Mean SD

Northen Sumatra 4 9.1 4.60 0.45

Honshu, Japan 4 9 4.61 0.44

Bio-Bio, Chile 4 8.8 4.62 0.45

Southern Sumatra 4 8.5 4.77 0.47

Southern Peru 4 8.4 4.66 0.49

The Flinn-Engdahl scheme deﬁnes 50 geo-spatial

regions and lists succinctly a total of 757 unique lo-

cations across. On the other hand, our captured event

recordings exposed dozens of afﬁliated place names

that are not registered in the standard seismic sites.

Secondly, and particularly in recent years, name de-

scriptions appear extremely verbose and embed ex-

cessive orientation information and absolute distance

in kilometers from the set location. This disparity

against the Flinn-Engdahl listings required both an

additional pass of earthquake data cleanup to tidy up

name strings, and to properly correlate the recorded

InferringGeo-spatialNeutralSimilarityfromEarthquakeDatausingMixtureandStateClusteringModels

100

0 10000 20000 30000 40000 50000

Figure 4: Agglomerative clustering dendrogram shown for the top one hundred seismic locations of the highest event count.

This process uses the Ward linkage method, known for producing a more evenly cluster distribution.

data with the standard representation, our implemen-

tation extends the source directory of Flinn-Engdahl

model by 42 sites. Thus bringing the total number of

seismic places to 789, all distributed and abide by the

originally speciﬁed, ﬁfty geographical regions.

4.2 Experimental Results

Our cluster analysis process is completely anonymous

and assumes no prior knowledge of earthquake event

locations. It solely relies on automatic feature ex-

traction from recorded data, and incorporates statis-

tical methods that facilitate the search of unsolicited

seismic patterns, to discover global relations of earth-

quake occurrences that are not necessarily bound to

geo-spatial proximity. In our software, both the num-

ber of seismic places to select from our earthquake

data and the number of generated clusters are system

level, user settable parameters. For our reported ex-

periments we use consistently the recorded data of

the top 200 geographical sites that underwent each at

least 300 seismic events, and further split the loca-

tions into 50 logical clusters. First, we derive the im-

plicit groups of geo-spatial proximity nature, by sim-

ply looking up an experimental place name from the

extended and manually constructed Flinn-Engdahl di-

rectory structure, incorporated into our software. This

distribution of places into already deﬁned regional

clusters, serves a useful comparativereference in ana-

lyzing our generic statistical approach, composed of a

mixture model, whose components directly entail the

partitions of places, and a Markov chain that follows

hierarchical clustering and a dynamic tree cutting pro-

cedure. To match the Flinn-Engdahl scheme for anal-

ysis, both the number of components and the number

of subtrees are set in our software to ﬁfty, respectively.

Figure 5: Seismic place distribution across 50 clusters: bot-

tom row is the geographically based Flinn-Engdahl model,

middle row depicts the mixture model results, and the top

row shows the Markov chain outcome. Lighter grey color

implies a higher membership place count.

Unless otherwise noted, for the Markov chain

model we apply the year-week resampling mode to

the time series, feature vector, and report agglomera-

tive clustering results using the single linkage method.

Figure 5 shows cluster distribution of seismic places

in Flinn-Engdahl, mixture model, and Markov chain

formulations. A grey stripe represents a group, and

the lighter its intensity the higher the membership

place count. In excluding empty clusters, identiﬁed

by black stripes, populated location collections total

40, 38, and 50 for our three clustering paradigms,

respectively. Our analysis experiments exploit 200

places spread across 50 relational arrays, or four

seismic sites per cluster, on average, and Table 6

provides complementary statistical summarization of

cluster place membership, emphasizing single mem-

ber groups of no association in the 1-Place column.

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement

1 5 10 15 20 25 30 35 40 45 50

Frequency

Cluster Id

Year-Week Monthly Bi-Monthly

(a) Single linkage method.

1 5 10 15 20 25 30 35 40 45 50

Frequency

Cluster Id

Year-Week Monthly Bi-Monthly

(b) Complete linkage method.

1 5 10 15 20 25 30 35 40 45 50

Frequency

Cluser Id

Year-Week Monthly Bi-Monthly

Figure 6: Place membership distribution in clusters for the Markov chain model, shown for the agglomerative single, complete,

and average linkage methods, and parameterized for each by year-week, monthly and bi-monthly resampling modes.

(a) Mixture model. (b) Markov chain.

Figure 7: Graphically visualized two cluster networks for each the mixture model and Markov chain clustering frameworks.

The Markov chain approach stands out in both ﬁnd-

ing seismic relations for at least a pair of places, and

moreover, it employs the full set of ﬁfty groups.

Figure 6 further depicts an interpretation of place

membership distribution for the Markov chain model,

reviewing the single, complete and average linking

methods, each parametrized by the seismic signal re-

sampling modes, including year-week, monthly and

bi-monthly intervals. Results pertaining to the Ward

linkage method are intentionally precluded to avoid

reporting any bias towards even place divisions. Par-

tition allocations for the complete and average link

functions appear on a fairly equal scale and show a

convincing behavior resemblance. Whereas at ﬁrst

inspection, the simple similarity method differs strik-

ingly from the rest and has three peaks that stand

apart for groups of about 20 to 30 place members.

However, in barring the outliers and rescaling the re-

maining member counts, a clear indication of equiv-

alence ensues. While the place term frequency in a

cluster varies orthogonally to any of modifying the

linkage method or the resampling mode, notably is

the strong inclusive correlation often observed across

classes generated out-of-order by different linkage

methods. Figure 7(b) shows for network node 0 a su-

per group created by the single linkage, and Figure

8 presents for that node, both the complete and aver-

age similarity methods, producing subgroups that are

fully contained in the aforementioned super class.

Table 6: Statistical measures of distributed, cluster place

membership for the three clustering paradigms. The 1-Place

column identiﬁes single member groups of no relations.

Model Min Max Med SD 1-Place

Flinn-Engdahl 0 24 2 4.48 8

Mixture Model 0 16 3 4.06 4

Markov Chain 2 24 3 4.07 0

Apart from the intuition of seismic similarity re-

sulting from geo-spatial proximity, as prescribed in

the Flinn-Engdahlmodel, we are interested in patterns

that relates places by their closeness in feature space,

for both the scale frequency and time series represen-

tations that feed into our mixture model and Markov

chain, respectively. Figure 7 shows graphically the

networks of two cluster nodes and their contextual

place descendants, for each of our clustering frame-

InferringGeo-spatialNeutralSimilarityfromEarthquakeDatausingMixtureandStateClusteringModels

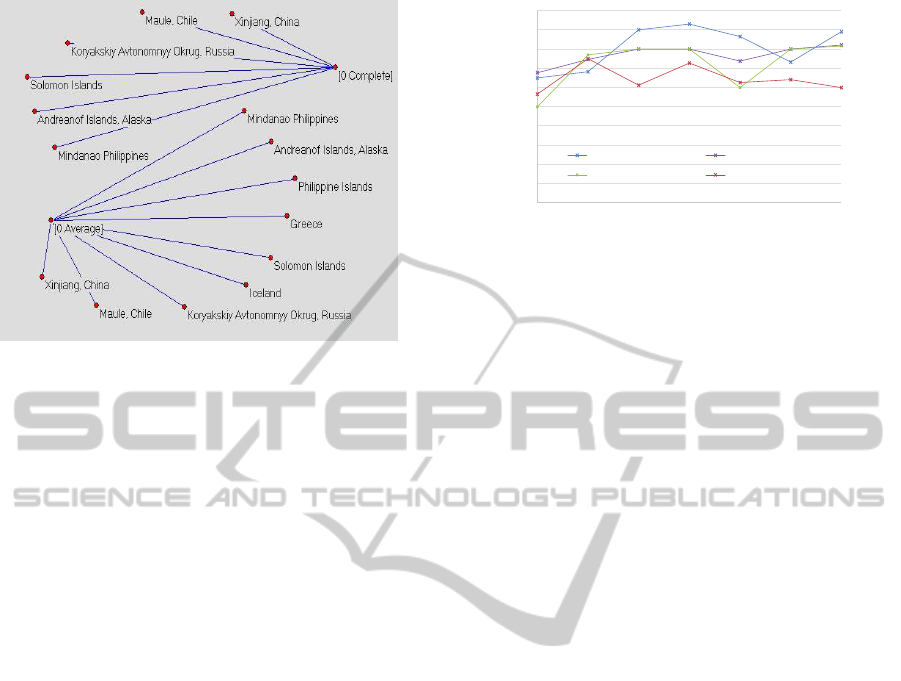
Figure 8: Graphically visualized cluster networks produced

by using complete and average linkage methods.

works. Emanating from a statistical process of group-

ing unlabeled earthquake bound locations, an imme-

diate observation of the cluster content identiﬁes seis-

mic behavior similarities in geographical places that

are both close and far apart physically. For example,

cluster id 15 (Figure 7(a)), originated in the composi-

tion of scale distribution features, incorporates Euro-

pean, African, North and South American, and Asian

countries including Iceland, Greece, Algeria, Alaska,

Mexico, and the Philippines. Similarly, cluster id

11 (Figure 7(a)) has California from North America,

Aden in Africa, Eastern Europe Russia, and Asian In-

donesia. Corollary, assemblies of time series features

(Figure 7(b)) conﬁgure sites of different continents

and show little resemblance to the Flinn-Engdahl geo-

spatial regional scheme. The discovery of unsolicited

seismic patterns promotes less dependence on a con-

straint physical partition proﬁle and encourages more

ﬂexible and autonomous ecological relations, based

on objective macroseismic effects (Hough, 2014).

Our software is ﬂexible to let the user set both

the number of quake affected places and the number

of clusters to generate, in each of the mixture model

and Markov chain formulations. Constructing groups

composed of a larger site count, enable us to perform

classiﬁcation and measure system level accuracy. For

classiﬁcation, we use a k-nearest neighbor (KNN)

(Cormen et al., 1990) baseline model that computes

a Euclidean-squared distance between a randomly se-

lected, test seismic vector against the remaining train-

ing feature vectors, in either a distribution scale or a

signal based representation. We then apply a normal-

ized majority rule to ten nearest samples to a test fea-

ture vector, and derive a seismic score. This score

is further accumulated and averaged for each cluster,

and the matching cluster corresponds to the highest

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

50 75 100 125 150 175 200

Maximum Accuracy

Places

Scale Distribution Signal, Year-Week

Signal, Monthly Signal, Bi-Monthly

Figure 9: Classiﬁcation maximum accuracy as a function

of ascending number of places, split into ﬁve clusters and

parametrized by seismic feature type.

average scoring, cluster id. Figure 9 shows classiﬁ-

cation maximum accuracy for a ﬁve-cluster partition

as a function of a non descending place count, and

parametrized by a seismic feature type. Scale distri-

bution features depict a slightly higher accuracy com-

pared to the seismic signal form, mostly ascribed to

sparseness of the latter due to samples of no seismic

action, and evidently, a coarser mode of time series

resampling results in a mild decline of accuracy rate.

To the best of our knowledge and based on lit-

erature published to date, we are unaware of seis-

mic analysis systems with similar goals to even-

handedly contrast our results against. The seismo-

surfer (Theodoridis, 2001), developed for seismic

data management and mining employs the k-means

algorithm for clustering. By specifying n geo-places

and k clusters, k-means time complexity is O (kn)

for each iteration, however the number of itera-

tions to converge can be very large. Conversely, in

our experiments both the EM and BW algorithms

ran efﬁciently well under 100 iterations to conver-

gence, along with setting the likelihood delta thresh-

old to 1e

−10

. Whereas computational complexity of

a bottom-up hierarchical clustering is O(n

logn), yet

the process terminates early once the desired num-

ber of clusters is reached. Another key architectural

difference is the localized spatio-temporal nature of

queries into the seismo-surfer database, as our design

seeks more broader shake relations that span the uni-

verse mostly unconditionally.

5 CONCLUSIONS

We have demonstrated the apparent potential in de-

ploying information retrieval and unsupervised ma-

chine learning methods, to accomplish the discov-

ery of geo-spatial free similarity of earthquake bound

places. By disregarding any prior location knowledge

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement

from presumed unlabeled seismic data, our proposed

system is generic and scalable and relies entirely on

objective closeness metrics in feature space that re-

moves dependency on a more constraining regional

scheme. For each of our distribution and signal type

feature vectors, both cluster analysis and classiﬁca-

tion results afﬁrm seismic pattern relations that cross

continent boundaries, suggesting similarity of impar-

tial macroseismic effects.

The data we acquired comprised of a large number

of hundreds of thousands earthquake events, recorded

in an extended period of time of four decades, and af-

fected a few thousands sites around the world. How-

ever, only a few hundreds of places, each bearing at

least several hundreds of shake occurrences, are sta-

tistically reasoned and pertinent to our probabilistic

system approach. Advancing the growth of the seis-

mic training set is imperative to our work and directly

affects classiﬁcation robustness. Yet using geograph-

ical locations that endured under one hundred seismic

events is a suboptimal choice for our system, giving

rise to highly sparse feature vectors. Alternatively, we

contend that by coalescing locations of a small event

count into a macro seismic site, based on geo-spatial

proximity considerations, our training collection size

is likely to increase further and proportionally let us

gain a more stable classiﬁcation process.

A direct progression of our work is to assume

no foregoing knowledge of the number of seismic

clusters to generate, and discover both the model ﬁt-

ting and the selection dimension directly from the in-

complete seismic training set, using a combination of

Akaike and Bayesian information criteria. We look

forward to further incorporate the three dimensional

geometrical data provided in a GeoJSON object, and

possibly detect seismic similarity along either a longi-

tude or a latitude extent perspective. Lastly, the ﬂex-

ibility of our software allows us to pursue a higher

level, inter-cluster network study to better understand

second order set of seismic relations.

ACKNOWLEDGEMENTS

We would like to thank the anonymous reviewers for

their insightful and helpful feedback.

REFERENCES

Akaike, H. (1973). Information theory and an extension of

the maximum likelihood principle. In International

Symposium on Information Theory, pages 267–281,

Budapest, Hungary.

Baeza-Yates, R. and Ribeiro-Neto, B., editors (1999). Mod-

ern Information Retrieval. ACM Press Series/Addison

Wesley, Essex, UK.

Baum, L. E. (1972). An inequality and associated maxi-

mization technique in statistical estimation for proba-

bilistic functions of Markov processes. In Symposium

on Inequalities, pages 1–8, Los Angeles, CA.

Baum, L. E. and Petrie, T. (1966). Statistical inference for

probabilistic functions of ﬁnite state Markov chains.

Annals of Mathematical Statistics, 37(6):1554–1563.

Cormen, T. H., Leiserson, C. H., Rivest, R. L., and

Stein, C. (1990). Introduction to Algorithms. MIT

Press/McGraw-Hill Book Company, Cambridge, MA.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the

EM algorithm. Royal Statistical Society, 39(1):1–38.

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Unsu-

pervised learning and clustering. In Pattern Classiﬁ-

cation, pages 517–601. Wiley, New York, NY.

Flinn-Engdahl (2000). Flinn-Engdahl seismic and geo-

graphic regionalization scheme. http://earthquake.

usgs.gov/learn/topics/ﬂinn

engdahl.php.

Fraley, C. and Raftery, A. E. (2002). Model-based

clustering, discriminant analysis and density estima-

tion. Journal of the American Statistical Association,

97(458):611–631.

Fraley, C. and Raftery, A. E. (2007). Bayesian regulariza-

tion for normal mixture estimation and model-based

clustering. Journal of Classiﬁcation, 24(2):155–181.

GeoJSON (2007). Geojson format for encoding geographic

data structures. http://geojson.org/.

Hough, S. E. (2014). Earthquake intensity distribution:

A new view. Bulletin of Earthquake Engineering,

12(1):135–155.

Johnson, S. C. (1967). Hierarchical clustering schemes.

Psychometrika, 32(3):241–254.

Kaufman, L. and Rousseeuw, P. J., editors (1990). Finding

Groups in Data: An Introduction to Cluster Analysis.

Wiley, New York, NY.

Langfelder, P., Zhang, B., and Horvath, S. (2007). Deﬁning

clusters from a hierarchical cluster tree: the dynamic

tree cut library for R. Bioinformatics, 24(5):719–720.

Manning, C. D., Raghavan, P., and Schutze, H. (2008). In-

troduction to Information Retrieval. Cambridge Uni-

versity Press, Cambridge, United Kingdom.

Manning, C. D. and Schutze, H., editors (2000). Founda-

tions of Statistical Natural Language Processing. MIT

Press, Cambridge, UK.

Mclachlan, G. J. and Basford, K. E. (1988). Mixture Mod-

els: Inference and Applications to Clustering. Marcel

Dekker, New York, NY.

Mclachlan, G. J. and Peel, D. (2000). Finite Mixture Mod-

els. John Wiley and Sons, New York, NY.

Ngatchou-Wandji, J. and Bulla, J. (2013). On choosing a

mixture model for clustering. Journal of Data Sci-

ence, 11(1):157–179.

R (1997). R project for statistical computing. http://

www.r-project.org/.

InferringGeo-spatialNeutralSimilarityfromEarthquakeDatausingMixtureandStateClusteringModels

Rabiner, L. R. (1989). A tutorial on hidden Markov models

and selected applications in speech recognition. Pro-

ceedings of IEEE, 77(2):257–286.

Rajaraman, R. and Ullman, J. D. (2011). Mining of Massive

Datasets. Cambridge University Press, New York,

NY.

Salton, G., Wong, A., and Yang, C. S. (1975). A vector

space model for automatic indexing. Communications

of the ACM, 18(11):613–620.

Schwarz, G. (1978). Estimating the dimension of a model.

The Annals of Statistics, 6(2):461–464.

Theodoridis, Y. (2001). SEISMO-SURFER: A prototype

for collecting, querying, and mining seismic data.

In Advances in Informatics, pages 159–171, Nicosia,

Cyprus.

USGS (2004). Real time feeds and notiﬁcations. http://

earthquake.usgs.gov/earthquakes/feed/v1.0/.

Ward, J. H. (1963). Hierarchical grouping to optimize an

objective function. American Statistical Association,

58(301):236–244.

Young, J. B., Presgrave, B. W., Aichele, H., Wiens, D. A.,

and Flinn, E. A. (1995). The Flinn-Engdahl region-

alization scheme: the 1995 revision. Physics of the

Earth and Planetary Interiors, 96(4):223–297.

GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement