
Genetic Algorithm Combined with Tabu Search in a Holonic Multiagent
Model for Flexible Job Shop Scheduling Problem
Houssem Eddine Nouri
1
, Olfa Belkahla Driss
1,2
and Khaled Gh´edira
1
1
Strat´egies d’Optimisation et Informatique intelligentE, Higher Institute of Management of Tunis, Bardo, Tunis, Tunisia
2
Higher Business School of Tunis, University of Manouba, Manouba, Tunisia
Keywords:
Scheduling, Flexible Job Shop, Genetic Algorithm, Tabu search, Holonic Multiagent.
Abstract:
The Flexible Job Shop scheduling Problem (FJSP) is an extension of the classical Job Shop scheduling Prob-
lem (JSP) presenting an additional difficulty caused by the operation assignment problem on one machine out
of a set of alternative machines. The FJSP is an NP-hard problem composed by two complementary problems,
which are the assignment and the scheduling problems. In this paper, we propose a combination of a genetic
algorithm with a tabu search in a holonic multiagent model for the FJSP. In fact, firstly, a scheduler agent ap-
plies a genetic algorithm for a global exploration of the search space. Then, secondly, a local search technique
is used by a set of cluster agents to guide the research in promising regions of the search space and to improve
the quality of the final population. To evaluate our approach, numerical tests are made based on two sets of
well known benchmark instances in the literature of the FJSP: Kacem and Brandimarte. The experimental
results show that our approach is efficient in comparison to other approaches.
1 INTRODUCTION
Scheduling is a field of investigationwhich has known
a significant growth these last years. The scheduling
problems appear in all the economic areas, from com-
puter engineering to industrial production and manu-
facturing. The Job Shop scheduling Problem (JSP),
which is among the hardest combinatorial optimiza-
tion problems (Sonmez and Baykasoglu, 1998), is a
branch of the industrial production scheduling prob-
lems. The JSP is known as one of the most popu-
lar research topics in the literature due to its potential
to dramatically decrease costs and increase through-
put (Jones and Rabelo, 1998). The Flexible Job Shop
scheduling Problem (FJSP) is an extension of the clas-
sical JSP that allows to process operations on one ma-
chine out of a set of alternative machines. Hence,
the FJSP is more computationally difficult than the
JSP. Furthermore the operation scheduling problem,
the FJSP presents an additional difficulty caused by
the operation assignment problem to a set of available
machines. This problem is known to be strongly NP-
Hard even if each job has at most three operations and
there are two machines (Garey et al., 1976).
To solve this problem, standard metaheuristic
methods are used for an approximate resolution and to
find near-optimal solutions for the FJSP with accept-
able computational time. (Brandimarte, 1993) pro-
posed a hierarchical algorithm based on Tabu Search
metaheuristic for routing and scheduling with some
known dispatching rules to solve the FJSP. (Hurink
et al., 1994) developed a Tabu Search procedure for
the job shop problem with multi-purpose machines.
(Dauz`ere-P´er`es and Paulli, 1997) presented a new
neighborhood structure for the problem, and a list of
Tabu moves was used to prevent the local search from
cycling. (Mastrolilli and Gambardella, 2000) used
Tabu Search techniques and presented two neighbor-
hood functions allowing an approximate resolution
for the FJSP. (Bozejko et al., 2010a) presented a Tabu
Search approach based on a new golf neighborhood
for the FJSP, and in the same year, (Bozejko et al.,
2010b) proposed another new model of a distributed
Tabu Search algorithm for the FJSP, using a cluster ar-
chitecture consisting of nodes equipped with the GPU
units (multi-GPU) with distributed memory. A new
version of Tabu Search algorithm with a fast Pub-
lic Critical Block neighborhood structure (TSPCB)
was proposed by (Li et al., 2011) to solve the FJSP.
For the Genetic Algorithm, it was adopted by (Chen
et al., 1999), where their chromosome representation
of solutions for the problem was divided into two
parts. The first part defined the routing policy and
the second part took the sequence of operations on
573
Nouri H., Belkahla Driss O. and Ghédira K..
Genetic Algorithm Combined with Tabu Search in a Holonic Multiagent Model for Flexible Job Shop Scheduling Problem.
DOI: 10.5220/0005348105730584
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 573-584
ISBN: 978-989-758-096-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

each machine. (Kacem et al., 2002a) used a Genetic
Algorithm with an approach of localization to solve
jointly the assignment and job shop scheduling prob-
lems with partial and total flexibility, and a second
hybridization of this evolutionary algorithm with the
fuzzy logic was presented in (Kacem et al., 2002b).
(Jia et al., 2003) proposed a modified Genetic Algo-
rithm for the FJSP, where various scheduling objec-
tives can be achieved such as minimizing makespan,
cost and weighted multiple criteria. (Ho et al., 2007)
developed a new architecture named LEarnable Ge-
netic Architecture (LEGA) for learning and evolv-
ing solutions for the FJSP, allowing to provide an
integration between evolution and learning in an ef-
ficient manner within a random search process. In
addition, other types of metaheuristics were devel-
oped in this last few years, such as (Yazdani et al.,
2010) implementing a Parallel Variable Neighbor-
hood Search (PVNS) algorithm to solve the FJSP us-
ing various neighborhood structures. A Knowledge-
Based Ant Colony Optimization (KBACO) algorithm
was presented by (Xing et al., 2010) for the FJSP.
Moreover, another branch of metaheuristic optimiza-
tion approaches appeared, by combining two or more
complementary approaches in order to create a supe-
rior solution procedure allowing to offer a more effi-
cient resolution for complex problems. That is why,
(Glover et al., 1995) elaborated a study about the na-
ture of connectionsbetween the genetic algorithm and
tabu search metaheuristics, searching to show the ex-
isting opportunities for creating a hybrid approach
with these two standard methods to take advantage
of their complementary features and to solve difficult
optimization problems. After this pertinent study, the
combination of these two metaheuristics has become
more well-known in the literature and is used to solve
many complex problems, such as the FJSP. An im-
proved genetic algorithm combined with local search
is proposed by (Zhang et al., 2008) to solve the FJSP.
In fact, this combination introduced a time-varying
the crossover probability for the genetic algorithm
and a time-varying maximum step size for the tabu
search, allowing to control the local search process
and the convergence to the global optimal solution.
After two years, (Zhang et al., 2010) presented a sec-
ond combined proposition of genetic algorithm with
tabu search to solve the multi-objective FJSP. They
adopted an additional external memory to save and
update the non-dominated solutions during the opti-
mization process. (Gao et al., 2008) adapted a hybrid
Genetic Algorithm (GA) and a Variable Neighbor-
hood Descent (VND) for FJSP. The GA used two vec-
tors to represent a solution and the disjunctive graph
to calculate it. Then, a VND was applied to improve
the GA final individuals. (Thamilselvan and Balasub-
ramanie, 2009) developeda new algorithm integrating
Genetic Algorithm and Tabu Search methods to solve
the JSP. The proposed algorithm is based on the net-
work central-clients node architecture inspired from
(Andresen et al., 2002), where the genetic algorithm
is run on a central node to generate n initial solutions,
to be used by n client nodes as a starting solution
for the Tabu Search algorithm. (Zhang et al., 2014)
proposed a model of low-carbon scheduling in the
FJSP considering three factors, the makespan, the ma-
chine workload for production and the carbon emis-
sion for the environmental influence. A metaheuristic
hybridization algorithm was proposed combining the
original Non-dominated Sorting Genetic Algorithm II
(NSGA-II) with a Local Search algorithm based on a
neighborhood search technique. Moreover, the Par-
ticle Swarm Optimization was implemented by (Xia
and Wu, 2005) in a metaheuristic hybridization ap-
proach with the Simulated Annealing for the multi-
objective FJSP. A combined Particle Swarm Opti-
mization and a Tabu Search algorithm were proposed
by (Zhang et al., 2009) to solve the multi-objective
FJSP. (Moslehi and Mahnam, 2011) presented a meta-
heuristic approach based on a hybridization of the
Particle Swarm Optimization and Local Search algo-
rithm to solve the multi-objective FJSP. Furthermore,
a new heuristic was developed by (Ziaee, 2014) for
the FJSP. This heuristic is based on a constructivepro-
cedure considering simultaneously many factors hav-
ing a great effect on the solution quality. Furthermore,
distributed artificial intelligence techniques were used
for this problem, such as the multiagent model pro-
posed by (Ennigrou and Gh´edira, 2004) composed by
three classes of agents, job agents, resource agents
and an interface agent. This model is based on a lo-
cal search method which is the tabu search to solve
the FJSP. Also, this model was improved in (Enni-
grou and Gh´edira, 2008) where the optimization role
of the interface agent was distributed among the re-
source agents. Similarly, (Azzouz et al., 2012) de-
veloped a combination of a tabu search and a ge-
netic algorithm based on a multiagent system to solve
the FJSP. This approach used two classes of agents,
a first class grouping resource agents responsible of
processing a local optimization technique based on
the tabu search of (Ennigrou and Gh´edira, 2008) and
a second class containing an interface agent responsi-
ble of processing a global optimization by a genetic
algorithm. (Henchiri and Ennigrou, 2013) proposed
a multiagent model based on a hybridization of two
metaheuristics, a local optimization process using the
tabu search to get a good exploitation of the good ar-
eas and a global optimization process integrating the
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
574

Particle Swarm Optimization (PSO) to diversify the
search towards unexplored areas.
In this paper, we present a combination of a ge-
netic algorithm with a tabu search in a holonic multi-
agent model for the flexible job shop scheduling prob-
lem. This new combined approach follows two prin-
cipal steps. In the first step, a scheduler agent ap-
plies a genetic algorithm for a global exploration of
the search space. Then, in the second step, a local
search technique is used by a set of cluster agents to
improve the quality of the final population. Numer-
ical tests were made to evaluate the performance of
our approach based on two data sets of (Kacem et al.,
2002b) and (Brandimarte, 1993) for the FJSP, where
the experimental results show its efficiency in com-
parison to other approaches.
The rest of the paper is organized as follows. In
section 2, we define the formulation of the FJSP with
its objective function and a simple problem instance.
Then, in section 3, we detail the proposed combined
approach with its holonic multiagent levels. The ex-
perimental and comparison results are provided in
section 4. Finally, section 5 rounds up the paper with
a conclusion.
2 PROBLEM FORMULATION
The flexible job shop scheduling problem (FJSP)
could be formulated as follows. There is a set of n
jobs J = {J
1
,...,J
n
} to be processed on a set of m
machines M = {M
1
,...,M
m
}. Each job J
i
is formed
by a sequence of n
i
operations {O
i,1
,O
i,2
,...,O
i,ni
}
to be performed successively according to the given
sequence. For each operation O
i, j
, there is a set of al-
ternative machines M(O
i, j
) capable of performing it.
The main objective of this problem is to find a sched-
ule minimizing the end date of the last operation of
the jobs set which is the makespan. The makespan
is defined by Cmax in equation (1), where C
i
is the
completion time of a job J
i
.
Cmax = max
1≤i≤n
(C
i
) (1)
The FJSP scheduling problem is divided in two
sub-problems:
• The operations assignment sub-problem that as-
signs each operation to an appropriate machine.
• The operations sequencing sub-problem that de-
termines a sequence of operations on all the ma-
chines.
Furthermore, the adopted hypotheses in this prob-
lem are:
• All the machines are available at time zero;
• All jobs are ready for processing at time zero;
• The order of operations for each job is predefined
and cannot be modified;
• There are no precedence constraints among oper-
ations of different jobs;
• The processing time of operations on each ma-
chine is defined in advance;
• Each machine can process only one operation at a
time;
• Operations belonging to different jobs can be pro-
cessed in parallel;
• Each job could be processed more than once on
the same machine;
• The interruption during the process of an opera-
tion on a machine is negligible.
To explain the FJSP, a sample problem of three
jobs and five machines is shown in table 1, where the
numbers present the processing times and the tags “–
” mean that the operation cannot be executed on the
corresponding machine.
Table 1: A simple instance of the FJSP.
Job Operation M
1
M
2
M
3
M
4
M
5
J
1
O
1,1
2 9 4 5 1
O
1,2
– 6 – 4 –
J
2
O
2,1
1 – 5 – 6
O
2,2
3 8 6 – –
O
2,3
– 5 9 3 9
J
3
O
3,1
– 6 6 – –
O
3,2
3 – – 5 4
3 GENETIC ALGORITHM
COMBINED WITH TABU
SEARCH IN A HOLONIC
MULTIAGENT MODEL
(Glover et al., 1995) elaborated a study about the na-
ture of connections between the genetic algorithm and
tabu search metaheuristics, searching to show the ex-
isting opportunities for creating a hybrid approach
with these two standard methods to take advantage
of their complementary features and to solve diffi-
cult optimization problems. After this pertinent study,
the combination of these two metaheuristics has be-
come more well-known in the literature, which has
motivated many researchers to try the hybridization
of these two methods for the resolution of different
complex problems in several areas.
(Ferber, 1999) defined a multiagent system as an
GeneticAlgorithmCombinedwithTabuSearchinaHolonicMultiagentModelforFlexibleJobShopSchedulingProblem
575
artificial system composed of a population of au-
tonomous agents, which cooperate with each other to
reach common objectives, while simultaneously each
agent pursues individual objectives. Furthermore, a
multiagent system is a computational system where
two or more agents interact (cooperate or compete, or
a combination of them) to achieve some individual or
collectivegoals. The achievementof these goals is be-
yond the individual capabilities and individual knowl-
edge of each agent (Botti and Giret, 2008).
(Koestler, 1967) gave the first definition of the
term “holon” in the literature, by combining the two
Greek words “hol” meaning whole and “on” meaning
particle or part. He said that almost everything is both
a whole and a part at the same time. In fact, a holon
is recursively decomposed at a lower granularity level
into a community of other holons to produce a hol-
archy (Calabrese, 2011). Moreover, a holon may be
viewed as a sort of recursive agent, which is a super-
agent composed by a sub-agents set, where each sub-
agent has its own behavior as a complementary part
of the whole behaviour of the super-agent. Holons
are agents able to show an architectural recursiveness
(Giret and Botti, 2004).
In this work, we propose a combined metaheuris-
tic approach processing two general steps: a first step
of global exploration using a genetic algorithm to find
promising areas in the search space and a clustering
operator allowing to regroup them in a set of clusters.
In the second step, a tabu search algorithm is applied
to find the best individual solution for each cluster.
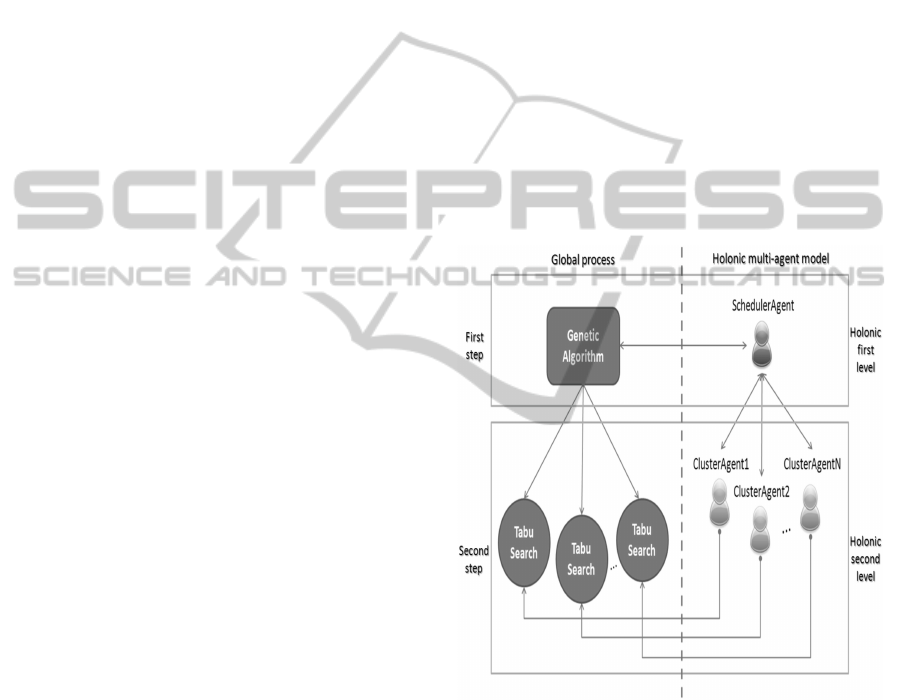
The global process of the proposed approach is imple-
mented in a two hierarchical holonic levels adopted
by a recursive multiagent model, named Genetic Al-
gorithm combined with Tabu Search in a Holonic
Multiagent model (GATS+HM), see figure 1. The
first holonic level is composed by a Scheduler Agent
which is the Master/Super-agent, preparing the best
promising regions of the search space, and the sec-
ond holonic level containing a set of Cluster Agents
which are the Workers/Sub-agents, guiding the search
to the global optimum solution of the problem. Each
holonic level of this model is responsible to process a
step of the hybrid metaheuristic algorithm and to co-
operate between them to attain the global solution of
the problem.
In fact, the choice of this new metaheuristic com-
bination is justified by that the standard metaheuristic
methods use generally the diversification techniques
to generate and to improve many different solutions
distributed in the search space, or by using local
search techniques to generate a more improved set of
neighbourhood solutions from an initial solution. But
they did not guarantee to attain promising areas with
good fitness convergingto the global optimum despite
the repetition of many iterations, that is why they need
to be more optimized. So, the novelty of our approach
is to launch a genetic algorithm based on a diversifica-
tion technique to only explore the search space and to
select the best promising regions by the clustering op-
erator. Then, applying the intensification technique of
the tabu search allowing to relaunch the search from
an elite solution of each cluster autonomously to at-
tain more dominant solutions of the search space.
The use of a multiagent system gives the opportu-
nity for distributed and parallel treatments which are
very complimentary for the second step of the pro-
posed approach. Indeed, our combined metaheuris-
tic approach follows the paradigm of “Master” and
“Workers” which are two recursive hierarchical lev-
els adaptable for a holonic multiagent model, where
the Scheduler Agent is the Master/Super-agent of its
society and the Cluster Agents are its Workers/Sub-
agents.
Figure 1: Genetic algorithm combined with tabu search in a
holonic multiagent model.
3.1 Scheduler Agent
The Scheduler Agent (SA) is responsible to process
the first step of the hybrid algorithm by using a genetic
algorithm called NGA (Neighborhood-based Genetic
Algorithm) to identify areas with high average fitness
in the search space. In fact, the goal of using the NGA
is only to explore the search space, but not to find
the global solution of the problem. Then, a clustering
operator is integrated to divide the best identified ar-
eas by the NGA in the search space to different parts
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
576

where each part is a cluster CL
i
∈ CL the set of clus-
ters, where CL = {CL
1
,CL
2
,...,CL
N
}. In addition,
this agent plays the role of an interface between the
user and the system (initial parameter inputs and final
result outputs). According to the number of clusters N
obtained after the integration of the clustering opera-
tor, the SA creates N Cluster Agents (CAs) preparing
the passage to the next step of the global algorithm.
After that, the SA remains in a waiting state until the
reception of the best solutions found by the CA for
each cluster. Finally, it finishes the process by dis-
playing the final solution of the problem.
3.1.1 Individual’s Solution Presentation
The flexible job shop problem is composed by two
sub-problems: the machine assignment problem and
the operation scheduling problem, that is why the
chromosome representation is encoded in two parts:
Machine Assignment part (MA) and Operation Se-
quence part (OS).
Figure 2: The chromosome representation of a scheduling
solution.
The first part MA is a vector V
1
with a length
L equal to the total number of operation and where
each index represents the selected machine to pro-
cess an operation indicated at position p, see fig-
ure 2 (a). For example p = 2, V
1
(2) is the se-
lected machine M
4
for the operation O
1,2
. The sec-
ond part OS is a vector V
2
having the same length
of V
1
and where each index represents an operation
O
i, j
according to the predefined operations of the
job set, see figure 2 (b). For example the opera-
tion sequence 1 − 2− 1 − 3 − 2 − 3− 2 can be trans-
lated to: (O
1,1
,M
5
) → (O
2,1
,M
1
) → (O
1,2
,M
4
) →
(O
3,1
,M
3
) → (O
2,2
,M
3
) → (O
3,2
,M
1
) → (O
2,3
,M
2
).
To convert the chromosome values to an active
schedule, we used the priority-based decoding of
(Gao et al., 2008). This method considers the idle
time which may exist between operations on a ma-
chine m, and which is caused by the precedence con-
straints of operations belonging to the same job i. Let
S
i, j
is the starting time of an operation O
i, j
(which
can only be started after processing its precedent op-
eration O
i,( j−1)
) with its completion time C
i, j
. In ad-
dition, we have an execution time interval [t
S
m
,t
E
m
]
starts form t
S
m
and ends at t
E
m
on a machine m to al-
locate an operation O
i, j
. So, if j = 1, S
i, j
takes t
S
m
,
else if j ≥ 2, it takes max{t
S
m
,C
i,( j−1)
}. In fact, the
availability of the time interval [t
S
m
,t
E
m
] for an oper-
ation O
i, j
is validated by verifying if there is a suffi-
cient time period to complete the execution time p
ijm
of this operation, see equation (2):
if j = 1,t
S
m
+ p
ijm
≤ t
E
m
(2)
if j ≥ 2, max{t
S
m
,C
i,( j−1)
} + p
ijm
≤ t
E
m
The used priority-based decoding method allows
in each case to assign each operation to its reserved
machine following the presented execution order of
the operation sequence vector V
2
. Also, to schedule
an operation O
i, j
on a machine m, the fixed idle time
intervals of the selected machine are verified to find
an allowed available period to its execution. So, if a
period is found, the operation O
i, j
is executed there,
else it is moved to be executed at the end of the ma-
chine m.
Noting that the chromosome fitness is calculated
by Fitness(i) which is the fitness function of each
chromosome i and Cmax(i) is its makespan value,
where i ∈ {1,...,P} and P is the total population size,
see equation (3).
Fitness(i) =
1
Cmax(i)
(3)
3.1.2 Population Initialization
The initial population is generated randomly follow-
ing a uniform law and based on a neighborhood pa-
rameter to make the individual solutions more diver-
sified and distributed in the search space. In fact, each
new solution should have a predefined distance with
all the other solutions to be considered as a new mem-
ber of the initial solution. The used method to deter-
minate the neighborhood parameter is inspired from
GeneticAlgorithmCombinedwithTabuSearchinaHolonicMultiagentModelforFlexibleJobShopSchedulingProblem
577

(Bozejko et al., 2010a), which is based on the per-
mutation level of operations to obtain the distance be-
tween two solutions. In fact, the dissimilarity distance
is calculated by verifying the difference between two
chromosomes in terms of the placement of each op-
eration O
i, j
on its alternative machine set in the ma-
chine assignment vector V
1
and its execution order in
the operation sequence vector V
2
. So, if there is a dif-
ference in the vector V
1
, the distance is incremented
by M(O
i, j
) (is the number of possible n placement
for each operation on its machine set, which is the
alternative machine number of each operation O
i, j
)
because it is in the order of O(n). Then, if there
is a difference in the vector V
2
, the distance is in-
cremented by 1 because it is in the order of O(1).
Let Chrom1(MA
1
,OS
1
) and Chrom2(MA
2
,OS
2
) two
chromosomes of two different scheduling solutions,
M(O
i, j
) the alternative number of machines of each
operation O
i, j
, L is the total number of operations of
all jobs and Dist is the dissimilarity distance. The
distance is calculated firstly by measuring the differ-
ence between the machine assignment vectors MA
1
and MA
2
which is in order of O(n), then by verify-
ing the execution order difference of the operation
sequence vectors OS
1
and OS
2
which is in order of
O(1), we give here how to proceed:
Noting that Distmax is the maximal dissimilar-
ity distance and it is calculated by equation (4), rep-
resenting 100% of difference between two chromo-
somes.
Distmax =
i,ni
∑
i,1
[M(Oi, j)] + L (4)
3.1.3 Selection Operator
The selection operator is used to select the best par-
ent individuals to prepare them to the crossover step.
This operator is based on a fitness parameter allow-
ing to analyze the quality of each selected solution.
But progressively the fitness values will be similar
for the most individuals. That is why, we integrate
the neighborhoodparameter, where we propose a new
combined parent selection operator named Fitness-
Neighborhood Selection Operator (FNSO) allowing
to add the dissimilarity distance criteria to the fitness
parameter to select the best parents for the crossover
step. The FNSO chooses in each iteration two parent
individuals until engaging all the population to cre-
ate the next generation. The first parent takes succes-
sively in each case a solution i, where i ∈ {1, . . . , P}
and P is the total population size. The second par-
ent obtains its solution j randomly by the roulette
wheel selection method based on the two Fitness and
Neighborhood parameters relative to the selected first
parent, where j ∈ {1,...,P} \ {i} in the P population
and where j 6= i. In fact, to use this random method,
we should calculate the Fitness-Neighborhood total
FN for the population, see equation (5), the selec-
tion probability sp
k
for each individual I
k
, see equa-
tion (6), and the cumulative probability cp
k
, see equa-
tion (7). After that, a random number r will be gener-
ated from the uniform range [0,1]. If r ≤ cp
1
then the
second parent takes the first individual I
1
, else it gets
the k
th
individual I
k
∈ {I
2
,...,I
P
} \ {I
i
} and where
cp
k−1
< r ≤ cp
k
.
• The Fitness-Neighborhood total for the popula-
tion:
FN =
P
∑
k=1
[1/(Cmax[k] × Neighborhood[i][k])]
(5)
• The selection probability sp
k
for each individual
I
k
:
sp
k
=
1/(Cmax[k] × Neighborhood[i][k])
FN
(6)
• The cumulative probability cp
k
for each individ-
ual I
k
:
cp
k
=
k
∑
h=1
sp
h
(7)
=⇒ For equations (5), (6) and (7), k =
{1,2, . . . , P} \ { i}
3.1.4 Crossover Operator
The crossover operator has an important role in the
global process, allowing to combine in each case the
chromosomes of two parents in order to obtain new
individuals and to attain new better parts in the search
space. In this work, this operator is applied with
two different techniques successively for the parent’s
chromosome vectors MA and OS.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
578

Machine Vector Crossover. A uniform crossover
is used to generate in each case a mixed vector
between two machine vector parents, Parent1-MA1
and Parent2-MA2, allowing to obtain two new chil-
dren, Child1-MA1
′
and Child2-MA2
′
. This uniform
crossover is based on two assignment cases, if the
generated number is less than 0.5, the first child gets
the current machine value of parent1 and the second
child takes the current machine value of parent2. Else,
the two children change their assignment direction,
first child to parent2 and the second child to parent1.
Operation Vector Crossover. An improved prece-
dence preserving order-based on crossover (iPOX),
inspired from (Lee et al., 1998), is adapted for the
parent operation vector OS. This iPOX operator is ap-
plied following four steps, a first step is selecting two
parent operation vectors (OS
1
and OS
2
) and generat-
ing randomly two job sub-sets Js
1
/Js
2
from all jobs.
A second step is allowing to copy any element in
OS
1
/OS
2
that belong to Js
1
/Js
2
into child individual
OS
′
1
/OS
′
2
and retain them in the same position. Then
the third step deletes the elements that are already in
the sub-set Js
1
/Js
2
from OS
1
/OS
2
. Finally, fill orderly
the empty position in OS
′
1
/OS
′
2
with the reminder ele-
ments of OS2/OS1 in the fourth step, see the example
in the figure 3.
Figure 3: An iPOX crossover example.
3.1.5 Mutation Operator
The mutation operator is integrated to promote the
children generation diversity. In fact, this operator is
applied on the chromosome of the new children gen-
erated by the crossover operation. Also, each part of a
child chromosome MA and OS has separately its own
mutation technique.
Machine Vector Mutation. This first operator uses
a random selection of an index from the machine vec-
tor MA. Then, it replaces the machine number in the
selected index by another belonging to the same alter-
native machine set, see figure 4.
Figure 4: A machine vector mutation example.
Operation Vector Mutation. This second operator
selects randomly two indexes index1 and index2 from
the operation vector OS. Next, it changes the position
of the job number in the index1 to the second index2
and inversely.
3.1.6 Replacement Operator
The replacement operator has an important role to
prepare the remaining surviving population to be con-
sidered for the next iterations. This operator replaces
in each case a parent by one of its children which has
the best fitness in its current family.
Figure 5: The final population transformation by applying
the clustering operator.
3.1.7 Clustering Operator
By finishing the last iteration of the genetic algorithm,
the Scheduler Agent applies a clustering operator us-
ing the hierarchical clustering algorithm of (Johnson,
GeneticAlgorithmCombinedwithTabuSearchinaHolonicMultiagentModelforFlexibleJobShopSchedulingProblem
579

1967) to divide the final population into N Clusters,
see figure 5, to be treated by the Cluster Agents in
the second step of the global process. The clustering
operator is based on the neighbourhood parameter
which is the dissimilarity distance between individu-
als. The clustering operator starts by assigning each
individual Indiv(i) to a cluster CL
i
, so if we have P
individuals, we have now P clusters containing just
one individual in each of them. For each case, we
fixe an individual Indiv(i) and we verify successively
for each next individual Indiv( j) from the remaining
population (where i and j ∈ {1,...,P},i 6= j) if the
dissimilarity distance Dist between Indiv(i) and
Indiv( j) is less than or equal to a fixed threshold
Dist fix (representing a percentage of difference X%
relatively to Distmax, see equation (8)) and where
Cluster(Indiv(i)) 6= Cluster(Indiv( j)). If it is the
case, Merge(Cluster(Indiv(i)),Cluster(Indiv( j))),
else continue the search for new combination with
the remaining individuals. The stopping condition is
by browsing all the population individuals, where we
obtained at the end N Clusters.
Dist fix = Distmax× X% (8)
Figure 6: Distribution of the Cluster Agents in the different
clusters of the search space.
3.2 Cluster Agents
Each Cluster Agent CA
i
is responsible to apply suc-
cessively to each cluster CL
i
a local search technique
which is the Tabu Search algorithm to guide the re-
search in promising regions of the search space and to
improve the quality of the final population of the ge-
netic algorithm. In fact, this local search is executed
simultaneously by the set of the CAs agents, where
each CA starts the research from an elite solution of
its cluster searching to attain new more dominant in-
dividual solutions separately in its assigned cluster
CL
i
, see figure 6. The used Tabu Search algorithm is
based on an intensification technique allowing to start
the research from an elite solution in a cluster CL
i
(a
promising part in the search space) in order to collect
new scheduling sequence minimizing the makespan.
Let E the elite solution of a cluster CL
i
, E
′
∈ N(E) is
a neighbor of the elite solution E, each CL
i
plays the
role of the tabu list with a dynamic length and Cmax
is the makespan of the obtained solution. So, this al-
gorithm applies in each case two steps, a move and
insert first step inspired from (Mastrolilli and Gam-
bardella, 2000) to generate new scheduling combina-
tion and a second step to save the best found solution
in the tabu list (which is CL
i
) after each generation
case. The stopping condition is by attaining the max-
imum allowed number of neighbors for a solution E
without improvement. We give here how to proceed:
By finishing this local search step, the CAs agents
terminate the process by sending their last best solu-
tions to the SA agent.
4 EXPERIMENTAL RESULTS
4.1 Experimental Setup
The proposed GATS+HM is implemented in java lan-
guage on a 2.10 GHz Intel Core 2 Duo processor and 3
Gb of RAM memory, where we use the IntegratedDe-
velopment Environment (IDE) eclipse to code the al-
gorithm and the multiagent platform Jade (Bellifem-
ine et al., 1999) to create the different agents of our
holonic model. To evaluate its efficiency, numerical
tests are made based on two sets of well known bench-
mark instances in the literature of the FJSP:
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
580

Table 2: Results of the Kacem instances (part 1).
Instance
Problem
n× m
AL+CGA (2002) LEGA (2007) KBACO (2010)
MOPSO+LS
(2011)
Best
Dev
(%)
Best
Dev
(%)
Best
Dev
(%)
Best
Dev
(%)
case 1 4×5 16 13,250 11 0 11 0 16 31,25
case 2 8×8 15 6,666 N/A – 14 0 14 0
case 3 10×7 15 26,666 11 0 11 0 15 26,666
case 4 10×10 7 0 7 0 7 0 7 0
case 5 15×10 23 52,173 12 8,333 11 0 11 0
Table 3: Results of the Kacem instances (part 2).
Instance
Problem
n× m
Hybrid NSGA-II
(2014) Heuristic (2014) GATS+HM
Best
Dev
(%) Best
Dev
(%) Best
Avg
Cmax
Avg CPU
(in seconds)
case 1 4×5 11 0 11 0 11 11,00 0,05
case 2 8×8 15 6,666 15 6,666 14 14,20 0,36
case 3 10×7 N/A – 13 15,384 11 11,40 0,72
case 4 10×10 7 0 7 0 7 7,60 1,51
case 5 15×10 11 0 12 8,333 11 11,60 29,71
• Kacem Data (Kacem et al., 2002b): The data set
consists of 5 problems considering a number of
jobs ranging from 4 to 15 with a number of op-
erations for each job ranging from 2 to 4, and a
number of operations for all jobs ranges from 12
to 56, which will be processed on a number of
machines ranging from 5 to 10.
• Brandimarte Data (Brandimarte, 1993): The data
set consists of 10 problems considering a number
of jobs ranging from 10 to 20 with a number of
operations for each job ranging from 5 to 15, and
a number of operations for all jobs ranges from
55 to 240, which will be processed on a number
of machines ranging from 4 to 15.
Due to the non-deterministic nature of the pro-
posed algorithm, we run it five independent times for
each case of the two data instances in order to ob-
tain significant results. The computational results are
presented by four metrics such as the best makespan
(Best), the average of makespan (Avg Cmax), the av-
erage of CPU time in seconds (Avg CPU), and the
standard deviation of makespan (Dev %) which is cal-
culated by equation (9). The Mko is the makespan
obtained by Our algorithm and Mkc is the makespan
of an algorithm that we chose to Compare to.
Dev = [(Mkc− Mko)/Mkc] × 100% (9)
The used parameter settings for our algorithm are
adjusted experimentally and presented as follow:
• Crossover probability 1.0
• Mutation probability 1.0
• Maximum number of iterations 1000
• The population size ranged from 15 to 300 de-
pending on the complexity of the problem.
4.2 Experimental Comparisons
To show the efficiency of our GATS+HM algorithm,
we compare its obtained results from the two previ-
ously cited data sets with other well known algorithms
in the literature of the FJSP. The chosen algorithms
are the TS of (Brandimarte, 1993), the AL+CGA of
(Kacem et al., 2002b), the LEGA of (Ho et al., 2007),
the MATSLO+ of (Ennigrou and Gh´edira, 2008), the
KBACO of (Xing et al., 2010), the TS3 of (Bozejko
et al., 2010a), the MOPSO+LS of (Moslehi and Mah-
nam, 2011), the MATSPSO of (Henchiri and Enni-
grou, 2013), the Hybrid NSGA-II of (Zhang et al.,
2014) and the Heuristic of (Ziaee, 2014). The differ-
ent comparative results are displayed in the tables 2,
3, 4 and 5, where the first column takes the name of
each instance, the second column gives the size each
instance, with n the number of jobs and m the num-
ber of machines (n × m), and the remaining columns
detail the experimental results of the different chosen
approaches in terms of the best Cmax (Best) and the
standard deviation (Dev %). The bold values in the
tables signify the best obtained results and the N/A
means that the result is not available.
By analyzing the table 2 and table 3, it can be
GeneticAlgorithmCombinedwithTabuSearchinaHolonicMultiagentModelforFlexibleJobShopSchedulingProblem
581

Table 4: Results of the Brandimarte instances (part 1).
Instance
Problem
n× m
TS (1993) LEGA (2007)
MATSLO+
(2008)
KBACO (2010)
Best
Dev
(%)
Best
Dev
(%)
Best
Dev
(%)
Best
Dev
(%)
MK01 10×6 42 4,761 40 0 40 0 39 -2,564
MK02 10×6 32 15,625 29 6,896 32 15,625 29 6,896
MK03 15×8 211 3,317 N/A – 207 1,449 204 0
MK04 15×8 81 20,987 67 4,477 67 4,477 65 1,538
MK05 15×4 186 6,989 176 1,704 188 7,978 173 0
MK06 10×15 86 24,418 67 2,985 85 23,529 67 2,985
MK07 20×5 157 8,280 147 2,040 154 6,493 144 0
MK08 20×10 523 0 523 0 523 0 523 0
MK09 20×10 369 15,718 320 2,812 437 28,832 311 0
MK10 20×15 296 25 229 3,056 380 41,578 229 3,056
Table 5: Results of the Brandimarte instances (part 2).
Instance
Problem
n× m
TS3 (2010) MATSPSO (2013) Heuristic (2014) GATS+HM
Best
Dev
(%)
Best
Dev
(%)
Best
Dev
(%)
Best
Avg
Cmax
Avg CPU (in
seconds)
MK01 10×6 40 0 39
-
2,564
42 4,761 40 40,80 0,93
MK02 10×6 29 6,896 27 0 28 3,571 27 27,80 1,18
MK03 15×8 204 0 207 1,449 204 0 204 204,00 1,55
MK04 15×8 65 1,538 65 1,538 75 14,666 64 65,60 4,36
MK05 15×4 173 0 174 0,574 179 3,351 173 174,80 8,02
MK06 10×15 68 4,411 72 9,722 69 5,797 65 67,00 110,01
MK07 20×5 144 0 154 6,493 149 3,355 144 144,00 19,73
MK08 20×10 523 0 523 0 555 5,765 523 523,00 11,50
MK09 20×10 326 4,601 340 8,529 342 9,064 311 311,80 79,68
MK10 20×15 227 2,202 299 25,752 242 8,264 222 224,80 185,64
seen that our algorithm GATS+HM is the best one
which solves the fives instances of Kacem. In fact,
the GATS+HM outperforms the AL+CGA in four out
of five instances, the LEGA, the MOPSO+LS and the
Hybrid NSGA-II in two out of five instances, and
the Heuristic in three out of five instances. Also,
our algorithm attains the same results obtained by
the KBACO, but the efficiency of GATS+HM can
be noted by the average of the CPU time in sec-
onds which is very acceptable for a real manufactur-
ing case.
From table 4 and table 5, the comparison re-
sults show that the GATS+HM obtains nine out of
ten best results for the Brandimarte instances. In-
deed, our algorithm outperforms the TS in nine out
of ten instances. Moreover, our GATS+HM outper-
forms the LEGA and the MATSLO+ in eight out of
ten instances. For the comparison with the KBACO,
the GATS+HM obtains the best solutions for the
MK02, MK04, MK06 and MK10 instances, but it gets
slightly worse result for the MK01 instance. Also, our
hybrid approach outperformsthe TS3 in fiveout of ten
instances. Furthermore, the MATSPSO attained the
best result for the MK01 instance, but our algorithm
obtains a set of solutions better than it for the remain-
ing instances. In addition, our algorithm outperforms
the Heuristic in all the Brandimarte instances. By
solving this second data set, our GATS+HM attains
the same results obtained by some approaches such
as the MK01 for LEGA, MATSLO+ and TS3; the
MK02 for MATSPSO; the MK03 for KBACO, TS3
and Heuristic; the MK05 and MK07 for KBACO and
TS3; the MK09 for KBACO; the MK08 for all the
algorithms only it is not the case for the Heuristic.
By analyzing the computational time in seconds
and the comparison results of our algorithm in term
of makespan, we can distinguish the efficiency of the
new proposed GATS+HM relatively to the literature
of the FJSP. This efficiency is explained by the flex-
ible selection of the promising parts of the search
space by the clustering operator after the genetic al-
gorithm process and by applying the intensification
technique of the tabu search allowing to start from an
elite solution to attain new more dominant solutions.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
582

5 CONCLUSIONS
In this paper, we present a new combination of a ge-
netic algorithm with a tabu search in a holonic multi-
agent model, called GATS+HM, for the flexible job
shop scheduling problem (FJSP). In this approach,
a Neighborhood-based Genetic Algorithm is adapted
by a Scheduler Agent (SA) for a global exploration
of the search space. Then, a local search technique is
applied by a set of Cluster Agents (CAs) to guide the
research in promising regions of the search space and
to improve the quality of the final population. Numer-
ical tests are made to measure the performance of the
proposed approach using two well known data sets
from the literature of the FJSP. The experimental re-
sults show that the proposed approach is efficient in
comparison to others approaches. In the future work,
improvements will be done on the tabu search of each
Cluster Agent. In fact, if a Cluster Agent CA
i
finds
a new dominant solution E
′
and it does not attain the
allowed number of neighbors from its current solu-
tion E, it does not stop, but it creates in each case a
new Sub-Cluster Agent SCA
i, j
allowing to relaunch
the search from the new obtained solution E
′
. Then
it continues to generate the remaining allowed neigh-
bors from its solution E searching other dominant so-
lutions. In other words, each Cluster Agent distributes
the new found solutions E
′
from its elite solution E
on a new sub-set of Sub-Cluster Agents SCA
i, j
to
launch from them their new search processes, which
enhances more the search in the selected promising
areas and shows more the efficient use of the notion of
the holonic agents (recursive agents) in our proposed
solution for the FJSP problem. Also, we will search
to treat other extensions of the FJSP, such as by inte-
grating new transportation resources constraints in the
shop process. So, we will make improvements to our
approach to adapt it to this new transformation and
study its effects on the makespan.
REFERENCES
Andresen, D., Kota, S., Tera, M., and Bower, T. (2002). An
ip-level network monitor and scheduling system for
clusters. In PDPTA, pages 789–795. CSREA Press.
Azzouz, A., Ennigrou, M., Jlifi, B., and Gh´edira, K. (2012).
Combining tabu search and genetic algorithm in a
multi-agent system for solving flexible job shop prob-
lem. In Proceedings of the 2012 11th Mexican In-
ternational Conference on Artificial Intelligence, MI-
CAI’12, pages 83–88, Washington, DC, USA. IEEE
Computer Society.
Bellifemine, F., Poggi, A., and Rimassa, G. (1999). Jade -
a fipa-compliant agent framework. In In Proceedings
of the fourth International Conference and Exhibition
on The Practical Application of Intelligent Agents and
Multi-Agent Technology, pages 97–108.
Botti, V. and Giret, A. (2008). ANEMONA: A Multi-
agent Methodology for Holonic Manufacturing Sys-
tems. Springer Series in Advanced Manufacturing.
Springer-Verlag.
Bozejko, W., Uchronski, M., and Wodecki, M. (2010a). The
new golf neighborhood for the flexible job shop prob-
lem. In In Proceedings of the International Confer-
ence on Computational Science, pages 289–296.
Bozejko, W., Uchronski, M., and Wodecki, M. (2010b).
Parallel hybrid metaheuristics for the flexible job shop
problem. Computers and Industrial Engineering,
59(2):323–333.
Brandimarte, P. (1993). Routing and scheduling in a flex-
ible job shop by tabu search. Annals of Operations
Research, 41(3):157–183.
Calabrese, M. (2011). Hierarchical-granularity holonic
modelling. Doctoral thesis, Universita degli Studi di
Milano, Milano, Italy.
Chen, H., Ihlow, J., and Lehmann, C. (1999). A genetic al-
gorithm for flexible job-shop scheduling. In In Pro-
ceedings of the IEEE International Conference on
Robotics and Automation, pages 1120–1125.
Dauz`ere-P´er`es, S. and Paulli, J. (1997). An integrated ap-
proach for modeling and solving the general multipro-
cessor job-shop scheduling problem using tabu search.
Annals of Operations Research, 70(0):281–306.
Ennigrou, M. and Gh´edira, K. (2004). Approche multi-
agents bas´ee sur la recherche tabou pour le job shop
flexible. In In 14`eme Congr`es Francophone AFRIF-
AFIA de Reconnaissance des Formes et Intelligence
Artificielle RFIA, pages 28–30.
Ennigrou, M. and Gh´edira, K. (2008). New local diversi-
fication techniques for the flexible job shop problem
with a multi-agent approach. Autonomous Agents and
Multi-Agent Systems, 17(2):270–287.
Ferber, J. (1999). Multi-Agent Systems: An Introduction
to Distributed Artificial Intelligence. Addison-Wesley
Longman Publishing Co., Inc., Boston, MA, USA, 1st
edition.
Gao, J., Sun, L., and Gen, M. (2008). A hybrid genetic and
variable neighborhood descent algorithm for flexible
job shop scheduling problems. Computers and Oper-
ations Research, 35(9):2892–2907.
Garey, M. R., Johnson, D. S., and Sethi, R. (1976). The
complexity of flow shop and job shop scheduling.
Mathematics of Operations Research, 1(2):117–129.
Giret, A. and Botti, V. (2004). Holons and agents. Journal
of Intelligent Manufacturing, 15(5):645–659.
Glover, F., Kelly, J. P., and Laguna, M. (1995). Genetic
algorithms and tabu search: Hybrids for optimization.
Computers & Operations Research, 22(1):111–134.
Henchiri, A. and Ennigrou, M. (2013). Particle swarm op-
timization combined with tabu search in a multi-agent
model for flexible job shop problem. In In Proceed-
ings of the 4th International Conference on Swarm
Intelligence, Advances in Swarm Intelligence, pages
385–394.
GeneticAlgorithmCombinedwithTabuSearchinaHolonicMultiagentModelforFlexibleJobShopSchedulingProblem
583

Ho, N. B., Tay, J. C., and Lai, E. M. K. (2007). An ef-
fective architecture for learning and evolving flexible
job-shop schedules. European Journal of Operational
Research, 179(2):316–333.
Hurink, J., Jurisch, B., and Thole, M. (1994). Tabu
search for the job-shop scheduling problem with
multi-purpose machines. Operations Research Spek-
trum, 15(4):205–215.
Jia, H., Nee, A., Fuh, J., and Zhang, Y. (2003). A modified
genetic algorithm for distributed scheduling problems.
Journal of Intelligent Manufacturing, 14(3):351–362.
Johnson, S. C. (1967). Hierarchical clustering schemes.
Psychometrika, 32(3):241–254.
Jones, A. and Rabelo, L. C. (1998). Survey of job shop
scheduling techniques. In National Institute of Stan-
dards and Technology, Gaithersburg, MD.
Kacem, I., Hammadi, S., and Borne, P. (2002a). Approach
by localization and multiobjective evolutionary opti-
mization for flexible job-shop scheduling problems.
IEEE Transactions on Systems, Man, and Cybernet-
ics, 32(1):1–13.
Kacem, I., Hammadi, S., and Borne, P. (2002b). Pareto-
optimality approach for flexible job-shop scheduling
problems: Hybridization of evolutionary algorithms
and fuzzy logic. Mathematics and Computers in Sim-
ulation, 60(3-5):245–276.
Koestler, A. (1967). The Ghost in the Machine. Hutchinson,
London, United Kingdom, 1st edition.
Lee, K., Yamakawa, T., and Lee, K. M. (1998). A ge-
netic algorithm for general machine scheduling prob-
lems. In In Proceedings of the second IEEE inter-
national Conference on Knowledge-Based Intelligent
Electronic Systems, pages 60–66.
Li, J., Pan, Q., Suganthan, P., and Chua, T. (2011). A hybrid
tabu search algorithm with an efficient neighborhood
structure for the flexible job shop scheduling problem.
The International Journal of Advanced Manufactur-
ing Technology, 52(5):683–697.
Mastrolilli, M. and Gambardella, L. (2000). Effective
neighbourhood functions for the flexible job shop
problem. Journal of Scheduling, 3(1):3–20.
Moslehi, G. and Mahnam, M. (2011). A pareto ap-
proach to multi-objective flexible job-shop schedul-
ing problem using particle swarm optimization and lo-
cal search. International Journal of Production Eco-
nomics, 129(1):14–22.
Sonmez, A. I. and Baykasoglu, A. (1998). A new dynamic
programming formulation of (nm) flow shop sequenc-
ing problems with due dates. International Journal of
Production Research, 36(8):2269–2283.
Thamilselvan, R. and Balasubramanie, P. (2009). Integrat-
ing genetic algorithm, tabu search approach for job
shop scheduling. International Journal of Computer
Science and Information Security, 2(1):1–6.
Xia, W. and Wu, Z. (2005). An effective hybrid op-
timization approach for multiobjective flexible job-
shop scheduling problems. Computers and Industrial
Engineering, 48(2):409–425.
Xing, L., Chen, Y., Wang, P., Zhao, Q., and Xiong, J.
(2010). A knowledge-based ant colony optimization
for flexible job shop scheduling problems. Applied
Soft Computing, 10(3):888–896.
Yazdani, M., Amiri, M., and Zandieh, M. (2010). Flexible
job-shop scheduling with parallel variable neighbor-
hood search algorithm. Expert Systems with Applica-
tions, 37(1):678–687.
Zhang, C., Gu, P., and Jiang, P. (2014). Low-carbon
scheduling and estimating for a flexible job shop
based on carbon footprint and carbon efficiency of
multi-job processing. Journal of Engineering Man-
ufacture, 39(32):1–15.
Zhang, G., Gao, L., and Shi, Y. (2010). A genetic algorithm
and tabu search for multi objective flexible job shop
scheduling problems. In International Conference on
Computing, Control and Industrial Engineering, vol-
ume 1, pages 251–254.
Zhang, G., Shao, X., Li, P., and Gao, L. (2009). An effec-
tive hybrid particle swarm optimization algorithm for
multi-objective flexible job-shop scheduling problem.
Computers and Industrial Engineering, 56(4):1309–
1318.
Zhang, G., Shi, Y., and Gao, L. (2008). A genetic algorithm
and tabu search for solving flexible job shop sched-
ules. International Symposium on Computational In-
telligence and Design, 1:369–372.
Ziaee, M. (2014). A heuristic algorithm for solving flexible
job shop scheduling problem. The International Jour-
nal of Advanced Manufacturing Technology, 71(1-
4):519–528.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
584
