
Relaxed Soundness Verification for Interorganizational Workflow
Processes
L´ıgia Maria Soares Passos
1,2
and St´ephane Julia
2
1
Computer Science Department, Federal Rural University of Rio de Janeiro, Nova Iguac¸u, Rio de Janeiro, Brazil
2
Computing Faculty, Federal University of Uberlˆandia, Uberlˆandia, Minas Gerais, Brazil
Keywords:
Interorganizational Workflow Processes, Relaxed Soundness, Verification, Linear Logic, Petri Nets.
Abstract:
This paper presents a method for the Relaxed Soundness verification of interorganizational workflow pro-
cesses. The method considers Interorganizational WorkFlow net models and is based on the analysis of Linear
Logic proof trees. To verify the Relaxed Soundness criterion, a Linear Logic proof tree is built for each differ-
ent scenario of an unfolded Interorganizational WorkFlow net. These proof trees are then analysed considering
two conditions: the first verifies if the analysed scenario can finish properly, without spare tokens and the sec-
ond verifies if every activity concerning the global process was covered by at least one possible scenario. The
Interorganizational WorkFlow net is then considered as relaxed sound if the scenarios satisfy these conditions.
1 INTRODUCTION
Workflow processes that involve several business pro-
cesses belonging to different organizations and which
need to coordinate their actions in order to reach a
common goal are known as interorganizational work-
flow processes (Captarencu, 2012).
According to (van der Aalst, 1998b), an interorga-
nizational workflow is essentially a set of loosely cou-
pled workflow processes where, typically, there ex-
ist local workflow processes that are involved in one
global workflow process. These local workflow pro-
cesses need to communicate for the correct execution
of those cases treated by the global workflowmanage-
ment system.
According to (Lim et al., 2012), interorganiza-
tional workflow systems play a fundamental role in
business partnerships and forming an alliance with
appropriate business partners is a common strategy
for enterprises to remain competitive by offering a
wider range of products and services to its clients.
Many studies have already considered the qual-
itative analysis of interorganizational workflow pro-
cesses. In (van der Aalst, 1998b; Yamaguchi et al.,
2007; Sun and Du, 2008; Soares Passos and Julia,
2013) for example, the proposed approaches are re-
lated to classical Soundness verification, a qualitative
property of Interorganizational WorkFlow nets. The
Soundness correctness criterion considers the interor-
ganizational workflow process as a whole, i.e if it
does not satisfy Soundness, it needs to be redesigned
to satisfy Soundness and guarantee that the model is
deadlock-free, for example. In (van der Aalst, 1998b;
Yamaguchi et al., 2007) and (Sun and Du, 2008), the
proposed approaches for classical Soundness verifi-
cation of interorganizational workflow processes are
based on the construction and analysis of reachability
graphs. In (Soares Passos and Julia, 2013), a Lin-
ear Logic based approach is presented for classical
Soundness verification in the context of interorgani-
zational workflow processes. The approach presented
in (Soares Passos and Julia, 2013) is based on the con-
struction and analysis of Linear Logic proof trees. It
is important to highlight that these studies are con-
cerned with the classical Soundness verification for
interorganizational workflow processes and the Re-
laxed Soundness verification for interorganizational
workflow processes is not taken into account.
The ideal scenario is the one in which the interor-
ganizational processes are sound, once that Sound-
ness ensures important criteria, such as absence of
deadlock and proper termination. However, according
to (Fahland et al., 2011), the checking of 735 indus-
trial business process models from financial services,
telecommunications, and other domains has shown
that only 46% of the process models were sound. So,
as an interorganizational workflow is essentially a set
of local workflow processes involved in one global
workflow process (van der Aalst, 1998b), and a large
percentage of these local workflow processes are un-
221
Soares Passos L. and Julia S..
Relaxed Soundness Verification for Interorganizational Workflow Processes.
DOI: 10.5220/0005349302210228
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 221-228
ISBN: 978-989-758-098-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

sound (Fahland et al., 2011), the global workflow pro-
cess that is based on unsound local workflow pro-
cesses will also be unsound according to the Sound-
ness definition proposed by (van der Aalst, 1998b).
In this context, a wide variety of interorganizational
workflowprocesses may be unsound and may lead the
services of the business organization to deadlock sit-
uations. Furthermore, workflow processes are impor-
tant assets for the organizations that are not always
willing to redesign or adjust their processes to fully
fit the specific need of a specific partner, specially as
different business partners may have different needs.
In the context of single workflow processes, i.e.
workflow processes that are not interorganizational,
(Dehnert and Rittgen, 2001) proposed to relax the
Soundness criterion. The new defined criterion is the
Relaxed Soundness criterion. The idea behind Re-
laxed Soundness is that the system’s behavior is cor-
rect if there exist sufficient executions which termi-
nate properly (Dehnert and Rittgen, 2001). So, the
notion of Relaxed Soundness ensures that there is at
least one run that enables each task of the workflow
process model which can be carried from the initial
state forward to the final state. In (Siegeris and Zim-
mermann, 2006), various workflow model composi-
tion proposals are summarized and the authors inves-
tigate the ability of these composition mechanisms
to preserve the Relaxed Soundness criterion. How-
ever, to preserve Relaxed Soundness, the workflow
processes that are used in the composition have to sat-
isfy the Relaxed Soundness criterion too. So, if this
is not the case, these workflow processes have to be
redesigned first to satisfy the Relaxed Soundness cri-
terion before they can be used in a composition.
Considering that a wide variety of interorganiza-
tional workflow processes may be unsound and that
the idea behind the Relaxed Soundness is that the sys-
tem’s behavior is correct if there exist sufficient ex-
ecutions which terminate properly, it is of great in-
terest to verify Relaxed Soundness in the context of
interorganizational workflow processes. In these cir-
cumstances, i.e. in the cases in which the interorga-
nizational workflow processes are unsound, the Re-
laxed Soundness criterion ensures that the main busi-
ness relationship between the involved organizations
can be provided safely, with no obligation to the re-
designing of the involved processes in order that they
satisfy the Soundness criterion. So, the approach pre-
sented in this paper considers the Relaxed Soundness
verification for an interorganizational workflow pro-
cess, where the set of local workflow processes are
not necessarily Relaxed Sound and the global work-
flow process is or may be unsound.
Therefore, this paper presents a method for Re-
laxed Soundness verification for interorganizational
workflow processes modelled by Interorganizational
WorkFlow nets (IOWF-nets) (van der Aalst, 1998b).
Thus, the organizations involved in the interorgani-
zational workflow process will be able to verify if
their main business services can finish properly, con-
sidering the global process, avoiding deadlock situa-
tions whenever they occur, without redesigning their
local or global workflow processes. This method is
based on the analysis of Linear Logic proof trees built
considering each scenario of the unfolded IOWF-net
(van der Aalst, 1998b).
This paper is structured as follows. In section 2
the definition of the Interorganizational WorkFlow
nets is provided. In section 3, an overview of Linear
Logic is given. The method for Relaxed Soundness
verification for Interorganizational WorkFlow nets is
presented in section 4. Finally, the last section con-
cludes this work with a short summary, an assessment
of the presented approach and an outlook on future
work proposals.
2 INTERORGANIZATIONAL
WORKFLOW NETS
In this section, the concepts related to Interorgani-
zational WorkFlow nets (IOWF-nets) are presented.
These concepts are necessary to better comprehend
the approach presented in section 4.
To define IOWF-nets, it is necessary first to intro-
duce the definition of WorkFlow nets. According to
(van der Aalst, 1998a), a Petri net (Murata, 1989) that
models a workflow process is called a WorkFlow net
(WF-net). A WF-net satisfies the following properties
(van der Aalst, 1998a): it has only one source place
named i and only one sink place named o, that are
special places such that the place i has only outgoing
arcs and the place o has only incoming arcs; a token
in i represents a case that needs to be handled and a
token in o represents a case that has been handled; ev-
ery task t (transition) and condition p (place) should
be on a path from place i to place o.
Following, the formal definition of WF-nets is
presented.
Definition 1 (WorkFlow-net). A Petri net PN =
{P, T, F}, where P is a finite set of places, T is a fi-
nite set of transitions (P∩T =
/
0) and F ⊆ (P × T) ∪
(T × P) is a set of arcs (flow relation), is a WF-net if,
and only if (van der Aalst, 1998a):
1. PN has two special places: i and o. Place i is
a source place: •i =
/
0. Place o is a sink place:
o• =
/
0.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
222

2. Every node is on a path from i to o.
An InterorganizationalWorkFlow net (IOWF-net)
is a Petri net that models an interorganizational work-
flow process and can be seen as a global workflow
process that has n business partners involved in it, ac-
cording to (van der Aalst, 1998b). Each partner has
its own local workflow process. So, an interorgani-
zational workflow is composed of at least two local
workflow processes. Thus, an IOWF-net is composed
of at least two Local WorkFlow nets (LWF-nets). In
(van der Aalst, 1998b), a global workflow process
consists of a set of local workflow processes plus an
interactive structure composed of asynchronous and
synchronous communication mechanisms. Accord-
ing to (van der Aalst, 1998b), synchronous commu-
nication corresponds to the melting (fusion) of some
transitions and the asynchronous communication cor-
responds to the exchange of messages between local
workflow processes. In this paper, the synchronous
case will not be considered, since we consider that
each organization controls its own process so that
there is no melting of transitions. Therefore, only
asynchronous communicationprotocols will be repre-
sented. Following this, the IOWF-net definition pro-
posed by Aalst in (van der Aalst, 1998b) is specially
adapted to the asynchronous case.
Definition 2 (IOWF-net). An Interorganizational
WorkFlow net (IOWF-net) is a tuple IOWF − net =
{PN
1
, PN
2
, ..., PN
n
, P
AC
, AC}, where:
1. n ∈ N is the number of LWF-nets;
2. for each k ∈ {1, ..., n}, PN
k
is a WF-net with a
source place i
k
and a sink place o
k
;
3. for all k, l ∈ {1, ..., n}, if k 6= l, then (P
k
∪ T
k
) ∩
(P
l
∪ T
l
) =
/
0;
4. T
∗
=
S
k∈{1,...,n}
T
k
, P
∗
=
S
k∈{1,...,n}
P
k
and F
∗
=
S
k∈{1,...,n}
F
k
(relations between the elements of
the LWF-nets);
5. P
AC
is the set of asynchronous communication el-
ements (communication places);
6. AC ⊆ P
AC
× P(T
∗
) × P(T
∗
) represents the asyn-
chronous communication relations
1
.
Each asynchronous communication element cor-
responds to a place name in P
AC
and the asynchronous
communication relation AC specifies a set of input
transitions and a set of output transitions for each
asynchronous communication element (van der Aalst,
1998b).
To clarify the concepts defined above, the interor-
ganizational workflow process presented in (van der
1
P(T
∗
) is the set of all non-empty subsets of T
∗
Aalst, 1998b) is contemplated. Such a process mod-
els a process that precedes the presentation of a pa-
per at a conference and its description can be found
in (van der Aalst, 1998b). The highlighted IOWF-
net area in Figure 1 shows the IOWF-net that mod-
els that process. This IOWF-net has two LWF-nets:
Author and PC (Program Committee). Each of these
has only one source and one sink place. In the LWF-
net Author, the source place is start flow author
and the sink place is end flow author. In the LWF-
net PC, the source and sink place are start
flow PC
and end flow PC, respectively. The places draft,
ack
draft, reject, accept, too late, final version
and ack final are examples of asynchronous commu-
nication places.
In (van der Aalst, 1998b), the Unfolded Interor-
ganizational WorkFlow net is defined. The unfolding
of an IOWF-net is a WF-net. In the unfolded net, i.e.
the U(IOWF-net), all the LWF-nets are included into
a single workflow process considering a start transi-
tion t
i
and a termination transition t
o
. A global source
place i and a global sink place o have to be added in
order to respect the basic structure of a simple WF-
net, and the asynchronous communication elements
are mapped into ordinary places according to (van der
Aalst, 1998b). Figure 1 shows an U(IOWF-net).
In (Dehnert and Rittgen, 2001), the authors pro-
posed to relax the Soundness criterion, a well-known
criterion defined by (van der Aalst, 1998a), to a new
criterion named Relaxed Soundness. They argue that
this criterion is closer to the intuition of the mod-
eller. According to (Dehnert and Rittgen, 2001), Re-
laxed Soundness is intended to represent a more prag-
matic view on correctness which is weaker (in a for-
mal sense) than the Soundness criterion. To (Dehn-
ert and Rittgen, 2001), Relaxed Soundness means
that there exist sufficient executions that terminate
properly (i.e. without spare tokens). In this context
sufficient means, according to (Dehnert and Rittgen,
2001), each transition of the process is covered at
least once when considering the set of sound firing
sequences.
The definition of Relaxed Soundness, proposed by
(Dehnert and Rittgen, 2001), is the following.
Definition 3 (Relaxed Soundness). A process speci-
fied by a WF-net PN = (P, T, F) is relaxed sound if
and only if every transition is in a firing sequence that
starts in state i and ends in state o.
Formally:
∀t ∈ T : ∃M, M
′
: (i
∗
−→ M
t
−→ M
′
∗
−→ o), where M
and M
′
are markings.
The Relaxed Soundness criterion was then defined
in the context of WF-nets only and the IOWF-nets
were not formally taken into account. However, this
RelaxedSoundnessVerificationforInterorganizationalWorkflowProcesses
223
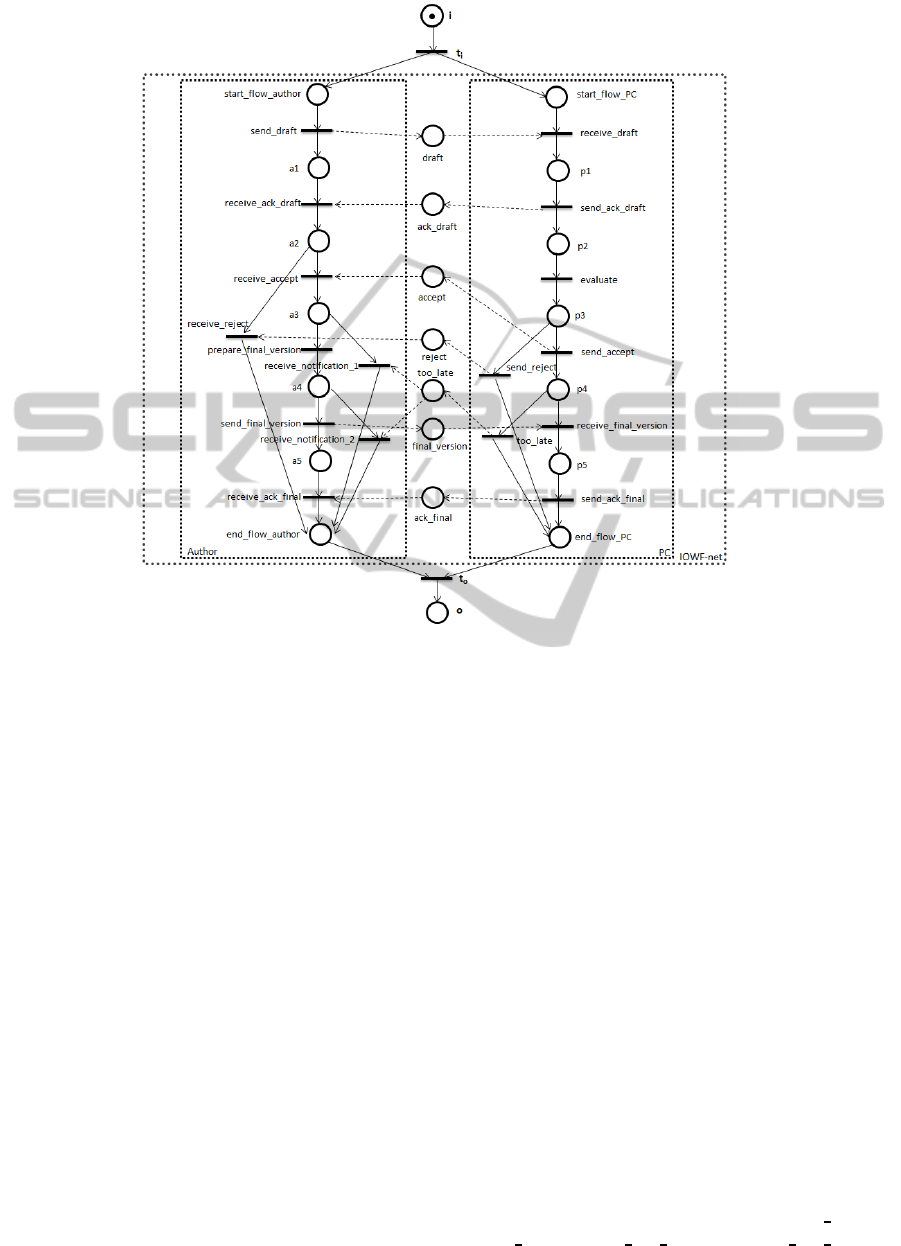
Figure 1: An unfolded IOWF-net.
criterion is also important in the context of IOWF-
nets, specially in the cases where the Soundness cri-
terion is not satisfied. Therefore, as the unfolding of
an IOWF-net, the U(IOWF-net), has the same struc-
ture of a WF-net, as shown in (van der Aalst, 1998b),
we can verify the Relaxed Soundness criterion for the
IOWF-nets, considering the analysis of its unfolded
net.
3 LINEAR LOGIC
In this section, an overview of Linear Logic is pre-
sented. The concepts presented here are necessary for
a better comprehension of the method presented in the
next section.
The first proposals for Linear Logic were made
in (Girard, 1987). In Linear Logic, propositions are
considered as resources, i.e. atoms, which are con-
sumed and produced at each state change (Riviere
et al., 2001). Linear Logic introduces new connec-
tives. In this paper just two Linear Logic connectives
will be used:
• The times connective, denoted by ⊗, that repre-
sents simultaneous availability of resources. For
instance, A⊗ B represents the simultaneous avail-
ability of resources A and B.
• The linear implies connective,denoted by ⊸, that
represents a state change. For instance, A ⊸ B
denotes that by consuming A, B is produced (it is
important to note that after the production of B, A
will not be available).
The translation of a Petri net into formulas of Lin-
ear Logic, presented in (Riviere et al., 2001), is the
following. A marking M is a monomial in ⊗ and
is represented by M = A
1
⊗ A
2
⊗ . . . ⊗ A
k
where A
i
are place names. For instance, the initial marking on
the U(IOWF-net) in Figure 1 is simply i because of
the token in place i. A transition is an expression of
the form M
1
⊸ M
2
where M
1
and M
2
are markings.
For example, transition evaluate of the LWF-net PC
in Figure 1 is noted evaluate = p2 ⊸ p3.
A sequent M, t
k
⊢ M
′
represents a scenario where
M and M
′
are respectively the initial and final
markings, and t
k
is a list of non-ordered transi-
tions. For instance, considering the U(IOWF-net)
shown in Figure 1, the sequent i, t
i
, send
draft,
receive draft, send ack dra ft, receive ack draft,
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
224

evaluate, send reject, receive reject, t
o
⊢ o repre-
sents one possible scenario of this U(IOWF-net),
where i is the initial marking, t
i
, send
draft,
receive dra ft, send ack draft, receive ack draft,
evaluate, send
reject, receive reject, t
o
is a list of
non-ordered transitions and o is the final marking. A
sequent can be proven by applying the rules of the se-
quent calculus. It was proven in (Girault et al., 1997)
that a proof of the sequent calculus is equivalent to the
corresponding reachability problem in a Petri net.
In this paper, only some rules of Linear Logic will
be considered. These rules will be used to build the
proof trees. In this context, F, G, and H are formulas
and Γ and ∆ are considered blocks of formulas. The
following rules will be those used in the present paper
(Riviere et al., 2001):
• The ⊸
L
rule,
Γ ⊢ F ∆, G ⊢ H
Γ, ∆, F ⊸ G ⊢ H
⊸
L
, expresses a
transition firing and generates two sequents such
that the right-hand sequent represents the subse-
quent which remains to be proven and the left-
hand sequent represents the tokens consumed by
this particular firing. For example, consider-
ing the transition t
i
= i ⊸ start
flow author ⊗
start
flow pc of the U(IOWF-net) shown in Fig-
ure 1, when this transition is fired, two sequents
are generated: i ⊢ i represents the token con-
sumed by this firing and start
flow author ⊗
start
flow pc the remaining subsequent to be
proven.
• The ⊗
L
rule,
Γ, F, G ⊢ H
Γ, F ⊗ G ⊢ H
⊗
L
, transforms a
marking in an atoms list. For example, the
subsequent start
flow author ⊗ start flow pc
generated by the firing of transition t
i
=
i ⊸ start
flow author ⊗ start flow pc of the
U(IOWF-net) shown in Figure 1 will use the
rule ⊗
L
to be transformed into a list of atoms
start
flow author, start flow pc.
• The ⊗
R
rule,
Γ ⊢ F ∆ ⊢ G
∆, Γ ⊢ F ⊗ G
⊗
R
, transforms a se-
quent such as A, B ⊢ A ⊗ B, into two identity se-
quents A ⊢ A and B ⊢ B. For example, consider-
ing the firing of the transition receive
accept =
a2 ⊗ accept ⊸ a3 of the U(IOWF-net) shown in
Figure 1, the sequent that represents the tokens
consumed by this firing, a2, accept ⊢ a2⊗ accept,
also needs to be proven, using the ⊗
R
rule, i.e.
a2 ⊢ a2 accept ⊢ accept
a2, accept ⊢ a2⊗ accept
⊗
R
.
In the approach presented in this paper, a Linear
Logic proof tree is read from the bottom up. The
proof stops when the atom that represents the place
o is produced, i.e. the identity sequent o ⊢ o appears
in the proof tree, when there is not any rule that can
be applied, or when all the leaves of the proof tree are
identity sequents.
4 RELAXED SOUNDNESS
VERIFICATION FOR IOWF-nets
To verify Relaxed Soundness for the IOWF-nets, it is
necessary to build and prove linear sequents of Lin-
ear Logic. This approach considers the analysis of
the unfolded IOWF-net, U(IOWF-net), which has the
same structure of a WF-net. So, it is then necessary
to built and prove linear sequents of Linear Logic that
represent the U(IOWF-net).
Initially, the U(IOWF-net) has to be represented
through the use of Linear Logic formulas. The
U(IOWF-net) can be represented by more than one
linear sequent, each linear sequent representing a pos-
sible scenario of the U(IOWF-net).
A scenario in the context ofU(IOWF-nets), corre-
sponds to a well defined route mapped into the cor-
responding U(IOWF-net). If the U(IOWF-net) has
more than one route (places with two or more out-
put arcs), it is necessary then to build a different lin-
ear sequent for each existing scenario (Soares Passos
and Julia, 2013). For example, for the U(IOWF-net)
shown in Figure 1, there exist five different scenar-
ios: the first scenario, Sc
1
, where task send
reject
will be executed (firing of transition send
reject);
the second scenario, Sc
2
, where tasks too late and
receive
notification 1 will be executed (firing of
transitions too late and receive notification 1); the
third scenario, Sc
3
, where tasks too
late and re-
ceive notification 2 will be carried out (firing of tran-
sitions too late and receive notification 2); the fourth
scenario, Sc
4
, where tasks send
final version and re-
ceive final version will be carried out (firing of transi-
tion send
final version and receive final version) and
the fifth scenario, Sc
5
, where tasks too late and
send
final version will be executed (firing of transi-
tions too late and send final version).
In this approach, each one of these scenar-
ios is then represented by a specific linear se-
quent that considers the initial and final markings
of the U(IOWF-net) and a non-ordered list of tran-
sitions involved in it. Each linear sequent has
only one atom which represents the initial mark-
ing of the U(IOWF-net). For example, the sce-
nario Sc
1
is represented by: i, t
i
, send
draft,
receive draft, send ack dra ft, receive ack draft,
evaluate, send
reject, receive reject, t o ⊢ o.
After the definition of the linear sequents that rep-
resent the different scenarios of theU(IOWF-net), the
RelaxedSoundnessVerificationforInterorganizationalWorkflowProcesses
225

linear sequents need to be proven through the build-
ing of Linear Logic proof trees. After the construc-
tion of these proof trees, each scenario of the anal-
ysed U(IOWF-net) must be analysed respecting the
following steps:
1. For each proof tree that represents a scenario:
(a) If just one atom o, that corresponds to an atom
in the sink place of the U(IOWF-net), was pro-
duced in the proof tree (this is represented in the
proof tree by the identity sequent o ⊢ o), then
the analysed scenario was finished properly.
(b) If there is not any available atom to be con-
sumed on the proof tree, i.e. all places are
empty, then the execution terminates without
spare tokens.
2. Considering the proof trees for scenarios
Sc
1
, Sc
2
, ..., Sc
i
of the analysed U(IOWF-net)
that satisfy step 1, each transition t ∈ T needs to
appear in, at least, one of these proof trees. This
proves that all transitions were fired at least once
and that every activity of the global process was
covered by at least one possible scenario.
If the conditions 1 and 2 are satisfied, the analysed
U(IOWF-net) is Relaxed Sound.
To illustrate the proposed approach, the IOWF-
net shown in Figure 1 is considered. To prove Re-
laxed Soundness for this IOWF-net, the correspond-
ing U(IOWF-net) is considered. It is necessary to
prove five linear sequents, each one representing one
of the following scenarios: Sc
1
, Sc
2
, Sc
3
, Sc
4
and Sc
5
.
The transitions of the U(IOWF-net) shown in
Figure 1 are represented by the following formulas of
Linear Logic:
t
i
= i ⊸ start flow author ⊗ start flow PC,
t
1
= send
draft = start flow author ⊸ a1⊗ dra ft,
t
2
= receive ack draft = a1⊗ ack draft ⊸ a2,
t
3
= receive
accept = a2⊗ accept ⊸ c3,
t
4
= receive reject = a2 ⊗ reject ⊸
end
flow author,
t
5
= prepare final version = a3 ⊸ a4,
t
6
= receive
notification 1 = a3 ⊗ too late ⊸
end flow author,
t
7
= send
final version = a4 ⊸ a5⊗ final version,
t
8
= receive noti fication 2 = a4 ⊗ too late ⊸
end
flow author,
t
9
= receive ack final = a5 ⊗ ack final ⊸
end
flow author,
t
10
= receive dra ft = start flow PC⊗ draft ⊸ p1,
t
11
= send ack dra ft = p1 ⊸ ack draft ⊗ p2,
t
12
= evaluate = p2 ⊸ p3,
t
13
= send
reject = p3 ⊸ reject ⊗ end flow PC,
t
14
= send
accept = p3 ⊸ accept ⊗ p4,
t
15
= too late = p4 ⊸ too late⊗ end flow PC,
t
16
= receive final version = final version ⊗ p4 ⊸
p5,
t
17
= send
ack final = p5 ⊸ ack final ⊗
end flow PC,
t
o
= end
flow author ⊗ end flow PC ⊸ o.
For readability, the atoms of the linear sequents
and proof trees will be represented just by the initial
letters of their complete name. For example, draft,
too
late and final version will be represented by d,
tl and fv, respectively. A set of transitions t
i
, t
j
, t
k
and
t
l
may be also represented as t
i, j,k,l
.
By considering the U(IOWF-net) shown in Fig-
ure 1, five different scenarios, and consequently linear
sequents, are defined:
Sc
1
= i, t
i
, t
1
, t
2
, t
4
, t
10
, t
11
, t
12
, t
13
, t
o
⊢ o,
Sc
2
= i, t
i
, t
1
, t
2
, t
3
, t
6
, t
10
, t
11
, t
12
, t
14
, t
15
, t
o
⊢ o,
Sc
3
= i, t
i
, t
1
, t
2
, t
3
, t
5
, t
8
, t
10
, t
11
, t
12
, t
14
, t
15
, t
o
⊢ o,
Sc
4
= i, t
i
, t
1
, t
2
, t
3
, t
5
, t
7
, t
9
, t
10
, t
11
, t
12
, t
14
, t
16,17,o
⊢ o,
Sc
5
= i, t
i
, t
1
, t
2
, t
3
, t
5
, t
7
, t
9
, t
10
, t
11
, t
12
, t
14
, t
15
, t
o
⊢ o.
Following are the proof trees for each one of these
scenarios. The proof tree for scenario Sc
1
is as fol-
lows:
ef a⊢efa ef p⊢ef p
ef a,e f p⊢ef a⊗e f p
⊗
R
o⊢o
⊸
L
a2⊢a2 r⊢r
a2,r⊢a2⊗r
⊗
R
ef p,ef a,efa⊗ef p⊸o⊢o
⊸
L
a1⊢a1 ad⊢ad
a1,ad⊢a1⊗ad
⊗
R
r,ef p,a2,a2⊗r⊸efa,t
o
⊢o
⊸
L
a1,ad,r,ef p,a1⊗ad⊸a2,t
4,o
⊢o
⊗
L
p3⊢p3 a1,ad,r⊗ef p,t
2,4,o
⊢o
⊸
L
p2⊢p2 a1,ad, p3, p3⊸r⊗ef p,t
2,4,o
⊢o
⊸
L
a1,ad, p2, p2⊸ p3,t
2,4,13,o
⊢o
⊗
L
p1⊢p1 a1,ad⊗p2,t
2,4,12,13,o
⊢o
⊸
L
sf p⊢sf p d⊢d
sf p,d⊢sf p⊗d
⊗
R
a1, p1, p1⊸ad⊗p2,t
2,4,12,13,o
⊢o
⊸
L
sf p,a1,d,sf p⊗d⊸ p1,t
2,4,11,12,13,o
⊢o
⊗
L
sf a⊢s f a sf p,a1⊗d,t
2,4,10,11,12,13, o
⊢o
⊸
L
sf a,s f p,sf a⊸a1⊗d,t
2
,t
4
,t
10
,t
11
,t
12
,t
13
,t
o
⊢o
⊗
L
i⊢i sf a⊗s f p,t
1
,t
2
,t
4
,t
10
,t
11
,t
12
,t
13
,t
o
⊢o
⊸
L
i,t
i
,t
1
,t
2
,t
4
,t
10
,t
11
,t
12
,t
13
,t
o
⊢o
For space reasons, just the first and the last linear
sequent are shown in the next proof trees. So, the
proof tree for scenario Sc
2
is as follows:
o⊢o
⊸
L
.
.
.
i,t
i
,t
1
,t
2
,t
3
,t
6
,t
10
,t
11
,t
12
,t
14
,t
15
,t
o
⊢o
The proof tree for scenario Sc
3
is as follows:
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
226

o⊢o
⊸
L
.
.
.
i,t
i
,t
1
,t
2
,t
3
,t
5
,t
8
,t
10
,t
11
,t
12
,t
14
,t
15
,t
o
⊢o
The proof tree for scenario Sc
4
is the following
one.
o⊢o
⊸
L
.
.
.
i,t
i
,t
1
,t
2
,t
3
,t
5
,t
7
,t
9
,t
10
,t
11
,t
12
,t
14
,t
16,17,o
⊢o
And finally the proof tree for scenario Sc
5
is as
follows:
tl,ef p,a5, f v,t
9
,t
o
⊢o
⊗
L
.
.
.
i,t
i
,t
1
,t
2
,t
3
,t
5
,t
7
,t
9
,t
10
,t
11
,t
12
,t
14
,t
15
,t
o
⊢o
The next step is to analyse the proof trees pro-
duced. By considering the proof trees for scenarios
Sc
1
, Sc
2
, Sc
3
, Sc
4
and Sc
5
, it is necessary to verify
the condition 1 for each scenario Sc
i
and the condi-
tion 2 for the scenarios that satisfy condition 1. It is
easy to note that the last sequent in the proof trees for
scenarios Sc
1
, Sc
2
, Sc
3
and Sc
4
is o ⊢ o. So, condi-
tions 1a and 1b are satisfied, i.e. just one atom o was
produced in these proof trees and as the last sequent
is an identity sequent, there is not any available atom
for consumption, i.e. the execution for these scenar-
ios finishes without spare tokens. The last sequent
for scenario Sc
5
is tl, ef p, a5, fv, t
9
, t
o
⊢ o, as no atom
o was produced by this scenario, the condition 1a is
not verified for this scenario. This sequent also con-
tains available atoms for consumption, as the atoms
tl, ef p, a5 and fv. Consequently, it does not satisfy
the condition 1b. Therefore, for the second part of the
verification (step 2), scenarios Sc
1
, Sc
2
, Sc
3
and Sc
4
will be considered. Each transition t ∈ T appears in
at least one of these scenarios. So, the condition 2 is
also satisfied and the IOWF-net shown in Figure 1 is
relaxed sound. The scenarios Sc
1
, Sc
2
, Sc
3
and Sc
4
are the ones that terminate properly. The scenario Sc
5
is the one where the process deadlocks.
According to (van der Aalst, 1998b), the classi-
cal Soundness verification for IOWF-nets is based on
the proof of liveness and boundedness for (n + 1)
WF-nets using standard techniques. According to
(Dehnert and Rittgen, 2001), there exist no structural
properties such as liveness and boundedness from
which the Relaxed Soundness property can be de-
rived. As presented in (Dehnert and Rittgen, 2001),
Relaxed Soundness can be proven only by enumer-
ation of sufficient sound firing sequences. For this
purpose, classical approaches based on reachability
graphs have to find sound firing sequences for ev-
ery transition (Dehnert and Rittgen, 2001). In par-
ticular, for classical Soundness verification of interor-
ganizational workflow processes as the one presented
in (van der Aalst, 1998b), if the analysed model is
not sound, it is then necessary to re-analyse and re-
explore the whole model to verify if it satisfies the
Relaxed Soundness criterion.
The Linear Logic based approach presented in
(Soares Passos and Julia, 2013) verifies classical
Soundness for IOWF-nets considering the construc-
tion and analysis of the Linear Logic proof trees that
represent each scenario of the Local WorkFlow nets
and each scenario of the corresponding U(IOWF-
net). The approach presented here to verify Relaxed
Soundness considers the construction and analysis of
the proof trees that represent each scenario of the
U(IOWF-net), i.e. the building and analysis of a sub-
set of the scenarios considered in the classical Sound-
ness verification. So, when an approach based on Lin-
ear Logic to verify the Soundness criterion for IOWF-
nets, as the one presented in (Soares Passos and Julia,
2013) is considered, if the analysed IOWF-net is un-
sound, a subset of the proof trees built to proveSound-
ness for the IOWF-net can be reused in the context
of this approach, performing only the analysis steps
of the proof trees that represent each scenario of the
U(IOWF-net) to decide whether the analysed IOWF-
net is relaxed sound. It is important to highlight that
the approach presented in this paper relaxes the con-
ditions of verification presented in (Soares Passos and
Julia, 2013), as well as Relaxed Soundness relaxes
the Soundness correctness criterion. And, although
the reuse of Linear Logic proof trees is achieved, the
verification methods are distinct.
5 CONCLUSIONS
This paper presented an approach for the Re-
laxed Soundness verification of interorganizational
workflow processes modelled by Interorganizational
WorkFlow nets (IOWF-nets). The approach was
based on the construction and analysis of proof trees
of Linear Logic that represent scenarios of the anal-
ysed unfolded IOWF-net. To verify Relaxed Sound-
ness for an IOWF-net, it is necessary in particular to
encounter all sound scenarios that allow the process
to reach the final state of the global business process
and to verify that every activity associated with the
transition of the U(IOWF-net) appears at least once
RelaxedSoundnessVerificationforInterorganizationalWorkflowProcesses
227

in one of the encountered scenarios.
The advantages of such an approach are diverse.
Initially, we extended the Relaxed Soundness crite-
rion to the context of the interorganizational work-
flow processes to guarantee that the main business re-
lationship between the involved organizations can be
provided safely, with no obligation of redesigning the
involved individual processes to satisfy the Relaxed
Soundness criterion before the composition, for ex-
ample.
The fact of working with Linear Logic permits
one to prove the Relaxed Soundness criterion consid-
ering the proper structure of the IOWF-net, without
considering the corresponding automata (reachability
graph). Furthermore,when an approachbased on Lin-
ear Logic to verify the Soundness criterion for IOWF-
nets, as the one presented in (Soares Passos and Julia,
2013) is considered, if the analysed IOWF-net is un-
sound, a subset of the prooftrees built to proveSound-
ness for the IOWF-net can be reused in the context
of this approach. Thus, performing only the analysis
steps in the proof trees that represent each scenario
of the U(IOWF-net) to decide whether the analysed
IOWF-net is relaxed sound.
As a future work proposal, it will be interesting
to implement a kind of real time supervisory control
able to follow the valid scenarios encountered during
the execution of the workflow management system,
avoiding in particular deadlock situations that may ex-
ist in the relaxed sound model, as is the case of sce-
nario Sc
5
of theU(IOWF-net) shown in Figure 1. It is
important since the Relaxed Soundness criterion does
not ensure that the process is deadlock-free.
REFERENCES
Captarencu, O. (2012). Modelling and verification of in-
terorganizational workflows with security constraints:
A petri nets-based approach. In Bajec, M. and
Eder, J., editors, Advanced Information Systems En-
gineering Workshops, volume 112 of Lecture Notes
in Business Information Processing, pages 486–493.
Springer Berlin Heidelberg.
Dehnert, J. and Rittgen, P. (2001). Relaxed soundness of
business processes. In Dittrich, K., Geppert, A., and
Norrie, M., editors, Advanced Information Systems
Engineering, volume 2068 of Lecture Notes in Com-
puter Science, pages 157–170. Springer Berlin Hei-
delberg.
Fahland, D., Favre, C., Koehler, J., Lohmann, N., V¨olzer,
H., and Wolf, K. (2011). Analysis on demand: In-
stantaneous soundness checking of industrial business
process models. Data Knowl. Eng., 70(5):448–466.
Girard, J.-Y. (1987). Linear logic. Theoretical Computer
Science, 50(1):1–102.
Girault, F., Pradin-Ch´ezalviel, B., and Valette, R. (1997). A
logic for Petri nets. Journal Europ´een des Syst`emes
Automatis´es, 31(3):525–542.
Lim, H. W., Kerschbaum, F., and Wang, H. (Sept.-Oct.
2012). Workflow signatures for business process com-
pliance. Dependable and Secure Computing, IEEE
Transactions on, 9(5):756–769.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Riviere, N., Pradin-Chezalviel, B., and Valette, R. (2001).
Reachability and temporal conflicts in t-time petri
nets. In Petri Nets and Performance Models, 2001.
Proceedings. 9th International Workshop on, pages
229–238.
Siegeris, J. and Zimmermann, A. (2006). Workflow model
compositions preserving relaxed soundness. In Pro-
ceedings of the 4th International Conference on Busi-
ness Process Management, BPM’06, pages 177–192,
Berlin, Heidelberg. Springer-Verlag.
Soares Passos, L. M. and Julia, S. (2013). Qualitative anal-
ysis of interorganizational workflow nets using linear
logic: Soundness verification. In Tools with Artificial
Intelligence (ICTAI), 2013 IEEE 25th International
Conference on, pages 667–673.
Sun, H. C. and Du, Y. Y. (2008). Soundness Analysis of
Inter-Organizational Workflows. Information Tech-
nology Journal, 7:1194–1199.
van der Aalst, W. M. P. (1998a). The application of Petri
nets to Workflow Management. In The Journal of Cir-
cuits, Systems and Computers, pages 21–66.
van der Aalst, W. M. P. (1998b). Modeling and analyzing
interorganizational workflows. In Application of Con-
currency to System Design, 1998. Proceedings., 1998
International Conference on, pages 262–272.
Yamaguchi, S., Matsuo, H., Ge, Q.-W., and Tanaka, M.
(2007). Wf-net based modeling and soundness ver-
ification of interworkflows. IEICE Trans. Fundam.
Electron. Commun. Comput. Sci., E90-A(4):829–835.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
228
