
Decision Guidance Analytics Language (DGAL)
Toward Reusable Knowledge Base Centric Modeling
Alexander Brodsky
1
and Juan Luo
2
1
Computer Science Department, George Mason University, Fairfax, VA 22030, U.S.A
2
Information Technology Services, George Mason University, Fairfax, VA 22030, U.S.A.
Keywords: Decision Support, Decision Guidance, Decision Optimization, Machine Learning, Data Management,
Decision Analytics.
Abstract: Decision guidance systems are a class of decision support systems that are geared toward producing
actionable recommendations, typically based on formal analytical models and techniques. This paper
proposes the Decision Guidance Analytics Language (DGAL) for easy iterative development of decision
guidance systems. DGAL allows the creation of modular, reusable and composable models that are stored in
the analytical knowledge base independently of the tasks and tools that use them. Based on these unified
models, DGAL supports declarative queries of (1) data manipulation and computation, (2) what-if
prediction analysis, (3) deterministic and stochastic decision optimization, and (4) machine learning, all
through formal reduction to specialized models and tools, and in the presence of uncertainty.
1 INTRODUCTION
Making decisions is prevalent in various domains
including supply chain and logistics, manufacturing,
power, energy and sustainability to name a few. To
support decision making, enterprises turned to
Decision Support Systems (DSS) (Shim et al., 2002)
and, more recently, to Decision Guidance Systems
(DGS) (Brodsky & Wang, 2008). Broadly, DSS
support decision makers in general ways, including
with useful well-organized information and
visualization. DGS is a class of DSS that are geared
toward producing actionable recommendations,
typically based on formal analytical models and
techniques. This paper proposes the Decision
Guidance Analytics Language (DGAL) and
Analytical Knowledge Base for easy iterative
development and reuse of models and applications
of DGS.
Consider an example of DGS for procurement
and sourcing, e.g., for a manufacturing facility.
Given databases and sources on possible suppliers, a
procurement officer needs to monitor, make and
execute procurement decisions, e.g., which items in
what quantities and from which suppliers should be
procured, as to satisfy business constraints
(production schedule, risk mitigation, inventory
capacity etc.) and minimize the total cost. The
technical tasks to be used by DGS can be broadly
divided into three categories of (1) descriptive, (2)
predictive, and (3) prescriptive decision analytics.
The descriptive analytics tasks resemble those of
database management systems, dealing with data
manipulation and transformation of data (especially
temporal sequences) from multiple sources. For
example, the procurement officer may want to
monitor the status of orders, inventories, schedules,
and DGS will need to generate different aggregated
views of this information, continuously, over time.
The predictive analytics may use the techniques of
stochastic simulation and statistical learning for
regression, classification and estimation (Shmueli &
Koppius, 2011). For example, given the current
inventory and orders status, as well as uncertainty in
future pricing and supply, the procurement officer
may want to estimate the level of inventories and
financial status over the next month and identify
risks. Prediction and estimation of uncertain
outcomes, in turn, may involve regression analysis
of functions (Montgomery, Peck & Vining, 2012)
such as for cost, time, risk, or building classifiers for
different categories of outcomes (e.g., normal
operation, schedule delay, financial default, etc.)
Prescriptive analytics involves optimization and
sensitivity analysis (Haas et al., 2011). For example,
the procurement officer may ask for a
67
Brodsky A. and Luo J..
Decision Guidance Analytics Language (DGAL) - Toward Reusable Knowledge Base Centric Modeling.
DOI: 10.5220/0005349600670078
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 67-78
ISBN: 978-989-758-096-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

recommendation on procurement, e.g., which items
in what quantities from which suppliers and at what
time should be purchased, as to satisfy business rules
and constraints and minimize the total procurement
cost. The prescriptive analytics tasks would typically
correspond to a deterministic or stochastic
optimization problem, possibly using multiple
criteria and under various business assumptions. The
goal of the Decision Guidance Analytics Language
(DGAL) and Analytical Knowledge Base (AKB),
which we propose in this paper, is to support easy
development and reuse of models of the descriptive,
predictive and prescriptive analytical tasks in
decision guidance systems.
As discussed in Section 2 (Related Work), due to
the diversity of computational tools, each designed
for a different task (such as data manipulation,
predictive what-if analysis, decision optimization or
statistical learning), modeling typically requires the
use of different mathematical abstractions
/languages. Essentially, the same underlying reality
must often be modelled multiple times using
different mathematical abstractions. Furthermore,
the modeling expertise required for these
abstractions/languages is typically not within the
realm of business analysts and business end users.
Most problematic in decision guidance modeling
today is the fact that it is task-centric: every
analytical task is typically implemented from
scratch, following a linear, non-reusable
methodology of gathering requirements, identifying
data sources, developing a model/algorithm using a
range of modeling languages and tools, performing
analysis (see upper part of Figure 1). Using this
conventional approach, which we call task-centric,
models and algorithms are difficult to develop,
modify and extend. Furthermore, they typically are
not modular or reusable, nor do they support
compositionality.
Figure 1: Conventional Approach vs. DGAL Approach.
Overcoming the outlined limitations of decision
guidance modeling is the focus of this paper. More
specifically, the contributions of this paper are
twofold. First, we introduce the concept of and the
design principles for the Decision Guidance
Analytics Language (DGAL) and the Analytical
Knowledge-Base (AKB). The key idea is a paradigm
shift from the non-reusable task-centric modeling
approach to reusable-AKB-centric approach (see
lower part of Figure 1). In the latter approach,
modular reusable and composable models, which we
call analytical objects (AOs), are created and stored
in the KB independently of the tasks and the tools
that may use these models. Second, we provide a
specification of DGAL and explain its features and
semantics through examples. DGAL supports the
creation, composition and easy modification of
unified AO’s which model (1) data and schema, (2)
decision variables, (3) computation of functions, (4)
constraints, and (5) uncertainty. Against the unified
AO’s in the AKB, DGAL users can pose declarative
queries for (1) data manipulation and computation,
(2) what-if prediction analysis, (3) deterministic and
1-stage stochastic decision optimization, and (4)
machine learning. In DGAL the declarative queries
are answered through a formal reduction to
specialized models and tools.
The paper is organized as follows. In Section 2
we discuss the related work and also its limitations.
Section 3 presents the design goals and key
functionalities of DGAL. Section 4 overviews JSON
and JSONiq for descriptive analytics, with its
computational DGAL extensions. Section 5
describes the construction and compositio of
Analytical Knowledge and explains how
computation, optimization and learning queries can
be posed against AOs and their semantics. Section 6
describes modeling of uncertainty in AO’s and the
corresponding declarative query operators. Section 7
concludes, provides more details on related work,
and outlines future research questions.
2 RELATED WORK & ITS
LIMITATIONS
To understand the current state of the art and its
limitations, consider the six classes of
tools/languages relevant to modelling analytical
tasks in decision guidance systems: (1) closed
domain-specific end-user oriented tools, e.g.,
strategic sourcing optimization modules within
procurement applications (Katz et al, 2011) (Xu &
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
68

Howitt, 2009); (2) data manipulation languages,
such as SQL, XQuery (Rys, Chamberlin &
Florescu, 2005) and JSONiq (Florescu & Fourny,
2013); (3) simulation modelling languages, such as
Modelica (Fritzson & Engelson, 1998); (4)
simulation languages, such as Jmodelica and
Simulink (Akesson et al., 2010); (5) optimization
modelling languages, such as AMPL (Fourer, Gay &
Kernighan, 1987), GAMS (Rosenthal, 2004), and
OPL (Van Hentenryck et al, 1999) for Mathematical
Programming (MP) and Constraint Programming
(CP); and (6) statistical learning
languages/interfaces, such as PMML (Guazzelli et
al, 2009). Domain specific tools may be easy to use
for a particular well-defined task, but are not
extensible to reflect the diversity of emerging
descriptive, predictive and prescriptive analytical
tasks. Nor do they support compositionality, i.e., the
ability to compose their (white-box) models to
achieve global (system-wide) optimal predictions
and/or prescriptions (e.g., actionable
recommendations), rather than local (silo) optimal
predictions and prescriptions. Data manipulation
languages, obviously, do not support predictive
what-if analysis, optimization or statistical learning.
Simulation languages and tools have the
advantage of their modelling expressivity,
flexibility, and OO modularity, which support
reusability and interoperability of (black-box)
simulation models. However, performing
optimization using simulation models/tools is based
on (heuristically-guided) trial and error. Because of
that, simulation-based optimization is significantly
inferior, in terms of optimality of results and
computational complexity, to MP and CP
tools/algorithms, for problems expressible in
supported analytical forms (e.g., MILP) (Jain &
Grossmann, 2001). Also, while sufficiently
expressive, simulation languages were not designed
for declarative and easy data manipulation provided
by data manipulation languages such as SQL,
XQuery and JSONiq.
Because optimization modelling languages such
as AMPL (Fourer, Gay & Kernighan, 1987), GAMS
(Rosenthal, 2004) or OPL (Van Hentenryck et al,
1999) are used with MP and CP solvers, which use a
range of sophisticated algorithms that leverage the
mathematical structure of optimization problems,
they significantly outperform simulation-based
optimization, in terms of optimality and running
time. However, optimization modelling languages
are not modular, extensible, reusable or support
compositionality; nor do they support low-level
granularity of simulation models (which is expressed
through OO programs.) Statistical learning
languages/tools have similar limitations and
advantages, because most are based on optimization.
Like the simulation tools, optimization and statistical
learning tools were not designed for easy data
manipulation, compared to data manipulation
languages such as SQL, XQuery, and JSONiq.
The Modelica simulation modeling language was
designed to reuse knowledge. It allows a detailed
level of abstraction, including Object-Oriented code
and differential equations (Fritzson & Engelson,
1998). However, Modelica by itself is not a
language for performing optimization, learning, or
prediction. But there are tools such as JModelica for
simulation, and Optimica for simulation-based
optimization (Akesson et al., 2010). However,
because of the low level of abstraction allowed in
Modelica, general Modelica models cannot be
automatically reduced to MP/CP models and solved
by MP/CP solvers.
3 DESIGN GOALS & KEY
FUNCTIONALITIES OF DGAL
The following are the design principles we identified
for the proposed DGAL language/system:
Reusable-KB-centric approach: DGAL must
support the paradigm shift from non-reusable
task-centric modelling approach to reusable-
KB-centric modelling approach.
Task-independent representation of analytical
knowledge: DGAL AOs must represent
analytical knowledge (including data and its
structure, parameters, control/decision
variables, constraints and uncertainty)
uniformly, regardless of the tasks (e.g.,
computation, prediction, optimization or
learning) that may be using it.
Unified language for analytical knowledge
manipulation: DGAL must uniformly support
(1) data manipulation (with the ease of data
manipulation languages like SQL and
JSONiq), (2) deterministic and stochastic
computation/prediction, (3) decision
optimization based on MP/CP, (4)
statistical/machine learning, and (5)
construction/composition of AOs.
Flexible construction of analytical knowledge:
DGAL must support modular AO
composition, generalization, specialization
and reuse.
DecisionGuidanceAnalyticsLanguage(DGAL)-TowardReusableKnowledgeBaseCentricModeling
69

Algebra over analytical KB: DGAL operators
must form an algebra over the set of well-
defined AOs, that is, operators applied to AOs
(in the AKB) must return an AO. Thus, the
resulting AOs can be put back into the AKB,
and then used by other operators. Note, this is
analogous to data manipulation languages
(such as SQL, XQuery and JSONiq), which
are algebras over the corresponding data
model (relational, XML or JSON).
Declarative high-level language: DGAL
analytical knowledge manipulation operators
(compute, optimize, learn) must be declarative
and simple for end users.
Compact language core: It is desirable for
DGAL to have a compact core, and allow
additional functionality through built-in and
user-developed libraries (in the knowledge-
base).
Ease of use by modellers: DGAL should be
easy to use by mathematical modellers and
software/DB developers.
Ease of use by end users: DGAL should
enable built-in KB libraries of AOs to raise
the level of abstraction (obscure mathematical
details, etc.), which would make it easy to use
by end users (such as business analysts and
managers)
Figure 2: DGAL Framework.
The high-level DGAL framework and
functionality is depicted in Figure 2. Central to the
framework is the Analytical Knowledge Base, which
is a collection of Analytical Objects (AO), possibly
organized in different Viewpoint Libraries. AO is
the base component of analytical knowledge. Each
AO can represent, uniformly:
Data and typing: we adopted the Java Script
Object Notation (JSON) as the data model,
which is becoming a de-facto standard for data
analytics.
Within the data, decision/control variables and
parameters over reals, integers and other
domains.
Computation of functions represented via
JSON data manipulation language, JSONiq,
extended with indexed access, and equation
syntax of OPL.
Constraints, using JSONiq syntax for Boolean
expressions, including for universal
quantification.
Uncertainty, by adding distribution functions
to expressions (in functions and constraints),
which implicitly define random variables. All
DGAL operators are applied to AO and return
an AO, and so DGAL constitutes an algebra
(like data manipulation languages SQL,
XQuery and JSONiq). The DGAL operators
are of four key types (Upper part of Figure 2).
Construct: this class of operators allows to
construct an AO from scratch, from another
AO by specialization/generalization, or by
composing an AO from previously defined
AOs.
Compute: this class of operators instantiate an
AO by perform computation of functions
(may involve uncertainty quantification).
Optimize: this class of operators instantiate an
AO by finding values of decision variables
that optimize an objective, and then compute
it with the optimal values.
Learn: this class of operators instantiate an
AO by funding values of its parameters, as to
minimize an estimation error against a
learning set.
The (deterministic) optimization and learning
operators are performed by creating a formal
mathematical or constraint programming model and
solving it using an appropriate solvers (Lower part
of Figure 2). The AO, AKB and DGAL operators
are designed according to the designed principles
outlined in this section.
4 OVERVIEW OF JSON AND
JSONIQ
JavaScript Object Notation (JSON) is rapidly
becoming a data model for descriptive (big data)
analytics. For that reason, we would like to use
JSONiq, a query language over JSON as a
foundation of DGAL. Both JSON and JSONiq are
reviewed in this section. We borrow here the
description of JSONiq from (JavaScript Object
Notation, 2014)(Fourny, 2013).
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
70

JSON data model is a “lightweight data-interchange
format. It is easy for humans to read and write. It is
easy for machines to parse and generate” (JavaScript
Object Notation, 2014). JSON is an open standard
format that uses human-readable text to transmit
data objects consisting of attribute-value pairs. It is
used primarily to transmit data between a server and
web application, as an alternative to XML (Fourny,
2013). Similar to the fact that Xquery is a query and
processing language designed for XML data model,
JSON data model also have a specially designed
powerful query language, JSONiq.
JSONiq is very similar to XQuery, adapted to
JSON, including “the structure and semantics of the
FLWR (FOR-LET-WHERE-RETURN) construct,
the functional aspect of the language, the semantics
of comparisons in the face of data heterogeneity, and
the declarative, snapshot-based updates” (JavaScript
Object Notation, 2014). However, Xquery is more
complex and has more language constructs than
JSONiq due to the fact that XML data model is more
complex than that of JSON. For example, the
element type of XML can be mixed with attributes,
elements, or text. The order of children elements in
XML is significant even with the same contents.
The namespaces, QNames, and XML schema can be
complicated to describe specific types of XML
documents (Fourny, 2013).
The FLWR construct is an iteration structure for
both JSONiq/Xquery. It is different from regular
control structure of programming languages by
considering the simplicity of JSON data model.
FLWR makes the JSONiq a powerful, clean, and
straightforward data processing language. In
addition to querying collections of data in JSON
format, JSONiq can extract, transform, clean, select,
enrich, or join hierarchical or heterogeneous data
sets (Fourny, 2013).
The main technical characteristics of JSONiq
(and XQuery) are as follows:
“It is a set-oriented language. While most
programming languages are designed to
manipulate one object at a time, JSONiq is
designed to process sets (actually, sequences)
of data objects” (Fourny, 2013).
It falls into the category of the functional
programming paradigm. Different from the
procedural programming paradigm such as
Object-Oriented programming languages,
expression is the basic unit of the JSONiq
programs. Every language construct is an
expression and expressions are composed
from one or more previous expressions
(Fourny, 2013).
It is a declarative language. It describes what
computation will be performed, instead of
how the computation (process) will be done.
It does not consider the implementation details
such as specific data structures, algorithms,
memory allocations, and indexing in
databases. The component of the declarative
language usually has clear corresponding
relationship to mathematical logic (Fourny,
2013).
It is designed to process hierarchical or
heterogeneous data which is sometimes semi-
structured. The JSON data type does not need
to follow any specific pattern but can be
heterogeneous. It can be nested structures in
multiple levels. Consequently it is hard to
define a schema which can describe the JSON
data well. Sometimes the schema may only be
able to describe the data partially (Fourny,
2013).
Figure 3: Collections “demand1.jsn” and “purchase1.jsn”.
To exemplify JSON and JSONiq, first consider
JSON collections “demand1.jsn” and
“purchase1.jsn” in Figure 3. JSON collections are
sequences of objects, identified by a name which is a
string, e.g. “demand1.jsn.” In the example, the
collection “demand1.jsn” is a sequence that contains
four objects, {item: 1, demQty: 100}, {item: 2,
demQty: 500}, {item: 3, demQty: 130}, and {item:
4, demQty: 50}. Objects are unordered sets of
key/value pairs, separated by comma. A key is a
string and a value can be any JSON building block.
Each key/value pair is separated by a semicolon.
DecisionGuidanceAnalyticsLanguage(DGAL)-TowardReusableKnowledgeBaseCentricModeling
71

Four items are defined in this collection, with the
quantity of demand specified.
Similarly the collection “purchase1.jsn” contains
a sequence of three suppliers objects. For each
supplier object, four sets of key/value pairs indicate
supplier identifier, the overall supplier cost before
and after volume discount, and the list of items
being purchased from this supplier. Given “items”
as the key of the key/value pair, a sequence of items
is assigned as the value and of the type JSON Array.
Array represents an ordered list of items (in any
category) and can nest. For example, for the first
supplier with key/value pair of “sup: 15”, two
different items are purchased as {item:1, ppu: 2.0,
availQty: 70, qty: 150} and {item:2, ppu: 7.5,
availQty: 2000, qty: 100}. Each item is
represented as a JSON object, with four key/value
pairs. Each item has a unique identifier (e.g. 1), price
per unit, available quantity from the specific
supplier, and purchased quantity.
JSONiq is a language that makes computations
of structures from the input collections easy. In the
JSONiq example of Figure 4, a JSONiq function
orderAnalytics is defined with variable
$purchase_and_demand as argument and object as
return type. The argument variable
$purchase_and_demand is of the composite structure
of both collections “purchase1.jsn” and
“demand1.jsn” as follows:
collection("purchaseAndDemand1.jsn"):
{purchase: [collection("purchase1.jsn")],
demand: [collection("demand1.jsn")] }
The function implements a small supply chain
with items, demand, and supplies. In the function
body, the variable $supInfo is assigned as an array
which contains the sequence of objects in the
collection “purchase1.jsn”. The variable $suppliers
is assigned as an array of all supplier identifiers such
as 15 or 17. The variable $orderedItems is assigned
as an array of all the items and demand quantities in
the collection “demand1.jsn”.
The variable $perSup is defined to calculate for
each supplier, the total cost charged for all items
supplied by this supplier. The “for” clauses is used
to iterate each supplier of $suppliers. For all items
supplied by that specific supplier, within the inner
“for” clause of the second “let” statement, the
variable $priceBeforeDisc represents the cost to
purchase items, which are calculated from price per
unit and item quantity. The variable $priceAfterDisc
is defined to adjust the item cost by considering the
volume discount rate. The cost after discount is
calculated based on a volume discount formula. If
the overall cost is more than the volumeDiscOver, it
will be calculated at a discount rate
volumeDiscRate. The variable $totalCost sums up
the total cost of all suppliers. The variable
$supAvailability is defined as a Boolean variable to
enforce the business rule that the item quantity
purchased must be less than or equal to the available
quantity to each specific supplier. The variable
$demandSatisfied is defined as another Boolean
variable to enforce the business rule that the total
market demand for each item cannot beyond the
total item supply from all suppliers. The Boolean
variable $constraint is the logical ‘&&’ of both
$supAvailability and $demandSatisfied.
Figure 4: JSONiq Example.
The object returned by this function consists of
six key-value pairs representing market demand,
detailed information for each supplier (identifier,
supplied items, price before volume discount, and
price after volume discount), total cost of all
purchases, if market demand has been satisfied, if
the supply availability has been satisfied, and if both
availability have been satisfied. The output of this
JSONiq example is displayed in Figure 5, given the
argument as composite collections in Figure 3.
The FLWOR expression is probably the most
powerful JSONiq construct, which corresponds to
the SQL Select-From-Where clause, but the JSONiq
construct is more general and flexible. The FOR
clause allows iteration over a sequence.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
72
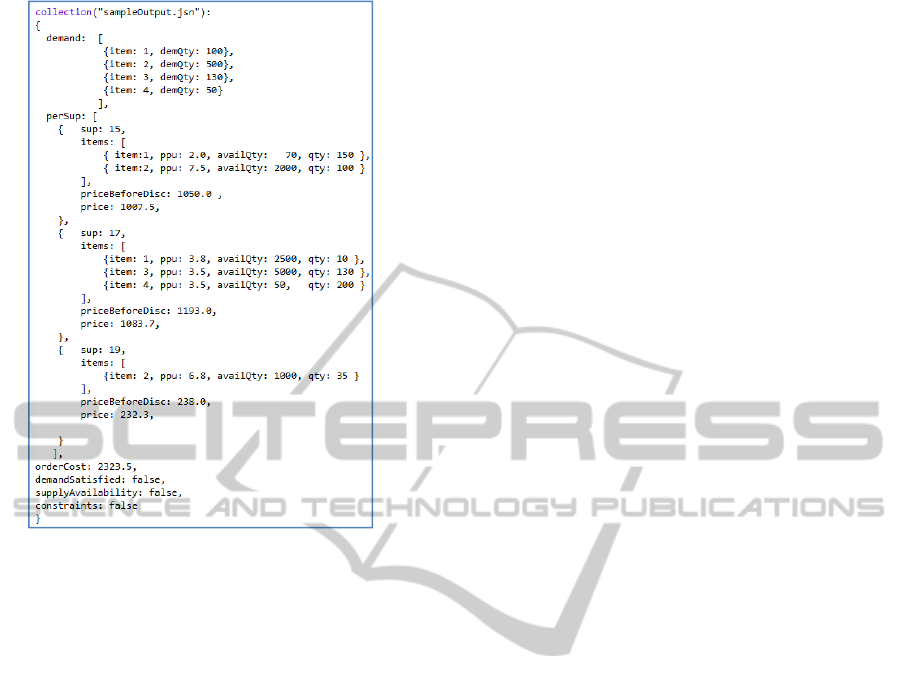
Figure 5: Output of JSONiq Example.
5 DETERMINISTIC
KNOWLEDGE
MANIPULATION
5.1 Construction and Composition of
Analytical Knowledge
To describe the concepts of DGAL knowledge-base,
modules, and analytical object (AO) functions, we
need the concept of an indexable object. Intuitively,
a JSON object is indexable if, in every array it
contains, the objects in that array are uniquely
identified by the value of the first key, which serves
as an index to the corresponding object. More
formally, we say that a JSON object is indexable if,
recursively, in every key-value pair, the value is one
of the following:
- atomic (i.e., not object or array)
- an indexable object
- an array of indexable objects with the same
keys, where there are no 2 objects with the same
value for the first key.
For example, in the collection
“purchaseAndDemand1.jsn”, which serves as input
to the orderAnalytics function, there are no two
“supplier” objects with the same value for the key
sup; similarly, there are no two “item” objects with
the same value for the key item.
A DGAL knowledge-base comprises of a set of
DGAL modules. A DGAL module is simply a
JSONiq module that contains analytical object (AO)
functions. An AO function is simply a JSONiq
function with the following two properties:
- The input and output of the function must be an
indexable object.
- The output object must contain the key
constraints with a value of type Boolean.
For example, the orderAnalytics function in the
previous section satisfies both conditions, i.e., it is
an AO function. Note that, while the orderAnalytics
function, like any JSONiq function, can be viewed
to describe data manipulation (of an input object into
an output object), it can also be viewed as an
integrity constraint on the input object. Namely, the
integrity constraint is satisfied by the input object if
and only if the Boolean value computed for the key
“constraint” in the output object is true. Similarly,
the orderAnalytics function, can be viewed as a
mathematical function that gives numerical values
(such as orderCost computed in the output object)
from the input object (including numerical values in
it).
Clearly, AO functions, like any JSONiq function,
perform data manipulation. For example, to compute
information about order analytics from the purchase
and demand data, one can simply invoke the JSONiq
function orderAnalytics, described in Figure 4.
However, we will also use AO functions for
optimization, statistical learning, simulation and
prediction with the same ease as data manipulation.
In the next subsections we explain, by examples,
how to perform (1) computation/data manipulation,
(2) deterministic optimization, and (3) learning in
DGAL.
5.2 Computation and Data
Manipulation
Performing computation/data manipulation with AO
function is just an invocation of a JSONiq function,
like in the example in Figure 6. First, we need to
import the module in which the function
orderAnalytics is defined. Then we assign values to
the argument of the function. The function is then
called to perform the computation. In the example, it
returns an object representing demand, cost of each
supplier, total cost, and a true/false Boolean value
for demand being satisfied, the supply availability
being satisfied, and both constraints being satisfied.
DecisionGuidanceAnalyticsLanguage(DGAL)-TowardReusableKnowledgeBaseCentricModeling
73
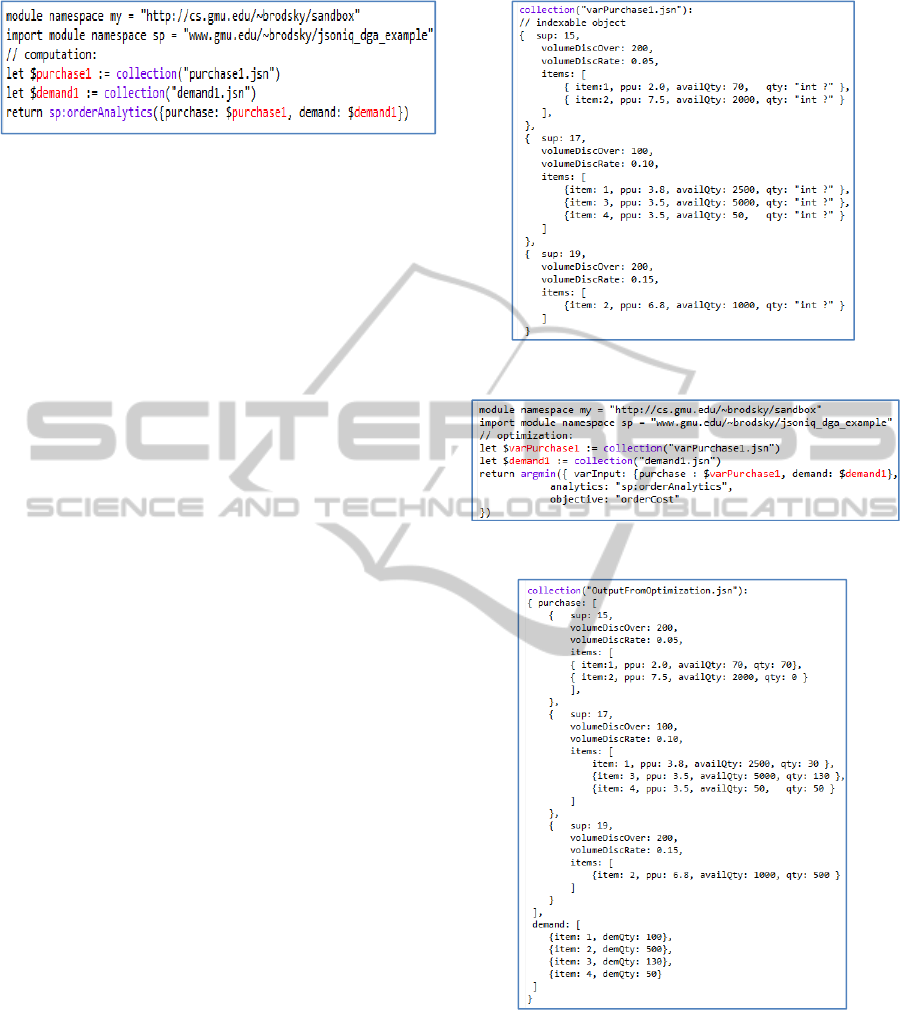
Figure 6: Computation.
5.3 Optimization
If the quantities in the collection “purchase1.jsn”
used as argument to JSONiq query in Figure 4 were
not known, the procurement officer may want to find
them as to make sure that the constraints of both
Boolean expressions “$demandSatisfied” and
“$supAvailability” are satisfied (i.e., computed to be
true), and the total cost is minimized. Intuitively,
the DGAL optimization operators are designed to do
this kind of “reverse” computation.
To perform optimization in DGAL, we first need
to annotate the input object to the AO function
(orderAnalytics in the example) to indicate which
values (qty’s in the example) are not known but we
would like the system to find (i.e., decision
variables). Figure 7 gives an example of such
annotation in the collection “varPurchase1.jsn.”
This collection is identical to the collection
“purchase1.jsn” in Figure 3, with the exception that
the key qty does not have a numerical value, but has
instead a special annotation “int ?” to indicate that
qty will now be a decision variable. The annotated
collection must have the following structural
limitation. Informally, the structure of the output
object should not depend on the values of the
annotated decision variables; only numerical values
in the output object may depend on the decision
variables.
With the annotated input collection, performing
optimization is very simple: it is performed by
invoking the DGAL function argmin (or argmax) as
exemplified in Figure 8.
The DGAL function argmin in Figure 8 is
invoked with the following input object. The first
key varInput has the value which is the annotated
input to orderAnalytics, i.e., when we use the
annotated collection “varPurchase1.jsn” from
Figure 7 instead of the original collection
“purchase1.jsn” from Figure 3. The second key
analytics has the value that indicates the name of the
AO function used, orderAnalytics in the example.
The third key objective has the value that indicates
the key of the numeric value in the output object of
orderAnalytics – orderCost in the example - that we
would like to use as the objective to be minimized.
Figure 7: varPurchase1.jsn.
Figure 8: Optimization.
Figure 9: Output of Optimization.
The output of the argmin function is an object
identical to the annotated input object, with the
exception that all annotations “int ?” (which denote
decision variables) are now replaced with actual
numerical values that (1) satisfy the constraints, i.e.,
result in the value true computed for the key
constraints in the output object; and (2) minimize
the numerical value computed for the key orderCost,
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
74

which was designated as the objective in the
invocation of the argmin function. The collection
“OutputFromOptimization.jsn” in Figure 9
exemplifies the optimization output. More generally,
given an invocation
argmin({varInput: I, analytics: A, objective:O})
let
- X be a vector of decision variables
corresponding to annotations “int ?” and “float
?” in I
- f: D
R be a function from the domain D of X
to Reals, that corresponds to the computation
of the value of the key O (for objective) in the
output object computed by the JSONiq
function A applied to I
- C(X) be a set of constraints in variables X, that
corresponds to the Boolean value for the key
constraints in the output object computed by
JSONiq function A applied to I
The semantics of the DGAL function argmin is
as follows:
- If C(X) is infeasible, argmin returns the
string“infeasible.”
- If C(X) is feasible, but f(X) does not have a
lower bound subject to C(X), argmin returns
the string “unbounded.”
- Otherwise, let Xo be a solution to the problem
min f(X) subject to C(X). DGAL argmin
function returns the annotated input object I in
which all annotations “int ?” and “float ?” are
replaced with the corresponding numerical
values from Xo.
The semantics of argmax is similar.
5.4 Learning
If the volume discount parameters, volumeDiscOver
and volumeDiscRate, were not known in the
collection “purchase1.jsn”, how can we learn them
(via regression analysis) from historical data? The
DGAL function learn is provided for this purpose.
To use the learn function in DGAL, we first need
to annotate the input object to the AO function
(orderAnalytics in the example) to indicate which
parameters we would like to learn. In the example
these parameters are volumeDiscOver and
volumeDiscRate for each supplier in collection
“varPurchase.jsn”. Figure 10 gives an example of
such annotation in the collection
“paramPurchase1.jsn”. This collection is identical
to the collection “varPurchase1.jsn in Figure 7, with
the exception that the keys volumeDiscOver and
volumeDiscRate do not have a numerical value, but
have instead a special annotation “float …” to
indicate that they will now be parameters to be
learned using regression.
Figure 10: paramPurchase1.jsn.
We also need to create a learning set collection,
which captures a set of (historical) input-output pairs
of a function we are trying to regress. The collection
“learningSet1.jsn” in Figure 11 exemplifies the
learning set. It contains a sequence of JSON objects,
each having keys input and output. The value for the
key output in every object gives a historical value
for orderCost. The value for the key input in every
object gives a “partial” input object for the AO
function orderAnalytics. It is “partial” because we
only need information on the quantities for each
item order from each supplier, but do not need any
other information. With the “paramPurchase1.jsn”
collection and the learning set object, performing
regression learning is done by invocation of DGAL
function learn, as shown in Figure 12.
Figure 11: Learning Set.
DecisionGuidanceAnalyticsLanguage(DGAL)-TowardReusableKnowledgeBaseCentricModeling
75

Figure 12: Learning.
Figure 13: Output from Learning.
The function learn is invoked with an object with
key-value pairs for paramInput; analytics to indicate
the AO function to be learned (orderAnalytics in the
example); outValue, to indicate which value the
function computes (orderCost in the example), and
the previously constructed learningSet.
The output of function learn is exemplified in
Figure 13. The structure of output is exactly as the
input collection “paramPurchaseAndDemand1”
with the exception that parametric annotations “float
…” replaced by values. However, the decision
variables annotations “int ?” are still left as they
were. Note that both parameters and decision
variables can be either of type int or float. The
values for parameters are constructed to minimize
the summation of squares of learning errors for each
input-output pair in the learning set.
6 UNCERTAINTY:
SIMULATION, PREDICTION
AND STOCHASTIC
OPTIMIZATION
Consider Figure 14, which exemplifies how
uncertainty is represented in AO functions.
Figure 14: AO with uncertainty.
In the example, the stochOrderAnalytics function
is identical to the (deterministic) orderAnalytics
function in Figure 4 with the exception that, in the
$ppu computation, a random value drawn from the
Gaussian distribution is used (see a box in Figure
14). When this is done, the variable $ppu on the left
of the assignment statement represents a random
variable. Furthermore, all expressions that are
dependent on it in the computation, directly or
indirectly, also represent random variables.
In the context of uncertainty, we can talk about
simulation, prediction and stochastic optimization
(see example in Figure 15). Simulation is done
exactly as computation, namely by invoking the AO
function stochOrderAnalytics. Because a random
value is drawn (see Figure 14), every invocation of
stochOrderAnalytics may result in a different
answer, which is a result of stochastic simulation.
We can also perform prediction, e.g., using the
Monte-Carlo method, to estimate the expectation of
the random variables ($ppu and all expressions that
depend on it in Figure 14). This is done using the
DGAL function predict, which is invoked with the
input object that has key-value pairs input, analytics,
sigmaUpperBound, confidence and timeUpperBound
(see prediction part in Figure 15). The value for
input is the same as in the computation (i.e.,
collection purchaseAndDemand1); analytics
indicates the used AO function (stochOrderAnalytics
in the example). The estimates of the random
variables are done so that the standard deviation
would not exceed the sigmaUpperBound with the
indicated statistical confidence, unless computation
time exceeds the indicated timeUpperBound, which
is an optional parameter. The form of the output is
the same as in the deterministic computation (the
example in Figure 5), with annotation, with the
exception that instead of the (deterministically)
computed numeric values, the output object contains
JSON objects that capture estimations of the
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
76
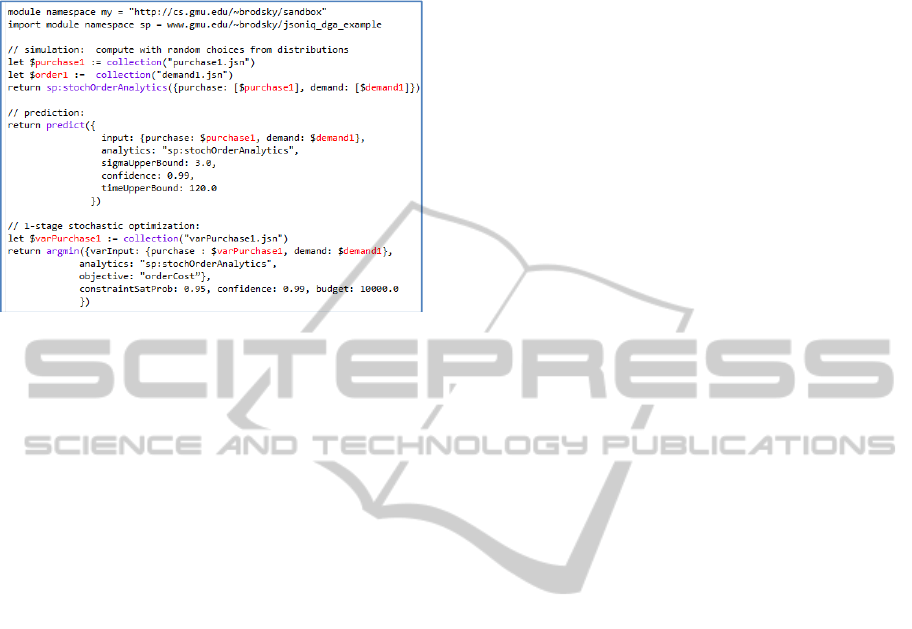
expectation and standard deviation of random
variables.
Figure 15: Simulation, prediction, 1-stage stochastic
optimization.
Finally, a one-stage stochastic optimization is
performed by invoking the DGAL function argmin
(or argmax). The input object is the same as in the
deterministic case, with the exception that it is
extended with key-value pairs for the required
constraintSatProb to indicate with what minimal
probability the constraints must be satisfied and with
what statistical confidence. Optionally, a maximum
computation budget can be indicated.
The output of the argmin function has the same
form as in the deterministic case. Semantically,
argmin in this case is interpreted as a (one-stage)
stochastic optimization to minimize the expectation
of the indicated objective (orderCost in the
example), which is now interpreted as a random
variable.
7 MORE ON RELATED WORK
AND CONCLUSIONS
In this paper we proposed the Decision Guidance
Analytics Language (DGAL) for easy iterative
development of decision guidance systems. The
work on DGAL leverages our prior work on
decision guidance and optimization languages. In
particular, the unification of computation and
equational syntax comes from CoJava (Brodsky &
Nash, 2006), SC-CoJava (Brodsky, Al-Nory &
Nash, 2012) and DGQL (Brodsky et al., 2011),
CoReJava (Brodsky, Luo & Nash, 2008; Luo &
Brodsky, 2011) on adding regression to DGAL, and
DG-Query (Brodsky, Halder & Luo, 2014) which
are designed to seamlessly add deterministic
optimization and machine learning to Java, SQL and
XQuery code, respectively, via automatic reduction
to MP, CP or specialized algorithms. Also, DGAL
fits into the framework of, but is significantly more
general than, Decision Guidance Management
Systems, proposed in (Brodsky and Wang, 2008).
Finally, the concept of centralized AKB is borrowed
from our work on the Process Analytics Formalism
(Brodsky, Shao & Riddick, 2013; Alrazgan &
Brodsky, 2014), which was limited to MP/CP
optimization only.
Many research questions remain open. They
include (1) specific reduction algorithms from
DGAL queries and AO functions to specialized
formal models of optimization, statistical learning,
and uncertainty quantification; it may be promising
to borrow from the work on constraint databases to
support symbolic constraint (2) development
specialized algorithms for stochastic optimization in
DGAL that can leverage deterministic
approximation encoded in DGAL analytical objects;
(3) development of specialized algorithms that can
utilize pre-processing of stored (and therefore, static)
AO’s, to speed up optimization, generalizing the
results in (Egge, Brodsky, & Griva, 2013); and, (4)
developing graphical user interfaces for domain
specific languages based on DGAL.
REFERENCES
Shim, J. P., Warkentin, M., Courtney, J. F., Power, D. J.,
Sharda, R., & Carlsson, C. (2002). Past, present, and
future of decision support technology. Decision
support systems, 33(2), 111-126.
Brodsky, A., & Wang, X. S. (2008). Decision-guidance
management systems (DGMS): Seamless integration
of data acquisition, learning, prediction and
optimization. In Proceedings of the 41
st
Hawaii
International Conference on System Sciences, (pp. 71-
71). IEEE.
Shmueli, G., & Koppius, O. R. (2011). Predictive
analytics in information systems research. Mis
Quarterly, 35(3), 553-572.
Montgomery, D. C., Peck, E. A., & Vining, G. G. (2012).
Introduction to linear regression analysis (Vol. 821).
John Wiley & Sons.
Haas, P. J., Maglio, P. P., Selinger, P. G., & Tan, W. C.
(2011). Data is Dead... Without What-If Models.
PVLDB, 4(12), 1486-1489.
Katz, S. B., Labrou, Y., Kanthanathan, M., & Rudin, K.
M. (2011). Method for managing a workflow process
that assists users in procurement, sourcing, and
decision-support for strategic sourcing. U.S. Patent
No. 7,870,012. Washington, DC: U.S. Patent and
Trademark Office.
DecisionGuidanceAnalyticsLanguage(DGAL)-TowardReusableKnowledgeBaseCentricModeling
77

Xu, K., & Howitt, I. (2009). Realistic energy model based
energy balanced optimization for low rate WPAN
network. In Proceedings of SOUTHEASTCON '09.
IEEE (pp. 261-266). IEEE.
Rys, M., Chamberlin, D., & Florescu, D. (2005). XML
and relational database management systems: the
inside story. In Proceedings of the 2005 ACM
SIGMOD international conference on Management of
data (pp. 945-947). ACM.
Florescu, D., & Fourny, G. (2013). JSONiq: The history of
a query language. Internet Computing, IEEE, 17(5),
86-90.
Fritzson, P., & Engelson, V. (1998). Modelica—A unified
object-oriented language for system modeling and
simulation. In ECOOP’98—Object-Oriented
Programming (pp. 67-90). Springer Berlin Heidelberg.
Akesson, J., Arzén, K. E., Gäfvert, M., Bergdahl, T., &
Tummescheit, H. (2010). Modeling and optimization
with Optimica and JModelica. org-Languages and
tools for solving large-scale dynamic optimization
problems. Computers & chemical engineering, 34(11),
1737-1749.
Fourer, R., Gay, D. M., & Kernighan, B. W. (1987).
AMPL: A mathematical programming language.
Murray Hill, NJ 07974: AT&T Bell Laboratories.
Rosenthal, E. (2004) GAMS: a user's guide. In GAMS
Development Corporation.
Van Hentenryck, P., Michel, L., Perron, L., & Régin, J. C.
(1999). Constraint Programming in OPL. In Principles
and Practice of Declarative Programming (pp. 98-
116). Springer Berlin Heidelberg.
Guazzelli, A., Zeller, M., Lin, W. C., & Williams, G.
(2009). PMML: An open standard for sharing models.
The R Journal, 1(1), 60-65.
Jain, V., & Grossmann, I. E. (2001). Algorithms for hybrid
MILP/CP models for a class of optimization problems.
INFORMS Journal on computing, 13(4), 258-276.
Fritzson, P., & Engelson, V. (1998). Modelica—A unified
object-oriented language for system modeling and
simulation. In ECOOP’98—Object-Oriented
Programming (pp. 67-90). Springer Berlin Heidelberg.
JavaScript Object Notation 2014. Available from:
<http://json.org/>. [17 November 2014]
Fourny, G. (2013). JSONiq The SQL of NoSQL.
Brodsky, A., Constraint Databases: Promising Technology
or Just Intellectual Exercise? Constraints Journal, 2(1),
1997.
Brodsky, A., & Nash, H. (2006). CoJava: Optimization
modeling by nondeterministic simulation. In
Principles and Practice of Constraint Programming-
CP 2006 (pp. 91-106). Springer Berlin Heidelberg.
Brodsky, A., Al-Nory, M., & Nash, H. (2012). SC-
CoJava: A Service Composition Language to Unify
Simulation and Optimization of Supply Chains. In
Modelling for Decision Support in Network-Based
Services (pp. 118-142). Springer Berlin Heidelberg.
Brodsky, A., Mana, S. C., Awad, M., & Egge, N. (2011,
January). A Decision-guided advisor to maximize ROI
in local generation & utility contracts. In Innovative
Smart Grid Technologies (ISGT), (pp. 1-7). IEEE.
Brodsky, A., Luo, J., & Nash, H. (2008). CoReJava:
learning functions expressed as Object-Oriented
programs. In Machine Learning and Applications,
2008. ICMLA'08. Seventh International Conference on
(pp. 368-375). IEEE.
Luo, J., and Brodsky, A. (2011). Piecewise Regression
Learning in CoReJava Framework, In International
Journal of Machine Learning and Computing, Vol.
1(2): 163-169 ISSN: 2010-3700.
Brodsky, A., Halder, S. G., & Luo, J. (2014). DG-Query:
An XQuery-based Decision Guidance Query
Language. In ICEIS 2014-16th International
Conference on Enterprise Information Systems.
Brodsky, A., & Wang, X. S. (2008). Decision-guidance
management systems (DGMS): Seamless integration
of data acquisition, learning, prediction and
optimization. In Hawaii International Conference on
System Sciences, Proceedings of the 41st Annual (pp.
71-71). IEEE.
Brodsky, A., Shao, G., & Riddick, F. (2013). Process
analytics formalism for decision guidance in
sustainable manufacturing. Journal of Intelligent
Manufacturing, 1-20.
Alrazgan, A., & Brodsky, A. (2014). Toward Reusable
Models: System Development for Optimization
Analytics Language (OAL). Technical Report GMU-
CS-TR-2014-4, Department of Computer Science,
George Mason University, Fairfax, VA 22030, USA.
Egge, N., Brodsky, A., & Griva, I. (2013). An Efficient
Preprocessing Algorithm to Speed-Up Multistage
Production Decision Optimization Problems. In
System Sciences (HICSS), 2013 46th Hawaii
International Conference on (pp. 1124-1133). IEEE.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
78
