Measuring Intrinsic Quality of Human Decisions

Tamal T. Biswas

Department of CSE, University at Buffalo, Amherst, NY, U.S.A.

1 RESEARCH PROBLEM

Decision making is a major area of AI. A central part

of it is emulating human decision making via super-

vised or unsupervised learning. Much of this research

is based on delivering systems that are capable of pro-

ducing optimal solutions based on rules for any given

problem. In most of the supervised learning mod-

els, a computational agent learns from the feedback

of the human supervisor. The other side, judging hu-

man decisions by an AI system, has not been explored

as much.

In most applications related to human decision

making, the actors are aware of the true or expected

value and cost of the actions. The available choices

are deterministic and known to the actor, and the

goal is to ﬁnd some choice or allowed combination

of choices that maximizes the expected utility value.

The decisions taken can be either dependent or inde-

pendent of actions taken by other entities that are part

of the decision-making problem. In bounded ratio-

nality, however, such optimization is often not possi-

ble due to time constraints, the lack of accurate com-

putation power by humans, the cognitive limitation

of mind, and/or insufﬁcient information possessed by

the actor at the time of taking the decision. With these

limited resources, the decision-maker in fact looks for

a solution that seems satisfactory to him rather than

optimal. Thus bounded rationality raises the issue of

getting a measure of the quality of decisions made by

the person.

Humans make decisions in diverse scenarios

where knowledge of the best outcome is uncertain.

This pertains to various ﬁelds, for example online

test-taking, trading of stocks, and prediction of future

events. Most of the time, the evaluation of decisions,

considers only a few parameters. For example, in test-

taking one might consider only the ﬁnal score; for

a competition, the results of the game; for the stock

market, proﬁt and loss, as the only parameters used

when evaluating the quality of the decision. We re-

gard these as extrinsic factors.

Although bounded-rational behavior is not pred-

icated on making optimal decisions, it is possible to

re-evaluate the quality of the decision, and thus move

from bounded toward strict rationality, by analyzing

the decisions made with entities that have higher com-

puting power and/or a longer timespan. This approach

gives a measure of the intrinsic quality of the decision

taken. Ideally, this removes all dependence on factors

beyond the agent’s control, such as, performance by

other agents (on tests or in games) or accidental cir-

cumstances (which may affect proﬁt or loss).

Decisions taken by humans are often effectively

governed by satisﬁcing, a cognitive heuristic that

looks for an acceptable sub-optimal solution among

possible alternatives. Satisﬁcing plays a key role in

bounded rationality contexts. It has been documented

in various ﬁelds, including but not limited to eco-

nomics, artiﬁcial intelligence and sociology (Wiki-

Books, 2012). We aim to measure the loss in qual-

ity and opportunity from satisﬁcing and express the

bounded-rational issues in terms of depth of thinking.

Let us illustrate the principles in the case of chess.

The problems of determining whether a given chess

position is winnable for the player to move, and ﬁnd-

ing a winning move if one exists, are held to be com-

putationally infeasible.

The limited capability of the

mind is responsible for this state of action, as the

agent knows it is not possible to be certain about the

optimal move in a limited time. There is again a key

difference between this setting and the situation when

solving any multiple-choice question, where the ex-

aminer usually knows the answer right away.

The other issue with satisﬁcing is the effect of

short-term gain. Most often short-term gains look

lucrative, but eventually turn out to have come from

poor choices. In chess, a similar scenario may occur

when an amateur player falls into the trap of capturing

a “hanging” piece on the board, which may however

be “poisoned”, meaning that the opponent can retali-

ate and win in a few moves.

In multiple-choice-question scenarios, there is no

standard metric to evaluate the answers. Any aptitude

In complexity theoretic terms, when chess is extended

to armies of 2n pieces each on an n ×n board, both problems

are complete for exponential time, or for polynomial space

in the presence of a generalized “50-move draw rule”.

T. Biswas T..

Measuring Intrinsic Quality of Human Decisions.

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

test allows multiple participants to answer the same

problem, and based on their responses, the difﬁculty

of the problem is measured. The desired measure of

difﬁculty is used when calculating the relative impor-

tance of the question on their overall scores. The ﬁrst

issue is how to distinguish the intrinsic difﬁculty of a

question from a simple poor performance by respon-

dents? A second issue is how to judge whether a ques-

tion is hard because it requires specialized knowledge,

requires deep reasoning, or is “tricky”—with plausi-

ble wrong answers. Classical test theory approaches

are less able to address these issues owing to design

limitations such as in test questions, with only one an-

swer receiving credit.

2 OUTLINE OF OBJECTIVES

We have identiﬁed three research goals:

1. Find an intrinsic way to judge the difﬁculty of de-

cision problems, such as test questions,

2. Quantify a notion of depth of thinking, by which

to identify satisﬁcing and measure the degree of

boundedness in rational behavior.

3. Use an application context (namely, chess) in

which data is large and standards are well known

so as to calibrate extrinsic measures of perfor-

mance reﬂecting difﬁculty and depth. Then trans-

fer the results to validate goals 1 and 2 in applica-

tions where conditions are less regular.

Putting together all these aspects, we have de-

veloped a model that can segregate agents by their

skill level via rankings based on their decisions and

the difﬁculty of the problems faced, rather than be-

ing based only on total test scores and/or outcomes of

games. Moreover, it is possible to predict an actor’s

future performance based on the past decisions made

by similar agents.

In our setting, we have chosen chess games played

by thousands of players spanning a wide range of

ranking. The moves played in the games are ana-

lyzed with chess programs, called engines, which are

known to play stronger than any human player. We

can assume that given considerable time, an engine

can provide an effectively optimal choice at any po-

sition along with the numeric value of the position,

which exceeds the quality of evaluation perceived by

even the best human players.

This approach can be extended to other ﬁelds of

bounded rationality, for example stock market trad-

ing and multiple choice questions, for several reasons,

one being that the model itself does not depend on any

game-speciﬁc properties. The only inputs are numer-

ical values for each option, values that have authori-

tative hindsight and/or depth beyond a human actor’s

immediate perception. Another is the simplicity and

generality of the mathematical components governing

its operation, which are used in other areas.

Our work aims to measure the intrinsic quality of

human decisions, identifying general features inde-

pendent of chess. This paper demonstrates the rich-

ness and efﬁcacy of our modeling paradigm. We show

how it embraces both values and preference ranks,

lends itself to multiple statistical ﬁtting techniques

that act as checks on each other, and gives consistent

and intelligible results in the chess domain. It is thus

both a rich testbed for methodological issues that arise

in other areas, and a fulcrum for transferring evalua-

tion criteria established with big data to other appli-

cations.

3 STATE OF THE ART

Various descriptive theories of decision models have

been proposed to date. Prospect theory, the most

popular decision model, was introduced by Kahne-

man and Tversky (Kahneman and Tversky, 1979).

Prospect theory handles a few fundamental require-

ments for dealing with decision measures, such as

eliminating clearly inferior choices and simplifying

and ordering outcomes. It introduced the concept of

‘reference dependence’, where outcomes are scaled to

the current evaluation, situation, or ‘status quo’. An-

other suggestion made in the model is measuring the

scaled outcome differently based on whether the deci-

sion causes gains or losses relative to the ‘status quo’.

That is, different utility functions are used for scaling

losses or gains related to the current status. The model

also introduced a notion of decision weights by con-

verting the probability p to π(p), where π is a convex

function that moderates initially extreme probability

estimates.

Fox and Tversky (Tversky and Fox, 1995; Fox,

1999; Fox and Tversky, 1998) extended this model to

decision making in a way that moved the focus from

risk (known event probabilities) to uncertainty (un-

known event probabilities). The measure of uncer-

tainty was used to derive weights for each decision.

Further improvement was done in the rank dependent

utility (RDU) theories, where the basis of decision

weighting function was changed from the probabil-

ity of ‘winning x’ to the probability of ‘winning x or

more’.

In response to prospect theory, Loomes and Sug-

dem (Loomes and Sugden, 1982) introduced regret

MeasuringIntrinsicQualityofHumanDecisions

theory – which yielded better justiﬁcation of some

empirical results than prospect theory. In this model,

the utility value is composed of two components: the

evaluation of the outcome obtained, and differences

between that outcome and the other discarded out-

comes. Lopes (Lopes, 1987) proposed a third ma-

jor theory, called security-potential/aspiration (SP/A)

theory. It assumes that the decision-maker simultane-

ously considers two distinct criteria in making deci-

sions: a utility value and a measure of progress toward

achieving some pre-set goal.

Sequential sampling/accumulation based models

are the most inﬂuential type of decision models to

date. Decision ﬁeld theory (DFT) applies sequential

sampling for decision making under risk and uncer-

tainty (Busemeyer and Townsend, 1993). One im-

portant feature of DFT is ‘deliberation’, i.e., the time

taken to reach a decision. DFT is a dynamic model

of decision making that describes the evolution of the

preferences across time. It can be used as a predic-

tor not only of the decisions, but also of the response

times. Deliberation time (combined with the thresh-

old) controls the decision process. The threshold is

an important parameter which controls how strong the

preference needs to be to get accepted.

Although IRT models do not involve any decision

making models directly, they provide tools to measure

the skill of a decision-maker. IRT models are used

extensively in designing questionnaires which judge

the ability or knowledge of the respondent. The item

characteristic curve (ICC) is central to the represen-

tation of IRT. The ICC plots p(θ) as a function of θ,

where θ and p(θ) represent the ability of the respon-

dent and his probability of choosing any particular

choice, respectively. Morris and Branum et al. have

demonstrated the application of IRT models to ver-

ify the ability of the respondents with a particular test

case (Morris et al., 2005).

On the chess side, a reference chess engine E ≡

E(d,mv) was postulated in (DiFatta et al., 2009). The

parameter d indicates the maximum depth the engine

can compute, where mv represents the number of al-

ternative variants the engine used. In their model, the

fallibility of human players is associated to a likeli-

hood function L with engine E to generate a stochastic

chess engine E(c), where E(c) can choose any move

among at max mv alternatives with non zero probabil-

ity deﬁned by the likelihood function L.

In relation to test-taking and related item-response

theories (Baker, 2001; Thorpe and Favia, 2012; Mor-

ris et al., 2005), our work is an extension of Rasch

modeling (Rasch, 1960; Rasch, 1961; Andersen,

1973; Andrich, 1988) for polytomous items (Andrich,

1978; Masters, 1982; Linacre, 2006; Ostini and Ner-

ing, 2006), and has similar mathematical ingredients

(cf. (Wichmann and Hill, 2001; Maas and Wagen-

makers, 2005)). Rasch models have two main kinds

of parameters, person and item parameters. These are

often abstracted into the single parameters of actor lo-

cation (or “ability”) and item difﬁculty. It is desir-

able and standard to map them onto the same scale in

such a way that ‘location > difﬁculty’ is equivalent to

the actor having a greater than even chance of getting

the right answer, or of scoring a prescribed norm in

an item with partial credit. For instance, the famil-

iar 0.0 − 4.0/F-to-A grading scale may be employed

to say that a question has exactly B level difﬁculty if

half of the B-level students get it right. The formulas

in Rasch modeling enable predicting distributions of

responses to items based on differences in these pa-

rameters.

4 METHODOLOGY

Our work builds on the original model of Regan and

Haworth (Regan and Haworth, 2011), which has two

person parameters called s for sensitivity and c for

consistency. The main schematic function E(s,c) is

determined by regression from training data to yield

an estimation of Elo rating, which is the standard

measure of player quality or strength in the chess

world. The threshold for “master” is almost univer-

sally regarded as 2200 on this scale, with 2500 serv-

ing as a rating threshold for initial award of the ti-

tle of Grandmaster, and 2000 called “Expert” in the

Unites States. The current world champion Magnus

Carlsen’s 2877 is 26 points higher than the previ-

ous record of 2851 by former world champion Garry

Kasparov. Computer programs running on consumer-

level personal computers are, however, reliably esti-

mated to reach into the 3200s, high enough that no hu-

man player has been backed to challenge a computer

on even terms since then-world champion Vladimir

Kramnik (currently 2760) lost a match on December

2006 to the Deep Fritz 10 program running on a quad-

core PC. This fact has raised the ugly eventuality of

human cheating with computers during games, but

also furnishes the reliable values for available move

options that constitute the only chess-dependent input

to the model.

Our main departure from Rasch modeling is that

the engine’s “authoritative” utility values are used to

infer probabilities for each available response, with-

out recourse to a measure of difﬁculty on the Elo

scale itself. That is, we have no prior notion of “a

position of Grandmaster-level difﬁculty”, or “expert

difﬁculty”, or “beginning difﬁculty” per-se. Chess

ICAART2015-DoctoralConsortium

problems, such as White to checkmate in two moves

or Black to move and win, are commonly rated for

difﬁculty of solution, but the criteria for these do

not extend to the vast majority of positions faced in

games, let alone their reference to chess-speciﬁc no-

tions (such as “sacriﬁces are harder to see”). Instead,

we aim to infer difﬁculty from the expected loss of

utility from that of the optimal move, and separately

from other features of the computer-analysis data it-

self. Hence we propose a new name for our paradigm:

“Converting Utilities into Probabilities”. Thus far, we

have worked with utility values from only the highest

depth of an engine’s search.

4.1 Chess Engines and their Evaluations

The Universal Chess Interface (UCI) protocol used by

most major chess engines speciﬁes two basic modes

of searching, called single-pv and multi-pv, and or-

ganizes searches in both modes to have well-deﬁned

stages of increasing depth.

Depth is in unit of plies,

also called half-moves.

In single-pv mode, at any

depth, only the best move is analyzed and reported

fully. If a better move is found at a higher depth, the

evaluation of the earlier selected move is not necessar-

ily carried forward any further. Whereas, in multi-pv

mode, we can select the number ` of moves to be ana-

lyzed fully. The engine reports the evaluation of each

of the ` best moves at each depth. In our work, we

run the engine in `-pv mode with ` = 50, which cov-

ers all legal moves in most positions and all reason-

able moves in the remaining positions. Table 1 shows

output from the chess engine Stockﬁsh 3 in multi-pv

mode at depths up to 19.

Prior to our paper (Biswas and Regan, 2015), all

work on the Regan-Haworth model used only the val-

ues in the rightmost column. This doctoral research

uses and interprets the data in all columns. We have

used multiple engines. Part of our research has in-

volved ﬁnding “correction factors” between engines

to bring their values for the same positions into line.

In all but a few engines the depths are successive in-

tegers. (The engine Junior used to produce evaluation at

depths at an interval of 3 i.e., 3-6-9-12. . . .) Also ‘pv’ stands

for “principal variation”.

A move by White followed by a move by Black equals

two plies.

The position is at White’s 29

move in the 5

game

of the 2008 world championship match between Kramnik-

Anand with Forsyth Edwards Notation (FEN) code

“8/1b1nkp1p/4pq2/1B6/PP1p1pQ1/2r2N2/5PPP/4R1K1 w

- - 1 29”. Values are from White’s point of view in units

of centipawns, ﬁguratively hundredths of a pawn.

5 RESEARCH PLAN

Decision making is studied from both normative and

descriptive standpoints. Normative theories concen-

trate on making the best decision in any situation,

whereas descriptive theories focus on how humans ac-

tually make decisions. In our proposed model, we

concentrate on the descriptive side. We assume we

have an AI agent that provides an ‘optimal’ or near-

optimal solution with the help of analytic machinery

developed within the normative approach. We ana-

lyze the authoritative data of the AI agent to infer

psychometric quantities about the nature of the posi-

tion/problem in advance of learning how humans give

response to them.

Our goal is to map IRT models in the chess con-

text, evaluate on our extensive data, and use the in-

verse mapping to make inferences about IRT model-

ing itself. The main motivation for using IRT mod-

els is the notion of discrimination, which is governed

by the difﬁculty of the problem. Rasch models, the

most popular specialization of IRT models, deﬁne an

item parameter as a measure of the intrinsic difﬁculty

apart from performance results and personal ability

parameters. IRT models include various other item

parameters to make the model robust and get a better

ﬁt. Contrary to the IRT models, where the probabil-

ity of choosing among the choices is derived from the

responses of humans, our model estimates the prob-

ability of choices from the evaluation by authorities,

namely AI chess engines of supreme strength.

We aim to incorporate the idea of depth or process

of deliberation by ﬁtting the moves of the chess play-

ers to itemized skill levels based on depth of search

and sensitivity. We will ﬁrst analyze the results and

later compare those to the reference fallible agents

in the game context model of (Regan and Haworth,

2011). The ability of a player can be mapped to vari-

ous depths of the engines. An amateur player’s search

depth for choosing any move may often not exceed

two plies, whereas for a grandmaster it might be pos-

sible to analyze moves at ply-depths as high as 20. In

this model, we will attempt to generate a mapping be-

tween engine depths and player ratings, and use it to

quantify depths of thinking of human players on all

rating levels.

The two central contributions of the proposed

work are the marriage of IRT models to traditional

decision making processes, as quantiﬁed in chess, and

the integration of depth as a concept. It may be possi-

ble to judge among various modern IRT models to de-

duce which yields better results in the chess context.

For now we consider the so-called two-parameter

(2PL) model (Baker, 2004). There are two varieties

MeasuringIntrinsicQualityofHumanDecisions

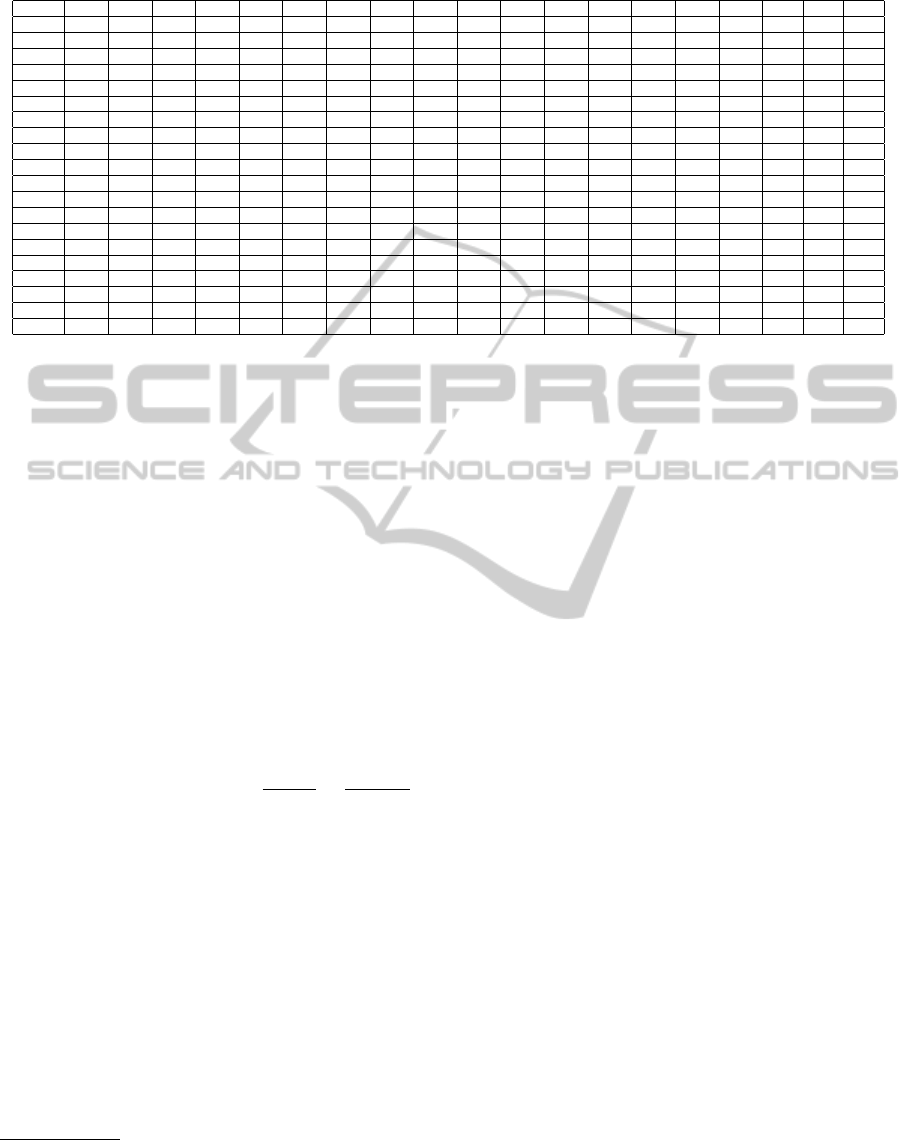
Table 1: Example of move evaluation by chess engines.

Moves 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Nd2 +230 +137 +002 +002 +144 +103 +123 +158 +110 +067 +064 +006 +002 +024 +013 -037 -018 000 000

Qg8 +205 +205 -023 -023 -059 -031 -058 -065 -066 -066 -053 -053 -103 -053 -053 -053 -053 -053 -053

Qh5 +101 +101 +034 +034 +034 -031 -058 -065 -066 -066 -053 -053 -103 -053 -053 -053 -053 -053 -053

Kf1 +108 +108 +108 +082 +029 +006 -087 -087 -090 -087 -048 -048 -087 -087 -077 -092 -092 -092 -092

Bxd7 +139 +139 -023 -023 -031 -039 -071 -071 -016 -020 -023 -023 -023 -017 -043 -042 -042 -083 -095

Rd1 +044 +044 +044 +016 -100 -094 -104 -124 -121 -121 -139 -143 -136 -150 -148 -122 -109 -122 -109

Nh4 +284 +161 +161 +161 +129 +116 +102 +046 +063 +028 +025 +028 -014 -078 -087 -097 -097 -127 -131

Kh1 +078 +078 +078 +051 -037 000 -019 -165 -165 -140 -140 -124 -157 -152 -185 -158 -158 -158 -172

Qg5 -107 -107 -091 -107 -113 -113 -130 -120 -202 -202 -197 -209 -200 -202 -200 -200 -189 -201 -174

Ng5 +402 +299 +299 +242 +163 +090 +008 +008 -033 -048 -041 -067 -067 -067 -115 -150 -150 -194 -177

Qh4 -107 -107 -107 -107 -113 -113 -130 -120 -202 -202 -186 -209 -203 -202 -200 -200 -189 -201 -191

Rf1 +003 +003 +003 -022 -138 -138 -138 -150 -168 -196 -183 -181 -220 -216 -205 -203 -211 -224 -205

h3 +084 +084 +084 +057 -237 -207 -230 -230 -257 -292 -279 -258 -249 -250 -253 -248 -249 -213 -236

Nxd4 -074 -074 -030 -054 -128 +243 +139 +139 +139 +091 +098 +098 +107 +093 +082 +061 -259 -250 -250

h4 +081 +081 +081 +055 -267 -267 -252 -243 -251 -255 -255 -247 -232 -246 -221 -244 -253 -253 -253

Ra1 +020 +020 +020 -007 -120 -120 -133 -145 -174 -196 -170 -211 -213 -172 -200 -217 -231 -231 -274

Rb1 +022 +022 +022 -005 -158 -158 -158 -145 -223 -196 -179 -172 -179 -209 -209 -217 -231 -231 -274

Qh3 +093 +093 +050 +050 -059 -019 -104 -104 -126 -208 -239 -210 -259 -217 -279 -310 -312 -312 -298

a5 +136 +136 +102 -191 -181 -181 -181 -288 -288 -288 -304 -327 -375 -376 -345 -428 -428 -430 -424

Be2 +097 +048 +062 +062 -051 -075 -205 -205 -278 -278 -282 -352 -379 -379 -375 -406 -447 -456 -451

to choose from, for 2PL models: normal and logis-

tic ogive models. We choose the logistic 2PL model

for its recent popularity, tractability, and compara-

ble performance to that of the normal ogive model.

The logistic ogive model employs a family of two-

parameter cumulative distribution functions (CDF).

For over a century, the logistic ogive has been used

as a model for the growth of plants, people and popu-

lations. However, the use of this as a model for IRT is

relatively new (Baker, 2004).

IRT models are widely used in the design, anal-

ysis, and scoring of test questions, and in measuring

human abilities or aptitude. When used for testing

scores, the two parameters in the model are called

item discrimination α

∈ (0,+∞) and item difﬁculty

∈ (−∞, +∞). They are related by:

(θ) = P(α

∗

,β

,θ) = Ψ(Z

) =

1 +e

−Z

(1)

where Z

is a logit with value Z

= α

∗

(θ − β

), and

∗

is the reciprocal of the standard deviation of the

logistic function.

5.1 Concept of Depth of Thinking

In most decision theory literature, deliberation time

is measured in units of seconds. In real-life decision

making, when we try to judge the quality of a deci-

sion, it is very difﬁcult to store the exact timing in-

formation for each decision. Moreover, the popular

belief that quality of decisions is directly proportional

The asterisk on α is the normalization factor relative

to a normal ogive model. I.e., to achieve the same item

characteristic curve, the α value calculated in the logistic

model needs to be multiplied by a factor of about 1.702.

to the deliberation time is not applicable in every sce-

nario. Sometimes the correct decision looks reason-

able at the beginning of deliberation, loses its ‘charm’

after a while, yet ﬁnally appears as the best choice to

the decision-maker. In the present setting, there is no

way possible to conclude that the correct decision has

come from a quick response or at an expense of higher

deliberation time.

Chess tournaments place limits on the collective

time for decisions, such as giving 120 minutes for a

player to play 40 moves, but allow the player to bud-

get this time freely. Meanwhile, chess offers an in-

trinsic concept of depth apart from how much time a

player chooses to spend on a given position. In game

theory, depth represents the number of plies a player

thinks in advance. In chess, a turn consists of two

plies, one for each player. We can visualize depth in

chess as the depth of the game tree. In our model,

the evaluation of each chess position comes from the

engine with values for each move at each depth in-

dividually. We use regression to derive the ability of

thinking by utilizing move-match statistics for various

depths.

5.2 Concept of Difﬁculty of a Problem

While the notion of difﬁculty of a problem is well

known in the IRT literature, the concept seems to

be little studied in decision making theories. We ar-

gue that having many possible options to choose from

does not make the problem hard. Rather the difﬁculty

lies in how close in evaluation the choices are to each

other, in how “turbulent” they are from one depth to

the next. The perception of difﬁculty differs among

decision-makers of various abilities. The difﬁculty

parameter β is the point on the ability scale where a

decision-maker has a 0.50 probability of choosing the

ICAART2015-DoctoralConsortium

correct response.

5.3 Concept of Discrimination

The discriminating power α is an item (or problem)

parameter. An item with higher discriminating power

can differentiate decision-makers around ability level

β better. For 2PL logistic IRT model, α contributes

to the slope of the ICC at β. In the decision making

domain, a problem with high “swing” may be a better

discriminator for decision-makers, since less compe-

tent decision-makers may be attracted to answers that

look good at low depths, but lose value upon greater

reﬂection.

5.4 Differential Weights for Questions

Following on from (Regan and Haworth, 2011), vari-

ous weighting mechanisms were designed to indicate

the importance of the position in measuring the intrin-

sic quality of the player. The two prominent weight-

ing used are ‘entropy weighting’

∑

log(1/p

) and

‘fall-off weighting’

∑

. Here p

and δ

represent the probability of the i

move and the

scaled deviation of the i

move in evaluation from

the best move, respectively. In this current model, an

explicit weighting mechanism is not required. This

is the fundamental advantage of using IRT models.

IRT models perform the statistical adjustment auto-

matically for differences between various test items

by means of item parameters, which in our case are

difﬁculty and discrimination parameters. We propose

to study them further.

6 IRT MODELING AND CHESS

DATA ANALYSIS

Each chess position can be compared to a question

asked to a student to answer. We treat the positions

as independent and identically distributed (iid). The

number of legal positions is astronomical (Shannon,

1950; Allis, 1994) and even in top level games, play-

ers often leave the “book” of previously played posi-

tions by move 15 or so. The lack of critical positions

that have been faced by many players makes it hard to

derive the item discrimination and difﬁculty parame-

ters for chess positions in the traditional IRT manners.

For typical IRT models, the expectation of the cor-

rect response for a particular examinee (of a certain

given ability) for a question is determined by the ratio

of the number m of respondents with correct answers

to the total number n of respondents. If we know the

abilities of the respondents beforehand, we can create

k subgroups of examinees, where each subgroup has

the same ability. Assuming each subgroup consists of

respondents where j ∈ (1..k), and r

in each sub-

group give the correct answer, the probability of an-

swering correctly is deemed to be p

= r

/ f

. But in

our chess domain we do not have ‘n’. So instead we

use the utility values (evaluations) of the engines to

generate the probability. There is a clear advantage in

adopting this approach. Besides mitigating the prob-

lem of having enough respondents/players, we do not

need any additional estimation to evaluate the abil-

ity parameter of the examines, rather the evaluation at

various depths yields this. The various depth param-

eters without any additional tweaks work comparable

to the ability parameter of the IRT models.

For achieving this goal, we need to address the

fundamental question of how to calculate the estimate

of the probability of playing the correct move, which

is a similar paradigm for a decision-maker’s proba-

bility of ﬁnding the optimal solution. This part plays

the most critical role in the whole design and requires

us to introduce the technique to convert utilities into

probabilities.

We can assume that a player of Elo rating e on av-

erage plays or thinks up to/around depth d. For any

particular depth d, for a position t, we have a number

` of available options a

,.. .,a

and a list of corre-

sponding values U

= (u

,.. .,u

). A player does

not know the values, but by means of his power of dis-

crimination can assign higher probability of playing a

move i with higher u

. For our basic dichotomous

model, we are only concerned about the probability

of playing the best move where there are only two bi-

nary decisions possible, namely P

and Q

, which rep-

resent the probability of playing the correct and some

incorrect move, respectively. Later we will extend

our model to the polytomous case, along the lines of

the Generalized Partial Credit Model (GPCM) (Mu-

raki, 1992) where we consider different probability

for each move and can evaluate the probability of the

played move.

This model is signiﬁcantly different from the

method analyzed in (Regan and Biswas, 2013). Here

we will ignore the consistency c parameter. Results

in (Regan and Haworth, 2011) show that in the hu-

man range from Elo 2000 to 2800, the c parameter

varies only between about 0.465 and 0.520 and for

constant s this makes a difference of under 200 Elo

points. Hence we focus on the sensitivity measure s,

which works as the decision-theoretic threshold pa-

rameter when ﬁnalizing any chosen move. The only

condition enforced in calculating the probabilities is

for any i, j, if u

> u

then p

> p

. Our thesis is that

deliberation time and deliberation capability limit the

MeasuringIntrinsicQualityofHumanDecisions

ability of the player to think beyond a certain ‘depth’.

6.1 Converting Utilities into

Probabilities

For calculating the probability, we measure the de-

viation of all the legal moves from the best evalua-

tion (u

∗,d

) at any particular depth d for any partic-

ular position. This generates the delta vector ∆

1,d

,δ

2,d

,.. .,δ

`,d

. If the best move at depth d is m

where j ∈ {1, .. . ,`}, then u

∗,d

= u

j,d

and δ

j,d

= 0. We

perform prior scaling based on the evaluation of the

position before the played move. In our paper (Re-

gan et al., 2014), we have shown how humans per-

ceive differences in the evaluation and are prone to

more error when either side has a tangible advantage.

This observation inspired and required us to calculate

the decision-makers’ δ

i,d

not simply as (u

∗,d

− u

i,d

but rather as the integral from u

∗,d

to u

i,d

. We adopt

the same scaling used in (Regan and Haworth, 2011),

where the differential dµ =

1+a

dz with a = 1, whose

integral gives ln(1 + z), was found to level the Aggre-

gate Difference (AD) histogram very well. For gen-

erating probabilities from utility values, we re-used

the exponential transformations from (Regan and Ha-

worth, 2011), but with ﬁxed parameters, via p

−2δ

∑

j=1

. (This also yields the depth-speciﬁc probabil-

ities p

i,d

used to quantify ‘trickiness’ in Section 7.2

below.) The choice of the constant 2 can be modiﬁed

by ﬁtting the sensitivity parameter s at a later stage,

but nonetheless promises to be a good starting point.

6.2 Fitting ICC for Estimating Item

Parameters

Once the probabilities of the moves are calculated,

our next task is to generate item parameters for the

two-parameter logistic ICC model. We simplify

Equation (1) by setting a = α , b = αβ and Z

a + bθ

. The resulting equation becomes:

= P(θ

) = P(a,b,θ

) =

1 + e

−(a+bθ

)

1 + e

−Z

(2)

For estimating the item parameters from the

probability we have already deduced, we use Least

Squares Estimation (LSE). We try to ﬁnd the min-

imum L (sum of squared residuals): L(a,b) =

∑

i=1

− P

)

. In our model, a residual is deﬁned

as the difference between the actual probability value

of the dependent variable and the value predicted by

the model. The details of the Newton-Raphson based

iterative procedure to estimate a and b are shown in

Appendix 8.

6.3 The ICC-move Choice

Correspondence

When an IRT model is deployed in the context of

a theory of testing, the major goal is to procure a

measure of the ability of each examinee. In item re-

sponse theory, this is standardly the maximum like-

lihood estimate (MLE) of the examinee’s unknown

ability, based upon his responses to the items on the

test, and the difﬁculty and discrimination parameters

of these items. When we apply this idea for chess

moves assessed by various chess engines, we follow

the same procedure. We ﬁrst calculate the MLE for

the moves the player played. This is performed by

evaluating the positions by various chess engines and

then assigning the probability of playing the correct

move at every depth. Finally, we use maximum like-

lihood estimation to get the ability parameter of the

player. We convert the ability parameter to the intrin-

sic rating by regressing on our milepost data set. Thus

dichotomous IRT corresponds to the “Move-Match”

(MM) test in chess (Regan and Haworth, 2011).

When we extend the model from dichotomous to

polytomous responses, we consider not only the best

move probability, but also the probabilities of all the

moves. This incurs methodological complications

whose empirical effects we have shown in (Regan and

Biswas, 2013) and in not-yet published work. Results

show that for chess move data, versions of MLE are

veriﬁably inferior to other ﬁtting methods. This may

not be a defect in the chess setting – rather, it argues

that the standard use of MLE in other applications

may be unwittingly inferior, and that alternatives to

MLE should be formulated and promoted.

For the completion of this estimation we make

four assumptions. First, the value of the item pa-

rameters are known or derived from engine evalua-

tion. Second, examinees are i.i.d sample or indepen-

dent objects and it is possible to estimate the param-

eters for examinees independently. Third, the posi-

tions given to the players are independent objects too.

Though the positions may come from the same game

we assume those to be uncorrelated. Fourth, all the

items used for MLE are modeled by the ICCs of the

same family.

If a player j ∈ {1,.. . ,N} faces n positions (either

from a single game or any set of random positions)

and the responses are dichotomously scored, we ob-

tain u

i, j

∈ {0,1} (1 for matching; 0 for not) where i ∈

{1,.. .,n} designates the items. This yields a vector

of item responses of length n: U

= (u

1 j

2 j

,.. .,u

n j

From our third assumption, all the u

i j

are i.i.d sam-

ples. Considering all the assumptions, the probability

of the vector of item responses for a given player can

ICAART2015-DoctoralConsortium

be produced by the likelihood function

Prob(U

|θ

) =

∏

i=1

i j

(θ

1−u

i j

(θ

). (3)

This yields the log-likelihood function

L = logProb(U

|θ

)

∑

i=1

i j

logP

i j

(θ

) + (1 − u

j) log Q

i j

(θ

)].

Since the item parameters for all the n items are

known, only derivatives of the log-likelihood with re-

spect to a given ability will need to be taken:

∂L

∂θ

∑

i=1

i j

(θ

)

∂P

i j

(θ

)

∂θ

∑

i=1

(1 − u

i j

)

i j

(θ

)

∂Q

i j

(θ

)

∂θ

. (4)

When Newton-Raphson minimization is applied

on L, an ability estimator θ

for the player is obtained.

6.4 The Ability-rating Correspondence

For converting the ability measure into the ratings in

the standard Elo scale, we perform linear regression

on our main data set. The data set comprises games

in which both the players were within 10 Elo rating

points of the ‘milepost’ values: 2700, 2600, . . . , 1800,

run under standard time controls in individual player

round-robin or small-Swiss tournaments. We use var-

ious ﬁtting methods and compare their performances

in estimating the ability for each milepost value. The

mapping between ability and Elo ratings gives us a

simple linear regression function for computing the

conversion. We name this rating the intrinsic perfor-

mance rating (IPR), which measures the performance

of the player based on the moves played instead of

game results. The use of Average Difference, not just

the MM test, makes this correspond to polytomous

settings.

6.5 The Master Plan

We aim to shed light on the following problems, for

application domains such as test-taking for which we

can establish a correspondence to our chess model:

Do the intrinsic criteria for mastery transferred from

the chess domain align with extrinsic criteria inferred

from population and performance data in the applica-

tion’s own domain? How close is the agreement and

what other scientiﬁc regularities, performance mile-

posts, and assessment criteria may be inferred from

it? What does this say about distributions, outliers,

and the effort needed for mastery, in relation to topics

raised popularly by Gladwell (Gladwell, 2002; Glad-

well, 2011)?

7 EXPECTED OUTCOME

Our model can be used for predictive analysis and

data mining. Moreover, the model represents how hu-

mans perceive differences in choices in case of un-

certainty. This information can be used for modeling

agents based on preferences. Modeling an agent also

depends on various other parameters speciﬁc to the

intuition or favoritism of the player. The approach

can be extended to various board games and strate-

gic (online) gaming. This model also gives an insight

about performances of an agent in time constrained

environments.

To extend the model for other domains, we only

need to conﬁgure any ‘artiﬁcial’ or ‘optimal’ de-

cision making agents to ‘think’ at some particular

strength/depth and use the data to analyze the prob-

lem. The model can also be used to ‘verify’ how

chosen decisions eventually impacted the outputs in

various applications, such as weather forecasting or

prediction of events.

7.1 Risk and Uncertainty

Risk and uncertainty, as deﬁned in (Kahneman and

Tversky, 1979; Tversky and Fox, 1995), are closely

related. Mauboussin (Mauboussin, 2013) distin-

guished them by the following means: while both

risk and uncertainty involve unknown outcomes, in

risk the underlying outcome distribution is known,

whereas for uncertainty it is not. Analyzing chess

positions up to a certain depth provides us the op-

portunity to model both risk and uncertainty. As the

number of legal moves is known for any position, the

outcome distribution can be calculated up to a limited

depth. But due to the exponential growth of the depth

tree in chess, a player cannot guarantee that his anal-

ysis of moves is correct. Even if the expected line of

the game is played, the player is uncertain of the ﬁnal

evaluation, let alone the issue of being surprised by an

overlooked line from the opponent.

For example, suppose a player thinks out to depth

d = 10, but we analyze (e.g. with Stockﬁsh) out to

depth D = 19. Moves by the opponent which, if

found, would yield disadvantageous values for the

player at depth d constitute risk. Values from depth

d + 1 to D represent uncertainty. Our research plan

aims to quantify and analyze these separate effects.

7.2 Trickiness

For measuring trickiness, we can compare the top

level exposure

∑

i=1

versus the w(d) depth-

weighted exposure

∑

w(d)p

i,d

. We expect tricky

MeasuringIntrinsicQualityofHumanDecisions

moves to be a good discriminator for decision-

makers.

7.3 Notion of Advantage

One prominent feature of chess positions that does

not have a clear correspondence in test taking is the

degree of advantage or disadvantage for the player to

move. In chess, this is connected to the player’s prob-

ability of winning the game, or more precisely, the

expectation counting wins and draws as 1 and 0.5, re-

spectively. Our research (Regan et al., 2014) shows

that this probability also depends on the difference in

ratings between the player and the opponent, whereas

in test taking there is no “opponent”. We would like to

infer some relations to the concepts of the test taker’s

probability of getting a question correct. One idea is

that “advantage” may reﬂect the degree of preparation

for certain parts of the test.

7.4 Speed-accuracy Trade-off

The model can be applied to verify the impact on ac-

curacy if faster decisions are taken. The effect is well

known in chess tournaments (Chabris and Hearst,

2003), almost all of which use a time control at move

40. Players often use up almost all of the allotted time

before move 30 or so, thus incurring ‘time pressure’

for 10 or more moves. The paper (Regan et al., 2011)

shows a steep monotonic increase in errors by move

number up to 40, then a sudden drop off as players

have more time. Our yet-unpublished work has quan-

tiﬁed the drop of intrinsic rating at Rapid and Blitz

chess played at faster controls. We expect that our

model will be capable of verifying the effect in other

decision applications as well.

7.5 Agent Modeling

This model can be extended to model decision-

makers which would be advantageous to plan strategy

for or against him/her. For player modeling, we need

to ﬁnd various characteristics unique to the player.

IPR, besides providing the measure of the quality of

decisions, is a strong indicator of the aptitude level. It

can be used to ﬁnd out any speciﬁc trend followed

by the player while taking decisions. In the con-

text of chess, this could be the players’ preference of

knight over the bishop, or propensity for positional

games rather than tactical ones. Measures of blunders

and the proclivity for procrastination also could con-

tribute in the player modeling. This may be relevant

for player proﬁling in other online battle games.

7.6 Cheating Detection and Veriﬁcation

Proved and alleged instances of cheating with com-

puters at chess have increased many-fold in recent

years. Technologies such as Google Glass, sensor net-

works, etc., have made the problem of cheating a per-

sistent threat. If a successful technique for detection

of cheating is possible, the same idea can be applied

to other ﬁelds of online gaming or online test-taking.

Our model provides the means of cheating detection

in a natural way. We aim to compare this model with

other predictive analytic models used in fraud detec-

tion.

7.7 Multiple-criteria Decision Analysis

Our model can be applied for multiple-criteria deci-

sion analysis and verifying the rationality of the in-

trinsic quality measured with respect to multi-criteria

decision rules. In standard chess tournaments, the to-

tal allotted time to play the ﬁrst 40 moves are ﬁxed.

The longer a player ponders on a given move, the

lesser time he can spend to make other moves. This

scenario is prevalent in any test-taking environment.

In a setting, where an examinee cannot return to pre-

vious questions, he often needs to split his time for

each question keeping in mind the difﬁculty of future

questions. In all these scenarios, the decision maker

eventually makes the ﬁnal decision in differentiate be-

tween alternatives based on his preference. Prior ar-

ticulation of preferences in multiple-criteria decision

problems plays a key role in agent modeling.

7.8 Decision Making in Multi-Agent

Environment

Does the quality of the decisions of any agent get af-

fected based on the presence of other agents? How

does a player play against a weaker versus a stronger

opponent? How does an examinee response when he

knows the other examinees are far either far supe-

rior or inferior than him? Our model tries to answer

these questions and measures the displacement from

the mean in these either extreme cases.

In this work, we have furnished various measure-

ment procedures to quantify the quality of human de-

cisions. Our proposed model generates the prediction

of choices made by any decision-makers for any prob-

lems. It also ranks the decision-makers by the quality

of the decisions made. The model is established via

the evaluations generated by an AI agent of supreme

strength, and represents the goodness of choice. We

expect that with improved processing power, higher

storage capacity, and sophisticated search algorithms,

ICAART2015-DoctoralConsortium

AI agents in the near future will produce results far

better in almost every aspect than a human possibly

can. We aim to leverage this phenomenon so as to

judge human decisions by ‘machines’ in our model.

These procedures can also be employed to model

a decision-maker by tuning down to match the

decision-maker’s native characteristics. Numerous

aspects like a speed-accuracy trade-off, effect of pro-

crastination and the impact of time pressure also can

be analyzed, and their effect on performances by the

decision-makers can be tested. Other ﬁelds where

this model can be applied include, but are not limited

to, economics, psychology, test-takings, sports, stock

market trading, and software benchmarking.

We wish to devise a tool to measure the qual-

ity of human decisions from the performances. We

hope this tool can be used for personnel assessment to

cheating detection. Though we have concentrated on

the chess domain which is a constrained environment,

we wish to apply the learning to adapt the model to

ﬁt in other domains, from test-taking to stock market

trading.

8 STAGE OF THE RESEARCH

Research on judging decisions made by fallible (hu-

man) agents is not as much advanced as research on

ﬁnding optimal decisions, and on the supervision of

AI agents’ decisions by humans. Human decisions

are often inﬂuenced by various factors, such as risk,

uncertainty, time pressure, and depth of cognitive ca-

pability, whereas decisions by an AI agent can be ef-

fectively optimal without these limitations. The con-

cept of ‘depth’, a well-deﬁned term in game theory

(including chess), does not have a clear formulation

in decision theory. To quantify ‘depth’ in decision

theory, we can conﬁgure an AI agent of supreme com-

petence to ‘think’ at depths beyond the capability of

any human, and in the process collect evaluations of

decisions at various depths. One research goal is to

create an intrinsic measure of the depth of thinking

required to answer certain test questions, toward a re-

liable means of assessing their difﬁculty apart from

the item-response statistics.

Currently, we are working on relating the depth of

cognition by humans to depths of searching alterna-

tives, and using this information to infer the quality

of decisions made, so as to judge the decision-maker

from his decisions. Our research extends the model

of Regan and Haworth to quantify depth, plus related

measures of complexity and difﬁculty, in the context

of chess. We use large data from real chess tourna-

ments and evaluations of chess programs (AI agents)

of strength beyond all human players. We then seek to

transfer the results to other decision-making ﬁelds in

which effectively optimal judgments can be obtained

from either hindsight, answer banks, or powerful AI

agents. In some applications, such as multiple-choice

tests, we establish an isomorphism of the underlying

mathematical quantities, which induces a correspon-

dence between various measurement theories and the

chess model. We provide results toward the objective

of applying the correspondence in reverse to obtain

and quantify the measure of depth and difﬁculty for

multiple-choice tests, stock market trading, and other

real-world applications and utilizing this knowledge

to design intelligent and automated systems to judge

the quality of human or artiﬁcial agents.

REFERENCES

Allis, L. V. (1994). Searching for solutions in games and

artiﬁcial intelligence. PhD thesis, Rijksuniversiteit

Maastricht, Maastricht, the Netherlands.

Andersen, E. (1973). Conditional inference for multiple-

choice questionnaires. Brit. J. Math. Stat. Psych.,

26:31–44.

Andrich, D. (1978). A rating scale formulation for ordered

response categories. Psychometrika, 43:561–573.

Andrich, D. (1988). Rasch Models for Measurement. Sage

Publications, Beverly Hills, California.

Baker, F. (2004). Item response theory : parameter estima-

tion techniques. Marcel Dekker, New York.

Baker, F. B. (2001). The Basics of Item Response Theory.

ERIC Clearinghouse on Assessment and Evaluation.

Biswas, T. and Regan, K. (2015). Quantifying depth and

complexity of thinking and knowledge. In proceed-

ings, International Conference on Agents and Artiﬁ-

cial Intelligence (ICAART).

Busemeyer, J. R. and Townsend, J. T. (1993). Decision

ﬁeld theory: a dynamic-cognitive approach to deci-

sion making in an uncertain environment. Psycholog-

ical review, 100(3):432.

Chabris, C. and Hearst, E. (2003). Visualization, pattern

recognition, and forward search: Effects of playing

speed and sight of the position on grandmaster chess

errors. Cognitive Science, 27:637–648.

DiFatta, G., Haworth, G., and Regan, K. (2009). Skill rating

by Bayesian inference. In Proceedings, 2009 IEEE

Symposium on Computational Intelligence and Data

Mining (CIDM’09), Nashville, TN, March 30–April 2,

2009, pages 89–94.

Fox, C. R. (1999). Strength of evidence, judged probability,

and choice under uncertainty. Cognitive Psychology,

38(1):167–189.

Fox, C. R. and Tversky, A. (1998). A belief-based account

of decision under uncertainty. Management Science,

44(7):879–895.

MeasuringIntrinsicQualityofHumanDecisions

Gladwell, M. (2002). The tipping point : how little things

can make a big difference. Back Bay Books, Boston.

Gladwell, M. (2011). Outliers : the story of success. Back

Bay Books, New York.

Kahneman, D. and Tversky, A. (1979). Prospect theory: An

analysis of decision under risk. Econometrica: Jour-

nal of the Econometric Society, pages 263–291.

Linacre, J. M. (2006). Rasch analysis of rank-ordered data.

JOURNAL OF APPLIED MEASUREMENT.

Loomes, G. and Sugden, R. (1982). Regret theory: An al-

ternative theory of rational choice under uncertainty.

The Economic Journal, pages 805–824.

Lopes, L. L. (1987). Between hope and fear: The psychol-

ogy of risk. Advances in experimental social psychol-

ogy, 20:255–295.

Maas, H. v. d. and Wagenmakers, E.-J. (2005). A psycho-

metric analysis of chess expertise. American Journal

of Psychology, 118:29–60.

Masters, G. (1982). A Rasch model for partial credit scor-

ing. Psychometrika, 47:149–174.

Mauboussin, M. (2013). More than you know : ﬁnding ﬁ-

nancial wisdom in unconventional places. Columbia

University Press, New York.

Morris, G. A., Branum-Martin, L., Harshman, N., Baker,

S. D., Mazur, E., Dutta, S. N., Mzoughi, T., and Mc-

Cauley, V. (2005). Testing the test: Item response

curves and test quality. Am. J. Phys., 74:449–453.

Muraki, E. (1992). A generalized partial credit model: Ap-

plication of an em algorithm. Applied psychological

measurement, 16(2):159–176.

Ostini, R. and Nering, M. (2006). Polytomous Item Re-

sponse Theory Models. Sage Publications, Thousand

Oaks, California.

Rasch, G. (1960). Probabilistic models for for some in-

telligence and attainment tests. Danish Institute for

Educational Research, Copenhagen.

Rasch, G. (1961). On general laws and the meaning of

measurement in psychology. In Proceedings, Fourth

Berkeley Symposium on Mathematical Statistics and

Probability, pages 321–334. University of California

Press.

Regan, K. and Biswas, T. (2013). Psychometric modeling of

decision making via game play. In proceedings,IEEE

Conference on Computational Intelligence in Games.

Regan, K., Biswas, T., and Zhou, J. (2014). Human and

computer preferences at chess. In Proceedings of the

8th Multidisciplinary Workshop on Advances in Pref-

erence Handling (MPref 2014).

Regan, K. and Haworth, G. (2011). Intrinsic chess ratings.

In Proceedings of AAAI 2011, San Francisco.

Regan, K., Macieja, B., and Haworth, G. (2011). Under-

standing distributions of chess performances. In Pro-

ceedings of the 13th ICGA Conference on Advances in

Computer Games. Tilburg, Netherlands.

Shannon, C. E. (1950). Xxii. programming a computer for

playing chess. Philosophical magazine, 41(314):256–

275.

Thorpe, G. L. and Favia, A. (2012). Data analysis using

item response theory methodology: An introduction

to selected programs and applications. Psychology

Faculty Scholarship, page 20.

Tversky, A. and Fox, C. R. (1995). Weighing risk and un-

certainty. Psychological review, 102(2):269.

Wichmann, F. and Hill, N. J. (2001). The psychometric

function: I. Fitting, sampling, and goodness of ﬁt. Per-

ception and Psychophysics, 63:1293–1313.

WikiBooks (2012). Bestiary of behavioral eco-

nomics/satisﬁcing — Wikibooks, the free textbook

project. [Online; accessed 7-August-2014].

APPENDIX

LSE Estimation of Logistic Model

Equation for 2PL logistic IRT model is:

= P(θ

) = P(a,b,θ

) =

1 + e

−(a+bθ

)

1 + e

−Z

(5)

This yields

∂P

∂a

= P

∂P

∂b

= P

∂Q

∂a

= −P

∂Q

∂b

= −P

Sum of squared residual L(a,b) =

∑

i=1

− P

)

where p

is the actual probability value of the depen-

dent variable. In the context of chess, which is the

probability we derive from engine evaluation. For

minimizing L, we need the ﬁrst and second partial

derivatives of L with respect to a and b.

∂L

∂a

∑

i=1

2(p

− P

)

∂P

∂a

= −

∑

i=1

2(p

− P

∂L

∂b

∑

i=1

2(p

− P

)

∂P

∂a

= −

∑

i=1

2(p

− P

∂

∂a

− 2(

∑

i=1

− P

) +

∑

i=1

− 2Q

))

= L

∂

∂a∂b

− 2(

∑

i=1

− P

) +

∑

i=1

− 2Q

))

∂

∂b

− 2(

∑

i=1

− P

) +

∑

i=1

− 2Q

))

ICAART2015-DoctoralConsortium

For minimizing:

∂L

∂a

= 0;

∂L

∂b

= 0; (6)

We use an iterative procedure based upon Taylor se-

ries to solve Eq. (6).We target to ﬁnd an approxima-

tion ˆa

to ˆa,

b, where ˆa = ˆa

+∆ ˆa and

b =

+∆

∆ ˆaand∆

b represent the error in approximation. By

Taylor series expansion, ignoring higher order terms,

we can rewrite Equation (6) as

+ L

∆ ˆa

+ L

∆

= 0

+ L

∆ ˆa

+ L

∆

= 0

Thus we need to solve the following equation for

∆ ˆa

and ∆





= −





∆ ˆa

∆

(7)

∆ ˆa

∆

= −





−1





(8)

This process is repeated t times until ∆ ˆa

and ∆ ˆa

are sufﬁciently small. This yields Eq 9.

ˆa

t+1

ˆa

−





−1





(9)

This equation is known as the Newton-Raphson

equation. Evaluating the inverse produces:

ˆa

t+1

ˆa

−

− L



−L





(10)

In order to start the iterative estimation process,

initial estimates of the item parameters are required.

For 2PL IRT model, often a and b parameters are set

to 1 and 0, respectively. Once the desired requirement

is met, no further iteration is performed. Item param-

eters α and β can be readily obtained from a and b by

α = ˆa and

β = −

b/ ˆa.

MeasuringIntrinsicQualityofHumanDecisions