Structure from Motion in the Context of Active Scanning

Johannes K

ohler, Tobias N

oll, Norbert Schmitz, Bernd Krolla and Didier Stricker

German Research Center for Artiﬁcial Intelligence, Trippstadter Str. 122, 67663 Kaiserslautern, Germany

Keywords:

Structured Light, Active Scanning, Bundle Adjustment, Structure from Motion.

Abstract:

In this paper, we discuss global device calibration based on Structure from Motion (SfM) (Hartley and Zis-

serman, 2004) in the context of active scanning systems. Currently, such systems are usually pre-calibrated

once and partial, unaligned scans are then registered using mostly variants of the Iterative Closest Point (ICP)

algorithm (Besl and McKay, 1992). We demonstrate, that SfM-based registration from visual features yields a

signiﬁcantly higher precision. Moreover, we present a novel matching strategy that reduces the inﬂuence of an

object’s visual features, which can be of low quality, and introduce novel hardware that allows to apply SfM

to untextured objects without visual features.

1 INTRODUCTION

3D scanning and reconstruction of static objects are

important applications of computer vision, in partic-

ular for cultural heritage preservation and reverse en-

gineering. Laser or structured light scanners are most

commonly used for this task and we focus on high-

precision reconstruction using such active scanning

systems in this paper.

To acquire a full reconstruction of an object, sev-

eral partial scans must be aligned, since the scanning

devices usually have a limited ﬁeld of view. The

transformation of these partial scans into a common

coordinate frame is customarily referred to as regis-

tration. Throughout the literature, registration is al-

most completely considered as the problem of ﬁnding

the (rigid) transformations between 3D data.

Structure from motion (SfM) algorithms that ex-

tract 3D geometry from images constitute a different

approach to object reconstruction. A respective sys-

tem usually reconstructs a scene from images by in-

cremental computation of new camera poses and con-

secutive triangulation of new points. This is done in a

common coordinate frame, the data is thus registered

implicitly.

Surprisingly and to the best of our knowledge,

this approach to the registration problem is hardly

discussed in the context of active scanning systems,

where variants of the iterative closest point algorithm

(Besl and McKay, 1992) are heavily dominating.

In this paper we break with this tradition. Instead

of registering individual scans computed in the local

Figure 1: Our proposed hardware, consisting of a struc-

tured light scanning unit (back) and a turntable with out-

riggers. Each outrigger holds a small projector, whose pro-

jected fringe patterns statically remain on the object.

frame of the scanner, we ﬁrst calibrate the scanner

globally by calibrating each of its individual devices

(projectors and cameras) using sparse visual features.

Global optimization by bundle adjustment, which ad-

justs both the sparse structure and all device parame-

ters simultaneously, is well studied in this context and

greatly improves the overall reconstruction accuracy.

In particular, it automatically adapts device parame-

ters that can slightly change over time, due to e.g. heat

generation. If the scanner calibration is, according to

the current predominant paradigm of precalibration,

kept constant instead, partial scans can suffer from

small distortions that cannot be corrected by the sub-

sequent registration anymore. This problem was ﬁrst

reported in (Furuakwa et al., 2009) and addressed by

global optimization after ICP-based alignment. How-

620

Köhler J., Nöll T., Schmitz N., Krolla B. and Stricker D..

Structure from Motion in the Context of Active Scanning.

DOI: 10.5220/0005353906200628

In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 620-628

ISBN: 978-989-758-091-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

ever, most approaches ignore this insight and assume

that partial scans can be aligned perfectly.

For calibration we use an SfM algorithm with au-

tocalibration, that is tailored to a projector-camera

scanning setup. In such a system, the projector in-

duces high-quality correspondences to the cameras.

We show that these correspondences can be used to

reduce the inﬂuence of the object’s natural features to

an acceptable minimum. Moreover, we present novel

hardware that makes the calibration fully independent

of the object’s own features. With our setup, it is pos-

sible to reconstruct any object that exhibits a reason-

able diffuse reﬂection component at very high preci-

sion. This holds in particular for featureless objects,

where optical registration will fail and symmetrical

objects, where geometry-based registration will fail.

We evaluate this method using a novel approach,

that expresses the error in terms of point accuracy in-

stead of pose accuracy. Our SfM-approach outper-

forms common, geometry-based methods. The main

contributions of this paper are:

• Analysis and discussion of registration by global

device calibration in the context of structured light

scanners.

• A novel matching strategy, that minimizes the in-

ﬂuence of potentially bad natural features.

• A novel hardware to gain independence of natural

features.

2 RELATED WORK

Existing methods for rigid shape registration process

geometry and/or optical features, either yield a coarse

or a ﬁne registration and align a single pair or mul-

tiple views. In this paper, we focus on multi-view

ﬁne registration and assume, that a coarse alignment

is already provided if required. A coarse alignment

is often computed from correspondences between ge-

ometrical features, a survey on computation of such

correspondences can be found in (van Kaick et al.,

2011).

The vast majority of existing registration methods

operate only on reconstructed geometry. This might

be due to the fact that off-the-shelf devices like laser

scanners, which are widely available nowadays, serve

as black box depth sensors and often output only point

clouds. In this case, registration must be performed

using only this data. Two surveys on geometry-

based registration are (Salvi et al., 2007) and the more

recent (Tam et al., 2013). The largest part of all

methods is undeniably based on the iterative closest

point (ICP) algorithm (Besl and McKay, 1992). This

method approximates unknown correspondences be-

tween two shapes by the closest point and iteratively

minimizes the distance between the shapes by updat-

ing an initial pose estimate. Many adaptations exist

that vary mostly in the point sampling, correspon-

dence weighting, outlier rejection and error measure-

ment (Rusinkiewicz and Levoy, 2001). Although the

closest point approximation becomes more difﬁcult

and costly among multiple views, numerous methods

extended ICP to this case, including (Bergevin et al.,

1996; Pulli, 1999; Williams and Bennamoun, 2001;

Toldo et al., 2010; Du et al., 2010).

Especially in the multi-view case, several new ap-

proaches were proposed recently. (Krishnan et al.,

2005) uses a manifold optimization on the constrained

manifold of rotations, (Huang et al., 2007) proposes a

bayesian formulation of the registration problem and

(Torsello et al., 2011) applies motion diffusion with

motion being expressed by dual quaternions. How-

ever, (Torsello et al., 2011) minimizes the error distri-

bution among multiple views and requires a pairwise

registration - ICP thus is also relevant in this context.

A different class of registration methods uses vi-

sual cues derived from images aligned to the recon-

structed points. 2D point correspondences among the

images induce 3D point correspondences, which can

be used to estimate the unknown transformation (Seo

et al., 2005; Dold and Brenner, 2006).

An entirely different approach to the registration

problem is given by SfM-algorithms. This class of

methods assumes a sequence of images and jointly

estimates camera motion and scene geometry. In the

context of an active scanner, SfM can be used to es-

timate all involved device parameters and optimize

them together with a sparse version of the ﬁnal re-

construction in a globally optimal way. In contrast to

the previously mentioned registration approaches that

keep the partial reconstructions and the device cali-

bration ﬁxed, this offers a larger ﬂexibility for align-

ing the data. While SfM is commonly used for passive

scene reconstruction from imagery, we are, surpris-

ingly, only aware of two publications that use it for

active scanners (K

ohler et al., 2013; Weinmann et al.,

2011).

Most active projector camera scanning setups that

could employ an SfM approach (e.g. (Holroyd et al.,

2010; Weise et al., 2009; Sadlo et al., 2005)) instead

rely on a local precalibration and register the partial

scans using a variant of ICP. We believe the main

reason for this to be the still dominant paradigm of

scanner precalibration. Up to the present day, the vast

majority of publications that address the problem of

scanner calibration only aim at such a local calibra-

tion that inevitably requires subsequent registration,

StructurefromMotionintheContextofActiveScanning

621

including (Audet and Okutomi, 2009; Griesser and

Van Gool, 2006; Moreno and Taubin, 2012).

The failure cases for all previously discussed

methods are obvious: The accuracy of all geometry-

based registration methods will degrade for objects

exhibiting a certain degree of symmetry, as the un-

known rigid transformation cannot be determined

uniquely in this case. Methods based on optical fea-

tures will fail for sparsely textured or textureless ob-

jects. We overcome these problems by introducing a

novel matching strategy that enables precise scanning

in case of sparse features, and new hardware, which

generates static, high-quality optical features. To the

best of our knowledge, it is the ﬁrst device that en-

ables to capture the geometry of symmetric and tex-

tureless objects at high precision.

3 SFM FOR ACTIVE SCANNING

In the following, we assume we are provided with a

rigid, active scanning unit consisting of a light emit-

ting device P (“projector”) and at least two cameras

. P is used to establish pixel-wise correspondences

of very high precision among the cameras for a partic-

ular scanner/object pose. Those correspondences are

commonly used to reconstruct dense, partial scans.

We refer to them as internal correspondences. In or-

der to capture a full object, either the object or the

scanning setup must be moved. We assume that each

scanner/object pose j generates new, virtual devices

and C

i j

with individual parameters each. Corre-

spondences among C

i j

of different scanner poses

j, l are called external correspondences. They can-

not be generated by P, and need to be computed by

other means. If external correspondences can be es-

tablished successfully, it is possible to estimate the

individual parameters of all virtual devices in a com-

mon frame.

The relationship to existing registration ap-

proaches is straightforward, if e.g. the projector’s

frame is used as the local scanner frame: SfM esti-

mates the scanner pose [R|t] for each scanner posi-

tion, which maps a point from the world to the local

scanner frame. In case of a precalibrated setup, recon-

structions are computed in the local scanner frame. A

registration algorithm thus computes the inverse pro-

jector pose [R

| − R

t], which maps the reconstruc-

tion to the common world frame.

In this section, we assume that a set of sparse cor-

respondences is provided among all virtual devices.

Correspondence generation is addressed in detail in

Sections 4 and 5.

We employ the following SfM-approach to esti-

mate the parameters of all virtual cameras C

i j

. As cus-

tomary, we assume that all C

can be modeled by the

pinhole model (Hartley and Zisserman, 2004). First,

we initialize a set of calibrated cameras and a sparse

point cloud:

1. Choose C

i j

and C

with most 2D-2D correspon-

dences.

2. If the intrinsic parameters of these cameras are not

known estimate them using an adaption of (Gher-

ardi and Fusiello, 2010).

3. Initialize the relative pose by epipolar matrix fac-

torization.

4. Triangulate all correspondences with a reprojec-

tion error ≤ t

Then, we iteratively apply the following steps to

all virtual cameras:

1. Choose an uncalibrated C

i j

with most 3D-2D cor-

respondences.

2. If the intrinsic parameters of C

i j

are not known,

compute a camera matrix P using direct linear

transform and factorize it into pose and intrinsic

parameters. Otherwise, compute the pose using

(Lepetit et al., 2009). In both cases, outliers are

rejected by RANSAC (Fischler and Bolles, 1981)

with a threshold of t

3. Update the set of triangulated points with a repro-

jection error ≤ t

4. Apply global bundle adjustment (Hartley and Zis-

serman, 2004).

5. Remove all 3D-2D correspondences with a repro-

jection error > t

During bundle adjustment, we optimize all trian-

gulated points as well as focal length, principal point,

distortion coefﬁcients and pose for each virtual cam-

era. The clear advantage of this process is, that a

sparse version of the ﬁnal reconstruction and all de-

vice parameters are simultaneously adjusted in a glob-

ally optimal way before the actual reconstruction. We

maintain a data structure that allows navigating from

each 3D point to all its valid projections and vice

versa. It is used to derive 3D-2D from 2D-2D cor-

respondences for calibrating a new device. Due to the

use of autocalibration, projectors can be easily inte-

grated, if required and a precalibration is not neces-

sary anymore.

4 CORRESPONDENCES FROM

NATURAL FEATURES

In this section, we adress external correspondence

generation from an object’s natural visual features.

For this purpose, descriptors such as SIFT (Lowe,

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

622

Camera Camera

Projector

Turntable

: Internal, P-generated matching

Figure 2: Left: Exemplary scanning unit with internal,

projector-generated matching. Right: Multiple positions of

the unit for complete object acquisition, circles illustrate ex-

ternally matched, virtual cameras. If the angle between the

scanning unit’s cameras is the same as the angle for turning

the object, virtual cameras of different scanner poses are

very close to each other.

1999) are commonly used to establish correspon-

dences. Passive SfM-approaches do not distinguish

between external and internal matches and use the

same descriptors for all camera pairs. In our context,

however, we can match using two different strategies,

i.e. use P for high quality internal matching and a fea-

ture descriptor for external matching with lower ro-

bustness. As natural features can be sparse and of low

quality (see (Zeisl et al., 2009) for details), it is impor-

tant to reduce their negative inﬂuence on the virtual

device calibration. We achieve this in two steps:

First, we do not allow low-quality SIFT-matches

internally. However, all external matches must be

internally matched to different cameras, as pairwise

matches do not allow to deduce 3D-2D correspon-

dences in the SfM process. Any point of an exter-

nal correspondence is thus extended internally using

P. Moreover, we generate additional internal matches

by regularly sampling the respective camera images.

An internal pair of virtual cameras thus always has

more matches than an external pair and thereby gets

a higher priority in our SfM algorithm. If a new

camera is initialized with 3D-2D correspondences de-

rived from potentially bad SIFT correspondences, the

3D points consequently were entirely computed from

high-quality P-generated matches. Moreover, the ma-

jority of these 3D points is valid, as P-generated cor-

respondences contain only few outliers. The high

quality of the internal matches can thus be propagated

to SIFT-matches to some extent, while global inﬂu-

ence of SIFT is kept low.

Second, we can exploit the characteristics of the

most common scanning setups (consisting of a scan-

ning unit and a turntable), to drastically increase qual-

ity and amount of external correspondences. In gen-

eral, the quality of correspondences decreases when

the angle between the principal axes of the associ-

ated cameras increases. This is a natural consequence

of perspective distortion, which changes the local ap-

pearance of the object. If the turntable of a scanning

setup is turned by n

◦

and two cameras of the scan-

ning unit are separated by a rotation of n

◦

around

the turntable axis, motion of the turntable will al-

ways move virtual cameras of different scanner/object

poses very close to each other (Figure 2). The corre-

sponding images will thus be almost identical. This

greatly increases both the quality and the amount of

correspondences. We restrict the external matching

to only these camera pairs. Note that this concept

of internal/external matches is not restricted to the

exemplary turntable scanning setup used in this sec-

tion. It is easily adapted to units with more cameras

and/or more rotational axes. If the scanner is freely

moved around the object however, it becomes more

difﬁcult to maintain a small baseline between exter-

nally matched cameras.

5 CORRESPONDENCES FROM

ARTIFICIAL FEATURES

The approach presented in Section 4 still relies on nat-

ural visual features and fails for textureless objects.

One possibility to generate new features would be to

add additional objects with strong texture information

as calibration targets. However, they will occlude the

actual object of interest.

In this section, we present a novel hardware setup

that makes scanning fully independent of both visual

features and the object geometry. The precision of

geometry-based registration deteriorates for objects

exhibiting a certain amount of symmetry, because the

correct transformation cannot be estimated uniquely.

Our results in Section 6 contain respective examples.

Optical registration approaches suffer from similar

problems: First, repetitive visual features cannot be

matched uniquely. Second, the features might be of

low quality (Zeisl et al., 2009). And third, textureless

objects yield no visual features at all. Consequently,

it is currently not always possible to acquire a precise,

full reconstruction of arbitrary objects, whose surface

reﬂectance properties are suitable for active scanning

based on strucured light.

We resolve this by proposing a novel hard-

ware layout (Figure 1), which consists of a cam-

era/projector scanning unit and a special turntable

construction. The turntable is equipped with three

outriggers, that allow to attach additional micro-

projectors. These additional devices allow us to

project data onto the object, similar to the internal

projector. However, this data statically remains on the

object and is thus invariant of the table rotation. The

StructurefromMotionintheContextofActiveScanning

623

(a) (b) (c) (d) (e)

(f) (g) (h) (i) (j)

Figure 3: Meshes used in our experiments. (a-d) were taken

from (Curless and Levoy, 1996), (e-g) were taken from

(Wang et al., 2010) and (h-j) were taken from our own col-

lection of scans.

external matching can thus be performed in the same

way as the internal matching. Each of these exter-

nal projectors is treated as individual feature source.

Therefore, it can be possible that a 3D point is triangu-

lated twice from a region where two projector images

overlap. Those regions are, however, small and the

duplicate points do not inﬂuence the calibration. The

devices used for evaluation are listed in Section 6.

Projectors commonly generate strong heat, which

causes their image to shift over time. This shift can be

signiﬁcant, we observed several millimeters until the

device reached constant operating temperature. For

the main unit, this is compensated by an individual

set of parameters for each virtual position. For the

additional units, the positions of the projected images

must be static, it is thus very important to comply with

a warming phase.

The high-quality external correspondences make

this setup more general than the approach of Section

4. Cameras of the scanning unit can be freely posi-

tioned without regarding the turntable rotation.

6 RESULTS

We evaluate the SfM-approach with the different fea-

ture generation methods presented in this paper using

both real and synthetic data and compare the precision

to state-of-the-art registration algorithms. In the fol-

lowing, we use phase shifting to generate high-quality

correspondences with all projectors; its advantages

are discussed in (K

ohler et al., 2013). The following

approaches are evaluated:

1. SfM with SIFT-features only

2. SfM with our minimal SIFT approach (Section 4)

3. SfM with our artiﬁcially generated features (Sec-

tion 5)

4. Multi-view ICP

(1) and (4) are considered as state of the art meth-

ods. (1) can be considered as standard SfM approach

as it is used with cameras only. We use it to demon-

strate the impact of the minimal SIFT approach (see

Section 4). We choose ICP as a geometric alignment

method, since it is undeniably the most common and

widespread registration method, which dominates the

state of the art up to the present day. Our implemen-

tation is an adaption of (Pulli, 1999).

In all experiments, we express the errors not in

terms of the pose parameters, but in terms of the

resulting reconstruction error or, in other words, in

terms of the error introduced to the reconstructed

points. This has the advantage that the error is ex-

pressed as a unidimensional quantity, which is easily

interpreted by a human being. Moreover, it allows us

to derive a simple, but highly expressive error thresh-

old from the scanner’s sampling density: An object

surface is sampled by the pixel grid of the cameras.

For a ﬁxed scanner to object distance, the sampling

density is thus the average distance between vertices

of neighboring pixels. We regard a registration as

good if the error it introduces is below this thresh-

old. In this case, the registration does not degrade the

theoretically achievable scanning precision. Note that

we do not regard the precision of the scanning unit,

but only the precision of the registration. In all exper-

iments, t

= 5 and t

= 2.

6.1 Synthetic Data

In our synthetic experiments, each evaluated method

is applied to a multi-view registration problem with

8 partial scans. These scans result from a full rota-

tion of an object and are thus separated by 45

◦

. We

generate 8 point clouds C

by rendering a given mesh

from 8 different camera poses P

, which are assumed

to be the scanner poses. The camera resolution is set

to 3296x2472 (8 megapixels) and the distance of the

camera to the object is automatically adjusted, such

that the rendering best occupies the resulting image.

For each pixel, the corresponding depth yields a 3D

point and each point cloud has approximately 2 mil-

lion points.

For the geometry-based registration, we apply a

small transformation T

to each point cloud but the

ﬁrst (rotation of 3

◦

around a random axis through

the mesh centroid, translation by 0.5% of the mesh’s

longest main axis). This transformation is small

enough for proper convergence and the transformed

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

624

(e) Multi-view ICP (Pulli,

1999)

(f) SIFT (g) Our min. SIFT (h) Our Phase

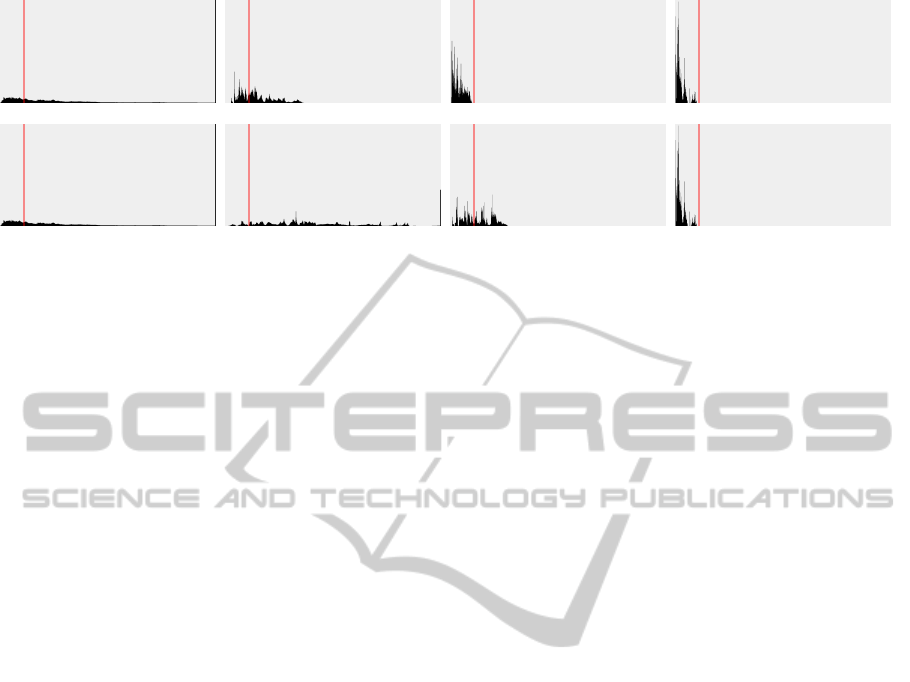
Figure 4: Results of our evaluation with synthetic data. Distribution of errors introduced to the reconstruction by wrong pose

estimates. Each histogram contains measurements from 509101060 vertices, resulting from 10 global registration problems

with 8 partial scans each. The top/bottom row illustrates results for a sharp/blurred texture, note that the ICP/Phase results

stay the same. The red line indicates our admissible error tolerance of 0.04 mm, see text for details. The large peaks at the

very right of the ICP and blurred SIFT histogram illustrate registration failures. The (linear) sizes of the x/y-axes are the same

for all plots.

point clouds can be considered as coarse initial align-

ment. The task then is to compute T

−1

For the different SfM-approaches, we assume a

scanner with 2 cameras separated by 40 degrees and

a projector centered in between. The projector frame

serves as local scanner frame, the scanner poses P

used for point cloud generation thus are the poses of

the respective projectors. For each SfM task (1-3),

the goal is to estimate P

. By separating the cameras

by 40 degrees, we account for an imprecise position-

ing most likely to occur in practice. Cameras that are

matched with our minimal SIFT approach (Section 4)

are thus separated by 5

◦

Using only SIFT-correspondences (task 1), cali-

bration of all P

was not always possible. We thus

added 6 additional cameras to the scanning unit (3

above, 3 below) to enable precise calibration from

only natural features. Note that these additional cam-

eras yield additional constraints for the registration

and naturally integrate into the SfM pipeline. In prac-

tice, imagery from these additional cameras could be

manually acquired to aid in calibration. The projector

is treated as an additional camera in this case, task 1

thus boils down to calibrate 8 ·(2 + 6 + 1) = 72 cam-

eras.

For each camera, we generate the corresponding

data for matching as follows: An image for generat-

ing SIFT-features is acquired by rendering the mesh

with a high-resolution (8196x8196 pixels) texture for

visual feature generation. This yields camera images

that have very similar characteristics compared with

real images. The internal and external phases are ac-

quired by tracing rays to the corresponding projec-

tors (we use 3 additional, static projectors for task 3).

We apply gaussian noise to both internal and external

phase correspondences, such that the reprojection er-

rors of the cameras and projectors are similar to the

values we measured in practice after calibration (0.5

pixels for the camera and 0.4 pixels for the projector).

For a given object/mesh, we compute the pose es-

timation error E

for each point cloud C

. Let in the

following Q

be the pose estimated by one of the reg-

istration methods for one of the point clouds. I.e. Q

maps from an initial position (either the common co-

ordinate frame or the coarse alignment position) to the

ﬁnal scanner position P

. For the geometry-based reg-

istration, E

= Q

◦T

≈ I, since Q

≈ T

−1

. For the SfM

methods, E

= Q

◦ P

−1

≈ I, since Q

≈ P

. For each

vertex V of a given point cloud C

, the reconstruction

error is then given by |V − E

(V )|.

We use 10 different meshes chosen from the Stan-

ford 3D Scanning Repository (Curless and Levoy,

1996), a mesh watermarking benchmark (Wang et al.,

2010) and our own collection of scans (Figure 3).

Each method thus must estimate 80 poses in total. The

set of objects contains both complex geometry and

more simple shapes with a certain degree of symme-

try. All per-vertex errors are accumulated in a single

histogram for each method (Figure 4). In all experi-

ments, the corresponding mesh was rescaled such that

the size along the major axis is 10 cm. The scanner’s

sampling density and thereby the admissible regis-

tration error threshold for such an object is 0.04mm.

Note, that this value can, at least in theory, be signif-

icantly lower for an increased device resolution. We

do the whole experiment with two different textures

mapped to the meshes. The ﬁrst is a complex forest

scene, that generates many visual features. The sec-

ond is a strongly blurred version of the ﬁrst and is

used to demonstrate the effects of sparse, low quality

StructurefromMotionintheContextofActiveScanning

625

Figure 5: Left: Small version of the forest texture, the red

square indicates the area magniﬁed on the right. Top right:

Original resolution (sharp), bottom right: original resolu-

tion, blurred.

features (Figure 5).

The ﬁrst row of Figure 4 illustrates the results for

the sharp texture. It is obvious that ICP clearly per-

forms worst. More than 50% of the errors are above

the admissible threshold and in particular for partially

symmetric objects, the alignment is of low quality.

This is, as expected, a major drawback of geometry-

based registration. SfM from only SIFT-features has

a signiﬁcantly higher quality but still more than 50%

of the points are above our quality threshold. How-

ever, if the SIFT-correspondences are constrained as

suggested in Section 4, the quality of the calibra-

tion/registration can be drastically increased - the

maximum per vertex error is 0.036 mm in all exper-

iments, which is below the scanner’s sampling fre-

quency. The artiﬁcal, phase-generated features per-

form best, the maximum per vertex error is 0.035

mm in all experiments. For ICP, the only datasets

that satisfy our quality threshold are those with very

sharp geometry features (Figure 3, (a,b,c,f)). For

smoother shapes like (Figure 3, (d,e,g,h,i,j)), several

partial views were always above our quality thresh-

old. For partially symmetric objects (Figure 3, (h,j)),

the alignment failed. This failure is reﬂected in the

large peaks at the right border of the histograms (Fig-

ure 4). The second row of Figure 4 illustrates the

effect of low quality visual features. The results of

ICP and our external phase registration stay the same,

while SIFT and our min. SIFT clearly deteriorate. In

contrast to the sharp texture case, our min. SIFT now

does not comply with the quality threshold anymore.

Constant quality thus could only be achieved with our

proposed hardware.

6.2 Real Data

For our real data evaluation, we use the setup illus-

trated in Figure 1 (see also Section 5). Our scanning

unit consists of 2+1 Allied Vision Technologies



Prosilica



GX 3300 cameras (3296x2472). The

third, centered camera enables calibration from only

SIFT features (similar to the synthetic case), it is not

used for reconstruction. Moreover, we use an Epson



EH TW 5910 projector (1920x1080) on the scanning

unit and three Dell



M115HD (1280x800) on the

turntable.

In the context of 3D-scanning, real data evalua-

tion is usually done by comparing a scan to a differ-

ent ground truth scan of known precision. In the fol-

lowing, we will thus use two scans: A ground truth

scan G and a scan S whose precision is to be evalu-

ated. In this situation, three types of registration are

potentially involved: First, the scan-internal registra-

tions, which combine multiple, partial shapes to a full

scan (G-internal registration GIR and S-internal regis-

tration SIR). Second, the external registration ER that

aligns S to G. This is necessary, as both scans have

different coordinate frames and often also different

scales. Since our focus is, however, on the precision

of the actual registration methods, an unbiased eval-

uation with real data is not possible - ER will always

add an unknown error to the ﬁnal result.

To keep the inﬂuence of ER, GIR and the sampling

density between G and S as low as possible, we use

the following approach: Both S and G are acquired

with the scanning setup proposed in Section 5. G is

not a full scan and therefore not biased by an internal

registration. S is computed by registering two partial

scans separated by 45

◦

, G is centered in between. S is

recorded once and then reconstructed/registered using

the following methods: ICP, SIFT, minimal SIFT and

Phase (see also Section 4). The external registration

is performed using 2D-2D phase correspondences be-

tween S and G, as the phase registration performed

best in the synthetic evaluation. Since both scans are

fully reconstructed, these 2D-2D correspondences in-

duce 3D-3D correspondences that are used to com-

pute the actual transformation. These 2D-2D cor-

respondences remain static, while the 3D-3D corre-

spondences depend on the given SIR and thus change.

The external registration bias introduced by wrong

2D-2D correspondences thus remains the same for

all evaluated registrations, changes in the error values

thus indeed result from the internal registration that

we want to evaluate. Note that the use of the scanner

itself as ground truth generator is valid in our context,

since we do not want to assess the precision of the

partial scan, but the precision of the inter-scan reg-

istration. Moreover, it has the following advantages:

First, the sampling density is exactly the same for all

scans. Second, phase correspondences can be used

for the external registration, which performed best in

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

626

(a) Lion (b) Vase (c) Shoe (d) Figurine

Figure 6: Objects used for real data evaluation, the amount

of features decreases from left to right, the vase is symmet-

ric.

the synthetic evaluation. For a different scanner, only

the geometry may be used, which performed worst in

the synthetic evaluation. After registering the scans to

the ground truth, we compute an error value (closest

distance to ground truth point) for each scan point in

the overlapping region.

We use four different objects with different char-

acteristics to demonstrate the capabilities of the indi-

vidual registration approaches: A Chinese lion statue

with many natural features and complex geometry,

a symmetric vase with a medium amount of natu-

ral features, a sports shoe with smooth geometry and

low amount of features and a white plastic ﬁgurine

without natural features (Figure 6). The amount of

points below our quality threshold is displayed in Ta-

ble 1. The amount does not reach 100%, because both

scans contain holes in regions not seen by all cam-

eras/projectors. In such a region, closest vertices are

not found at the correct position, but across the hole

at its border. The distance is thus automatically high.

Although we consider the simpler pairwise align-

ment instead of a multi-view problem, the results have

similar characteristics: SIFT-based registration con-

stantly deteriorates, when the amount of features is re-

duced and fails for the untextured ﬁgurine. However,

a high-quality registration can still be achieved using

our proposed minimal SIFT matching strategy. It has

constant quality, even for the shoe (sparse visual fea-

tures) and fails only for the untextured ﬁgurine. This

is resolved by our proposed hardware: The phase-

only matching exhibits constant quality. ICP is only

successful for complex geometry. It fails for the sym-

metric vase and deteriorates for objects with smooth

geometry, just as in the synthetic case. A failure case

is illustrated in Figure 7.

7 DISCUSSION

In this paper, we showed that the precision of pro-

jector/camera based active scanning systems greatly

Figure 7: Geometry cannot be used to align (partially)

symmetric objects. Left: Vase correctly registered with

SfM, right: Vase wrongly registered with ICP. Red/green:

Left/right scanner position, yellow: Overlapping area.

Table 1: Results for real datasets. The values indicate the

amount of errors below the quality threshold, ”-” indicates

registration failure. See text for details.

Lion Vase Shoe Figurine

ICP 90% - 73% 82%

SIFT 91% 85% 53% -

min. SIFT 91% 91% 91% -

Phase 91% 92% 91% 92%

beneﬁts from a global calibration. While SfM ap-

proaches are widely used in the context of imagery,

the predominant paradigm for such active scanners is

still a pre-calibration followed by a geometry-based

registration. In our experiments, the SfM-based re-

constructions could always beat traditional registra-

tion based on ICP.

We introduced a novel minimal SIFT matching

strategy that greatly reduces the inﬂuence of poten-

tially bad SIFT-features and presented a novel hard-

ware platform that makes SfM fully independent from

natural features. With this hardware, it is possible

to successfully scan any object suitable for diffuse

structured light. In particular, it allows one to scan

(partially) symmetric objects that cannot be registered

with geometry-based methods and textureless objects

that cannot be registered with optical methods.

ACKNOWLEDGEMENTS

The work presented in this paper has been partially

funded by the project DENSITY (01IW12001).

REFERENCES

Audet, S. and Okutomi, M. (2009). A user-friendly

method to geometrically calibrate projector-camera

systems. 2012 IEEE Computer Society Conference on

Computer Vision and Pattern Recognition Workshops,

0:47–54.

StructurefromMotionintheContextofActiveScanning

627

Bergevin, R., Soucy, M., Gagnon, H., and Laurendeau, D.

(1996). Towards a general multi-view registration

technique. IEEE Trans. Pattern Anal. Mach. Intell.,

18(5):540–547.

Besl, P. J. and McKay, N. D. (1992). A method for registra-

tion of 3-d shapes. IEEE Trans. Pattern Anal. Mach.

Intell., 14(2).

Curless, B. and Levoy, M. (1996). A volumetric method

for building complex models from range images. In

Proceedings of SIGGRAPH, pages 303–312.

Dold, C. and Brenner, C. (2006). Registration of terres-

trial laser scanning data using planar patches and im-

age data. In Int. Arch. Photogramm. Remote Sens.,

pages 25–27.

Du, S., Zheng, N., Xiong, L., Ying, S., and Xue, J. (2010).

Scaling iterative closest point algorithm for registra-

tion of m-d point sets. J. Vis. Comun. Image Repre-

sent., 21(5-6):442–452.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: A paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Commun. ACM, 24(6):381–395.

Furuakwa, R., Inose, K., and Kawasaki, H. (2009). Multi-

view reconstruction for projector camera systems

based on bundle adjustment. In CVPR Workshops.

Gherardi, R. and Fusiello, A. (2010). Practical autocalibra-

tion. In ECCV (1), volume 6311 of Lecture Notes in

Computer Science, pages 790–801. Springer.

Griesser, A. and Van Gool, L. (2006). Automatic interac-

tive calibration of multi-projector-camera systems. In

CVPR Workshops.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Second edition.

Holroyd, M., Lawrence, J., and Zickler, T. (2010). A coax-

ial optical scanner for synchronous acquisition of 3D

geometry and surface reﬂectance. Proceedings of SIG-

GRAPH.

Huang, Q.-X., Adams, B., and Wand, M. (2007). Bayesian

surface reconstruction via iterative scan alignment to

an optimized prototype. In Proceedings of Eurograph-

ics SGP.

ohler, J., N

oll, T., Reis, G., and Stricker, D. (2013). A

full-spherical device for simultaneous geometry and

reﬂectance acquisition. In IEEE Workshop on Appli-

cations of Computer Vision (WACV).

Krishnan, S., Lee, P. Y., Moore, J. B., and Venkatasub-

ramanian, S. (2005). Global registration of multiple

3d point sets via optimization-on-a-manifold. In Pro-

ceedings of Eurographics SGP.

Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). Epnp:

An accurate o(n) solution to the pnp problem. Int. J.

Comput. Vision, 81(2):155–166.

Lowe, D. (1999). Object recognition from local scale-

invariant features. In Proceedings of ICCV.

Moreno, D. and Taubin, G. (2012). Simple, accurate, and

robust projector-camera calibration. In Proceedings of

3DIMPVT.

Pulli, K. (1999). Multiview registration for large data sets.

In Proceedings of 3DIM.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants

of the ICP algorithm. In Proceedings of 3DIM.

Sadlo, F., Weyrich, T., Peikert, R., and Gross, M. (2005). A

practical structured light acquisition system for point-

based geometry and texture. Proceedings Eurograph-

ics/IEEE VGTC Symposium Point-Based Graphics,

0:89–145.

Salvi, J., Matabosch, C., Foﬁ, D., and Forest, J. (2007).

A review of recent range image registration meth-

ods with accuracy evaluation. Image Vision Comput.,

25(5):578–596.

Seo, J. K., Sharp, G. C., and Lee, S. W. (2005). Range data

registration using photometric features. In Proceed-

ings of CVPR.

Tam, G. K. L., Cheng, Z.-Q., Lai, Y.-K., Langbein, F. C.,

Liu, Y., Marshall, D., Martin, R. R., Sun, X.-F., and

Rosin, P. L. (2013). Registration of 3d point clouds

and meshes: A survey from rigid to nonrigid. IEEE

Trans. Vis. Comput. Graphics, 19(7).

Toldo, R., Beinat, A., and Crosilla, F. (2010). Global reg-

istration of multiple point clouds embedding the gen-

eralized procrustes analysis into an icp framework. In

Proc. 3DPVT 2010 Conf.

Torsello, A., Rodola, E., and Albarelli, A. (2011). Multi-

view registration via graph diffusion of dual quater-

nions. CVPR.

van Kaick, O., Zhang, H., Hamarneh, G., and Cohen-Or, D.

(2011). A survey on shape correspondence. Computer

Graphics Forum, 30(6):1681–1707.

Wang, K., Lavou

e, G., Denis, F., Baskurt, A., and He, X.

(2010). A benchmark for 3D mesh watermarking. In

Proc. of the IEEE International Conference on Shape

Modeling and Applications, pages 231–235.

Weinmann, M., Schwartz, C., Ruiters, R., and Klein,

R. (2011). A multi-camera, multi-projector super-

resolution framework for structured light. In Proceed-

ings of 3DIMPVT.

Weise, T., Wismer, T., Leibe, B., and Van Gool, L. (2009).

In-hand scanning with online loop closure. In ICCV

Workshops.

Williams, J. A. and Bennamoun, M. (2001). Simulta-

neous registration of multiple corresponding point

sets. Computer Vision and Image Understanding,

81(1):117–142.

Zeisl, B., Georgel, P. F., Schweiger, F., Steinbach, E., and

Navab, N. (2009). Estimation of location uncertainty

for scale invariant feature points. In Proc. BMVC,

pages 57.1–57.12.

VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications

628