
Image Labeling by Integrating Global Information by 7 Patches
and Local Information
Takuto Omiya, Takahiro Ishida and Kazuhiro Hotta
Meijo University, 1-501 Shiogamaguchi, Tempaku-ku, Nagoya, 468-8502, Japan
Keywords: Bag of Visual Words, K-Nearest Neighbor, Image Labeling and Integration of Local and Global Features.
Abstract: We propose an image labeling method by integrating the probabilities of local and global information.
Many conventional methods put label to each pixel or region by using the features extracted from local
regions and local contextual relationships between neighboring regions. However, labeling results tend to
depend on a local viewpoint. To overcome this problem, we propose the image labeling method using not
only local information but also global information. The probability by global information is estimated by K-
Nearest Neighbor. In the experiments using the MSRC21 dataset, labeling accuracy is much improved by
using global information.
1 INTRODUCTION
The goal of image labeling is to associate a class
label such as sky, water, road, etc. with every pixel
in the image. Image labeling is one of the most
crucial steps toward image understanding and has a
variety of applications such as image retrieval and
classification. The most fundamental approach put
labels to each region using the local features (e.g.,
color, texture, etc.) extracted from the region.
However, labels in an object tend to be inconsistent
since this approach puts labels to each region
independently.
Some approaches have been proposed to
overcome this problem recently. Popular approaches
use information not only from local features but also
from local contextual relationships between regions.
In those methods, Conditional Random Field (CRF)
model is used. Shotton et al. (2006) used a CRF
model which joints the appearance of different
semantic categories. Tu (2008) introduced the auto-
context model to use contextual information.
The common problem in these approaches is that
recognition results tend to be a local optimum. It is
consider that the reason of the problem is the lack of
a global viewpoint. Since only local features and
local relationship are used, the regions easily
recognized by a global viewpoint are recognized
incorrectly.
Omiya et al. (2013) used not only local
information but also the global information to
overcome with the problem. They used local
appearance histogram and Bag of Visual Words
(BoVW) as the global similarity. However, they
assumed that each image includes only one class.
Hence, the method did not work well when there are
plural classes in an image.
Therefore, we propose a novel image labeling
method that can cope with images including plural
objects. Specifically, we choose similar patches
which are similar to an input patch from the training
patches by K-Nearest Neighbor (K-NN). The objects
in the similar patches are likely to be the same as the
objects in the input patch. Hence, we vote ground-
truth labels in K similar patches and estimate the
probabilities of each pixel. This is the global
probability in our method. We integrate local and
global probabilities, and labels on a test image are
estimated.
In experiments, we used the MSRC21 dataset
(Shotton et al., 2006). When we estimated class
labels by using only local information, class average
accuracy was 49.5% and pixel-wise accuracy was
63.6%. When we use only global information, class
average and pixel-wise accuracies were 55.7% and
61.8%. When we estimated class labels by
integrating local and global information, class
average and pixel-wise accuracies were improved to
64.2% and 82.3%. The results demonstrated the
effectiveness of integration. The accuracies are
comparable to those of recent methods.
536
Omiya T., Ishida T. and Hotta K..
Image Labeling by Integrating Global Information by 7 Patches and Local Information.
DOI: 10.5220/0005356005360541
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 536-541
ISBN: 978-989-758-090-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
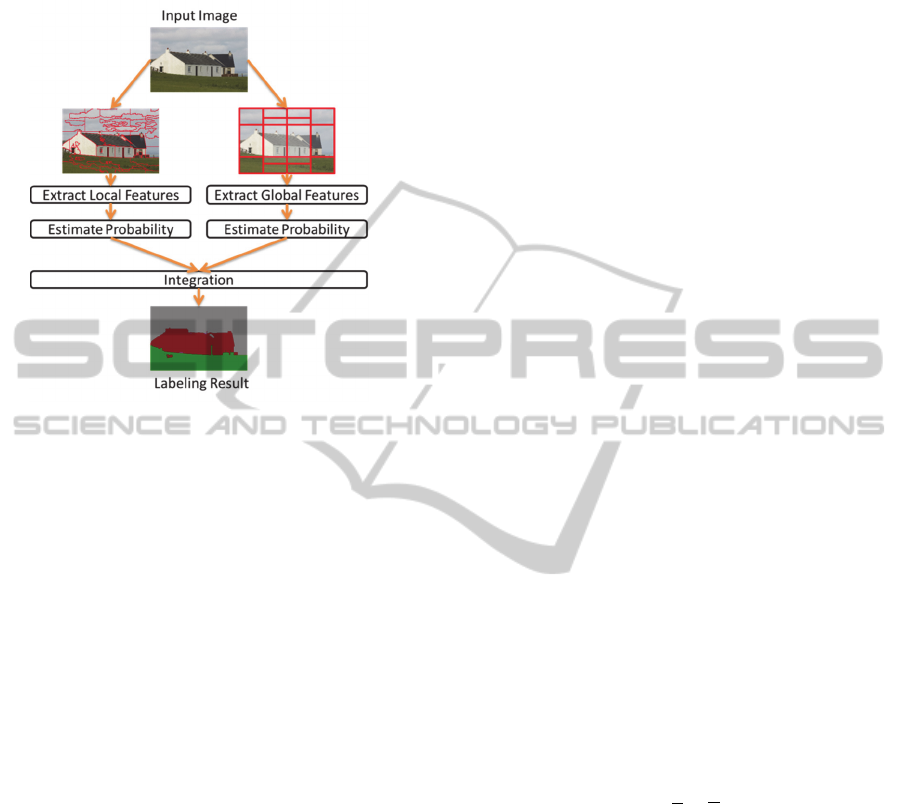
2 OVERVIEW OF THE
PROPOSED METHOD
Figure 1: Overview of the proposed method.
We show the overview of the proposed method in
Figure 1. The proposed method consists of two
phases; local and global information. An input
image is segmented by Simple Linear iterative
Clustering (SLIC) (Achanta et al, 2012) to acquire
local information, and we extract color and texture
features from each superpixel. Local feature vectors
of each superpixel are represented as the local co-
occurrence histogram of the color and texture
features. The posterior probability of each class is
estimated by Support Vector Machine (SVM).
We divide an input image into 7 patches to
acquire global information, and we extract RootSIFT
(Arandjelovic and Zisserman, 2012) from each patch
and represent it by BoVW. We choose similar
patches by using K-NN from the training patches
and estimate the probability by voting the ground-
truth labels attached to the similar patches.
Integration is performed by the product of both
probabilities every pixel. After integration, the label
of each pixel is determined to be the class with the
highest probability.
2.1 Local Information
We explain how to extract local feature vectors in
section 2.1.1. In section 2.1.2, the probability of
local information is explained.
2.1.1 Extraction of Local Features
We estimate the class labels of each superpixel
based on color and texture features. Color features
are effective to identify objects which have their
own characteristic color (e.g., sky, grass, etc.).
However, color features are sensitive to various
illumination conditions. In addition, some objects
have a wide range of color (e.g., red car, blue cars,
etc.). Therefore, we also use texture feature which is
robust to various illumination conditions and is not
affected by color variation. We used HSV as color
features and LBP (Ojala et al., 2002) as texture
features.
The local co-occurrence histogram is composed
of HSV and LBP. If we use a large number of
features, we may represent fine difference of objects.
However, the computational cost is high. Therefore,
we used clustering by k-means in each features.
In experiments, the number of dimensions of
HSV is 100 and the number of dimensions of LBP is
50. Thus, the number of dimensions of the local co-
occurrence histogram is 5,000. These values were
determined by using validation images. This local
co-occurrence histogram is used as the local feature
vectors.
2.1.2 Probability of Local Information
We use SVM to estimate the posterior probability of
each class label. Since SVM is a binary classifier,
we use one-against-one strategy. The label of each
superpixel becomes the class which has maximum
posterior probability.
We use Hellinger kernel as the kernel function.
Hellinger kernel is reported that high accuracy with
low computational cost can be realized (Vedaldi and
Zisserman, 2012). Hellinger kernel is defined as
,
√
.
(1)
In this paper, we use LIBSVM (Chang and Lin,
2001) to compute the posterior probability. The local
probability
of the -th class for the -th pixel
in an image is defined as
|
(2)
where
corresponds to the -th class and
is a
local feature vector for superpixel .
|
is
the posterior probability which is estimated by SVM.
Therefore, all pixels in the superpixel have the
same posterior probability.
ImageLabelingbyIntegratingGlobalInformationby7PatchesandLocalInformation
537

2.2 Global Information
There are trends in the distribution of the object in
images (e.g., there is the grass in the lower part of
the image, or there is the sky in the upper part of the
image). The similar image has the similar
distribution of classes in common with the input
image. By utilizing such properties, the distribution
of the object in the input image can be estimated.
Figure 2 shows the overview of the label
estimation by global information. We choose some
similar patches which are similar to the input patch
from the training patches. We use the K-NN of
BoVW histogram to select similar patches. We vote
the ground-truth label of similar patches to the input
patch, and we convert the voting result into
probability by dividing the number of votes of each
class by the total number of votes at each pixel. This
is the global probability. In this method, the
probabilities of multiple classes are estimated if
multiple objects are present in the test image. Of
course, we can estimate the position of the multiple
objects.
Figure 2: How to estimate label by global information.
When we estimate the class label from the entire
image, there is a possibility that the labeling result of
small objects is difficult since small objects are
strongly influenced by large objects such as
background. Therefore, the proposed method is
divided the image into 7 patches as shown in Figure
3. The reason for using the patch on the center of the
image is to capture the foreground objects well, and
we also obtain spatial information by using these 7
patches. The size of each patch is fixed to 160 × 160
pixels. In addition, each patch is cropped with
overlap from the image, and it is represented by
BoVW of RootSIFT (Arandjelovic and Zisserman,
2012).
We explain how to extract global feature vectors
in section 2.2.1. In section 2.2.2, the probability of
global information is explained.
Figure 3: 7 patches for K-NN.
2.2.1 Extraction of Global Features
We extract RootSIFT of 4 scales (4, 8, 12, and 16)
per 2 pixels from 7 patches. It has been reported that
RootSIFT gives higher accuracy than SIFT in
(Arandjelovic and Zisserman, 2012). We compose
BoVW histogram of RootSIFT in each patch. This
BoVW histogram becomes the global feature vector.
In experiments, the number of visual words is set to
2,000.
2.2.2 Probability of Global Information
We search similar patches from the training patches
by using K-NN. If the value of K is small, the
reliability of the estimated class label is low. On the
other hand, patches that do not similar to the input
patch are selected if the value of K is large. In this
paper, we set K = 40 which gives the optimal result
in section 3.2.
The global probability
of the -th class
for the -th pixel in an image is defined as
∑∑
∑∑∑
(3)
where
∑∑∑
represents the sum of
weighted votes at the -th pixel and
∑∑
represents the sum of weighted votes of the -th class
at the -th pixel. When the label on the -th pixel in
the -th patch is not ,
is 0.
is the weight of
the -th patch and it is computed as
(4)
where
is the distance of the -th nearest
neighbor and
is the distance of the most similar
patch.
is the distance of the K-th nearest neighbor.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
538

The weight of the most similar patch is one and the
weight gradually decreases in accordance with the
distance. The weight of the K-th patch is zero.
2.3 Information Integration
In this section, we explain the integration of local
and global information. The probabilities of local
and global information are calculated in every pixel.
Since we assume that the local and global
information is independence, we integrate both
probabilities by the product. Therefore, it is defined
as
∙
(5)
where
,
and
express the
probability of the -th class for the -th pixel in an
image. After integration, the class label
of the -th
pixel is defined as
argmax
.
(6)
3 EXPERIMENTS
We show the experimental results of our method. In
section 3.1, we describe the MSRC21 dataset
(Shotton et al., 2006) and how to evaluate the
accuracy. We show preliminary experiment in
section 3.2. In section 3.3, we show the accuracy of
our method. We show the comparison with related
works in section 3.4.
3.1 How to Evaluate Accuracy
We use the MSRC21 dataset (Shotton et al., 2006) in
the following experiments. The dataset has 591
images and contains 21 classes (building, grass, tree,
cow, sheep, sky, aeroplane, water, face, car, bicycle,
flower, sign, bird, book, chair, road, cat, dog, body,
boat). In this paper, we use 276 images for training,
59 images for validation, and 256 images for testing.
Therefore, the number of test patches is 1792 (= 256
× 7), the number of training patches is 1932 (= 276 ×
7) and the number of validation patches is 413 (= 59
× 7).
We use pixel-wise accuracy and class average
accuracy for evaluation. Class average accuracy is
the average percent of correctly labeled pixel in each
class. Pixel-wise accuracy is the percent of correctly
labeled pixels in total. Since the number of pixels in
each class is different, the two accuracies become
different value.
3.2 Preliminary Experiment for Global
Information
We show class average and pixel-wise accuracy
after integration in Figure 4. These accuracies were
obtained using validation images. After K = 40,
class average and pixel-wise accuracy are almost
unchanged. The larger K is, the higher
computational cost is. Therefore, we set K = 40 in
the following experiments.
Figure 4: Class average and pixel-wise accuracy (%) after
integration. The value of K in K-NN is different.
3.3 Results on the MSRC21 Dataset
Table 1 shows the accuracies of our method. We see
that integration of local and global information is
effective for image labeling. The accuracy of cow
class is 48.6% by only local information, while the
accuracy is 57.9% by only global information. In the
case of building, the accuracy is 41.1% by only local
information and the accuracy is 33.4% by only
global information. Thus, local and global
information have a complementary relationship each
other, and the accuracy of our method is improved
by using local and global information.
We show the examples of labeling results in
Figure 5. As shown in Figure 5, chair, boat and bird
are not labeled well. Common points of those classes
are that within-class variance is large and the
number of training sample is small. Boat class in the
MSRC21 dataset includes various ships, e.g. small
craft or large passenger ship. Chair class includes
various kinds of chairs, e.g. plastic chair or wooden
chair. It is considered that the class with large
within-class variance could not be characterized well
by using local color and texture feature. The label by
global information is estimated by voting the
ground-truth label which is attached to the similar
patches. Hence, the vote of the class with a small
number of training samples decreases and the class
is not easily classified. For example, the grass
classified with high accuracy has 2,574,052 pixels in
ImageLabelingbyIntegratingGlobalInformationby7PatchesandLocalInformation
539

training samples, but the boat classified with low
accuracy has only 91,320 pixels in training samples.
Therefore, those objects tend to be mislabeled by
only global information.
Figure 5: Examples of image labeling. (a) original image.
(b) ground-truth. (c) only local information. (d) only
global information. (e) integration of local and global
information. (A), (B) and (C) are the examples that
classification accuracy is improved by integrating local
and global information. (D), (E) and (F) are the examples
that our method did not work well.
3.4 Comparison with Related Works
We show the comparison with related works in
Table 2. Shotton et al. (2006) used a CRF model
which joints the appearance of different semantic
categories. They used only local features and local
contexts without using global information. In
comparison with their method, our method gives
higher accuracy in both measures because we used
global information.
Tu (2008) introduced the auto-context model to
use contextual information. Tu (2008) also use only
local information but their class average accuracy is
higher than one of our method. This is because
global information of our method is difficult to
classify the objects with large within-class variance.
Gould (2012) proposed a method which
considers a non-local constraint that penalizes
inconsistent pixel labels between disjoint image
regions having similar appearance. Pixel-wise
accuracy of our method is higher than one of this
method. This is because our method is able to
estimate the position of the object by only global
information and is not easy to intersperse the image
with the wrong labels.
We compare our method with the method
(Omiya et al., 2013). Class average of our method is
lower than one of Omiya et al. (2013). This is
because it is difficult for global information in the
proposed method to classify infrequent and small
objects (e.g. bird, chair, boat, etc.). On the other
hand, pixel-wise accuracy is improved. Since global
information in Omiya et al. (2013) cannot estimate
the position of objects, their pixel-wise accuracy is
lower than ours. Moreover, the classes which often
appear in background are classified with high
accuracy since our global information can recognize
spatial information by using 7 patches. For example,
our accuracies of sky, grass, water, etc. are higher
than those of Omiya et al. (2013). Omiya et al.
(2013) used the result of object categorization as
global information. Therefore, humans must
determine the main object in an image manually, and
other objects in the image are ignored. However, our
global information can estimate class label
automatically by using K-NN and is able to
recognize multiclasses. Consequently, the proposed
method is superior to the method of Omiya et al.
(2013).
4 CONCLUSIONS
In this paper, we introduced the global information
that can support multiple objects in an image. In
experiments, good class average accuracy and pixel-
wise accuracy are obtained by integrating local and
global information. In comparison with related
works, the proposed method gave high pixel-wise
accuracy and sufficient class accuracy.
Our global information is obtained by voting the
ground-truth label attached to K similar patches. The
labeling result tends to be influenced by objects with
large area (e.g. sky and grass). Thus, we plan to
decide the region with high probability and carry out
K-NN without the region that already determined.
The proposed method will estimate the label for
small objects correctly by estimating the probability
iteratively. This is a subject for future works.
Table 1: The accuracy (%) of our method.
Local Global Integration
Building
41.1 33.4 61.2
Grass
87.7 80.0 93.0
Tree
73.1 66.3 81.3
Cow
48.6 57.9 61.3
Sheep
59.2 61.2 72.4
Sky
89.1 82.8 95.3
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
540

Table 1: The accuracy (%) of our method (cont.).
Local Global Integration
Aeroplane
44.7 86.9 69.6
Water
60.6 63.8 80.4
Face
61.3 80.1 74.5
Car
52.3 57.9 66.7
Bicycle
69.8 97.0 89.4
Flower
42.2 61.0 70.7
Sign
27.4 72.2 55.6
Bird
17.5 12.5 30.2
Book
65.7 58.5 68.4
Chair
8.7 46.2 34.0
Road
75.3 41.7 73.0
Cat
48.4 41.6 57.9
Dog
32.7 22.7 41.2
Body
27.4 37.9 59.6
Boat
7.0 7.1 13.6
Class ave
49.5 55.7 64.2
Pixel-wise
63.6 61.8 82.3
Table 2: Comparison with related works.
Class ave(%) Pixel-wise(%)
Our method 64.2 82.3
Omiya et al.
(2013)
72.5 76.2
Shotton et al.
(2006)
57.7 72.2
Tu
(2008)
68.4 77.7
Gould
(2012)
71.1 81.0
ACKNOWLEDGEMENTS
This work was supported by KAKENHI
No.24700178.
REFERENCES
Shotton, J., Winn, J., Rother, C., Criminisi, A., (2006).
‘Textonboost: joint appearance, shape and context
modeling for multi-class object recognition and
segmentation.’ European Conference on Computer
Vision, pp. 1-15.
Tu, Z., (2008). ‘Auto-context and its application to high-
level vision tasks.’ Computer Vision and Pattern
Recognition, pp. 1-8.
Omiya, T., Hotta, K., (2013). ‘Image labeling using
integration of local and global features.’ International
Conference on Pattern Recognition Applications and
Methods, pp. 613-618.
Csurka, G., Dance, C., Fan, L., Willamowski, J., Bray, C,
(2004). ‘Visual categorization with bags of keypoints.’
ECCV Workshop on statistical learning in computer
vision, pp. 1-22.
Fix, E., Hodges, J., (1951). ‘Discriminatory analysis
nonparametric discrimination: Consistency properties.’
Technique Report No. 4, U.S. Air Force School of
Aviation Medicine, Randolf Field Texas.
Achanta, R., Shaji A., Smith, K., Lucchi, A., Fua, P.,
Susstrunk, S., (2012). ‘SLIC Superpixels Compared to
State-of-the-art Superpixel Methods.’ IEEE
Transactions on Pattern Analysis and Machine
Intelligence, Vol. 34, No. 11 pp. 2274-2282.
Arandjelovic, R., Zisserman, A., (2012). ‘Three things
everyone should know to improve object retrieval.’
Computer Vision and Pattern Recognition. pp. 2911-
2918.
Ojala, T., Pietikainen, M., Maenpaa, T., (2002).
‘Multiresolution gray-scale and rotation invariant
texture classification with local binary patterns.’ IEEE
Transactions on Pattern Analysis and Machine
Intelligence, Vol. 24, No. 7, pp. 971-987.
Vedaldi, A., Zisserman, A., (2012) ‘Efficient additive
kernels via explicit feature maps.’ IEEE Transactions
on Pattern Analysis and Machine Intelligence, Vol. 34,
No. 3, pp. 480-492.
Chang, C.-C., Lin, C.-J., (2001). LIBSVM: a library for
support vector machines. Available at:
http://www.csie.ntu.edu.tw/~cjlin/libsvm/ (Accessed:
11 November 2014).
Fei-Fei, L., Perona, P., (2005). ‘A Bayesian hierarchical
model for learning natural scene categories.’
Computer Vision and Pattern Recognition, Vol. 2, pp.
524-531.
Gould, S., (2012). ‘Multiclass pixel labeling with non-
local matching constraints.’ Computer Vision and
Pattern Recognition, pp. 2783-2790.
ImageLabelingbyIntegratingGlobalInformationby7PatchesandLocalInformation
541
