PGP2X: Principal Geometric Primitives Parameters Extraction

Zahra Toony, Denis Laurendeau and Christian Gagné

Computer Vision and System Laboratory, Department of Electrical and Computer Engineering,

Université Laval, Québec, QC, Canada

Keywords:

Parameter Extraction, Geometric Primitives, Principal Component Analysis.

Abstract:

In reverse engineering, it is important to extract the 3D geometric primitives that compose an object. It is

also important to ﬁnd the values of the parameters describing each primitive. This paper presents an approach

for the estimation of the parameters of geometric primitives once their type is known using 3D information.

The primitives of interest are planes, spheres, cylinders, cones, tori and partial instances of the latter four

types. The proposed approach extends methods found in the literature for planes, spheres, cylinders and

cones and proposes a new method for dealing with tori. The results of the proposed method are compared to

approaches found in the literature as well as with ground truth values. The proposed method can be applied to

the estimation of parameters of geometric primitives of synthetic CAD models as well as for models of real

objects acquired with 3D scanners.

1 INTRODUCTION

Recognizing 2D objects and ﬁnding their primitives

was one of the most popular topics in computer vi-

sion and still remains a challenging task. Accurate

3D scanners have started a challenging domain of re-

search in object detection and recognition which con-

sists of recognizing objects based on their geometry

rather than their appearance. Such 3D sensors cap-

ture the geometry of the objects and allow the type

of 3D objects to be recognized and their descriptive

parameters to be estimated.

Estimating the parameters of 3D models can be

helpful in different applications such as reverse en-

gineering, 3D model retrieval, and classiﬁcation of

3D models. Some methods have been proposed to

recognize different types of primitives (Toony et al.,

2014; Osada et al., 2002; Kazhdan et al., 2003; Zhu

et al., 2012). Once a primitive has been recognized,

we need an approach to extract the parameters of each

primitive. Some methods, (Attene et al., 2006; Attene

and Patanè, 2010; Fayolle and Pasko, 2013), ﬁrst ﬁt a

primitive model to the data and then ﬁnd the parame-

ters of the model. Our goal is to extract the primitive

parameters directly from the original model without a

ﬁtting process. The motivation of our work is to es-

timate the parameters of the principal types of primi-

tives encountered in reverse engineering applications

and object modelling. Since 95% of industrial objects

can be described by spheres, planes, cones, cylinders,

and tori (Rabbani and Van Den Heuvel, 2005), we

proposean approach for estimating the descriptivepa-

rameters of these types of primitives.

The rest of the paper is organized as follows. Re-

lated work is presented in Section 2. The proposed

approach for extracting the parameters of each prim-

itive type is explained in detail in Section 3. Section

4 presents experimental results and demonstrates the

efﬁciency of our approach in different situations and

in comparison with other methods. Section 4 also

presents results obtained on real scans of 3D objects

composed of the primitives of interest. Finally, we

conclude the paper in Section 5.

2 RELATED WORK

In order to estimate the parameters of primitives, dif-

ferent approaches can be considered. The methods

that have been proposed so far can be divided into two

categories. The ﬁrst category consists of techniques

that segment the model at ﬁrst and then determine the

type of each segment as well as their descriptive pa-

rameters. Authors usually use different primitives in

order to identify the type of each segment. The sec-

ond category contains methods which start directly

from the original model without any pre-processing

such as segmentation. These methods apply a ﬁtting

process to identify the type of primitive and then the

Toony Z., Laurendeau D. and Gagné C..

PGP2X: Principal Geometric Primitives Parameters Extraction.

DOI: 10.5220/0005356400810093

In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 81-93

ISBN: 978-989-758-087-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

parameters of the best ﬁtted primitive are returned.

Our approach deals with original models without any

pre-processing but the assumption is made that the

model contains only one primitive which can be in the

ﬁrst category but without a prior segmentation pro-

cess. Since several methods have been proposed to

determine the type of primitives, (Toony et al., 2014;

Osada et al., 2002; Kazhdan et al., 2003; Zhu et al.,

2012), in this paper, we assume that the type of each

primitive is known and focus on an accurate estima-

tion of primitive parameters.

The methods in the ﬁrst category require a seg-

mentation step and a non-linear ﬁtting approach with

reliable initial seeds. One of the methods in this cat-

egory, presented in (Lukács et al., 1998), uses a seg-

mentation approach based on initial seeds and region

growing. The segmentation and ﬁtting stop based on

the ﬁtting error. This method works for spheres, cylin-

ders, cones, and tori. The method is sensitive to the

choice of the initial seed and is also very time con-

suming.

Another approach in this category is presented in

(Benko et al., 2002). The authors assume that the in-

put point cloud is already segmented into primitives

and the type of primitive is already known. They sup-

pose that there is a set of parametrized objects for

which the parameters need to be estimated. They con-

sider some “primary objects” such as surfaces, curves,

etc. and some “auxiliary objects” that describe the

constraints between primary objects. A ﬁtting process

is used in order to ﬁnd the parameters of the primary

and auxiliary objects.

In the paper presented in (Fayolle and Pasko,

2013), which belongs the ﬁrst category, the authors

use a set of primitives from a user-speciﬁed list of

primitives. They then ﬁt these primitives and extract

the points that correspond to the best ﬁtted primitive

and the parameters are obtained from the best ﬁt. The

list of primitives includes spheres, cylinders, planes,

tori, cones, and super-ellipsoids.

The approaches in the second category extract the

primitives directly from the input point cloud using

RANSAC-based methods for instance (Li et al., 2011;

Schnabel et al., 2007; Bolles and Fischler, 1981; Fis-

chler and Bolles, 1981). In (Schnabel et al., 2007), an

automatic method is presented based on random sam-

pling which detects planes, spheres, cylinders, cones,

and tori. This RANSAC-based method is time con-

suming like all random based methods and it also de-

pends on the selected points. The method presented in

(Olson, 2001) is splitting and pruning the parametric

space in order to implement a faster algorithm. Some

other methods use the Gaussian sphere for extracting

primitives (Chaperon et al., 2001; Rabbani and Van

Den Heuvel, 2005; Liu et al., 2013).

The methods presented in (Borrmann et al., 2011;

Kotthäuser and Mertsching, 2012) are extracting

planes only but other methods are proposed to extract

cylinders (Bolles and Fischler, 1981; Lozano-Perez

et al., 1987; Chaperon et al., 2001; Rabbani and Van

Den Heuvel, 2005; Liu et al., 2013).

A hierarchical ﬁtting approach which deals di-

rectly with input data is introduced in (Attene et al.,

2006) and (Attene and Patanè, 2010). The method

presented in (Attene et al., 2006) produces a bi-

nary tree of primitives, extracting planes, spheres,

and cylinders. Another approach (Attene and Patanè,

2010) exploits more accurate hierarchical clustering

in order to extract more primitives such as planes,

spheres, cylinders, cones, and tori. Since we compare

our results with these approaches, they are described

in detail in the following section.

2.1 A Review of Two Hierarchical

Fitting Approaches

2.1.1 Method Proposed in (Attene et al., 2006)

The basic idea of the method presented in (Attene

et al., 2006) is to merge neighboring triangles into

representative clusters. The idea is to build a dual

graph from the input mesh model. At the beginning

of the algorithm, each node of the graph represents a

cluster. The authors assign a weight to each edge of

the graph. They then build a priority queue based on

the edges’ weights and they merge the edges with the

minimum weights in the priority queue. After each

merging operation, edge weights and clusters are up-

dated. The algorithm stops based on some criteria.

Fitting is applied to each cluster and the primitive

which has the minimum evaluation error is selected.

Planes, spheres, and cylinders are considered. To

extract planes, the authors use a classical method

based on PCA (Principal Component Analysis) (Gar-

land et al., 2001; Cohen-Steiner et al., 2004). First the

covariance matrix of each cluster is computed. The

normal of the plane is the eigenvector corresponding

to the smallest eigenvalue of the covariance matrix.

The ﬁtting error is calculated afterwards.

In order to ﬁnd the parameters of the spheres (ra-

dius and location of the center), several different radii

and centers are tested and those that minimize the dis-

tance between the points and the ﬁtted sphere are se-

lected. These parameters can be found by solving a

Gauss-Newton minimization problem (Scales, 1985)

but, as mentioned in the paper (Attene et al., 2006),

this is a time consuming process so an algebraic dis-

tance approach (Pratt, 1987) has rather been used to

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

(a) (b) (c) (d) (e)

Figure 1: The parameters extracted for: (a) plane, (b) sphere, (c) cylinder, (d) cone, and (e) torus.

determine the sphere’s parameters.

For cylinders, the parameters that need to be es-

timated are the radius, the axis direction, and a point

belonging to the axis which is called the center. In

order to estimate the axis direction, they ﬁrst compute

a covariance matrix on the edges of the dual graph.

Then, they select the eigenvector related to the largest

eigenvalue of the covariance matrix as the axis of the

cylinder. A plane is then deﬁned with a normal in the

same direction of the axis of the cylinder and a point

as the center of mass of the cylinder points. Then, all

points of the cylinder are projected onto the plane and,

using a direct circle ﬁtting approach, the radius and

the center location of the created circle on the plane

are computed. Finally the ﬁtting error is calculated.

2.1.2 Method Proposed in (Attene and Patanè,

2010)

In this method, the authors consider spheres, planes,

cylinders, cones, and tori. They present an algorithm

to convert a 3D surface into a hierarchical represen-

tation. A k-nearest neighbor graph is built on the in-

put point-set which is a time consuming process. The

procedure for estimating the parameters of planes and

spheres is the same as the one presented in (Attene

et al., 2006). For cylinders, the Gaussian sphere con-

cept is used. First the normals of the cylinders are

mapped on the Gaussian sphere, the axis of the cylin-

der is found using PCA. A plane is then mapped on

the points located on the Gaussian sphere and, ﬁnally,

all of these points are projected onto the plane and a

direct circle ﬁtting approach is used to ﬁnd the radius

of the projected circle.

For cones, the normals are mapped on the Gaus-

sian sphere and a plane is ﬁtted on the normals. PCA

is used to ﬁnd the normal vector to the plane. The

apex of the cone is found using a minimization pro-

cess and, ﬁnally, the semi-apical angle that shows the

deviation of the cone surface from the axis is com-

puted.

For tori, a center point, a height vector and a ra-

dius are calculated. The curvature properties of the

torus are used to estimate the height vector and the

small radius of the torus. Each point of the torus is

moved on the opposite direction of its normal with

a signed distance obtained from the curvature value.

So, all of the points are placed on a circular axis.

The plane passing through the transformed points is

then found. The direction of the plane’s normal is the

height vector. These transformed points are projected

onto the plane, and the center and the radius are found

by applying a circle ﬁtting algorithm on the projected

points.

In this paper, we compare our results with (At-

tene and Patanè, 2010)’s method and also with the

result of a non-linear least-squares ﬁtting algorithm

of the LSGE library developed for ﬁtting primitives

(LSGE, 2004). In our method, we extract the param-

eters of planes, spheres, cylinders, cones, and tori as

well as partial instances of the former four types of

primitives. The methodology for extracting the pa-

rameter values of each type of primitive is detailed in

the following section.

3 PROPOSED METHOD (PGP2X)

Regardless of the type of input data, mesh or point

cloud, we estimate the normal at each vertex of each

primitive. If the model is a mesh, we consider the

normal at a vertex as the average between the nor-

mals of its connected faces. The normal to a tri-

angular face is the cross product of its two adjacent

sides. If the model is a point cloud, we compute the

normal at each point using the method presented in

(Zhang et al., 2013) which is a robust normal esti-

mation method based on a low-rank subspace clus-

tering approach. A covariance analysis of the neigh-

borhood is used to ﬁnd the smooth and sharp regions

around the points. A guiding matrix using an un-

supervised learning process based on neighborhood

features is built. Finally, the anisotropic neighbor-

hoods are segmented into some isotropic neighbor-

hoods using the guiding matrix and the low-rank sub-

space clustering approach. For a point near smooth

regions, the normal can be obtained easily and accu-

rately but for points near sharp regions, the normal is

estimated as the normal of a ﬁtted plane to the consis-

tent sub-neighborhoods (Zhang et al., 2013).

Now that the procedure for obtaining the normals

to the vertices has been presented and the type of each

primitive is known, we go through the details of pa-

rameter extraction for each primitive. The primitives

PGP2X:PrincipalGeometricPrimitivesParametersExtraction

(a) (b) (c)

Figure 2: (a) Real scanned plane with vertices and normals,

(b) principal components obtained from vertices, (c) ﬁtted

plane using the normal obtained from PCA and the median

of vertices as the point.

that are considered in this paper are planes, spheres,

cylinders, cones, and tori as well as partial models

of the latter four types of primitives. Based on the

method presented in (Toony et al., 2014), the type of

primitive is found. The parameters are extracted for

each primitive type are listed in ﬁgure 1.

3.1 Plane

The parameters of a plane are the normal to the plane,

~n, as well as a point p lying on the plane (ﬁgure 1 (a)).

In order to ﬁnd the normal to the plane, a good method

is the Principal Component Analysis (PCA). We ap-

ply the PCA on the vertices of the input data. The

eigenvector corresponding to the smallest eigenvalue

is selected as the normal to the plane. The median of

the points is chosen as a point lying on the plane.

Figure 2 presents a scanned plane. Part (a) shows

the plane with vertices and normals; the principal

components are presented in part (b) and, ﬁnally, the

ﬁtted plane using the normal extracted from PCA and

the median of the points are shown in part (c).

3.2 Sphere

The parameters that need to be extracted for a sphere

are the center c and the radius r (see ﬁgure 1 (b)). In

order to estimate the two parameters, different meth-

ods can be used. The simplest but the most time con-

suming is the ﬁtting approach. In this paper we rather

use a fast method which relies on four non-coplanar

points (Schmitt, 2005). A sphere can be extracted

uniquely from four points if they are not on the same

plane (Schmitt, 2005). The details of the approach are

presented in the following:

1. In order to have four non-coplanar points, we

select three non-collinear points P

, and P

Then we ﬁnd the plane passing through these three

points and the fourth point is the one whose dot

product with the plane’s normal is nonzero, mean-

ing that this fourth point is non-coplanar with the

other three points.

2. Once four points have been selected, we need to

solve the following determinant equation:



+ y

+ z

x y z 1

+ y

+ z

+ y

+ z

+ y

+ z

+ y

+ z



= 0. (1)

3. This determinant can be written as:

) M

−xM

+yM

−zM

= 0.

(2)

4. Considering x

+ y

+ z

= r

, we write the sphere

equation as follows:

(x− x

)

+ (y− y

)

+ (z− z

)

− r

= 0. (3)

5. After equating the expansion of equation 3 with

equation 2, the parameters of the sphere are ob-

tained as,

= +0.5

, y

= −0.5

, z

= +0.5

= x

+ y

+ z

−

(4)

see (Schmitt, 2005) for the deﬁnition of each M

3.3 Cylinder

For a cylinder, we need to extract the direction of the

axis,

d, the height of the cylinder, h, the center, c, and

the radius, r, of the basis as presented in ﬁgure 1 (c).

The proposed method to estimate the parameters of

cylinders is presented in the following steps:

1. Map all normals of the cylinder on the Gaussian

sphere. This creates a great circle on the sphere.

2. Find the plane passing through the normals. To

achieve this, we apply PCA on the normals and

we select the vector corresponding to the small-

est eigenvalue as the normal to the plane which is

the direction of the cylinder’s axis,

d. Selecting

one of the points on the Gaussian sphere and the

normal direction of the plane, we have the plane

that is passing through the normals on the Gaus-

sian sphere.

3. Once the plane has been determined, all points of

the cylinder are projected onto the plane which cre-

ates a circle on the plane.

4. In order to obtain the radius of the circle, most

methods, such as the one proposed by Attene

in (Attene et al., 2006) and (Attene and Patanè,

2010), use direct circle ﬁtting. In this paper, we

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

(a) (b) (c)

(d) (e) (f)

Figure 3: Extracting the parameters of a cylinder: (a) 3D

model of a cylinder with its normals; (b) normals of the

cylinder on the Gaussian sphere; (c) the ﬁtted plane on the

normals; (d) projected points on the plane and the result

of Taubin’s circle ﬁtting; (e) projected cylinder points on

the plane’s normal (axis vector), the blue point shows the

minimum value; and (f) the basis of the cylinder with it’s

center (green dot).

rather use Taubin’s method (Taubin, 1991) to esti-

mate the radius. Taubin’s method is fast and robust

and it works well even in the case of a partial circle

with a small arc (Chernov, 2009). Taubin’s method

is more stable than the circle ﬁtting approach pro-

posed by Kasa (Kasa, 1976) and is faster than the

direct circle ﬁtting by Pratt (Pratt, 1987).

5. To estimate the center of the cylinder, if the 2D

center of the Taubin’s ﬁtted circle is transformed

into 3D, it returns a point on the axis vector, as

in Attene’s method, but is not exactly the center

of the cylinder base. So, we ﬁrst determine the

points right at the base of the cylinder and then

we extract the center. To achieve this, all points

on the cylinder are projected onto the axis vec-

tor and the minimum projected value is found.

Afterwards, all cylinder points whose projected

values are in a small neighborhood of the mini-

mum value are selected. This creates a circle as

shown in ﬁgure 3. Then, three points on this circle

are chosen, knowing the radius r

from the pre-

vious step, the general circle equation is solved,

(x − x

)

+ (y − y

)

+ (z − z

)

= r

, to ﬁnd the

center,c = (x

),of the cylinder base.

6. In the last step, to ﬁnd the height of the cylinder,

the difference between the min and the max values

of the projected points on the axis vector are found

and the height is computed as h = max − min.

3.4 Cone

The parameters of a cone that need to be extracted are

the axis direction,

d, the height of the cone, the radius,

r, and the center of the cone base, c. In the following

(a) (b) (c)

(d) (e) (f)

Figure 4: Extracting the parameters of a cone: (a) 3D model

of a cone with its normals; (b) normals of the cone on the

Gaussian sphere; (c) the ﬁtted plane on the normals; (d)

projected points on the plane with Taubin’s circle ﬁtting;

(e) projected cone points on the plane normal (axis vector),

the blue point shows the minimum value; and (f) the base

of the cone with its center (green dot).

we explain the details of our approach to extract these

parameters:

1. The ﬁrst step is similar to the case of cylinders and

consists in mapping all normals of the cone on the

Gaussian sphere. This creates a small circle on the

sphere (ﬁgure 4 (b)).

2. A plane is ﬁtted through the normals. The direc-

tion of the plane’s normal is the direction of the

axis vector.

3. All of the 3D points of the cone are projected

onto the plane which creates several circles. Us-

ing Taubin’s method, circles are ﬁtted and the one

with the greatest radius is selected.

4. To estimate the height of the cone, all 3D points are

projected onto the axis vector, and the difference

between the minimum and the maximum projected

values is considered as the height of the cone.

5. In order to estimate the center of the cone base,

the base of the cone must be estimated ﬁrst, as

for cylinders. In a case of an upward cone, all

3D points correspondingto the minimum projected

value on the axis direction, or the points related

to the maximum projected value, in the case of a

downward cone, are located on the cone base. For

the estimation to be independent from the direc-

tion of the cone, the points in a small neighbor-

hood of the minimum and the maximum projected

values on the axis direction are selected. So, two

sets are considered, one around the minimum pro-

jected value and the other one includes the points

around the maximum projected value. The set that

consists of one point, the apex, is rejected. As for

cylinders, knowing the radius and three points of

PGP2X:PrincipalGeometricPrimitivesParametersExtraction

the base, the circle equation is solved in order to

determine the center of the cone base.

This procedure is applied on a cone that is presented

in ﬁgure 4.

3.5 Torus

Estimating the parameters of the torus primitive is the

most challenging task of primitive parameter extrac-

tion. In fact, approaches reported in the literature fol-

lowing the research presented by (Attene and Patanè,

2010) have failed. However, here, we present a novel

algorithm to extract the parameters of a torus. The

method is accurate for different instances of tori. The

parameters to be extracted are the direction vector,

which is orthogonal to the torus model, the center, c,

the radius for the great circle, R, and the radius for the

small circle, r. In the following we explain the de-

tails of the approach that is proposed to extract these

parameters:

1. PCA is applied on the 3D points of the torus

model. The eigenvector corresponding to the

smallest eigenvalue is considered as the direction

vector,

2. A plane is located with

d as its normal vector and

the point that is the average of the points on the

torus. This point is considered as the center, c, of

the torus.

3. All 3D points of the torus are projected onto

the plane. This produces several circles. Using

Taubin’s method, the parameters of these circles

are found. The smallest and the greatest radii, r

and r

respectively, are used to compute the radii

of the torus model. As presented in ﬁgure 5 (d),

the two radii, r

and r

are used to compute R and

(a) (b)

Figure 5: Extracting the parameters of a torus: (a) 3D model

of a torus with its normals; (b) 3D points of the torus with

the PCA ﬁtted plane and the direction vector; (c) projected

points on the plane with the greatest and smallest ﬁtted cir-

cles, red and blue circles respectively; and (d) two new radii,

and r

are used to compute R and r.

r, with the following equations:

R = r

− r

+ r

, (5)

r =

− r

. (6)

This methodology works well for complete CAD

models or real scans of complete tori. However, for

partial tori, especially small ones, the eigenvector cor-

responding to the smallest eigenvalue is not always

the vector perpendicular to the model. To deal with

such cases, the three principal components of the

points on the models are computed. The vector as-

sociated with each component is considered in turn

as the normal to the torus plane which produces three

different projection results. Figure 6 depicts these dif-

ferent projections.

In order to identify the right plane, for each of

these three conditions, the points outside of a mar-

gin distance ε to the plane are ignored and then the

distance of the remaining points to the plane are cal-

culated. When the diagram of the sorted distances

for each plane is plotted, the three diagrams in ﬁgure

7 plot (a)-(c) are obtained. For a torus model, espe-

cially CAD models, the points on the torus are located

on circles but on different levels. We thus have sev-

eral points at the same distance to the plane and then

another series of points with a different common dis-

tance to the plane and so on for the different levels.

The difference of sorted distances shows many zero

valuesin the diagram with sharp steps which is caused

by the points with the same distance to the plane. If

the plane is the right one, with the normal perpendic-

ular to the model, the diagram of differences of dis-

tances has several zeros and sharp peaks. However

(b) (c) (d)

(a) (e) (f) (g)

Figure 6: Finding the right direction of the plane for a par-

tial torus: (a) the 3D CAD model of a partial torus with

its three principal components; (b) selecting the eigenvec-

tor corresponding to the smallest eigenvalue as the normal

to the plane; (c) selecting the eigenvector corresponding to

the second smallest eigenvalue as the normal to the plane;

(d) selecting the eigenvector corresponding to the largest

eigenvalue as the normal to the plane; and (e)-(g) projecting

3D points on the plane presented in (b), (c), and (d) respec-

tively.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

(a) (b) (c)

(d) SF M = 0.0236 (e) SF M = 0.0001 (f) SF M = 0.0171

Figure 7: Diagram of the distances to the plane: (a)-(c) di-

agrams of the distances to the planes presented in ﬁgure 6

(b)-(d), respectively; while (d)-(f) show difference of dis-

tances between contiguous points of the diagrams presented

in plot (a)-(c), respectively. The spectral ﬂatness value is

calculated for the difference of distances diagrams, plot (d)-

(f) and the values are presented for each diagram. The min-

imum value ((e) in this case) corresponds to the right direc-

tion of the plane.

if the plane is the wrong one, there is no regularity

between the distance of points from the plane. The

ﬂatness of the diagram of differences of distances can

be considered as a measure that can be used to ﬁnd the

right plane. This regularity is more observable when

the model is a CAD model as it is the case for ﬁg-

ure 7. However, the approach has also been applied

successfully to real scanned models.

When the plane is the wrong one, there is no

regularity in the distribution of the distances of the

points to the plane. The Kurtosis of the difference of

distances diagram or its ﬂatness are parameters that

could be used to ﬁnd the most regular one. Based on

our experiments, ﬂatness has demonstrated to be more

efﬁcient than Kurtosis. For this reason, the Spectral

Flatness Measure (SFM) (Johnston, 1988) was used

to estimate the ﬂatness. SFM is obtained by com-

puting the ratio between the geometric mean of the

diagram and the arithmetic mean of the diagram:

SFM =

∏

i=1

∑

i=1

(7)

where, N + 1 is the number of points, y

is the dif-

ference of distance to the plane between point i and

i+ 1.

(a) (b)

Figure 8: Finding the parameters of the circles for the par-

tial torus of ﬁgure 6 using (a) Taubin’s method and (b) the

RCD approach. The results show that Taubin’s method is

not suitable for two partial circles while the RCD approach

is able to extract the parameters correctly.

Using the spectral ﬂatness, the direction vector

of the torus model,

d, can be found for both com-

plete and partial models. Once the plane is obtained,

the points within a small margin distance ε to the

plane are selected and are projected onto the plane.

For a complete torus, this creates two full circles and

Taubin’s method can be used to ﬁnd the radius of the

two circles and, using equation 5 and 6, the two radii

of the torus can be computed. For partial models only

two partial circles are observed and Taubin’s method,

which also works in the case of a single partial circle,

fails to ﬁnd the correct radii since there are two par-

tial circles. The Randomized Circle Detection (RCD)

method can be used instead (Chen and Chung, 2001).

Figure 8 shows that the Taubin’s method fails for the

partial torus of ﬁgure 6 but works well for a complete

torus as observed in ﬁgure 5 plot (c).

RCD can also be applied to full circles but since

Taubin’s method is fast and accurate, RCD is only

used in the case of partial tori. In order to decide

which approach to be used, Taubin’s method is ap-

plied ﬁrst and then the small and great circles are

found. The points located on these two circles are re-

moved. If more than 30% of the points remain, RCD

is used instead.

The Randomized Circle Detection (Chen and

Chung, 2001) was introduced for detecting circles

on images. Here, the RCD is used to detect circles

made of 2D points, which are 3D points projected

on a plane. RCD begins with a set of pixels V, and

then selects three non-collinear points, v

, and v

The fourth point, v

, is selected such that it is non-

collinear with two of the three other points. Then, the

parameters of four circles, C

ijk

, obtained by each of

the three points, (x − a

ijk

)

+ (y − b

ijk

)

= r

ijk

, are com-

puted as follows:

ijk



+ y

− (x

+ y

) 2(y

− y

)

+ y

− (x

+ y

) 2(y

− y

)



4((x

− x

)(y

− y

) − (x

− x

)(y

− y

))

, (8)

PGP2X:PrincipalGeometricPrimitivesParametersExtraction

ijk



2(x

− x

) x

+ y

− (x

+ y

)

2(x

− x

) x

+ y

− (x

+ y

)



4((x

− x

)(y

− y

) − (x

− x

)(y

− y

))

, (9)

ijk

− a

ijk

)

+ (y

− b

ijk

)

, for any l = 1, 2,3,4.

(10)

Once the parameters of the four circles,C

123

124

134

, and C

234

, are found, the distance between point

, i = 1, 2, 3, 4 to the circle obtained from the

three other points is computed: d

→ C

234

, d

→ C

134

→ C

124

, and d

→ C

123

. If one of these distances is

less than a threshold, T

, the four points are called co-

circular (Chen and Chung, 2001) and the three pixels

composing the circle are referred to as agent pixels.

The distance between each pair of agent points must

be greater than a threshold, T

If all these conditions are satisﬁed, the number

of points, n

that are lying on the circle obtained by

agent pixels are found. If n

is larger than a global

threshold T

, the circle is considered as a true circle

and all the points that are lying on this circle are re-

moved from set V. The algorithm iterates until only a

small number of points remain in set V.

Since this approach requires that several parame-

ters be set, it was modiﬁed by removing some thresh-

olds and some steps are also changed so the algo-

rithm adapts to our application. Eliminating several

thresholds of the original RCD method decreases the

number of failures and makes the algorithm converge

faster while maintaining the same level of accuracy.

In the following, the modiﬁed RCD approach is ex-

plained:

1. Suppose V to be a set of input points (pixels),

which is a set of projected 3D points on the plane.

First, the counters and thresholds are initialized as

follows:

f: failure counter is set to 0.

: failure threshold, maximum number of failures

that are tolerated by the algorithm.

min

: the minimum number of points that can

remain in set V in order to stop the algorithm.

: the distance threshold between each point and

the ﬁtted circle.

2. If f = T

or |V| < T

min

, the algorithm stops; other-

wise four pixels are selected from set V so they are

co-circular.

3. The four possible circles associated with these four

points are computed and then the number of points

lying on the circles are identiﬁed. To achieve this,

the distance between each point in set V and each

circle is determined. The number of points, N

whose distance is less than threshold T

is stored.

4. The circle with the largest N

is selected as the best

ﬁtted circle. If N

is less than one percent of V, the

failure counter f is incremented by one and the al-

gorithm returns to step 1. If N

is greater than 45%

of V, the sum of distances from the best ﬁtted cir-

cle is computed and divided by N

. If this value is

less than ε

, the circle is selected as the true circle,

the circle’s parameters are stored and all points in

V lying on the circle are removed and one returns

to step 1.

With the above procedure the great and small radii

of the torus, R and r, and the axis direction,

d can be

estimated. The other parameter that remains to be ex-

tracted is the center of the torus. Using either RCD

or Taubin’s method, we have the centers of the cir-

cles on the plane, c

and c

, while we need to extract

the center of the torus in 3D. As mentioned before,

all points of the torus were projected onto a plane

whose normal is

d. This vector is one of the eigen-

vectors of the PCA, so the two other eigenvectors,

and

B, are the vectors lying on the plane onto which

the torus points are projected. If we consider (x, y, z)

as the coordinates of torus points,

d = (d

, d

A = (a

, a

), and

B = (b

, b

) as the PCA

eigenvectors, the projection of points on these vectors

are expressed as follows:































x+ a

y+ a

x+ b

y+ b

x+ d

y+ d







(11)

so, considering M =













we have,













= M

−1







x+ a

y+ a

x+ b

y+ b

x+ d

y+ d







= M

−1







′







(12)

′

, y

′

, z

′

) are the coordinates of the projection of

(x, y, z) on

A, and

B, respectively. All values of ma-

trix M are know. The x-coordinate and y-coordinate

of the circles center, c

and c

respectively, are the

same as the x and y coordinates of the torus center,

so, x

′

= c

and y

′

= c

. The only missing param-

eter is z

′

which is exactly the mean value of the torus

points projected on

d. Now, using equation 12 the 3D

coordinate of the torus center, (x, y, z)can be com-

puted.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

0 10 20 30 40 50 60 70 80 90 100

100

120

Model number

Radius

Ground Truth

PGP2X

Attene Method

LSGE

0 10 20 30 40 50 60 70 80 90 100

0.001

0.002

0.003

0.004

0.005

0.006

0.007

0.008

0.009

0.01

Model number

SSD for center

PGP2X

Attene Method

LSGE

(a) (b)

0 10 20 30 40 50 60 70 80 90 100

Model number

Run Time(s)

PGP2X

Attene Method

LSGE

0 5 10 15 20 25 30

100

Model number

Radius

Ground Truth

PGP2X

Attene Method

LSGE

0 5 10 15 20 25 30

Model number

SSD for center

PGP2X

Attene Method

LSGE

0 5 10 15 20 25 30

Model number

Run Time(s)

PGP2X

Attene Method

LSGE

(e) (f)

Figure 9: Comparison of sphere parameters between ground

truth values, our method (PGP2X), Attene’s method and

LSGE. The ﬁrst row shows the result for complete spheres

and the second row presents the results for partial spheres.

Plots (a) and (d) compare radius values, the comparison of

the sum of square differences for the center values is pre-

sented in plots (b) and (e). plots (c) and (f) show the run

times for the different approaches.

4 EXPERIMENTAL RESULTS

In order to study the result of our method for differ-

ent models, we prepared 620 CAD models with the

3DsMax software: 100 planes, 100 cones, 100 cylin-

ders, 100 spheres, 100 tori, 30 partial cones, 30 partial

cylinders, 30 partial spheres and, 30 partial tori which

is called GPrimDB (Geometric Primitive Data Base).

We selected the parameters of the models in order to

design small, large, sparse, and dense models (from

1mm to 100mm). The database includes cones with

the cap (100 full cones and 30 partial cones) which

is not used in this paper. In this section, we compare

our parameter detection method with two other ap-

proaches: Attene’s method (Attene and Patanè, 2010)

and LSGE (Least Squares Geometric Element Soft-

ware) (LSGE, 2004). Attene’s method has been ap-

plied for Planes, cones, cylinders, and spheres but it

does not achieve good results for tori. The LSGE uses

least-squares ﬁtting in order to ﬁnd the parameters of

the primitives. For all primitives, an initial value for

each parameter is required which limits the use of the

algorithm. Consequently, we use Attene’s method re-

sults as the initial values for LSGE for spheres and

cylinders. Since Attene’s method does not achieve

good results for tori, initial values are not available

for torus ﬁtting in LSGE. For cones, Attene’s method

does not return the radius of the base which is one of

the initial values that is required by LSGE.

Since Attene’s method and LSGE perform well

for spheres and cylinders, we compare our results to

these two approaches and to ground truth values. The

parameters that are introduced in section 3.5 are cho-

sen empirically and are set to the following values:

ε: the distance associated with the second peak in the

difference of sorted distances’ diagram, T

: 30000,

min

: |V| × 0.1, T

: 0.5, and ε

: 0.3.

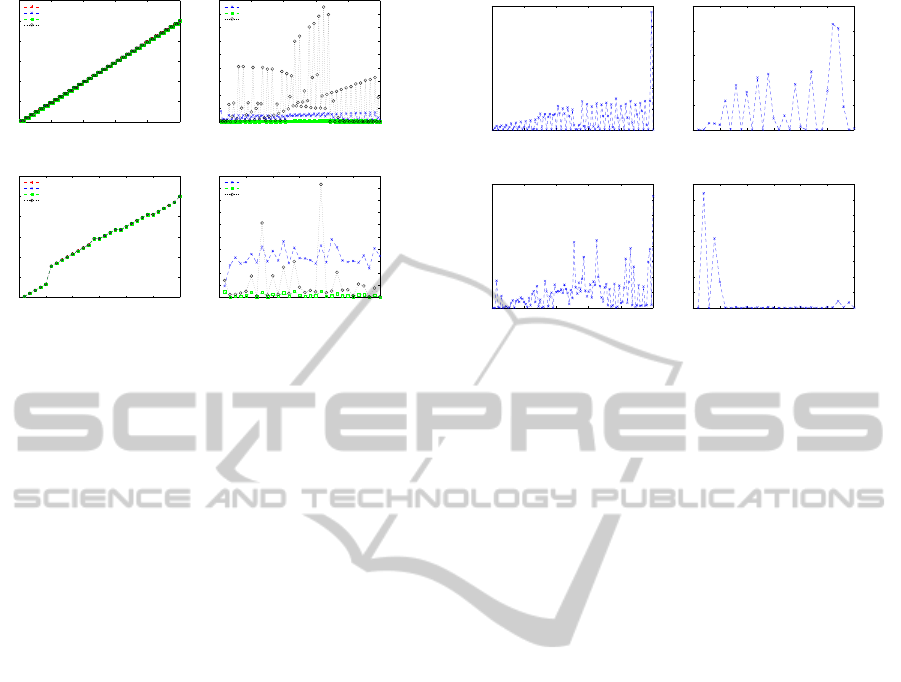
Figure 9 presents six diagrams for sphere models.

The ﬁrst row shows the results of the comparison for

100 complete spheres of the database with respect to

both the radius and the center of the sphere with the

run time of the algorithms. The second row presents

the results for 30 partial spheres of the database. In

order to compare the computed center, (c

′

, c

′

, c

′

with the ground truth center, (c

, c

), the Sum of

Square Differences (SSD) is calculated as follows:

SSD =

− c

′

)

+ (c

− c

′

)

+ (c

− c

′

)

. (13)

Where the SSD is close to zero, the method is judged

as accurate. The SSD values are presented in the sec-

ond plot for both complete and partial spheres. The

ﬁrst plots show the computed radii in comparison with

ground truth radii. The run time of the different ap-

proaches is plotted in the last plots. The results show

that all methods perform well for estimating the ra-

dius. For the center, all methods provide good re-

sults. PGP2X for complete spheres varies somewhat

for some models but is signiﬁcantly more efﬁcient

than other methods in processing time.

For cylinders, Attene’s method and LSGE return

the radius of the cylinder, the direction of the axis and

a point on the axis while PGP2X returns the radius,

the direction axis, the height, and the center of the

base. If the direction axis is not correct, the radius

of the cylinder will not be correct either. In the fol-

lowing, we compare the parameters that are common

to the other approaches and ours. Figure 10, shows

the computed radius and run time for the different ap-

proaches for both complete and partial cylinders.

The results show that all methods perform well for

the radius. PGP2X is slightly slower than the others

since it estimates more parameters (i.e. the exact lo-

cation of the center on the base). We also compare

PGP2X with ground truth values for the height and

center of cylinders. Figure 11 shows the difference

between the computed height and center estimated by

PGP2X and the ground truth values for both complete

PGP2X:PrincipalGeometricPrimitivesParametersExtraction

0 20 40 60 80 100

100

120

Model number

Radius

Ground Truth

PGP2X

Attene Method

LSGE

0 20 40 60 80 100

Model number

Run Time(s)

PGP2X

Attene Method

LSGE

(a) (b)

0 5 10 15 20 25 30

100

120

Model number

Radius

Ground Truth

PGP2X

Attene Method

LSGE

0 5 10 15 20 25 30

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

Model number

Run Time(s)

PGP2X

Attene Method

LSGE

Figure 10: Comparison of cylinder parameters between

ground truth values, our method (PGP2X), Attene’s method

and LSGE. The ﬁrst row shows the result for complete

cylinders and the second row presents the results for par-

tial cylinders. Plots (a) and (c) present the comparison for

the radius and plots (b) and (d) show the run times for the

different approaches.

and partial models.

For cone models, Attene’s method (Attene and

Patanè, 2010), identiﬁes the direction of the axis, the

apex and the semi-apical angle which expresses the

deviation of the cone border from the direction of the

axis. The ground truth values of the cones designed

with 3DsMax do not correspond to these parameters.

The rotation of the 3D model is entered as an input

to 3DsMax, so the ground truth axis direction can be

estimated based on the rotation information given by

3DsMax (multiplying the rotation matrix by unit axis

direction (0, 0, 1) ). The semi-apical axis is the arc-

tangent of the cone radius over its height. The posi-

tion of the apex cannot be estimated from ground truth

parameters.

For cones, our approach estimates the center, the

radius of the cone base, the height, and the direction

of the axis plus the semi-apical angle and the position

of the apex. So, in order to make the comparison of

the axis direction computed by different methods, the

SSD is calculated using the ground truth values (see

part (a) in ﬁgures 12 and 13 for complete and par-

tial models, respectively). For the semi-apical angle,

Attene’s method and our approach are compared to

ground truth values in part (b) of ﬁgures 12 and 13 for

complete and partial models, respectively. For the po-

sition of the apex, we have Attene’s results and our re-

sult without the ground truth values as a reference, so,

we have not provided any comparison for this param-

eter. For the center of the cone base, the heightand the

radius, we compare the results of our method with the

ground truth for both complete and partial models in

0 20 40 60 80 100

x 10

−3

Model number

Difference between ground truth height and our result

0 5 10 15 20 25 30

0.5

1.5

2.5

x 10

−3

Model number

Difference between ground truth height and our result

(a) (b)

0 20 40 60 80 100

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Model number

SSD for center

0 5 10 15 20 25 30

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

Model number

SSD for center

Figure 11: The difference between ground truth values for

height and center of cylinders and results obtained by our

method (PGP2X). Plots (a) and (c) shows the results of the

complete models (height and center). Plots (b) and (d) show

the results of partial models for height and center, respec-

tively.

ﬁgures 12 and 13 in part(c), (d), and (e), respectively.

The run time is presented in part (f) in ﬁgures 12 and

13 for both complete and partial models. The results

in ﬁgure 12 and 13 show that our method can estimate

more parameters in comparison with Attene’s method

and thus provides a more detailed description of the

primitive. Our results are very close to ground truth

values. The run time of our method is less than At-

tene’s approach even though our approach provides

more parameters.

For torus primitives, since no other method deals

with this primitive, our method is compared to ground

truth values only. Therefore, we present the compari-

son between our method and ground truth in a tabular

manner as the average of the sum of square differ-

ences. Torus models are described by the center, the

great and small radii, and the direction of the axis. For

the center and the direction of the axis, we compute

the average of SSD values for all models and for the

two radii we compute the average of Euclidean dis-

tances between ground truth values and our results.

These results are presented in table 1. The results

show that our method can identify all parameters of

the torus models with an acceptable error.

In order to study our method in the case of real

models, we scanned objects such as a ball (sphere), a

life saver (torus), a pipe (cylinder), and a paper cone.

It is clear that a ball is not a perfect sphere, a life

saver is also not a perfect model since it is slightly

twisted, see ﬁgure 14. Since the exact parameters

of these models are not known and there is no easy

means of measuring them in order to verify the accu-

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

0 20 40 60 80 100

x 10

−4

Model number

SSD for axis direction

PGP2X

Attene Method

0 20 40 60 80 100

−5

Model number

tg(angle)

Ground Truth

PGP2X

Attene Method

(a) (b)

0 20 40 60 80 100

0.005

0.01

0.015

0.02

0.025

Model number

SSD for center

0 20 40 60 80 100

100

Model number

Radius

Ground Truth

PGP2X

0 20 40 60 80 100

−6

−4

−2

x 10

−4

Model number

Difference between ground truth height and our result

0 20 40 60 80 100

Model number

Run Time(s)

PGP2X

Attene method

(e) (f)

Figure 12: Cone parameters comparison between ground

truth values, our method (PGP2X) and Attene’s method.

Plot (a) shows the sum of square differences for the axis di-

rection between PGP2X, Attene’s method and ground truth.

Plot (b) presents the tangent of the angle for PGP2X, At-

tene’s method in comparison with ground truth values. The

comparison for the center, the radius and the height between

PGP2X and ground truth is provided in plots (c)-(e), respec-

tively. Finally plot (f) shows the run time for PGP2X in

comparison with Attene’s approach.

racy of our method, we scanned the objects with the

Creaform Go!Scan 3D handheld scanner, applied our

method to the primitives to identify their parameters

and used the Polyworks inspection software in order

to measure the parameters manually.

For the real sphere, cone, and cylinder, we se-

lected points on the models and used Polyworks’s

primitive ﬁtting function to determine the parame-

ters. Since the software does not provide torus ﬁt-

ting, for the scanned torus, we mapped two spheres

on the model in order to estimate the radii. One

Table 1: Partial and complete torus models parameters er-

ror. The values that are provided in the tables are the av-

erage of differences between ground truth values and our

results. The difference that is computed for the center and

the axis direction is the sum of square distances. The Eu-

clidean distance is computed for the two radii.

Complete Torus Partial Torus

Great Radius 0.0174 0.2226

Small Radius 0.0189 0.0844

Center 1.426× 10

−4

0.2268

Axis Direction 5.933× 10

−7

1.187× 10

−5

0 5 10 15 20 25 30

0.2

0.4

0.6

0.8

1.2

1.4

Model number

SSD for axis direction

PGP2X

Attene Method

0 5 10 15 20 25 30

−4

−2

Model number

tg(angle)

Ground Truth

PGP2X

Attene Method

(a) (b)

0 5 10 15 20 25 30

0.005

0.01

0.015

0.02

0.025

0.03

0.035

Model number

SSD for center

0 5 10 15 20 25 30

100

120

Model number

Radius

Ground Truth

PGP2X

0 5 10 15 20 25 30

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

Model number

Difference between ground truth height and our result

0 5 10 15 20 25 30

Model number

Run Time(s)

PGP2X

Attene method

(e) (f)

Figure 13: Comparison of partial Cone parameters between

ground truth values, our method (PGP2X), and Attene’s

method. Plot (a) shows the sum of square differences for

the axis direction between PGP2X, Attene’s method and

ground truth values. Plot (b) presents the tangent of the an-

gle for PGP2X, Attene’s method in comparison with ground

truth values. The comparison for the center, the radius and

the height between our result and ground truth values is pro-

vided in plots (c)-(e), respectively. Plot (f) shows the run

times for PGP2X in comparison with Attene’s approach.

small sphere inside the torus and one great sphere

around the torus. In absence of ground truth param-

eters, a visual comparison is also provided in ﬁgure

14 to assess which method determines the best pa-

rameters for the primitives. The numerical values are

also provided in the same ﬁgure. The results indicate

that our method provides parameter values compara-

ble to Polyworks. Our approach functions automati-

cally while Polyworks involves a manual process.

5 CONCLUSION

In this paper, we presented a novel method for com-

puting the parameters of geometric primitives such as

plane, sphere, cylinder, cone, and torus. Most meth-

ods presented in the literature do not provide accurate

results for tori. We compared our method (PGP2X)

with two other approaches in the case of common

primitives (spheres, cylinders and, cones). For tori,

we provided a comparison with ground truth values.

Our method works well for both complete and partial

primitives. The experiments show that our method is

PGP2X:PrincipalGeometricPrimitivesParametersExtraction

Scanned model PGP2X result The result obtained with Polyworks

Center = (−1.128, −3.22, 552.079)

Radius = 192.5097

Center = (−0.843, −2.978, 552.789)

Radius = 192.219

Orientation = (−0.0585, 0.701, 0.71)

Height = 81.482, Radius = 45.217

Apex = (6.398, −60.937, 341.699)

Semi − apicalangle = 29.028

Orientation = (−0.091, 0.708, 0.701)

Height = 79.14

Apex = (8.271, −61.816, 341.712)

Semi − apicalangle = 27.603

Orientation = (0, 0, 1)

Height = 100, Radius = 50.008

Center = (−36.159, 72.951, 0)

Orientation = (0, 0, 1)

Height = 100.004, Radius = 50.002

Center = (−36.154, 72.913, −0.001)

Center = (−113.781, −119.821, 487.169)

Great radius = 239.0103

Small radius = 109.309

Center = (−115.658, 125.371, 500.384)

Great radius = 238.857

Small radius = 109.125

Figure 14: Parameter Extraction for real scanned models. The parameters are extracted using our method (PGP2X) and the

Polyworks software. Each row shows the result for one model using both methods.

accurate and performs well even in the case of real

noisy models acquired with 3D sensors.

ACKNOWLEDGEMENTS

This work was supported by the NSERC-Creaform

Industrial Research Chair on 3D Scanning. Z. Toony

was supported by a FRQNT post-graduate schol-

arship. The authors thank Trung-Thien Tran for

providing us with the implementation of Attene’s

method for cylinders and spheres (Attene and Patanè,

2010) and Annette Schwerdtfeger for proofreading

this manuscript.

REFERENCES

Attene, M., Falcidieno, B., and Spagnuolo, M. (2006). Hi-

erarchical mesh segmentation based on ﬁtting primi-

tives. The Visual Computer, 22(3):181–193.

Attene, M. and Patanè, G. (2010). Hierarchical structure

recovery of point-sampled surfaces. In Computer

Graphics Forum, volume 29, pages 1905–1920. Wi-

ley Online Library.

Benko, P., Kós, G., Várady, T., Andor, L., and Martin, R.

(2002). Constrained ﬁtting in reverse engineering.

Computer Aided Geometric Design, 19(3):173–205.

Bolles, R. C. and Fischler, M.A. (1981). A RANSAC-based

approach to model ﬁtting and its application to ﬁnd-

ing cylinders in range data. In 7th Int. Joint Conf. on

Artiﬁcial Intelligence (IJCAI’81), volume 1981, pages

637–643.

Borrmann, D., Elseberg, J., Lingemann, K., and Nüchter,

A. (2011). The 3D Hough transform for plane detec-

tion in point clouds: A review and a new accumulator

design. 3D Research, 2(2):1–13.

Chaperon, T., Goulette, F., and Laurgeau, C. (2001). Ex-

tracting cylinders in full 3D data using a random sam-

pling method and the gaussian image. In Proc. of the

Vision Modelling and Visualization Conf., volume 1,

pages 35–42. Citeseer.

Chen, T.-C. and Chung, K.-L. (2001). An efﬁcient random-

ized algorithm for detecting circles. Computer Vision

and Image Understanding, 83(2):172–191.

Chernov, N. (2009). Circle Fitting by Taubin method. http://

www.mathworks.com/matlabcentral/ﬁleexchange/

22678-circle-ﬁt–taubin-method-. [Online; accessed

January-2009].

Cohen-Steiner, D., Alliez, P., and Desbrun, M. (2004).

Variational shape approximation. In ACM Trans. on

Graphics (TOG), volume 23, pages 905–914.

Fayolle, P.-A. and Pasko, A. (2013). Segmentation of dis-

crete point clouds using an extensible set of templates.

The Visual Computer, 29(5):449–465.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM, 24(6):381–395.

Garland, M., Willmott, A., and Heckbert, P. S. (2001). Hi-

erarchical face clustering on polygonal surfaces. In

Proc. of the 2001 Sym. on Interactive 3D graphics,

pages 49–58. ACM.

Johnston, J. D. (1988). Transform coding of audio signals

using perceptual noise criteria. IEEE Journal on Se-

lected Areas in Communications, 6(2):314–323.

Kasa, I. (1976). A circle ﬁtting procedure and its error anal-

ysis. IEEE Trans. on Instrumentation and Measure-

ment, 1001(1):8–14.

Kazhdan, M., Funkhouser, T., and Rusinkiewicz, S. (2003).

Rotation invariant spherical harmonic representation

of 3D shape descriptors. In Proc. of the 2003 Eu-

rographics/ACM SIGGRAPH Sym. on Geometry pro-

cessing, pages 156–164. Eurographics Association.

GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications

Kotthäuser, T. and Mertsching, B. (2012). Triangulation-

based plane extraction for 3D point clouds. In In-

telligent Robotics and Applications, pages 217–228.

Springer.

Li, Y., Wu, X., Chrysathou, Y., Sharf, A., Cohen-Or, D.,

and Mitra, N. J. (2011). Globﬁt: Consistently ﬁtting

primitives by discovering global relations. In ACM

Transactions on Graphics, volume 30, page 52.

Liu, Y.-J., Zhang, J.-B., Hou, J.-C., Ren, J.-C., and Tang,

W.-Q. (2013). Cylinder detection in large-scale point

cloud of pipeline plant. IEEE Trans. on Visualization

and Computer Graphics, 19(10):1700–1707.

Lozano-Perez, T., Grimson, W., and White, S. (1987). Find-

ing cylinders in range data. In Proc. of IEEE Intl.

Conf. on Robotics and Automation, volume 4, pages

202–207.

LSGE (2004). LSGE: The Least Squares Geometric El-

ements Library. http://www.eurometros.org/metros/

key_functions/ﬁtting_routines/.

Lukács, G., Martin, R., and Marshall, D. (1998). Faith-

ful least-squares ﬁtting of spheres, cylinders, cones

and tori for reliable segmentation. In 5th European

Conf. on Computer Vision (ECCV’98), pages 671–

686. Springer.

Olson, C. F. (2001). Locating geometric primitives by

pruning the parameter space. Pattern Recognition,

34(6):1247–1256.

Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D.

(2002). Shape distributions. ACM Transactions on

Graphics (TOG), 21(4):807–832.

Pratt, V. (1987). Direct least-squares ﬁtting of algebraic

surfaces. ACM SIGGRAPH Computer Graphics,

21(4):145–152.

Rabbani, T. and Van Den Heuvel, F. (2005). Efﬁcient

Hough transform for automatic detection of cylinders

in point clouds. Proc. of ISPRS WS on Laser Scan-

ning, 3:60–65.

Scales, L. (1985). Introduction to non-linear optimization.

Springer-Verlag New York, Inc.

Schmitt, S. R. (2005). Center and Radius of a Sphere

from Four Points. http://www.abecedarical.com/

zenosamples/zs_sphere4pts.html.

Schnabel, R., Wahl, R., and Klein, R. (2007). Efﬁcient

RANSAC for point-cloud shape detection. In Com-

puter graphics forum, volume 26, pages 214–226. Wi-

ley Online Library.

Taubin, G. (1991). Estimation of planar curves, surfaces,

and nonplanar space curves deﬁned by implicit equa-

tions with applications to edge and range image seg-

mentation. IEEE Trans. on Pattern Analysis and Ma-

chine Intelligence, 13(11):1115–1138.

Toony, Z., Laurendeau, D., and Gagné, C. (2014). Recog-

nizing 3D principal primitives using gaussian sphere

and gaussian accumulator. Internal Report. Computer

Vision and System Laboratory, Laval University, Au-

gust 2014.

Zhang, J., Cao, J., Liu, X., Wang, J., Liu, J., and Shi,

X. (2013). Point cloud normal estimation via low-

rank subspace clustering. Computers & Graphics,

37(6):697–706.

Zhu, K., Wong, Y. S., Loh, H. T., and Lu, W. F. (2012). 3D

CAD model retrieval with perturbed laplacian spectra.

Computers in Industry, 63(1):1–11.

PGP2X:PrincipalGeometricPrimitivesParametersExtraction