
Convex Hull Brushing in Scatter Plots
Multi-dimensional Correlation Analysis
Miguel Nunes, Kresimir Matkovic and Katja B
¨
uhler
VRVis Research Center, Vienna, Austria
Keywords:
Visual Analytics, Convex Hull Brush, Scatter Plots, Linked Views, Correlation.
Abstract:
Interactive Visual Analysis has been widely used for the reason that it allows users to investigate highly
complex data in coordinated multiple views, showing different perspectives over data. In order to relate data,
multiple techniques of brushing have been introduced. This work extends the state of the art by introducing
the Convex Hull (CH) Brush, which is a new way of selecting and interpreting high dimensional data in scatter
plot (SP) views. By using a combination of brushes through linked views, the CH-Brush allows the selection
and clustering of values that are not typically defined by SP ranges, in spite of sharing similarities. In CH-
Brushing is also able to visually report the existence of correlation between variables. Furthermore, we discuss
CH-Brushing sensitivity and the application of smoothness. We use synthetic data to support our rationale and
clarify the intrinsic meanings of CH-Brushing in scatter plots. We also report on the first experience on using
the CH-Brush in a real-world medical case.
1 INTRODUCTION
Through Interactive Visual Analysis (IVA), a range
of linked views displaying different data visualiza-
tion techniques is available for visual inspection
of relations between variables of complex datasets.
It is consistently used in numerous fields such as
science (Mart
´
ınez-G
´
omez et al., 2014), engineer-
ing (Sedlmair et al., 2011) or finance (Inselberg,
2009) for hypothesis generation, evaluation and sense
making. According to task and domain of the
data, different visualization methods can be com-
bined. These include scientific visualization, statisti-
cal graphics and computational tools (Konyha et al.,
2006) which are used to uncover hidden informa-
tion in multi-dimensional datasets by making use of
human intuition and respective domain knowledge
for data analysis. It is through coordinated multi-
ple views (Roberts, 2007) that users are able to com-
pare different values, perspectives or interpretations
of data.
The scatter plot is one of the most often used
views in data visualization and has been extensively
studied (Li et al., 2010; Rensink and Baldridge,
2010). Scatter plots are often used to visually de-
termine existence of clusters in data and respective
correlations between two variables. However, often
times is not feasible for users to fully visualize and
understand complex clusters of points when a high
number of variables are being analysed. Relationship
between variables become harder to visually inspect
when hundreds or thousands of data points are plot-
ted in coordinated multiple views. Convex hulls have
been used in scatter plots to support the construction
of convexity measures (Wilkinson et al., 2006) and to
allow navigation and query sculpting in scatter plots
matrices (Elmqvist et al., 2008).
Obtaining clusters from convex hulls was al-
ready achieved (Sainath et al., 2011; Pratt et al.,
2014) showing how they can be generically applica-
ble (Wilderjans et al., 2013). A review on literature
about methods and techniques for clustering (Estivill-
Castro, 2002) shows how well developed this field of
research is. However, it is argued that different algo-
rithms may not run in the same datasets, forcing users
to be aware of the best method for each case. Through
IVA, composite brushing and Convex Hull brushing,
we believe users may obtain clusters and respective
information in a visual and intuitive manner.
To enable CH-brushing and to support analysis
and visualization tasks in coordinated multiple views,
navigating between overview and detail of datasets is
fundamental. Typically, this is achieved by brushing,
which is an important tool for visually inspecting data
in an interactive manner. Brushing in one linked view
highlights subsets of data displayed in other linked
182
Nunes M., Matkovic K. and Bühler K..
Convex Hull Brushing in Scatter Plots - Multi-dimensional Correlation Analysis.
DOI: 10.5220/0005356501820189
In Proceedings of the 6th International Conference on Information Visualization Theory and Applications (IVAPP-2015), pages 182-189
ISBN: 978-989-758-088-8
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Details of synthetic datasets.
Dataset ID Dimensions Data Points
1 7 300
2 10 500
3 13 300
4 6 1550
5 4 1500
6 4 1000
7 6 500
8 7 680
views, facilitating the understanding of relationships
between a high number of variables. This iterative
and interactive process of brushing in different con-
nected views, allows information drill-down where
previously selected data points become the new focus
of analysis, enabling further brushing in a sub-context
of the data. It is also possible to use a combination of
multiple brushes across linked views to extract mul-
tiple features or discover patterns in data (Martin and
Ward, 1995; Roberts, 2007). Respective selected data
points are highlighted in the respective brush’s colour.
The CH-Brush is different from typical brushing since
the brush range selection is no longer the user’s re-
sponsibility, but is automatically created by taken in
consideration linked data points originated from com-
posite brushing in other linked views.
The major contribution of this work is the intro-
duction of Convex Hull Brush in scatter plots. We dis-
cuss what are the implications and interpretations of
combining linked brushing with CH-Brush in linked
views. In addition, we also consider the potential of
including a smoothness factor (Doleisch and Hauser,
2002) for CH-Brushes, together with an interpretation
of brush sensitivity and how to tackle such issue with
smooth brushing. Multidimensional datasets from an
online data repository and a real medical case were
used in this work.
2 DATA
To support the reasoning behind the use of the CH-
Brush, we used 8 synthetic datasets that were ex-
plored by means of a coordinated multiple views sys-
tem (Matkovic et al., 2008). The system supports par-
allel coordinates (PC), histograms and scatter plots.
Synthetic datasets were obtained from an open
data generator, Sketchpad N-D (Wang et al., 2013),
with dimensions ranging from 4 to 13 variables. The
number of points present in these datasets ranged
from 300 to 1550. Table 1 shows details about each
dataset. None of our datasets was targeted with di-
mension reduction techniques, nor were they previ-
Figure 1: Parallel Coordinates obtained in Sketchpad N-D
while generating dataset 8 with manually set probability
density functions and quadrilateral data connection.
ously classified. We used the original dimensions and
data points delivered by the synthetic data generator.
Figure 1 depicts the generated PC for dataset 8 in
Sketchpad N-D. It can be seen that six probability
density functions were set to create clusters and one
quadrilateral data connection was added between the
last two axes.
3 BRUSHING IN SP
Introduced more than 25 years ago (Becker and
Cleveland, 1987; Fisherkeller et al., 1988), brush-
ing in scatter plots became one of the most com-
mon methods for displaying and interacting with
multi-dimensional data in the information visualiza-
tions scope. Scatter plots relate two dimensions of a
dataset and, together with other linked scatter plots or
other views, many variables of a dataset can be vi-
sually assessed at the same time in a straightforward
way (Sedlmair et al., 2013).
Brushing in scatter plots is routinely done by se-
lecting a cross-section of two ranges, which is visu-
ally represented by a rectangular box (Figure 2 (a)).
Other forms of brushing in scatter plots include, but
not limited to, circular brushes (Figure 2 (b)) and
lasso brushes (Figure 3 (a)), which gives flexibility on
how users select ranges in scatter plots. Data relations
within Circular brushes are hard to interpret if units
and scales of parameters are different. Brushed data
points will be inside a circular area around a point. As
for lasso brushes, these have more complicated inter-
pretations but are used for selection of complex sub-
sets. It is also possible to obtain complex subsets by
using a composite brushing where brushes are be log-
ically combined (Figure 3 (b)).
Figures 4 (a) and (b) show two linked scatter plots.
Data from dataset 3 is plotted so variables M, E and I
can be used for brushing and analysis. After plotting
data in both linked scatter plots, a box brush is created
which selects data points for M and E axes (Figure 4
(a). While brushing the first scatter plot data points, in
ConvexHullBrushinginScatterPlots-Multi-dimensionalCorrelationAnalysis
183

(a) (b)
Figure 2: Examples of a Box Brush (a) and of a Circle Brush
(b) in 2D Scatter Plots.
(a) (b)
Figure 3: Example of a Lasso Brush in a 2D Scatter Plot (a)
and a composite brush of Box Brushes selecting different
ranges (b).
the second scatter plot (Figure 4 (b)) the correspond-
ing linked points get highlighted with the same colour.
However, since the second scatter plot is comparing
two other dimensions of the dataset, which have dif-
ferent ranges and distribution of values, these points
do not visually correspond to the same area as in the
first scatter plot.
As such, brushing in coordinated multiple views
systems introduces two terms to define data points:
brushed data and linked data. The first one defines
data points that are inside the area of a brush, as seen
in Figures 2 and 3. Linked data are data points that
have been brushed in one view, but are displayed in
another view relating other dimensions of the dataset
(Figure 4 (b)). These data points are highlighted with
the same colour as the brush that originally selected
them. Brushed data and linked data will later be used
to help define the CH-Brush.
To facilitate the definition of a gradual change
between brushed data and not brushed data, and to
avoid the sudden tumble present in binary brushes’
edges, smoothness enhances the focus+context work-
flow by applying a degree of continuity between 1 and
0 to surrounding data points (Oeltze et al., 2012). It
supports users in discerning a degree of interest over
brushed data. An example is the definition of a range
of opacity values to depict flow in volume render-
ing (Doleisch et al., 2003).
Smooth brushing can also be used to extract mean-
ing from neighbouring data points that have simi-
lar characteristics to the ones inside the brushed re-
gion. Applying a smoothness factor to a brush has
the power to elucidate expert users about properties of
data points that were not initially selected. Depending
on the context, these properties can range from corre-
lation of selected data points and signature similarities
to uncertainty.
Brush sensitivity can be seen as how much linked
data changes when a brush is changed. If a small
change in the brush (e.g.: panning, resizing) results
in a large change over linked data, then the brush can
be considered very sensitive, otherwise it has low sen-
sitivity. The sensibility of brushes should always be
evaluated by the domain expert in its corresponding
context. Smooth brushing can then be used to guar-
antee that the brush is not placed in a highly sensitive
range.
4 THE CONVEX HULL BRUSH
Parallel Coordinates, for example, are a good method
to find patterns and certain clusters of information.
However, the selection of values in PC are translated
to SP as rectangular brushes. Trying to do so, would
most probably incur in adding data points that would
not be taken into consideration by the convex hull
algorithm. We will introduce now the Convex Hull
brush which overcomes this problem.
For any subset of points in a 2D plane, its convex
hull is the smallest convex polygon that contains that
subset. So, for the case of creating a CH-Brush in
a scatter plot, all linked data points brushed in other
linked views will be used for the construction of the
convex hull, together with points that were not se-
lected but are inside of the 2D subset.
In cases where visual clusters arise by (more or
less complex) brushing, existing brushes are not able
to efficiently and quickly gather all points inside the
originally brushed subset. The addition of the CH-
Brush quickly overcomes this issue. The CH-Brush
facilitates this process by geometrically analysing the
linked data points and creating a convex hull around
the previously selected data points, automatically cre-
ating a cluster which can then be focused on and anal-
ysed. As an example to illustrate this, a scatter plot
gets set up and data points get brushed (Figure 4 (a)).
As a result, in another linked scatter plot, comparing
two other variables of the same dataset, linked data
points get highlighted (Figure 4 (b)) with the colour
of the original brush. Only then, the creation of a CH-
Brush becomes possible. Because there is linked data
IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications
184
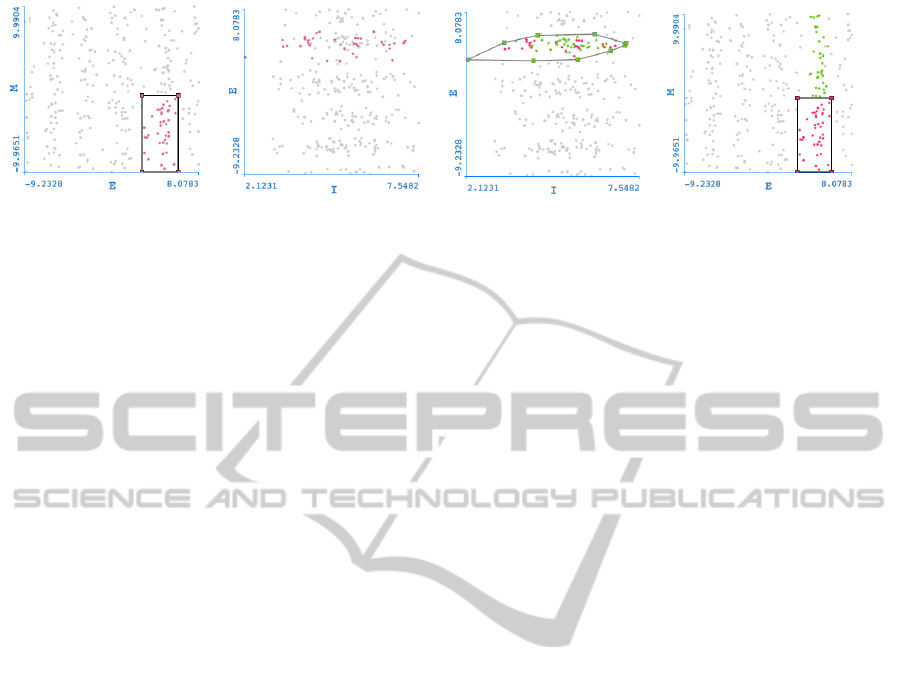
(a) (b) (c) (d)
Figure 4: Scatter plot with brushed data (a) and respective highlighted linked data in a second Scatter Plot (b). Automatically
created Convex Hull brush from linked data (c). Original scatter plot displaying new green linked points as a result of creating
a Convex Hull brush (d).
highlighted, the generation of a convex brush hull of
those linked points is a quick operation and results
in a new brush, with a new colour, selecting all data
points inside of it (Figure 4 (c)).
Following the same logic, these new brushed data
points (in green) will then be highlighted in the pre-
vious linked scatter plots, giving instant information
about how many new data points got brushed, as seen
in Figure 4 (d). From the differences found in the
quantity of brushed data points and the size of the CH-
Brush, different conclusions about data points and
variables can be reached.
4.1 Interpretations
Generating a convex hull in a scatter plot can help
disclose properties of the brushed data. Furthermore,
including a smooth region to the CH-Brush allow
users investigating its sensitivity. The result of CH-
Brushing can help:
• to verify how much correlation exist between the
two variables plotted in the SP (M1),
• to verify how similar the newly added points are
in relation to previously selected data points (M2),
• to check for the existence of clustering data points
(M3),
• to contextualize data points that were not initially
selected (M4).
Correlation between variables (M1) can be vi-
sually obtained by brushing ranges of data points
of interest and later visualized across linked views
of plotted data. Yet, when users are dealing with
datasets containing dozens of variables and thousands
of points, such task can eventually become higher in
complexity and prone to human error due to clutter
of information and time spent in focus+context sub-
tasks. Correlation can be intuitively visualized by
analysing the size of the CH-Brush in relation to the
total of data points spread in the SP. If the CH-brush
focus in a small area of the SP, it can be concluded that
a correlation exists between the two plotted variables,
in relation to the brushed data points. Otherwise, se-
lected data points hold little correlation between se-
lected data points.
Gathering data points by applying a CH-Brush in
a SP after users brush and focus+context will return
points with similar characteristics. Users can then es-
timate how meaningful the newly added data points
are in comparison to the originally brushed points
(e.g., following the same trend, having similar rela-
tions to other variables).
Clustering of highly complex data has been
broadly studied and many methods have been eval-
uated. By introducing the CH-Brush, we propose a
visual check of clusters by making use of IVA (M3).
Keeping in mind points (M1) and (M2), by creating
a CH-Brush over previously brushed linked data, it
is possible to check clustering in other dimensions.
A good example of this would be the case where
a multi-dimensional dataset consisting of clusters of
data could be well represented and easily brushed in a
linked view where two variables are compared. How-
ever, the same cluster would be hard to distinguish by
using different variables. Generating the CH-Brush
would easily select all points previously selected to-
gether with data points inside the CH-Brush. (M1)
and (M2) could then be used to assess how well these
two new variables can be used for further clustering
of data, focus and contextualization.
IVA allows visualizing data in different paradigms
(e.g.: volume rendering) which can contribute to a
better understanding of the extent of the CH-Brush
(M4). By (M1), (M2) and (M3) users are given
the possibility to evaluate and contextualize all data
points inside the CH-Brush and how well they cor-
relate or cluster. In Section 5, we use the results of
linked brushing and CH-brushing in scatter plots to
further clarify the intrinsic meaning of these 4 points.
ConvexHullBrushinginScatterPlots-Multi-dimensionalCorrelationAnalysis
185

Figure 5: Example of a Convex Hull Brush with a smooth-
ness factor in a 2D Scatter Plot. Points inside smooth area
are highlighted with a faded colour of the brush.
4.2 CH-Brush Sensitivity
We define sensitivity of the CH-Brush differently as
reported in Section 3. When generating a new CH-
Brush, two things can happen: no extra data points
are included or new data points are included. For
the first case, sensitivity is null since no changes in-
curred. This supports on saying that, for the origi-
nally brushed data points, total correlation exist be-
tween the two variables plotted in the SP (M1).
On the other hand, if new data points are included
in the CH-Brush, several possibilities arise. If a high
percentage of data points are included, we can say
that the sensitivity of the CH-Brush is very high, for
it changes much of the linked data. This can also be
an indication of low correlation between plotted vari-
ables (M1). If the data points selected by the CH-
Brush present similarities to other data points in other
linked views (e.g.: the same pattern in PC) the brush
has low sensitivity. An example of this can be seen
in Figure 4 (c) where red points belong to the original
brush and green points are the points selected by the
CH-brush.
Including a smoothness factor (Figure 5) impacts
the sensibility of the brush as data points that were not
initially inside the CH-Brush might be included. This
addition can check if near-by data points also have
correlation to the data points inside the CH-Brush
(M1), verify if these points belong to the same or sim-
ilar context of brushed data points (M2 and M4) and,
finally, check how these data points in the smooth re-
gion might integrate a cluster (M3).
4.3 Implementation
Our implementation of the CH-brush is based on An-
drew’s monotone chain convex hull algorithm (An-
drew, 1979). All brushed data points from the data
table are taken in consideration to build the convex
hull. After the user brushes a series of ranges across
dimensions of a dataset in one or more linked views
using one or more brushes, s/he can investigate in a
scatter plot how two dimensions relate. In case new
data points are selected after the CH-Brush is gener-
ated, and because all views are linked, it is possible to
immediately see the effect of how the linked data gets
changed/highlighted.
We incorporated smooth brushing in our CH-
brush in order to allow inspection of uncertainty and
also deal with brush sensitivity. Smoothness is seen
as an outside doted contour (Figure 5) that is created
by first calculating the centroid of the CH-brush, next
calculating the vectors of the centroid to each vertex
of the CH-Brush and then applying a smoothness fac-
tor to each vector. This creates the vertices of the CH-
brush’s smoothness line. Points inside the smoothness
area are given values between 0 and 1.
To actually create the CH-brush, the user has to
select values from a data table using available linked
views. After values are selected, a scatter plot dis-
playing selected linked points should be made avail-
able to allow the creation of the CH-Brush. In our
prototype, to create it, the user only has to click the
option for Convex Hull Generation. Immediately, a
lasso brush is calculated gathering the linked points
in that view space, by means of the convex hull algo-
rithm. As soon as the brush is created, all other views
are updated with the newly selected values with the
respective CH-brush colour.
5 RESULTS AND DISCUSSION
Linked views were used to analyse, brush and com-
pare our synthetic and real datasets (Section 2). Since
our synthetic datasets did not contain more then 1550
samples, visual recognition of clusters and correla-
tions between certain dimensions were usually easily
achieved. We make use of the CH-Brush to reach the
same observations.
5.1 Dataset 4
For dataset 4, we started by plotting values of vari-
able B in a histogram, and brushed a single bin with a
red brush (Figure 6 (a)). We then plotted in a scatter
plot the values of A and C. It was noticeable that both
variables had a certain degree of local correlation for
the brushed data points of B. We then created a CH-
Brush, as seen in Figure 6 (b)) for those linked data
points and realized that the histogram in Figure 6 (a)
displayed extra selected data points all across dimen-
sion B.
IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications
186

(a) (b) (c)
Figure 6: Linked histogram view plotting values of B from dataset 4. Red values selected from red brush and blue values
selected by blue CH-brush (a). Linked SP view plotting values of A and C from dataset 4 with a CH-Brush (b). Resulting PC
linked view showing local correlation between variables A and C from dataset 4 (c).
Figure 7: Parallel Coordinates overview of dataset 8.
We then plotted all dimensions of dataset 4 in a
linked PC view (Figure 6 (c)). We were able to ob-
serve the relationship between all variables and anal-
yse the level of correlations between A, B and C. It
is easy to observe that, for the selected range of B in
red, a very small range of A is selected, showing high
correlation between these two variables (M1). How-
ever, such a high degree of correlation is not noted
between B and C. Actually, the creation of the CH-
Brush shows that many values of B get selected (M2),
and that these values have very little correlation to
variable C. Yet, it is still possible to observe that, for
the newly range of C values, there is a high degree of
local correlation with A (M3).
5.2 Dataset 8
Dataset 8 was purposely built in a way that some vari-
ables are highly correlated while others have no cor-
relation at all. By visually inspecting the PC view
of dataset 8 (Figure 7), it is visually perceptible that
variables A and B, and C and D are highly correlated,
while variables E, F and G have no apparent correla-
tion.
Next, by brushing high values of F, we were able
to see that there was, in fact, a local correlation be-
tween E and F (M1). Figure 8 (a) shows the high val-
ues of F brushed in green, while Figure 8 (b) depicts
the generated CH-Brush in a scatter plot comparing E
to F. It can then be seen in the PC view that variables
E and F have a certain correlation for high values of
F (Figure 8 (c)). Also, Figure 8 (b) shows that no ex-
tra values of F were selected by the CH-Brush (green
colour), pointing in the direction that these brushed
data points form a cluster (M3). Observing the result-
ing PC and histogram we can see no extra data points
are selected by the CH-Brush. This is a special case of
the CH-Brush that, when correlation is total, the same
operation could be performed by simply brushing the
same ranges in the PC.
5.3 An Example with Medical Data
Datasets from an ongoing project, where we closely
collaborate with medical experts (Nunes et al., 2014),
were composed of between 7 and 12 variables
and number of points ranging between 35.000 and
550.000. These variables correspond to medical im-
ages such as Magnetic Resonance (MR) T1-weighted,
molecular components of MR Spectroscopy Imag-
ing (MRSI), manual segmentations and X, Y, Z co-
ordinates of patients with brain cancer. Following
medical guidance, three more dimensions relating
three molecular components through their ratios were
added to the datasets.
An initial version of the CH-Brush was used to
answer a real medical need. Magnetic Resonance
Spectroscopy Imaging (MRSI) was evaluated in an
IVA system connecting a Visual Analytics system to
a medical imaging framework, which allowed doc-
tors to analyse MRSI data in an intuitive and flexi-
ble manner for the first time. By plotting MRSI val-
ues in linked views, and using multiple brushes, pat-
terns arouse and there was a need to create clusters
of data. CH-Brushing gathered extra 3D MRSI vox-
ConvexHullBrushinginScatterPlots-Multi-dimensionalCorrelationAnalysis
187

(a) (b) (c)
Figure 8: Linked histogram view plotting values of F from dataset 8. Values in green are brushed from the green brush.
Yellow values originate from CH-Brushing (a). Linked SP view plotting values of E and F from dataset 8 with a yellow
CH-Brush (b). Resulting PC linked view showing local correlation between variables E and F from dataset 8. Yellow and
green lines are overlapped (c).
els that were not previously taken into account by the
doctors segmentations. It was found that data points
included in the CH-Brush had correlation (M1) and
presented very similar signatures as segmented vox-
els (M2). By visually inspecting the newly selected
voxels in anatomical rendering, it was noted that 3D
voxels bordering the original segmentation were high-
lighted (M4). These results point in the direction that,
by using IVA, a better understanding about cancer
can be achieved, to ultimately design better treatment
plans for patients.
It was also observed that the CH-Brush selected
values that corresponded to very specific and sparse
ranges in PC. This goes in line to what was indicated
in Section 4 that brushing a range in a PC axis is the
same as creating a rectangular brush in a SP and does
not allow flexibility in this sort of cluster discovering.
The CH-Brush overcame this issue.
The examples and results herein presented and
discussed show the potential of using CH-Brushing
for clustering, contextualizing and correlation find-
ing. Synthetic datasets and one real world case sup-
port our initial hypothesis (M1–M4) that CH-Brushes
can positively impact the way users interact and anal-
yse multi-dimensional datasets in scatter plots.
6 LIMITATIONS AND FUTURE
WORK
We understand that there are datasets that might
not follow the patterns and clustering presented
here (Sedlmair et al., 2013). As such, an alterna-
tive to the CH-Brush could be a Concave Hull Brush
from where similar meanings could be extracted from,
but where brushed data is presented in a way that
would not be meaningful while employing a CH-
Brush (Moreira and Santos, 2007).
Another key point for further CH-Brush valida-
tion would be to extend its applicability into more
real world multi-dimensional datasets. A proper eval-
uation of the performance of this brush with the re-
spective domain experts will certainly add value and
better definitions for this brush. Also, using CH-
Brushing with SP matrices would further enlighten
the true power of the presented brush.
Lastly, smoothness in CH-Brush can be alterna-
tively approached. Another way we can envision the
construction of the smoothness region would be to
sample neighbouring points from the original CH-
Brush’s vertices, and then use these new points to
create a new CH-brush region. This, and other al-
ternatives, would have to be properly evaluated and
compared in order to assess the respective usefulness,
not only as a general application but also in specific
domains.
7 CONCLUSIONS
This work introduced a new way of brushing for IVA.
We used linked views and a rendering system to vi-
sualize linked brush data and analyse the result of
including Convex Hull brushing. Synthetic multi-
dimensional datasets were used to show the general
applicability of the CH-Brush as well as real data
from medical studies.
Our approach suggests that CH-Brush can be use-
ful for cases where interpretation of data inside clus-
ters might not be trivial. Also, we consider that visu-
ally inspecting the existence of clusters and relation-
ships between high number of variables is simplified.
IVAPP2015-InternationalConferenceonInformationVisualizationTheoryandApplications
188

ACKNOWLEDGEMENTS
The authors wish to thank the reviewers for their care-
ful reading of the manuscript and helpful comments.
This work is part of the SUMMER Marie Curie Re-
search Training Network (PITN-GA-2011-290148),
which is funded by the 7th Framework Programme
of the European Commission (FP7-PEOPLE-2011-
ITN). The centre of excellence, VRVis, is financed by
COMET – Competence Centers for Excellent Tech-
nologies by BMVIT, BMWFJ and ZIT – The Tech-
nology Agency of the City of Vienna. The COMET
Programme is managed by FFG.
REFERENCES
Andrew, A. M. (1979). Another efficient algorithm for con-
vex hulls in two dimensions. Information Processing
Letters, 9(5):216–219.
Becker, R. A. and Cleveland, W. S. (1987). Brushing scat-
terplots. Technometrics, 29(2):127–142.
Doleisch, H., Gasser, M., and Hauser, H. (2003). Inter-
active feature specification for focus+ context visual-
ization of complex simulation data. In Proceedings
of the symposium on Data visualisation 2003, pages
239–248. Eurographics Association.
Doleisch, H. and Hauser, H. (2002). Smooth brushing for
focus+context visualization of simulkation data in 3d.
Elmqvist, N., Dragicevic, P., and Fekete, J.-D. (2008).
Rolling the dice: Multidimensional visual explo-
ration using scatterplot matrix navigation. Visualiza-
tion and Computer Graphics, IEEE Transactions on,
14(6):1539–1148.
Estivill-Castro, V. (2002). Why so many clustering algo-
rithms: A position paper. SIGKDD Explor. Newsl.,
4(1):65–75.
Fisherkeller, M. A., Friedman, J. H., and Tukey, J. W.
(1988). Prim-9: An interactive multi-dimensional data
display and analysis system. In In Dynamic Graphics
for Statistics, pages 111–120.
Inselberg, A. (2009). Parallel coordinates. Springer.
Konyha, Z., Matkovic, K., Gracanin, D., Jelovic, M., and
Hauser, H. (2006). Interactive visual analysis of fam-
ilies of function graphs. Visualization and Computer
Graphics, IEEE Transactions on, 12(6):1373–1385.
Li, J., Martens, J.-B., and Van Wijk, J. J. (2010). Judging
correlation from scatterplots and parallel coordinate
plots. Information Visualization, 9(1):13–30.
Martin, A. R. and Ward, M. O. (1995). High dimen-
sional brushing for interactive exploration of multi-
variate data. In Proceedings of the 6th Conference on
Visualization’95, page 271. IEEE Computer Society.
Mart
´
ınez-G
´
omez, E., Richards, M. T., and Richards, D. S. P.
(2014). Distance correlation methods for discovering
associations in large astrophysical databases. The As-
trophysical Journal, 781(1):39.
Matkovic, K., Freiler, W., Gracanin, D., and Hauser, H.
(2008). Comvis: A coordinated multiple views sys-
tem for prototyping new visualization technology. In
Information Visualisation, 2008. IV ’08. 12th Interna-
tional Conference, pages 215–220.
Moreira, A. and Santos, M. Y. (2007). Concave hull: A
k-nearest neighbours approach for the computation
of the region occupied by a set of points. Proceed-
ings of the 2nd International Conference on Computer
Graphics Theory and Applications.
Nunes, M., Rowland, B., Schlachter, M., Ken, S., Matkovic,
K., Laprie, A., and B
¨
uhler, K. (2014). An integrated
visual analysis system for fusing mr spectroscopy and
multi-modal radiology imaging. In Proceedings of
IEEE VAST 2014.
Oeltze, S., Doleisch, H., Hauser, H., and Weber, G. (2012).
Interactive visual analysis of scientific data. Tutorial
at the IEEE VisWeek 2012.
Pratt, J., Busse, A., Mueller, W.-C., Chapman, S., and
Watkins, N. (2014). Anomalous dispersion of la-
grangian particles in local regions of turbulent flows
revealed by convex hull analysis. arXiv preprint
arXiv:1408.5706.
Rensink, R. A. and Baldridge, G. (2010). The perception
of correlation in scatterplots. volume 29, pages 1203–
1210. Wiley Online Library.
Roberts, J. C. (2007). State of the art: Coordinated & mul-
tiple views in exploratory visualization. In Coordi-
nated and Multiple Views in Exploratory Visualiza-
tion, 2007. CMV’07. Fifth International Conference
on, pages 61–71. IEEE.
Sainath, T. N., Nahamoo, D., Kanevsky, D., Ramabhad-
ran, B., and Shah, P. (2011). A convex hull ap-
proach to sparse representations for exemplar-based
speech recognition. In Automatic Speech Recognition
and Understanding (ASRU), 2011 IEEE Workshop on,
pages 59–64. IEEE.
Sedlmair, M., Isenberg, P., Baur, D., Mauerer, M., Pigorsch,
C., and Butz, A. (2011). Cardiogram: visual analyt-
ics for automotive engineers. In Proceedings of the
SIGCHI Conference on Human Factors in Computing
Systems, pages 1727–1736. ACM.
Sedlmair, M., Munzner, T., and Tory, M. (2013). Empirical
guidance on scatterplot and dimension reduction tech-
nique choices. Visualization and Computer Graphics,
IEEE Transactions on, 19(12):2634–2643.
Wang, B., Ruchikachorn, P., and Mueller, K. (2013).
Sketchpadn-d: WYDIWYG sculpting and editing in
high-dimensional space. CoRR, abs/1308.0762.
Wilderjans, T. F., Ceulemans, E., and Meers, K. (2013).
Chull: A generic convex-hull-based model selection
method. Behavior research methods, 45(1):1–15.
Wilkinson, L., Anand, A., and Grossman, R. (2006). High-
dimensional visual analytics: Interactive exploration
guided by pairwise views of point distributions. Visu-
alization and Computer Graphics, IEEE Transactions
on, 12(6):1363–1372.
ConvexHullBrushinginScatterPlots-Multi-dimensionalCorrelationAnalysis
189
