
Interactive Relighting of Virtual Objects under Environment Lighting
Nick Michiels, Jeroen Put and Philippe Bekaert
Hasselt University - tUL - iMinds, Expertise Centre for Digital Media, Wetenschapspark 2, 3590 Diepenbeek, Belgium
Keywords:
Rendering, Spherical Gaussians, Real-time, Triple Product, Gpu.
Abstract:
Current relighting applications often constrain one or several factors of the rendering equation to keep the ren-
dering speed real-time. For example, visibility is often precalculated and animations are not allowed, changes
in lighting are limited to simple rotation or the lighting is not very detailed. Other techniques compromise on
quality and often coarsely tabulate BRDF functions. In order to solve these problems, some techniques have
started to use spherical radial basis functions. However, solving the triple product integral does not guarantee
interactivity. In order to dynamically change lighting conditions or alter scene geometry and materials, these
three factors need to be converted to the SRBF representation in a fast manner. This paper presents a method to
perform the SRBF data construction and rendering in real-time. To support dynamic high-frequency lighting,
a multiscale residual transformation algorithm is applied. Area lights are detected through a peak detection
algorithm. By using voxel cone tracing and a subsampling scheme, animated geometry casts soft shadows
dynamically. We demonstrate the effectiveness of our method with a real-time application. Users can shine
with multiple light sources onto a camera and the animated virtual scene is relit accordingly.
1 INTRODUCTION
Interaction between the real environment and virtual
scenes is crucial in real-time relighting applications.
Realistic integration of computer generated objects in
real environments is used in movie post-production
and in augmented reality applications. Fully inter-
active applications allow immediate changes of three
important factors. Firstly, they allow changes in the
lighting in the scene. These changes can affect both
distant and near-field changes in illumination. Sec-
ond, the geometry of the objects in the scene can
change with animations or with user input. Lastly, the
materials that constitute the objects can change. How-
ever, the evaluation of the required rendering equation
in real-time has so far remained impossible without
constraining at least one of these three factors. Be-
sides, it is also important that the representable con-
tent can contain high-frequency details. There are
several problems to solve before reaching real-time
framerates. Our approach combines the advantages
of previous approaches and allows real-time relight-
ing of dynamic virtual scenes with real-time captured
environment lighting. The data is represented using
spherical radial basis functions (SRBFs). This paper
will explain how to construct such a representation
efficiently. Each factor needs to be dynamic and re-
(a) (b)
(c) (d)
Figure 1: Interactive rendering where all factors are dy-
namic. (a) Rendering of a virtual object in a real envi-
ronment. (b) Real-time change of material specularity. (c)
Change in geometry requires real-time cone tracing of vis-
ibility. The virtual object can be animated or changed by
user input. (d) Real-time change of lighting. The environ-
ment map is captured real-time.
quires a fast transformation to the SRBF representa-
tion. For environment lighting, we show how a mul-
tiscale residual algorithm can be used for SRBF fit-
ting. The visibility needs to be sampled in real-time
and we show how voxel cone tracing together with
an efficient sampling scheme allow for accurate soft
shadows.
220
Michiels N., Put J. and Bekaert P..
Interactive Relighting of Virtual Objects under Environment Lighting.
DOI: 10.5220/0005360102200228
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 220-228
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Comparison to other techniques that use precomputed radiance transfer for triple product rendering. All compared
techniques use spherical harmonics wavelets or spherical Gaussians to solve the rendering equation. However, they all con-
strain at least one of the factors. Our approach allow for a real-time update for as well lighting, materials and visibility.
all-frequency dynamic lighting dynamic geometry dynamic reflectance
Sloan et al., 2003 × × × ×
Ng et al., 2004 X × × ×
Tsai and Shih, 2006 X rotation only × ×
Haber et al., 2009 X × × ×
Wang et al., 2009 X rotation only × X
Lam et al., 2010 X rotation only × ×
Meunier et al., 2010 X limited sources rigid transformations X
Iwasaki et al., 2012 X rotation only low-poly X
our method X X X X
2 RELATED WORK
Our technique is related to Precomputed Radiance
Transfer techniques (PRT) (Sloan et al., 2002; Ng
et al., 2003; Sun et al., 2007; Imber et al., 2014),
in that we factorize rendering and represent the es-
timated data in efficient bases.
Ng et al. (Ng et al., 2004) represent the visibility
term, the environment map and the BRDF slice that
corresponds to the viewing direction ω
o
in the Haar
wavelet basis Ψ. This basis is defined over the hemi-
sphere using the hemi-octahedral parameterization as
introduced by Praun and Hoppe (Praun and Hoppe,
2003). Later this approach is extended to work with
high-order wavelets (Michiels et al., 2014). Wavelet
representations are good for compression and can be
used efficiently in the triple product integration of
PRT rendering. However, the factors themselves can-
not be transformed easily to the wavelet representa-
tion and require offline processing.
Haber et al. (Haber et al., 2009) use the afore-
mentioned approach to efficiently compress and ren-
der with the three factors. However, none of the three
factors are dynamic. For example, all BRDF slices
are first sampled in pixel domain and are then trans-
formed to wavelets and the visibility is preprocessed
with ray tracing.
A new basis to represent the three factors of
the rendering are spherical radial basis functions
(SRBFs). The advantage of SRBFs is that they have
an efficient rotation operator. Tsai et al. (Tsai and
Shih, 2006) proposed a method for rendering with all-
frequency lighting using SRBFs. The lighting Gaus-
sians are fitted using an optimization process which
results in high compression ratios, but can take up to
several minutes to fit the full lighting factor. Further-
more, the visibility is precomputed and compressed
using Clustered Tensor Approximation (CTA) and is
therefore limited to static scenes only.
Wang et al. (Wang et al., 2009) also presented ren-
dering with SRBFs for all-frequency lighting. They
lack the possibility to render dynamic scenes since the
visibility is precalculated using a spherical singed dis-
tance function (SSDF). Moreover, SSDFs are not able
to accurately render detailed shadows. To represent
the lighting factor, they use the same elaborate fitting
process as Tsai et al. (Tsai and Shih, 2006).
Lam et al. (Lam et al., 2010) proposed a hierar-
chical method for transforming environment lighting
to a SRBF representation. The positions and band-
width parameters of the SRBF are determined by the
Healpix (Gorski et al., 2005) distribution. The coeffi-
cients are obtained by a least-square projection (Sloan
et al., 2003).
Meunier et al. (Meunier et al., 2010) explain how
cosine lobes can be used to represent each term of
the rendering equation. The use of a cosine lobe rep-
resentation for compactly representing a reflectance
function is common. The authors also show how di-
rect spherical light sources can be approximated with
cosine lobes as well as show how to off-line simplify
the geometry into a tree of spheres. By splatting these
spheres onto a quad-tree, the visibility is sampled.
Only rigid transformations of the geometry are pos-
sible.
Iwasaki et al. (Iwasaki et al., 2012) developed a
real-time renderer for dynamic scenes which is able
to render under all-frequency lighting using spheri-
cal Gaussians. The lighting can be rotated, but cannot
be updated dynamically. The visibility is dynamically
estimated by projecting bounding volumes onto a grid
of patches of the hemisphere. Occluded patches are
represented with spherical Gaussians. However, up-
dating the bounding volume tree is strongly depen-
dent on the complexity of the scene. Besides, their
tree traversal uses suboptimal branching operation on
InteractiveRelightingofVirtualObjectsunderEnvironmentLighting
221

GPUs.
Our method also uses spherical radial basis func-
tions to represent all three factors. In contrast to pre-
vious techniques, we are able to construct and up-
date all three factors in real-time. We show how a
residual transformation technique can be used to effi-
ciently transform the lighting information to spherical
Gaussians. Cone tracing together with peak-detection
of powerful and high-frequent lights allow for inter-
active rendering of soft shadows. Table 1 gives an
overview of all the discussed techniques. Note that
only our technique allows real-time adjustment of the
lighting. Other techniques support only static lighting
or rotation of the environment map. Furthermore, the
performance of our real-time visibility tracing is not
dependent on the amount of polygons.
3 TRIPLE PRODUCT
INTEGRATION
A key part in our framework is the simulation of light
propagation in a scene based on the reflectance equa-
tion over the hemisphere Ω (Kajiya, 1986; Ng et al.,
2004):
B(v, ω
o
) =
Z
Ω
ρ(v, ω
i
, ω
o
)V (v, ω
i
)
˜
L(v, ω
i
)dω
i
(1)
where ρ is the BRDF, incorporating the cosine term
for the incident illumination from ω
i
, at position v
and the outgoing direction ω
o
. V is the hemispherical
visibility term evaluated around v and
˜
L is the inci-
dent illumination rotated in the local frame of v. The
components are illustrated in Figure 2, where each of
relighting
BRDF
visibility environment
lighting
Figure 2: Rendering and relighting. The rendering equa-
tion is factorized in material (BRDF), visibility and envi-
ronment map. All the factors are represented over the hemi-
sphere. Rendering is the integration over the hemisphere
of the three factors. Each factor can be changed and will
immediately influence the rendered result. For example, a
change in environment lighting will result in a relit scene.
the factors affect the appearance of the rendered re-
sult. Now the rendering equation can be evaluated as
a triple-product integral at each point in the scene:
B(v, ω
0
) =
∑
k
∑
l
∑
m
C
klm
ρ
k
V
l
e
L
m
(2)
where C
klm
=
R
Ω
Ψ
k
Ψ
l
Ψ
m
dω
i
are called the binding
or tripling coefficients of the three bases. The effi-
ciency of this calculation is dependent on the choice
of basis to represent the factors. Calculations in
the pixel domain will be inefficient, as pixels can-
not sparsely represent the information of the factors.
Other techniques using spherical harmonics (Sloan
et al., 2002), Haar wavelets or eigenbases are often
able to more compactly represent the content. These
bases, however, place their own restrictions on the
data or the operations that can be performed on it. For
example, spherical harmonics are not able to sparsely
represent high-frequency signals. On the other hand,
wavelets are very good at compression but lack flexi-
bility. Wavelets are constrained to static scenes, since
the visibility needs to be precomputed. Moreover,
rotation is a complex operation in the wavelet do-
main (Wang et al., 2006). We choose to represent all
three factors in the triple product integral with hierar-
chical spherical Gaussians. A spherical Gaussian G is
defined as
G(v · p, λ, µ) = µe
λ(v·p−1)
(3)
where v · p is the dot product between a vector v on the
sphere and the center of the Gaussian, λ the Gaussian
bandwidth and µ the amplitude. Spherical Gaussians
have several advantages:
• A hierarchy of spherical Gaussians allows the
efficient representation of both low- and high-
frequency information.
• Spherical Gaussians are rotationally symmetric
and therefore allow the efficient rotation of the en-
vironment map to the local vertex coordinate sys-
tem by rotating the center of the Gaussian.
• BRDF functions can be well approximated with
spherical Gaussians, allowing run-time evaluation
of reflectance.
• The mixing of Gaussians is additive and allows
for a less complex implementation, compared to
spherical harmonics or wavelet theory.
Additionally, Gaussians have an extra interesting
characteristic. The product and convolution of Gaus-
sians can be solved analytically (Tsai and Shih, 2006):
Z
S
2
G
1
(v · p
1
, λ
1
, µ
1
)G
2
(v · p
2
, λ
2
, µ
2
)G
3
(v · p
3
, λ
3
, µ
3
)dv
=
4πµ
1
µ
2
µ
3
e
λ
1
+λ
2
+λ
3
sinh(krk)
krk
(4)
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
222

where r = kλ
1
p
1
+ λ
2
p
2
+ λ
3
p
3
k. The binding coef-
ficients out of Equation 4 are now reduced to a simple
formula. However, solving the triple product integral
efficiently is not enough for real-time relighting appli-
cations. In order to interactively change lighting con-
ditions or alter scene geometry and materials, these
three factors need to be converted to the SRBF rep-
resentation in a fast manner. In the next sections, we
will demonstrate how we can make the visibility, ma-
terials and lighting factors dynamic by using spherical
radial basis functions.
4 DYNAMIC MATERIALS
There are a few characteristics a good material repre-
sentation must have:
1. The representation should be compact.
2. Easy rotation of the BRDF into the global lighting
and visibility frame.
3. Fast evaluation of double and triple product inte-
grals.
SRBF functions can approximate almost any
BRDF. They are rotationally symmetric and easily ro-
tatable. They also allow for a compact all-frequency
representation, due to their multiscale nature. It is
known that BRDF functions expressed in terms of
a normal distribution function can be approximated
with Gaussian lobes (Ngan et al., 2005; Wang et al.,
2009). These Gaussians are then integrated in the
triple product rendering integral.
Figure 3: Dynamic materials. The lobe of a BRDF is ap-
proximated using one or few Gaussians. This direct map-
ping allows for real-time changes in appearance of the ma-
terial. For example a virtual object can be rendered with
different kinds of materials: Lambertian (top left), dif-
fuse Phong (top right), glossy Phong (bottom left), specular
Phong (bottom right), Cook-Torrance, ...
5 DYNAMIC VISIBILITY
To evaluate the complex visibility term in the render-
ing equation in real-time, a fast and dynamic approxi-
mation is required. Previous techniques have relied on
precomputation, but such a solution is no longer fea-
sible when changes in the geometry occur frequently.
In our framework, we combine PRT techniques with
voxel cone tracing (Crassin et al., 2011), to evaluate
the visibility in real-time entirely on the GPU.
The first step in our processing pipeline is to
voxelize the geometry to a 3D texture. This is
done by implementing a one-pass voxelization algo-
rithm (Crassin and Green, 2012). We use a geometry
shader to project all polygon fragments to their domi-
nant axis. Voxelization is a real-time process and only
needs to be partially updated every frame for dynamic
geometry. For this we use a dirty flag mechanism that
leaves the static geometry untouched.
The second step is to perform cone tracing in the
voxel volume. Each visible pixel corresponds to a 3D
position in voxel space. From this position, new cones
can be constructed and traced throughout the voxels.
Current voxel cone tracing is often used to perform
ambient occlusion or low frequency global illumina-
tion effects. However in our application, we shoot
cones to evaluate the visibility factor of the triple
product integral. For this to work, a mapping from
cones to spherical Gaussians is essential. Suppose we
have a Gaussian with size λ. Let us fit a cone that co-
incides with the distance α where the Gaussian eval-
uates 0.5:
e
λ(cos(α)−1)
= 0.5 (5)
Solving for α:
α = cos
−1
(
log(0.5)
λ
+ 1.0) (6)
where α is used as the solid angle for the cone to trace.
The last step is to select the appropriate cones to
trace. A straightforward method would trace one vis-
ibility cone for each BRDF lobe. However, important
high-frequency detail might be missed. For BRDF
lobes with a large solid angle, all visibility details
are integrated over a large area of the hemisphere.
A better approach is to subsample the BRDF lobe
with smaller visibility cones. The subsampling den-
sity depends on the characteristics of the BRDF. A
circle packing algorithm is used to determine the cen-
ter position and radius. Figure 4 shows our subsam-
pling scheme. For diffuse Lambertian BRDF lobes,
a small number of uniformly traced visibility cones
suffice. For more glossy BRDF lobes, the cones are
scaled and rotated into the lobe. The number of cones
used for subsampling determines the desired level of
InteractiveRelightingofVirtualObjectsunderEnvironmentLighting
223
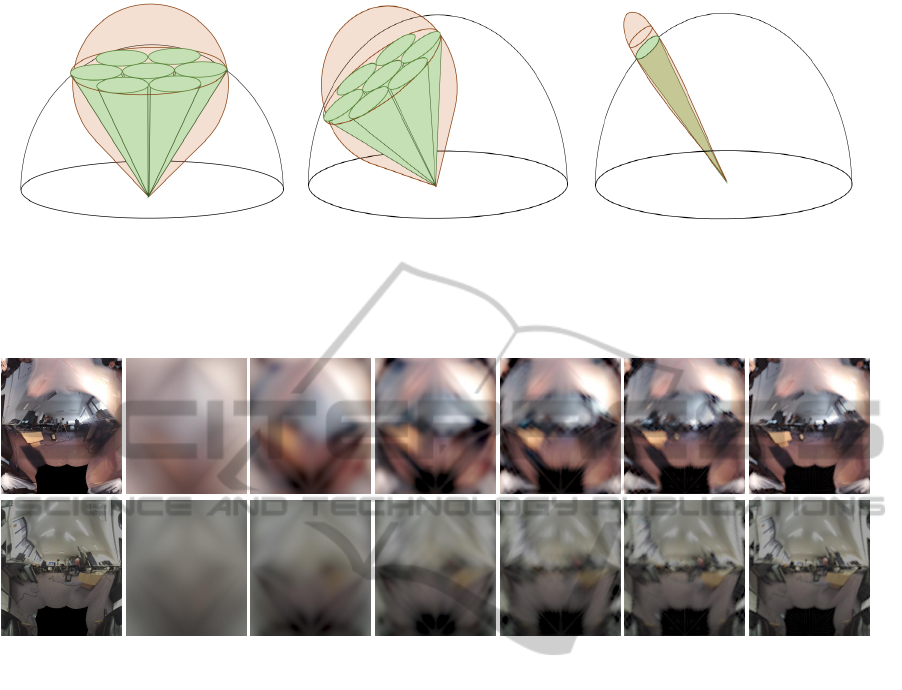
(a) (b) (c)
Figure 4: Adaptive subsampling of visibility cones. Left: Gaussian of a Lambertian BRDF lobe (orange) approximated with
a number of visibility cones (green). Middle: Gaussian of a glossy BRDF lobe (orange) approximated with the same number
of visibility cones (green), rotated and scaled to enclose the BRDF. Right: for a Gaussian of a specular BRDF lobe (orange)
it suffices to only trace a single visibility cone (green) that coincides the lobe.
Figure 5: Multiscale residual transformation of environment map into SRBF representation from a coarse scale (left) to more
refined scales (right). Each level adds extra detail to the reconstruction.
quality. Because the size of a BRDF lobe dictates
the recoverable frequencies (Ramamoorthi and Han-
rahan, 2001), our subdivision of scaled cones within
the BRDF lobe retains approximately the same level
of quality for all lobe sizes. In our implementation we
obtained good quality renderings using a subdivision
of 7 cones.
6 DYNAMIC LIGHTING
Real-time changes to the lighting environment can
drastically alter the look of three-dimensional models.
To capture the entire distant lighting sphere, we use
HDR omnidirectional video frames extracted from
the Ladybug3 (PointGrey, 2014) camera. To convert
the lighting to an RBF representation, we perform an
RBF fitting algorithm based on Ferrari et al. (Ferrari
et al., 2004). We apply the algorithm on the sphere
using the Healpix (Gorski et al., 2005) distribution,
utilizing a multiscale algorithm. The algorithm starts
from the environment map as input to the first scale.
The input of each scale is approximated with a fixed
grid of SRBFs. The difference of the approximated
reconstruction and the input data is the residue and is
passed as input to the next scale. This process contin-
ues until the residual error is below a certain thresh-
old or the maximum level of detail is reached. The
described algorithm is fast and allows for a real-time
transformation. Unlike other methods, no complex
optimization is used (Tsai and Shih, 2006; Lam et al.,
2010). An example of a multiscale approximation is
shown in Figure 5.
The subsampling scheme described in Section 5
performs well for large area light sources and low-
frequency lighting. For these cases, the visibil-
ity cones can stay relatively large. In the case
of very bright area lights, subsampling of visibility
cones would quickly become too fine-grained to be
tractable. We treat these lights as a special case. Their
areas are easily identified with a peak detection algo-
rithm. First, the incoming environment map lighting
is thresholded, so that only the peaks with the most
influence remain. Then, the connected component al-
gorithm is used to group pixels into the lights they
constitute. Lastly, a number of Gaussians (1-3) are
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
224
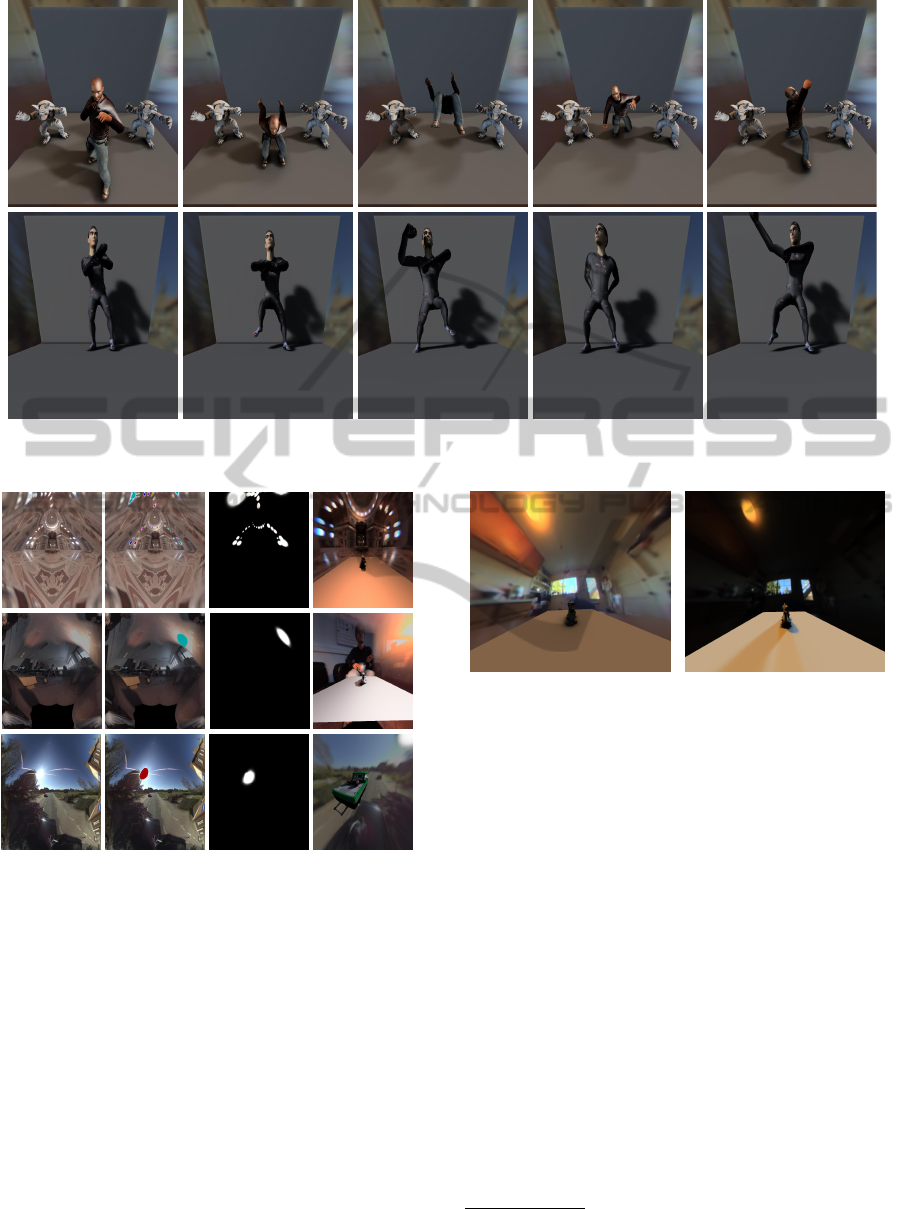
Figure 7: Dynamic visibility
1
. Geometry can be changed using animations or user input. Adaptive cone tracing in the voxel
volume based on the subsampling scheme and peak detection allows for real time rendering of soft shadows.
Figure 6: Peak detection. The input HDR environment map
is thresholded to keep only the high-intensity values. These
peaks are then detected using connected components. Each
connected component can now be represented with a num-
ber of Gaussians. These Gaussians are used to accurately
render soft shadow for high-frequency lighting.
fitted to match the shape of each connected compo-
nent. We trace a visibility cone for every Gaussian.
Figure 6 shows a few examples of our peak detection
algorithm applied on different environment maps.
7 RESULTS
We have designed a custom application to demon-
strate the relighting capabilities of our technique. The
(a) (b)
Figure 8: Peak detection is mandatory for finding the impor-
tant visibility cones to trace. Left: traced visibility cones
over entire hemisphere using the subsampling scheme of
Section 5. Further subsampling of the hemisphere in more
smaller cones will accurately solve the visibility, but will be
intractable for real-time applications. Right: extra impor-
tance sampling of the hemisphere by using peak detection
of bright light sources. By tracing extra cones in the direc-
tion of the main area light sources, realistic soft shadows
are acquired.
application was tested on an Intel Core i7 3.4 GHz
processor with 8 GB of RAM and a GeForce 770
GTX. The triple product calculation for material, visi-
bility and lighting is done entirely with GLSL shaders
on the GPU. The application can be used to place vir-
tual models under real-world lighting conditions. Our
peak detection process of Section 6 is performed on
the distant illumination environment map in real-time.
Afterwards, the model can be viewed under these
lighting conditions and changes can be made. Unique
to our approach is that all factors can be changed si-
multaneously and in real-time. The lighting can be
1
Animations are courtesy of Mixamo. https://
www.mixamo.com/motions
InteractiveRelightingofVirtualObjectsunderEnvironmentLighting
225

Figure 9: Dynamic lighting
1
. The environment lighting is captured using the Ladybug3 (PointGrey, 2014) omnidirectional
camera. Our peak detection algorithm is performed in real-time and passed to the renderer. The virtual object is now rendered
with the lighting conditions from the captured frames. Note how the virtual shadow positions are aligned with the real light
source.
altered, the model can be moved or deformed and the
materials can be edited. If there are spatially-varying
material parameters in the scene, they can be encoded
in textures defined over the virtual model.
Figure 7 shows results with animated geometry.
This geometry causes dynamic changes in the visi-
bility factor. Our algorithm is able to cope with this
in real-time by using voxel cone tracing. The sam-
pling scheme of visibility cones, as explained in Sec-
tion 5, is implemented to quickly get an integrated
visibility value over a certain solid angle, defined by
the BRDF properties. Extra importance sampling of
visibility cones is done by finding peaks in the light-
ing and is a key feature to efficiently render accurate
high-frequency area light sources. Figure 7 clearly
shows that a change in geometry caused different vis-
ibility and that our system is able to render with soft
shadows. Figure 8 illustrates the importance of peak
detection for shadows. The same environment map is
used to render both images, but the right rendering is
done with peak detection and the left with only the
subsampling scheme for visibility.
To demonstrate dynamic visibility, we placed an
omnidirectional camera, such as the Ladybug3 (Point-
Grey, 2014) of Point Grey, near the desired position of
the virtual object in the scene. The residual transfor-
mation algorithm is implemented to extract the spher-
ical Gaussians to render with. Now, a virtual model
can be relit with one or more flashlights, held before
the omnidirectional camera. The results are given in
Figure 9. Note the high-quality soft shadows resulting
from our peak detection algorithm.
To measure the influence of scene complexity on
performance, the scene was rendered with models of
varying complexity and lighting conditions with a dif-
ferent amount of peaks. An overview of these exper-
iments is given in Table 2. It can be seen that geo-
Table 2: Influence of scene complexity on performance. All
results are rendered at 1280x720 resolution.
scene peaks triangles FPS
fighter: Fig. 1 6 16k 43
dragon: Fig. 2 top 6 871k 45
dragon: Fig. 2 bottom 1 871k 75
dragon: Fig. 8 11 871k 36
sphere: Fig. 3 6 3k 58
fighter/armadillo: Fig. 7 top 11 708k 34
dancer: Fig. 7 bottom 1 16k 67
dancer: Fig. 9 1 16k 75
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
226

metric complexity has only a small influence on the
framerate. Environmental complexity has a more no-
ticeable influence, but scales well with the number of
peaks.
8 CONCLUSION
We have presented a unique combination of tech-
niques to allow real-time triple product rendering
where all three factors are dynamic. We use spherical
Gaussians to represent the incoming light, the BRDF
lobes and the visibility over a solid angle. This rep-
resentation enables efficient light integration on the
GPU. Important regions of visibility detail is cone
traced using an adaptive subsampling scheme. Fur-
thermore, peak detection is used to trace complex area
shadows. We have shown in the previous section that
the three factors of material, visibility and lighting are
dynamic and can be updated in real-time. We there-
fore combine all features of previous techniques as
listed in Table 1. We explained how we use cone trac-
ing to support dynamic scenes. Note that our tech-
nique inherits some of the difficulties of cone tracing
with respect to the handling of large scenes as well as
well as thin geometry. This is because our current 3D
texture voxelization is not sparse. This limitation will
be overcome by the new partially resident textures on
new GPUs (Sellers, 2013). A second limitation is the
amount of visibility cones. Each new visibility cone
introduces a new triple product calculation. The visi-
bility subsampling scheme together with the peak de-
tection algorithm will limit the amount of visibility
Gaussians. However, environment maps filled with
different small HDR light sources will influence the
rendering performance.
ACKNOWLEDGEMENTS
This work has been made possible by the Fund for
Scientific Research-Flanders (FWO-V Remixing re-
ality) and with the help of a PhD specialization bur-
sary from the IWT. The authors acknowledge finan-
cial support from the European Commission (FP7 IP
SCENE).
REFERENCES
Crassin, C. and Green, S. (2012). Octree-based sparse vox-
elization using the gpu hardware rasterizer. In Cozzi,
P. and Riccio, C., editors, OpenGL Insights, pages
303–318. CRC Press.
Crassin, C., Neyret, F., Sainz, M., Green, S., and Eise-
mann, E. (2011). Interactive indirect illumination us-
ing voxel-based cone tracing: An insight. In ACM
SIGGRAPH 2011 Talks, SIGGRAPH ’11, pages 20:1–
20:1, New York, NY, USA. ACM.
Ferrari, S., Maggioni, M., and Borghese, N. A. (2004).
Multiscale approximation with hierarchical radial ba-
sis functions networks. IEEE Transactions on Neural
Networks, 15(1):178–188.
Gorski, K., Hivon, E., Banday, A., Wandelt, B., Hansen,
F., et al. (2005). HEALPix - A Framework for high
resolution discretization, and fast analysis of data dis-
tributed on the sphere. Astrophys.J., 622:759–771.
Haber, T., Fuchs, C., Bekaer, P., Seidel, H.-P., Goesele, M.,
and Lensch, H. (2009). Relighting objects from image
collections. In Computer Vision and Pattern Recogni-
tion, 2009. CVPR 2009. IEEE Conference on, pages
627–634.
Imber, J., Guillemaut, J.-Y., and Hilton, A. (2014). Intrinsic
textures for relightable free-viewpoint video. In Fleet,
D., Pajdla, T., Schiele, B., and Tuytelaars, T., edi-
tors, Computer Vision ECCV 2014, volume 8690 of
Lecture Notes in Computer Science, pages 392–407.
Springer International Publishing.
Iwasaki, K., Furuya, W., Dobashi, Y., and Nishita, T.
(2012). Real-time rendering of dynamic scenes under
all-frequency lighting using integral spherical gaus-
sian. Comp. Graph. Forum, 31(2pt4):727–734.
Kajiya, J. T. (1986). The rendering equation. In Pro-
ceedings of the 13th annual conference on Computer
graphics and interactive techniques, SIGGRAPH ’86,
pages 143–150, New York, NY, USA. ACM.
Lam, P.-M., Ho, T.-Y., Leung, C.-S., and Wong, T.-T.
(2010). All-frequency lighting with multiscale spheri-
cal radial basis functions. Visualization and Computer
Graphics, IEEE Transactions on, 16(1):43–56.
Meunier, S., Perrot, R., Aveneau, L., Meneveaux, D., and
Ghazanfarpour, D. (2010). Cosine lobes for interac-
tive direct lighting in dynamic scenes. Computers &
Graphics, 34(6):767–778.
Michiels, N., Put, J., and Bekaert, P. (2014). Product
integral binding coefficients for high-order wavelets.
In Proceedings of the 11th International Conference
on Signal Processing and Multimedia Applications
(SIGMAP 2014). INSTICC.
Ng, R., Ramamoorthi, R., and Hanrahan, P. (2003). All-
frequency shadows using non-linear wavelet lighting
approximation. In ACM SIGGRAPH 2003 Papers,
SIGGRAPH ’03, pages 376–381, New York, NY,
USA. ACM.
Ng, R., Ramamoorthi, R., and Hanrahan, P. (2004). Triple
product wavelet integrals for all-frequency relighting.
ACM Trans. Graph., 23(3):477–487.
Ngan, A., Durand, F., and Matusik, W. (2005). Experi-
mental analysis of brdf models. In Proceedings of
the Sixteenth Eurographics conference on Rendering
Techniques, EGSR’05, pages 117–126, Aire-la-Ville,
Switzerland, Switzerland. Eurographics Association.
PointGrey (2014). Ladybug3. Web page. http://
www.ptgrey.com/. Accessed October 13 , 2014.
InteractiveRelightingofVirtualObjectsunderEnvironmentLighting
227

Praun, E. and Hoppe, H. (2003). Spherical parametrization
and remeshing. ACM Trans. Graph., 22(3):340–349.
Ramamoorthi, R. and Hanrahan, P. (2001). A signal-
processing framework for inverse rendering. In Pro-
ceedings of the 28th annual conference on Computer
graphics and interactive techniques, SIGGRAPH ’01,
pages 117–128, New York, NY, USA. ACM.
Sellers, G. (2013). Opengl extension specifica-
tion: Arb sparse texture. Web page. https://
www.opengl.org/registry/specs/ARB/sparse texture.txt.
Accessed October 11, 2014.
Sloan, P.-P., Hall, J., Hart, J., and Snyder, J. (2003). Clus-
tered principal components for precomputed radiance
transfer. In ACM SIGGRAPH 2003 Papers, SIG-
GRAPH ’03, pages 382–391, New York, NY, USA.
ACM.
Sloan, P.-P., Kautz, J., and Snyder, J. (2002). Precomputed
radiance transfer for real-time rendering in dynamic,
low-frequency lighting environments. In Proceedings
of the 29th annual conference on Computer graph-
ics and interactive techniques, SIGGRAPH ’02, pages
527–536, New York, NY, USA. ACM.
Sun, X., Zhou, K., Chen, Y., Lin, S., Shi, J., and Guo, B.
(2007). Interactive relighting with dynamic brdfs. In
ACM SIGGRAPH 2007 papers, SIGGRAPH ’07, New
York, NY, USA. ACM.
Tsai, Y.-T. and Shih, Z.-C. (2006). All-frequency precom-
puted radiance transfer using spherical radial basis
functions and clustered tensor approximation. In ACM
SIGGRAPH 2006 Papers, SIGGRAPH ’06, pages
967–976, New York, NY, USA. ACM.
Wang, J., Ren, P., Gong, M., Snyder, J., and Guo, B. (2009).
All-frequency rendering of dynamic, spatially-varying
reflectance. In ACM SIGGRAPH Asia 2009 Papers,
SIGGRAPH Asia ’09, pages 133:1–133:10, New
York, NY, USA. ACM.
Wang, R., Ng, R., Luebke, D., and Humphreys, G. (2006).
Efficient wavelet rotation for environment map ren-
dering. In Proceedings of the 17th Eurographics Con-
ference on Rendering Techniques, EGSR ’06, pages
173–182, Aire-la-Ville, Switzerland, Switzerland. Eu-
rographics Association.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
228
