
Visualization of Enrollment Data using Chord Diagrams
Laia Blasco-Sopl
´
on
1
, Josep Grau-Valldosera
2
and Juli
`
a Minguill
´
on
1
1
Computer Science, Multimedia and Telecommunication Studies, Universitat Oberta de Catalunya,
Rambla Poblenou 156, Barcelona, Spain
2
Marketing Department, Universitat Oberta de Catalunya, Rambla Poblenou 156, Barcelona, Spain
Keywords:
Enrollment, Dropping Out, Chord Diagrams, Radial Visualization, Distance Education, Higher Education.
Abstract:
Distance and online universities have usually more flexible academic requirements than brick-and-mortar ones,
so students do not uniformly advance within the programme they enroll into as they are supposed to. Further-
more, due to their intrinsic nature, distance students need additional support for deciding which subjects they
will take every semester. On the other hand, teachers have usually no idea about what other subjects are tak-
ing the students enrolled in their subjects. This paper proposes the use of chord diagrams for visualizing the
relationships between pairs of subjects taken by students, with the aim of providing both university managers
and students with a clear picture of possible bottlenecks, that is, combinations of subjects that might affect
students’ performance. Chord diagrams can be used to analyze intra-semester data (subjects taken simultane-
ously) and inter-semester data (sequences of subjects taken by students) and provide a fast overview of what
is happening within a given programme at subject level. Furthermore, it is possible to interact with chord
diagrams in order to filter and obtain additional subject details if desired.
1 INTRODUCTION
Enrollment and dropping out in higher education are
two sides of the same coin. In the case of distance
and online universities, dropping out mostly occurs
after the end of the first academic semester or year
(Grau-Valldosera and Minguill
´
on, 2014; Tyler-Smith,
2006). In (Campbell et al., 2007), the authors de-
scribe several examples of learning analytics related
to enrollment, some of them oriented towards improv-
ing student retention. Usually, all these studies are
used-centered, trying to determine whether a student
will be accepted or not, or trying to predict her aca-
demic performance. Although such data-driven de-
cision support systems can be built using historical
enrollment data (see (Sac
´
ın et al., 2011; Siraj and
Abdoulha, 2009), for instance), we are more inter-
ested in obtaining a fast overview of what is happen-
ing within a given programme, adopting a subject-
centered approach and following the basic premises
of information visualization (Card et al., 1999). In
(Grau-Valldosera and Minguill
´
on, 2014), the authors
proposed a novel definition of dropping out adapted
to the specific characteristics of distance universities,
based on the minimum number of break semesters (N)
a student takes, needed to determine that such student
never enrolls again (i.e. drops out), for a given er-
ror rate (less than 5% of students come back after N
semesters). Using such definition, the authors were
able to compute the dropping out rate for different
programmes, which lead to strong evidences: half of
the dropouts occur after the first academic semester,
and up to 75% of accumulated dropouts occur after
the second semester (i.e. the first year). As most stu-
dents take only two or three subjects during their first
semester, they should know which combinations are
known to be problematic, using accumulated enroll-
ment data. Therefore, it is very important to provide
both university managers and students with visualiza-
tion tools that allow them to detect possible bottle-
necks for a given programme and help them to adjust
their expectations about subject enrollment, respec-
tively. As stated in (Park and Choi, 2009), “internal
factors such as subject design strategies and learners’
motivation should be prioritized at the subject devel-
opment stage in order to make the subject participa-
tory and interesting and to keep learners engaged”.
We think that these strategies should be moved one
level upward, trying to detect problems not only at
subject level but at programme level, visualizing how
students advance within programmes and the possible
barriers caused by wrong enrollment decisions.
This paper is structured as follows: the dataset
with enrollment data used in this paper is analyzed
511
Blasco-Soplón L., Grau-Valldosera J. and Minguillón J..
Visualization of Enrollment Data using Chord Diagrams.
DOI: 10.5220/0005360505110516
In Proceedings of the 10th International Conference on Computer Graphics Theory and Applications (GRAPP-2015), pages 511-516
ISBN: 978-989-758-087-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
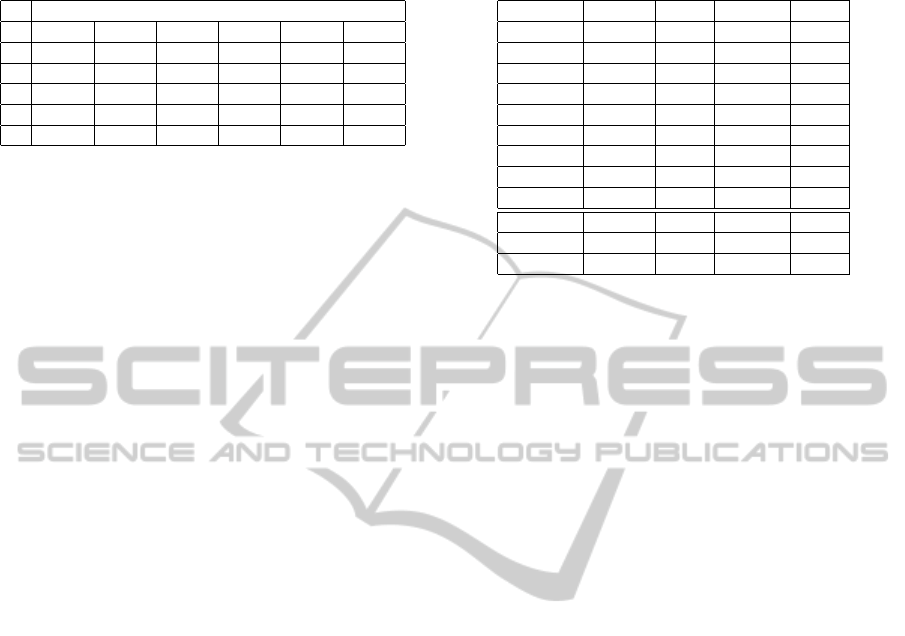
Table 1: subjects and degree plans for the Economics pro-
gramme.
S subjects
1 01.001 01.079 01.003 01.004 00.010 00.002
2 01.005 01.006 01.007 01.078 01.009 00.003
3 01.080 01.021 01.086 01.020 00.004 x.x
4 01.014 01.015 01.012 01.087 01.011 x.x
5 01.018 01.019 01.016 01.022 x.x x.x
6 01.008 01.023 x.x x.x x.x x.x
in Section 2. Section 3 proposes the use of chord di-
agrams for visualizing subject relationships with re-
spect to enrollment. Finally, conclusions and future
work are stated in Section 4.
2 ENROLLMENT DATA
The dataset used in this paper is taken from Universi-
tat Oberta de Catalunya (UOC) academic databases.
Only valid enrollments have been included, i.e. ones
that have been formalized and paid for, thus excluding
enrollments that were subsequently canceled. As we
are just exploring the possibility of using chord dia-
grams for visualizing relationships between subjects,
we have chosen the largest programme amongst all
available data, i.e., students enrolled into Economics
between Spring 1999 and Spring 2011, containing
data about 21792 students and 501 different subjects,
giving a total of 328467 subject enrollments during
25 consecutive semesters.
Table 1 shows the expected sequence of subjects
for the Economics programme. It is supposed to be
finished in 6 semesters (3 years), taking 6 subjects ev-
ery semester. Here x.x means subjects chosen from a
pool of optional subjects or from other programmes.
This structure is only a recommendation, so students
can take subjects in any order and number. Actually,
the only requirement is subject 00.010 (a basic sub-
ject on online competencies) which is mandatory for
all students during the first semester. A more com-
plete version of Table 1 is what students have before
they decide which subjects they will enroll into, in-
cluding information about each subject. As expected,
due to the nature of distance students (most of them
have a full-time work, family responsibilities, and so),
they usually do not enroll into a complete semester
(i.e. 6 subjects), but fewer. Furthermore, they do
not even follow the predetermined order of subjects,
that is, they can enroll into subjects from the second
semester without having taken subjects from the first
one. Therefore, the concept of cohort is completely
undermined.
Table 2 partitiones students according to the num-
ber of subjects (C) they enroll into, as well as the
Table 2: Number of students taking / passing C subjects
during the two first academic semesters.
C 1st Sem. Pass 2nd Sem. Pass
0 — 6069 — 3924
1 814 3155 1289 2641
2 5518 5190 5760 4284
3 9451 5102 5286 3367
4 4181 1692 2557 1450
5 1130 388 929 463
6 521 150 354 167
7 or more 177 46 181 60
Total 21792 15723 16356 12432
Mean 3.073 1.78 2.873 1.888
Median 3 2 3 2
1st-3rd Qs. [1,4] [0,3] [1,3] [1,3]
number of subjects they successfully pass. Notice
that students take more subjects in average during the
first semester than during the second one. This could
be a sign that students learn to regulate their learn-
ing process by narrowing their enrollment once they
have acquired the experience of being online learners.
As stated in (Kiernan et al., 2004), the process of be-
coming a good “e-learner” depends not only on the
student herself but also on the institutional support,
so the more information the learners have, the better
decisions they might take.
On the other hand, Table 2 shows also that, in
the first semester, most students fail to pass all sub-
jects they enrolled into. Preliminary results show that
the most important variable for predicting dropping
out after the first semester is the number of subjects
successfully taken, so adjusting the number of sub-
jects taken during the first semester becomes a key
issue, for both the institution and the students. One of
the main differences between brick-and-mortar uni-
versities and distance ones is that the latter have more
flexible requirements: no minimum enrollment, pos-
sibility of taking one or more consecutive semester
breaks, and so. But, are students following the institu-
tional recommendations? We propose to analyze the
subjects taken by students, in order to determine the
most common subject combinations and try to visu-
ally detect any relationship with the fact of passing or
not a subject. We call this “intra-semester analysis”.
We are also interested in analyzing how students ad-
vance within a given programme, that is, which sub-
jects they will enroll in the next semester according to
the results of the preceding one. We call this “inter-
semester analysis”.
2.1 Intra-semester Analysis
Table 3 shows the most popular subjects taken by
students in their first academic semester. From the
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
512

Table 3: Number of students (N) taking / passing a given
subject the first academic semester sorted by popularity.
Rank subject N Pass Acum. Pct.
1 00.010 15229 10500 15229 69.9 %
2 01.001 7433 4519 17566 80.6 %
3 01.079 6662 3481 18528 85.0 %
4 01.005
∗
6615 3698 19328 88.7 %
5 00.002 4654 2621 19795 90.8 %
... ... ... ... ... ...
10 01.009
∗
1432 756 20790 95.4 %
... ... ... ... ... ...
18 01.020
∗
527 233 21562 98.9 %
total pool of 501 possible subjects, students choose
only among 128, following a long-tail distribution.
Roughly, 90% percent of the students take at least one
of the first five most popular subjects, 95% of the stu-
dents take one of the first ten most popular subjects
and 99% take one of the first eighteen. These will be
the subjects selected for the visualization using chord
diagrams, in order to see whether the density of the
graph is appropriate enough to include as much as in-
formation as possible without being too complex. No-
tice also that there are students enrolling into subjects
that are not supposed to be taken during the first aca-
demic semester (those marked in Table 3 with
∗
). This
is a typical situation in distance universities where
students are not compelled to enroll a predetermined
set of subjects.
Table 4 reproduces the same analysis but for the
most popular subjects taken in the second academic
semester. Notice that in this case, “second” has a
more complex definition, as we take into account
breaks taken by students. For instance, if a student
takes a break during her second semester, the next
semester she is taking a subject is used as her second
one. Notice also that, as some students drop out after
the first semester, the number of students is smaller
(16356). Compared to Table 3, the accumulated per-
centage of students taking one of the most popular
subjects grows more slowly. In fact, students choose
among 181 subjects out of the total pool of 501, so
the number of possible combinations is larger than in
the first academic semester. Therefore, in order to an-
alyze the same percentage of students (90%, 95% and
99%) it is necessary to include more subjects in the
visualization (12, 16 and 24 respectively).
This analysis can be repeated for the third and fur-
ther semesters. In summary, in the third semester, at
least one of the 15, 18 and 26 most popular subjects is
taken by the 90%, 95% and 99% of the total students
(13718) from a pool of 200 subjects. In the fourth
semester, figures are 16, 20 and 30 respectively, for
a total of 11831 students and 191 different subjects.
Notice that 30 different subjects generate
30
2
differ-
Table 4: Number of students (N) taking / passing a given
subject the second academic semester sorted by popularity.
Rank subject N Pass Acum. Pct.
1 01.005 4022 2470 4022 24.6 %
2 01.006 3704 2699 6611 40.4 %
3 01.079
∗
3369 2005 8670 53.0 %
4 01.001
∗
3362 2135 10266 62.8 %
5 01.078 2942 2247 11172 68.3 %
... ... ... ... ... ...
12 00.002
∗
1827 1087 14810 90.5 %
... ... ... ... ... ...
16 00.004
∗
1299 1059 15665 95.8 %
... ... ... ... ... ...
24 01.012
∗
481 333 16185 99.0 %
Table 5: Most popular combinations of subjects taken in
consecutive enrollments.
subject 01.005 01.006 01.079 01.001 01.078
00.010 3230 3026 2533 2654 2061
01.001 1915 1711 1473 898 1447
01.079 1597 1434 1048 1166 1775
01.005 1075 1398 1178 1321 886
00.002 915 807 725 767 644
ent combinations (i.e. 435), which is probably a fig-
ure too large for visualization purposes. Therefore, in
the following sections we will use the 95% level for
visualizing relationships between subjects.
2.2 Inter-semester Analysis
In this case we are interested in analyzing the se-
quence of subjects taken by students, that is, what
subjects they enroll into once they know the results
of the previous semester. Usually, when a student
fails to pass a subject, she is more likely to enroll into
such subject again the next semester, altogether with
other new subjects, following (or, unfortunately, not)
the recommendations given by the university (Table
1).
Table 5 shows, for each subject in the first
semester (rows), the number of students that take a
specific subject the second semester (columns), for
the first five most popular subjects each semester.
Only 65.3% of the 16356 students take one of these
25 combinations. In order to represent the 95% of stu-
dents’ enrollments, this table should have at least, 10
rows × 16 columns, which is clearly unwieldy.
3 VISUALIZING ENROLLMENT
DATA
Visualizing large volumes of data is not a trivial prob-
lem, specially when several dimensions are involved
VisualizationofEnrollmentDatausingChordDiagrams
513

Figure 1: Example of chord diagram.
(temporal, relationships among elements, and so). As
stated by (Shneiderman, 1996), it is very important to
find the appropriate visual representations of different
types of relationships between data entries. Among
the huge amount of possibilities (see (McCandless,
2009; Yau, 2011)), we have chosen to explore radial
visualizations (Draper et al., 2009) as they are well
suited for describing relationships between hierarchi-
cal data. We will focus in visualizing adjacency edges
(i.e. relationships between subjects), following the
approach described in (Holten, 2006), as well as con-
sidering the e-learning visualization context (G
´
omez-
Aguilar et al., 2010).
3.1 Chord Diagrams
In the light of the results described in the previous
section, we propose to use chord diagrams for visual-
izing both intra-semester and inter-semester data (not
included due to paper length restrictions). A chord
diagram is composed by segments, namely nodes and
chords. Nodes are arranged radially, drawing thick
curves (i.e. chords) between them. The thickness of
the curve encodes the frequency of a given aspect be-
tween the two connected nodes. In our case, each
node is a subject, the more students take a subject,
the bigger the node is, while chords between nodes
represent the number of students taking both subjects
at the same time.
For building chord diagrams we used D3.js, a
Javascript library for manipulating data (Bostock
et al., 2011). The aspect of a chord diagram is de-
termined by the following variables: the number of
subjects N, a vector of N elements containing sev-
eral attributes for each subject (in our case, num-
ber of students and success rate, which will deter-
mine node size and color respectively), a N × N ad-
jacency matrix containing elements in the form of
N
i j
= N
i j
00
+ N
i j
01
+ N
i j
10
+ N
i j
11
where N
i j
is the num-
Figure 2: Relationships between the 10 most popular sub-
jects in the first academic semester.
ber of students simultaneously taking subjects i and
j and subscripts describe the 2 × 2 matrix containing
the number of students failing/passing (0/1) each sub-
ject respectively. Due to printing restrictions, chord
diagrams are shown here using gray tones only. In-
teractive chord diagrams use color for increasing the
ability of discovering patterns: success rate [0, 1] is
mapped to a continuous [red, green] interval (contain-
ing yellow). Such interval could be quantized into
three bins [0, a), [a, b) and [b, 1] (a < b) representing
“under average”, “average” and “above average”, re-
spectively. More complex coloring strategies could
be designed as well, specially when visualizing sub-
ject combinations as chords.
3.2 Visualization of Intra-semester Data
Figure 2 shows the generated chord diagram for the
data described in Table 3, for the 10 most popular
subjects of the first semester. We have used a = 0.4
and b = 0.6 for quantizing node colors. subjects are
in clockwise order according to the number of stu-
dents taking each subject. On the other hand, Figure
3 reproduces the same visualization for the 16 most
popular subjects of the second semester. In this case
we show only the chords starting from a particular
subject, as an example of the interaction described in
Section 3.4. The complexity of these diagrams with
10 and 16 subjects is quite high, so 90% will be prob-
ably a better level for exploration purposes, including
more subjects dynamically if desired.
3.3 Visualization of Inter-semester Data
In this case we will think of chord diagrams as having
two halves: the left one contains the subjects from the
first semester, while the right one contains the sub-
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
514

Figure 3: Relationships between the 16 most popular sub-
jects in the second academic semester, showing some data
only for a given subject.
jects from the second one. Obviously some subjects
can be repeated in both halves (i.e. students taking
the same subject again), but no chords will be drawn
between subjects on the same half. Actually, it is like
visualizing a bipartite graph but maintaining the same
metaphor. Segment width and color follow the same
rules described in the previous sections. Chord width
is determined by the number of students taking one
subject from the right half after having taken one from
the left one. Chord color can be determined by the
percentage of students successfully passing both sub-
jects, showing dangerous/suitable subject enrollment
sequences. Figure 4 shows the chord diagram gener-
ated with the data in Table 5. This diagram could also
be created trying to reproduce the institutional rec-
ommendations (Table 1), including one more subject
every semester, in order to see reality compared to the
predetermined programme sequence. Nevertheless,
as some of the most popular subjects in the second
semester are from the first one (because students have
not taken them yet or they have but failed to do so),
the number of subjects should be larger in the right
half of the chord diagram, increasing its complexity.
3.4 Adding Interaction
Following Shneiderman’s mantra, “overview first,
zoom and filter, then details on demand” (Shneider-
man, 1996), we can use the possibilities of D3.js to
add some interaction to chord diagrams. While the
basic chord diagram (as shown in Figure 2) would
be the first task (“overview”), it is possible to move
forward the second task (“zoom and filter”) and the
third one (“details on demand”) using the following
approach:
• “zoom and filter”: if the user moves the cursor
(i.e. the mouse) over any segment, only those
Figure 4: Relationships between the 5 most popular sub-
jects each semester seen as consecutive enrollments.
other segments directly connected to such seg-
ment are visualized, the rest are filtered out by
fading. Therefore, if the user moves the cursor
over a node, only the node and the chords con-
necting such node to other nodes are visible. On
the other hand, if the user moves the cursor over
a chord, only that chord and the two nodes con-
nected by such chord are visible. Zoom can help
users to perform the “filter” task for small seg-
ments.
• “details on demand”: if the user selects (i.e. by
clicking) any segment, a small window contain-
ing information about such segment is displayed.
If the segment is a node, data about such sub-
ject is displayed, namely its code, name, academic
semester, percentage of students passing it and
percentage of students taking it for second and
further times. If the segment is a chord, the per-
centage of students taking the two subjects simul-
taneously (or consecutively) as well as the 2 × 2
matrix with the pass/fail rates are shown.
4 CONCLUSIONS
Enrollment in educational institutions with flexible
requirements (such as distance and online universi-
ties) does not follow uniform patterns with respect
to the subjects each student enrolls into or with re-
spect to the recommended sequence proposed by the
institution. The concept of cohort (students taking the
same subjects and advancing within a programme at
the same pace) is completely unsuitable. Students get
scattered between semesters, so their only nexus are
subjects taken simultaneously. Therefore, programme
planning becomes a complex issue involving large ta-
VisualizationofEnrollmentDatausingChordDiagrams
515

bles of numbers which are too large to comprehend
by university managers. On the other hand, students
have no support for determining which combinations
of subjects are more suitable, specially in their first
academic semester when they have no experience in
what means being an online learner.
In this paper we have described the use of chord
diagrams for visualizing intra-semester enrollment
data, namely the combinations of subjects taken by
students simultaneously. The number of subjects (and
their relationships) visualized as chord diagrams is
determined by a threshold, trying to capture as many
students as possible. We have created diagrams that
include 95% of the students, but they are quite com-
plex, so probably a threshold of 90% is enough for
exploration purposes. Currently now, university man-
agers are using tabular data for detecting programme
bottlenecks; we expect to introduce and evaluate the
use of chord diagrams as a simple way to visualize
such information as part of an internal institutional in-
novation project. These visualizations will be part of
an enrollment support system that will guide students
and their mentors through the large amount of subject
combinations, according to both their personal inter-
ests and background, but taking into account the aca-
demic performance of previous students with similar
enrollment patterns.
Current and future work in this topic should in-
clude the creation of more complex visualizations in-
volving more than two semesters, using concentric
chords or a 3D version, arranging chords in an imag-
inary 3D cone or cylinder. More experimentation for
determining the best number of subjects and the color-
ing scheme is also needed, as well as the information
provided by the interaction with the chord diagram.
ACKNOWLEDGEMENTS
This work is supported by Spanish Ministry of Sci-
ence and Innovation project MAVSEL (ref. TIN2010-
21715-C02-02).
REFERENCES
Bostock, M., Ogievetsky, V., and Heer, J. (2011). D
3
data-
driven documents. IEEE Transactions on Visualiza-
tion and Computer Graphics, 17(12):2301–2309.
Campbell, J., DeBlois, P., and Oblinger, D. (2007). Aca-
demic analytics: A new tool for a new era of educa-
tional research. EUCAUSE Review, 42(4):40–57.
Card, S. K., Mackinlay, J. D., and Shneiderman, B. (1999).
Readings in information visualization - using vision to
think. Academic Press.
Draper, G. M., Livnat, Y., and Riesenfeld, R. F. (2009).
A survey of radial methods for information visualiza-
tion. IEEE Transactions on Visualization and Com-
puter Graphics, 15(5):759–776.
G
´
omez-Aguilar, D. A., Su
´
arez-Guerrero, C., Theron-
S
´
anchez, R., and Garc
´
ıa-Pe
˜
nalvo, F. (2010). Visual
analytics to support e-learning. In Advances in Learn-
ing Processes.
Grau-Valldosera, J. and Minguill
´
on, J. (2014). Rethink-
ing dropout in online higher education: The case of
the universitat oberta de catalunya. The International
Review of Research in Open and Distance Learning,
15(1).
Holten, D. (2006). Hierarchical edge bundles: Visualiza-
tion of adjacency relations in hierarchical data. IEEE
Transactions on Visualization and Computer Graph-
ics, 12(5):741–748.
Kiernan, M., Woodroffe, M., and Thomas, P. (2004). Open
24/7: The journey from e-user to e-learner. In Nall, J.
and Robson, R., editors, Proceedings of World Con-
ference on E-Learning in Corporate, Government,
Healthcare, and Higher Education 2004, pages 95–
97, Washington, DC, USA. AACE.
McCandless, D. (2009). Information is beautiful. Collins,
London.
Park, J.-H. and Choi, H. J. (2009). Factors influencing adult
learners’ decision to drop out or persist in online learn-
ing. Educational Technology & Society, 12(4):207–
217.
Sac
´
ın, C. V., Chue, J., Peche, J. P., Alvarado, G., Vinatea,
B., Estrella, J., and Ortigosa, A. (2011). A data min-
ing approach to guide students through the enrollment
process based on academic performance. User Model-
ing and User-Adapted Interaction, 21(1-2):217–248.
Shneiderman, B. (1996). The eyes have it: A task by
data type taxonomy for information visualizations. In
Proceedings of the IEEE Symposium on Visual Lan-
guages, pages 336–343.
Siraj, F. and Abdoulha, M. A. (2009). Uncovering hid-
den information within university’s student enroll-
ment data using data mining. In Al-Dabass, D., Tri-
weko, R., Susanto, S., and Abraham, A., editors, Asia
International Conference on Modelling and Simula-
tion, pages 413–418. IEEE Computer Society.
Tyler-Smith, K. (2006). Early attrition among first time
elearners: A review of factors that contribute to drop-
out, withdrawal and non-completion rates of adult
learners undertaking elearning programmes. Journal
of Online Learning and Teaching, 2(2).
Yau, N. (2011). Visualize This: The FlowingData Guide to
Design, Visualization, and Statistics. John Wiley &
Sons.
GRAPP2015-InternationalConferenceonComputerGraphicsTheoryandApplications
516
