
Compressive Video Sensing with Adaptive Measurement Allocation for
Improving MPEGx Performance
George Tzagkarakis
1,3
, Panagiotis Tsakalides
1
and Jean-Luc Starck
2
1
Foundation for Research & Technology-Hellas (FORTH) - Institute of Computer Science (ICS), Crete, Greece
2
CEA, Service d’Astrophysique, Centre de Saclay, Gif-Sur-Yvette, France
3
EONOS Investment Technologies, Paris, France
Keywords:
Compressive Video Sensing, Measurement Allocation, Remote Imaging, MPEGx
Abstract:
Remote imaging systems, such as unmanned aerial vehicles (UAVs) and terrestrial-based visual sensor net-
works, have been increasingly used in surveillance and reconnaissance both at the civilian and battlegroup
levels. Nevertheless, most existing solutions do not adequately accommodate efficient operation, since limited
power, processing and bandwidth resources is a major barrier for abandoned visual sensors and for light UAVs,
not well addressed by MPEGx compression standards. To cope with the growing compression ratios, required
for all remote imaging applications to minimize the payloads, existing MPEGx compression profiles may re-
sult in poor image quality. In this paper, the inherent property of compressive sensing, acting simultaneously
as a sensing and compression framework, is exploited to built a compressive video sensing (CVS) system by
modifying the standard MPEGx structure, such as to cope with the limitations of a resource-restricted visual
sensing system. Besides, an adaptive measurement allocation mechanism is introduced, which is combined
with the CVS approach achieving an improved performance when compared with the basic MPEG-2 standard.
1 INTRODUCTION
Modern high-resolution visual sensing devices, with
processing and communication capabilities, largely
based on the seminal Shannon and Nyquist studies,
have enabled the acquisition, storage, and transmis-
sion of ever increasing amounts of visual data. How-
ever, the increasing demand for higher acquisition
rates and even improved resolution is placing signifi-
cant burden on existing hardware architectures.
An area which could benefit significantly by
the introduction of efficient computational models
is video acquisition. A characteristic example is
the design of remote imaging systems, such as un-
manned aerial vehicles (UAVs) and terrestrial visual
sensor networks, which have been increasingly used
in surveillance and reconnaissance applications. Re-
cent technological advances enable the design of low-
cost devices that incorporate multimodal sensing, pro-
cessing, and communication capabilities. At the same
time, the limited resources of the compression hard-
ware still is a major issue for such light-weight re-
mote imaging systems. To cope with such growing
compression ratios existing MPEGx techniques may
result in poor image quality.
The framework of compressive video sensing
(CVS) was introduced recently as an extension of
compressive sensing (CS) theory (Cand
`
es et al.,
2006). In particular, CVS methods aim at enabling
low-complexity onboard remote image acquisition
and compression using a reduced amount of linear
incoherent random projections, while maintaining a
similar reconstruction performance when compared
to standard video compression techniques.
In existing CVS methods, a non-overlapping
block splitting is applied first for each frame, followed
by full sampling of the reference frames and CS-
based acquisition of the non-reference frames. Then,
the reconstruction is performed separately (Stankovi
´
c
et al., 2008), or jointly by either considering a joint
sparsity model as in (Kang and Lu, 2009), or by de-
signing an adaptive sparsifying basis using neighbor-
ing blocks in previously reconstructed frames (Do
et al., 2009; Prades-Nebot et al., 2009). The ma-
jor drawback in the first case is that, since potential
spatio-temporal redundancies are not exploited, the
corresponding CVS methods usually result in higher
bit-rates, while also being sensitive to reconstruction
failures. The propagation of reconstruction errors
along the video sequence is also a common charac-
254
Tzagkarakis G., Tsakalides P. and Starck J..
Compressive Video Sensing with Adaptive Measurement Allocation for Improving MPEGx Performance.
DOI: 10.5220/0005360602540259
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 254-259
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

teristic of CVS methods performing joint decoding,
since inter-frame correlations are still not considered
at the encoder.
An efficient video representation must remove po-
tential spatio-temporal redundancies, which is an im-
portant issue towards the reduction of the transmitted
information. In recent studies (Marcia and Willett,
2008; Jacobs et al., 2010; Park and Wakin, 2009), a
first attempt was made to account for inter-frame cor-
relations expressed via the estimated motion between
consecutive frames. However, these approaches still
suffer from several drawbacks, such as the separate
encoding of each frame, thus without removing a sig-
nificant part of the inherent temporal redundancy, or
the attainment of a satisfactory performance only for
video sequences with slowly varying content.
In the present work, we address the above draw-
backs by introducing a CVS scheme, which combines
the advantages of MPEGx in traditional video com-
pression along with the power of CS in represent-
ing and reconstructing highly sparse signals with in-
creased accuracy. The performance of our method is
further enhanced by introducing a simple, yet very ef-
ficient, adaptive measurement allocation mechanism.
We demonstrate that the proposed approach satis-
fies the restrictions of a remote imaging system with
limited resources, while outperforming the standard
MPEGx implementation under certain conditions. We
emphasize though that the present study does not in-
tend to compete optimally designed MPEGx-based
industrial solutions, but to highlight the potential of
embedding CS-based modules in existing MPEGx
standards towards improving the overall performance
of the combined system.
The paper is organized as follows: in Section 2,
the CS frame acquisition model is reviewed. Sec-
tion 3 describes in detail the structure of the proposed
CVS system, along with key-factors that affect its ro-
bustness, and compares its performance against the
standard MPEG-2 approach. Finally, conclusions and
further extensions are outlined in Section 4.
2 CS FRAME MODEL
For convenience, we consider the case of N × N
frames, with the main disadvantage being the high
computational and memory expense when we deal
with high resolutions, which may be prohibitive for
a system with limited capabilities. A straightfor-
ward solution is to proceed in a non-overlapping
block-wise fashion. In the proposed CVS system,
each frame is divided into equally-sized n
B
× n
B
non-
overlapping blocks. Then, a random measurements
(a) GOP of MPEG-2 (b) GOP of CVS
Figure 1: GOP formations for MPEG-2 and CVS.
vector g
j
, j = 1,... ,B, is generated for each one of
the B blocks by employing a suitable measurement
matrix Φ (for simplicity the same matrix is used for
each block) as follows,
g
j
= Φ(Ψ
c
x
j
) , (1)
where x
j
∈ R
n
B
×n
B
denotes the j-th block of frame
x using a predetermined enumeration pattern, Ψ
c
∈
R
n
B
×n
B
is a coding transform basis and Φ ∈ R
M
B
×n
2
B
is a random measurement matrix with M
B
n
2
B
. No-
tice that Φ is applied on a vectorized version of Ψ
c
x
j
,
which is reshaped into an n
2
B
×1 column vector. If the
j-th block has a K-sparse representation in an appro-
priate sparsifying transform domain, and if the mea-
surement operator along with the sparsifying trans-
formation satisfy a sufficient incoherence condition,
then x
j
can be recovered from M
B
& O(2K logn
B
)
measurements by solving the following optimization
problem,
min
w
j
kw
j
k
1
+ τkg
j
− ΦΨ
c
Ψ
−1
s
w
j
k
2
2
, (2)
where Ψ
s
is an appropriate sparsifying transforma-
tion, such as an orthonormal basis (e.g., discrete
wavelet transform (DWT)) or an overcomplete dic-
tionary (e.g., undecimated DWT (UDWT)), w
j
is the
transform-domain representation of x
j
in Ψ
s
, and τ
is a regularization parameter that controls the trade-
off between the achieved sparsity (first term) and the
data fidelity (second term). If Ψ
s
is different than the
identity, then the reconstruction of the j-th block is
first performed in the transform domain,
ˆ
w
j
, followed
by an inversion to obtain the final spatial-domain es-
timate,
ˆ
x
j
= Ψ
−1
s
ˆ
w
j
. Otherwise, the spatial-domain
solution is obtained directly, that is,
ˆ
x
j
≡
ˆ
w
j
.
In a remote imaging system, some additional re-
quirements should be posed on the choice of the mea-
surement matrix Φ, such as the use of a minimal
number of compressed measurements, as well as their
fast and memory-efficient computation along with
a “hardware-friendly” implementation. A class of
matrices satisfying these requirements, the so-called
structurally random matrices, was introduced in (Do
et al., 2008). The block Walsh-Hadamard (BWHT)
operator is a typical member of this class, which is
employed in our proposed method.
CompressiveVideoSensingwithAdaptiveMeasurementAllocationforImprovingMPEGxPerformance
255

3 PROPOSED CVS SYSTEM
In this section, our proposed CVS system is in-
troduced and analyzed with respect to various key-
factors that affect its performance. We start with a
brief review of the core components of MPEG-2, to
which we compare in the rest of the paper.
3.1 Overview of MPEG-2
At the core of all MPEGx coding standards is the ex-
ploitation of spatio-temporal redundancies among ad-
jacent frames. Focusing on MPEG-2, each frame is
divided in non-overlapping 8 × 8 blocks. Compres-
sion along the temporal dimension is achieved us-
ing motion estimation (ME) and motion compensation
(MC), followed by a 2-D DCT applied on each block
to account for spatial redundancies. The encoding
process is completed with the quantization of DCT
coefficients, followed by Huffman coding. The video
sequence is viewed as a set of consecutive groups-of-
pictures (GOPs), consisting of I, B, and P frames, as
shown in Fig. 1(a). More specifically, I-frames are
fully sampled and encoded using a standard compres-
sion algorithm, such as JPEG. On the other hand, P-
frames are encoded with prediction from previous I
or P frames, while B-frames are encoded using pre-
diction from both previous and subsequent I and/or P
frames, depending on their position in the GOP.
During the ME step, the best match, under a mini-
mum mean absolute error (MAE) or mean squared er-
ror (MSE) criterion, of each block in the current frame
is searched among the blocks in a previously stored
reference frame (or frames). The success of MPEGx
is primarily based on the use of the (highly) sparse
residual frames, which are simply the prediction er-
rors between the predicted and the actual block. Mo-
tivated by this, we exploit directly the inherent spar-
sity of the residual-frame domain in the framework of
CS for the design of our proposed CVS system. Be-
sides, note that the GOP formation used in MPEG-2 is
not suitable for remote imaging systems with limited
memory resources, since the frames must be stored in
a buffer and reordered in order to compute the resid-
uals. An alternative and more memory-efficient GOP
formation is used in our CVS system, which consists
of I and P frames only, and thus it requires a single-
frame buffer (ref. Fig. 1(b)). Doing so, there are two
options: either estimate the residuals between the cur-
rent P and the previous I frame (IP mode), or between
two adjacent frames (PP mode). To avoid the error
propagation, which is inherent in the PP mode, the IP
mode is employed instead.
Figure 2: Proposed CVS system.
3.2 Proposed CVS System Structure
The structure of our proposed CVS scheme is shown
in Fig. 2. Specifically, it consists of an encoder - de-
coder pair, where appropriate CS-based modules are
embedded in both sides of an MPEGx architecture.
In the subsequent analysis, the similarity between
two frames, and also the reconstruction quality, is
measured in terms of the structural similarity index
(SSI), which resembles more closely the human vi-
sual perception than the commonly used peak signal-
to-noise ratio (PSNR). For a given pair of images I,
ˆ
I
the SSI is defined by,
SSI(I,
ˆ
I) =
(2µ
I
µ
ˆ
I
+ c
1
)(2σ
I
ˆ
I
+ c
2
)
(µ
2
I
+ µ
2
ˆ
I
+ c
1
)(σ
2
I
+ σ
2
ˆ
I
+ c
2
)
, (3)
where µ
I
, σ
I
are the mean and standard deviation of
the luminance of image I (similarly for
ˆ
I), σ
I
ˆ
I
denotes
the correlation coefficient of the two images, and c
1
,
c
2
stabilize the division with a weak denominator. In
particular, when SSI is equal to 0 the two images are
completely distinct, while when the two images are
matched perfectly SSI is equal to 1.
3.2.1 CVS Encoder
In this section, the main constituent parts of the pro-
posed CVS encoder are described, along with the pa-
rameters affecting their performance.
a) Motion Estimation. The reconstruction quality
of our CVS system depends highly on the achieved
sparsity of the residual frames, controlled by the ME
process. To this end, we tested the efficiency of well-
established ME algorithms, each one differing from
the others in the way the neighborhood of the cur-
rent block is scanned to find the best match. Among
them, the Adaptive Rood Pattern Search (ARPS) (Nie
and Ma, 2002) was shown to follow closely the opti-
mal Exhaustive Search (ES) approach, while also per-
forming a minimum average number of search steps
in the neighborhood of the current block until the best
matching is found. Based on that, ARPS was chosen
in our proposed CVS system.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
256
We note that the experimental evaluations in the
rest of the paper are performed on the luminance
component of three infrared (IR) videos of distinct
content
1
: i) iruw02 (static background, moving fore-
ground), ii) irw06 (static background, moving fore-
ground), and iii) UAV (complex motion content).
b) Block Size. Two distinct types of blocks must
be distinguished clearly. The first is related to the ME
process, for which we adopt the option of MPEG-2
setting the block-size equal to 8 × 8 and performing
the ME on macro-blocks of size 16 × 16. The second
is related to the CS measurement acquisition and con-
trols the degree of sparsity of a residual frame. We
found experimentally that a satisfactory trade-off be-
tween the CS block-size and the achieved sparsity is
obtained for blocks of size 32 × 32.
c) Sampling Operator. The sampling operator
in (1) is determined by the coding transformation Ψ
c
and the measurement matrix Φ. Common choices for
Ψ
c
are the discrete cosine transform (DCT) and the
DWT (with the 9/7 wavelet as in JPEG2000), which
have been shown to achieve a high degree of sparsity
for a broad range of images, while Φ is chosen to be a
BWHT matrix, which is computationally efficient, as
it was mentioned in Section 2.
d) Quantization & Coding. The simple uniform
quantizer used in MPEG-2 is also adopted by the
quantization module of our system, so as to make a
fair comparison between the two architectures. The
quantized CS measurements for all blocks of the cur-
rent residual frame are then encoded using an im-
proved Huffman coding scheme using recursive split-
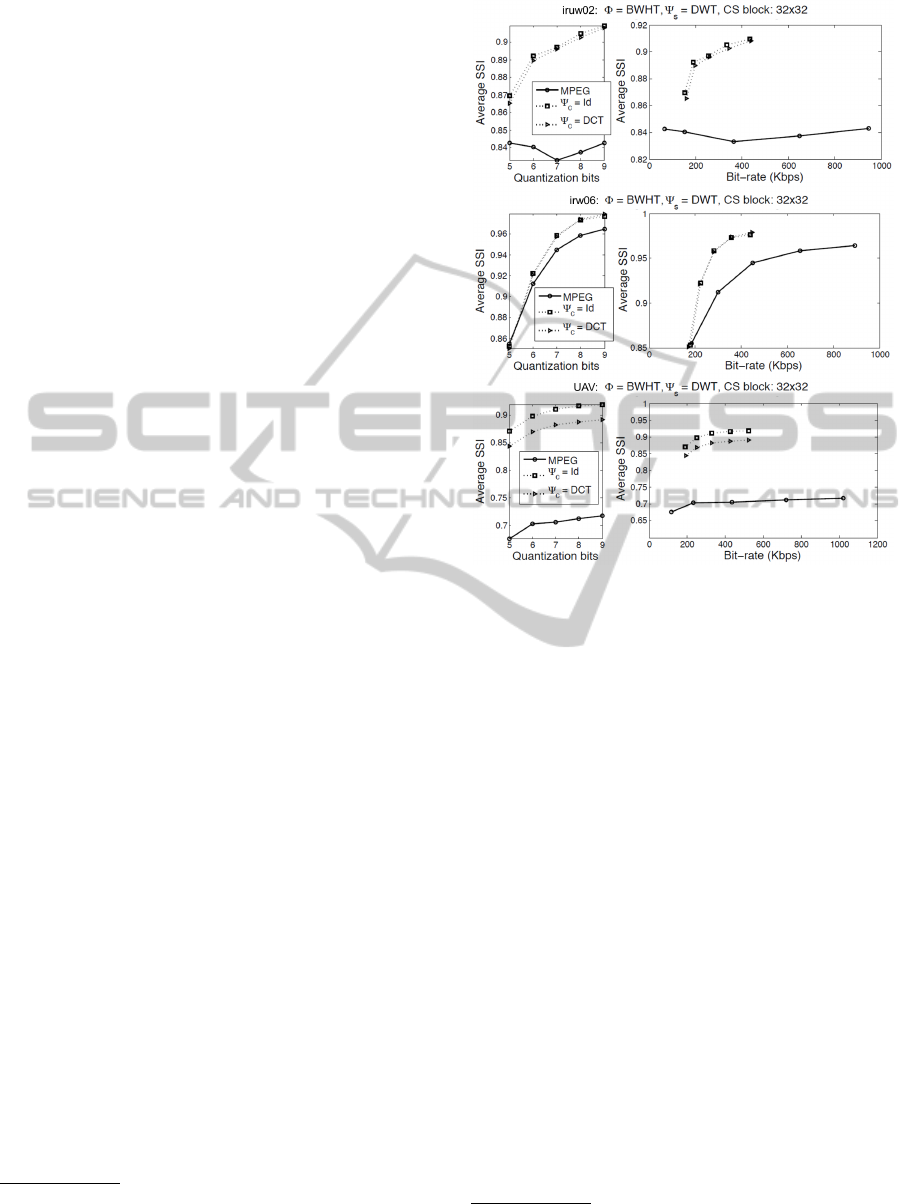
ting (Skretting et al., 1999). Fig. 3 shows the average
SSI as a function of the number of quantization bits
for the three video sequences. First, we observe that
CVS outperforms MPEG-2 as the number of quanti-
zation levels decreases, that is, as the resolution of the
available information at the decoder becomes coarser.
This difference is more prominent for the UAV se-
quence, whose motion content is more complex when
compared with iruw02 and irw06.
e) CS Sampling Ratio. The reconstruction qual-
ity improves with an increasing CS sampling ratio
(r = M
B
/n
2
B
) of the acquired CS measurements (M
B
)
over the CS block-size (n
B
× n
B
), but at the cost of
higher bit-rates. A reduction of the total bit-rate is
achieved by designing an adaptive measurement allo-
cation approach, as it is described in Section 3.3.
1
iruw02 and irw06 were obtained from http://www.cse.
ohio-state.edu/otcbvs-bench/; UAV was provided by
SAGEM.
Figure 3: Reconstruction performance as a function of
quantization levels.
3.2.2 CVS Decoder
At the decoder side, the main components along with
the associated factors affecting their performance are
analyzed below.
a) Sparsifying Transformation. In general, the
sparsifying transformation Ψ
s
used in (2) can be dif-
ferent from the coding transformation Ψ
c
. In the later
case, an orthonormal basis is preferred for the coding
of the residual blocks, whereas in the former case the
sparsifying transformation can be either a basis or an
overcomplete dictionary, such as an UDWT. In fact,
an overcomplete dictionary usually results in sparser
representations, and consequently in an improved re-
construction quality at lower bit-rates, but at the cost
of increased decoding time.
b) Reconstruction Algorithm. In our implementa-
tion, the TwIST
2
algorithm is used to solve the opti-
mization problem (2), since it was shown to achieve
a good trade-off between the computational complex-
ity and the resulting reconstruction quality. However,
a more thorough study concerning the optimal choice
of the reconstruction method is left as a future work.
c) Noisy Data. In practice, we deal with data
2
Matlab code and paper: http://www.lx.it.pt/∼bioucas/
TwIST/TwIST.htm.
CompressiveVideoSensingwithAdaptiveMeasurementAllocationforImprovingMPEGxPerformance
257

corrupted by noise (e.g., instrumental, quantization,
and channel). In the noisy case, an MPEGx-based
approach requires denoising of at least the I and P
frames in each GOP, since they are used together with
the reconstructed residuals to obtain the rest of the P
and B frames. On the other hand, one of the main ad-
vantages of CS is its inherent property to act as a de-
noising process by suppressing the reconstructed non-
sparse part of the residual introduced by the noise.
Thus, in our CVS system the denoising of only the
I-frames should suffice. For the denoising, a double-
density dual-tree complex DWT thresholding tech-
nique was employed
3
. The same denoising method
is also used for the I and P frames of the MPEG-2
system for a fair comparison.
Fig. 4 compares for the three videos the aver-
age SSI between the proposed CVS system and the
MPEG-2 approach, as a function of the input SNR,
ranging from 10 dB to 40 dB, as well as the number of
quantization bits, q ∈ [5, 9]. Clearly, the CVS system
achieves a significant improvement against MPEG-2
in the case of noisy data, requiring a significantly re-
duced bit-rate especially for low input SNR values,
while it achieves a comparable reconstruction quality
when compared with MPEG-2 in the medium to high
input SNR regime.
3.3 Adaptive Measurement Allocation
The superiority of MPEGx, which is usually observed
for videos with slowly varying content is primarily
due to the large number of small-amplitude DCT co-
efficients of the residual blocks because of the (al-
most) static regions in the original frames. A way to
account for this redundancy is to perform a uniform
thresholding on each CS block by applying the CVS
scheme on the same percentage (α%) of the largest
amplitude DCT coefficients.
The main drawback of a uniform measurement ac-
quisition is that it does not exploit the true sparsity of
each individual residual block. Motivated by this, we
design an adaptive CS measurement allocation mech-
anism, which is then added in the “Block CS” mod-
ule of Fig. 2, analogously to the bit allocation process
used by many modern compression architectures.
To this end, for a given N × N residual frame R,
the noise standard deviation, σ
η
, is estimated first us-
ing the median absolute deviation (MAD) rule. Then,
a block-wise DCT is applied followed by a thresh-
olding of the transform coefficients with threshold
ρ
T h
= λσ
η
p
2log(N
2
), where λ is a predefined scal-
ing factor. Let K
max
= r · n
2
B
be the maximum number
3
Matlab code and paper: http://taco.poly.edu/selesi/
DoubleSoftware/
of CS measurements corresponding to a sampling ra-
tio r, where n
B
× n
B
is the CS block size. Doing so,
the adaptive sampling ratio for the j-th CS block is
given by
r
j
=
1
n
2
B
· min(card({C
j
> ρ
T h
}), K
max
) , (4)
where C
j
denotes the set of DCT coefficients of the
j-th block. Finally, the associated number of CS mea-
surements to be acquired for the j-th block is equal to
M
j
= br
j
· n
2
B
c.
The bit-rate gain of the adaptive measurement al-
location process is quantified by bit-rate
gain
=
B
0
−B
1
B
0
,
where B
0
is the total number of bits for CVS coding
of the original residual frames R using our adaptive
measurement allocation method, and B
1
is the total
number of bits for coding the residual frames obtained
by zeroing all except for the α % largest DCT coeffi-
cients of R and reconstructing using the IDCT.
Next, results are presented for the iruw02 se-
quence only, whilst a similar behavior was observed
for the other two sequences. The achieved gains with
respect to the required bit-rates are shown in Fig. 5.
As it can be seen, a significant bit-rate gain is attained
by applying the intermediate thresholding step fol-
lowed by the adaptive allocation of CS measurements.
Specifically, this gain is higher for smaller sampling
ratios and quantization bits.
4 CONCLUSIONS
In this work, a variant of an MPEGx-based video
compression system was introduced based on the
principles of CS. Motivated by the success of
MPEGx to remove spatio-temporal redundancies
among frames by working with the residual frames,
we exploited the sparse nature of the residual frames
in conjunction with the power of CS to achieve a high
reconstruction quality at reduced bit-rates. The per-
formance was further improved by means of an adap-
tive measurement allocation scheme. Preliminary ex-
perimental results on infrared sequences revealed that
the proposed CVS system is competitive with the
well-established MPEG-2 approach, under appropri-
ate specification of the several system components.
Several extensions of the current CVS design are
possible. First, regarding the ME/MC modules, the
simple but efficient ARPS method used in the current
implementation can be substituted by a more accu-
rate method resulting in even sparser residual frames.
However, we must be always aware of keeping a bal-
ance between the estimation accuracy and the compu-
tational complexity in an imaging system with limited
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
258

Figure 4: Average SSI as a function of bit-rate and input SNR.
Figure 5: Effect of thresholding and adaptive measurement
allocation on the bit-rate gain for the iruw02 sequence.
resources. Furthermore, the use of a uniform quan-
tizer is by no means a sub-optimal choice. Instead,
we expect that a quantizer adapted to the character-
istics of CS measurements along with an appropriate
reconstruction approach, as proposed in (Baig et al.,
2010), could increase the compression rates at the en-
coder and the reconstruction quality at the decoder.
Finally, concerning the CS reconstruction, especially
in the noisy case, a challenging task will be to find
systematic ways to set the optimal sampling opera-
tors, as well as the regularization parameters so as to
adapt to the statistics of the noisy signals.
ACKNOWLEDGMENT
This work was supported by CS-ORION Marie Curie
Industry - Academia Partnerships and Pathways
(IAPP) project funded by the European Commis-
sion in FP7 (PIAP-GA-2009-251605). It has been
co-financed by the European Union and Greek
national funds through the National Strategic Ref-
erence Framework (NSRF), Research Funding Pro-
gram: “Cooperation-2011”, Project “SeNSE”,
grant number: 11ΣYN-6-1381.
REFERENCES
Baig, Y., Lai, E. M.-K., and Lewis, J. (2010). Quantiza-
tion effects on compressed sensing video. In ICT ’10,
Doha, Qatar.
Cand
`
es, E., Romberg, J., and Tao, T. (2006). Robust
uncertainty principles: Exact signal reconstruction
from highly incomplete frequency information. IEEE
Trans. on Information Theory, 52(2):489–509.
Do, T., Chen, Y., Nguyen, D., Nguyen, N., Gan, L., and
Tran, T. (2009). Distributed compressed video sens-
ing. In ICIP ’09, Cairo, Egypt.
Do, T., Tran, T., and Gan, L. (2008). Fast compressive sam-
pling with structurally random matrices. In ICASSP
’08, Las Vegas, NV.
Jacobs, N., Schuh, S., and Pless, R. (2010). Compressive
sensing and differential image-motion estimation. In
ICASSP ’10, Dallas, TX.
Kang, L.-W. and Lu, C.-S. (2009). Distributed compressive
video sensing. In ICASSP ’09, Taipei, Taiwan.
Marcia, R. and Willett, R. (2008). Compressive coded aper-
ture video reconstruction. In EUSIPCO ’08, Lau-
sanne, Switzerland.
Nie, Y. and Ma, K.-K. (2002). Adaptive rood pattern search
for fast block-matching motion estimation. IEEE
Trans. Image Processing, 11(12):1442–1448.
Park, J. Y. and Wakin, M. (2009). A multiscale frame-
work for compressive sensing of video. In PCS ’09,
Chicago, IL.
Prades-Nebot, J., Ma, Y., and Huang, T. (2009). Distributed
video coding using compressive sampling. In PCS
’09, Chicago, IL.
Skretting, K., Husoy, J. H., and Aase, S. O. (1999).
Improved huffman coding using recursive splitting.
In Norwegian Signal Processing Symposium, Asker,
Norway.
Stankovi
´
c, V., Stankovi
´
c, L., and Cheng, S. (2008). Com-
pressive video sampling. In EUSIPCO ’08, Lausanne,
Switzerland.
CompressiveVideoSensingwithAdaptiveMeasurementAllocationforImprovingMPEGxPerformance
259
