
Comparison of Statistical and Artificial Neural Networks Classifiers
by Adjusted Non Parametric Probability Density Function Estimate
Ibtissem Ben Othman, Wissal Drira, Faycel El Ayeb and Faouzi Ghorbel
GRIFT Research Group, Cristal Laboratory, School of Computer Sciences, Manouba 2010, Tunisia
Keywords: Artificial Neural Networks, Classifier Stability, Dimension Reduction, Error Rate Probability Density
Function, Kernel-diffeomorphism Plug-in Algorithm, Patrick-Fischer Distance Estimator, Stability.
Abstract: In the industrial field, the artificial neural network classifiers are currently used and they are generally
integrated of technologic systems which need efficient classifier. Statistical classifiers also have been
developed in the same direction and different associations and optimization procedures have been proposed
as Adaboost training or CART algorithm to improve the classification performance. However, the objective
comparison studies between these novel classifiers stay marginal. In the present work, we intend to evaluate
with a new criterion the classification stability between neural networks and some statistical classifiers based
on the optimization Fischer criterion or the maximization of Patrick-Fischer distance orthogonal estimator.
The stability comparison is performed by the error rate probability densities estimation which is valorised by
the performed kernel-diffeomorphism Plug-in algorithm. The results obtained show that the statistical
approaches are more stable compared to the neural networks.
1 INTRODUCTION
In high dimension spaces, the precision of the
estimation requires non realistic size of training
sample since the sample data size required to obtain
satisfactorily classification accuracy increases
exponentially with dimension of data space. Hence,
dimension reduction step is one of the important and
efficient issues to overcome this problem. Among
statistical methods for this purpose, we consider here
a standard one called Fisher Linear Discriminate
Analysis (LDA) and a second one based on a
probabilistic distance. Artificial Neural Networks
(ANNs or NNs) have been in use for some time now
and we can find them working in data classification
and non-linear dimension reduction.
Various experimental comparisons of neural and
statistical classifiers have been reported in the
literature. Paliwal and Kumar presented in (Paliwal,
2009) a recent review of these studies. Tam and
Kiang showed in (Tam, 1992), by comparing the NNs
with the linear classifiers as: Discriminate Analysis,
the logistic regression and the k Nearest Neighbor
ones for bank bankruptcy prediction in Texas. A
performance evaluation of the neural networks
against linear discriminate analysis was presented by
Patuwo and al, in (Patuwo, 1993), for some
classification problems. Their study proved that
neural approaches are not better than the LDA but
they are comparable in two-group two-variable
problems.
Most of researchers compare the neural and
statistical techniques performance while forgetting
the NNs instability criterion. This paper studies the
stability of neural network classifier results compared
to the statistical ones. In our work we propose to
evaluate the stability by estimating the error rate
probability density function (pdf) of each classifier.
Such pdf is estimated by applying the Plug-in kernel
algorithm (Saoudi, 2009), which optimizes the
integrated mean square error criterion to search the
best smoothing parameter of the estimator. The
misclassification error is a positive real value
bounded by the unity. Therefore we choose to
improve the pdf estimation precision by using the
performed kernel-diffeomorphism Plug-in algorithm
recently developed in (Saoudi, 2009).
Therefore this paper will be organized as follow.
We begin in the section 2 by presenting the neural
approach. Section 3 recalls the statistical classifiers
which are based on two tasks. The first one consists
on the dimensionality reduction after that, the
classification procedure will be applied in the reduced
space. The classifier based on Patrick-Fischer
672
Othman I., Drira W., El Ayeb F. and Ghorbel F..
Comparison of Statistical and Artificial Neural Networks Classifiers by Adjusted Non Parametric Probability Density Function Estimate.
DOI: 10.5220/0005360906720678
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 672-678
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

distance will be described. After that, we will devote
section 4 to the introduction of the criterion which
will be given as the comparison study between the
neural and the statistical classifiers. Simulation
results are presented and analyzed in section 5. In the
last section, we will apply this comparative study to
the evaluation of real pattern recognition problem. So
we intend to test the different classifiers stability and
performance for the handwritten digits recognition
problem by classifying their corresponding Fourier
Descriptors. Such features form a set of invariant
parameters under similarity transformations and
closed curve parameterizations. This set has good
proprieties as completeness and stability.
2 NEURAL APPROACHES
The most used and studied networks category is the
mixed NNs, which present a combination of the
features extractors NNs and the classifiers ones. Once
the first networks layers carry out the primitive
extraction, the last layers classify the extracted
features. An interesting example is the Multi-Layer
Perceptron.
2.1 Multi-Layer Perceptron: MLP
Based on the results from (Steven, 1991), a MLP with
one hidden layer is generally sufficient for most
problems including the classification. Thus, all used
networks in this study will have a unique hidden
layer. The number of neurons in the hidden layer
could only be determined by experience and no rule
is specified. However, the number of nodes in the
input and output layers is set to match the number of
input and target parameters of the given process,
respectively. Thus, the NNs have a complex
architecture that the task of designing the optimal
model for such application is far from easy.
In order to reduce the difference between the
ANN outputs and the known target values, the
training algorithm estimates the weights matrices,
such that an overall error measure is minimized. The
proposed technique requires improvements for MLP
with the back-propagation algorithm.
2.2 Neural Networks Critics
Although the effectiveness and significant progress of
ANNs in several applications, and especially the
classification process, they present several limits.
First, the MLP desired outputs are considered as
homogeneous to a posterior probability. Till today, no
proof of this approximation quality has been
presented. Second, the NNs have a complex
architecture that the task of designing the optimal
model for such application is far from easy. Unlike
the simple linear classifiers which may underfit the
data, the NNs architecture complexity tends to overfit
the data and causes the model instability. Breiman
proved, in (Breiman, 1996), the instability of ANNs
classification results. Therefore, a large variance in its
prediction results can be introduced after small
changes in the training sets. Thus, a good model
should find the equilibrium between the under-fitting
and the over-fitting processes.
Qualified by their instability, the neural classifiers
produce a black box model in terms of only crisp
outputs, and hence cannot be mathematically
interpreted as in statistical approaches. Thus, we
recall in the next section some statistical methods
such the basic linear discriminate analysis and the
proposed Patrick-Fischer distance estimator.
3 STATISTICAL APPROACHES
The traditional statistical classification methods are
based on the Bayesian decision rule, which presents
the ideal classification technique in terms of the
minimum of the probability error. However, in the
non parametric context, applying Bayes classifier
requires the estimation of the conditional probability
density functions. It is well known that such task
needs a large samples size in high dimension.
However, a dimension reduction is required in the
first step.
3.1 Linear Discriminate Analysis: LDA
The linear discriminate analysis is the most well-
known approach in supervised linear dimension
reduction methods since this popular method is based
on scatter matrices. In the reduced space, the between
scatter matrices are maximized while the within class
ones are minimized. To that purpose, the LDA
considers searching for orthogonal linear projection
matrix W that maximizes the following so-called
Fisher optimization criterion (Fukunaga, 1990):
)(
)(
)(
WSWtrace
WSWtrace
WJ
w
T
b
T
(1)
S
w
is the within class scatter matrix and S
b
is the
between class scatter one. Their two well-known
expressions are given by:
ComparisonofStatisticalandArtificialNeuralNetworksClassifiersbyAdjustedNonParametricProbabilityDensity
FunctionEstimate
673

c
k
T
kkkw
XXES
1
)))(((
1
()()
c
T
bkk k
k
S
(2)
where μ
k
is the conditional expectation of the original
multidimensional random vector X relative to the
class k. μ corresponds to the mean vector over all
classes. c is the total number of classes and π
k
denotes
the prior probability of the k
th
class. E(.) is the
expectation operator.
Fisher reduction space is generated by the d-
eigenvectors having the d-largest eigen values of the
matrix S
w
-1
S
b
. Note that this method is based on the
scatter matrices which are defined from first and
second order statistical moments of the conditional
random variable. Therefore, for complex situations as
the multimodal conditional distributions the low
order moments do not enable to describe completely
statistical dispersions. So, Fisher discriminate
analysis could give wrong feature selection. In order
to get rid this limitation, we have proposed in (Drira,
2012) the method based on distances between the
conditional probability density functions weighted by
the prior probabilities.
3.2 Patrick-Fischer Distance Estimator
based on Orthogonal Series
It is well known that the most suitable criteria for the
discriminate analysis is defined from the distance
between probability density functions whether
conditional or mixture. Despite its theoretical interest,
its use is still limited in practice while this distance
does not admit practically no explicit estimator in the
non parametric case.
We recall here the Patrick-Fischer distance, which
has links of decrease and increase with the probability
error of classification, as following:
2
1
2
221121
)(),( dxffffd
D
R
PF
(3)
In (Drira, 2012), the authors introduce a Patrick-
Fischer distance estimator using orthogonal
functions. Using orthogonal property of the function
basis in the sense of L
2
(U), they replace in the Patrick-
Fischer distance expression, the different quantities
by their corresponding estimators. The obtained
estimator results in the following quantity:
11 22
12
12
12
11 2 2
2
11 11
12
min( , )
11
1
ˆ
(, ) ( , )
2Re ( , )
NN NN
P
Fmljmlj
lj lj
NN
mm l j
lj
dKXXKXX
N
KXX
(4)
Where
k
i
X is the i
th
observation of the k
th
class.
i
N
is
the sample size of the i
th
class and N is the total size
of all classes. m
N
is the smoothing parameter for kernel
density function estimator.
),( yxK
N
m
is the kernel
function associated to the orthogonal system of
functions{e
m
(x)} used in (Drira, 2012).
PF
d
ˆ
is an
unbiased estimator of the Patrick Fischer distance.
The estimator in the reduced space could be
expressed as a function of the linear form W in R
D
:
12
21
22
2
11
1
11
21
),min(
11
22
11
11
2
),(Re2
),(
),(
1
ˆ
N
l
N
j
jlmm
N
l
N
j
jlm
N
l
N
j
jlmPF
XXK
XWXWK
XWXWK
N
d
(5)
where
VW represents the scalar product operator of
the two vectors V and W of the space R
D
and Re(z) is
the real part of a complex z.
For dimensionality reduction purpose, this
distance is considered as the criterion function to be
maximized with respect to a linear projection matrix
W that transform original data space onto a d-
dimensional subspace so that classes are most
separated. This functional maximization problem
cannot be solved analytically. Since this estimator
equation is highly nonlinear according to the element
of W and an analytical solution is often practically not
feasible. Thus, we have resorted to a numerical
optimization methods to compute a suboptimal
projection matrix W.
4 STABILITY STUDY
The first step before comparing is to train the two
classifiers, and then we proceed by measuring the
error rate produced by each classifier with each one
of N independent test sets. Let’s consider (X
i
)
1≤i≤N
the
N generated error rates of a given classifier (ANN or
Bayes). These random variables are supposed to be
independent and identically distributed and having
the same probability density function (pdf), f
X
.
4.1 Non-parametric Error Estimation
based on the Gaussian Kernel
We suggest to use the kernel method proposed in
(Fukunaga, 1990), to estimate the classifiers error
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
674

rates pdfs. For this method, an approximation of the
Mean Integrated Square Error (MISE) is optimized in
order to estimate the involved smoothing parameters
h
N
.
The choice of the optimal value for the smoothing
parameter will determine the estimation goodness
level. Recently, the researchers try to determine it by
the iterative resolution called the Plug-in algorithm.
Actually, a fast variant of known conventional Plug-
in algorithm has been developed in (Saoudi, 2009).
4.2 The Performed
Kernel-Diffeomorphism Plug-in
Algorithm
The observed misclassification error rates (X
i
)
1≤i≤N
of
each classifier are positive real values bounded by the
unity. Thus, there won’t be any interest to use the
conventional kernel density estimation method while
the pdfs are defined on a bounded or semi-bounded
space. During their estimation phase, some
convergence problems called the Gibbs phenomenon
may occur at the edges. Several researchers have tried
to solve this issue and some methods got described in
order to estimate the probability densities under
topological constraints on the support. Two
interesting solutions mentioned in (Saoudi, 1994)
present interesting results: the orthogonal functions
method and the kernel diffeomorphism one. The last
procedure is based on a suitable variable change by a
C1-diffeomorphism. Although, the smoothing
parameter value must be optimized, otherwise there
won’t be any warranty to get a good estimation
quality. The Plug-in diffeomorphism algorithm which
is a generalization of the conventional Plug-in one
(Saoudi, 2009) is used to perform the smoothing
parameter optimization.
For complexity and convergence reasons, we have
suggested in (Othman, 2013) a new variant of the
kernel-diffeomorphism semi-bounded Plug-in
algorithm. This new procedure is based on the
variable change
)( XLogY
of the positive error
rates. So, the kernel estimator expression becomes:
(6)
In order to specify a new classification quality
measure, we iterate the conventional Plug-in
algorithm for the transformed data. Finally, we
compute
ˆ
()
ˆ
()
Y
X
f
Logx
fx
x
.
5 PERFORMANCE EVALUATION
BY SIMULATIONS
The stability comparison between the ANN, the LDA-
Bayes and the Patrick-Fischer estimator proposed in
our previous works (Drira, 2012) is first summarized
by stochastic simulations. For this purpose, we have
considered a binary classification problem adapted to
a mixture of two different Gaussian distributions.
For the training phase, we generate one adjusted
set including 1000 samples for each class. By using
this training set, we look to find the optimum
transformation that represents the dimension
reduction for both LDA and the proposed Patrick-
Fischer methods before applying the Bayesian rule,
and then to fix the optimal neural model parameters.
For the generalisation phase and in order to
analyse the classifiers stability, we generate 100
supervised and independent test sets (including 1000
samples for each class). Then a set of 100 error rates
are retained for each approach. Their probability
densities are estimated using the performed kernel-
diffeomorphism Plug-in algorithm proposed in the
previous section.
Figure 1 shows the estimated error rates
probability densities. In Fig.1.a and Fig.1.b, we
illustrate respectively homoscedastic and classical
heteroscedastic Gaussians. In Fig.1.c, we treated the
case of two superposed distributions having the same
means vector and different covariance matrices.
Finally, Fig.1.d shows the case of two truncated
Gaussians in a tridimensional space. In this last case,
the second samples cloud surrounds the first one in a
ball centred at the origin. In table 1, the classifiers
stability and performance are also valorised by
presenting their error rates bias and variances.
By analysing the four illustrations of figure 1, we
can observe that the neural density curve is generally
situated on the right. Thus, the statistical classifiers
(LDA-Bayes and PF-Bayes) are more efficient than
the neural networks since they admit the smallest error
rates means. Furthermore, the neural approach
remains the least stable classifier for the four cases that
presents the greatest variance and thus the widest
curve. The results show also the performance and
stability improvement of the Patrick-Fischer distance
estimator against the conventional Fisher LDA.
N
i
N
i
N
Y
h
Yy
K
Nh
yf
1
**
1
)(
ˆ
ComparisonofStatisticalandArtificialNeuralNetworksClassifiersbyAdjustedNonParametricProbabilityDensity
FunctionEstimate
675
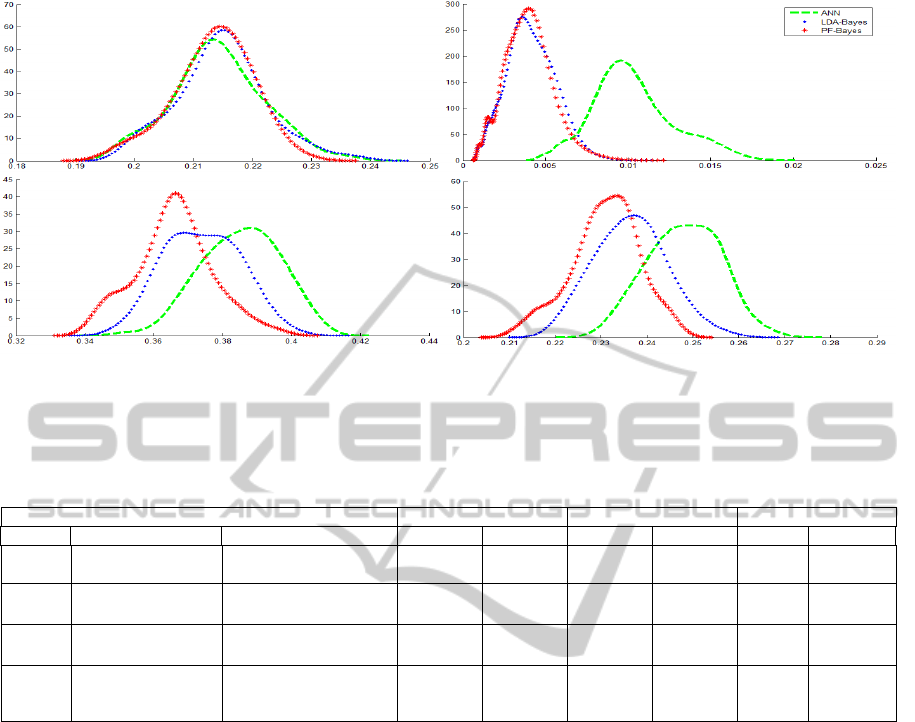
Figure 1: Error rate densities of ANN (in green(--)), LDA-Bayes (in blue(..)) and PF-Bayes (in red(*)), for various simulations:
homoscedastic (a), heteroscedastic (b), superposed (c) and truncated (d) Gaussians.
Table 1:
Comparison results of the presented approaches: Low (mean/variance) ==> Better (performance/stability) of the
classifiers.
Simulations ANN LDA-Bayes PF-Bayes
Cases
Class 1 Class 2 Mean Variance Mean Variance Mean Variance
a
μ
1
=(1,..,1)
10
∑
1
=I
10
μ
2
=(1.5,..,1.5)
10
∑
2
=I
10
0.2147 0.5883 0.2145 0.5590 0.2134 0.3978
b
μ
1
=(0,..,0)
10
∑
1
=I
10
μ
2
=(2,..,2)
10
∑
2
=2* I
10
0.0103 0.0550 0.0041 0.0181 0.0040 0.0175
c
μ
1
=(0,..,0)
10
∑
1
=I
10
μ
2
=(0,..,0)
10
∑
2
=2*I
10
0.3853 0.1224 0.3741 0.1145 0.3660 0.1224
d
μ
1
=(0,0,0)
∑
1
=[0.06 0.01 0.01
]*I
3
μ
2
=(0.1,0.1,0.1)
∑
2
=[0.01 0.06 0.05 ] *I
3
0.2481 0.5988 0.2364 0.5762 0.2309 0.5383
6 APPLICATION TO
HANDWRITTEN DIGIT
RECOGNITION
In order to compare the classifiers stability and
performance, we refer in the present section to the
handwritten digit recognition problem. This task is
still one of the most important topics in the automatic
sorting of postal mails and checks registration. The
database used to train and test the different classifiers
described in this paper was selected from the
publicly available MNIST database of handwritten
digits (yann). For the training and test sets, we select
randomly, from the MNIST training and test sets
respectively, single digit images (the both sets
contain 1000 images for the 10 digit classes).
The most difficult task in handwritten digit
recognition problems is the suitable features
selections. The extracted characteristics must satisfy
a non-exhaustive set of criteria such as fast
computation, completeness, powerful discrimination
and invariance. The Fourier descriptors (FD) verify
such criteria. The FD are calculated from the digit
outline boundary and are invariant regarding to the
elementary geometrical transformations, such as
translation, rotation and scaling. In this experiment,
we compute a Fourier descriptors vector to each
digit. The FD vector size is chosen to be equal to
fourteen. This vector size is demonstrated in
(Ghorbel, 1990) to be sufficient to represent a
contour digit. The FD vectors set obtained for the
whole digits in the selected sample will form the
shape descriptors dataset to be tested.
We intend to compare the classifiers stability by
evaluating their respective performances for 100
times using the 10-folds (default) Cross Validation
(CV) algorithm. We use the CV algorithm from the
MNIST test set to select the test sets (N=1000 images
for each class). With these sets, we calculate the
(c)
(d)
(b)
(a)
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
676
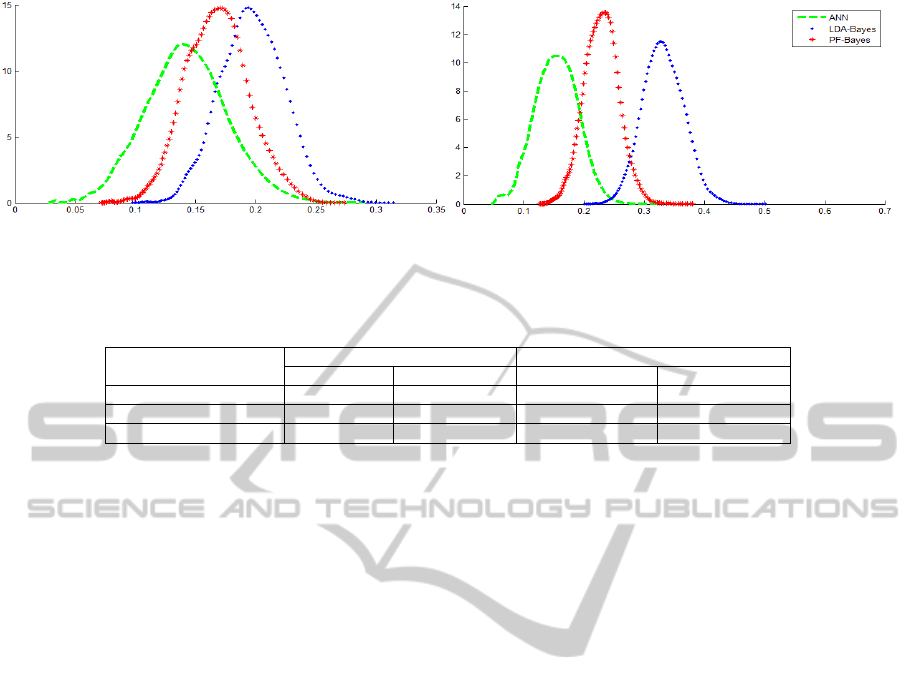
Figure 2: Error rate densities of ANN (in green(--)), LDA-Bayes (in blue(..)) and PF-Bayes (in red(*)) for binary classification
of digits ‘2’ and ‘3’ (in the left) and ‘3’ and ‘4’ (in the right).
Table 2: Comparison results of the presented approaches on the MNIST database: Low (mean/variance) ==> Better
(performance/stability).
Digit classes: ‘2’ and ‘3’ Digit classes: ‘3’ and ‘4’
Mean Variance Mean Variance
ANN
0.1425 0.7285 0.1545 0.0012
LDA-Bayes
0.1975 0.6803 0.3319 0.0011
PF-Bayes
0.1682 0.6791 0.2292 0.0010
classifiers misclassification rates (MCR).
Figure 2 shows the classifiers error rate
probability densities estimated using the suggested
performed kernel-diffeomorphism Plug-in algorithm
for Fourier descriptors. In table 2, we summarize the
obtained MCR means and variances. The results
show the performance of the ANN against the
Bayesian classifier, but the superiority of its error
rate variances proves their low stability against the
statistical approaches. For these two complex real
cases, the LDA fails to find the optimal projection
subspace.
Whereas, the Patrick-Fischer distance estimator
performs better than the conventional LDA. By
providing a better performance, the proposed
Patrick-Fischer distance estimator is relatively more
stable than the Fisher LDA. Thus, we can approve
that the stability and performance of the Bayesian
classifier increases with the use of the proposed
Patrick-Fischer distance estimator as reduction
dimension method.
7 CONCLUSIONS
In this paper, we have introduced a new criterion to
evaluate the results stability of the artificial neural
networks and some statistical classifiers based on the
optimization Fischer criterion and the maximization
of Patrick-Fischer distance orthogonal estimator.
The stability comparison is valorised by the use of
the performed kernel-diffeomorphism Plug-in
algorithm. The stochastic simulations and the real
dataset experiments demonstrated the neural
networks are not stable as the statistical approaches.
The results show also the performance and stability
progress of the Patrick-Fischer orthogonal distance
estimator against the conventional Fisher LDA.
Associating different classifiers to improve their
stabilities can be a quiet interesting point to focus on
in our future works as combining the neural
networks classifier with the ones based on the
Patrick-Fischer distance or the CART algorithm.
REFERENCES
Breiman, L., 1996. Bagging predictors, Machine learning,
vol. 24, no. 2, pp. 123-140.
Drira, W., Ghorbel, F., 2012. An estimator of the L-2-
probabilistic dependence measure for vectorial
reduction dimension. Multiclass case, Traitement du
Signal, 29(1-2), 143-155.
Fukunaga, K., 1990. Introduction to Statistical Pattern
Recognition, Academic Press, 2nd edition.
Ghorbel, F., LT, J., 1990. Automatic control of
lamellibranch larva growth using contour invariant
feature extraction. Pattern Recognition.
Othman, I.B., Ghorbel, F., 2013. The Use of the Modified
Semi-bounded Plug-in Algorithm to Compare Neural
and Bayesian Classifiers Stability, Neural Networks
and Fuzzy Systems.
Paliwal, M., Kumar, U. A., 2009. Neural networks and
statistical techniques: A review of applications,
Expert Syst. Appl., vol. 36, no. 1, pp. 2–17.
Patuwo, W., Hu, M.Y., Hung, M.S., 1993. Two-group
classification using neural networks, Decision
Sciences, vol. 24, pp. 825–845.
Saoudi, S., Ghorbel, F., Hillion, A., 1994. Nonparametric
probability density function estimation on a bounded
ComparisonofStatisticalandArtificialNeuralNetworksClassifiersbyAdjustedNonParametricProbabilityDensity
FunctionEstimate
677

support: applications to shape classification and
speech coding, Applied Stochastic Models and Data
Analysis Journal, vol. 10, no. 3, pp. 215–231.
Saoudi, S., Troudi, M., Ghorbel, F., 2009. An iterative
soft bit error rate estimation of any digital
communication systems using a non parametric
probability density function, Eurasip Journal on
wirless Communications and Networking.
Steven, K., Rogers, Kabrisky, M., 1991. An Introduction
to Biological and Artificial Neural Networks for
Pattern Recognition, SPIE Optical Engineering Press,
vol. 4.
Tam, K.Y., Kiang, M.Y., 1992. Managerial applications
of neural networks: The case of bank failure
predictions, Management Science, vol. 38, no. 7, pp.
926–947.
yann.lecun.com/exdb/mnist/.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
678
