
Low Level Statistical Models for Initialization of Interactive 2D/3D
Segmentation Algorithms
Jan Kolomazn
´
ık, Jan Hor
´
a
ˇ
cek and Josef Pelik
´
an
Department of Software and Computer Science Education, Faculty of Mathematics and Physics,
Charles University in Prague, Prague, Czech Republic
Keywords:
Statistical Models, Interactive Segmentation, Active Contours, Graph-cuts.
Abstract:
In this paper we present two models which are suitable for interactive segmentation algorithms to decrease
amount of user work. Models are used during initialization step and do not increase complexity of segmen-
tation algorithms. Model describe spatial distribution of image values and classification as either foreground
or background. Second part of the model is vector field which constrains direction of boundary normals.
We show how to use these models in parametric snakes/surfaces framework and minimal graph-cut based
segmentation.
1 INTRODUCTION
Image segmentation is one of the most essential prob-
lems in the field of computer vision. Although this
topic has been extensively studied, common seg-
mentation algorithms often serve as a preprocessing
method of other algorithms. Automatic segmentation
can hardly obtain satisfied results without high level
knowledge of interest object (Heimann and Meinzer,
2009; Cremers et al., 2007; Leventon et al., 2002; Yue
and Tagare, 2009).
In medical imaging is often the situation compli-
cated by the fact that we often need to segment or-
gan affected by certain pathologies (tumors, deforma-
tions, scar tissue), which are hard to model due to
their unpredictability.
Also, methods suitable for automatic segmenta-
tion tend to be time consuming especially when deal-
ing with low quality input (low resolution, noise,
scanning artifacts, etc.).
Besides automatic and semi-automatic methods
variety of fast interactive methods (Zhao and Xie,
2013) were published. User provides information
about segmented object in form of constrains, seeds
or similar mechanism. By evaluation of the segmen-
tation output user can improve the result by updating
input interactively. Session ends when object is seg-
mented with desired precision.
Main disadvantage of the interactive segmentation
algorithm is the amount of work user must do to get
satisfying results, particularly for 3D volume segmen-
tation.
We tried to address these issues by designing low
level statistical models, which can provide most of the
required input information and user can focus on the
most problematic (blurred, damaged) parts of the seg-
mented object.
We call these models low level because they do
not describe complex properties and relations to sur-
rounding objects like other sophisticated but slow
methods (Tsai et al., 2003), (Okada et al., 2008).
We chose presented models with these properties
in mind:
• Easily embedable into various segmentation algo-
rithms.
• Low computational complexity.
• Applicable during preprocessing step.
We ended up using two models. One describing
spatial distribution of intensity values and the other
directions of possible contour normals.
These models were embedded and tested in two
segmentation frameworks. As energy minimization
problem in parametric snakes/surfaces (Jacob et al.,
2001) and in minimal graph-cut based segmentation
(Boykov and Jolly, 2001; Yi and Moon, 2012; Kolo-
maznik et al., 2012).
686
Kolomazník J., Horá
ˇ
cek J. and Pelikán J..
Low Level Statistical Models for Initialization of Interactive 2D/3D Segmentation Algorithms.
DOI: 10.5220/0005361506860692
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 686-692
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

2 INTENSITY DISTRIBUTION
2.1 Formulation
We model spatial intensity distribution of seg-
mented object (foreground) and its surroundings
(background). Model provides two probabilities for
pixel/voxel on position x of intesity I(x) being in-
side the segmented region (R
in
) resp. outside the seg-
mented region (R
out
).
P
in
(I(x),x) = P(I(x) ∧ x ∈ R
in
)
P
out
(I(x),x) = P(I(x) ∧ x ∈ R
out
) (1)
In special case when foreground/background in-
tensities are independent of position (homogeneous
object on homogeneous background) we can use ba-
sic properties of conditional probability and get these
equations:
P(I(x) ∧ x ∈ R
in
) = P(I(x)|x ∈ R
in
) · P(x ∈ R
in
)
P(I(x) ∧ x ∈ R
out
) = P(I(x)|x ∈ R
out
) · P(x ∈ R
out
) (2)
In (Jacob et al., 2001) authors used energy term
E
original
E
original
=
ˆ
S
in
−log
P(I(x)|x ∈ R
in
)
P(I(x)|x ∈ R
out
)
dx(3)
It relates probability of point being inside seg-
mented region (R
in
) having some intensity value and
probability of being outside (R
out
) with actual inten-
sity value. This energy term reaches its minimum
when regions S
in
(intermediate segmentation result)
and R
in
are the same. It works well if we are trying to
select object of homogeneous intensity on homoge-
neous background. Segmentation driven by this en-
ergy often fail if there is an area with similar intensity
as the segmented object, because there are no spatial
constrains (if not introduced in another way).
We decided to extend this model by spatial in-
formation and use 3-dimensional (2D segmentation)
or 4-dimensional (3D segmentation) probability dis-
tribution function instead of 1-dimensional from the
original term. So we propose formulation (4).
E
region
=
ˆ
S
in
−log
P
in
(I(x),x)
P
out
(I(x),x)
dx (4)
E
region
=
ˆ
S
in
−log
P(I(x) ∧ x ∈ R
in
)
P(I(x) ∧ x ∈ R
out
)
dx (5)
In cases when we can assume independence of in-
tensity and position (homogeneous regions), we can
use equations 2 Using this and the fact that logarithm
of a product is sum of logarithms we get simplified
version of the energy term.
E
region2
= −
ˆ
S
in
log
P(I(x)|x ∈ R
in
)
P(I(x)|x ∈ R
out
)
+
+log
P(x ∈ R
in
)
P(x ∈ R
out
)
dx (6)
When intesity and position are independent
E
region2
equals E
region
. First term is same as E
original
and the second term is based only on spatial distri-
bution. Second term was used for example in (Jacob
et al., 2001) as constrain energy, defined by user or
trained from samples. We can introduce another pa-
rameter α into this equation and by convex combina-
tion of these two models we can influence behavior of
segmentation process.
E
region3
= −
ˆ
S
in
α · log
P(I(x)|x ∈ R
in
)
P(I(x)|x ∈ R
out
)
+
+(1 − α) · log
P(x ∈ R
in
)
P(x ∈ R
out
)
dx (7)
This simplified model works well only for homo-
geneous regions on homogeneous background due to
intensity-location independence assumption.
2.2 Training
First step is proper alignment of the images from the
training set (section 4.1). For each aligned image we
need binary mask representing segmented object.
Intensity of each image element is recorded to one
of the histograms available for its spatial coordinates.
One histogram is for P
in
probability and the second is
for the P
out
probability. Decision about which should
be used is made by the binary mask query.
These histograms tend to be sparse due to the low
number of images from training set in comparison to
the number of possible values in the intensity range.
We use Parzen window to get smooth density esti-
mation. Also, the resolution of the model is lower
than resolution of the input images to ensure spatial
smoothness of the trained model.
3 SHAPE MODEL
Previous model works quite well but still it has some
flaws. With increasing variability of data in training
set there grows larger area around segmented region,
where P
in
and P
out
are almost the same. Boundary
LowLevelStatisticalModelsforInitializationofInteractive2D/3DSegmentationAlgorithms
687

tends to fluctuate or takes the shortest path (depending
on internal and constrain energy) in these regions. So
we need some other energy, which forces boundary to
have proper shape.
3.1 Formulation
We use a vector field which tries to model behavior
of the boundary normals. The shape energy is based
on dot product of boundary normal and vector in our
field on the same position. We use curve integral in
2D and surface integral in 3D over object’s boundary.
E
shape2D
= −
˛
C
u · υ
+
dr (8)
E
shape3D
= −
‹
S
u · υ
+
dS (9)
Where u is trained vector field and υ
+
is vector
field of curve/surface unit normals oriented outwards
from segmented region.
As will be shown in section 4 it is useful to ex-
press shape energy as region integral (surface, vol-
ume) instead of integral over curve/surface. For that
we apply Divergence theorem (Green’s theorem in
2D, Gauss–Ostrogradsky theorem in 3D) on previous
equations.
E
shape2D
= −
ˆ
S
∇ · u(x,y)dxdy (10)
E
shape3D
= −
ˆ
S
∇ · u(x,y,z)dxdydz (11)
3.2 Training
We need either binary masks, or contour represen-
tation of segmented objects for each aligned image
from training set. We compute vector field containing
region normals for each dataset either by computing
normals from boundary representation or by comput-
ing normalized gradient of region binary mask. These
vector fields are too sparse and rough (those computed
as binary mask gradient). So we need to smooth them
and increase the area of influence.
For this purpose we already have mechanism in
form of Gradient Vector Flow (Xu and Prince, 1997),
(Paragios et al., 2001), which is used for image gra-
dient enhancement in snake based segmentation algo-
rithms. Parameters for diffusion depend on size of
training set and properties of segmented regions.
Now we should have set of vector fields with in-
creased support (nonzero area). We want to compute
one final vector field with following properties:
• Vectors have same direction as segmented region
boundary passing that point.
• Size of vector reflects certainty of the direction.
• Vector field should be smooth.
We try to achieve these properties by minimizing
energy functional based on GVF.
v
1
,v
2
,v
3
,... are vector fields of dimension n from
training set.
E(u) =
ˆ
Ω
−
∑
i
v
i
·u+λ
∑
i
∑
j
∂u
i
∂x
j
2
+κku−
∑
i
v
i
k
2
(12)
Our desired vector field u should minimize this
energy formulation, which consist from three parts.
First term ensures minimal direction deviation from
each training vector field. Second forces our field
to be smooth by minimizing partial derivatives and
the third term prevent divergence by trying to keep u
close to training vector field. Regularization parame-
ters λ and κ tune the tradeoff between the first, second
and third term.
Using basic properties of dot product we can sim-
plify the equation by introducing sum of training vec-
tor fields w =
∑
i
v
i
.
E(u) =
ˆ
Ω
−w · u + λ
∑
i
∑
j
∂u
i
∂x
j
2
+ κku − wk
2
(13)
u = [u
1
,u
2
,...,u
n
] where n is field dimension.
We solve this problem using set of Euler-Lagrange
equations. For i in 1,2,. . . ,n, where n is field dimen-
sion.
−w
i
+ 2κ(u
i
− w
i
) − 2λ
∑
j
∂
∂x
j
∂u
i
∂x
j
= 0
2κu
i
− (2κ + 1)w
i
− 2λ∆u
i
= 0 (14)
This can be used in steepest descent or similar op-
timization algorithm.
4 MODEL USAGE
4.1 Alignment
Quality of the trained model and its usefulness de-
pends on the proper alignment of the training images
and alignment between model and the segmented ob-
ject in the processed image.
Various approaches to this task exist (Yao and
Summers, 2009), but most of them would again
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
688
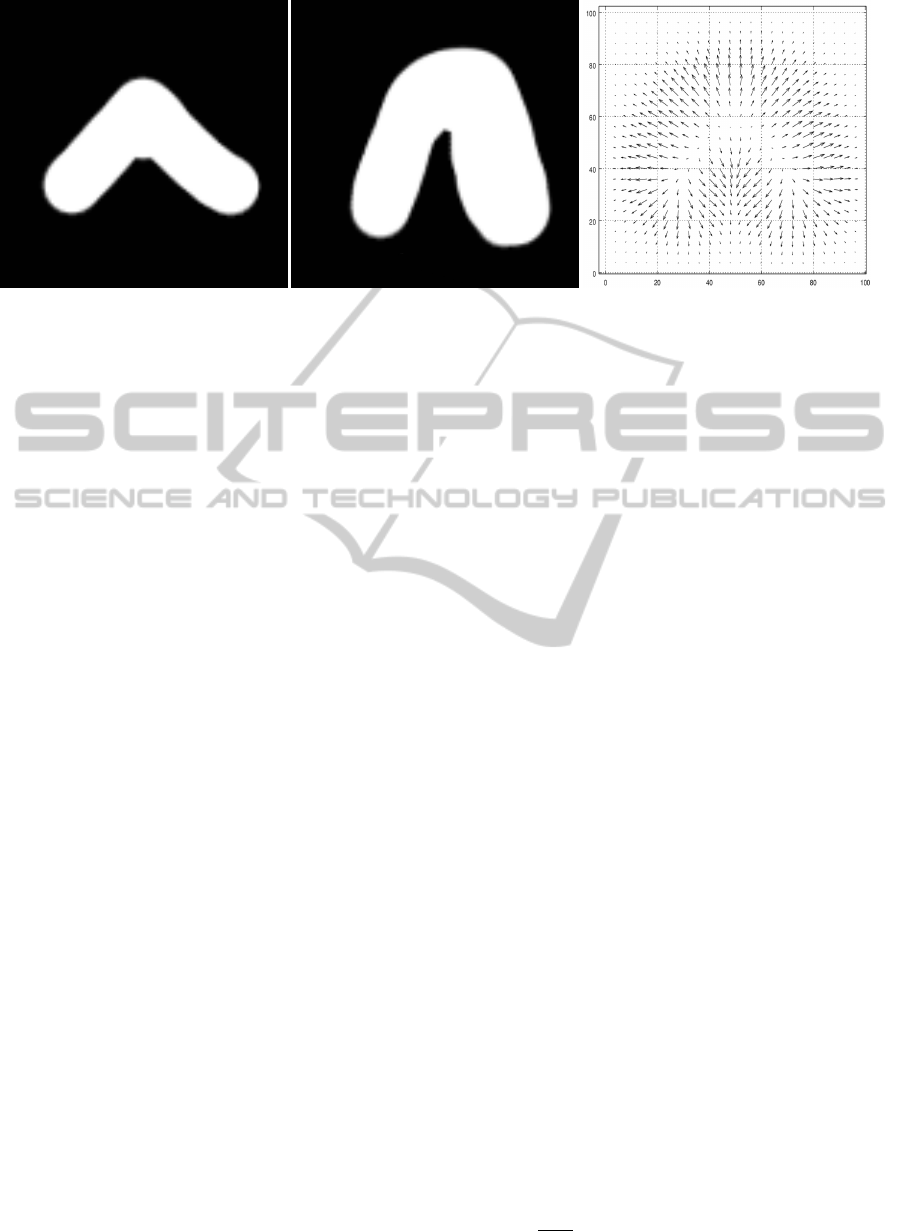
Figure 1: Two binary masks from training set and computed vector field.
increase computational complexity of the whole
pipeline. Since we design method for interactive seg-
mentation we decided to let user select important fea-
tures from which we compute the aligning transfor-
mation.
For our test case (section 5) we let the user spec-
ify extreme points (poles) of segmented kidney in
transversal slices of CT scan.
4.2 Parametric Contours/Surfaces
From wide range of segmentation methods based on
deformable models (snakes, levelsets, etc.) we used
parametric snakes/surfaces where contour is defined
as spline curve/patch and its shape is controlled by
set of control points.
In comparison to shape representation in form of
a levelset the parametric boundary representation can
be easily used only for segmentation of objects with
simple topologies. It is quite problematic to introduce
shape with holes.
Our motivation for usage of the parametric bound-
ary representation is again speed. Whole framework
is easilly paralelizable. Also, curves and surfaces ma-
nipulated by set of control points is well known con-
cept from other graphical software tools. These prop-
erties makes it good candidate for interactive segmen-
tation algorithm.
If we want to use models from previous sections in
parametric boundary segmentation it is useful to com-
pute curve/surface integral instead of surface/volume
integral (divergence theorem), which is more time
consuming. (Jacob et al., 2001) used this step to bind
all energy terms into one unified energy term. We use
the exactly same approach.
We assume that surface Φ is oriented, so normal
vectors (Φ
u
× Φ
v
)/kΦ
u
× Φ
v
k are oriented outwards.
F(x,y) and F(x, y,z) are 2D/3D unified energy terms.
ˆ
S
F(x,y)dxdy =
˛
C
(
ˆ
y
−∞
F(x,τ)dτ)dx (15)
= −
˛
C
(
ˆ
x
−∞
F(τ,y)dτ)dy(16)
ˆ
V
F(x,y,z)dxdydz =
‹
S
G
x
·dS =
‹
S
G
y
·dS =
‹
S
G
z
·dS (17)
G
x
= (
ˆ
x
−∞
F(τ,y,z)dτ,0,0) (18)
G
y
= (0,
ˆ
y
−∞
F(x,τ,z)dτ,0) (19)
G
z
= (0,0,
ˆ
z
−∞
F(x,y,τ)dτ) (20)
But for usage in optimization scheme we need
partial derivatives with respect to control parameters
(control points). We show only 3D version, 2D is spe-
cial case and was presented in (Jacob et al., 2004).
We use definition of surface integral of second
kind.
‹
S
G
x
·dS =
ˆ
u
ˆ
v
G
x
(Φ)·(Φ
u
× Φ
v
)dudv (21)
And now we show how to compute partial deriva-
tive of our equation in respect to x-coordinate of i-th
control point.
∂
∂c
i,x
ˆ
u
ˆ
v
G
x
(Φ)·(Φ
u
× Φ
v
)dudv (22)
LowLevelStatisticalModelsforInitializationofInteractive2D/3DSegmentationAlgorithms
689

=
ˆ
u
ˆ
v
∂
∂c
i,x
[G
x
(Φ)·(Φ
u
× Φ
v
)]dudv
=
ˆ
u
ˆ
v
∂
∂x
[G
x
(Φ)·(Φ
u
× Φ
v
)]
∂x
∂c
i,x
dudv
=
ˆ
u
ˆ
v
h
∂G
x
(Φ)
∂x
·(Φ
u
× Φ
v
) +
+G
x
(Φ)·
∂(Φ
u
× Φ
v
)
∂x
| {z }
=0
i
∂x
∂c
i,x
dudv
=
ˆ
u
ˆ
v
(F(Φ),0,0)· (Φ
u
× Φ
v
)
∂x
∂c
i,x
dudv
∂x(u,v)
∂c
i,x
will be often in simple form. For splines we
get basis functions.
So we obtain equation for each partial derivative
in respect to curve/surface control point, which is eas-
ily computable.
4.3 Minimal Graph-cut
Another method we used the models for is segmenta-
tion based on computing minimal graph cut (Boykov
and Jolly, 2001; Yi and Moon, 2012; Kolomaznik
et al., 2012). Each image element (pixel, voxel, subre-
gion) is represented as vertex in the constructed graph.
We also add another two special vertices (source and
sink)
Information about neighbors is integrated in form
of the edges (n-links) with weight based on image val-
ues or image gradient magnitude. All vertices in the
graph are connected to the source and sink by t-links.
User marks segmented object and background.
This information is then incorporated into the graph
in form of t-link weights.
By finding minimal graph cut we divide vertices in
two sets. One is for foreground and second for back-
ground. If user is not satisfied with the result he can
update markers (modify t-links) and run segmentation
again.
Drawing foreground/background markers can be
tedious especially in 3D. So we apply thresholding to
input image using conditions 23. So we obtain initial
markers automaticaly from the model. t
F
and t
B
are
foreground/background probability thresholds.
M(x) =
F P
in
(I(x),x) > t
F
B P
out
(I(x),x) > t
B
0 Rest
(23)
We use the second part of our model to modulate
n-link weights. Boundaries of objects tend to follow
strong edges/ridges in the input image. So it means
that contour goes through parts of the image with big
gradient magnitude and its normals at those parts have
same direction as the gradient.
We have vector field which should represent nor-
mal directions of possible boundaries, so we can boost
influence of parts of image with properly oriented gra-
dient.
G
new
(x) = G(x)
1 + α
max(0,
ˆ
G(x)·u(x))
(24)
Where G is original image gradient,
ˆ
G normalized
image gradient, u our shape model and α parameter
controlling strength of the effect.
To prevent distortion of vector field we don’t
change direction of the vector, we only modulate its
length. We do not shorten vectors. We only elon-
gate those with proper direction. Example of gradient
modulation in figure 2.
5 RESULTS
Presented models are aimed for initialization of inter-
active segmentation algorithms. So the quality the re-
sult also depends on user input. To rule out influence
of the user input we implemented two tests, which
work without user input.
First one was modified thresholding, where
aligned model serves as classifier. We counted how
many voxels were properly tagged, number of false
positives and false negatives. We express these val-
ues relatively to object volume obtained from manual
segmentation.
As a second method we used parametric snakes
based on our model and term which attracts contour
to areas with bigger gradient magnitude. Error was
again expressed as a percentage of whole object vol-
ume.
In tables 1 and 2 are results of left kidney segmen-
tation in CT images (with and without contrast agent
– model trained for each case separatelly).
Measured errors show that our models work pre-
cise initialization in almost all cases – degenerated or
damaged organs (patients 2 and 16) aren’t covered by
models.
6 CONCLUSIONS
We introduce low level statistical models which suc-
cessfully address inititialization problem of interac-
tive segmentation algorithms for class of compact ob-
jects.
Presented models describe only few certain prop-
erties of the segmented objects, but not their topology
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
690
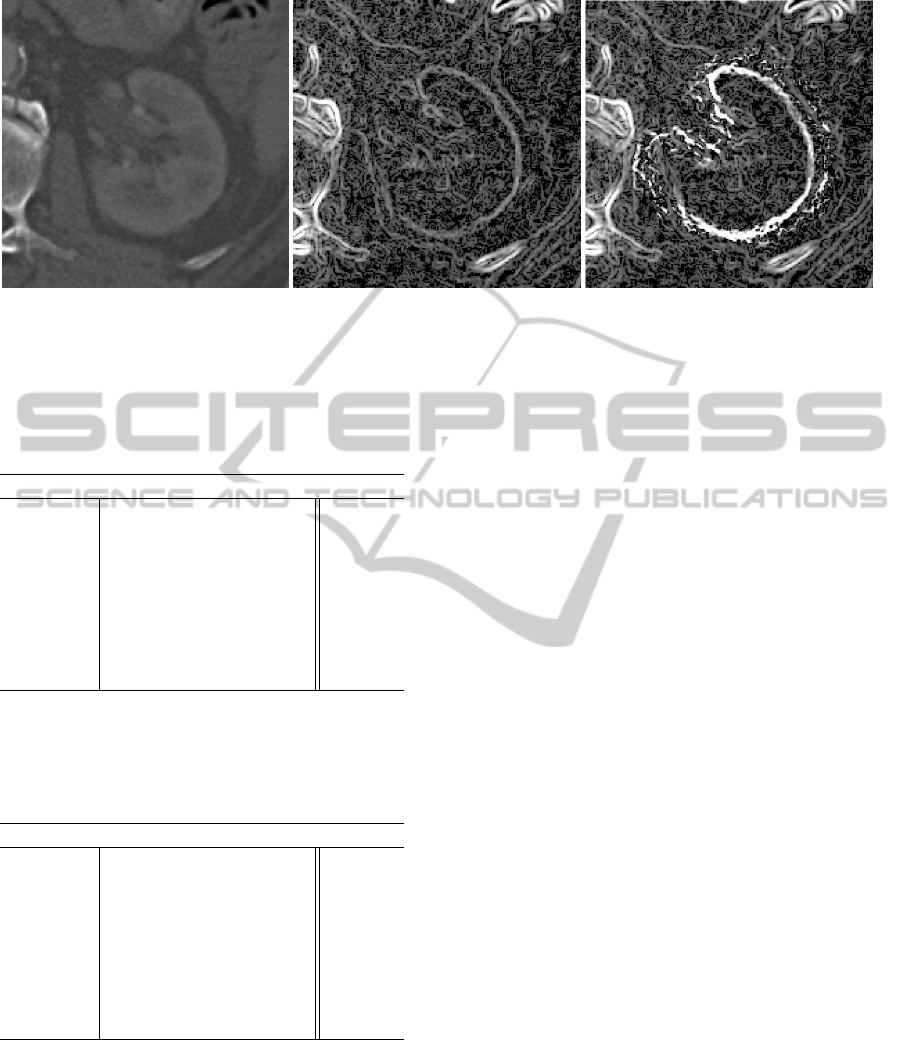
Figure 2: a) Human kidney image - part of abdominal CT scan b) Gradient magnitude c) Modulated gradient magnitude.
Table 1: Left kidney (post-contrast): Correct – part of organ
volume correctly classified; E
out
– false positive; E
in
– false
negative; E
snakes
error of snake based segmentation (false
positive and negative)
patientID Correct E
out
E
in
E
snakes
1 88,9% 8.6% 11.0% 7.1%
2 70.0% 6.0% 30.0% 26.3%
3 96.6% 13.0% 3.3% 6.2%
4 91.5% 4.5% 8.5% 1.6%
5 91.9% 3.5% 8.0% 1.9%
6 65.2% 9.5% 34.8% 4.2%
7 84.0% 2.4% 15.9% 10.3%
8 89.1% 2.2% 10.9% 5.4%
Table 2: Left kidney (without contrast agent): Correct –
part of organ volume correctly classified; E
out
– false posi-
tive; E
in
– false negative; E
snakes
error of snake based seg-
mentation (false positive and negative)
patientID Correct E
out
E
in
E
snakes
9 84.5% 6.4% 15.4% 2.2%
10 91.5% 29.3% 8.5% 20.6%
11 89.5% 3.6% 10.5% 1.0%
12 92.8% 11.1% 7.1% 10.4%
13 93.4% 17.4% 6.6% 17.2%
14 71.7% 2.3% 28.3% 9.4%
15 91.4% 2.8% 8.6% 0.2%
16 61.8% 3.7% 38.2% 2.6%
or shape variability. This leaves us with very rough
initialization in case of complicated objects or objects
with big shape variability. But even in this case we
decrease amount of user labor needed for initializa-
tion of the full-fledged segmentation algorithm which
follows.
REFERENCES
Boykov, Y. and Jolly, M.-P. (2001). Interactive graph cuts
for optimal boundary amp; region segmentation of ob-
jects in n-d images. In Computer Vision, 2001. ICCV
2001. Proceedings. Eighth IEEE International Con-
ference on, volume 1, pages 105–112 vol.1.
Cremers, D., Rousson, M., and Deriche, R. (2007). A re-
view of statistical approaches to level set segmenta-
tion: Integrating color, texture, motion and shape. In-
ternational Journal of Computer Vision, 72:215.
Heimann, T. and Meinzer, H.-P. (2009). Statistical shape
models for 3d medical image segmentation: A review.
Medical Image Analysis, 13(4):543 – 563.
Jacob, M., Blu, T., and Unser, M. (2001). A unifying ap-
proach and interface for spline-based snakes. In in
Proc. SPIE Med. Imaging, l. 4322, pages 340–347.
Jacob, M., Blu, T., and Unser, M. (2004). Efficient Energies
and Algorithms for Parametric Snakes. IEEE Trans-
actions on Image Processing, 13(9):1231–1244.
Kolomaznik, J., Horacek, J., Krajicek, V., and Pelikan, J.
(2012). Implementing interactive 3d segmentation on
cuda using graph-cuts and watershed transformation.
International Conferences in Central Europe on Com-
puter Graphics, Visualization and Computer Vision.
Leventon, M., Grimson, W., and Faugeras, O. (2002). Sta-
tistical shape influence in geodesic active contours. In
Biomedical Imaging, 2002. 5th IEEE EMBS Interna-
tional Summer School on, page 8 pp.
Okada, T., Yokota, K., Hori, M., Nakamoto, M., Nakamura,
H., and Sato, Y. (2008). Construction of hierarchi-
cal multi-organ statistical atlases and their application
to multi-organ segmentation from ct images. In Pro-
ceedings of the 11th international conference on Med-
ical Image Computing and Computer-Assisted Inter-
vention - Part I, MICCAI ’08, pages 502–509, Berlin,
Heidelberg. Springer-Verlag.
Paragios, N., Mellina-Gottardo, O., and Ramesh, V. (2001).
Gradient vector flow fast geodesic active contours.
In Computer Vision, 2001. ICCV 2001. Proceedings.
Eighth IEEE International Conference on, volume 1,
pages 67 –73 vol.1.
LowLevelStatisticalModelsforInitializationofInteractive2D/3DSegmentationAlgorithms
691

Tsai, A., Yezzi, A., Wells, W., Tempany, C., Tucker, D.,
Fan, A., Grimson, W. E., and Willsky, A. (2003). A
shape-based approach to the segmentation of medical
imagery using level sets. IEEE transactions on medi-
cal imaging, 22(2):137–154.
Xu, C. and Prince, J. L. (1997). Gradient vector flow: A
new external force for snakes. In IEEE Proc. Conf.
On, pages 66–71.
Yao, J. and Summers, R. (2009). Statistical location model
for abdominal organ localization. In Yang, G.-Z.,
Hawkes, D., Rueckert, D., Noble, A., and Taylor,
C., editors, Medical Image Computing and Computer-
Assisted Intervention - MICCAI 2009, volume 5762
of Lecture Notes in Computer Science, pages 9–17.
Springer Berlin, Heidelberg.
Yi, F. and Moon, I. (2012). Image segmentation: A survey
of graph-cut methods. In International Conference on
Systems and Informatics.
Yue, Y. and Tagare, H. (2009). Learning to segment us-
ing machine-learned penalized logistic models. 2012
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition Workshops, 0:58–65.
Zhao, F. and Xie, X. (2013). An overview of interactive
medical image segmentation. Annals of the BMVA,
2013(7):1–22.
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
692
