
SymPaD: Symbolic Patch Descriptor
Sinem Aslan
1
, Ceyhun Burak Akgül
2
, Bülent Sankur
2
and E.Turhan Tunalı
3
1
International Computer Institute, Ege University, Bornova, Izmir, Turkey
2
Electrical & Electronics Engineering Department, Boğaziçi University, Bebek, İstanbul, Turkey
3
Department of Computer Engineering, Izmir University of Economics, Balçova, İzmir, Turkey
Keywords: Image Feature, Model-driven Visual Dictionary, Primitive Structures of Natural Images, Object Recognition,
Image Understanding.
Abstract: We propose a new local image descriptor named SymPaD for image understanding. SymPaD is a probability
vector associated with a given image pixel and represents the attachment of the pixel to a previously designed
shape repertoire. As such the approach is model-driven. The SymPad descriptor is illumination and rotation
invariant, and extremely flexible on extending the repertoire with any parametrically generated geometrical
shapes and any desired additional transformation types.
1 INTRODUCTION
The origins of research on qualitative image
structures date back to Marr (Marr, 1982) in 1980’s.
In his three-step representation framework, Marr
described primal sketch of images qualitatively in
terms of the feature categories of edges, lines and
blobs based on the quantitative responses of linear
filters (Marr, 1982). Marr’s scheme was further
improved by (Koenderink, 1984) so that the
localization of detected edges is estimated on the
points of highest gradient rather than simply near
them. (Griffin, 2007) extended the idea in 2000’s by
using 1
st
order, 2
nd
order and 1
st
and 2
nd
order filters
with which a wider range of image symmetries can be
probed compared to Marr’s “edge”, “line”, “blob”
feature sets. This set of approaches leads to the
paradigm of model-guided shape dictionaries to
describe images via pixel neighbourhoods.
The alternative paradigm in classifying and
categorizing images or recognizing objects in images
via local features uses data-driven dictionaries. As a
case in point, SIFT (Lowe, 1999) or HOG (Dalal and
Triggs, 2005) features represent local image
structures based on the magnitude and orientation of
gradients at pixel locations. A visual dictionary is
then constructed typically by the k-means clustering
algorithm (Csurka et. al, 2004).
Both approaches have their own advantages and
disadvantages. In the data-driven scheme, which is
presently by far more popular in the literature, one
learns the descriptor prototypes statistically from
local image descriptors computed on a training set of
image patches. This entails some dependency on the
training dataset, hence might limit generalizability
and there may be some loss of accuracy due to the
clustering algorithm chosen (Jurie and Triggs, 2005).
In contrast, model-driven approaches do not need an
elaborate training step to learn a visual dictionary.
The dictionary is created based on variations of shape
models such as ramps, ridges, valleys, corners, lines,
spots, and their various combinations. In this study,
we pursue the model-driven framework to generate
new descriptors that would best capture the image
characteristics in a database-independent manner.
Basic Image Features (BIFs) proposed by (Crosier
and Griffin, 2010) is the most current model-driven
dictionary construction study in the literature. It is
based on determining image symmetries by using re-
parameterized derivatives of gradient filters (DtG).
The method is invariant to some geometric
transformations such as rotation, reflection, and some
grayscale transformations such as intensity
multiplications and addition of a constant intensity
(Griffin and Lillholm, 2007). They re-parameterize
the jet space of DtG filters, called 2
nd
order local
image structure solid, which they partition into
Voronoi-like regions in order to obtain seven feature
categories corresponding to the symmetries of “flat”,
“ramp”, “dark/light line”, “dark/light circle”,
“saddle” patches on natural images.
BIF features tested on texture classification
266
Aslan S., Akgül C., Sankur B. and Tunalı T..
SymPaD: Symbolic Patch Descriptor.
DOI: 10.5220/0005361802660271
In Proceedings of the 10th International Conference on Computer Vision Theory and Applications (VISAPP-2015), pages 266-271
ISBN: 978-989-758-089-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

(Crosier and Griffin, 2010), object recognition
(Lillholm and Griffin, 2008), handwriting recognition
(Newell and Griffin, 2014) with a bag of words
implementation yield modest performance. (Crosier
and Griffin, 2010) then introduce a multi-scale
version of with BIFs and achieve state-of-the-art
performance competing with the data-driven
schemes.
Our proposed Symbolic Patch Descriptor
(SymPaD) uses a shape repertoire, as detailed in the
sequel, based on patch shapes described by
sigmoidals of polynomials and some transcendental
functions. Pixels are then characterized by their
posterior probability vector to belong to the members
of the shape repertoire. The probability vectors from
all pixels of an image are then accumulated into a
frequency vector, in much the same way as the Bag-
of-Words approach. The advantages of SymPaD can
be summarized as follows:
The model driven approach makes SymPaD a
dataset independent tool bypassing the
computational step required by clustering-
based dictionary construction methods.
SymPaD is illumination invariant as we use the
BRIEF features (Calonder, et. al, 2010), that
essentially encode the signs of local image
derivatives. Furthermore robustness against
rotation and scaling is obtained by
accomodating the prototypical shapes in an
adequate number of orientations and scales.
The repertoire of patch shapes can be enriched
by incorporating different parametric functions
and/or by considering their linear and nonlinear
combinations.
At the first section of the paper, we define the
main components of the framework of proposed
descriptor SymPaD. We present the performance of
the SymPaD for an object recognition application and
compare it with state of the art at the second section.
Finally we address the conclusion and the future
work.
2 SymPaD FRAMEWORK
The SymPaD framework consists of three
computational components: (i) Generation of the
Primitive Shape Library (PSL), in other words, the
model-driven dictionary, (ii) Posterior computation
module in which we compute the SymPaD vectors on
dense image points, and (iii) Pooling module in which
we construct the final descriptor or code vector for the
input image. The block diagram of the system is given
Figure 1: SymPaD framework.
in Figure 1 and the pooling module is illustrated in
Figure 2.
2.1 Primitive Shape Library (PSL)
The primitive shape library contains a variety of
shape appearances generated by input functions in
Table 1, which are fed into the standard logistic
function shown in Eq. 1.
,
1
1
,
(1)
In a preliminary proof of concept study (Aslan, et. al,
2014), we experimented with a limited set of the
dictionary (functions
to
).
If the primitive shape structure of a natural image
is probed in patches of characteristic size, it would
mostly appear as step edges in various orientations
and scales (Griffin et. al, 2004) or as flat regions
However, if an image is probed in constant size
patches, the primitive local structure can have
appearances in different forms, such as combinations
of oriented, translated or scaled step edges, circular or
elliptical pits or hills, ridges corners, saddles, three
step edges etc. all at different orientations and scales.
We use sigmoidal outputs of the chosen ,
shape functions, as in Table 1, in order to add one
more control parameter, , that adjust the steepness
of the shapes. An alternative monotonically
increasing function generating sigmoidal curves is
hyperbolic tangent function, whose outcome is
symmetric around the origin. While this symmetry
behaviour has some advantages for the neural
networks, (LeCun et. al, 2012), in our case this is not
relevant.
To achieve invariance against rotation and scaling
effects, each sized prototypical shape is
generated in an adequate number of orientations and
scales. The orientations are created by the
SymPaD:SymbolicPatchDescriptor
267

Table 1: Parametric patch generators (
,
denote the
rotated versions of and with angle , a is the minor and
b is the major axes of the elliptic shape).
Generator function Appearance
,
,
,
,
,
,
,
/
/
,
/
/
,
,
,
,
,
,
,
,
,
,
,
,
cos
2
⁄
,
cos
parameter as in Table 1; the scales are controlled by
the parameter in Eq. 1. In addition, elliptical
trenches and ridges have the eccentricity parameter.
To generate patch varieties, we randomly sample the
,
plane with instances for every PSL class.
2.2 Posterior Computation Module
We characterize each patch (test or prototype)
by its BRIEF feature vector with length
256
using a sampling geometry of (Calonder et. al, 2010)
that corresponds to random point locations drawn
from the uniform distribution.
BRIEF features
for a patch centered on a pixel
are computed densely on the image, that is, on every
pixel of the image. Similarly, BRIEF features
,
,…,
of the PSL patches
,
,…,
are
precomputed where , is the number of
scale and orientation varieties for a shape as in Table
1 that construct the class of that particular shape and
is the number of words in the dictionary or number
of functions in Table 1 taking place in PSL
generation.
When the BRIEF feature
of a test image patch
is given, we estimate its class posterior probability
among
,
,…,
by counting votes among the
-nearest neighbours (1). We execute the
linear -NN search with FLANN library (Muja and
Lowe, 2012) using Hamming distance. For each test
patch , let the
, 1,⋯, be the nearest
neighbour class occurrences. Then the patch posterior
probability is computed by Eq. 2 where ∈
1,2…,
,
,
1 if , and 0otherwise.
|
,
∑
,
(2)
2.3 Pooling Module
In Section 2.2, the image has been converted into a D-
band image where each pixel is represented by the jet
of the estimated posterior probabilities. We examined
two types of pooling methods, one with max pooling
rule, where we assign the label of maximum
posteriori of
|
to the pixel p as in Eq. 3:
if argmax
,,…,
|
(3)
An image is then represented by the histogram of
pixels
consisting of number of bins. The other
scheme does not discard the probability estimates in
the second, third ranking decisions. Instead, we build
a separate histograms for each of ranks, where the
first histogram is as in the max pooling case; the
histogram is considers label assignments at the
rank among the labels resulting in the K-NN
scheme. Here . The pooling process of
posterior jets is illustrated in Figure 2.
3 EXPERIMENTS
We examined the proposed descriptor on the COIL-
20 “processed” corpus, which contains 20 object
categories with a pose interval of 5 degrees between
72 images of 128128 pixels in each category. For
the test setup, we tried two scenarios: (i) in
coil20_rand, we randomly select 6, 12 and 24 images
from each object category for training, and use the
remaining ones for testing and repeat the whole
process ten times, (ii) in coil20_seq, for the training
set, we chose images with the pose interval of 15
degrees for coil20_seq_tr24, 30 degrees for
coil20_seq_tr12, and 60 degrees for coil20_seq_tr6
sequentially and throw the remaining ones into the
test set for each object category, this scheme was also
used in (Shekar, et. al, 2013). We also compare the
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
268

accuracy of SymPaD with the conventional
clustering-based dictionary construction method
using dense SIFT features with the default stride
parameter in (Law et. al, 2014) and with equal
number of visual words in the dictionary used in
SymPaD. Since we are interested in the performance
of the descriptor, we did not use an advanced
classifier but a simple K-nearest neighbour classifier
using chi-square distance with 5-fold cross validation
to accomplish object recognition.
First we used the visual dictionary in (Aslan, et.
al, 2014) that consists of eight shape classes that are
generated by input functions
to
in Table 1 into
the sigmoid function in Eq. 1. Then the whole process
is repeated for the extended dictionary created by
using the whole set of functions
to
Since the
Flat label is assigned mostly to the (background
region in images, we can exclude it during the coding
to exploit the effect of structural regions arising from
the foreground object. Hence, we also considered the
without flat scheme by omitting the effect of the PSL
class generated by
function.
We generated 50 number of 1515 sized
gray-level patches of varying orientation and
coarseness level for each of the PSL classes. Since
the higher values of represents the characteristics
of uniform distribution better, more transformational
variations could be simulated by generating a higher
number of patches in a PSL class. 20, 50,
100 are examined and we observed that the
decision of should be given by considering the
pooling method used, that is, in hard assignment
based pooling higher performs better than the lower
ones, however in soft-assignment based pooling
performance of both gets similar. This is not a big
surprise that, since we exploit the uncertainty of pixel
labels on the image pixels about their affiliation to the
PSL classes by soft assignment, the performance
improves.
Orientation: Since the shapes generated by the
functions
,
and
exhibit rotational symmetry,
we do not assign orientation to them, ramp-like
structures generated by the functions
,
,
,
,
and
has the orientation range of
0,2
, and the
remaining ones has the orientation range of
0,
. So,
for each shape class we randomly sample number
of orientation values drawn from uniform distribution
in each function’s orientation range in order to be able
to represent every possible orientation of a form in its
own class.
Transition rate: Since we want an approximately
uniformly distributed appearances of coarseness
levels for a particular shape, we sampled the values
of α from exponential distribution with pdf in Eq. 4,
with mean of µ, and we shift the sampled values by a
constant τ to prevent collapse on the coarsest and
finest levels.
1
exp
∈0,∞
0
(4)
The values of
μ,
that we used for the functions
with degree of (i)1 are (µ=0.3, τ = 0.3), (ii) 2 are (µ
in [0.004,0.1], τ =0.04), (iii) 3 are (µ in [0.01,0.02], τ
= 0.01), (iv)4 are (µ=0.0035, τ = 0.0008), and (v) for
the exponential functions (µ in [0.15,0.3], τ =0.15)
and (vi) transcendental functions (µ=0.3, τ = 0.3).
Figure 2: Pooling scheme of SymPaD framework for a sized input image.
SymPaD:SymbolicPatchDescriptor
269
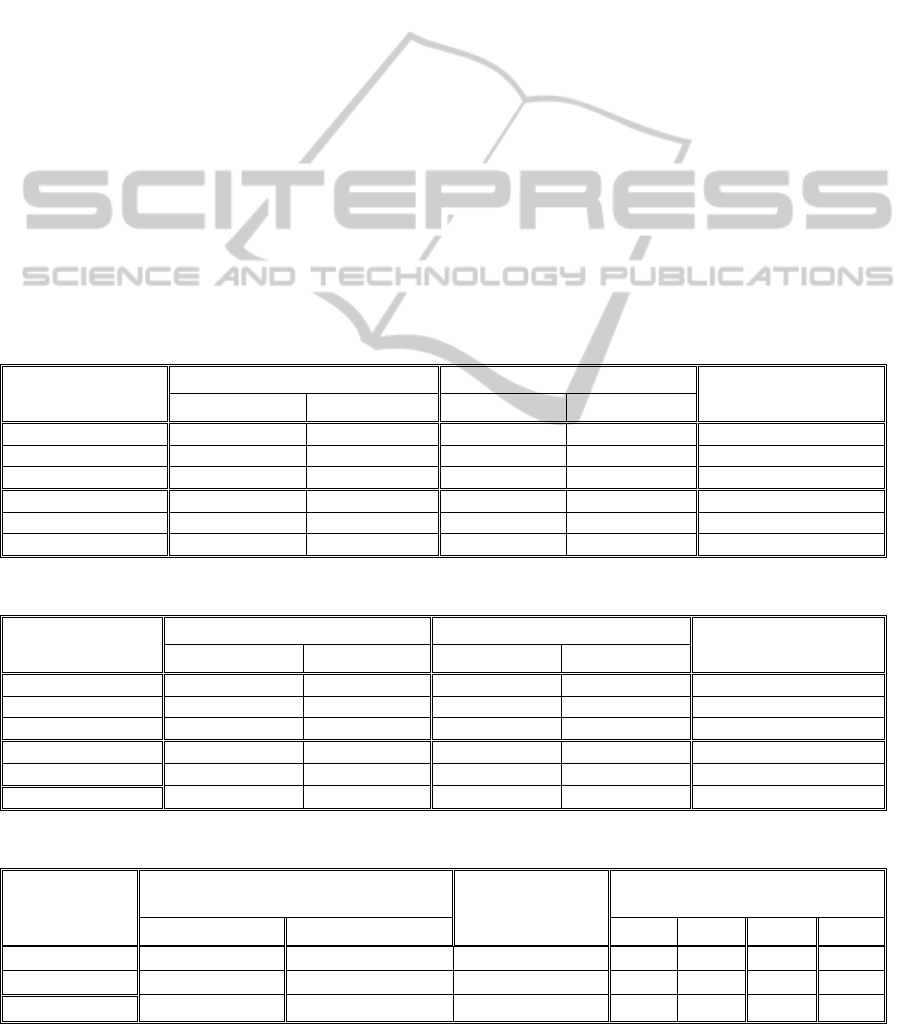
The performance results obtained with the
dictionary of eight words (of functions
to
) are
given in Table 2 and 21 words (of functions
to
)
are given in Table 3. We also present the results of
(Shekar, et. al, 2013) which used the same test setup
on COIL20 in Table 4. Some outcomes of the tests
are:
SymPaD performs best in every test setup,
when soft assignment based encoding with
rank 4 was used. We could also outperform the
results given in (Shekar, et. al, 2013).
For 8 hard assignment based encoding,
withFlat is slightly better than withoutFlat
scheme. However, when 21 is used, the
situation becomes reversed, probably because
when 21 is used, classes except Flat
becomes more descriptive compared to the
same case when 8 is used
Soft-assignment based encoding improves
performance whether Flat was included or not.
The amount of improvement is higher for
8 than 21 which can be interpreted as, for
the low dimensional dictionaries soft
assignment based encoding has a more vital
role.
Both methods, SymPaD and conventional
Dense SIFT + BoW, exhibited performance
achievements when the training set was
designed with sequentially selected images of
each category, however, when the smaller sized
dictionary was used, amount of improvement
acquired by conventional method was higher
than the amount of improvement acquired by
SymPaD, that shows robustness of SymPaD for
the test setup designed by random elements.
The larger dictionary provided improvement
when hard assignment based encoding was
used, but it did not have a significant effect
when soft assignment based encoding was
used.
4 CONCLUSIONS
In this study, we propose a new descriptor, generated
by a model-driven framework. Since model-driven
Table 2: Recognition performance. (D = 8, HA: Hard Assignment, SA: Soft Assignment).
Test SymPaD, withFlat SymPaD, withoutFlat Dense SIFT + BoW
HA SA_Rank(1:4) HA SA_Rank(1:4)
coil20_rand_tr6 78.84 ± 1.72 85.86 ± 1.01 77.15 ± 2.71
87.55 ± 2.50
77.58 ± 1.27
coil20_rand_tr12 86.81 ± 1.46 92.66 ± 1.36 84.28 ± 3.55
94.36 ± 1.05
85.04 ± 1.03
coil20_rand_tr24 92.35 ± 0.73 96.72 ± 0.80 91.86 ± 0.62
98.42 ± 0.62
90.91 ± 1.24
coil20_seq_tr6 79.39 85.61 80.38
90.91
79.92
coil20_seq_tr12 89.83 95.42 89.17
97.00
89.92
coil20_seq_tr24 93.65 97.71 94.58
99.38
95.00
Table 3: Recognition performance. (D=21, HA: Hard Assignment, SA: Soft Assignment).
Test SymPaD, withFlat SymPaD, withoutFlat Dense SIFT + BoW
HA SA_Rank(1:4) HA SA_Rank(1:4)
coil20_rand_tr6 82.69 ± 1.96 85.27 ± 1.93 83.65 ± 1.92
84.37 ± 2.13
83.06 ± 1.87
coil20_rand_tr12 90.81 ± 1.39 92.54 ± 1.00 92.19 ± 1.16
92.97 ± 1.11
90.25 ± 1.17
coil20_rand_tr24 95.77 ± 0.72 96.94 ± 0.48 97.22 ± 0.56
97.66 ± 0.45
95.39 ± 0.99
coil20_seq_tr6 85.83 88.56 87.65
89.39
86.66
coil20_seq_tr12 94.5 95.83 94.92
96.25
95.00
coil20_seq_tr24 97.29 97.71 98.65
98.96
98.54
Table 4: Overall comparison.
Test SymPaD, Without Flat,
SA_Rank(1:4)
Dense SIFT +
BoW
Results in
(Shekar, et. al,
2013)
D = 8 D = 21 KID SIFT SURF ORB
coil20_seq_tr6
90.91
89.39 86.66
86.97 84.47 48.94 81.81
coil20_seq_tr12
97.00
96.25 95.00
96.67 93.42 72.00 92.25
coil20_seq_tr24
99.38
98.96 98.54
98.75 96.56 83.33 95.73
VISAPP2015-InternationalConferenceonComputerVisionTheoryandApplications
270

approaches do not need to be tuned for databases of
different image understanding applications, we
believe that a carefully designed system would be a
solution for generalizability. We worked in single
scale in this study and it is a fact that some of the PSL
shape structures such as circulars or ellipticals, or the
star shape generated by
and
could only be met
explicitly at some particular scales. Hence, as a future
work, we intend to examine the method in multiscale.
Moreover, we plan to extend the dictionary by (i)
judiciously quantizing the shape parameter space to
generate the shape varieties, (ii) deriving new shape
classes by various combinations of the current shape
classes that would be filtered by a feature selection
method. Finally, we need to consider the localization
of the descriptors on the image in a more accurate
coding scheme. SymPaD will also be examined in
various databases as a future work.
REFERENCES
Marr, D., 1982. Vision: A computational investigation into
the human representation and processing of visual
information, Henry Holt and Co. Inc., New York, NY,
2-46.
Koenderink, J. J., 1984. The structure of images. Biological
cybernetics, 50(5), 363-370.
Griffin, L. D., 2007. The second order local-image-
structure solid. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, 29(8), 1355-1366.
Lowe, D. G., 1999. Object recognition from local scale-
invariant features. In 7th IEEE international conference
on Computer vision, Vol. 2, pp. 1150-1157.
Dalal, N., and Triggs, B., 2005. Histograms of oriented
gradients for human detection. In IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition, (Vol. 1, pp. 886-893).
Csurka, G., Dance, C., Fan, L., Willamowski, J., and Bray,
C., 2004. Visual categorization with bags of keypoints.
In Workshop on statistical learning in computer vision,
ECCV (Vol. 1, No. 1-22, pp. 1-2).
Jurie, F., and Triggs, B., 2005. Creating efficient codebooks
for visual recognition, In 10th IEEE International
Conference on Computer Vision, (1), 604-610.
Crosier, M., and Griffin, L. D., 2010. Using basic image
features for texture classification. International Journal
of Computer Vision, 88(3), 447-460.
Griffin, L. D., and Lillholm, M., 2007. Feature category
systems for 2nd order local image structure induced by
natural image statistics and otherwise. In IS&T/SPIE
Electronic Imaging, 6492(09). International Society for
Optics and Photonics.
Lillholm, M., and Griffin, L. D., 2008. Novel image feature
alphabets for object recognition. In ICPR (pp. 1-4).
Newell, A. J., and Griffin, L. D., 2014. Writer identification
using oriented Basic Image Features and the Delta
encoding. Pattern Recognition, 47(6), 2255-2265.
Aslan, S., Akgül, C. B., and Sankur, B., 2014. Symbolic
feature detection for image understanding. In
IS&T/SPIE Electronic Imaging (pp. 902406-902406).
International Society for Optics and Photonics.
LeCun, Y. A., Bottou, L., Orr, G. B., and Müller, K. R.,
2012. Efficient backprop. In Neural networks: Tricks of
the trade (pp. 9-48). Springer Berlin Heidelberg.
Griffin, L. D., Lillholm, M., and Nielsen, M., 2004. Natural
image profiles are most likely to be step edges. Vision
Research, 44(4), 407-421.
Calonder, M., Lepetit, V., Strecha, C., and Fua, P., 2010.
Brief: Binary robust independent elementary features.
In ECCV 2010 (pp. 778-792).
Muja, M., and Lowe, D. G., 2012. Fast matching of binary
features. In 9th IEEE Conference on Computer and
Robot Vision, pp. 404-410.
Law, Marc T., Nicolas Thome, and Matthieu Cord, 2014.
Bag-of-Words Image Representation: Key Ideas and
Further Insight, Fusion in Computer Vision. Springer
International Publishing, 29-52.
Shekar, B. H., Holla, K. R., and Kumari, M. S., 2013. KID:
Kirsch Directional Features Based Image Descriptor. In
Pattern Recognition and Machine Intelligence (pp. 327-
334). Springer Berlin Heidelberg.
SymPaD:SymbolicPatchDescriptor
271
