Modeling, Analysis and Design of a Closed-loop Power Regulation

System for Multimedia Embedded Devices

Qiong Tang, Ángel M. Groba, Eduardo Juárez and César Sanz

Centro de Investigación en Tecnologías del Software y Sistemas Multimedia para la Sostenibilidad (CITSEM),

Universidad Politécnica de Madrid (UPM), Madrid, Spain

Keywords: Multimedia, Embedded, Power Consumption, Modeling, Closed-loop Regulation.

Abstract: In this paper, the plant modeling as well as the theoretical analysis and design and simulation of a closed-

loop control system for the power consumption of a hand-held multimedia embedded device are presented.

This is a first validation step for a target system in which the power consumption will be regulated based on

estimation feedback. Prior to the availability of power estimation data, actual power consumption

measurements are used to obtain a mathematical model of the controlled plant. Then, classic control-theory

methods are applied to get a closed-loop integral controller able to regulate the power consumption of a

video decoder running in an embedded development platform. The simulation results show how the system

output keeps track of the set point without average steady-state error, even in the presence of consumption

fluctuations, thus announcing promising results for the closed-loop approach to the final power regulation

system.

1 INTRODUCTION

The optimization of not only the quality of

experience (QoE) but also the energy consumption is

a necessity in present multimedia embedded and

mobile systems. For example, the wide spectrum of

usual available applications for current smart phones

make them to have quite limited operating times,

especially when they execute common video

encoding, decoding and/or presentation applications.

Furthermore, the introduction of emerging standards

such as High Efficiency Video Coding (HEVC)

(Sullivan, 2012) will probably increase this

limitation, with respect to other previous ones like

H.264/AVC (ITU-T, 2012). Since it is not

foreseeable that the density of energy stored in

lithium batteries will increase considerably in

coming years, there is an increasing effort into trying

to reduce the energy consumption of this kind of

systems from different points of view. Particularly,

we are interested in optimizing their energy

consumption in relation with applications of video

decoding. Although our research group has been

already working on these issues since several years

ago (Juárez et al., 2010; Ren et al., 2012; Ren et al.,

2013; Ren et al., 2014), we are opening now a new

research subline which aims to turn the work to a

less heuristic and more systematic approach. In this

sense, we are interested in applying the closed-loop

control theory to the aforementioned optimization

problem and, therefore, its validity and efficiency

need to be tested.

As a first step of this new proposed approach, in

this paper we present the formal and theoretical

application of classic closed-loop control techniques

to the power consumption regulation of a video

decoding application running in an embedded

multimedia platform (the plant). For this purpose,

the system should be modeled as a real-time closed-

loop control system, in which the controlled output

follows the target (set-point) signal regardless of the

influence of possible disturbance effects. This is

achieved by a controller which processes the system

error between the target and the feedback

information coming from a sensor and generates the

action signal to the plant under control. In a typical

industrial process control, the plant is normally

designed to be controlled in this way, so it normally

offers action inputs able to vary the plant output(s)

and even sensors for feeding the output values back.

This work has been supported by the Spanish Ministry o

Economy and Competitiveness under grant TEC2013-48453-

C02-2-R.

363

Tang Q., Groba Á., Juárez E. and Sanz C..

Modeling, Analysis and Design of a Closed-loop Power Regulation System for Multimedia Embedded Devices.

DOI: 10.5220/0005365603630372

In Proceedings of the 5th International Conference on Pervasive and Embedded Computing and Communication Systems (ESAE-2015), pages 363-372

ISBN: 978-989-758-084-0

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

In our case, we face the previous problem of

adapting our plant to this topology, because it is not

initially thought to be controlled in this way.

Therefore, the first milestone is to identify and setup

both an action and a feedback signal in the plant,

being clear that the controlled output will be the

power consumption. For the former, we have

identified and used the DVFS (Dynamic Voltage and

Frequency Scaling) mechanism, present in many

commercially available platforms and able to act on

the system consumption by varying the OPP

(Operating Performance Point) of the

microprocessor unit (MPU). For the later, what we

have identified is a lack of direct consumption

sensors in the majority of present commercial

embedded platforms. Hence, we have decided to

adopt an intermediate solution, which is to estimate

the power consumption from other available signals

(event counts) in the plant. This leads to a structure

like the one shown in Figure 1, which decouples the

consumption optimization infrastructure from

specific instrumentation needed to obtain actual

power measurements, thus increasing the platform

autonomy and the control-system applicability.

Figure 1: Diagram of a closed-loop consumption control

system based on estimation feedback.

Our power consumption estimation is based on

previous work (Ren et al., 2012; Ren et al., 2013) in

which static energy estimations are mathematically

calculated for completed multimedia tasks for a

fixed OPP by off-line correlation between actual

energy measurements and significant-events counts

taken from the processor PMCs (Performance

Monitoring Counters). Now this estimation method

has to be extended to a system in which the OPP will

be variable and the estimations will be periodically

calculated in real time. Besides, the estimator has to

be connected to and synchronized with the

controller, which, in turn, has to drive the operating-

system (OS) support for the DVFS subsystem. For

all these reasons, the estimation-based closed-loop

system is being implemented within the OS kernel.

But before the estimator can be implemented,

first it is being suitably tuned through an extensive

off-line procedure of correlation with actual power

consumption measurements captured with an

external data acquisition system in response to

changes in the OPP. While this estimation-based test

bed is being developed and hoping the estimations

will be accurate enough, a first approach to the

control system design can be done in advance by

getting a dynamic model of the plant through the

analysis of the same consumption profiles acquired

for tuning the estimator. This initial design task and

its results are presented in this paper, with the

following structure. In Section 2 related work is

presented; Section 3 describes the test bed used; in

Section 4 a model of the plant is obtained; Section 5

presents the design of a first-approach closed-loop

controller; Section 6 includes the main results

achieved with that controller; and Section 7

concludes.

2 RELATED WORK

The energy consumption optimization in

microprocessor-based systems is a matter of concern

since several years ago in fields which range from

small battery-operated systems (Ren et al., 2012; Le

and Wang, 2010) to larger data centers or web

servers (Wang and Wang, 2009; Horvath et al.,

2007), focusing also in multimedia applications (Ren

et al., 2013; Juárez et al., 2010; Lu et al., 2003).

Furthermore, the use of the DVFS method to act on

the system consumption is not new (Jejurikar and

Gupta, 2004; Choi et al., 2005; Snowdon et al.,

2007). On the other hand, the application of closed-

loop techniques also appears in the literature of all

these fields (Le and Wang, 2010; Wang and Wang,

2009; Lu et al., 2003), with widespread use of

DVFS. However, where there is a broader variety of

proposals is in how to feed back the closed-loop

system, mainly because there is not a clear feedback

signal available in conventional platforms, as

mentioned above:

In (Xia et al., 2008; Ahmadian et al., 2010) the

controlled variable is the processor utilization factor

(U), which is varied through the DVFS system by

means of a PI controller. The energy savings

increase as U approaches 100%, meeting the task

deadlines. Also based on targeting a suitable value

of U, in (Poellabauer et al., 2005) the feedback

signal is the memory access rate (MAR), calculated

from PMC values.

Another set of approaches are found in which the

controlled variable is the occupancy level of certain

system queues, given that keeping it constant

implies that just the needed energy is being

consumed. Some examples based on DVFS are (Wu

et al., 2005), in which a PID controller is used to

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

364

minimize the energy-delay product by controlling

the number of data/instructions stored in

uniprocessor multiple-clock domain queues and

threads in chip multiprocessor queues; and

(Alimonda et al., 2009), where a nonlinear controller

is used in queue-based streaming applications.

Other closed-loop approaches are those in which

the controlled variable is a time for which a

relationship with energy consumption can be found,

for example, end-to-end delay in (Horvath et al.,

2007) or average slack time in (Lu et al., 2006; Zu

and Mueller, 2007), all of them based again on

DVFS.

There are cases in which the control loop adapts

the DVFS OPP to the just needed frequency by

estimating the processor workload, like (Gu and

Chakraborty, 2008) where the clock cycles for each

game frame are estimated by a PID controller; and

(Bang et al., 2009) where a Kalman filter estimates

the computation time needed by MPEG-2 decoded

frames.

In specific cases in which the target system is

provided with a power monitor unit, it is possible to

feed actual consumption data back to the closed-loop

controller, like in (Minerick et al., 2002) for a laptop

with an I controller, (Lefurgy et al., 2007) for a high-

density server with a P controller or (Wang et al.,

2009) for a chip multiprocessor with an optimal

controller. However, although in the first design

phases, like those which this paper focuses on, the

availability of off-line power measurements is

useful, our final aim, beyond the scope of this paper,

is to reach a control system which can regulate the

power consumption of an autonomous embedded

system without the need of added power monitors

but basing it on power estimations. It is an approach

similar to the one used in (Wang et al., 2010), where

the use of PMCs is proposed for estimating L2 cache

consumption, but which has to be extended in our

case to the processor and to act on its DVFS

mechanism.

3 TEST BED

In order to not add more complexity than necessary

to the test bed when our focus is put in analyzing the

control-system behavior, our test bed uses a single-

CPU hardware development platform for mobile

multimedia embedded systems (Beagleboard, n.d.).

It features, apart from a number of peripherals, 2Gb

NAND and 2Gb MDDR SDRAM of memory and an

OMAP3530 processor system (TI-Omap3530, n.d.).

This system includes a MPU based on an up to 720-

MHz ARM Cortex-A8 core, with separated L1

instruction and data caches of 16KB each and a

shared 256KB L2 cache, as well as a DSP core and

other coprocessors. Related to the BeagleBoard

peripherals, it is worth mentioning the possibility a

subset of them brings for changing the MPU supply

voltage and clock frequency (DVFS subsystem).

This development platform allows us to execute

video decoding applications while monitoring the

global power consumption. To drive this monitoring

process an Agilent set of programmable power

supply, battery emulator and PC-based GPIB-linked

acquisition system has been used (Agilent, 2009).

Through this set, the whole platform is electrically

supplied while records of current consumption can

be stored in a PC hard disk and/or graphically

represented on the monitor. To simplify the work

and focus on the energy consumption caused by the

MPU, the memory subsystem and the related I/O

buses, the board has been configured as a minimal

system that disables the unnecessary components.

With respect to the software part, a Linux 3.8.0

kernel, patched to support the platform DVFS

mechanism, is running in the processor. On the other

hand, trying again to keep the system complexity

and performance at reasonable levels and taking

advantage of our expertise in the Open RVC-CAL

Compiler (Orcc) (Ren et al., 2013; Ren et al., 2014),

a MPEG4-Part2 decoder is built from (ORC-RVC-

MPEG, n.d.) to be used as the consuming video

application. Besides, several video sequences are

used to characterize the system (RVC-CAL-

Sequences, n.d.).

The DVFS subsystem is managed through the

cpufreq Linux driver. This driver includes four

predefined governors to fix the MPU OPP, two static

and two dynamic which react to the system load.

This is achieved by a function called

cpufreq_driver_target, one of whose input

parameters is the target frequency of the desired

OPP to switch to. This function searches the target

frequency among the ones of the OPPs defined in an

internal table and selects the appropriate one by

applying a ceil or a floor rounding algorithm,

depending on another input parameter. The function

then sets the frequency and the voltage

corresponding to the selected OPP. The default

cpufreq definitions for the BeagleBoard only

consider 6 OPPs. This implies a strong nonlinearity

for the closed-loop system in the form of a

quantization process, which makes the analysis and

design more difficult and leads to worse system

behaviour. In order to decrease this nonlinearity in

the DVFS-based plant input, additional valid OPPs

Modeling,AnalysisandDesignofaClosed-loopPowerRegulationSystemforMultimediaEmbeddedDevices

365

were searched. For this purpose, following an

approach similar to that exposed in (Barbalace and

Ravindran, 2012) for another OMAP-based board,

new frequencies were tested for the MPU and

accompanied by a corresponding interpolated

voltage level in an empirical way. Those OPPs

which were suitably verified to have differentiated

execution times and MPU supply voltages were kept

into the cpufreq table, reaching a total of 27. Their

corresponding pairs frequency/voltage are shown in

the first three columns of Table 1. The code of one

of the cpufreq governors was modified with the aim

of changing the MPU OPP under our criterion,

whereas a system call was used to synchronize the

user-space video decoder with the kernel-space

DVFS interface in the right moments of the

measuring experiments.

4 GETTING A LINEAR MODEL

OF THE PLANT

One means of designing the system controller is to

base it on a suitable model of the plant. As a first

approach to the problem, still working with actual

consumption data and not with practical estimations,

we use a simplified model to facilitate the

application of the classic control theory. Later, this

model could be refined and sophisticated and

different advanced closed-loop control strategies

could be applied.

For modeling purposes, a capture of the actual

consumption of the whole board while decoding

different video files has been acquired for a

sequence of OPPs changing every 3 seconds. The

OPP sequence includes steps up, steps down and

variable-size steps, resulting all of them in the fixed

average consumption values that are given for each

OPP in the fourth column of Table 1.

The repetition of the capture experiment for the

same video sequence indicates that there is a certain

basis of (average) consumption for each OPP, more

or less constant for all repetitions, plus a number of

big consumption spikes that appear in different

moments in each repetition. For this reason, those

spikes are not considered to be due to the video task

executed in the CPU but to other “unknown” sinks

in the board. Moreover, by adjusting suitably the

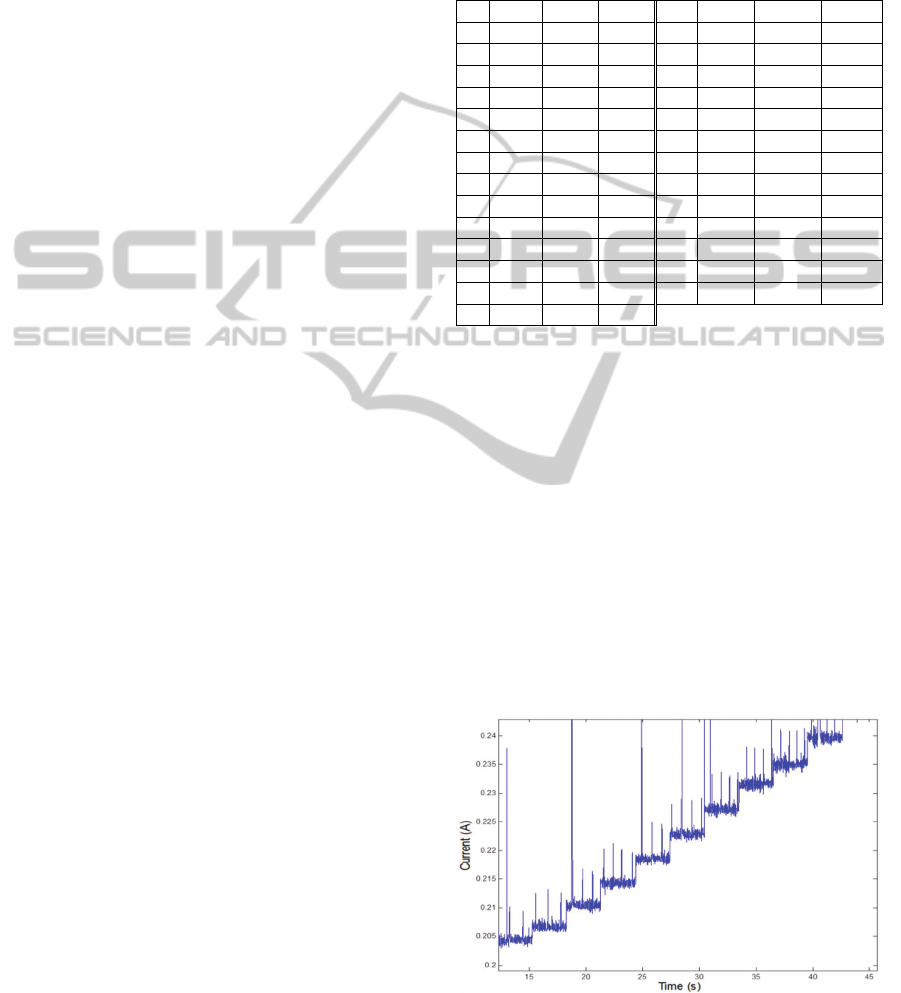
zoom in the graphs, it can be observed, apart from

the biggest “random” consumption spikes, a second

level of pseudo-periodic consumption peaks, whose

period decreases as the OPP frequency increases.

These can be due to accesses to the SD card to get

the video file data packets but not to decoding

activities. Hence, these current peaks should not be

taken into account to model the plant, given that

neither the on-going power estimation procedure

will reflect them. Figure 2 shows these details.

Table 1: OPP data.

No. MHz

1 125 0.978 0.186 15 430 1.156 0.245

2 200 0.991 0.197 16 500 1.168 0.259

3 210 1.003 0.199 17 510 1.181 0.263

4 220 1.018 0.201 18 520 1.193 0.266

5 240 1.031 0.205 19 530 1.206 0.270

6 250 1.043 0.207 20 540 1.218 0.274

7 270 1.056 0.211 21 550 1.230 0.278

8 290 1.068 0.215 22 560 1.243 0.282

9 310 1.081 0.219 23 570 1.256 0.288

10 330 1.093 0.224 24 580 1.280 0.290

11 350 1.106 0.228 25 590 1.293 0.297

12 370 1.118 0.233 26 600 1.306 0.301

13 390 1.131 0.236 27 720 1.306 0.327

14 410 1.143 0.241

Frequency (MHz);

Voltage (V);

Average consumption (A)

If the zoom is focused on how the consumption

changes from one OPP to another, the dynamics of

this change can be analyzed. From this analysis, a

mathematical model of the system plant can be

obtained. Thus, for example, starting with a simple

linear first-order Laplace transfer function,

G(s)=1/(2.75·10

-3

s+1) can be obtained (Ogata,

2010), which relates the current consumption with

input OPP average current level. Figure 3 shows the

comparison between the time response of this model

and the actual consumption for an input step from

OPP26 to OPP27 levels. The time response of G(s)

has been compared also with the rest of steps of the

OPP sequence described above and its validity has

been verified.

Figure 2: Detail of the real board consumption profile for

increasing OPPs.

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

366

Figure 3: Actual consumption and model response for

OPP26 to OPP27 step.

The proposed model G(s) is a continuous one,

which has to be discretized depending on the action

period T to be considered. If a digital-to-analog

converter (zero-order hold) + continuous process +

analog-to-digital converter (sample & hold) scheme

model is considered for the discretization, a Z

transfer function can be derived from the continuous

model: G(z)=(1-e

)/(z-e

) (Phillips and Parr,

2010), where p is the pole of G(s), i.e. p = –363.63.

5 ANALYSIS AND DESIGN OF

THE CLOSED-LOOP SYSTEM

Once a mathematical model of the plant is obtained,

different analysis techniques can be applied to

foresee the system behavior. A first approach is

addressed with a linear model, which will be

completed later with more realistic (nonlinear)

characteristics.

5.1 Linear Model

Thinking on implementing a closed-loop automatic

power regulation system, one of the parameters to be

fixed is the action period (sample period T of G(z)).

Apart from other technological issues, the stability

of the closed-loop system is one of the

characteristics that must be ensured. As a first

approach, the simplest controller that can be used in

closed loop is a proportional (P) one (Phillips &

Parr, 2010). If we call K the gain of this controller,

the transfer function of the closed-loop system is

M(z)=K(1-e

)/(z-e

+K(1-e

)). Therefore, the

critical gain which leads the system to instability is

=(1+e

)/(1-e

). If K

is represented versus the

sample period, from 1ms to 1s, the graph shown in

Figure 4 is obtained. From that figure it can be

realized that in order to have K

values higher than

1, T must be lower than 10ms, which can be a too

low value in terms of system overhead. It is worth

noting that this overhead will come not only from

the execution time of the control algorithm itself but

also from the OPP switching time.

Figure 4: Critical gain of closed-loop system vs sample

period.

Hence, a realistic P controller would have a limit

of 1 for its gain. With this upper bound, the lower

bound for the closed-loop system error in steady

state is min(e

)=100/(1+max(K

))=50% (Ogata,

2010), which is too high. In order to avoid this

limitation and still keeping a classic linear

controller, an integral action (I) should be added to

it.

As a first and simple approach to the integral

action, one can choose between a forward and a

backward rectangular rule (FRR and BRR,

respectively) (Franklin and Powell, 1997). Their

corresponding Z transfer functions differ only on a

zero in z=0 which appears in the second case. Given

that for overhead reasons a realistic sample period

cannot be very short, the pole of G(z) will be close

to 0. For example, for a sample time T of 100ms the

pole of G(z) is z=e

=1.6·10

-16

. Therefore, the

practical zero-pole cancellation in a series of a BRR

I and G(z) will enable shorter settling times than

with a FRR I when closing the control loop because

the system dominant pole can be closer to z=0. This

can be deduced from the Z-plane root loci shown in

Figure 5. In the FRR case, the modulus of the

system dominant pole is always greater than or equal

to 0.5, whereas in the BRR case the system

dominant pole can reach the minimum value of 0

thus enabling settling times shorter than the sample

period.

Modeling,AnalysisandDesignofaClosed-loopPowerRegulationSystemforMultimediaEmbeddedDevices

367

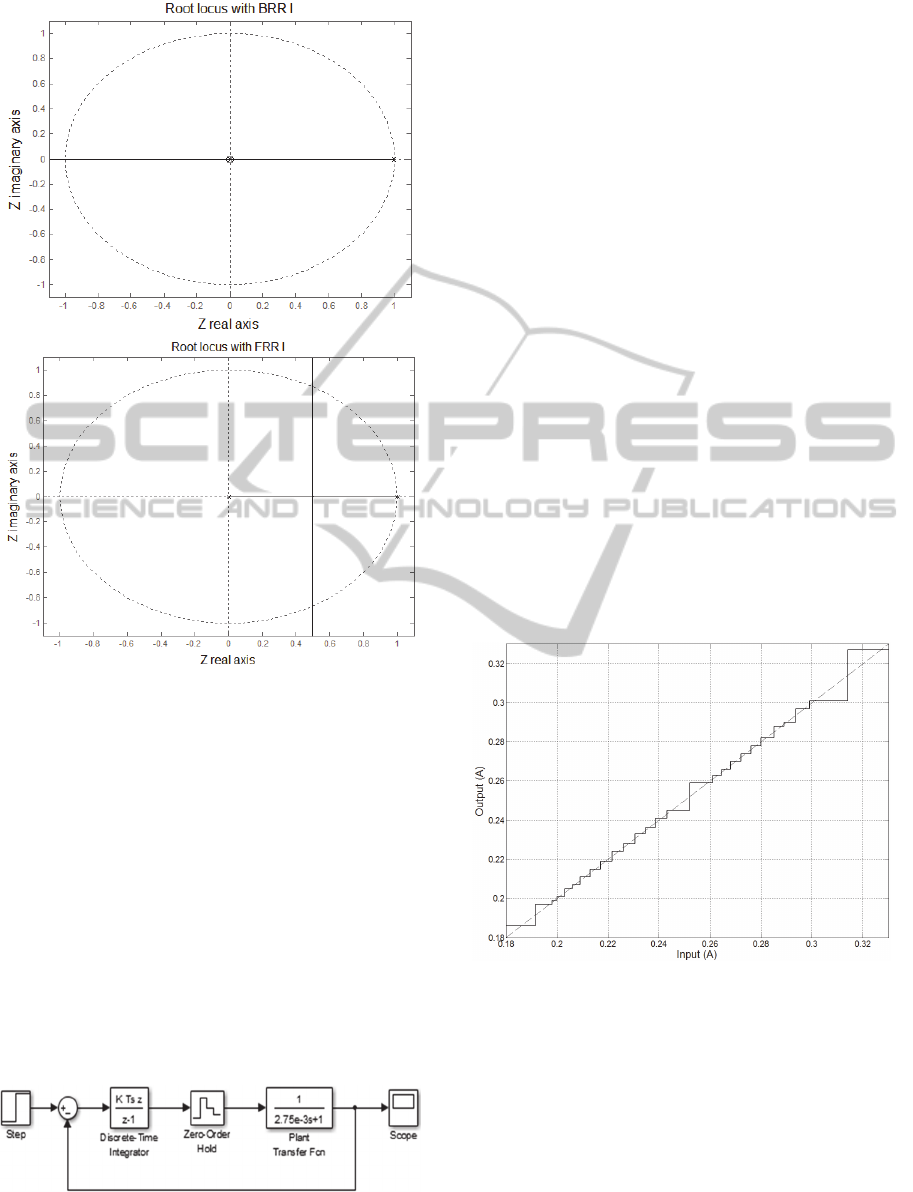
Figure 5: System root locus with BRR (up) and FRR

(down) integrators.

Thus, considering the BRR option, the closed-

loop pole of the system for a long enough sample

period is p

=1-KT, being again K the controller

gain. Let us consider a sample period T of 100ms,

which seems to be a good trade-off value for

keeping reasonable relative overhead, immunity to

jitter effects and frequency of control actions. For

this period, the critical gain which leads the system

to instability (p

=-1) is K

=20, whereas the gain for

the shortest settling time (p

=0) is K=10. This is the

gain used for the I controller in the Simulink closed-

loop linear system model of Figure 6, characterized

by null steady-state error and the same settling time

as the plant.

Figure 6: Block diagram of the linear closed-loop control

system.

5.2 Adding Nonlinearities to the

System Model

The initial linear model must be enhanced with more

real system details. For example, perhaps the

clearest nonlinearity of the system is that the

interface to the plant only admits 27 different levels,

i.e. the 27 available OPPs. As mentioned above, this

implies a strong quantization process previous to the

plant, whose steps are even irregular. Hence, the

diagram of Figure 6 must include a block, previous

to the plant, implementing this quantization, which

can even overcome the zero-order hold functionality

and substitute it (see Figure 8). The quantization also

includes implicitly the nonlinear effect of saturation

beyond the limits of the extreme OPPs. From the

OPP average consumption values included in Table

1, the transfer function of this quantization block is

graphically represented with the stepped line of

Figure 7 in 27 irregular steps. The diagonal line of

that figure is a reference to identify how the input

breakpoints should be fixed in the middle of the step

values in order to limit the maximum quantization

error to ±step/2. This is a feature to be added to the

final implementation because our default cpufreq

interface offers both ceil and floor functionality but

not rounding to the nearest valid OPP value.

Figure 7: Transfer function of the discrete OPP

quantization effect.

One of the main advantages of closed-loop

systems is their capability to react to disturbances on

the controlled output. Therefore, the system model

should be completed with a disturbance input, like

shown in Figure 8, in order to analyze its influence.

The disturbance input would simulate the effect of a

consumption variation when the system is following

the set point in steady state, due, for example, to a

variation in the processor load.

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

368

Figure 8: Diagram of the nonlinear closed-loop system

with disturbance input.

Another non-ideal feature that can be added to

the model is what we can call noise in the

consumption signal. I.e. the last column of Table 1

represents average values of current consumption for

each OPP but the actual values do fluctuate around

those averages, as can be distinguished in Figure 3.

If, as explained above, the consumption peaks not

directly due to the video decoding task are omitted

(see Figure 2), then the resulting consumption signal

can be modeled in each OPP as a constant (its

corresponding average value) plus a random-like

“noise” of about 2mA peak to peak and zero mean.

Figure 9 shows an example of this noise. The

disturbance input of the diagram of Figure 8 can be

used to inject a noise like that of Figure 9 into the

system output (consumption) in order to analyze

how it influences the control system.

Figure 9: Simulated noise to be added to the consumption

signal.

6 RESULTS

The Simulink system model of Figure 8 has been

tested in simulation for a number of set points and

disturbances, mainly step shaped. It is worth noting

that a step-shaped input would simulate a constant

current desired for the system consumption (set

point) or modifying the system consumption

(disturbance). In turn, the set-point level might

depend on a number of factors, ranging from system

load to battery state of charge. As a summary, Figure

10 shows the system time response for a set-point

step from OPP1 level to OPP15 level in t=0 and a

disturbance step (undesirable and unexpected

increase of consumption) of a 40% of the input step

in t=0.45s. In that figure it can be seen how, first, the

settling time is shorter than the sample period

(T=100ms) after the initial input step, and second,

the I controller assures a null error in steady state

given that the full target current level is reached after

the settling time (see its corresponding value in

Table 1). Afterwards, with the system consumption

stable at OPP15 level, a sudden consumption

increase arises at t=0.45s and this higher

consumption keeps until the next sample time at

t=0.5s. At that moment, the integral controller

detects the anomaly and corrects it immediately by

decreasing its output to the plant (i.e. by setting a

lower OPP). However, since the disturbance value

probably will imply that there is not any OPP which

cancels exactly its effect, i.e. none OPP applied to

the plant reaches a consumption equal to the target,

the I controller makes the response oscillate.

Something similar would happen also if the set point

did not match any of the OPP levels defined in Table

1, even in the absence of disturbance. The oscillation

in the system current consumption can be seen, on

one hand, as an undesirable behavior of the system,

given that the set point is not oscillating, or, on the

other hand, as the only way the control system can

satisfy the set-point requirement, in average. In fact,

the system is acting as a kind of pulse-width

modulator (PWM), switching between two adjacent

OPPs.

If the disturbance input of Figure 8 is used to

inject the characteristic noise of the system

consumption (see Figure 9) and we let enough

response time, the system output for an example set

point equivalent to OPP3 level is the one shown in

Figure 11. In that figure it can be seen how the

system reaches a current consumption with the

average value of OPP3 (see Table 1), as desired, but

some glitches appear occasionally. What happens is

that, although the average value of the noise is zero,

the sampling process inherent in the control system

may lead to a biased error sequence. This implies

that the integrator output increases or decreases

gradually until it reaches an OPP breakpoint

threshold, thus generating the undesirable glitches of

Figure 11. This can be better understood by

observing Figure 12, which shows the output of the I

controller during the same time interval as in Figure

11. Besides, Figure 12 includes also the two OPP

Modeling,AnalysisandDesignofaClosed-loopPowerRegulationSystemforMultimediaEmbeddedDevices

369

breakpoint levels adjacent to the OPP3 value as a

couple of horizontal lines at 198mA and 200mA,

respectively. The glitches in Figure 11 appear when

the integrator output crosses the breakpoint lines in

Figure 12, which triggers an OPP change.

Figure 10: Closed-loop time response for an OPP1 to

OPP15 input step and disturbance of 40% at t=0.45s.

Figure 11: Closed-loop response for OPP3 level target and

noise disturbance.

The example illustrated in Figure 11 and Figure

12 has been based on an OPP3 target value, the one

closest to its neighbours, as it can be realized from

Table 1. This implies that the glitches in the

consumption will be the lowest but the most

frequent ones, because the integrator output reaches

the breakpoints in less time. In the worst general

case, the highest glitch would have the amplitude of

the highest OPP step, which can be easily identified

in Figure 7 to be between OPP26 and OPP27 with a

value of 26mA from Table 1 data. Anyway, the

glitch width is only one sample period. This issue is

one of the disadvantages of the I controller which

have to be treated, but we will wait to have

consumption estimation data available, in order to

compare its associated noise with that of the actual

consumption used in this paper.

Figure 12: Integrator output for OPP3 level target and

noise disturbance.

7 CONCLUSION AND FUTURE

WORK

A mathematical model of the power consumption

process of a video decoding application running in a

commercial embedded development platform has

been obtained from measured data. Then, classic

analysis and design techniques have been applied to

get a suitable controller able to keep track of the

power consumption in closed loop. Prior to the

availability of real-time power estimation data for

implementing the target system, simulation results

have validated the controller in the presence of

consumption variations. I.e., the control system is

stable and able to make the decoder consumption

follow the set point with a null average steady-state

error regardless the existence of consumption noise

or disturbance. This paves the way for optimizing

the power consumption of multimedia hand-held

devices by applying closed-loop techniques.

From now on, a suitable power estimator has to

be achieved for the video decoder such that its

estimations are as close as possible to the real

consumption. The effects of the possible differences

between estimation and consumption on the control

system have to be analyzed prior to implement the

target system with real-time estimation feedback.

Once the target system is implemented, its response

has to be contrasted with previous simulation results.

This will open the door to further improvements

such as the refinement of the I controller or the test

of different (advanced) controllers. Moreover, the

subsequent power savings will come from the

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

370

suitable programming of the set point, which will be

followed by the decoder consumption by means of

the closed-loop control system. The set point will be

programmed to achieve different objectives

involving battery life time, performance or QoE

parameters among others, and the corresponding

power savings will be compared to other existing

solutions in order to evaluate the efficiency of our

proposal. Other further work can lead to more

complex scenarios in which, for example, the

hardware offers more than one CPU, like in

OMAP4-based platforms (TI-Omap4460, n.d.), and

the software is partitioned among different

processing cores. Then the closed-loop control of

power consumption in several CPUs or coprocessors

will be worth researching.

REFERENCES

Agilent 2009, Agilent 14565B Software and 66319B/D

and 66321B/D Mobile Communications DC Sources,

Available from: <http://cp.literature.agilent.com/

litweb/pdf/5990-3503EN.pdf>. [2014.11.26].

Ahmadian, A. S., Hosseingholi, M. and Ejlali, A., 2010. A

control-theoretic energy management for fault-tolerant

hard real-time systems. IEEE International

Conference on Computer Design (ICCD).

Alimonda, A., Carta, S., Acquaviva, A., Pisano, A. and

Benini, L., 2009. A feedback-based approach to DVFS

in data-flow applications. IEEE Transactions on

Computer-Aided Design of Integrated Circuits and

Systems, vol. 28, no. 11, pp. 1691-1704.

Bang, S. Y., Bang, K., Yoon, S. and Chung, E. Y., 2009.

Run-time adaptive workload estimation for dynamic

voltage scaling. IEEE Transactions on Computer-

Aided Design of Integrated Circuits and Systems, vol

28, no. 9, pp. 1334-1347.

Barbalace, A. and Ravindran, B., 2012. Quantitative

evaluation of single and multicore real time DVFS

schedulers in Linux. Technical report available from:

<http://chronoslinux.org/papers/rtdvfs_emb_tech.pdf>.

[2014.12.26]

Beaglboard, n.d. Available from: <http://beagleboard.org/

beagleboard>. [2014.11.26].

Choi, K., Soma, R. and Pedram, M., 2005. Fine-grained

dynamic voltage and frequency scaling for precise

energy and performance trade-off based on the ratio of

off-chip access to on-chip computation times. IEEE

Transactions on Computer-Aided Design of Integrated

Circuits and Systems, vol. 24, no. 1, pp. 18-28.

Franklin, G. F. and Powell, J. D., 1997. Digital Control of

Dynamic Systems. Addison Wesley, 3rd edition.

Gu, Y. and Chakraborty, S., 2008 .Control theory-based

DVS for interactive 3D games. Design Automation

Conference (DAC).

Horvath, T., Abdelzaher, T., Skadron, K., and Liu, X.,

2007. Dynamic voltage scaling in multitier web

servers with end-to-end delay control. IEEE

Transactions on Computers, vol.56, no. 4, pp. 444-

458.

ITU-T and ISO/IEC JTC 1 2012. Advanced Video Coding

for Generic Audiovisual Services. ITU-T Rec. H.264

& ISO/IEC 14496-10.

Jejurikar, R. and Gupta, R., 2004. Dynamic voltage

scaling for systemwide energy minimization in real-

time embedded systems. International Symposium on

Low Power Electronics and Design (ISLPED).

Juárez, E., Pescador, F., Lobo, P., Groba, A. and Sanz, C.,

2010. Distortion-energy analysis of an OMAP-based

H.264/SVC decoder. 6th International Mobile

Multimedia Communications Conference

(MobiMedia).

Le, D. and Wang, H., 2010. An effective feedback-driven

approach for energy saving in battery powered

systems. 18th IEEE International Workshop on

Quality of Service (IWQoS).

Lefurgy, C., Wang, X. and Ware, M., 2007. Server-level

power control. 4th International Conference on

Autonomic Computing (ICAC).

Lu, Z., Lach, J., Stan, M. and Skadron, K., 2003. Reducing

multimedia decode power using feedback control.

International Conference on Computer Design

(ICCD).

Lu, Z., Lach, J., Stan, M. and Skadron, K., 2006. Design

and implementation of an energy efficient multimedia

playback system. Asilomar Conference on Signals,

Systems and Computers.

Minerick, R. J., Freeh, V. W. and Kogge, P. M., 2002.

Dynamic power management using feedback.

Workshop on Compilers and Operating Systems for

Low Power.

Ogata, K., 2010. Modern control engineering, Prentice

Hall, 5th edition.

ORC-RVC-MPEG, n.d. Available from:

<https://github.com/orcc/orc-

apps/tree/master/RVC/src/org/sc29/wg11/mpegh/part2

>. [2014.11.26]

Phillips, C. L. and Parr, J. M., 2010. Feedback Control

Systems, Prentice Hall, 5th edition.

Poellabauer, C., Singleton, L. and Schwan, K., 2005.

Feedback-based dynamic voltage and frequency

scaling for memory-bound real-time applications. 11th

IEEE Real Time and Embedded Technology and

Applications Symposium (RTAS).

Ren, R., Juárez, E., Pescador, F. and Sanz, C., 2012. A

stable high-level energy estimation methodology for

battery-powered embedded systems. 16th IEEE

International Symposium on Consumer Electronics

(ISCE).

Ren, R., Wei, J., Juárez, E., Garrido, M., Sanz, C. and

Pescador, F., 2013. A PMC-driven methodology for

energy estimation in RVC-CAL video codec

specifications. Signal Processing: Image

Communication, vol. 28, no. 10, pp. 1303-1314.

Ren, R., Juarez, E., Sanz, C., Raulet, M., and Pescador, F.,

2014. Energy-Aware decoder management: a case

study on RVC-CAL specification based on just-in-

Modeling,AnalysisandDesignofaClosed-loopPowerRegulationSystemforMultimediaEmbeddedDevices

371

time adaptive decoder engine. IEEE Transactions on

Consumer Electronics, vol. 60, no. 3. pp. 499-507.

RVC-CAL-Sequences, n.d. Available from:

<http://sourceforge.net/projects/orcc/files/Sequences>.

[2014.11.26]

Snowdon, D. C., Petters, S. M. and Heiser, G., 2007.

Accurate on-line prediction of processor and memory

energy usage under voltage scaling. 7th International

Conference on Embedded Software (EMSOFT).

Sullivan, G. J., Ohm, J. R., Han, W. J. and Wiegand, T.,

2012. Overview of the High Efficiency Video Coding

(HEVC) Standard. IEEE Transactions on Circuits and

Systems for Video Technology, vol. 22, no. 12, pp.

1649-1668.

TI-Omap3530, n.d. Available from: <http://www.ti.com/

product/omap3530>. [2014.11.26].

TI-Omap4460, n.d. Available from: <http://www.ti.com/

product/omap4460>. [2014.12.26].

Wang, X. and Wang, Y., 2009. Co-Con: coordinated

control of power and application performance for

virtualized server clusters. 17th IEEE International

Workshop on Quality of Service (IWQoS).

Wang, X., Ma, K. and Wang, Y., 2010. Achieving fair or

differentiated cache sharing in power-constrained chip

multiprocessors. 39th International Conference on

Parallel Processing (ICPP).

Wang, Y., Ma, K. and Wang, X., 2009. Temperature-

constrained power control for chip multiprocessors

with online model estimation. 36th International

Symposium on Computer Architecture (ISCA).

Wu, Q., Juang, P., Martonosi, M., Peh, L. S. and Clark, D.

W., 2005. Formal control techniques for power-

performance management. IEEE Micro, vol. 25, no. 5,

pp. 52-62.

Xia, F., Tian, Y. C., Sun, Y. and Dong, J., 2008. Control-

theoretic dynamic voltage scaling for embedded

controllers. IET Computers & Digital Techniques, vol.

2, no. 5, pp. 377-385.

Zhu, Y. and Mueller, F., 2007. Exploiting synchronous

and asynchronous DVS for feedback EDF scheduling

on an embedded platform. ACM Transactions on

Embedded Computing Systems, vol. 7, no. 1, pp. 3:1-

3:26.

PECCS2015-5thInternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

372