Dimensionality Reduction for Supervised Learning in

Link Prediction Problems

Antonio Pecli, Bruno Giovanini, Carla C. Pacheco, Carlos Moreira, Fernando Ferreira,

Frederico Tosta, Júlio Tesolin, Marcio Vinicius Dias, Silas Filho, Maria Claudia Cavalcanti

and Ronaldo Goldschmidt

Military Institute of Engineering, Pr. General Tiburcio, 22290-270, Rio de Janeiro, RJ, Brazil

Keywords: Link Prediction, Supervised Learning, Machine Learning, Dimensionality Reduction.

Abstract: In recent years, a considerable amount of attention has been devoted to research on complex networks and

their properties. Collaborative environments, social networks and recommender systems are popular

examples of complex networks that emerged recently and are object of interest in academy and industry.

Many studies model complex networks as graphs and tackle the link prediction problem, one major open

question in network evolution. It consists in predicting the likelihood of an association between two not

interconnected nodes in a graph to appear. One of the approaches to such problem is based on binary

classification supervised learning. Although the curse of dimensionality is a historical obstacle in machine

learning, little effort has been applied to deal with it in the link prediction scenario. So, this paper evaluates

the effects of dimensionality reduction as a preprocessing stage to the binary classifier construction in link

prediction applications. Two dimensionality reduction strategies are experimented: Principal Component

Analysis (PCA) and Forward Feature Selection (FFS). The results of experiments with three different

datasets and four traditional machine learning algorithms show that dimensionality reduction with PCA and

FFS can improve model precision in this kind of problem.

1 INTRODUCTION

For the last years, the constant advances in

information technology have significantly

contributed to increase the amount of interconnected

data around the world. In this scenario, many large,

complex and dynamic digital networks have

emerged. For example, social networks,

collaborative environments and recommender

systems, just to name a few, are complex networks

provided by Web 2.0 and e-Science. Both scientific

and industrial communities have devoted a

considerable amount of attention to the investigation

of such networks and their properties (Liben-Nowell

and Kleinberg, 2003). Many studies model networks

as graphs, where a vertex (node) represents an item

in the network (e. g. person, web page, product,

movie, photo, etc) and an edge represents some sort

of association between the corresponding items (e.g.

a purchase connects the product and the client).

Complex networks are very dynamic, since new

vertices and edges can be added to the graph over

the time. Understanding the reasons that make the

networks evolve is a complex question that has not

been properly answered yet. One major but

comparatively easier problem in the study of

network evolution is the link prediction task. It

consists in predicting the likelihood of an association

between two not interconnected nodes in the graph

to appear (Lü and Zhou, 2011). We have noticed that

link prediction has been applied for two different

tasks: predicting “future” links (Liben-Nowell and

Kleinberg, 2003), when the goal is to discover which

links will appear in the future, and predicting

“missing” links (Lü and Zhou, 2011), used for

inferring links that already exist in the network, but

are not represented yet.

One of the approaches to the link prediction

problem is based on supervised learning (Hasan et

al, 2006; Li and Chen, 2009; Pujari and Kanawati,

2012; Sa and Prudencio, 2011; Benchetarra et al.,

2010). Such approach converts original data to a

binary classification problem. In this problem, each

data point corresponds to a pair of vertices with a

class label denoting their link status: positive if the

association between the two vertices exists,

295

Pecli A., Giovanini B., C. Pacheco C., Moreira C., Ferreira F., Tosta F., Tesolin J., Vinicius Dias M., Filho S., Claudia Cavalcanti M. and Goldschmidt R..

Dimensionality Reduction for Supervised Learning in Link Prediction Problems.

DOI: 10.5220/0005371802950302

In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 295-302

ISBN: 978-989-758-096-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

negative, otherwise. Additional features must be

added to the dataset in order to describe its data

points and represent some sort of proximity between

the pair of vertices. A machine learning algorithm is

applied to the enriched dataset in order to generate a

classification model.

Many features have been experimented in

supervised learning for link prediction problems

(Hasan and Zaki, 2011). Typically, these features are

classified in three groups: (a) node and edge

information (e.g. client’s age, job location, etc); (b)

aggregated features (e.g. sum of e-mails, sum of

contacts, etc); (c) topological measures extracted

from the graph (e.g. common neighbors, jaccard’s

coefficient, etc). Choosing which features to add to

the dataset is crucial for the learning process. It is a

typical optimization problem where there is a search

for a reduced set of features that preserves, as much

as possible, the original amount of information

available in the dataset.

Although many works have reported promising

results with the binary classification approach for

link prediction, choosing the set of features to train

the classifiers is acknowledged to be a major

challenge (Hasan and Zaki, 2011).

The machine learning community has developed

many methods to deal with the high-dimensional

space problem (Yu and Liu, 2003; Caruana et al.,

2008). In general, these methods are based on two

approaches (Kohavi and John, 1997): filter and

wrapper. The filter approach consists in calculating

some evaluation metric (such as correlation or

information gain) from the dataset in order to select

the features that lead to better evaluations. On the

other hand, the wrapper approach is iterative and, for

each iteration, selects a subset of features, reduces

the original dataset (using the selected features) and

uses it to construct and evaluate a predictive model.

This process is repeated until a stopping criterion is

satisfied.

Dimensionality reduction techniques can also be

classified in two groups: feature selection and

feature extraction. The main difference between

them is that the first group does not change original

attributes and the second one transforms original

features in new attributes.

Despite its acknowledged importance for

supervised learning tasks, few works have

investigated the effects of dimensionality reduction

in link prediction. Table 1 shows examples of

dimension reduction techniques according to the

classifications presented above.

Feature Selection for Link Prediction – FESLP

(Xu and Rockmore, 2012) and Cross-Temporal Link

Prediction – CTLP (Oyama et al., 2011) have been

specifically designed to be used in link prediction

applications. FESLP selects features based on their

correlation and information gain. CTLP assumes that

features useful for link prediction change over time

and, thus, searches for sets of features which best

describes nodes and theirs variations as time passes

by. Oyama et al., (2011) used CTLP in a dynamic,

time evolving environment to determine the

identities of real entities represented by data objects

observed in different time periods. Xu and

Rockmore (2012) ran their experiments with

datasets generated from an email network of a large

academic university.

Forward Feature Selection – FFS (Freitas, 2002)

and Principal Component Analysis – PCA (Jackson,

1991) are methods traditionally used by the machine

learning community.

FFS is iterative. In each iteration, FFS searches

for a feature that, combined to a set of selected

features, builds a reduced dataset that leads to the

best predictive model (according to some criterion,

such as precision or recall, for example). Its loop

will perform until no predictive model built in the

current iteration shows improvement. Initially, the

set of selected features is empty and FFS builds as

many reduced datasets as the number of attributes in

the original dataset (each reduced dataset contains

exactly one attribute plus the class, target of the

problem).

PCA is a statistical technique that uses an

orthogonal transformation to convert a dataset of

possibly correlated features into a set of linearly

uncorrelated attributes called principal components.

The number of principal components is less than or

equal to the number of original features. Such

components are orthogonal because they are the

eigenvectors of the covariance matrix, calculated

with the attributes of the original dataset.

To the best of our knowledge, both FFS and PCA

have never been used to reduce dimension in link

prediction applications.

Table 1: Examples of Dimensionality Reduction Methods.

Methods Approach Feature Treatment

FESLP Filter Selection

CTLP Filter Selection

PCA Filter Extraction

FFS Wrapper Selection

So, this paper evaluates the effects of PCA and

FFS as dimensionality reduction preprocessing

techniques to the binary classifier construction in

link prediction applications. In constrast to FESLP

and CTLP, we have run our experiments over three

ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems

296

open and popular datasets (DBLP, Amazon, Flickr).

Traditional learning algorithms like SVM, Naïve

Bayes, K-NN and CART (Hasan et al, 2006) were

tested with both dimensionality reduction methods.

The results show that dimensionality reduction with

FFS and PCA can improve model precision in this

kind of problem when compared to the use of the

complete set of features (CS).

This work was organized in four other sections.

Section 2 presents details about the experimental

setup. Configurations of the classification algorithms

and information about the used datasets are also

described in Section 2. Section 3 presents and

analyses the results obtained. Conclusions and future

work are posed in Section 4.

2 EXPERIMENTAL SETUP

2.1 Datasets

We have selected three different datasets to perform

our experiments: DBLP, Amazon and Flickr. All of

them are available on the web for download (Ley,

2009; Leskovec and Krevl, 2014). The first one

contains data about co-authoring scientific

publications and has been used in many works

concerning future link prediction (Hasan et al, 2006;

Oyama et al., 2011; Benchettara et al., 2010). The

idea is to predict future interactions (links) that

could occur between the authors (vertices). The

second dataset is formed by product co-purchasing

(with products as vertices and their relations of

being sold together as links). The Flickr dataset

contains pictures (vertices) and their associations

(links). The link prediction task in DBLP is slightly

different from the ones in Amazon and Flickr. While

in DBLP dataset the goal is “future” link prediction,

the task in both Amazon and Flickr datasets is to

predict “missing” links among products (Amazon)

and photos (Flickr).

2.2 Feature Set

For this work, a feature set with 15 attributes was

selected. Most of them were selected due to their use

and relevance in many applications of link

prediction (Hasan and Zaki, 2011). However, some

other features that were not so common in the link

prediction task were chosen as well, in order to

evaluate their relevance in the datasets used in the

experiments. The features are described as follows:

1. Shortest path length (Hasan and Zaki, 2011):

this traditional feature corresponds to the

smallest number of edges that forms a path

between a pair of vertices;

2. Second shortest path length (Hasan et al, 2006):

the length of the shortest path different from the

previous one;

3. Common neighbours (Hasan and Zaki, 2011):

the number of common neighbours between two

given vertices;

4. Sum of neighbours (Hasan et al., 2006): the total

of neighbours of each vertex from a pair;

5. Jaccard’s Coefficient (Hasan and Zaki, 2011):

the ratio between the number of common

neighbours and the number of total neighbours

of each vertex;

6. Sum of intermediate elements: taking into

account the structure of a bipartite graph, the

sum of intermediate elements refers to the total

number of elements connected to both vertices

that form a pair;

7. Adamic/Adar similarity (Adamic and Adar,

2003): it is the sum of the secondary common

neighbors (neighbors of neighbors), with a

smaller weight (relevance) than the primary

neighbors (direct neighbors).

8. Preferential attachment (Barabasi et al., 2002):

product of the number of neighbours of both

vertices that form a pair;

9. Katz measure (Katz, 1953): sum of lengths of all

paths existing between each pair of vertices,

providing higher relevance to paths with smaller

lengths.

10. Leicht-Holme-Newman Index (Leicht et al.,

2006): ratio between the number of common

neighbours of a pair of vertices and their

preferential attachment;

11. Clustering coefficient (Hasan and Zaki, 2011):

this metric is related to the number of triangles

that each vertex is part of;

12. Closeness centrality (Freeman, 1978): the

inverse value of the average distance of each

vertex of the pair to all other vertices in the

graph;

13. Average clustering of the nodes (Saramäki et al.,

2007): the mean of the local clustering

coefficient of the vertices;

14. Average neighbour degree (Barrat et al., 2004):

the average of the degree of the neighbours of

the pair of vertices;

15. Square clustering coefficient (Lind et al., 2005):

this metric is related to the number of squares

that each vertex is part of.

DimensionalityReductionforSupervisedLearninginLinkPredictionProblems

297

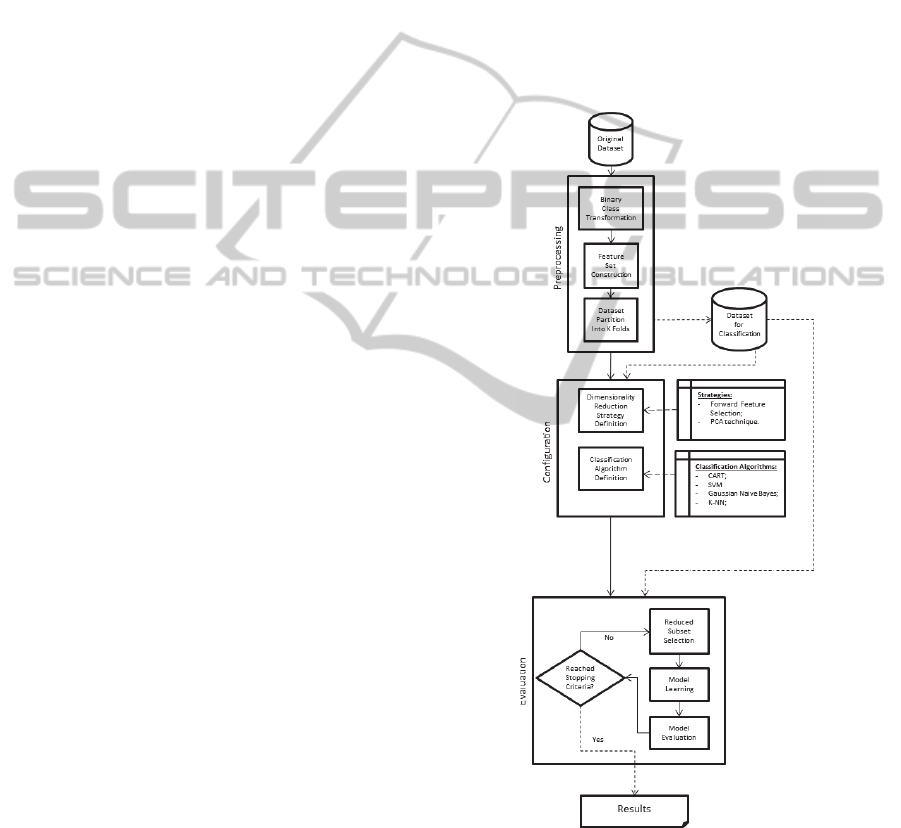
2.3 Method

Figure 1 depicts the process performed for each

group of experiments.

Conceptually, our experimental process has three

major stages: preprocessing, configuration, and

evaluation. The first stage prepares the data for the

next stages; the second one defines the settings of

both dimensionality reduction strategy and

classification algorithm, and the last stage trains and

evaluates the learning model over the reduced

datasets.

All the stages were developed in Python and

were based on Scikit-learn (Pedregosa et al, 2011), a

well known machine learning library, and on

NetworkX (Hagberg et al., 2008) a development

environment frequently used to implement and

process graph structures.

2.3.1 Pre-processing

This stage is performed only once for each dataset. It

randomly selects samples from the original data in

order to build a dataset for the classification task.

The new dataset is the one used by the other stages.

This stage has the following steps:

a) Binary Class Transformation: this step is

responsible for taking a sample from the original

dataset modelled as a graph G and turning it into

a dataset formed by the pairs of vertices and their

classes. Each of the randomly selected pairs of

vertices is classified as positive or negative. The

classification process will depend on the kind of

task performed: for the future link prediction, the

original dataset is divided into two range of years

(Hasan et al., 2006) – the training years (which

represents the “present” period of time, and is

represented by the graph G

, originated from the

graph G), and the test years (which represents the

“future” period of time, and is represented by the

graph G

t+1

, also originated from the graph G). A

selected pair of vertices cannot have a link

between them in the training range, but may or

may not have a link in the test range, being

classified as positive or negative example,

respectively. This process was used with the

DBLP dataset. For the missing link prediction

task, the sample is selected from the graph G,

and the pairs of vertices are classified as positive

or negative if they have a link between them or

not. However, once the positive examples are

selected, their links are removed from the graph

, which is a copy from the original graph G (in

order to simulate their absence and consider

them the “missing” links). This criterion was

applied to Amazon and Flickr datasets.

b) Feature Set Construction: after building the

sample, the features of each selected pair of

vertices are calculated. As we have used only

topological features for this work, the features

are calculated based on the graph structure G

(which can represent different versions of the

original graph G, depending on the task

performed). We normalized the features values

using the standard score (Hasan et al., 2006).

After normalized, the calculated features are

attached to the tuple corresponding to its pair of

vertices in the dataset for classification.

Figure 1: The sequence of stages and their steps performed

for each experiment.

c) Dataset Partition into K-Folds: this step divides

the dataset for the classification task into K

different folds, adding the index of the fold of

each pair of nodes to its corresponding tuple. The

purpose of keeping the folds previously defined

ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems

298

was to consider the same dataset partition for the

k-fold cross-validation process to be executed

with every classification algorithm.

2.3.2 Configuration

The data analyst uses this stage to select both the

dimensionality reduction strategy and the

classification algorithm (and its parameters to be

employed in the evaluation stage). This stage has the

following steps:

a) Dimensionality Reduction Strategy Definition: in

this step, the dimensionality reduction strategy

that will be used for future evaluation is chosen.

There are two available strategies: FFS and PCA.

The former has no parameter. For the latter, the

maximum number of principal components that

will be generated from the dataset must be

defined by the user.

b) Classification Algorithm Definition: this step is

responsible for defining the classification

algorithm and its configuration to be used in the

supervised learning process. The tested

algorithms and their configurations are listed in

section 2.4.

2.3.3 Evaluation

The supervised learning process and dimensionality

reduction strategy evaluation effectively happen in

this stage. As depicted in the figure 1, the evaluation

stage is iterative, executing its steps in a loop. If the

PCA technique is chosen as dimensionality

reduction strategy, this loop will perform until the

maximum number of principal components are

evaluated. Otherwise, the FFS will be used, and as it

is an incremental strategy, its loop will perform until

there is no improvement of precision of the built

predictive models. The results of this stage are the

precision of the most accurate predictive model and

the number of principal components or features

(depending on the strategy) used to build this model.

This stage has the following steps:

a) Reduced Dataset Selection: this step applies the

dimensionality reduction strategy in the pre-

processed dataset, creating the reduced datasets.

If the FFS strategy is selected, at its first

iteration, a reduced dataset with each attribute of

the original feature set will be generated.

However, if the PCA technique is selected, there

will be as many reduced datasets as the

previously defined maximum number of

principal components.

b) Model Learning: In order to obtain a predictive

model, this step applies the classification

algorithm to the reduced dataset produced by the

previous step. The predefined configuration of

the algorithm is always used during the process.

As we are using the k-fold cross validation, we

build k different predictive models for each

reduced dataset. We have parallelized this

process, building these predictive models

simultaneously.

c) Model Evaluation: the predictive model is

evaluated in this step. All the k predictive models

are evaluated using the traditional k-fold cross

validation. We have used the precision of the

classification model to evaluate the reduced

dataset. As mentioned before, the validation was

parallelized, so the evaluation of each predictive

model happens simultaneously, and the final

precision is the average precision of these

predictive models.

2.4 Classification Algorithms

Although there are many classification algorithms

for supervised learning, we had to choose some of

them to perform our experiments. Summarized in

Table 1, our choices followed the ones reported in

(Hasan et al., 2006).

We performed some preliminary experiments

with each dataset, in order to set the parameter

values depicted in Table 2. For example, we ranged

k of k-NN from 3 to 9 in order to choose the one

(k=5) with the best classification results in the

evaluated datasets. Once set, such configurations

were used in all experiments.

Table 2: Classification algorithms used in this work.

Algorithm Comment

SVM

‘RBF’ Kernel; penalty = 100; kernel coeff.

= 0.1

K-NN K=5

Naïve Bayes (NB) Gaussian Distribution

CART Random State = 10

3 RESULTS AND DISCUSSIONS

We performed three groups of experiments. Each

group considered one of the three datasets. For the

future link prediction task in the DBLP dataset, we

have used a period of time from 1990 to 2000 as the

training years, and from 2001 to 2005 as test years.

As we have used the Amazon and Flickr datasets for

the missing link prediction task, we did not have to

define a period of time for them. We preprocessed

DimensionalityReductionforSupervisedLearninginLinkPredictionProblems

299

each dataset only once, at the beginning of the

experiments of its group. Then, we have applied

PCA, FFS and CS strategies with each classification

algorithm in each dataset using the 10-fold cross

validation process. The CS (Complete Set)

“strategy” was considered our baseline. It always

used the complete set of attributes (15 features). In

fact, no dimensionality reduction was performed

with it. With PCA, we have used 14 as the

maximum number of principal components for each

dataset. The FFS strategy demanded no parameter.

We have built a total of 5280 predictive models.

Table 3 summarizes our results. Each triple (dataset,

dimensionality reduction strategy, classification

algorithm) defines a cell that contains two numbers.

The first one is the average precision (%) of the

classification models produced by the subset of

experiments that applied the corresponding

dimensionality reduction strategy to the respective

classification algorithm and dataset during the 10-

fold cross validation process. The second one

(presented between brackets) indicates the number

of features (or principal components) of the most

precise classification model produced in such subset

of experiments.

The FFS strategy outperformed CS in eight of

twelve cases (66.6%). Only in the subset of

experiments with the Amazon dataset and SVM

algorithm, FFS presented the same average precision

of CS, but with a smaller feature subset. The PCA

outperformed CS in half of the cases (50%), having

the same average precision in three of them.

FFS overcame PCA in nine of twelve cases

(75%), while PCA only overcame FS in two of all

cases (16.6%).

It is worth to mention the improvement of the

Gaussian Naïve Bayes (NB) algorithm when

evaluated with a reduced dimension space. Not

surprisingly, for all datasets, this algorithm

performed much better with less correlated attributes

or principal components than with the complete

original feature set.

4 CONCLUSIONS

Link prediction is an important task in the scenario

of complex networks and supervised learning is an

approach to deal with it. High dimensionality is one

major problem in machine learning applications.

And so it is in the supervised learning link prediction

task. In spite of the importance of this problem, just

a few works related to dimensionality reduction in

link prediction have been developed. However, none

of them have used classical techniques from the

machine learning literature, such as principal

components analysis (PCA) and forward feature

selection (FFS).

Table 3: Summary of results obtained with the three

groups of experiments.

Dataset

Algorithm

Dimensionality Reduction Strategy

CS (%) FFS (%) PCA (%)

DBLP

CART 73.7 [15] 79.9 [02] 73.6 [10]

SVM 81.3 [15] 81.2 [07] 81.3 [11]

K-NN 80.0 [15] 79.2 [04] 80.1 [10]

NB 64.2 [15] 80.5 [05] 78.0 [01]

Amazon

CART 96.4 [15] 97.3 [03] 95.8 [04]

SVM 97.5 [15] 97.5 [07] 97.5 [11]

K-NN 97.2 [15] 97.5 [04] 97.3 [09]

NB 91.8 [15] 97.0 [03] 92.9 [03]

Flickr

CART 89.5 [15] 89.2 [02] 77.3 [07]

SVM 82.6 [15] 83.7 [03] 82.6 [10]

K-NN 79.2 [15] 86.4 [06] 79.8 [08]

NB 65.5 [15] 79.3 [01] 71.0 [04]

In this paper, we have explored the effects of

dimensionality reduction in the link prediction task,

by applying the traditional techniques of PCA and

FFS. The main contributions of our experiments

include: (a) results that showed that traditional

dimensionality reduction techniques can lead to

more precise and compact models in link prediction;

(b) the use of open datasets (which makes it easier

for other researchers to reproduce the experiments)

that cover “future” (DBLP) as well as “missing”

(Amazon and Flickr) link prediction applications; (c)

insertion of some topological measures (the last

three ones described in subsection 2.2) not usually

employed in link prediction state of art to describe

the datasets.

As future work, we consider the use and

evaluation of other classical feature selection

techniques in link prediction, including optimization

meta-heuristics, such as genetic algorithms. It would

be also interesting to use other datasets that include

not only the topological information, but information

from the graph nodes as well, in order to consider a

wider range of features. Experiments with other

classification algorithms for those link prediction

tasks and the use of other evaluation measures such

as recall, F-measure and AUC are also desirable.

ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems

300

ACKNOWLEDGEMENTS

This work has been partially supported by CNPq

(307647/2012-9), FAPERJ (E- 26/111.147/2011)

and CAPES (MSc scholarship).

REFERENCES

Adamic, L. A., Adar, E., 2003. Friends and neighbors on

the web. Social Networks, 25 (3), 211-230.

Barabasi, A. L., Jeong, H., Neda, Z., Ravasz, E., 2002.

Evolution of the social network of scientific

collaboration. Physica A: Statistical Mechanics and its

Applications, 311 (3), 590-614.

Barrat, A., Barthelemy, M., Pastor-Satorras, R. and

Vespignani, A., 2004. The architecture of complex

weighted networks. Proceedings of the National

Academy of Sciences, 101. 3747-3752.

Benchettara, N., Kanawati, R., Rouveirol, C., 2010.

Supervised Machine Learning applied to Link

Prediction in Bipartite Social Networks. International

Conference on Advances in Social Networks Analysis

and Mining, 326-330.

Caruana, R., Karampatziakis, N., Yessenalina, A., 2008.

An empirical evaluation of supervised learning in high

dimensions. International Conference on Machine

Learning (ICML). ACM. 96-103.

Freeman, L. C., 1978. Centrality in social networks

conceptual clarification. Social Networks, 1 (3).

Freitas, A. A., 2002. Data Mining and Knowledge

Discovery with Evolutionary Algorithms, Springer.

New York.

Hagberg, A. A., Schult, D. A., Swart, P. J., 2008.

Exploring network structure, dynamics, and function

using NetworkX. Proceedings of the 7th Python in

Science Conference (SciPy2008). 11-15.

Hasan, M. A., Chaoji, V., Salem, S., Zaki, M., 2006. Link

Prediction using Supervised Learning In Proc. of SDM

06 workshop on Link Analysis, Counterterrorism and

Security, Counterterrorism and Security, SIAM Data

Mining Conference.

Hasan, M. A., Zaki, M. J., 2011. A survey on Link

Prediction in Social Networks. Social Network Data

Analytics. Springer. 243-275.

Huang, Z., Li, X., Chen, H., 2005. Link prediction

approach to collaborative filtering. Proceedings of the

5th ACM/IEEE-CS joint conference on Digital

libraries. ACM. 141-142.

Izudheen, S., Mathew, S., 2013. Link Prediction in

Protein Networks. Indian Journal of Applied

Research, 3 (5).

Jackson, J. E., 1991. A User's Guide to Principal

Components, Wiley. New York.

Katz, L., 1953. A new status index derived from

sociometric analysis. Psychometrika, 18 (1). 39-43.

Kohavi, R., John, G. H., 1997. Wrappers for feature subset

selection. Artificial Intelligence, 97 (1). 273-324.

Leicht, E. A., Holme, P., Newman, M. E. J., 2006, Vertex

similarity in networks. Physical Review E, 73 (2).

Li, X., Chen, H., 2009. Recommendation as link

prediction: a graph kernel-based machine learning

approach. Proceedings of the 9th ACM/IEEE-CS joint

conference on Digital libraries. 213-216.

Liben-Nowell, D., Kleinberg, J., 2003. The link prediction

problem for social networks. Proceedings of the

twelfth international conference on Information and

knowledge management. 556-559.

Lind, P. G., Gonzalez, M. C., Herrmann, H. J., 2005.

Cycles and clustering in bipartite networks. Physical

Review E, 72.

Leskovec, J., Krevl, A., 2014. SNAP Datasets: Stanford

Large Network Dataset Collection. Retrieved from:

http://snap.stanford.edu/data.

Ley, M., 2009. DBLP: some lessons learned. Proceedings

of the VLDB Endowment, 2 (2).

Lü, L., Jin, C., Zhou, T., 2009. Similarity index based on

local paths for link prediction of complex networks. In

Physical Review, 80.

Lü, L., Zhou, T., 2011. Link prediction in complex

networks: A survey. Physica A, 390.

Narang, K.; Lerman, K. & Kumaraguru, P., 2013.

Network flows and the link prediction problem.

Proceedings of the 7th Workshop on Social Network

Mining and Analysis.

Oyama, S., Hayashi, K., Kashima, H., 2011, Cross-

temporal Link Prediction. Proceedings of the 11th

International Conference on Data Mining (ICDM).

Papadimitriou, A., Symeonidis, P., Manolopoulos, Y.,

2012. Fast and Accurate Link Prediction in Social

Networking Systems. Journal of Systems and

Software, 85 (9).

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P.,

Weiss, R., Dubourg, V., VanderPlas, J., Passos, A.,

Cournapeau, D., Brucher, M., Perrot, M., Duchesnay,

E., 2011. Scikit-learn: Machine Learning in Python.

Journal of Machine Learning Research, 12.

Pujari, M., Kanawati, R., 2012. Tag Recommendation by

Link Prediction Based on Supervised Machine

Learning. Proceedings of the Sixth International

Conference on Weblogs and Social Media.

Sa, H. R., Prudencio, R. B. C., 2011. Supervised link

prediction in weighted networks. The 2011

International Joint conference on Neural Networks

(IJCNN).

Saramäki, J.; Kivelä, M.; Onnela, J.; Kaski, K. & Kertesz,

J., 2007. Generalizations of the clustering coefficient

to weighted complex networks. Physical Review, 75

(2).

Shojaie A., 2013. Link Prediction in Biological Networks

using Penalized Multi-Mode Exponential Random

Graph Models. Proceedings of the 13th KDD

Workshop on Learning and Mining with Graphs.

Symeonidis, P., Iakovidou, N., Mantas, N.,

Manolopoulos, Y., 2013. From biological to social

networks: Link prediction based on multi-way spectral

clustering. Data & Knowledge Engineering, 87.

DimensionalityReductionforSupervisedLearninginLinkPredictionProblems

301

Wang, L., Hu, K., Tang, Y., 2013. Robustness of Link-

prediction Algorithm Based on Similarity and

Application to Biological Networks. Current

Bioinformatics, 9 (3).

Xu, Y., Rockmore, D., 2012. Feature selection for link

prediction. Proceedings of the 5th Ph.D. workshop on

Information and knowledge. 25-32.

Yu, L., Liu, H., 2003. Feature selection for high-

dimensional data: a fast correlation-based filter

solution. Machine Learning International Workshop

Then Conference, 20 (2).

ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems

302