
Plane-Sweep Algorithms for the K Group Nearest-Neighbor Query
George Roumelis
1
, Michael Vassilakopoulos
2
, Antonio Corral
3
and Yannis Manolopoulos
1
1
Department of Informatics, Aristotle University, GR-54124 Thessaloniki, Greece
2
Department of Electrical and Computer Engineering, University of Thessaly, GR-38221 Volos, Greece
3
Department of Informatics, University of Almeria, 04120 Almeria, Spain
groumeli@csd.auth.gr, mvasilako@uth.gr, acorral@ual.es, manolopo@csd.auth.gr
Keywords:
Spatial Query Processing, Plane-Sweep, Group Nearest-Neighbor Query, Algorithms.
Abstract:
One of the most representative and studied queries in Spatial Databases is the (K) Nearest-Neighbor (NNQ),
that discovers the (K) nearest neighbor(s) to a query point. An extension that is important for practical ap-
plications is the (K) Group Nearest Neighbor Query (GNNQ), that discovers the (K) nearest neighbor(s) to a
group of query points (considering the sum of distances to all the members of the query group). This query
has been studied during the recent years, considering data sets indexed by efficient spatial data structures. We
study (K) GNNQs, considering non-indexed data sets, since this case is frequent in practical applications. And
we present two (RAM-based) Plane-Sweep algorithms, that apply optimizations emerging from the geometric
properties of the problem. By extensive experimentation, using real and synthetic data sets, we highlight the
most efficient algorithm.
1 INTRODUCTION
Spatial database is a database that offers spatial data
types (for example, types for points, line segments,
regions, etc.), a query language with spatial predi-
cates, spatial indexing techniques and efficient pro-
cessing of spatial queries (Rigaux et al., 2002). It has
grown in importance in several fields of application
such as urban planning, resource management, trans-
portation planning, etc. Together with them come
various types of complex queries that need to be an-
swered efficiently.
One of the most representative and studied queries
in Spatial Databases is the (K) Nearest-Neighbor
Query (NNQ), that discovers the (K) nearest neigh-
bor(s) to a query point. An extension that is impor-
tant for practical applications is the (K) Group Near-
est Neighbor Query (GNNQ), that discovers the (K)
nearest neighbor(s) to a group of query points (con-
sidering the sum of distances to all the members of
the query group). This query has been studied during
the recent years, considering data sets indexed by effi-
cient spatial data structures. An example of its utility
could be when we have a set of meeting points (data
set) and a set of user locations (query set), and we
want to find the set of one (K) meeting point(s) that
minimizes the sum of distances for all user locations,
since each user will travel from his location to each
of the K meeting points. More specifically, user lo-
cations may represent residence locations and meet-
ing points may represent points of interest (cultural
landmarks). Each of the K points is visited by each
user for whole day inspection and the user returns to
his residence overnight, before visiting the next land-
mark on the following day. We may interested to
solve such a problem for a specific pair of data and
query sets only once, but we may face several such
problems for different pairs of sets. Note that, buid-
ing indexes for the data sets would be needed only if
several queries would be answered for the these data
sets, which might evolve gradually in the course of
time and not be completely replaced by new data sets.
One of the most important techniques in the com-
putational geometry field is the Plane-Sweep (PS) al-
gorithm, which is a type of algorithm that uses a con-
ceptual sweep line to solve various problems in the
Euclidean plane, E
2
, (Preparata and Shamos, 1985).
The name of PS is derived from the idea of sweep-
ing the plane from left to right with a vertical line
(front) stopping at every transaction point of a geo-
metric configuration to update the front. All process-
ing is done with respect to this moving front, without
any backtracking, with a look-ahead on only one point
each time (Hinrichs et al., 1988). For instance, the
PS technique has been successfully applied in spatial
query processing, mainly for intersection joins (Jacox
83
Roumelis G., Vassilakopoulos M., Corral A. and Manolopoulos Y..
Plane-Sweep Algorithms for the K Group Nearest-Neighbor Query.
DOI: 10.5220/0005375300830093
In Proceedings of the 1st International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM-2015), pages
83-93
ISBN: 978-989-758-099-4
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

and Samet, 2007).
In (Roumelis et al., 2014), the problem of process-
ing K Closest Pair Query between RAM-based point
sets was studied, using PS algorithms. Two improve-
ments that can be applied to a PS algorithm and a
new algorithm that minimizes the number of distance
computations, in comparison to the classic PS algo-
rithm, were proposed. By extensive experimentation,
using real and synthetic data sets, the most efficient
improvement was highlighted and it was shown that
the new PS algorithm outperforms the classic one.
In this paper, we study (K) GNNQs, considering
non-indexed data sets (a frequent case in practical ap-
plications, see the example given previously), unlike
previous research presented in Section 2 that consider
that both data sets are indexed by structures of the
R-tree family. Our target is to design efficient non-
index based algorithms for (K) GNNQs and highlight
the most efficient among them. Thus, we present two
(RAM-based) PS algorithms, that apply optimizations
emerging from the geometric properties of the prob-
lem. Several experiments have been performed, using
real and synthetic data sets, to show the most efficient
algorithm. In the future, we plan to compare the best
of our algorithms to existing index based solutions.
The paper is organized as follows. In Section 2,
we review the related literature and motivate the re-
search reported here. In Section 3, two new PS al-
gorithms for GNNQs are presented. In Section 4, a
comparative performance study is reported. Finally,
in Section 5, conclusions on the contribution of this
paper and future work are summarized.
2 RELATED WORK AND
MOTIVATIONS
GNN queries are introduced in (Papadias et al., 2004)
and it consist in given two sets of points P and Q,
a GNN query retrieves the point(s) of P with the
smallest sum of distances to all points in Q. GNN
queries are also known as aggregate nearest neighbor
(ANN) queries (Papadias et al., 2005). In (Papadias
et al., 2004), the authors have developed three differ-
ent methods were developed, MQM (multiple query
method), SPM (single point method) and MBM (min-
imum bounding method), to evaluate a GNN query
that minimizes the total distance from a set of query
points to a data point. In (Papadias et al., 2005) these
methods have been extended to minimize the mini-
mum and maximum distance in addition to the total
distance with respect to a set of query points. All
these methods assume that the data points are indexed
using an R-tree and can be implemented using both
depth-first search and best-first search algorithms.
In general terms, MQM performs an incremental
search for the nearest data point of each query point
in the set and compute the aggregate distance from
all query points for each retrieved data point. The
search ends when it is ensured that the aggregate dis-
tance of any non-retrieved data point in the database is
greater than the current K-th minimum aggregate dis-
tance, that is the K GNNs are found. It means MQM
is a threshold algorithm, since it computes the nearest
neighbor for each query point incrementally, updat-
ing different thresholds according to the target of the
KGNN. The main disadvantage of MQM is that it tra-
verses the R-tree multiple times and it can access the
same data point more than once.
The other methods, SPM and MBM, find the K
GNNs in a single traversal of the R-tree. SPM ap-
proximates the centroid of the query distribution area
and continues the searching with respect to the cen-
troid until the current KGNNs are determined. Dur-
ing the search, some heuristics based on triangular
inequality are used to prune intermediate nodes and
determine the real nearest neighbors to Q. MBM re-
gards Q as a whole and uses its MBR M to prune the
search space in a single query, in either a depth-first
or best-first manner. Moreover, two pruning heuristics
involving the distance from an intermediate node to M
or query points are proposed and they can be used in
either traversal policy. Experimental results showed
that the performance of MBM is better than SPM and
MQM for memory and disk resident queries, since
it traverses the R-tree once and takes the query dis-
tribution area into account. Moreover, according to
the comparison conducted in (Papadias et al., 2004),
MBM is better than SPM in terms of node access and
CPU cost while MQM is the worst.
In (Li et al., 2005), the authors propose two prun-
ing strategies for KGNN queries which take into ac-
count the distribution of query points. Such methods
employ an ellipse to approximate the extent of mul-
tiple query points, and then derive a distance or min-
imum bounding rectangle using that ellipse to prune
intermediate nodes in a depth-first search via an R
∗
-
tree. These methods are also applicable to the best-
first traversal. The experimental results show that the
proposed pruning strategies are more efficient than the
methods presented in (Papadias et al., 2004).
A new method to evaluate a KGNN query for non-
indexed data points using projection-based pruning
strategies was presented in (Luo et al., 2007). Two
points projecting-based ANNQ algorithms were pro-
posed, which can efficiently prune the data points
without indexing. This new method projects the query
points into a special line, on which their distribution
GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement
84

is analysed, for pruning the search space.
In (Namnandorj et al., 2008), a new property in
vector space was proposed and, based on it some effi-
cient bound estimations were developed for two most
popular types of ANN queries (sum and maximum).
Taking into account these bounds, indexed and non-
index ANN algorithms were designed. The proposed
algorithms showed interesting results, especially for
high dimensional queries.
Other related contributions in this research line
have been proposed in the literature. In (Hashem
et al., 2010) an efficient algorithm for KGNN query
considering privacy preserving was proposed, and the
existing KGNN algorithms (Papadias et al., 2005)
for point locations were extended to regions in or-
der to preserve user privacy. In (Zhu et al., 2010),
the KGNN query in road networks based on network
voronoi diagram was solved. In (Jiang et al., 2013),
the reverse top-K group nearest neighbor search is
presented. In (Zhang et al., 2013), the KNN and
KGNN queries are extended to get a new type of
query, so-called K Nearest Group (KNG) query. It
retrieves closest elements from multiple data sources,
and it finds K groups of elements that are closest to
a given query point, with each group containing one
object from each data source. And recently, for uncer-
tain databases, probabilistic KGNN query was studied
by (Lian and Chen, 2008; Li et al., 2014).
Therefore, the KGNN is an active research line
nowadays and most of the contributions have used in-
dexes (of the R-tree family) for their solutions. The
main motivation of this paper is to use the Plane-
Sweep technique to solve the problem proposed in
(Papadias et al., 2004), when neither of the inputs
are indexed. Due to not using indexes, the algorithms
proposed in this paper are completely different to pre-
vious solutions. To the best of our knowledge, there
are not any existing solutions for the (K) GNNQ with-
out indexes. The unnecessity of indexes is not in-
frequent in practical applications, when the data sets
change at a very rapid rate, or the data sets are not
reusable for subsequent queries (see the example in
Section 1).
3 PLANE-SWEEP ALGORITHMS
FOR GNNQ
In this section we introduce two Plane-Sweep algo-
rithms for processing GNNQ. The input of this query
consists of a set P = {p
0
, p
1
,··· , p
N−1
} of static data
points in the Euclidean plane, E
2
, and a group of
query points Q = {q
0
,q
1
,··· , q
M−1
}. The output
contains the K (≥ 1) data point(s) with the small-
est sum of distances to all points in Q. The dis-
tance between a data point p ∈ P and Q is defined as
sumdist(p, Q) =
∑
M−1
i=0
dist(p, q
i
), where dist(p, q
i
) is
the Euclidean distance between p ∈ P and a query
point q
i
∈ Q. A simple application of Plane-Sweep,
assuming that both data sets are sorted in ascending
order of their X -values, would compute the sum of
distances of each data point to all the query points, by
examining the data points from left to right, along the
sweeping axis (e.g. X-axis). In the following we will
denote the sum of distances (dx-distances) of a data
point p to the set of query points Q by sumdist(p, Q)
(sumdx(p, Q)). Note that, while the sweep line ap-
proaches (moves away from) the median point(s),
sumdx will be decreasing (increasing). This is proved
in the Appendix. And, sumdx(p, Q) ≤ sumdist(p, Q),
for a data point p ∈ P. Besides, we must empha-
size that dx-distance (dx dist(p,q), ∆x(p,q)) is the
distance function between two points p and q over
the X -axis, an analogous expression is for dy-distance
(dy dist(p, q), ∆y(p,q)) over the Y-axis. And the
sum of dx-distances between one given point p ∈ P
and all query points of Q (q
i
∈ Q) is defined as
sumdx(p, Q) =
∑
M−1
i=0
dx
dist(p, q
i
).
A max binary heap (keyed by sumdist and called
MaxKHeap) that keeps the K data points with the
smallest sum of distances to the query points found so
far is used. The sumdist of the root of the MaxKHeap
is denoted by δ. In case the heap is not full (it contains
less than K points), p will be inserted in the heap, re-
gardless of sumdist(p,Q). Otherwise, for each data
point p being compared with the query set Q, there
are 2 cases:
1. Case 1: If sumdx(p,Q) is larger than or equal to
δ, then there is no need to calculate sumdist(p, Q)
(rule 1).
2. Case 2: If the sumdist(p,Q) is smaller than δ,
then p will be inserted in the heap (rule 2).
Let p with sumdx(p, Q) ≥ δ, then, for every
p
0
with p
0
.x ≥ p.x, sumdx(p
0
,Q) ≥ sumdx(p, Q).
Moreover, sumdist(p
0
,Q) ≥ sumdx(p
0
,Q). Thus,
sumdist(p
0
,Q) ≥ δ and we do not need to calculate
any distance for p
0
.
In the algorithms that we have developed, we find
a data point p
i
∈ P that is X-closest to the median
point of the query set Q (in case that the query set
contains an even number of points, we choose the
right of the two median points). This data point is
found by binary search. The sweep line is located
on p
i−1
and moves to left until a data point p with
sumdx(p, Q) ≥ δ is found (termination condition 1).
Then, the sweep line is located on p
i
and moves to
the right until a data point p with sumdx(p, Q) ≥ δ
(termination condition 2). At this stage, MaxKHeap
Plane-SweepAlgorithmsfortheKGroupNearest-NeighborQuery
85

Algorithm 1: GNNPS.
Input: Two X-sorted arrays of points P = {p[0], p[1],· ·· , p[N − 1]}, Q = {q[0], q[1],··· ,q[M − 1]}, and MaxKHeap.
Output: MaxKHeap storing the K Nearest Neighbors having smallest sums of distances to all query points.
1: i = f ind closest point(P, q[m]) STEP 1 : Preperation. q[m] is the median point of query set Q.
2: j = i − 1
3: while j > −1 do STEP 2 : Search in the range p[ j].x ≤ q[m].x, descending j
4: if calc sum dist(p[ j − −], Q,MaxKHeap) == err code dx then Termination condition 1
5: break
6: while i < N do STEP 3 : Search in the range p[i].x > q[m].x, ascending i
7: if calc sum dist(p[i + +],Q,MaxKHeap) == err code dx then Termination condition 2
8: break
Algorithm 2: calc sum dist.
Input: One point p, the sorted array of query points Q = {q[0],q[1], ··· ,q[M − 1]}, and MaxKHeap.
Output: Value success f ul insertion or err code dx or err code dist and MaxKHeap updated with p if rule 2 was true.
1: function calc sum dist(p, Q, MaxKHeap)
2: sumdist = 0.0, sumdx = 0.0
3: if MaxKHeap is not f ull then
4: for k = 0;k < M; k + + do for each query point q
5: sumdist+ = dist(p,q[k]) dist() computes the Euclidean distance between p and q[k]
6: MaxKHeap.insert(p,sumdist)
7: return sucess f ul insertion
8: else
9: for k = 0;k < M; k + + do for each query point q
10: sumdx+ = dx dist(p,q[k]) dx dist() computes the dx-distance between p and q[k] (∆x(p, q[k]))
11: if sumdx ≥ MaxKHeap.root.dist then Rule 1
12: return err code dx exit k, all other points have longer distance
13: for k = 0;k < M; k + + do for each query point q
14: sumdist+ = dist(p,q[k]) add the distance (dist) from the current point
15: if sumdist < MaxKHeap.root.dist then Rule 2
16: MaxKHeap.insertFull(p,sumdist)
17: return sucess f ul insertion
18: else
19: return err code dist not inserted because of sum of distances (sumdist)
will contain the K data points with the smallest sum
of distances to the query points.
In (Papadias et al., 2004) it was proved that
for every data point p with |Q| · dist(p,c) ≥ δ +
sumdist(c, Q), p can be ignored, without calculating
any distance. In the second algorithm that we have de-
veloped, the centroid c of the query points is also used
and the above condition is a pruning condition for
points that saves a significant number of calculations.
Moreover, in the second algorithm, when the sweep
line is outside of the area of query points, then for the
current data point p, sumdx(p, Q) = |Q| · |p.x − c.x|.
Using this condition, we save numerous calculations.
In the Appendix, we prove that the sum of dx-
distances between one given point p(x, y) ∈ P and all
points of the query set Q (sumdx(p, Q)):
A Is minimized at the median point q[m] (where q[m]
is the array notation of q
m
),
B For all p.x ≥ q[m].x, sumdx is constant or increas-
ing with the increment of x, and
C For all p.x < q[m].x, sumdx is increasing while x
decreases.
The first algorithm (that is only based on median)
is called GNNPS and it uses the helper algorithm
calc sum dist and the function f ind closest point.
Firstly, it calculates the initial position of the sweep-
ing line (preparation state). For this, the algorithm
must find the first point p[i] ∈ P which is on the right
of the median of query set q[m] (p[i].x > q[m].x), by
calling the function f ind closest point (line 1). After
this, the algorithm sets the sweeping line at the point
p[i − 1] (line 3) and continues scanning the points of
set P decreasing the index i until the termination con-
dition 1 will be true or the points of set p will have fin-
ished (lines 3-5). Lastly, the algorithm sets the sweep-
ing line at the point p[i] and continues scanning the
points of set P increasing the index i until the termi-
nation condition 2 will be true or the points of the set
P will have finished (lines 6-8).
The second algorithm (that is based on median and
centroid) is called GNNPSC and it uses the helper
GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement
86

Algorithm 3: GNNPSC.
Input: Two X-sorted arrays of points P = {p[0], p[1],· ·· , p[N − 1]}, Q = {q[0], q[1],··· ,q[M − 1]}, and MaxKHeap.
Output: MaxKHeap storing the K Nearest Neighbors having smallest sums of distances to all query points.
1: i = f ind closest point(P, q[m]) STEP 1 : Preperation. q[m] is the median point of query set Q.
2: j = i − 1
3: c(x,y) = Calculate Centroid coord(Q) calculate the coordinates of the Centroid
4: sumdistCQ = 0.0
5: for k = 0; k < M;k + + do for each query point q
6: sumdistCQ+ = dist(c, q[k])
STEP 2 : Search in the range p[ j].x ≤ q[m].x, descending j
7: cont search = true initialize the flag
8: while j > −1 and p[ j].x > q[0].x do for each point p[ j] inside the query MBR in sweeping axis (X-axis)
9: if calc sum dist in(p[ j − −], Q,c,sumdistCQ,MaxKHeap) == err code dx then Termination condition 1
10: cont search = f alse
11: break
12: if cont search = true then
13: while j > −1 do for each point p[ j] on the left of the query MBR in sweeping axis
14: if calc sum dist out(p[ j − −],Q, c,sumdistCQ, MaxKHeap) == err code dx then Termination condition 1
15: break
STEP 3 : Search in the range p[i].x > q[m].x, ascending i
16: cont search = true
17: while i < N and p[i].x < q[M − 1].x do for each point p[i] inside the query MBR in sweeping axis
18: if calc sum dist in(p[i + +],Q,c,sumdistCQ,MaxKHeap) == err code dx then Termination condition 2
19: cont search = f alse
20: break
21: if cont search = true then
22: while i < N do for each point p[i] on the left of the query MBR in sweeping axis
23: if calc sum dist out(p[i + +],Q,c,sumdistCQ,MaxKHeap) == err code dx then Termination condition 2
24: break
algorithms calc sum dist in and calc sum dist out
and the function f ind closest point. Firstly, the
algorithm calculates the initial position of the
sweeping line and the coordinates of the cen-
troid (preparation state). For these, the algorithm
calls the functions f ind closest point (line 1) and
Calculate Centroid coord(Q) (line 3). In the next
step, it continues scanning the points of set P decreas-
ing the index j until the termination condition 1 will
be true or the x-coordinate of the current point of set
P is smaller than or equal to the X -coordinate of the
first query point q[0] (p[ j].x ≤ q[0]). In this state,
GNNPSC calls the function calc sum dist in to cal-
culate the sum of distances. After exiting the previous
loop and if the termination condition 1 has not arisen
(line 12), the algorithm continues decreasing j until
the termination condition 1 will be true or the points
of set P will have finished (lines 13-15). Lastly, the
algorithm sets the sweeping line at the point p[i] and
continues scanning the points of set P increasing the
index i just like in the previous step (lines 17-20 in-
side query set Q and lines 21-24 outside query set Q).
We must highlight that the function calc sum dist in
is the same as calc sum dist, adding two new param-
eters (the centroid of Q (c) and its sum of distances to
all query points (sumdistCQ)) and the following state-
ments just after the line 9.
9 : dist pc = calc dist(p, c)
10 : if M ·dist pc ≥ maxKheap.root.dist + sumdistCQ then
11 : return err code dist centroid
And the remaining statements of calc sum dist in
from line 12 (12-22) are the same as calc sum dist.
The following examples illustrate the execution
of the algorithms. The point data set P is defined as
P = {p
0
(1,7); p
1
(2,4); p
2
(3,1); p
3
(3,13); p
4
(8,2);
p
5
(8,18); p
6
(9,10); p
7
(10,19); p
8
(12,12); p
9
(13,4);
p
10
(14,12); p
11
(16,6); p
12
(19,8); p
13
(19,17);
p
14
(20,3); p
15
(22,7) }, and the point query set Q
is defined as Q = {q
0
(9,7); q
1
(10,11); q
2
(12,4);
q
3
(17,7); q
4
(19,11) }. In Figure 1, P and Q (they
are sorted in ascending order of their X -values), the
centroid and the median of the query points and the
initial position of the sweep line are drawn.
In GNNPS, firstly (in Step 1) the algorithm
searches for the point of the P set which is on
the right of the median q
2
(12,4) query point (line
1). That is p
9
(13,4) point. In Step 2 (lines 3-5)
it starts calculating the sum of distances between
point p
8
(12,12) and all query points. The result
is sumdist(p
8
,Q) = 30.209 and the point p
8
is in-
serted in the MaxKHeap (calc sum dist:lines 2-7).
In the next iteration the point p
7
(10,19) is examined.
The MaxKHeap is full and the second part of the
calc sum dist function (lines 9-19) is executed. The
sum of distances is sumdist(p
7
,Q) = 61.108 larger
than the MaxKHeap.root.dist = 30.209 (condition in
Plane-SweepAlgorithmsfortheKGroupNearest-NeighborQuery
87

Algorithm 4: calc sum dist in.
Input: One point p, set of query points Q, centroid c, its sum of distances to all query points sumdistCQ and MaxKHeap.
Output: Value success f ul insertion or err code dx or err code dist and MaxKHeap updated with p if rule 2 was true.
1: function calc sum dist in(p, Q, c, sumdistCQ, MaxKHeap)
2: sumdist = 0.0, sumdx = 0.0
3: if MaxKHeap is not f ull then
4: for k = 0;k < M; k + + do for each query point q
5: sumdist+ = dist(p,q[k]) dist() computes the dx-distance between p and q[k]
6: MaxKHeap.insert(p,sumdist)
7: return sucess f ul insertion
8: else
9: d pc = dist(p,c) dist() computes the distance between p and c
10: if M · d pc − sumdistCQ ≥ MaxKHeap.root.dist then prune p without computing distances
11: return err
code dist; not inserted because of sum of distances
12: for k = 0;k < M; k + + do for each query point q
13: sumdx+ = dx dist(p,q[k]) dx dist() computes the dx-distance between p and q[k] (∆x(p, q[k]))
14: if sumdx ≥ MaxKHeap.root.dist then Rule 1
15: return err code dx exit k, all other points have longer distance
16: for k = 0;k < M; k + + do for each query point q
17: sumdist+ = dist(p,q[k]) add the distance (dist) from the current point
18: if sumdist < MaxKHeap.root.dist then Rule 2
19: MaxKHeap.insertFull(p,sumdist)
20: return sucess f ul insertion
21: else
22: return err code dist not inserted because of sum of distances (sumdist)
Figure 1: The points of P and Q, the centroid, the median of
the query points and the initial position of the sweep line.
the calc sum dist:line 15 is false), so the point is re-
jected (calc sum dist:line 19). In the third iteration
the point p
6
(9,10) is examined and the sum of dis-
tances is sumdist(p
6
,Q) = 29.716 which is smaller
(condition of calc sum dist:line 15 is true) than the
MaxKHeap.root.dist therefore the point p
6
is in-
serted in the MaxKHeap (calc sum dist:lines 16,17)
by replacing the previous root (p
8
). In the fourth
and fifth iterations for the points p
5
and p
4
the
sum of distances are sumdist(p
5
,Q) = 60.317 and
sumdist(p
4
,Q) = 43.299, respectively; both larger
than the MaxKHeap.root.dist and the points are
rejected. In the sixth iteration, the point p
3
has
sumdx(p
3
.x,Q) = 52 (condition in calc sum dist:line
11) which is larger than the MaxKHeap.root.dist
and the process (scanning the P set on the left)
ends (calc sum dist:line 12) because it is impossi-
ble to find other points of set P on the left of p
3
having sum of distances smaller than 52. The al-
gorithm continues scanning the points of set P to
the right of the median q
2
, starting from the p
9
point. Its sumdist(p
9
,Q) = 27.835 is smaller than
the MaxKHeap.root.dist = 29.716 so it replaces
the existing point in the root of MaxKHeap. The
next point p
10
has sumdist(p
10
,Q) = 30.370 and it
is rejected. The next iteration will try the point
p
11
which has sumdist(p
11
,Q) = 26.599 the small-
est sum of distances and this point (p
11
) is in-
serted in the MaxKHeap replacing the previous root
p
9
. In the last iteration the algorithm examines
the point p
12
which has sumdx(p
12
,Q) = 28 larger
than the MaxKHeap.root.dist = 26.599 and the pro-
cess is finally finished. While executing this algo-
rithm we made 46 complete point-point distance cal-
culations, 84 point-point dx-distance calculations, 4
points with their sum of distances were inserted in the
MaxKHeap and 10 of the 16 points of set P were ex-
amined.
GNNPSC starts (Step 1) by finding the first point
of set P which is on the right of the median point of
query set Q. That is the point p
9
. Afterwards it calcu-
lates the coordinates of centroid point c(x,y) = (13,8)
and then calculates the sum of distances between the
centroid and the query points sumdist(c,Q) = 23.374.
GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement
88

Algorithm 5: calc sum dist out.
Input: One point p, set of query points Q, centroid c, its sum of distances to all query points sumdistCQ and MaxKHeap.
Output: Value success f ul insertion or err code dx or err code dist and MaxKHeap updated with p if rule 2 was true.
1: function calc sum dist out(p, Q, c, sumdistCQ, MaxKHeap)
2: sumdist = 0.0, sumdx = 0.0
3: if MaxKHeap is not f ull then
4: for k = 0;k < M; k + + do for each query point q
5: sumdist+ = dist(p,q[k]) dist() computes the dx-distance between p and q[k]
6: MaxKHeap.insert(p,sumdist)
7: return sucess f ul insertion
8: else
9: dx = dx dist(p,c) dx dist() computes the dx-distance between p and c (∆x(p, c))
10: if M · dx ≥ MaxKHeap.root.dist then Rule 1
11: return err code dx; exit k, all other points have longer distance
12: dy = dy dist(p,c) dy dist() computes the dy-distance between p and c (∆y(p,c))
13: dist pc =
p
dx
2
+ dy
2
14: if M · dist pc ≥ MaxKHeap.root.dist + sumdistCQ then
15: return err code dist centroid;
16: for k = 0;k < M; k + + do for each query point q
17: sumdist+ = dist(p,q[k])
18: if sumdist < MaxKHeap.root.dist then Rule 2
19: MaxKHeap.insertFull(p,sumdist)
20: return sucess f ul insertion
21: else
22: return err code dist not inserted because of sum of distances (sumdist)
GNNPSC continues with Step 2. In that step,
the points of set P are scanned on the left of the
p
9
in two particular steps. First from p
8
up to
p
7
which have X-coordinate larger than q
0
.x = 9
by calling the calc
sum dist in function. There
is sumdist(p
8
,Q) = 30.209 and this point is in-
serted in the MaxKHeap as the first point while
the maxKHeap is empty (calc sum dist in:lines 3-
7). The point p
7
is examined next and it is rejected
without a need to calculate sumdist(p
7
,Q) because
the condition of the function calc sum dist in:line
10 is true. Step 2 continues scanning the points
of set P which are on the left (outside) of the q
0
query point by calling the function calc sum dist out.
The point p
6
with sumdist(p
6
,Q) = 29.716 is in-
serted (calc sum dist in:lines 9-20), while points p
5
and p
4
are rejected with sumdist(p
5
,Q) = 60.137
and sumdist(p
4
,Q) = 43.299 respectively, both larger
than the MaxKHeap.root.dist = 29.716 with the
point p
6
. The next point p
3
is the last point to be
examined because it has sumdx(p
3
,Q) = 52 larger
than the current MaxKHeap.root.dist. The algo-
rithm continues by executing Step 3, scanning the
points of set P on the right of the median query
point q
2
. The algorithm continues scanning the
points of set P to the right starting from the p
9
point. Its sumdist(p
9
,Q) = 27.835 is smaller than
the MaxKHeap.root.dist = 29.716 so it replaces the
existing point in the root of MaxKHeap. The next
point p
10
has sumdist(p
10
,Q) = 30.370 and it is re-
jected. The next iteration will try the point p
11
which
has sumdist(p
11
,Q) = 26.599 the smallest sum of dis-
tances and this point is inserted in the MaxKHeap re-
placing the previous root p
9
. In the last iteration we
examine the point p
12
which has sumdx(p
12
,Q) = 28
larger than the MaxKHeap.root.dist = 26.599 and
the process is finally finished. While executing this
algorithm we made 42 complete point-point distance
calculations, 38 point-point dx-distance calculations,
4 points with their sum of distances were inserted in
the MaxKHeap and 10 of 16 points of set P were ex-
amined.
4 EXPERIMENTATION
In order to evaluate the behaviour of the proposed
algorithms, we have used 6 real spatial data sets of
North America, representing cultural landmarks (CL
with 9203 points) and populated places (PP with
24493 points), roads (RD with 569120 line-segments)
and railroads (RR with 191637 line-segments). To
create sets of points, we have transformed the MBRs
of line-segments from RD and RR into points by tak-
ing the center of each MBR (i.e., |RD| = 569120
points, |RR| = 191637 points). Moreover, in order to
get the double amount of points from RR and RD, we
chose the two points with min and max coordinates of
the MBR of each line-segment (i.e. |RDD| = 1138240
points and |RRD| = 383274 points). The data of these
Plane-SweepAlgorithmsfortheKGroupNearest-NeighborQuery
89
6 files were normalized in the range [0, 1]
2
. The real
data sets we used are geographical. In order to test
the performance of our algorithms with data appear-
ing in Science, we have created synthetic clustered
data sets of 125000 (125K), 250000 (250K), 500000
(500K) and 1000000 (1000K) points, with 125 clus-
ters in each data set (uniformly distributed in the
range [0,1]
2
), where for a set having N points, N/125
points were gathered around the center of each cluster,
according to Gaussian distribution (this distibution is
common for natural properties of systems within Sci-
ence). The first real data set (CL) was used to make
the query set (Q) by selecting the appropriate num-
ber of points randomly. Then the coordinates of these
points were appropriately scaled in order to get the
MBR of the query points to get a pre-defined size in
comparison to the MBR of the data set (P). The other
9 data sets were used as data sets (P) within which we
were looking for the NNs.
All experiments were performed on a PC with In-
tel Core 2 Duo, 2.2 GHz CPU with 4 GB of RAM and
several GBs of secondary storage, with Ubuntu Linux
v. 14.04, using the GNU C/C++ compiler (gcc). The
performance measurements were: (1) the response
time (total query execution time) of processing the
(K) GNNQ, not counting reading from disk files to
main memory and sorting, (2) the number of points
involved in calculations, and (3) the number of X-axis
distance computations (dx-distance).
In every experiment the query set was moved on
X-axis in 8 equal size steps from the top left corner
of the area of the data set (P) up to the right corner
and after this, one step down on the Y -axis and so on.
The total execution time, and the other experimenta-
tion metrics, for each one experiment, were computed
as an average of all (the 64) queries.
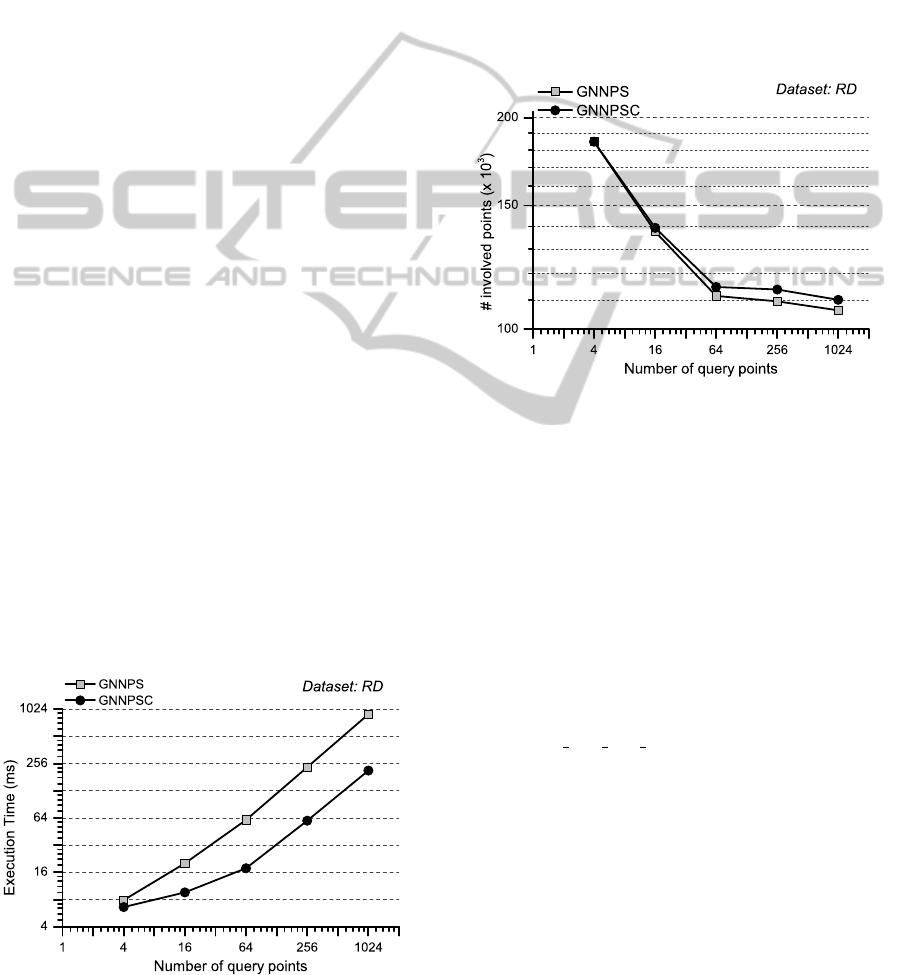
In Figure 2, we depict the effect of the number
of query points, N, on execution time of both al-
Figure 2: Execution time of the algorithms as a function of
N (RD data set).
gorithms for the RD data set (the number of group
nearest-neighbors, K, was equal to 8 and the size of
query-set MBR was 8% of the data set space). Anal-
ogous diagrams created for dx-distance and dist cal-
culations had similar appearance. It is obvious that
the increase of N leads to an increase of the execution
time, but with a smaller rate of increase. GNNPSC
needs less time than GNNPS, because of the use of
centroid (the computation of the distance between the
centroid and the reference point of set P needs one
calculation of distance while the computation of the
sum of distances between the reference point and all
query points needs N distance calculations).
Figure 3: # Points involved in calculations of the algorithms
as a function of N (RD data set).
For the same parameter settings and data set, in
Figure 3, we depict the effect of N on the number
of data set points involved in calculations. We ob-
serve that this number of points is reduced as N in-
creases. The sums of distances of the points of data
set P near the median are enlarged to a smaller ex-
tent, compared to the sumdist of the points outside
the MBR. This enables the termination conditions and
makes it possible to get nearest to the median query
point. Moreover, we can observe in Figure 3 that GN-
NPSC needs more involved points and from Figure 2
it is the fastest. This behaviour could be due to that in
function calc sum dist in we firstly apply the pruning
condition of centroid and next the termination condi-
tion 1 or 2 is checked. So it is possible that some
points may be pruned in GNNPSC rather than being
the cause of termination of the scanning.
In Figure 4, we depict the effect of the size of
the query-set MBR, on dx-distance calculations of
both algorithms for the 1000K data set (the number
of group nearest neighbors, K, was equal to 8 and the
number of query points was equal to 128).
Analogous diagrams created for executions time
and distance calculations had similar appearance. It
is obvious that the increase of the size of the query-
GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement
90
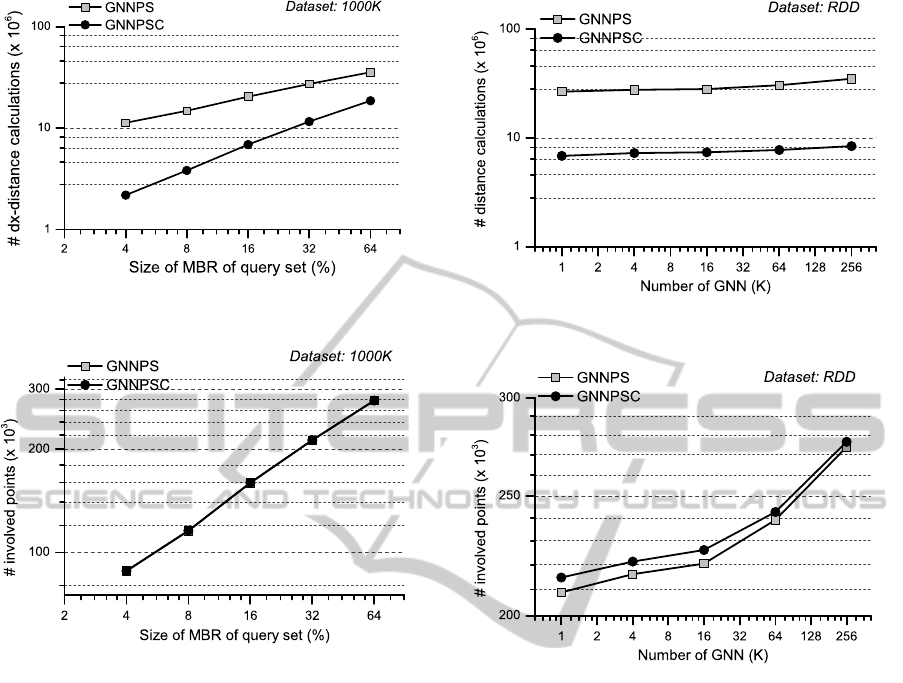
Figure 4: # dx-distance calculations of the algorithms as a
function of the size of MBR (1000K data set).
Figure 5: # Points involved in calculations of the algorithms
as a function of the size of MBR (1000K data set).
set MBR leads to an increase of the execution time,
but with a smaller rate of increase. The size of MBR
M was increased with a ratio of 4. The execution time,
dx-distance and complete distance (dist) calculations
was increased with ratio in the range 1.2 up to 2 for
all data sets of real and synthetic data. For the same
parameter settings and data set, in Figure 5, we de-
pict the effect of the size of the query-set MBR on
the number of points involved in calculations. We ob-
serve that this number of points is increased as M in-
creases with a ratio smaller than 1.4. We observe in
this figure that the number of points involved almost
identical and the two lines are overlapped.
In Figure 6, we depict the effect of the number
of group nearest-neighbors, K, on distance calcula-
tions of both algorithms for the RDD data set (the
number of query points, N, was equal to 128 and the
size of query-set MBR was 8% of the data set space).
Analogous diagrams created for execution times and
dx-distance calculations had similar appearance. It is
obvious that the increase of K does not significantly
affect the execution time, dx-distance and complete
distance (dist) calculations. For the same parameter
Figure 6: # distance calculations of the algorithms as a func-
tion of K (RDD data set).
Figure 7: # Points involved in calculations of the algorithms
as a function of K (RDD data set).
settings and data set, in Figure 7, we depict the effect
of K on the number of points involved in calculations.
We observe that this number of points is increased so
slowly that it is going to be seen for values of K larger
than 64.
From the above experiments, we conclude that:
• The number of points of data sets (P) involved
in the calculations of both algorithms is almost
equal. However, the execution time for GNNPSC
remains always lower than the execution time of
GNNPS, due to the pruning condition and the
lower dx-distance calculations cost.
• The main advantages of the Plane-Sweep method
are the absence of recalculation, as each point is
used in calculations once at most, and the absence
of backtracking.
• The decrease of the number of points involved in
the calculations with respect to number of query
points can be justified when the MBR size is con-
stant.
Plane-SweepAlgorithmsfortheKGroupNearest-NeighborQuery
91

5 CONCLUSIONS AND FUTURE
WORK
Processing of GNNQs has been based on index struc-
tures, so far. In this paper, for the first time, we
present new PS algorithms that can be efficiently ap-
plied on RAM-based data for processing the GNNQ.
As the experimentation that we performed, using syn-
thetic and real data sets, shows the use of median (in
GNNPS) and, even more, the use of median and cen-
troid (in GNNPSC), prunes the number of points in-
volved in processing and the number of calculations.
Although, in this paper, we do not present a com-
parison of our algorithms with respect to the algo-
rithms presented in (Papadias et al., 2004), compar-
ing the results that we have presented to the results of
(Papadias et al., 2004) for data sets of similar size (ap-
proximately 24.5K and 192/195K points) we observe
that our algorithms achieve competitive performance.
This is an initial observation. A detailed compari-
son could be performed in the future, using the same
data sets on the same machine. Moreover, the algo-
rithms we present could be transformed / extended to
work on high volume, disk resident data that are trans-
ferred in RAM in blocks. Moreover, the application
of Plane-Sweep to other spatial queries (like Reverse
NNQ) could lead to interesting techniques.
ACKNOWLEDGEMENTS
Work supported by the GENCENG project (SYN-
ERGASIA 2011 action, supported by the Euro-
pean Regional Development Fund and Greek Na-
tional Funds); project number 11SYN 8 1213. Work
also supported by the MINECO research project
[TIN2013-41576-R] and the Junta de Andaluc
´
ıa re-
search project [P10-TIC-6114].
REFERENCES
Ahn, H., Bae, S. W., and Son, W. (2013). Group nearest
neighbor queries in the L
1
plane. In TAMC Confer-
ence, pages 52–61. Springer.
Hashem, T., Kulik, L., and Zhang, R. (2010). Privacy
preserving group nearest neighbor queries. In EDBT
Conference, pages 489–500. ACM.
Hinrichs, K., Nievergelt, J., and Schorn, P. (1988). Plane-
sweep solves the closest pair problem elegantly. In-
formation Processing Letters, 26(5):255–261.
Jacox, E. H. and Samet, H. (2007). Spatial join techniques.
ACM Trans. Database Syst., 32(1):7.
Jiang, T., Gao, Y., Zhang, B., Liu, Q., and Chen, L.
(2013). Reverse top-k group nearest neighbor search.
In WAIM Conference, pages 429–439. Springer.
Li, H., Lu, H., Huang, B., and Huang, Z. (2005).
Two ellipse-based pruning methods for group near-
est neighbor queries. In ACM-GIS Conference, pages
192–199. ACM.
Li, J., Wang, B., Wang, G., and Bi, X. (2014). Efficient pro-
cessing of probabilistic group nearest neighbor query
on uncertain data. In DASFAA Conference, pages 436–
450. Springer.
Lian, X. and Chen, L. (2008). Probabilistic group nearest
neighbor queries in uncertain databases. IEEE Trans.
Knowl. Data Eng., 20(6):809–824.
Luo, Y., Chen, H., Furuse, K., and Ohbo, N. (2007). Ef-
ficient methods in finding aggregate nearest neighbor
by projection-based filtering. In ICCSA Conference,
pages 821–833. Springer.
Namnandorj, S., Chen, H., Furuse, K., and Ohbo, N. (2008).
Efficient bounds in finding aggregate nearest neigh-
bors. In DEXA Conference, pages 693–700. Springer.
Papadias, D., Shen, Q., Tao, Y., and Mouratidis, K. (2004).
Group nearest neighbor queries. In ICDE Conference,
pages 301–312. IEEE.
Papadias, D., Tao, Y., Mouratidis, K., and Hui, C. K.
(2005). Aggregate nearest neighbor queries in spatial
databases. ACM Trans. Database Syst., 30(2):529–
576.
Preparata, F. P. and Shamos, M. I. (1985). Computational
Geometry - An Introduction. Springer, New York, NY.
Rigaux, P., Scholl, M., and Voisard, A. (2002). Spatial
databases - with applications to GIS. Elsevier, San
Francisco, CA.
Roumelis, G., Vassilakopoulos, M., Corral, A., and
Manolopoulos, Y. (2014). A new plane-sweep algo-
rithm for the k-closest-pairs query. In SOFSEM Con-
ference, pages 478–490. Springer.
Zhang, D., Chan, C., and Tan, K. (2013). Nearest group
queries. In SSDBM Conference, page 7. ACM.
Zhu, L., Jing, Y., Sun, W., Mao, D., and Liu, P. (2010).
Voronoi-based aggregate nearest neighbor query pro-
cessing in road networks. In ACM-GIS Conference,
pages 518–521. ACM.
APPENDIX
Lemma: The sum of dx-distances between one given
point p(x,y) ∈ P and all points of the query set Q
(sumdx(p, Q)):
A Is minimized at the median point q[m] (where q[m]
is the array notation of q
m
),
B For all p.x ≥ q[m].x, sumdx is constant or increas-
ing with the increment of x, and
C For all p.x < q[m].x, sumdx is increasing while x
decreases.
GISTAM2015-1stInternationalConferenceonGeographicalInformationSystemsTheory,ApplicationsandManagement
92

*
*
*
*
*
*
*
x
0
x
1
x
k-1
x
k
x
m
x
m+1
x
M-1
q
0
q
1
q
k-1
q
k
q
m
q
m+1
q
M-1
//
// //
*
x
k΄-1
q
k -1΄
//
p
p΄
x x΄
Figure 8: The point p has K query points on the left and the
point p
0
(p
0
.x > p.x) has K
0
query points on the left.
Proof: Property A has been proved in (Ahn et al.,
2013). To prove property B, for every point p ∈ P
and q ∈ Q, we use
∆x(p, q) =
p.x − q.x if p.x ≥ q.x
q.x − p.x if p.x < q.x
If the point p has K query points on
the left (p.x < q[K − 1].x) and M − K
query points on the right (Figure 8), then:
sumdx(p,Q) =
K−1
∑
i=0
(p.x − q[i].x) +
M−1
∑
i=K
(q[i].x − p.x)
= K p.x −
K−1
∑
i=0
q[i].x +
M−1
∑
i=K
q[i] − (M − K)p.x
= (2K − M)p.x −
K−1
∑
i=0
q[i].x +
M−1
∑
i=K
q[i].x
For another point p
0
∈ P with p
0
.x > p.x which
has K
0
query points on the left (Figure 8)
and M − K
0
query points on the right, it is:
sumdx(p
0
,Q) = (2K
0
− M)p
0
.x −
K
0
−1
∑
i=0
q[i].x +
M−1
∑
i=K
0
q[i].x
The difference between dx-distances of the points p
0
and p is:
∆sumdx = sumdx(p
0
,Q) − sumdx(p, Q)
= (2K − M)(p
0
.x − p.x)
+2
"
(K
0
− K)p
0
.x −
K
0
−1
∑
i=K
q[i].x
#
If the set of the query points Q has cardinality M and
this is an even number then there are two medians
q[m1] and q[m2], while if M is odd then there is only
one median point q[m].
B.1 M is even and q[m1].x ≤ p.x < p
0
.x then
M ≤ 2K ≤ 2K
0
so (2K − M) ≥ 0, (p
0
.x − p.x) ≥ 0 and
(K
0
− K)p
0
.x −
K
0
−1
∑
i=K
q[i].x ≥ 0
because p
0
.x ≥ q[i].x, whereas K ≤ i ≤ K
0
B.2 All of the above apply to M if it is odd and it
is only one median point q[m].x ≤ p.x < p
0
.x. It is
proven that for all points p on the right of the median
query point the sum of dx-distances is increasing.
C For both types of cardinality of the query set Q and
for the case p.x < p
0
.x < q[m].x it is:
∆sumdx = (2K − M)(p
0
.x − p.x) + 2(K
0
− K)p
0
.x
−2
K
0
−1
∑
i=K
q[i].x
≤ (2K − M)(p
0
.x − p.x) + 2(K
0
− K)p
0
.x
−2(K
0
− K)p.x
= 2(K − M)(p
0
.x − p.x)
+2(K
0
− K)(p
0
.x − p.x)
= (2K − M + 2K
0
− 2K)(p
0
.x − p.x)
= (2K
0
− M)(p
0
.x − p.x) < 0
It is proven that for all points p on the left of the
median query point the sum of dx-distances is strictly
decreasing.
Plane-SweepAlgorithmsfortheKGroupNearest-NeighborQuery
93
