Privacy-preserving Hybrid Peer-to-Peer
Recommendation System Architecture
Locality-Sensitive Hashing in Structured Overlay Network
Alexander Smirnov
1,2
and Andrew Ponomarev
1
1
St. Petersburg Institute for Informatics and Automation of the RAS, 14
th
line, 39, St. Petersburg, Russia
2
ITMO University, Kronverksky, 49, St. Petersburg, Russia
Keywords: Distributed Collaborative Filtering, Recommendation Systems, Locality-Sensitive Hashing, Peer-to-Peer,
Anonymization, Privacy.
Abstract: Recommendation systems are widely used to mitigate the information overflow peculiar to current life. Most
of the modern recommendation system approaches are centralized. Although the centralized
recommendations have some significant advantages they also bear two primary disadvantages: the necessity
for users to share their preferences and a single point of failure. In this paper, an architecture of a collaborative
peer-to-peer recommendation system with limited preferences’ disclosure is proposed. Privacy in the
proposed design is provided by the fact that exact user preferences are never shared together with the user
identity. To achieve that, the proposed architecture employs a locality-sensitive hashing of user preferences
and an anonymized distributed hash table approach to peer-to-peer design.
1 INTRODUCTION
Recommendation systems play an important role in
modern e-commerce systems by helping users to
make their ways through the abundant variety of
goods and services offers. From an architectural point
of view, most of the widely used recommendation
systems have a centralized design. This design is
beneficial mainly because it allows employing a
broad spectrum of user preference models to predict
the future user behaviour. It also puts all the relevant
user information under control of the
recommendation system provider allowing to
perform various research activities on this
information besides providing online
recommendations to users.
However, the centralized approach has several
drawbacks. First, it introduces a quandary about
privacy and, in a wider perspective, about rights on
the preferences data collected about users. As a rule,
a user is not aware of what information the system
collects about his/her behaviour and cannot extract
this information from the centralized system. On the
other hand, if a recommendation system is abandoned
by its maintainer, all the collected user profiles may
be lost. Second, the centralization usually results in
some kind of preferences partitioning. A user may
communicate with several recommendation systems,
sharing with each system some part of his/her
preferences profile, therefore all user’s preferences
become spread over several recommendation systems
with no chance of being united. This is not desirable,
because a complete preferences profile can
potentially lead to recommendations that are more
accurate. Third, any centralization usually leads to a
single point of failure, however, in modern computer
systems, this drawback is usually alleviated by
multilevel duplication and replication.
On the other hand, decentralization of
recommendation systems brings two main
advantages:
- the recommendation functions can be distributed
among all users, thus, removing the need for a costly
central server and enhancing scalability;
- a decentralized system may improve the users’
privacy, as there exists no central entity owning the
users’ private information (however, this topic is
subtle due to the inherent security issues of peer-to-
peer systems).
There are several approaches to recommendation
system decentralization. In this paper, a user-centric
approach is examined. According to this approach the
532
Smirnov A. and Ponomarev A..
Privacy-preserving Hybrid Peer-to-Peer Recommendation System Architecture - Locality-Sensitive Hashing in Structured Overlay Network.
DOI: 10.5220/0005376905320542
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 532-542
ISBN: 978-989-758-097-0
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

user holds all his/her preferences on his/her own
system. This entirely removes the quandary about
rights – the user fully controls his/her preferences
storage. This can also remove the preferences’
partitioning as all the user preferences become
centralized in a device controlled by the user. When
recommendations are needed, the users’ device sends
recommendation requests to other devices.
Albeit all enumerated issues of the centralized
recommendation systems design are alleviated by the
user-centric decentralized recommendation system
design, it poses several new issues. The main problem
that is addressed in this paper is how to make
recommendations based on collaborative filtering
approach respecting user privacy by not sharing
complete profiles between members of distributed
recommendations network.
In this paper, the recommendation system
architecture that follows the user-centric approach is
proposed. It is based on a structured peer-to-peer
(P2P) network, where each peer corresponds to one
user and holds preferences thereof.
Recommendations are made by means of anonymized
communication between peers. The proposed
architecture enforces privacy by providing limited
preferences disclosure. It means that there is no way
to reliably match ratings and a user’s network address
having no global control over the entire P2P network.
The proposed architecture is a hybrid P2P as it uses
one special node for the data-driven coordination that,
however, is not used directly in the recommendation
process.
The rest of the paper is structured as follows.
Section 2 presents an overview of existing P2P
recommendation systems and approaches. In section
3, the locality-sensitive hashing approach to
recommendations is discussed. Section 4 contains the
description of the proposed recommendation
system’s architecture. Section 5 contains an
experimental evaluation of the proposed ideas. Main
results are summarized in the conclusion.
2 RELATED WORK
Peer-to-peer recommendation systems design is
already addressed in literature.
In Draidi et al. (2011a) and Draidi et al. (2011b)
P2Prec system is proposed. The idea of this system is
to recommend high quality documents related to
query topics and content hold by useful friends (or
friends of friends) of the users, by exploring
friendship networks. To disseminate information
about relevant peers, it relies on gossip algorithms.
For publishing and discovering services a distributed
hash table is used.
The authors of P2Prec employ two-level Latent
Dirichlet Allocation to automatically model topics. At
the global level performed by a bootstrap server a
sample of documents is collected from peers and a set
of topics is inferred. Then at the local level performed
by each peer the local documents are analysed with
respect to common topics. Each user maintains the
friendship network. A user enlarges the friendship
network by accretion of new friends relevant to
queries and overlapping with this users’ friendship
network.
To establish friendship P2Prec use gossip
protocols. Keyword queries are routed recursively
through friends networks, based on user trust and
usefulness.
In a number of methods described in literature, an
overlay network structure based on a similarity
between nodes is built and recommendation
algorithm is defined on this network (Draidi, Pacitti
and Kemme, 2011; Pitsilis and Marshall, 2006).
Recommendations are searched for among
neighbours up to certain depth or certain similarity
threshold.
One of the algorithms of an aligning network
structure to peer similarities is T-Man (Jelasity,
Montresor and Babaoglu, 2009). T-Man relies on the
ability of a peer to measure how it «likes» peers.
Having defined this relation, T-Man algorithm aligns
the structure of the overlay network to juxtapose
peers that «like» each other.
The similarity-based overlay network structure is
extensively studied in Ormandi et al. (2010) where
authors showed that overlay topologies defined by
node similarity have highly unbalanced degree
distributions to be taken into account when load-
balancing the P2P recommendation network. They
also proposed algorithms with favourable
convergence of speed and prediction accuracy taking
load balancing into account, considering
collaborative filtering system where similarity of
users is measured as cosine similarity.
In the proposed architecture, the exact ratings are
not exposed together with a node identity, so there is
no way to say how similar the two nodes are. Using
the locality-sensitive hash values one can possibly say
whether they are likely to be close enough or not.
Another approach is to rely on random walk
search for similar nodes in the ordinary P2P network
using some form of the flooding technique (Tveit,
2001). Similarly Bakker et al. (2009) show that it is
enough to take a random sample of the network and
use the closest elements of that sample to make
Privacy-preservingHybridPeer-to-PeerRecommendationSystemArchitecture-Locality-SensitiveHashinginStructured
OverlayNetwork
533

recommendations.
In Kermarrec et al. (2010), the random walks
approach to collaborative filtering recommendations
is examined in the context of P2P systems. The
authors argue that the effect of random walk in
decentralized environment is different than the
centralized one. They also propose a system where
epidemic protocols (gossip protocols) are used to
disseminate the user similarity information. They
start from a random set of peers and then in series of
random exchanges compare their local-view with the
local view of the remote node, leaving only the most
similar peers in the local view (clustering gossip
protocol). This process converges to form some
overlay based on the peers’ similarity. Then peers that
are not farther than two hops from the given one are
used to make recommendations.
In epidemic protocols, peers have access to a
Random Peer Sampling service (RPS) providing
them with a continuously changing random subset of
the network peers. Each peer maintains a view of the
network, which is initialized at random through RPS
when a peer joins the network. Gossip protocols are
fully decentralized, can handle high churn rates, and
require no specific protocol to recover from massive
failures.
There also published research papers where
structured P2P networks are used. For example, in
Hecht et al., (2012) and Han et al., (2004), distributed
hash tables are used to store ratings. The proposed
approach stands close to this way except the point that
ratings are not stored in a distributed hash table,
instead a fast lookup capability provided by this kind
of P2P architecture is employed for searching similar
peers.
Most of the approaches involve sharing the rating
data between nodes, while in the proposed
architecture it is avoided.
Privacy concerns are directly addressed in Pussep
et al., (2009). The authors propose a file sharing
network where users exchange their data only with
their friends and the recommendation system on the
top of it. They propose a privacy-conserving
distributed collaborative filtering approach that is
based on exchanges of anonymized items’ relevance
ranks between peers. Their approach, however,
allows only unary ratings (initially, the fact of owning
a specific file).
Distributed recommendation systems are also
analysed in quite different context, seeking for
efficient parallel implementations of centralized
recommendation techniques. This research direction
is entirely beyond the scope of this paper.
3 LOCALITY-SENSITIVE
HASHING FOR
RECOMMENDATIONS
Locality-sensitive hashing (LSH) is a method widely
used for a probabilistic solution of k-NN (k Nearest
Neighbours) problem. The idea of this method is to
hash multidimensional objects in such a way that
similar objects (w.r.t. some distance measure defined
on them) are likely to have the same hash value.
3.1 The Idea of LSH
The problem of finding the nearest neighbours is
closely related to the recommendation systems
research area. The reason is rather straightforward
and is based on an assumption that users that had
similar preferences in the past are likely to have
similar preferences now (and in the future).
Therefore, if user preferences are represented as a
numerical vector and some measure is introduced in
that vector space that corresponds to preference
similarity, then the problem of finding similar users
translates into the nearest neighbours search. In this
section, a formal description of collaborative filtering
recommendation method based on the locality-
sensitive hashing is provided.
Let d
1
< d
2
be two distances according to some
distance measure d. А family F of functions is said to
be (d
1
, d
2
, p
1
, p
2
)-sensitive if for every f in F
(Rajaraman and Ulman, 2012):
• If d(a, b) ≤ d
1
, then probability that f(a) = f(b) is
at least p
1
.
• If d(a, b) ≥ d
2
then probability that f(a) = f(b) is
at most p
2
.
An important concept in the locality-sensitive
hashing theory is an amplification. Given a (d
1
, d
2
, p
1
,
p
2
)-sensitive family F, a new family F’ can be
constructed by either AND-construction or OR-
construction.
AND-construction of F’ is defined as follows.
Each member of F’ consists of r members of F for
some fixed r. If f is in F’ and f is constructed from the
set {f
1
, f
2
, …, f
r
} of members of F, f(x) = f(y) if, and
only if f
i
(x) = f
i
(y) for all i {1, ..., r}. As members of
F’ are independently chosen from F, F’ is an (d
1
, d
2
,
p
1
r
, p
2
r
)-sensitive family (Rajaraman and Ulman,
2012).
OR-construction of F’ is defined as follows. Each
member of F’ consists of b members of F for some
fixed b. If f is in F’, and f is constructed from the set
{f
1
, f
2
, …, f
b
} of members of F, f(x) = f(y) if and only
there exists i {1, ..., b}, such that f
i
(x) = f
i
(y).
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
534

Similarly, F’ is an (d
1
, d
2
, 1 – (1 – p
1
)
b
, 1 – (1 – p
2
)
b
)
-sensitive family.
Generally, it is desirable that p
1
is as large as
possible and p
2
is as small as possible. If p
1
is less than
1, then there exists some possibility that similar
objects will have different hash values. On the other
hand, if p
2
is greater than 0, some possibility exists
that distant objects will have similar hash values.
Therefore, family F is chosen in such a way that p
1
is
large (close to 1) and p
2
is small (close to 0). There is
a finite set of well-studied locality-sensitive function
families and the desired levels of p
1
and p
2
cannot
always be achieved with one “pure” family, and here
the amplification comes into play.
If family F
Ar
is obtained as AND-construction of
r functions from family F, and G is then obtained as
OR-construction of b functions from family F
Ar
, then
G is a (d
1
, d
2
, 1 – (1 – p
1
r
)
b
, 1 – (1 – p
2
r
)
b
)-sensitive
family. Informally, AND-construction mostly lowers
the initially low p
2
probability and subsequent OR-
construction raises the initially high p
1
probability.
The idea of the nearest neighbours search based
on LSH is described in many papers like Rajaraman
and Ulman, (2012) and Slanley and Casey (2008).
First, a hash family F (to be discussed in greater detail
later) is chosen and b ordinary hash tables are
arranged. Each hash table corresponds to some hash
function f
Ar
i
, i = 1,…,b, where f
Ar
i
is an AND-
construction of r random functions from F. Every
object x is stored into each of the b hash tables. Key
is the f
Ar
i
(x) and value is either some identity of x or x
itself. It is natural that several objects can fall into one
hash table bucket.
When searching for the nearest neighbours of an
object y, at first, f
Ar
i
(y), i=1,..,b is calculated and then
all values from the corresponding hash maps are
retrieved resulting in a set of the nearest neighbour
candidates. Precise distance to each of the candidates
is then assessed and the false positives are removed.
Particular choice of the hash function family
depends on data representation and distance function
d. For Hamming distance a bit sampling locality
sensitive hash was proposed in Indyk and Motwani
(1998), for cosine distance a random projections
method was proposed in Charikar (2002), a well-
performing hash function for Euclidean distance is
proposed in Datar et al. (2004).
In the proposed architecture the random
projections method is used, i.e. function f from F
corresponds to one random hyperplane and checks
whether a point being hashed is above or under this
hyperplane.
3.2 Recommendations Generation
User-based collaborative filtering system is the
recommendation system that infers recommendations
from the similarity of users measured by the degree
known user ratings coincide.
More formally, let r
uj
be the rating assigned to the
item j by the user u, which corresponds to how user u
liked item j, or what was the subjective utility of j for
u. Let U be the set of all users, I – the set of all items,
I
u
– the set of items rated by user u, and I
uv
– the set
of items rated by both user u and user v. Usually, a
user has ratings for relatively small number of items,
|I
u
| << |I|. Neighbourhood methods of user-based
collaborative filtering employ some similarity
measure between users which is calculated based on
common ratings (sim(u, v) = f
s
({r
uj
, r
vj
| j  I
uv
})) and
estimate unknown rating r*
uj
based on known ratings
r
vj
and estimated similarities sim(u, v).
In the recommendation systems research several
user similarity measures were introduced: Pearson
and Spearman correlation coefficients, Jaccard
similarity, Hamming distance, cosine similarity
(Amatriain et al., 2011). In this paper, the cosine
similarity is employed as the similarity measure
between users. Therefore:



uvuv
uv
I
vj
I
uj
vj
I
uj
rr
rr
vusim
22
),(
(1)
The similarity measure choice is caused mostly by the
fact that there exists a known way to approximate this
measure by a set of locality-sensitive hash functions
(Charikar, 2002), which is not the case for other wide-
spread similarity measures (e.g., Pearson correlation
coefficient). It is also supported by the evidence that
the cosine similarity works well in many
recommendation system settings (Amatriain et al.,
2011).
User ratings are normalized in such a way that
r
uj
= 1 corresponds to a strong positive attitude of user
u to item j, and r
uj
= -1 corresponds to a strong
negative attitude respectively.
The prediction of an unknown rating r*
uj
requires
the search of users v that are similar to u, or the
nearest neighbours of u according to cosine similarity
measure.
Recommendation system using LSH follows the
nearest neighbour approach. At the known set of hash
values for some user u, the system checks the
respective hash tables and retrieves all users whose
interests are likely (due to hash function properties)
to be similar to u’s. Then an exact similarity may be
Privacy-preservingHybridPeer-to-PeerRecommendationSystemArchitecture-Locality-SensitiveHashinginStructured
OverlayNetwork
535

assessed and high rated items of similar users are
provided to u.
In the proposed system, the exact user similarity
is not computed, as it would lead to user profile
exposure, which is avoided. Instead, approximate
similarity measure s’(u,v) is introduced as the number
of locality-sensitive hash functions whose values are
equal for users u and v. The recommendation
algorithm, at first, retrieves all approximate
neighbours Q
u
of user u from hash tables and
computes s’(u,v) (where v  Q
u
). Then, each of the
neighbours v  Q
u
is asked for the recommended
items R
v
. The proposed algorithm and the system as a
whole do not predict ratings, instead it ranks all items
that were recommended by approximate neighbours
with respect to some attractiveness estimate
ui
a
~
of
item i for user u defined by the following expression:



u
Qv
R
viui
Pvusa ),('
~
.
(2)
Here
R
vi
P
is an indicator function that checks if item
i is in the list of items recommended by user v:






v
v
R
vi
Ri
Ri
P
,0
,1
.
(3)
In other words, the attractiveness estimate
ui
a
~
 [0;
Q
u
] is the sum of approximate similarities between
user u and neighbours that “recommended” item i to
user u.
To sum it up, in the proposed system architecture,
a profile of user u is a set of pairs (i, r
ui
), where i are
item identifiers. To compute the hash function, a
profile is transformed to a vector of length |I| in such
a way that for each known rating r
ui
the respective (i
th
)
vector component is set to normalized rating value,
and for each unknown rating it is set to 0. Each of b
locality-sensitive hash functions is represented by r
vectors, whose dimensionality equals to a number of
the known items (|I|). Finding a hash of a profile
vector corresponds to computing inner products of the
profile vector and hash functions vectors, resulting in
1 if the inner product is positive and 0 if the inner
product is negative or equals to zero. After
application of all these hash functions b r-
dimensional binary vectors are obtained and stored
into hash table. When looking for recommendations,
b lookups are performed, then each found
approximate neighbour is queried for recommended
items and the list of recommended items is sorted
according to
ui
a
~
value.
The values of b and r аre the parameters of
recommendation system. In the section 5, impact of
these parameters on the recommendations quality is
assessed.
4 SYSTEM ARCHITECTURE
The proposed hybrid architecture enables the
personalized recommendations exchange with the
limited user preferences disclosure. In this section,
target use cases are discussed, as well as components
of the proposed system and scenarios that implement
the target use cases.
4.1 Use Cases
Recommendation systems may provide for somewhat
different end-user features. Specifically, in this paper
the following recommendation use cases are
considered: a) attractiveness estimation of a given
item (or set of items); b) recommendations query.
Attractiveness estimation of a given item (or a set
of items) is involved when a user encounters some
item and wants to check if it is potentially interesting
or useful for him/her. In this case, the user passes this
item (item identity) to recommendation system and
the recommendation system should return an
expected attitude of this user to this item. Certainly,
the user is not required to perform this request
intentionally by hand; some other program or GUI
element acting on behalf of the user can mediate this
action. Attractiveness estimation request may contain
several items. Though estimation for multiple items
can always be implemented as a series of single item
estimations, it is interpreted here as a use case
extension, because in some circumstances the
estimation for multiple items is potentially more
efficient than multiple separate single item requests.
Recommendations query is launched in quite
another situation. Here, the user just wants to see
some recommendations – maybe recommendations
of new, previously unseen and actual items.
4.2 Components
In the proposed architecture, the recommendation
system is split into two parts: Peer-to-Peer (P2P)
recommendations network and the Master node
(Figure 1). The Master node breaks the conceptual
purity of the P2P design, making it a hybrid P2P
system, but it does not play a significant role in the
primary use cases of the system, namely the
assessment of a given item and recommendation
query. Both enumerated earlier use cases are
implemented by the P2P network solely and the
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
536

Master node is responsible for synchronizing
supplementary information between peers.
Figure 1: Connections between nodes in the proposed
architecture.
In Figure 1, two types of connection between nodes
are shown: connections between similar peers used to
get recommendations are shown by solid lines, and
occasional connections of peers to the Master node
for retrieving the supplementary information are
depicted by dashed lines.
1) Peer-to-Peer recommendations network: In the
proposed architecture, each user corresponds to
exactly one node (or peer – these terms are used here
interchangeably). That node holds all the information
about one user’s preferences, ratings, browsing
history etc, but does not share this information with
the other nodes, instead it shares only the locality-
sensitive hash values of this information in order to
find similar users to query for recommendations.
P2P network is based on the Distributed Hash
Table (DHT) (Korzun and Gurtov, 2013) model
widely employed in various P2P networks. The
general idea of DHT is rather straightforward. It holds
a collection of key/value pairs scattered over a
distributed set of nodes, supporting key/value pair
migration in case of node disconnection. DHT usually
refers to a class of systems rather than to some
specific system or algorithm.
Original DHT has some severe security
vulnerabilities. To overcome these vulnerabilities a
variety of secure and anonymous DHT lookup
implementations were designed. The proposed
architecture relies on one of these anonymized
implementations, namely Octopus (Wang and
Borisov, 2012). The idea behind the most of secured
DHT implementations is that all the DHT lookups are
made through other nodes accessible by anonymous
paths through anonymization relays. Each node in the
anonymization path knows only the neighbour nodes
and does not know whether some request originated
in the neighbour node, or was passed over from some
other node.
DHT in the proposed system is used as a set of
hash tables needed for nearest neighbour search, as
described in section 3. Each key/value pair stored in
DHT holds information about one locality-sensitive
hash value and the list of nodes corresponding to that
hash value. As it was discussed in the respective
section, several (b) hash tables are needed to perform
the nearest neighbour search. Each of the b tables uses
its own locality-sensitive hash function. It is proposed
to store all of these b hash tables in one DHT. In order
to achieve this key of the DHT pair should include a
global unique identifier of the locality-sensitive hash
function and the value of that function.
Each node of the P2P network has its unique
identifier assigned to the node when it first connects
to the network. In most DHT implementations the
node identifier is a 160-bit value that is produced by
applying SHA-1 to the network address of the node.
Before a node advertises itself in DHT it creates
an anonymized path and uses the endpoint
specification of this path as an address it shares with
other nodes. These anonymized paths are created
each time when the node connects network, resulting
in different public identifiers of the same node.
Figure 2: Peer-to-Peer layers.
As user preferences expressed in ratings are not
changing very fast, it is reasonable for each node to
locate other nodes with the similar profiles through
DHT and store links to them. Therefore, a new
overlay network of similar users is formed over the
P2P network. It is important to differentiate between
the three employed connection layers (Figure 2). The
first layer is the underlying network, that provides a
physical connection between P2P nodes. The second
Users/Peers
Master
node
Similar nodes (neighbours)
Peer-to-Peer (DHT)
Physical network
Router
IP address
Node ID
Anonymized
node ID
Privacy-preservingHybridPeer-to-PeerRecommendationSystemArchitecture-Locality-SensitiveHashinginStructured
OverlayNetwork
537

layer is DHT connection layer that provides DHT key
search, key redistribution etc. This layer is formed by
links to adjacent nodes in structured P2P, the so-
called “fingers”. The third layer is formed by
connections between similar nodes, where the
similarity is interpreted like an equality of locality-
sensitive hashes.
It is important to note, that links to neighbour
nodes in the third layer are not exactly identifiers of
nodes in P2P network, they are entrances to
anonymized paths to these nodes.
2) The Master node: The distributed nature of the
proposed system causes one hindrance. LSH-based
nearest neighbour search implies that when searching
for the neighbours of object x, all the locality-
sensitive hash functions that were used to hash other
objects and fill hash tables are applied to x. In the
proposed architecture, an object being hashed is a
vector of normalized ratings assigned by the user to
different items of interest and hashing functions
family is represented by random hyperplane
projections. To define a hyperplane the
dimensionality of the space has to be known. In some
cases, for instance, when the rating storage is
centralized, when ratings are immutable or all
possible items are known in advance, knowing
dimensionality is not a problem. However, in case of
distributed rating storage when each node holds only
ratings of one user, overall item space dimensionality
can be found out only though communication
between nodes. Dimensionality means the number of
dimensions as well as their order. It is easy to see that
if one user encounters items in the following order:
(Item1:1, Item2:-0.5, Item3:1), and another user
encounters and rates the same items in another order:
(Item1:1, Item3:1, Item2:-0.5), then their hashes with
hyperplane (0, 1, 0) would be different although the
ratings match perfectly.
Hence, it is needed to synchronize item space
characteristics and random projection hyperplanes
across all nodes. The problem of maintaining a global
shared state in the P2P network is rather nettlesome,
and there are numerous papers dedicated to this
problem, e.g. (Hu, Bhuyan and Feng, 2012; Oster et
al., 2006; Chen et al., 2005). In the proposed system
this problem is addressed in a way similar to the one
presented in (Mastroianni, Pirro and Talia, 2008) and
sacrificing the P2P-purity of the system. It is the
Master node that, first, collects all new items
discovered and rated by peers, maintains their
ordering and generates new locality-sensitive hash
functions. So, each peer must connect to the Master
node in two situations: first, to notify about some
previously unknown item (which should become a
new dimension), second, to get a new set of locality-
sensitive hash functions. It must be noted, that there
is no necessity in generation of new hash functions
after an assessment of each new item. Using outdated
hash functions with lower dimensions is still possible,
but it gradually decreases the quality of
recommendations. So, each user node collects the
new rated items (which were not assigned identifiers
yet) and then sends a batch of these items to the
Master node. The Master node, in turn, accumulates
new items, and when their number is great enough
assigns them an ordering and issues a new set of
locality sensitive hash functions. It is also important
that the new set is not an entire replacement of the
previous, but contains only several new hash
functions.
4.3 Scenarios
This subsection describes how five main scenarios of
the recommendation system are implemented by
means of the proposed architecture. These scenarios
are: attractiveness estimation for a given item,
recommendations query, rating an item, refreshing
hash functions, and the search for similar peers.
1) Attractiveness estimation of a given item:
attractiveness estimation on a node is possible only
after the integration of this node into the P2P network
and locating the nodes of the users with similar
ratings (hereinafter these nodes are referred to as
neighbour nodes). Let the neighbour nodes for the
given one be stored in the Neighbours list. Then
attractiveness estimation for the item is performed by
sending requests to each node from the Neighbours
list passing the item identifier over. Each neighbour
node answers with a binary value meaning if it can
recommend this item to others or not. Attractiveness
estimation for the set of items is done mostly in the
same way, except that the requester node passes the
list of item identifiers instead one identifier and the
answer contains a list of pairs (itemId,
recommend_flag) for all items that the neighbour
node is able to recommend.
Informally, attractiveness estimation scenario can
be interpreted as asking an advice from co-minded
people. In centralized systems it is performed in some
conceptual way, in the proposed hybrid P2P system it
is performed literally sending requests to the
respective nodes. When answering attractiveness
estimation request, a node can base the response on
the rating that is stored for the given item, or infer the
rating from some other information. This is an
extension point of the proposed system architecture.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
538

These requests are sent and answered through
anonymization relays, so the node does not expose
both its identity and an exact rating for any item.
2) Recommendations query: In this case, node that
needs recommendations just sends corresponding
requests to each of the neighbour nodes. Each
neighbour node answers with a list of (item, rating)
pairs. Unlike the previous scenario, here the
neighbour node needs to send not just identifiers of
the recommended items, but their entity, something
that the receiver side can use directly.
The way neighbour node forms the
recommendations list is also an extension point. In the
simplest case, it should return some random sample
of the high-rated items, it may also return only new
high-rated items.
Anonymization relays make sure that the
recommendations provider does not expose both
ratings and its identity.
3) Rating an item: The main issue of rating items
is the generation of new locality-sensitive hash
functions that must follow it. To address this issue
each node has two lists: Known and New. The Known
list holds all the items the Master node is aware of.
This list is received from the Master node during the
bootstrap process of periodical synchronization
process. The order of items in this list is also
important as it corresponds to the order of dimensions
of locality-sensitive hash functions. The New list, on
the other hand, holds the items that are discovered by
this node and are not yet approved by the Master
node. When the user rates an item, the rating is saved
and then, if the item is neither in Known, nor in New
lists it is added to the New list.
When New list exceeds some predefined size or
once in a predefined period (whatever happens first),
the node sends its New list to the Master node and
retrieves the global shared state from the Master node.
Global shared state from the Master node includes up-
to-date version of the Known list. Each node
augments its Known list according to the one received
from the Master node and removes from New list
items that are present in Known list.
4) Refreshing hash functions (supplementary
scenario): Each node periodically queries the Master
node for the global shared state. As it was described
earlier, there are b functions, and each hash function
is a vector of r m-dimensional random vectors
(representing random hyperplanes). To reduce the
amount of information exchange and load of the
Master node, each hash function posted by the Master
node is represented by three integers: function unique
identifier (funcId), random seed and current number
of items m (i.e. item space dimensionality). When a
node gets this information it generates random
hyperplanes constituting each of the b locality-
sensitive hash function as a sequence of r*m (m
dimensions for each of r hyperplanes) random
numbers from the specified seed using Mersenne
twister (Matsumoto and Nishimura, 1998).
5) The search for similar peers (supplementary
scenario): The search for similar, or neighbour, peers
is initiated when a node is registered in the P2P
network. Then this search is performed regularly.
Before searching for neighbours a node have to
refresh item list and hash functions from the Master
node. Then each function from an up-to-date set of
hash functions is applied to this node ratings vector.
The results are merged into pairs (funcId, value) and
these pairs are used as keys to look up in DHT. DHT
look up returns a list of node identifiers similar to this
one according to the respective locality-sensitive
function. These lists are then merged and stored as the
Neighbours list.
5 EXPERIMENTAL STUDY
Experimental study of the proposed approach was
performed with the MovieLens 100k dataset shared
by GroupLens research lab. This dataset fits well with
e-commerce scenarios (specifically, media streaming
services), as it contains 100,000 real-life ratings
assigned by 943 users to 1682 movies.
The purpose of the experimental study was
twofold. First, to gain some insights into the internal
quantitative characteristics of the proposed approach
and to estimate time and spatial complexity of the
DHT-based LSH recommendation system. Second, to
evaluate the quality of recommendations with respect
to some well-known baselines.
Ratings are normalized by centring over the user’s
mean rating and scaling to [-1; 1] range.
5.1 Time, Space and Network Load
It was already noted that b (the number of hash
functions) and r (the number of hyperplanes in each
hash function) are parameters of the LSH-based
recommender. Values of these parameters have
significant impact both system performance and
accuracy.
As each node puts itself into DHT b times, the size
of the DHT is n*b it means that on the average only b
records of the DHT are located on each node. In most
cases, this burden is negligible. More important is the
fact that the search for the neighbour nodes takes b
lookups which is O(b log(n)) of internode
Privacy-preservingHybridPeer-to-PeerRecommendationSystemArchitecture-Locality-SensitiveHashinginStructured
OverlayNetwork
539

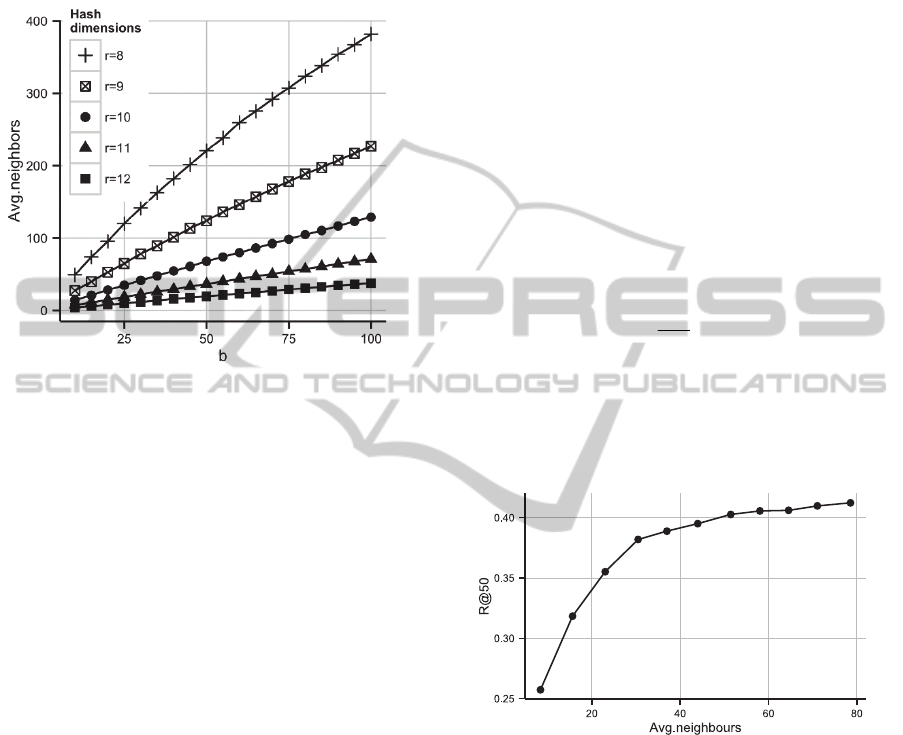
communications. Even more important is the number
of neighbours, as this number corresponds to the
number of network queries performed to obtain
recommendations, and it is desirable to keep the
number of these queries as small as possible.
Figure 3: Average number of neighbours depending on the
number of hash functions (b) and their dimensionality (r).
Figure 3 shows the dependency between b and r
parameters of recommender and the average number
of neighbours found through hash table look up. It can
be seen that the number of neighbours increases with
the growth of b, and the speed of growth significantly
depends on the dimensionality of hash functions. It is
expected behaviour, as small dimensionality of hash
functions and large number of “alternative” hash
functions make neighbour search procedure
indiscriminative. In this experiment, we assume that
the reasonable number of hash functions is under 100
and the reasonable number of neighbours is under 50.
The numbers are different as neighbours search is
one-time action and queries to neighbours happen
more often.
The number of neighbours selection is also
supported by the experiment, presented in Figure 4.
For fixed dimensionality (r) different values of b were
tried and the average number of neighbours and the
respective recall were evaluated. It can be seen, that
when the number of neighbours is less than
approximately 50, the quality of recommendations is
growing fast, whereas for bigger values of the number
of neighbours it reaches a plateau.
Having this in mind, three configurations were
selected to examine recommendations quality: (r=12,
b=100), (r=10, b=35), (r=8, b=10). These
configurations were selected because each of them
gives on the average approximately 50 neighbours for
a user in the explored dataset (see Figure 3).
5.2 Recommendations Quality
As the proposed recommendation system does not
predict item ratings, the conventional root mean
square error metric for measuring recommendations
quality is irrelevant. Instead, recall is used as a quality
metric better tailored to top-n recommendation
systems. The authors follow the approach described
in Cremonesi et al. (2010). Ratings dataset is split into
two subsets: training set and testing set in 80/20
proportion. Training set is used to fill the hash table.
Then, for each high rating (4 or 5) from the testing set
a check is performed whether this item is in top n
recommended items for that user. The outcome of this
check may be either 1 (if it is in the top n) or 0 (if it is
not). These outcomes are summed for all high ratings
of the testing set to produce N
p
value. Recall is
calculated according to formula:
H
p
N
N
nR @
,
(4)
where N
H
is the number of high ratings. In other
words, this value can be interpreted as a probability
that a randomly taken high rated item is in fact
recommended by the algorithm.
Figure 4: R@50 depending on the number of nearest
neighbours for LSH with r=10 and b varying from 5 to 55.
Recall of the proposed recommendation method was
compared with two baseline non-personalized
recommenders. First, a random recommender
(RandRec) which recommends just n random items to
any user, second, popular items recommender
(PopRec) which recommends the items that have the
most number of ratings. Figure 5 shows the recall of
each of the recommenders at different values of n.
All the tested variants of LSH recommendation
method give similar results. It may be explained by
the fact that in all of the tested variants there are
nearly the same number of neighbour nodes (about
50, see Figure 3). It can also be seen that the proposed
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
540

Figure 5: Comparison of R@n for different
recommendation methods.
recommendation algorithm significantly outperforms
the non-personalized recommendation algorithms in
terms of recall.
6 CONCLUSIONS
In this paper, the architecture of a user-centric hybrid
peer-to-peer recommendation system, based on
locality-sensitive hashing is proposed. In the
proposed architecture, privacy is enforced by the fact,
that user ratings are shared only in an anonymized
way and complete profiles are not shared at all (only
their hash values).
The proposed approach was evaluated on a widely
used dataset from an e-commerce scenario (movie
ratings) and it was shown that the estimated recall of
the proposed recommendation system is sufficiently
higher than that of the trivial baselines.
However, some limitations of this approach can
also be enumerated. First, due to DHT limitations it is
not applicable to the P2P networks with high churn,
second, it most likely does not fit highly dynamical
domains, such as news recommendation, because of
the need of sharing information about all objects all
over the P2P network.
In the future, the authors are planning to consider
alternative solutions of sharing the global set of
locality-sensitive hash functions among peers.
ACKNOWLEDGEMENTS
The research was partially supported by projects
funded by grants # 13-07-00271, # 13-07- 00039, and
# 14-07-00345 of the Russian Foundation for Basic
Research, project 213 (program 8) of the Presidium
of the Russian Academy of Sciences, and project
# 2.2 of the basic research program “Intelligent
information technologies, system analysis and
automation” of the Nanotechnology and Information
technology Department of the Russian Academy of
Sciences. This work was also partially financially
supported by Government of Russian Federation,
Grant 074-U01.
REFERENCES
Amatriain, X., Jaimes, A., Oliver, N., Pujol, J.M., (2011)
Data Mining Methods for Recommender Systems. In:
Ricci, F., Rokach, L., Shapira, B., Kantor, P. (Eds.)
Recommender Systems Handbook, Springer.
Bakker, A., Ogston, E. and van Steen, M., 2009
Collaborative filtering using random neighbours in
Peer-to-Peer networks. Workshop on Complex
Networks in Information & Knowledge Management,
pp. 67-75.
Charikar, M.S., 2002. Similarity Estimation Techniques
from Rounding Algorithms. In STOC’02 Proceedings
of the 34th annual ACM symposium on Theory of
Computing, pp. 380-388.
Chen, X. et al., 2005. SCOPE: Scalable Consistency
Maintenance in Structured P2P Systems. In Proc. of
IEEE INFOCOM, 2005, pp. 1502-1513.
Cremonesi, P., Koren, Y. and Turrin, R., 2010.
Performance of recommender algorithms on top-n
recommendation tasks. In Proceedings of the fourth
ACM conference on Recommender systems (RecSys
'10). ACM, New York, NY, USA, pp. 39-46.
Datar, M. et al., 2004. Locality-Sensitive Hashing Scheme
Based on p-Stable Distributions. In SCG’04
Proceedings of the 20
th
annual symposium on
Computational geometry, pp. 253-262.
Draidi, F., Pacitti, E. and Kemme, B., 2011a. P2Prec: a P2P
recommendation system for large-scale data sharing.
Journal of Transactions on Large-Scale Data and
Knowledge-Centered Systems (TLDKS), vol. 3, 2011,
pp. 87-116.
Draidi, F. et al., 2011b. P2Prec: a social-based P2P
recommendation system. In Proceedings of the 20
th
ACM international conference on Information and
knowledge management, pp. 2593-2596.
Han, P. et al., 2004. A scalable P2P recommendation
system based on distributed collaborative filtering.
Expert Systems with Applications 27(2), pp. 203-210.
Hecht, F. et al., 2012. Radiommendation: P2P on-line radio
with a distributed recommendation system. In
Proceedings of the IEEE 12
th
International Conference
on Peer-to-Peer computing, pp. 73-74.
Hu, Y., Bhuyan, L. N. and Feng, M., 2012. Maintaining
Data Consistency in Structured P2P Systems. IEEE
Transactions on Parallel and Distributed Systems,
Vol.23, Issue 11, 2012, pp. 2125-2137.
Indyk, P., Motwani, R., 1998. Approximate Nearest
Neighbors: Towards Removing the Curse of
Dimensionality. In STOC’98 Proceedings of the 30th
Symposium on Theory of Computing, pp. 604-613.
Privacy-preservingHybridPeer-to-PeerRecommendationSystemArchitecture-Locality-SensitiveHashinginStructured
OverlayNetwork
541

Jelasity, M., Montresor, A., Babaoglu, O., 2009. T-Man:
Gossip-based fast overlay topology construction,
Computer Networks, 53, 13 (August 2009), pp. 2321-
2339.
Kermarrec, A.-M. et al., 2010. Application of random walks
to decentralized recommendation systems. In
Proceeding of the 14
th
international conference on
Principles of distributed systems, pp. 48-63.
Korzun, D., Gurtov, A., 2013. Structured Peer-to-Peer
Systems. Fundamentals of Hierarchical Organization,
Routing, Scaling and Security. Springer.
Mastroianni, C., Pirro, G. and Talia, D., 2008. Data
Consistency and Peer Synchronization in Cooperative
P2P Environments. Technical Report, unpublished.
Matsumoto, M., Nishimura, T., 1998. Mersenne twister: a
623-dimensionally equidistributed uniform pseudo-
random number generator, ACM Transactions on
Modeling and Computer Simulation, Vol. 8, Issue 1,
1998, pp. 3-30.
Ormandi, R., Hegedus, I. and Jelasity, M., 2010. Overlay
management for fully distributed user-based
collaborative filtering, Euro-Par 2010, pp. 446-457.
Oster, G. et al., 2006. Data consistency for P2P
collaborative editing. In Proceedings of the 20th
anniversary conference on Computer supported
cooperative work, 2006, pp. 259-268.
Pitsilis, G., Marshall, L., 2006. A trust-enabled P2P
recommendation system. In Proc. 15
th
IEEE
International Workshops on Enabling Technologies:
Infrastructure for Collaborative Enterprises, pp. 59-64.
Pussep, K. et al., 2009. A Peer-to-Peer Recommendation
System with Privacy Constraints. In CISIS: IEEE
Computer Society, 409-414.
Rajaraman, A., Ullman, J., 2012. Mining of Massive
Datasets. Cambridge University Press.
Slanley, M., Casey, M., 2008. Locality-Sensitive Hashing
for Finding Nearest Neighbors, IEEE Signal Processing
Magazine, vol.25, no.2, March.2008, pp. 128-131.
Tveit, A., 2001. Peer-to-peer based recommendations for
mobile commerce. In Proc. 1
st
Intl. workshop on Mobile
commerce (WMC’01), ACM, pp. 26-29.
Wang, Q., Borisov, N., 2012. Octopus: A Secure and
Anonymous DHT Lookup. In Proceedings of the IEEE
32nd International Conference on Distributed
Computing Systems, 2012, pp. 325-334.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
542