
Optimizing Routine Maintenance Team Routes
Francesco Longo, Andrea Rocco Lotronto, Marco Scarpa and Antonio Puliafito
Dipartimento DICIEAMA, Universit
`
a degli Studi di Messina,
Viale F. Stagno d’Alcontres, 31 - 98166 Messina (ME), Italy
Keywords:
Routine Maintenance Interventions, Metaheuristic Approaches, Simulated Annealing, Scheduling Problems,
Optimization Problems.
Abstract:
Simulated annealing is a metaheuristic approach for the solution of optimization problems inspired to the
controlled cooling of a material from a high temperature to a state in which internal defects of the crystals
are minimized. In this paper, we apply a simulated annealing approach to the scheduling of geographically
distributed routine maintenance interventions. Each intervention has to be assigned to a maintenance team and
the choice among the available teams and the order in which interventions are performed by each team are
based on team skills, cost of overtime work, and cost of transportation. We compare our solution algorithm
versus an exhaustive approach considering a real industrial use case and show several numerical results to
analyze the effect of the parameters of the simulated annealing on the accuracy of the solution and on the
execution time of the algorithm.
1 INTRODUCTION
The use of limited resources with utilization re-
quests over time originates a class of problems called
scheduling problems (W. Herroelen et al., 1999). The
contexts with this type of problems are multiple and,
consequently, for each of such contexts the final ob-
jectives, the number and kind of the limited resources,
and the number and kind of the utilization requests
can be different. Moreover, the same problem could
not exhibit a unique solution. Instead, a set of solu-
tions that are all admissible can be generated, differ-
entiated by their cost. The nature of such a cost and
the way it is evaluated and determined is of course
different in different application contexts. However,
even if the application context changes, the follow-
ing property is usually satisfied: making a minimal
change to a particular solution of a scheduling prob-
lem can produce a substantial change in its cost. This
determines, in the general economy of any applica-
tion context, the necessity to find a solution to a spe-
cific scheduling problem that is as less expensive as
possible. Moreover, it makes such a task particularly
difficult given that small perturbations can heavily in-
fluence the overall cost.
An algorithm exploited to solve this kind of prob-
lems usually tests if a given solution is admissible
for the problem and, defining a cost function (usu-
ally depending on the aspects of the problem that is
necessary to minimize/maximize), calculates its cost.
Problems of this nature where the goal is to mini-
mize/maximize a cost function are generally identi-
fied as optimization problems.
In this paper, we take into consideration the prob-
lem of scheduling a list of geographically distributed
routine maintenance interventions among a set of
maintenance teams, taking into account team skills,
cost of overtime work, and cost of transportation.
This kind of problems can present a set of admissible
solutions that is too large to implement an algorithm
that assesses all of them in order to determine the one
with the minimum cost, in a finite time. Therefore, we
follow a different approach exploiting a metaheuristic
technique (F. Glover and G. Kochenberger, 2003).
In particular, we exploit the simulated annealing
(SA) (Fleischer, 1995) metaheuristic to solve our rou-
tine maintenance scheduling problem with the goal of
optimizing the routes of the maintenance teams mini-
mizing the cost and trying to maximize the number of
maintenance operations actually performed in a given
day. In order to show the effectiveness of our ap-
proach, we take into consideration a real industrial
use case provided by Meridionale Impianti
1
, a com-
pany active in the industrial and electrical plant de-
sign sector. We compare the solution obtained by
1
http://www.merimp.com/en/
535
Longo F., Rocco Lotronto A., Scarpa M. and Puliafito A..
Optimizing Routine Maintenance Team Routes.
DOI: 10.5220/0005400105350546
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 535-546
ISBN: 978-989-758-096-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

our approach with the exact solution obtained by ap-
plying an exhaustive algorithm that comprehensively
enumerates all the solutions finding the one that pro-
duces the minimal cost. We also perform a large set
of experiments evaluating the impact of the different
parameters of our SA approach to the accuracy of the
solution and the efficiency of the algorithm in terms
of execution time, with the aim of tuning the optimal
values of such parameters for future execution of the
same algorithm.
2 RELATED WORK
In this paper, we present an efficient and general
method for solving routine maintenance scheduling
problems based on SA metaheuristic. Several works
in literature propose the use of SA for the solution
of scheduling problems in the context of the main-
tenance of specific installations, especially power
plants. In (J.T. Saraiva et al., 2011), authors address
the problem of the periodic maintenance of electric
generators by using SA. They aim at scheduling sys-
tem maintenance operations along a planning horizon
assuming that the time interval between maintenance
actions for the same generator is fixed. In our ap-
proach, we do not take into consideration the time in-
terval between maintenance actions but we deal with
the scheduling of interventions that are supposed to
be conducted in a certain working day accordingly to
a predetermined business policy. As in (J.T. Saraiva
et al., 2011), (Keshav P. Dahal and Nopasit Chakpi-
tak, 2006) deals with the maintenance of generators
in a power plant by using a hybrid approach based
on a combination of genetic algorithms and SA. In
(Ibrahim El-Amin et al., 1999), the tabu search meta-
heuristic is applied to the maintenance of generators
in a power station with the aim of reducing the cost
associated with the management of the maintenance
operations and to increase the time interval between
two maintenance operations for the same generator.
In our case a pure SA approach is exploited mainly
focusing on the overall cost of performing a set of ge-
ographically distributed maintenance operations dur-
ing a working day taking into account transportation
and overtime costs.
More generally, the SA metaheuristic and its vari-
ations are often used for the solution of optimiza-
tion problems in several application fields spanning
from ICT to biomedicine. In (Chun-Cheng Lin et al.,
2014), SA, combined with additional momentum
terms in order to improve cooling rate, is exploited to
solve the problem of router node placement with ser-
vice priority constraint to improve the performance of
a wireless mesh network. In (Allen G. Brown et al.,
2014), the SA algorithm is adopted for creating ma-
neuver plans for the guidance of a satellite cluster. In
a gene expression data matrix, a bicluster is a subma-
trix of genes and condition. The problem of detecting
the most significant bicluster has been shows to be
NP-Complete. In (Kenneth Bryan et al., 2006), the
authors present a biclustering technique based on SA
to efficiently discover the more significant biclusters.
In this paper, we use SA to solve a maintenance
operation scheduling problem. During problem for-
malization we do not take into consideration any spe-
cific application context. However, we show its ap-
plication to a real industrial use case dealing with the
maintenance of energy plants. We are interested in
routine maintenance operations, i.e., maintenance op-
erations that are not related to an actual failure of the
considered system but are scheduled in advance. We
start from the assumptions that a set of maintenance
operations are scheduled to be conducted in a specific
day and our goal is to optimize the maintenance team
routes and maximize the number of interventions that
are actually performed. Contrary to maintenance op-
erations upon failures, such routine operations can be
postponed if it is not possible to guarantee that all
the operations that are supposed to be conducted in
a day will be actually fulfilled. However, our algo-
rithm is also able to deal with maintenance operations
that need to be executed with a higher priority.
3 REFERENCE SCENARIO
We take into consideration a company that needs to
perform maintenance operations in a set of geograph-
ically distributed locations. We only deal with routine
maintenance interventions, i.e., interventions that are
scheduled in advance. However, our approach also
takes into account that some higher priority interven-
tions could be necessary, representing failures and/or
specific situations that need immediate attention. We
focus on the set of maintenance operations that need
to be performed in a single day by a limited set of
maintenance resources. The maintenance resources
are represented by a number of teams, each composed
of a set of company employees and one vehicle. The
teams leave from the company principle headquarters
in the morning, follow a specific route established in
advance, perform all the maintenance interventions
that they have been assigned to, and return to their
starting point. This kind of problems falls under the
class of scheduling problems.
The problem we need to solve is to assign the
maintenance operations that are supposed to be con-
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
536

ducted in the considered day to the teams. Constraints
are present related to the nature of each maintenance
intervention. In fact, all maintenance operations have
specific characteristics in terms of both the location
where the intervention needs to be conducted and the
technical skills that are necessary to accomplish the
intervention. Being each intervention team composed
of one or more workers and one vehicle, accordingly
to the technical skills that each worker presents and
to the characteristics of the vehicle (that can reach a
specific location or not), it is possible to understand
which teams are able to perform a specific interven-
tion (it may be a subset of all the teams).
Of course, maintenance activities represent a cost
for the company. In our reference scenario, costs are
related to the hourly wage of the workers and to the
transportation expenses. A worker hourly wage in-
creases if the worker needs to do overtime, so a solu-
tion algorithm assigning interventions to teams needs
to minimize the possibility to go into overtime taking
into consideration both the time that is needed to per-
form each maintenance intervention and the traveling
time for a team to move from one intervention site to
the following. Transportation expenses are mainly re-
lated to fuel and maintenance for all the vehicles used
during the working day.
The main objective of this paper is to provide an
algorithm that automatically assigns the maintenance
interventions to the worker teams, taking into consid-
eration the above reported constraints with the aim of
minimizing the overall cost for the company.
4 PROBLEM FORMULATION
This section provides a formalization of the scenario
described in Section 3 unambiguously describing all
the characteristics of the considered scheduling prob-
lem, together with all the constraints and the costs that
need to be taken into account. Starting from our for-
malization, in Section 5, we will first provide the so-
lution based on SA and then we will present an ex-
haustive algorithm that will be used as a reference for
the solution of the problem.
Let Q indicate the set of available maintenance
teams and let Q be the cardinality of such a set (Q =
|Q |), i.e., the total number of teams. Moreover, let
C indicate the set of all the possible technical skills
of the company workers, while C is the total number
of skills (C = |C|). We use I to indicate the set of
all the possible kinds of maintenance operations and
I to indicate their total number (I = |I|). Finally, let
P indicate the set of all the possible geographic loca-
tions for the maintenance interventions and let P be
the cardinality of such a set (P = |P |), i.e., the total
number of sites where maintenance operations can be
conducted.
Each day, a total number of L maintenance inter-
ventions need to be carried out by the Q teams. We
indicate with L the list of such interventions, with
L = |L|. Each maintenance intervention l ∈ L is char-
acterized by the following information:
• geographic location: the geographical coordinates
of the site p
l
∈ P where the maintenance interven-
tion l needs to be performed;
• maintenance operation: the maintenance opera-
tion i
l
∈ I that actually needs to be performed dur-
ing intervention l;
• execution time: the time t
l
∈ R that is necessary
to carry out the maintenance intervention l, once
on site;
• priority: the level of priority c
l
∈
{normal,urgent} assigned to intervention
l.
The goal of the scheduling algorithm that we need
to design is to determine:
• the optimal number of maintenance interventions
that each team has to carry out (denoted with L
q
≤
L where 1 ≤ q ≤ Q);
• the actual list L
q
of maintenance operations each
team has to perform among those in L;
• the optimal order each team has to perform the
maintenance operations, i.e., the optimal ordering
of list L
q
;
Note that L
q
= |L
q
| and that the following constrains
apply:
Q
∑
q=1
L
q
≤ L, (1)
Q
[
q=1
L
q
⊆ L. (2)
Eq. (1) and (2) explicitly take into consideration the
possibility that, in the considered working day, not
all the scheduled maintenance interventions are actu-
ally performed (presence of ≤ and ⊆ symbols). This
could happen if an overtime is needed to exhaustively
perform all the maintenance operations for some of
the teams and if such a cost overcomes the cost asso-
ciated with the missing interventions.
If there are maintenance operations that require
specific skills, they necessarily have to be included
in the list of one of the teams whose components have
those skills. Let us define
F
c
q
: Q → 2
C
(3)
OptimizingRoutineMaintenanceTeamRoutes
537

associating to each maintenance team the set of skills
they possess, and
F
c
i
: I → 2
C
(4)
that associates to each specific maintenance opera-
tion the set of skills that are necessary to carry it out.
Then, a maintenance operation l ∈ L can be assigned
to team q ∈ Q if and only if F
c
i
(l) ⊆ F
c
q
(q).
Finally, if some of the maintenance interventions
in L exhibit a urgent priority they need to be included
in lists L
q
in the top positions. In the following, we
will indicate with L
q
[i].priority the priority assigned
to the i
th
intervention assigned to team q.
Let us denote the list of the geographical positions
and the execution times of the maintenance operations
assigned to team q as follows:
M
q
=
(p
1
q
,t
1
q
),(p
2
q
,t
2
q
),... ,(p
i
q
,t
i
q
),... ,(p
N
q
q
,t
N
q
q
)
where:
• p
i
q
∈ P is the position of the i
th
maintenance op-
eration assigned to team q;
• t
i
q
∈ R is the execution time of the i
th
maintenance
operation for team q;
with 1 ≤ i ≤ L
q
. In particular, let p
0
q
indicate the po-
sition of the location from where team q leaves at the
beginning of the working day and let p
L
q
+1
q
indicate
the final position to where the team has to go back.
Let v
i
q
define the travel time associated with the i
th
maintenance operation for the q team. Of course, v
i
q
depends on p
i−1
q
and p
i
q
and can be obtained by ap-
plying a routing algorithm finding the best route from
one geographical location to another. As an assump-
tion, v
L
q
+1
q
is the travel time that is necessary for the
team to go back to the final position.
For each team q to which a list of maintenance
operations L
q
has been assigned, the duration of the
working day D
q
can be computed as follows:
D
q
=
L
q
+1
∑
i=1
(v
i
q
+t
i
q
) (5)
with t
L
q
+1
q
= 0.
Denoting with D the maximum duration of the
working day, we want D
q
< D for each team. If it
is not possible to perform all the maintenance opera-
tions L in the working day, we define
¯
L as the number
of maintenance operations that can be carried out dur-
ing the standard working hours. This
¯
L operations are
associated with a normal cost, while we associate a
cost of overtime for the remaining maintenance oper-
ations. For each travel of each team, we associate a
cost CV
i
q
that can be computed as a function of the to-
tal distance associated with the i
th
maintenance opera-
tion of team q also including vehicles wear out. It can
be assumed that there is an additional cost for each
team whose duration of the working day exceeds D.
Therefore, if D
q
> D, this generates a cost of overtime
and we indicate it with CS
q
.
All this assumed, the multi-objective optimization
problem for our scenario can be formally defined as
follows:
Problem 1:
Find L
q
(with 1 ≤ q ≤ Q) such that:
i)
∑
Q
q=1
∑
L
q
i=1
CV
i
q
is minimized;
ii)
∑
Q
q=1
CS
q
is minimized;
iii)
¯
L is maximized;
iv) ∀q,∀i : F
c
i
(i) ⊆ F
c
q
(q);
v) ∀q,∀i : L
q
[i].priority ≤ L
q
[i + 1].priority.
5 SOLUTION ALGORITHMS
5.1 Background on SA
Simulated annealing (SA) is commonly considered to
be the oldest meta-heuristic which explicitly applies
a strategy to avoid getting stuck in local minimum,
while searching the problem solution space (C. Blum
and A. Roli, 2003). The name and the inspiration of
SA derive from the physical phenomenon known as
annealing. The annealing process consists in firstly
heating a material to high temperature and then cool-
ing it in a controlled manner. This process increases
the size of the material crystals, while reducing their
internal defects.
The SA algorithm has been firstly introduced as
an adaptation of the Metropolis-Hasting algorithm, a
Montecarlo method to generate states of a thermody-
namic system (N. Metropolis et al., 1953). In such a
work, the SA algorithm produces a sequence of mate-
rial states:
...,s
i
,s
i+1
,s
i+2
,...,s
i+n−1
,s
n
,....
Starting from the system initial state, the next state of
the sequence is generated by applying a perturbation
mechanism. Such a mechanism randomly produces a
new state which is close to the given one in terms of
their amount of thermodynamic energy. A sequence
of energy levels is then produced:
...,E
s
i
,E
s
i+1
,E
s
i+2
,...,E
s
i+n−1
,E
s
n
,...
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
538

with the aim of reaching the system state with the
lower possible energy level. To this aim, as already
reported above, the SA exploits a strategy that seeks
to avoid local minimum.
At each algorithm iteration, starting from a state s
i
with energy E
s
i
, the SA algorithm randomly generates
a new state s
i+1
with energy E
s
i+1
. If the new state has
an amount of energy such that ∆E = (E
s
i+1
−E
s
i
) ≤ 0,
the new state is accepted as the current state, thus low-
ering the energy of the system. On the other hand,
if ∆E > 0, i.e., the energy of the system would be
increased, the algorithm accepts the new state, even
if it is worst than the previous one, accordingly to
a probabilistic approach that depends on the actual
temperature of the system. In fact, as in the physi-
cal annealing process, in the SA algorithm, starting
from a state with a high temperature, the temperature
is gradually lowered while advancing in the genera-
tion of new system states. When a newly generated
state produces a difference in energy greater than zero
(∆E > 0), the new state is accepted with a probabil-
ity equal to e
(−∆E/T )
, where T is the current temper-
ature (so called Metropolis criterion (N. Metropolis
et al., 1953)). This results in a high probability to ac-
cept new states, even if they are worst than the previ-
ous one, during the initial iterations of the algorithm.
However, while lowering the temperature also the ac-
ceptance probability will decrease. This strategy al-
lows SA not to get stuck in local minimum.
Applying the SA meta-heuristic to a given opti-
mization problem involves designing all its character-
istic aspects adapting them to the specific context (D.
T. Pham and D. Karaboga, 2000) as detailed in the
following.
Solutions Space. The solution space S represents the
set of all the possible solutions to the given problem
that the SA approach has to be able to generate. Tak-
ing into consideration the above reported discussion,
it represents all the possible states s
i
that the system
can assume.
Cost Function. In optimization problems, defining a
cost function that is used as the objective function to
minimize is needed. In the SA annealing metaphor,
the cost function of the optimization problem is asso-
ciated with a function f determining, for each system
state, the value of the associated energy:
E
s
i
= f (s
i
). (6)
Generation Mechanism of the Neighboring Solu-
tions. When using SA for the solution of a problem,
it is necessary to formally define a mechanism that,
given the current solution, allows to generate a new
neighboring solution. In the SA metaphor, it is neces-
sary to define a function Ψ determining a new system
state s
i+1
from current state s
i
:
s
i+1
= Ψ(s
i
). (7)
Of course, while designing such a function, it is nec-
essary to take into consideration a criteria that allows
to determine if a new solution is near to the current
one. This is strictly related to the nature of the given
optimization problem.
Cooling Scheme. The way cooling is performed in
SA is characterized by four aspects: i) initial temper-
ature; ii) temperature updating mechanism; iii) num-
ber of iterations for each temperature value; iv) stop
criterion. Also in the case of the solution of an opti-
mization problem, it is necessary to design a specific
cooling scheme that allows to reach a good solution,
while still containing execution time.
Acceptance Rule. A newly generated solution need
to be accepted or discarded accordingly to a certain
criterion. In SA, to accept or discard a newly gener-
ated state, Metropolis criterion or one of its variations
are often used. Such criteria are usually exploited also
in the case of the solution of an optimization problem.
5.2 Formalization of a Solution
In order to show how SA has been exploited for
the solution of our optimization problem, namely the
problem of scheduling a list of geographically dis-
tributed routine maintenance interventions among a
set of maintenance teams, taking into account team
skills, cost of overtime work, and cost of transport,
it is first necessary to define how a possible problem
solution can be represented in a formal way.
With this aim, let us consider a specific case in
which L = 10 maintenance interventions need to be
scheduled among Q = 4 maintenance teams. A pos-
sible solution of such a problem consists in find-
ing the four lists L
1
, L
2
, L
3
, and L
4
associating to
each team the interventions to perform in a specific
order. An example is the following: L
1
= {1,8},
L
2
= {2, 9,10}, L
3
= {4, 3}, L
4
= {7, 6,5}, i.e., the
first team is scheduled to perform interventions num-
ber 1 and 8 in this order, the second team is scheduled
to perform interventions number 2, 9, and 10 in this
order, and so on. Such a problem solution can be for-
mally represented in a matrix form as follows:
1 0 0 0 0 0 0 2 0 0
0 1 0 0 0 0 0 0 2 3
0 0 2 1 0 0 0 0 0 0
0 0 0 0 3 2 1 0 0 0
. (8)
In such a matrix each row is associated with a main-
tenance team while each column refers to a mainte-
nance intervention. The values of nonzero elements
OptimizingRoutineMaintenanceTeamRoutes
539

indicates the order in which each intervention is per-
formed by the corresponding team. So, for exam-
ple, the element belonging to the first row and to
the eight
th
column is equal to 2 because intervention
number 8 is scheduled to be performed by the first
team as the second intervention in its list.
Generalizing such an example, a generic solution
of a generic instance of our scheduling problem is
given by a specific distribution of L maintenance in-
terventions among Q maintenance teams. Thus, if we
want to formally represent it in a matrix form, we
need a Q × L matrix A = {a
i, j
} such that i ∈ [1, Q],
j ∈ [1,L], and a
i, j
∈ [1,L]:
A =
a
1,1
a
1,2
·· · a
1,L
.
.
.
.
.
.
.
.
.
a
Q,1
a
Q,2
·· · a
Q,L
. (9)
In particular, being L the interventions to be per-
formed, the matrix in eq. (9) represents a solution
of our optimization problem only if a maximum of
L among its Q · L elements are nonzero:
nz(A) ≤ L (10)
where nz : R × R → N is a function that provides the
number of nonzero elements in a given matrix. More-
over, given that each matrix column is associated with
a specific intervention and given that each interven-
tion can be assigned only to one team, it follows that
in each column of matrix A only one element can be
nonzero, indicating the team to which the correspond-
ing intervention is assigned. Thus, indicating with c
j
the j
th
column of matrix A with j ∈ [1,L] (it is con-
sidered as a Q × 1 matrix):
c
1
=
a
1,1
a
2,1
.
.
.
a
Q,1
,c
2
=
a
1,2
a
2,2
.
.
.
a
Q,2
,··· ,c
L
=
a
1,L
a
2,L
.
.
.
a
Q,L
(11)
then:
nz(c
j
) ≤ 1, ∀ j ∈ [1, L]. (12)
The use of symbol ≤ in both eq. (10) and (12) is due to
the fact that some interventions may not be scheduled
due to overtime cost.
Finally, the value of the nonzero element of each
column c
j
has to represent the execution order of the
maintenance intervention j ∈ [1,L] within the list of
interventions associated with the corresponding team.
In formula:
a
x, j
6= 0 ⇔ L
x
[(a
x, j
)] = j (13)
with x ∈ [1,Q] and j ∈ [1,L] and x is the index as-
sociated with the team to which the intervention j is
assigned.
Summarizing, a possible solution of our optimiza-
tion problem can be formally represented as the ma-
trix in eq. (9) subject to the structural constraints re-
ported in eq. (10), (12), and (13). Moreover, Problem
1 constraints iv) and v) should also be checked in or-
der to verify that the solution represented by a given
matrix is admissible for the given problem.
5.3 Applying SA to our Optimization
Problem
SA is a meta-heuristic for general applications.
Therefore, as already mentioned in Section 5.1, it is
necessary to design all its characteristic aspects adapt-
ing them to the specific context. In the case of our op-
timization problem, such aspects have been designed
as follows.
Solution Space. Accordingly to what reported in
Section 5.2, the solution space of our optimization
problem can be formally represented as the set of all
the possible Q × L matrices in the form of eq. (9):
S = {A
i
} (14)
with Q and L depending on the specific problem and
satisfying eq. (10), (12), and (13), and Problem 1 con-
straints iv) and v).
Cost Function. In our optimization problem, the cost
function associates a cost to each possible matrix in
S. Accordingly to the definition of Problem 1 and to
what has been exposed in Section 4, our cost function
is the following:
E
A
= f (A) =
Q
∑
q=1
L
q
∑
j=1
CV
j
q
+
Q
∑
q=1
CS
q
. (15)
Generation Mechanism of the Neighboring Solu-
tions. In our optimization problem, function Ψ :
S × {row,column} → S operates on a matrix in S re-
turning another matrix that is close to the first one in
terms of disposal of its elements:
A
i+1
= Ψ(A
i
, p) (16)
with A
i+1
,A
i
∈ S, p ∈ {row, column}.
The parameter p is used to define two ways of
modifying matrix A
i
in terms of element disposal ob-
taining matrix A
i+1
. In particular:
• Row Swapping. If p = row, two elements in a
row of the matrix are swapped. Specifically, we
randomly select one of the matrix rows in which
two or more nonzero elements are present, i.e., we
randomly select a team whose list of interventions
contains two or more interventions:
generate q ∈ [1, Q] : |L
i
q
| > 1.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
540

Then, we randomly select two different nonzero
elements in the row:
generate x, y ∈ [1, L] : a
i
q,x
6= a
i
q,y
6= 0
and we swap them, i.e., we invert the order in
which two interventions in the list are performed:
a
i+1
q,x
= a
i
q,y
, (17)
a
i+1
q,y
= a
i
q,x
.
• Column Swapping. If p = column, the nonzero
element of a column of the matrix is moved from
one row to another one, possibly modifying its
value if necessary. In particular, we randomly
select one of the matrix columns c
l
in which a
nonzero element is present, i.e., we select an in-
tervention l that is already assigned to a team:
generate l ∈ [1,L] : nz(c
l
) 6= 0, i.e., l ∈
Q
[
q=1
L
i
q
.
Then, we randomly select one matrix row z in
which the corresponding element a
i
z,l
of the ma-
trix column c
l
is equal to zero:
generate z ∈ [1, Q] : a
i
z,l
= 0.
The value of the nonzero element in the column
vector c
l
is set to zero. Finally, if all the elements
of the row z in matrix A
i
are zero then element
a
i+1
z,l
in matrix A
i+1
is set to 1:
a
i+1
z,l
= 1 (18)
while, if in the row z in matrix A
i
there are
nonzero elements, we compute the maximum
value among all the elements in the row and we
assign to element a
i+1
z,l
in matrix A
i+1
the value:
a
i+1
z,l
= max(z,A
i
) + 1, (19)
i.e., we take one intervention from one team and
we give it to another one that will perform it as its
last intervention.
Cooling Scheme. The aspects of the cooling scheme
have been designed as follows:
• (a) initial temperature - An initial problem solu-
tion A
1
is generated and the initial temperature is
set to its cost:
T = E
A
1
(20)
• (b) temperature updating mechanism - We de-
signed an updating mechanism based on a cooling
factor α ∈ R
+
such that:
T = T − (α · T ) (21)
• (c) number of iterations for each temperature
value - n
t
∈ N iterations are performed for each
temperature value T by correspondingly generat-
ing n
t
solutions though the use of eq. (16):
A
1
,A
2
,··· ,A
n
t
• (d) stop criterion - We designed a criterion which
is based on both the value of the temperature and
the progress of the SA algorithm itself. We de-
fined a target temperature T
low
∈ [0, T [ at which
the SA algorithm is terminated. Moreover, we use
a vector vectE to store the cost associated with the
last |vectE| solutions:
vectE = {E
A
y
,E
A
y+1
,··· ,E
A
y+|vectE |
} (22)
If the cost associated with such solutions is ex-
actly the same for a number of temperature levels
equal to |vectE| the algorithm is terminated:
E
A
y
(Q,L)
= E
A
y+1
(Q,L)
= ·· · = E
A
y+|vectE |
(Q,L)
(23)
Acceptance Rule. The solutions generated for each
temperature value T are compared using Metropolis
criterion. When solution A
i+1
is generated its cost
is computed by eq. (15) and the cost variation with
respect to solution A
i
is computed:
∆E = f (A
i+1
) − f (A
i
). (24)
If ∆E ≤ 0 the new solution is accepted. Otherwise, if
∆E > 0 the new solution is accepted only if
ξ < e
(−∆E/T )
(25)
where ξ is a random number uniformly distributed
over [0,1] and T is the current temperature. If ξ >
e
(−∆E/T )
the new solution is discarded and current
solution A
i
is used to generate a new one through
eq. (16).
Algorithm 1 reports all the steps of the SA algo-
rithm as applied to our routine maintenance problem.
Specifically, in lines 1-7 all the necessary vari-
ables are declared: s and s
0
represent the current solu-
tion and the neighboring solution, respectively; vec-
tor vectE of size d stores the cost of the last d solu-
tions; α is the cooling factor; T contains the initial
temperature of the system and the following tempera-
ture values while T
low
is the minimum temperature to
be reached; E and E
0
represent the cost of the current
solution s and of the neighboring solution s
0
, respec-
tively; n
t
is the number of iterations to be performed
for each temperature value. In line 9 the initial solu-
tion is generated through generate initial solution()
and in line 10 f () returns its cost (see eq. (6)). Such a
cost is used to set the temperature initial value in line
11. The SA algorithm itself consists of two nested
OptimizingRoutineMaintenanceTeamRoutes
541

Algorithm 1: SA algorithm for the solution of the routine
maintenance problem.
1: declare s, s
0
;
2: declare d;
3: declare α;
4: declare vectE[d];
5: declare T , T
low
;
6: declare E, E
0
;
7: declare n
t
;
8:
9: s ← generate initial solution()
10: E ← f (s);
11: T ← E;
12: while T > T
low
do
13: i ← 1;
14: while i < n
t
do
15: s
0
← Ψ(s);
16: E
0
← f (s
0
);
17: ξ ← rand();
18: if E
0
≤ E or e
−(E
0
−E)/T
> r then
19: s ← s
0
;
20: E ← E
0
;
21: end if
22: i ← i + 1;
23: end while
24: vectE ← store last cost(vectE, E);
25: if check stop criteria(vectE,d) then
26: break;
27: end if
28: T ← T − (α · T );
29: end while
30: return s, E;
loops. The outer loop (lines 12-29) is used for tem-
perature cooling while the inner loop (lines 14-23)
is used to perform the n
t
iterations for each temper-
ature value. In particular, in lines 24-27 functions
store last cost() and check stop criteria() are used
to check if the last |vectE| = d solutions are exactly
the same. In such a case the algorithm is stopped.
Otherwise the algorithm stops as soon as temperature
T
low
is reached. In both cases, the current solution and
its cost are returned (line 30).
5.4 Exhaustive Algorithm
Through the use of the SA, we are not guaranteed that
the found solution is the best solution for our opti-
mization problem. It is therefore necessary to identify
a reference value to evaluate the quality of the solu-
tions found with the SA. To this purpose, we designed
an exhaustive algorithm.
Exhaustive algorithm is composed of two parts.
The first part has the role to find all the possible dis-
tributions of the L maintenance interventions to the Q
maintenance teams. The distribution operation sim-
ply executes the division of the L maintenance inter-
ventions to the Q maintenance teams by creating Q
unordered lists identified as U
q
:
Q
[
q=1
U
q
⊆ L (26)
Where U
q
= |U
q
| : U
q
≤ L and U
q
[i] ∈ [1,Q] : i ∈
[1,L]. To solve the distribution operation a method
which use a vector with dimension L has been devel-
oped:
V
L
= {v
1
,v
2
,··· v
L
} (27)
Each elements of the V
L
vector represents one of the
maintenance interventions of the list L:
v
i
∈ L (28)
The value of each element of the vector V
L
determines
at which U
q
unordered list is assigned, whereas the
position in the vector determines the identifier of the
maintenance operation:
U
v
i
[x] = i : x ∈ [1,L] (29)
The V
L
vector allows us to implement and automate
the generation of all the possible distributions of the L
maintenance operations to the Q maintenance teams,
using the V
L
vector like a number in Q basis with L
digits, it is possible to generate all the numbers in Q
in the range [0,Q
L
] by defining the following function
V
i
L
= next(V
i−1
L
,b) (30)
where i ∈ [0, Q
L
] and V
0
L
= {0}. The function (30) re-
ceives in input a number V
i−1
L
expressed in array form
(27), and its basis b. Therefore the function generates
the next number of the input in basis b. This last num-
ber is always expressed in array form (27).
The second part of the exhaustive algorithm, us-
ing all vector form numbers found with function (30),
computes all the possible solutions for our problem
which are later evaluated to determine the best solu-
tion.
For each vector numbers all possible simple per-
mutations of the U
q
are evaluated. Therefore, for
each U
q
several solutions are generated for our prob-
lem, each evaluated to determine the best solution.
6 EXPERIMENTAL RESULTS
The use case, where the SA algorithm was applied, is
related to a real Italian company, located in the north
west of Sicily, with the responsibility of managing
the maintenance related to electrical installations. As
mentioned in Section 1 to perform the maintenance
operations the company needs to solve a scheduling
problem to minimize the overall cost for maintenance.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
542

The solution of the optimization problem must be
found respecting the formalization of the objectives
and constraints specified in Problem 1.
In particular, the use case is related to a typical
working day, where the company needs to schedule
the daily maintenance operations to its maintenance
teams. The maintenance operations, occur in the elec-
trical installations managed by the company. The ge-
ographical points of installations and company head-
quarters compose the all possible geographical loca-
tions P defined in Section 4 and listed in Table 1.
Table 1: Geographical points of installations.
Installation ID Latitude Longitude Name
1 38.000000 13.283333 Kaggio (A)
2 38.083333 13.500000 Bagheria (B)
3 38.050000 13.000000 Balestrate (C)
4 38.150000 13.083333 Terrasini (D)
5 38.033333 13.450000 Misilmeri (E)
6 38.116667 13.366667 Company (F)
As introduced in Section 4, L maintenance ser-
vices are provided in a typical working day; each of
them is characterized by an execution time, a set of
skills needed to perform the maintenance and a loca-
tion. We applied our optimization algorithm to the
L = 10 maintenance services of the referred company
reported in Table 2, where the maintenance services
are identified by an ID and the location where the
maintenance has to be done is identified by the same
ID used in Table 1 (Installation ID). In order to main-
tain the scenario as simple as possible, we assume that
all the maintenance intervention have the same prior-
ity.
Table 2: Maintenance interventions.
Interventions ID Duration Installation ID Skills ID Skills
1 120 1 1 {3}
2 180 2 2 {1,2}
3 120 2 1 {3}
4 90 3 3 {1}
5 180 3 2 {1,2}
6 60 5 4 {2}
7 120 4 2 {1,2}
8 120 1 5 {2,3}
9 180 5 6 {1,3}
10 120 4 5 {2,3}
The company has four maintenance teams (Q =
4), composed of one or more workers and a single
vehicle. These teams are the elements of Q . Each
worker has one or more skills, collected in C . In
our use case three possible skills have been identified
(C = 3) and they have been associated to each worker
as described in Table 3, where the cost per hour and
the maintenance team have been specified.
The vehicles owned by the company are summa-
rized in Table 4 together with the fuel type (petrol or
Table 3: Workers cost per hour and skills.
Worker ID Cost/h Skills Team ID
1 6.80 {1,2,3} 1
2 6.50 {1,2,3} 1
3 7.00 {1,2,3} 2
4 6.40 {1,2} 2
5 6.25 {1,2,3} 3
6 6.90 {3} 3
7 6.20 {1,2,3} 4
8 6.00 {3} 4
Table 4: Vehicles characteristics.
Vehicle ID Fuel type l/Km Wear/Km($) Team ID
1 Diesel 8.2 0.57 1
2 Diesel 8.2 0.57 2
3 Petrol 5.9 0.25 3
4 Petrol 5.9 0.25 4
diesel), the costs, and the maintenance team ID which
are assigned to.
Each maintenance team is characterized by both
the skills of its workers and the characteristics of its
vehicle. This means that each teams can perform only
the maintenance services fitting adequate skills spec-
ified through eq. (3) and (4). In the specific case of
the use case here considered, columns Skills ID and
Skills of Table 2 represents the function of eq. (4).
It is easy to see that the monetary cost of each team
depends on the workers hourly cost (Table 3) and on
the travel cost (Table 4).
To completely define the optimization problem,
we have to define the cost functions introduced in
Problem 1 (items i) and ii)). These functions depends
on the working day duration D, that is assumed to be
eight hours long (D = 8) in our use case. Let C
q
be
the hourly cost by each maintenance team during the
regular working time, C
q
is calculated by adding the
hourly wage of each worker of the team shown in Ta-
ble 3. In ii) is defined the cost function to be applied
after the first eight working hours. The cost CS
q
de-
fined in Problem 1, representing the cost during the
extra working time, is defiend as CS
q
= 2 ∗ C
q
. The
cost CV
i
q
is computed using the data in Table 4 and
fixed values for diesel and petrol cost that are 1.746
for the petrol and 1.627 for the diesel.
In the following, we will present the results ob-
tained by applying the optimization Algorithm 1 to
the problem defined above. Since the SA is a based
on a meta-heuristic approach, we compare the results
with the real optimum solution computed through the
exhaustive algorithm (Section 5.4). The purpose of
the comparison is twofold: 1) evaluate the quality of
the solution, and 2) evaluate the time efficiency of the
algorithm. During our experiments, we varied the SA
parameters in order to show their impact on the final
OptimizingRoutineMaintenanceTeamRoutes
543
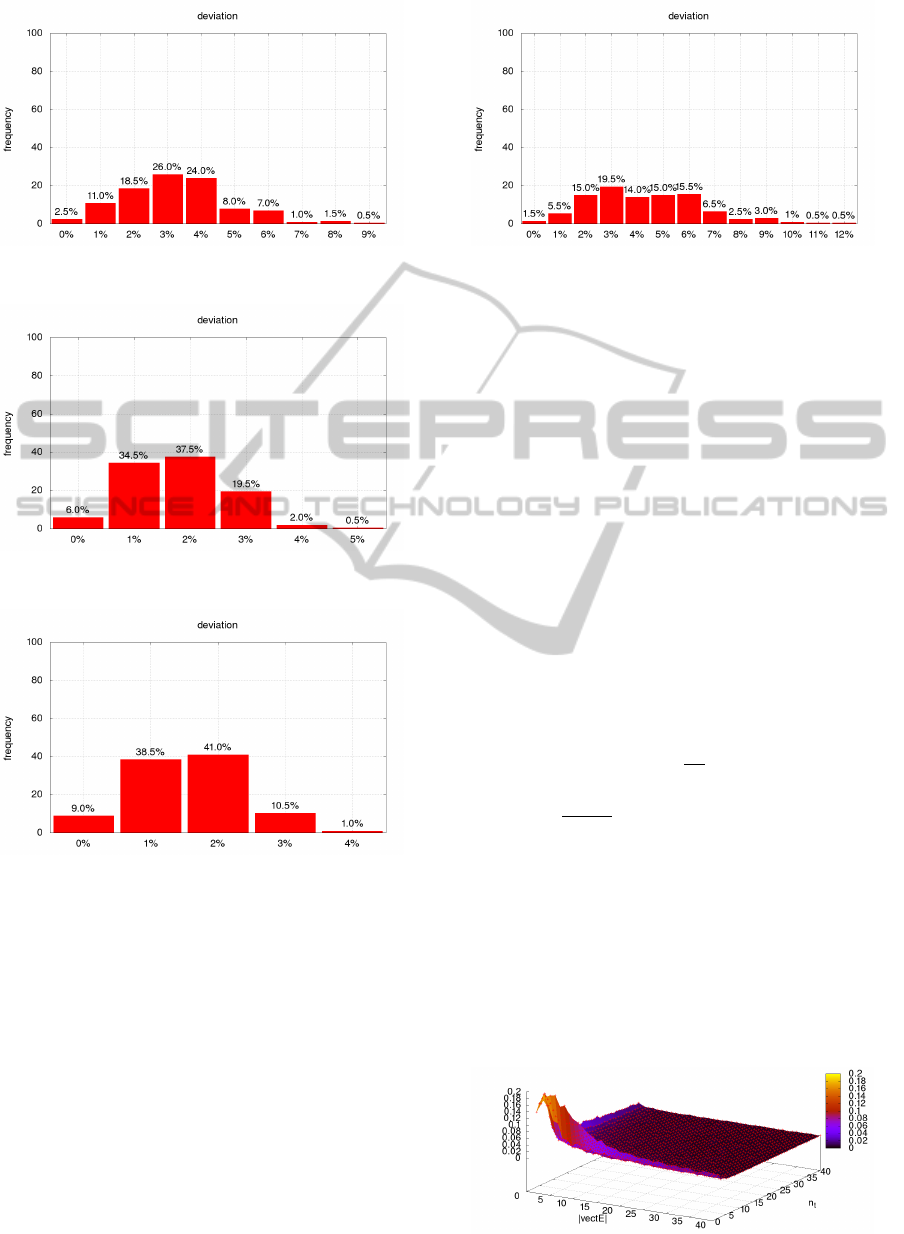
Figure 1: α = 0.3, n
t
= 30, T
low
= T − (T ∗ 0.999),
|vectE| = 20.
Figure 2: α = 0.03, n
t
= 30, T
low
= T − (T ∗ 0.999),
|vectE| = 20.
Figure 3: α = 0.003, n
t
= 30, T
low
= T − (T ∗ 0.999),
|vectE| = 20.
solution. We considered the parameters related to the
cooling (21) and to the stop criterion (23), specifically
α and n
t
for the cooling scheme, T
low
and |vectE| for
the stop criterion.
Given a set of fixed parameters, we run the SA
algorithm 200 times and we computed the distance
of each obtained optimal solution with respect to that
evaluated by the exhaustive algorithm. The overall re-
sults are synthesized in Figures 1, 2 and 3 by varying
the α and with fixed n
t
and T
low
; each histogram de-
picts the distribution of the deviations. As an example
Figure 1 shows that the Algorithm 1 has a probabil-
ity equal to 26% to give an estimation of the optimum
with an error equal to 3%. The graphs show that de-
Figure 4: α = 0.003, n
t
= 30, T
low
= T − (T ∗ 0.990),
|vectE| = 20.
creasing the value of α the accuracy of the result de-
creases accordingly, ranging from an an average devi-
ation of 3.275% with α = 0.3 to an average deviation
of 1.56% with α = 0.003.
Another set of experiments has been performed by
fixing the value of α to 0.003 and varying the param-
eter T
low
from T
low
= T − (T ∗ 0.999) (Figure 3) to
T
low
= T − (T ∗ 0.990) (Figure 4), thus increasing the
value of the target temperate. This change produces a
sharp deterioration of the solutions found with Algo-
rithm 1 to an average deviation of 4.319 in Figure 4.
This deterioration is justified by the fact that fewer it-
erations are performed with Algorithm 1 to search the
solution of the optimization problem.
To evaluate how the parameters n
t
and |vectE| af-
fect the Algorithm 1 in the search of the solution, we
considered as a quality index the relative error E
r
of
the solution obtained by the exhaustive algorithm:
E
r
=
E
a
x
m
(31)
where E
a
=
|x
m
−V
a
|
2
is the mean absolute error affect-
ing the solution, V
a
is the result of exhaustive algo-
rithm, and x
m
is the average value of the solutions ob-
tained from Algorithm 1. Figure 5 depicts E
r
versus
both n
t
and |vectE|. As can be seen in Figure 5, E
r
decreases when n
t
and |vectE| increase starting from
0 but its value does not substantially change when n
t
and |vectE| reach a certain threshold.
To better analyze the behavior of the SA algo-
rithm, we also considered the execution time, other
than the quality of the result, through the following
Figure 5: E
r
with α = 0.003 and T
low
= T − (T ∗ 0.999).
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
544

function:
F
q
(E
r
,τ) = 1−
β ·
E
r
− min
E
r
∆
Er
+
γ ·
τ − min
τ
∆
τ
(32)
The quantities used to define F
q
() are the following:
∆
E
r
= max
E
r
− min
E
r
, where max
E
r
and min
E
r
are the
maximum and the minimum relative error obtained by
varying n
t
and |vectE|; τ is the measured execution
time of the Algorithm 1; ∆τ = max
τ
− min
τ
, where
max
τ
and min
τ
are the maximum and the minimum
execution time obtained by varying the parameters n
t
and |vectE|; the parameters β and γ, such that β + γ =
1, are two constants used to give a different weight to
the quality of the solutions and to the execution time
of the Algorithm 1 respectively.
Figure 6: F
q
(E
r
,τ) with β = 0.7 and γ = 0.3.
The graph in Figure 6 shows the trend of function
(32) computed with α and T
low
set to the optimal val-
ues found in the first set of experiments (α = 0.003
and T
low
= T − (T · 0.999)) and by varying n
t
and
|vectE|. The values of β and γ are fixed to β = 0.7
and γ = 0.3 in order to give more weight to the solu-
tion quality than to the execution speed of the Algo-
rithm 1. The analysis of the graph reveals a maximum
identifying the best pairs of parameters to optimize
the behavior with respect either the precision and the
execution time.
To better identify the value of the parameters, we
depicted in Figures 7 and 8 the 2-D versions of the
graph in Figure (6). In Figure 7, each line corresponds
to a single value of n
t
(z axis in Figure 6) whereas in
Figure 8 each line corresponds to a single value of
|vectE| (x axis in Figure 6).
Parameters n
t
and |vectE| carry out a comple-
mentary role. Using hight values of |vectE|, we im-
pose a stop criterion heavily based on temperature T ;
this configuration produces excellent results as long
as n
t
doesn’t excessively increase otherwise a perfor-
mances degradation is manifested. As well shown in
Figure 8, the graph has a maximum located around
n
t
= 5 and |vectE| = 35.
As final experimental results, we reported in Ta-
ble 5 the execution times obtained by running Algo-
rithm 1 with different sets of parameters and the exe-
Figure 7: F
q
(E
r
,τ) with β = 0.7 and γ = 0.3.
Figure 8: F
q
(E
r
,τ) with β = 0.7 and γ = 0.3.
Table 5: Execution Time Algorithm 1 and Exhaustive Al-
gorithm.
Execution Time Algorithm 1 (ms)
n
t
|vectE|
5 5 485.0
5 20 639.4
5 35 697.4
10 5 1057.2
10 20 1313.8
10 35 1442.4
20 5 2332.0
20 20 2746.4
20 35 2977.2
35 5 4304.8
35 20 4986.2
35 35 5259.0
Execution Time Algorithm 2 (ms)
2100000
cution time of the exhaustive algorithm. As can be ob-
served, Algorithm 1 completes in some milliseconds,
irrespective of the set of parameters, whereas the ex-
haustive algorithm needs a lot of minutes to find the
final problem solution.
7 CONCLUSIONS AND FUTURE
WORK
In this paper, we proposed the use of simulated an-
nealing for the solution of the scheduling problem of a
OptimizingRoutineMaintenanceTeamRoutes
545

set of geographically distributed routine maintenance
interventions. We based the choice of which team to
pick among the available ones for each intervention
and the order in which each team performs its inter-
ventions on several parameters, i.e., team skills, cost
of overtime work, and cost of transportation. We ap-
plied the proposed algorithm to a real industrial use
case provided by an electrical plant design company
and we compared it versus an exhaustive approach.
Several numerical results have been shown highlight-
ing the effects of the parameters of the simulated an-
nealing on the accuracy of the solution and on the ex-
ecution time of the algorithm. Future work will be
focused on implementing a complete tool for mainte-
nance intervention scheduling, testing and stressing
it on the ground of realistic use cases. Moreover,
we plan to combine the proposed approach with ad-
vanced routing algorithms analyzing the influence of
their efficiency on our solution technique.
ACKNOWLEDGEMENT
The research leading to these results has re-
ceived funding from the Italian National project
“SIGMA - Integrated Cloud-Sensor System for Ad-
vanced Multirisk Management” under grant agree-
ment PON01 00683.
REFERENCES
Allen G. Brown, Dr. Matthew, C. Ruschmann, Dr. Brenton
Duffy, Lucas Ward, Dr. Sun Hur-Diaz, Eric Ferguson,
and Shaun M. Stewart (2014). Simulated annealing
maneuver planner for cluster flight. In 24th Interna-
tional Symposium on Space Flight Dynamics, Laurel,
MD, April 2014.
C. Blum and A. Roli (2003). Metaheuristics in combinato-
rial optimization: overview and conceptual compari-
son. In ACM Computing Surveys, Vol. 35, No. 3.
Chun-Cheng Lin, Lei Shu, and Der-Jiunn Deng (2014).
Router node placement with service priority in wire-
less mesh networks using simulated annealing with
momentum terms. In Systems Journal, IEEE (Vol-
ume:PP , Issue: 99 ).
D. T. Pham and D. Karaboga (2000). Intelligent optimisa-
tion techniques: genetic algorithms, tabu search, sim-
ulated annealing and neural networks. In Springer.
F. Glover and G. Kochenberger (2003). Handbook of meta-
heuristics. massachusetts. In Eds. New York: Kluwer
Academic Publish-ers.
Fleischer, M. (1995). Simulated annealing: past, present
and future. In Proceedings of the 1995 Winter Simu-
lation Conference, C. Alexopoulos, K. Kang, W. Lileg-
don, and G. Goldsman, Eds. 155161.
Ibrahim El-Amin, Salih Duffuaa, and Mohammed Abbas
(1999). A tabu search algorithm for maintenance
scheduling of generating units. In Electric Power Sys-
tems Research 54 (2000) 9199.
J.T. Saraiva, M.L. Pereira, V.T. Mendes, and J.C. Sousa
(2011). A simulated annealing based approach to
solve the generator maintenance scheduling prob-
lem. In Electric Power Systems Research 81 (2011)
12831291.
Kenneth Bryan, Padraig Cunningham, and Nadia Bol-
shakova (2006). Application of simulated annealing to
the biclustering of gene expression data. In Informa-
tion Technology in Biomedicine, IEEE Transactions
on (Volume:10 , Issue: 3 ).
Keshav P. Dahal and Nopasit Chakpitak (2006). Genera-
tor maintenance scheduling in power systems using
metaheuristic-based hybrid approaches. In Electric
Power Systems Research 77 (2007) 771779.
N. Metropolis, A. W. Rosenbluth, M.N. Rosenbluth, A.H.
Teller, and E. Teller (1953). Equation of state cal-
culations by fast computing machines. In Journal of
Chemical Physics, vol. 21, no. 6, pp. 10871092.
W. Herroelen, E. Demeulemeester, and B. De Reyck
(1999). Metaheuristics in combinatorial optimization:
overview and conceptual comparison. In J. Weglarz
(Ed.), Project Scheduling: Recent Models, Algorithms
and Applications, Kluwer Academic Publishers, pp.
126.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
546
