Optical Limiting Characteristics of Fabry–Perot Microresonators at
Third-order Nonlinear Absorption and Refraction of the
Intracavity Medium
A. A. Ryzhov
1,2
and I. M. Belousova
1,2
1
Institute for Laser Physics, Vavilov State Optical Institute, Kadetskaya lin. 5/2, Saint Petersburg, Russia
2
Laser Physics Department, ITMO University, Kronverksky pr. 49, Saint Petersburg, Russia
Keywords:
Optical Limiting, Fabry–Perot, All-optical Devices, Nonlinear Optics.
Abstract:
Calculating steady-state optical limiting characteristics of nonlinear Fabry–Perot resonators, we noticed that
the input-output characteristic shape does not depend on any resonator parameter. The intracavity medium
was assumed to have either third-order nonlinear refraction or absorption. In a double logarithmic diagram the
input-output characteristic can be divided into two regions, linear and nonlinear, which are both almost straight
lines with a relatively short curved section between them. The only dependent variable is the position of that
curved section (limiting threshold). Simple relations between resonator parameters, nonlinear coefficients and
the limiting threshold, enabling one to easily get nonlinear characteristics of such resonators whithout doing
nonlinear calculations, are presented.
1 INTRODUCTION
In a nonlinear Fabry–Perot resonator (NFPR) indices
of reflection and absorption of a medium contained
between the mirrors depend on light intensity. Such
resonators have been well studied since the second
half of the 1970s. Theoretically predicted effects of
optical bistability, differential gain and limiting have
been experimentally observed for resonators contain-
ing Na vapors, nonlinear liquids (liquid crystals, ni-
trobenzene, CS
2
), and solid plates of semiconductor.
A detailed review of these works has been presented
in (Abraham and Smith, 1982).
In general, application of NFPRs for creation of
low-threshold nonlinear optical devices is promising
because of two following reasons. Firstly, the res-
onator is a narrowband optical filter, for which spec-
tral position of the line of transparencydepends on the
optical distance between the mirrors not on medium
resonant properties. Along with it a small change in
the refractive index of a medium contained between
the mirrors results in a significant spectral shift of the
line. Whereas a small increase in the absorption index
drops considerably transmittance (T) at the peak of
the line (however, in this case a decrease in T results
mainly from an increase in reflectance (R) not from
an increase in absorbance (A) of the whole structure).
Secondly, light intensity at the resonant wavelength
many-fold increases in the space between the mirrors
by interference, which leads to a correspondent de-
crease in the nonlinear threshold.
An NFPR works as an optical power limiter if
the incident radiation wavelength is a resonant wave-
length. The potential of NFPR in the capacity
of quick-response one-wavelength optical limiters is
currently under investigation. Such limiters could be
useful in a variety of laser systems, for example, in a
laser rangefinder to protect the detector from intensive
reflected (back-scattered) radiation. Currently there is
a lack of experimental works realising that approach,
whereas interest in optical power limiting is very ac-
tive.
There are also some features restricting the range
of possible application of NFPRs as optical limiters:
• an NFPR operates as an optical limiter only at a
predetermined resonant wavelength while being
simply a linear mirror in the neighborhood of this
wavelength;
• an NFPR must be placed in a collimated beam
propagating in a specified direction.
Recently we presented an experimental observa-
tion of optical limiting effect provided by a thin-film
multilayer NFPR (Ryzhov et al., 2014). The ex-
perimental characteristics were in a good agreement
with corresponding numerical simulation results. The
140
Ryzhov A. and Belousova I..
Optical Limiting Characteristics of Fabry–Perot Microresonators at Third-order Nonlinear Absorption and Refraction of the Intracavity Medium.
DOI: 10.5220/0005404301400143
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 140-143
ISBN: 978-989-758-093-2
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

same calculation program was used in the present
work.
2 THE APPROACH
A monochromatic uniform plane wave, characterized
by intensity I
inp
and wavelength λ
0
, enters into a sym-
metric NFPR, characterized by mirror reflectance R
m
,
geometricalthickness L, intracavity medium linear re-
fractiveindex n
0
and complex nonlinear coefficient n
2
(cm
2
/W). There is no absorption in the mirrors and no
linear absorption in the medium.
The intracavity medium is assumed to be a third-
order nonlinear material with instant response so that
at any location x
n(x) = n
0
+ n
2
I(x), (1)
where I(x) is light intensity (W/cm
2
) at location x.
The real part of n
2
defines nonlinear refraction
and is commonly denoted as γ: γ = ℜ(n
2
). Nonlin-
ear absorption is usually characterized by coefficient
β (cm/W), which is proportional to the imaginary part
of n
2
:
β =
4π
λ
0
ℑ(n
2
). (2)
Optical limiting characteristic of an NFPR is ei-
ther output intencity I
out
or transmittance T depen-
dence on input intencity I
inp
. In case of nonlinear ab-
sorption absorbance A versus I
inp
can be considered
as a separate characteristic.
Numerical simulation of optical limiting charac-
teristics at different parameters of the NFPR shows
that shapes of the characteristics are constant. More
precisely, there is one shape when the medium has
nonlinear absorption, and another (but quite similar)
shape when the medium has nonlinear refraction.
When one or several parameters of the NFPR vary,
its nonlinear characteristic only moves along the ab-
sciss. The characteristic position can be evaluated by
just one value — the limiting threshold. We define
the limiting threshold I
th
as a value of I
inp
, at which
T decreases to 0.8 of its initial value, which is a quite
common definition:
T(I
th
) = 0.8T(0). (3)
The task is to derive relations between I
th
, λ
0
and
the NFPR parameters: R
m
,L,n
0
,n
2
.
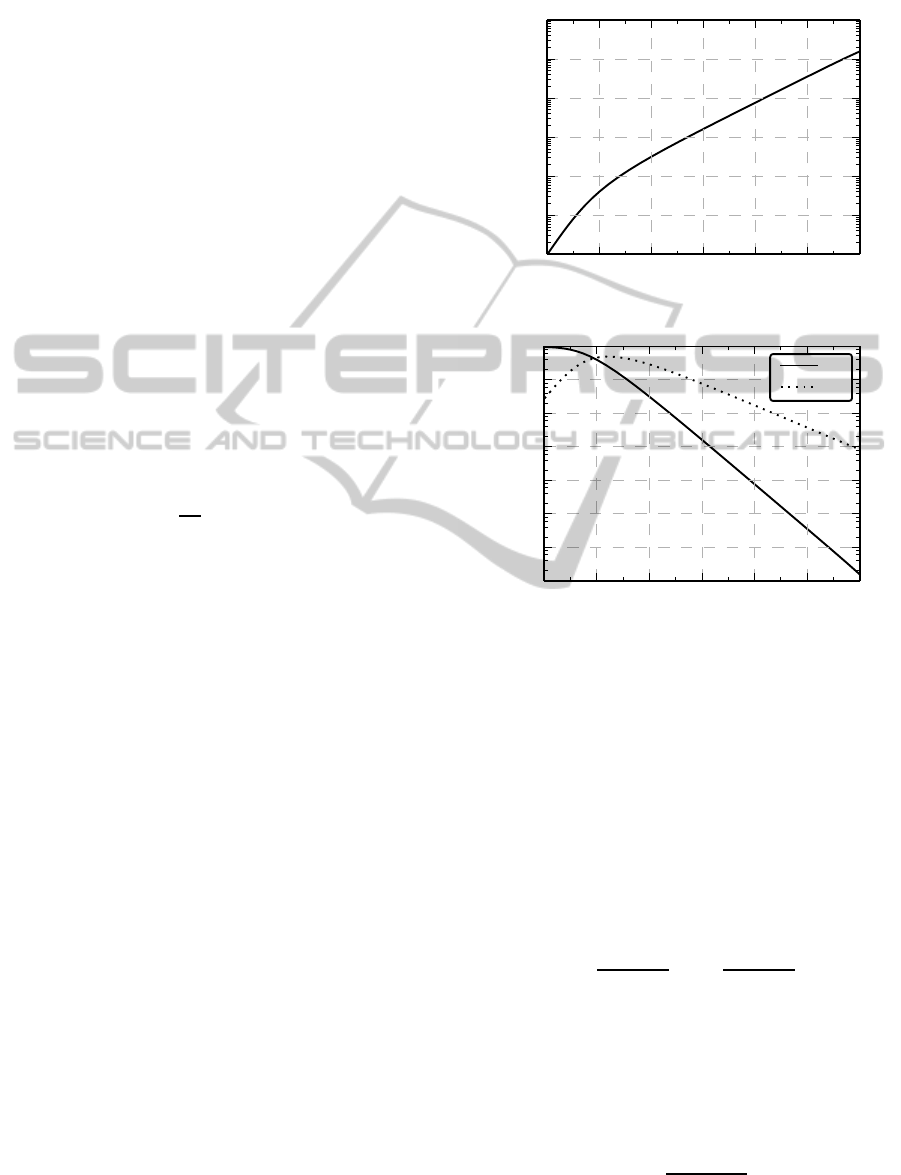
3 NONLINEAR ABSORPTION
This section deals with the case when only nonlin-
ear absorption exists and γ = 0. In Figure 1 limiting
characteristics of such an NFPR in terms of I
th
are
presented.
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
I
inp
/I
th
10
−1
10
0
10
1
10
2
10
3
10
4
10
5
I
out
/I
th
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
I
inp
/I
th
10
−7
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
T , A
T
A
Figure 1: Limiting characteristics of an NFPR at nonlinear
absorption.
A noticable feature of these characteristics is that
absorbance A is at its maximum when I
inp
is in the
range (10;100) ×I
th
. Low A at high I
inp
means that
the absorptive medium is in some degree protected
from optical breakdown or overheating by the mirror.
As it was mentioned above, light intensity at the
resonant wavelength many-fold increases in the space
between the mirrors. The field inside the resonator is
a standing wave, and it is clear that in the absence of
absorption intensity at the loops
max{I
inside
} =
4
(1−R
m
)
I
out
=
4
(1−R
m
)
TI
inp
. (4)
It is evident that I
th
is inversely proportional to
I
inside
/I
inp
and β. It also must be proportional to the
finesse of the resonator because the finesse, in some
sense, determines the number of passes. So, for a high
finesse NFPR (1−R
m
<< 1), the required equation
can be written as
I
th
≃ 0.07
(1−R
m
)
2
Lβ
; (5)
OpticalLimitingCharacteristicsofFabry-PerotMicroresonatorsatThird-orderNonlinearAbsorptionandRefractionofthe
IntracavityMedium
141

where the coefficient 0.07 was defined by the numer-
ical calculations.
Recently a quite comprehensive theoretical analy-
sis of the same case — plane microresonator at third-
order nonlinear absorption of the intracavity medium
— was published (Makri et al., 2014). One can find
there a plot looking exactly like Figure 1, but there is
no relation comparable to Equation 5.
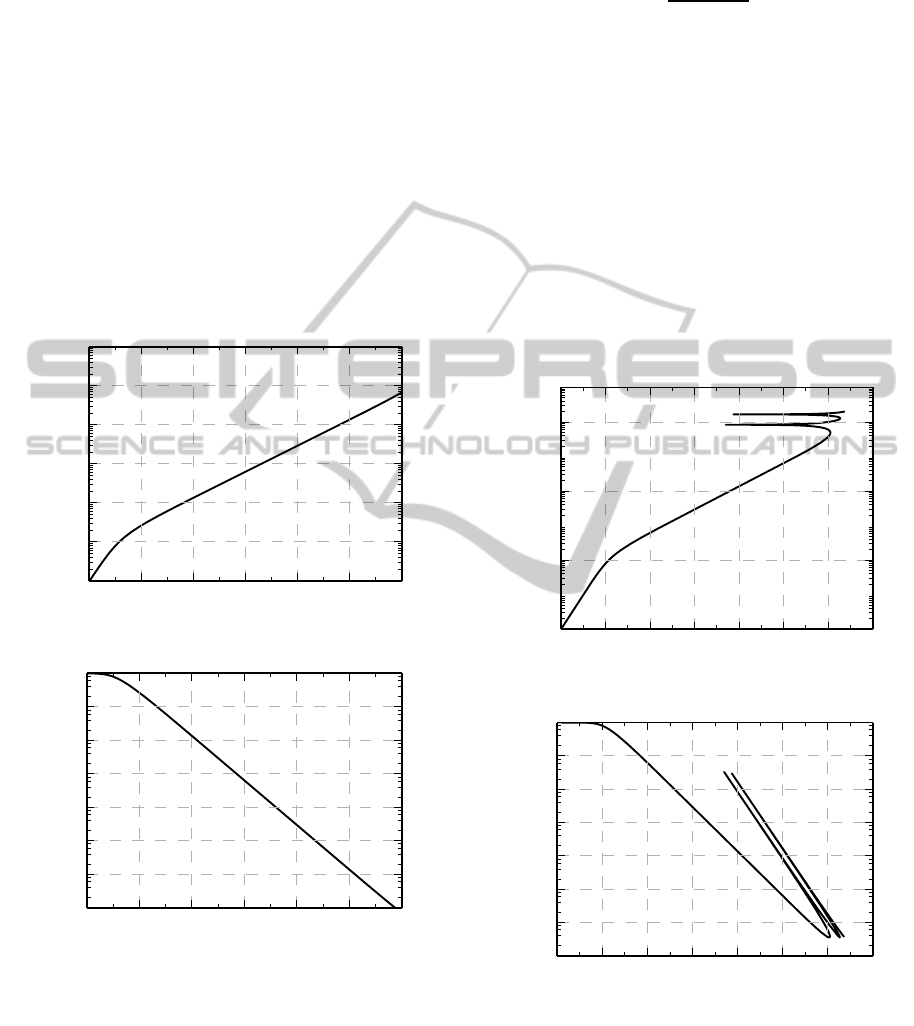
4 NONLINEAR REFRACTION
Here it is assumed that only nonlinear refractionexists
and β = 0. Limiting characteristic of such an NFPR
in terms of I
th
is shown in Figure 2.
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
10
11
I
inp
/I
th
10
−1
10
0
10
1
10
2
10
3
10
4
10
5
I
out
/I
th
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
I
inp
/I
th
10
−7
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
T
Figure 2: Limiting characteristics of an NFPR at nonlinear
refraction.
As opposed to the case of nonlinear absorption,
at nonlinear refraction T does not decrease with no
limit. Considering that the decrease in T results from
a spectral shift of the resonance line, one can easily
realize that the minimal possible value of T is equal
to the minimum of the initial (at very low I
inp
) trans-
mission spectrum. That value is well known from the
theory of Fabry–Perot resonators:
T
min
=
(1−R
m
)
2
(1+ R
m
)
2
. (6)
As far as T
min
depends on R
m
, it is different for
NFPR with different R
m
. So the presented limiting
characteristic in terms of I
th
is appropriate to an NFPR
only for a range of I
inp
, at which T > T
min
and the
nonlinear characteristic is almost straight in a double
logarithmic diagram. At higher I
inp
T at first slightly
increases, then jumps to higher branches — the input-
output characteristic is multiple-valued. Of course,
limiting characteristics of different NFPR are differ-
ent in this area.
For example, the limiting characteristic of a spec-
ified NFPR, for which I
th
= 10 (W/cm
2
), is shown
in Figure 3. Here λ
0
= 1.5 µm,R
m
= 0.9988,L =
53.57 µm,n
0
= 3.5,γ = 10
−10
(cm
2
/W).
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
10
13
I
inp
(W/cm
2
)
10
−1
10
1
10
3
10
5
I
out
(W/cm
2
)
10
−1
10
1
10
3
10
5
10
7
10
9
10
11
10
13
I
inp
(W/cm
2
)
10
−7
10
−6
10
−5
10
−4
10
−3
10
−2
10
−1
10
0
T
Figure 3: Multiple-valued limiting characteristics of an
NFPR with specified parameters.
In fact upper branches of T reach unity. It is
not shown in the given plot due to a lack of cal-
culation points, although their number is very high
— 951 points in the range of I
out
from 1.5 ·10
4
to
2·10
4
W/cm
2
.
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
142

Unlike the case of nonlinear absorption, at nonlin-
ear refraction I
th
is inversely proportional to δλ — the
full-width half-maximum of the resonant line. I
th
also
must be inversely proportional to I
inside
/I
inp
and γ. Fi-
nally, for a high finesse NFPR the following equation
was derived:
I
th
≃ 0.16(1−R
m
)
n
γ
δλ
λ
0
. (7)
By means of the linear Fabry–Perot resonators
theory δλ can be expressed through other variables:
δλ =
1−R
m
π
√
R
m
λ
2
0
2n
0
L
; (8)
so that
I
th
≃ 0.025
(1−R
m
)
2
γ
√
R
m
λ
0
L
; (9)
or, if (1−R
m
) << 1,
I
th
≃ 0.025
(1−R
m
)
2
λ
0
γL
. (10)
5 CONCLUSION
The derived simple equations (5) and (10) enable one
to estimate the limiting threshold of an NFPR in cases
of third-order nonlinear absorptionor third-ordernon-
linear refraction of its intracavity medium. Together
with the limiting characteristics in relative units (Fig-
ures 1 and 2) these relations easily give correspond-
ing absolute limiting characteristics, so that there is
no need to calculate them for each new set of NFPR
parameters.
The following additional consequences can be for-
mulated:
1. At given parameters of the intracavity medium
(L,n
0
,n
2
) an increase in mirror reflectance R
m
leads to an increase in the field intensity multipli-
cation (inside relative to outside) and a decrease
in resonance line width δλ. All that results in
quadratic reduction of the limiting threshold I
th
which is proportional to (1 −R
m
)
2
at both non-
linear absorption and refraction.
2. With the other things being equal an increase in
the resonator length L leads to proportional de-
creases in δλ and in I
th
also at both nonlinear ab-
sorption and refraction. In this case the rate of I
th
reduction with δλ narrowing is lower. To realize
that one should take into account that the field in-
tensity multiplication depends only on R
m
. So if
a decrease in I
th
is needed but a narrower resonant
line is undesirable, it is more advantageous to en-
hance R
m
not L.
ACKNOWLEDGEMENTS
This work was partially supported by the Russian
Foundation for Basic Research (No. 14-02-00851)
and the Government of Russian Federation (No. 074-
U01)
REFERENCES
Abraham, E. and Smith, S. D. (1982). Nonlinear Fabry-
Perot interferometers. Journal of Physics E: Scientific
Instruments, 15(1):33–39.
Makri, E., Ramezani, H., Kottos, T., and Vitebskiy, I.
(2014). Concept of a reflective power limiter based
on nonlinear localized modes. Physical Review A,
89(3):031802.
Ryzhov, A. A., Belousova, I. M., Wang, Y., Qi, H., and
Wang, J. (2014). Optical limiting properties of a
nonlinear multilayer Fabry-Perot resonator containing
niobium pentoxide as nonlinear medium. Optics Let-
ters, 39(16):4847–50.
OpticalLimitingCharacteristicsofFabry-PerotMicroresonatorsatThird-orderNonlinearAbsorptionandRefractionofthe
IntracavityMedium
143