Modelling and Analysis of Process Execution based on

Data Acquired from Sensors Networks

Repta Dragos, Ioan Stefan Sacala, Mihnea Alexandru Moisescu,

Calin Munteanu and Aurelian Mihai Stanescu

University Politehnica of Bucharest,

Faculty of Automatic Control and Computers, Bucharest, Romania

Keywords: Process Mining, Future Internet Enterprise Systems.

Abstract: This paper proposes a new approach for the analysis of physical processes. Based on several assumptions

regarding the information available regarding the physical processes, we constrain the generation of the

transition system. The method is based on the theory of regions that allows for the building compact

representations as Petri Nets of transition systems and a set of explicit descriptions for some of the

activities. The resulting compact model will exhibit the same behaviour as the input transition system. In

order to evaluate the resulting process model, several quality dimensions have been established.

1 INTRODUCTION

This paper proposes a new approach for the analysis

of physical processes. For this, we employ a

technique from the field of process mining – the two

step approach (Aalst, 2010) which works by

constructing a transition system from an observed

event log, followed by its transformation into a Petri

Net using an algorithm based on the theory of

regions.

We propose a new method of building the

transition system based on state variables. In order to

achieve this, we make several assumptions about the

information available regarding the processes:

knowledge of the preconditions and effects of the

actions that triggered the events and the initial state

of the system.

2 RELATED WORK

Process mining is a newly developed research field

that provides methods for analysing processes

starting from their observed behaviour.

This observed behaviour is encapsulated in event

logs and it is readily available in most PAIS (Process

Aware Information Systems) usually deployed in

enterprise environments. Furthermore, the

information contained in the event logs, can also be

collected from other types of systems, such as

embedded systems, using an array of sensors.

Each event in a log is referring to an activity or

action performed in the system (that led to a change

in the system’s state) and to a process instance or

case. An event log contains sequences of events

collected from the observed processes instances or

cases. Each of these sequences is also called a

process trace. For different process instances the

same trace may be recorded, but the order in which

different cases are logged is not relevant to the

analysis. Because of this, the event log is

represented as a multi-set or bag of event sequences.

The three main tasks considered in the field of

process mining are process discovery, conformance

checking and process model enhancement.

The process discovery problem is concerned with

finding a process model which best represents an

observed behaviour contained in an event log.

Usually, a simple event log is considered, one that

contains events that only refer to an activity and a

process case. (Moisescu, 2013), (Repta, 2013).

Several algorithms have been proposed as

solutions to the process discovery problem, such as:

the (extended) alpha algorithm, heuristic miner

(Weijters, 2003), genetic miner, fuzzy miner, ILP

miner (Werf, 2008) and the two-step approach based

on state-space theory of regions (Aalst, 2010). An

analysis of the proposed process discovery

algorithms is beyond the scope of this paper, but

618

Dragos R., Sacala I., Moisescu M., Munteanu C. and Stanescu A..

Modelling and Analysis of Process Execution based on Data Acquired from Sensors Networks.

DOI: 10.5220/0005407506180625

In Proceedings of the 3rd International Conference on Model-Driven Engineering and Software Development (MDE4SI-2015), pages 618-625

ISBN: 978-989-758-083-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

several reviews have been made such as (Tiwari,

2008) in which various approaches to process

discovery are comparatively described and

evaluated.

Conformance checking is used to evaluate a

process model against an event log. Techniques

proposed in this subfield of process mining can be

used in a variety of scenarios such as assessing a

discovered process model or analysing the

implementation of a process by comparing the base

model with the observations from the production

system. Recently, several quality dimensions have

been established in order to evaluate process models:

fitness, simplicity, precision and generality. Fitness

quantifies the amount of observed behaviour that can

be generated by the evaluated model. It is desirable

for the process model to have perfect fitness,

meaning that all the observed traces can be

generated by it. This quality metric is evaluated by

replaying each collected trace on the process model

and penalizing misalignments (Aalst, 2012). The

“simplicity” quality dimension refers to the size and

complexity of the process model and it is related to

the Occam’s razor principle. A metric based on the

number of elements in the process model is usually

used to evaluate this quality dimension. It should be

noted that in some cases, a compact process model

will not be the best representation of a process from

an analysts’ perspective. Lastly, precision and

generality refer to the amount of unobserved

behaviour that the process model can generate. They

are concerned with the problems of under-fitting

(too general) and over-fitting (too precise) process

models. A balance must be reached between the

amount of behaviour that the resulting model allows

and the behaviour expressed in the input event log.

On one hand, we cannot expect that all possible

behaviour will be found in the observed log. This is

particularly obvious in the case of parallel activity

sequences, where not all possible instantiations are

expected to appear in the log. On the other hand, a

process model that allows too much behaviour won’t

be useful for the user or analyst as it discards the

dependencies / constraints of the real process.

Finally, the task of process model enhancement

takes as input an existing process model and event

log and aims at improving or extending the model

using the information provided in the log. These

techniques require more information than what is

contained in a simple event log. Decision mining (de

Leoni, 2013) – identifying the conditions associated

with the decision points in process models – requires

additional data attributes associated with the events

in the log, based on which classification problems

are instantiated. Social network analysis (Aalst,

2004), (Song, 2008) that aims at identifying the

relations between the actors involved in the

execution of the process require that each event

references the entities that participated in the

completion of the activity. Furthermore, timestamp

of the events can be used analyse the execution time

of processes and determine performance data or

identify bottlenecks.

The ability of the proposed process discovery

and enhancement techniques to tackle problems

from various domains has been extensively studied.

In (Rozinat, 2009), the Heuristic Miner and the

Decision Miner are used to analyse and diagnose a

multi-agent system composed of soccer playing

robots. In (Aalst, 2007) a billing process in a public

administration office is analysed using various

process mining techniques demonstrating their

utility in the case of large organizations. Finally, a

case study on industrial production systems is

discussed and analysed in (Rozinat, 2009) (Gunther,

2010). This last example reveals some of the

shortcomings of existing approaches to process

discovery in the case of less-structured processes.

The approach presented in this paper belongs to

the process discovery task, but requires additional

information beyond an elementary event log.

Namely, we investigate the use of an explicit state-

space representation of the actions associated with

the events from the input log, as prior information.

This information is used in the two-step process

discovery approach (Aalst, 2010) to construct a

“more accurate” transition system.

3 PROBLEM STATEMENT

We consider that the assumptions we make

regarding the availability of the additional prior

information are feasible in the considered scenario

of physical processes.

In this case, it is conceivable that at least a subset

of the events in the log is retrieved using data from

sensors deployed in the environment, thus making

available at least a part of the real state of the

system. This additional information will result in the

discovery of a process model that is closer to the

reality.

In fig. 1 depicts the example process considered

in this paper (the implicit places in the Petri Net are

hidden).

The example process can depict two vehicles (A

and B) that move independently in an environment

partition into several areas. The events “Ax” and

ModellingandAnalysisofProcessExecutionbasedonDataAcquiredfromSensorsNetworks

619

Figure 1: Example process model.

“Bx” correspond to movement actions of vehicle A

and B between the areas of the environment. The

goal of this process is to perform 2 “work” actions –

X and Y - in two separate, pre-determined areas.

These “work” action require that both vehicles are in

the same area, at the same time.

In this case, the events regarding the movement

of the vehicles in the environment can be

automatically collected, leveraging an existing

access-control system.

4 TWO STEP PROCESS

DISCOVERY

In this section we make a short description of the

two step method of process discovery, discussed in

(Aalst, 2010) with a focus on the impact of various

methods of building the transition system on the

precision and generality of the discovered model.

The method is based on the theory of regions that

provides a method of building compact

representations as Petri Nets of transition systems.

The resulting compact model will exhibit the same

behaviour as the input transition system.

The considered process discovery method first

builds a transition system based on the information

from the log and then converts it - the second step -

in a compact Petri Net representation.

DEF (Transition system) – A transition system

TS = (S, E, T), in which S represents the set of

states, E is the set of transition labels (including the

silent transition) and T ⊂ S × E × S is the transition

relation.

The transition system can be viewed as a directed

graph in which the initial states are the states with no

incoming arcs, while the final states have no

outgoing arcs.

In fig. 2 the first step of the process discovery

process – the construction of the transition system –

is depicted. Each state is constructed using a

Figure 2.

function “state(σ, k)” that takes as arguments a

sequence of events and an index k. The state

function assigns to each k-length prefix or suffix of

the sequence σ a state from the state space of the

transition system. In order to build a transition

system from the input event log, the state function

must be applied on each sequence of events to all of

its indexes. In the original approach, the authors

propose several method of representing each state –

as a set of events, a bag (multi-set) or list. In the

example presented in fig.2, each state is constructed

by transforming the prefix of each sequence of

events into a set.

Beyond these simple transformations, the state

generation function can be enhanced through the use

several “abstractions” that limit the horizon on

which the transformation is applied, the size of the

resulting collection, or the labels that are included in

the final state representation.

After the creation of the transition system,

several operations that can be applied on it in order

to improve the quality of resulting process model –

removing self-loops or closing “diamond”

structures.

The second step of the process discovery

approach involves the creation of a Petri Net that

exhibits the same behaviour as the transition system.

This step is based on the results of the research into

the synthesis problem – the problem of synthesising

a Petri Net whose behaviour coincides with a

specified behaviour.

There are two approaches to this problem – state-

based region theory and language-based theory of

regions. Although the basic principle is similar, the

input – the behaviour specification – is different.

While the state-based approach uses as input a

transition system, the language-based methods uses

a regular language – a finite set of sequences (the

log). Naturally, given the generated transition

system, a state-based approach will be used in the

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

620

second step of the described approach.

A region represents a set of states that fulfil the

condition that all transitions having the same label

either enter, exit or don’t cross the region. In the

simplest case, of excitation-closed transition systems

(Carmona, 2008), the employed algorithm will

identify the minimal, non-trivial (empty set of states)

regions, and each one will correspond to a place in

the resulting Petri Net. For each place, the events

that enter the region correspond to a transition

generating tokens in that place and events that exit to

transitions that consume tokens. The resulting Petri

Net will be able to simulate the specified transition

system – “bi-similarity property”. In the case of

arbitrary transition system, the “excitation-closure”

property must be first enforced. A proposed

technique uses “label splitting” (Cortadela, 1998) in

which the sets of transitions having the same label

are partitioned thus adding new labels to the system.

5 EXPLICIT STATE

REPRESENTATION

In this section we present a slightly modified

procedure of generating the transition system

required in order to build the Petri Net.

In order to enable this method that uses an

explicit representation of the system’s state, we

make several assumptions:

- Activity definitions based on state variables can

be defined for a subset of the events

- The initial state of the transition system,

expressed in terms of state variable values is known

- The explicit description of activities must be

accurate and the actors involved in the process use

the optimal path in the state-space in order to

achieve their goal

We consider these to be feasible assumptions

given that the focus of our approach is represented

by physical processes. In these scenarios, it is

considered that at least some events in the input log

are derived from sensor observations – and a subset

of the real system state in known.

We redefine the generic definition of state and

transition system used in the two-step process

discovery technique using state variable.

DEF (State) – A state S ∈ D

× D

× .. × D

where D

...D

are the (finite) domains of the state

variable v

...v

∈ V, where V is the set of state

variables. Each state variable has a unique index

assigned by the function idx: V → N.

DEF (Explicit action definition) – An explicit

action definition is a pair (P, E) of conditions and

effects:

- P ⊆ D

× D

× ... × D

– the set of states in

which the action A is enabled

- E ∈ 





× 





× … × 





– the effect of

executing the action. For each state variable v

, the

set 





=



∪{} , where e is the null element,

signifying that the action doesn’t affect the value of

the state variable.

In the following sections, we will use a simpler

notation of states and actions: s

= (pos_vehicle_1 =

gate_1, pos_vehicle_2 = work_area),

move_1_vehicle_1 = (pos_vehicle_1 = gate_1,

vehicle_inactive = true; pos_vehicle_1 = work_area)

We distinguish between two types of actions –

explicit, for which descriptions of the conditions and

effects are available and expressed using the state

variables and implicit, for which these descriptions

and missing.

In order to enable the correct generation of the

transition system, for each implicit action a new

state variable will be introduced. The state

representation of the implicit actions will be

automatically generated and will have an empty

condition expression and, as the effect, a change of

the associated state variable from the initial state to a

new value. Although the empty condition expression

for the implicit actions means that the action is

enabled in any state, when building the transition

system, it will be ignored.

Notice that this representation of implicit actions

is equivalent to representing states as sets of actions

in the original approach. For other ways of

representing states, such as multi-sets or lists, a

different approach for creating the state definitions

of implicit actions is required.

We assume that implicit actions will correspond

to events from high-level activities that are logged

by human operators or by other information systems,

while the explicit events are logged using sensor

data.

In the extreme case of an event log that refers

only to implicit actions, the resulting transition

system will be equivalent to the one generated by the

original approach.

The method of generating the transition system

will make use the available information regarding

the state changes. First, a transition system that

contains just the initial state will be created. After

that, each trace from the input event log will be

processed. Starting by considering the initial state as

the current state, for each event, the procedure will

insert a new transition labelled with the event name

between the current and the next state. The next state

ModellingandAnalysisofProcessExecutionbasedonDataAcquiredfromSensorsNetworks

621

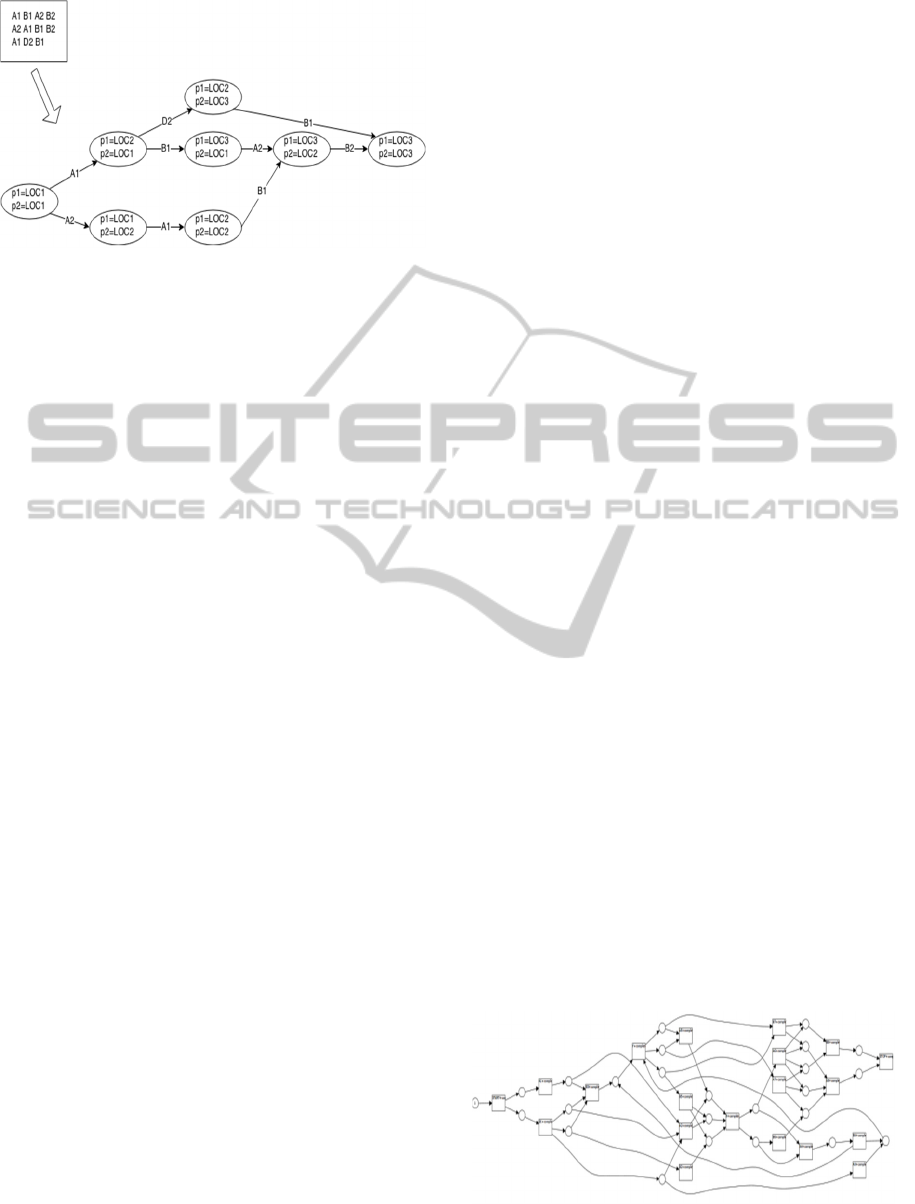
Figure 3.

will be computed using the available information

about the effects of the action related to the event. If

the next state doesn’t exist in the transition system, it

will be added. After the transition is added to the

system, the next state becomes the current state and

the next transition is the sequence of the event trace

is considered.

An example of transition system generated using

this procedure is depicted in fig. 3. In this case, the

state variables “p1” and “p2” are used and they have

the save domain D

= D

= {LOC1, LOC2, LOC3}.

Starting from the initial state (p1=LOC1,

p2=LOC2), the procedure will fist consider the

transition “A1” for which the state description is

(p1=LOC1; p1=LOC2). As the initial state validates

the action’s conditions, the effects are applied and

the state (p1=LOC2, p2=LOC1) is added to the

system.

Notice that the algorithm will be able to detect

inconsistencies in the definitions of the conditions of

the explicit actions by checking them against the

definition of the current state.

The second part of the proposed approach will

leverage the explicit description of the actions to add

possible, but missing behaviour to the system.

It is expected that the log will not contain all

possible behaviour that can be generated by the

system, especially in the case of parallel sequences.

This is a major problem to existing process mining

algorithms as it prevents the accurate detection of

the real causal relations between the activities.

Our approach aims at alleviating this problem by

using the state description of the actions to introduce

new states and transitions in the system.

In order to achieve this, the algorithm determines

the set of goal states for each state of the system. A

final state F is a goal state for state S if an optimal

path from the initial state to F passes through S. The

cost of a path is equal to its length.

Then, for each state S, the procedure will search

for new optimal paths towards all the associated goal

states. For this, all explicit action definitions whose

conditions match the current state S are considered

as the first transition T of the new path. A next state

is created by applying the effects described by the

action definition to the state S. If S

is already

present in the transition system, the currently

considered action will be added only if a path that

starts with T and passes through S

has the same cost

as the optimal paths from S to the goal state.

Otherwise, the procedure will use a planning

algorithm in order to find an optimal path that starts

with T towards the final goal. A planning domain

will be created that contains all the observed values

of the state variables as PDDL predicates and all

explicit action definitions as PDDL actions. If a

valid optimal plan is found and its length is the same

as the optimal paths from S to the goal state, the

algorithm will embed it the transition system by

adding the missing states and transitions.

The updated transition system will then be

transformed into the final Petri Net process model

using an existing algorithm based on the theory of

regions.

In our experiments we used petrify (Cortadela,

1998) to generate the final process model from the

transition system and LPRPG planner (Coles, 2011)

for searching for new optimal paths in the system.

6 EVALUATION

In order to evaluate our approach, we considered 20

types of traces (behaviours) that can be generated by

the example process. These traces were compiled

into an event log that was used as input to various

process discovery algorithms.

We compared the process models generated by

various existing process mining algorithms with the

ones that were generated from the transition system

enhanced using the procedure described in the

previous section.

In fig. 4, the process model discovered by the

“ILP Miner” plugin from the ProM suite is depicted.

Figure 4: Process model generated using the ILP Miner.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

622

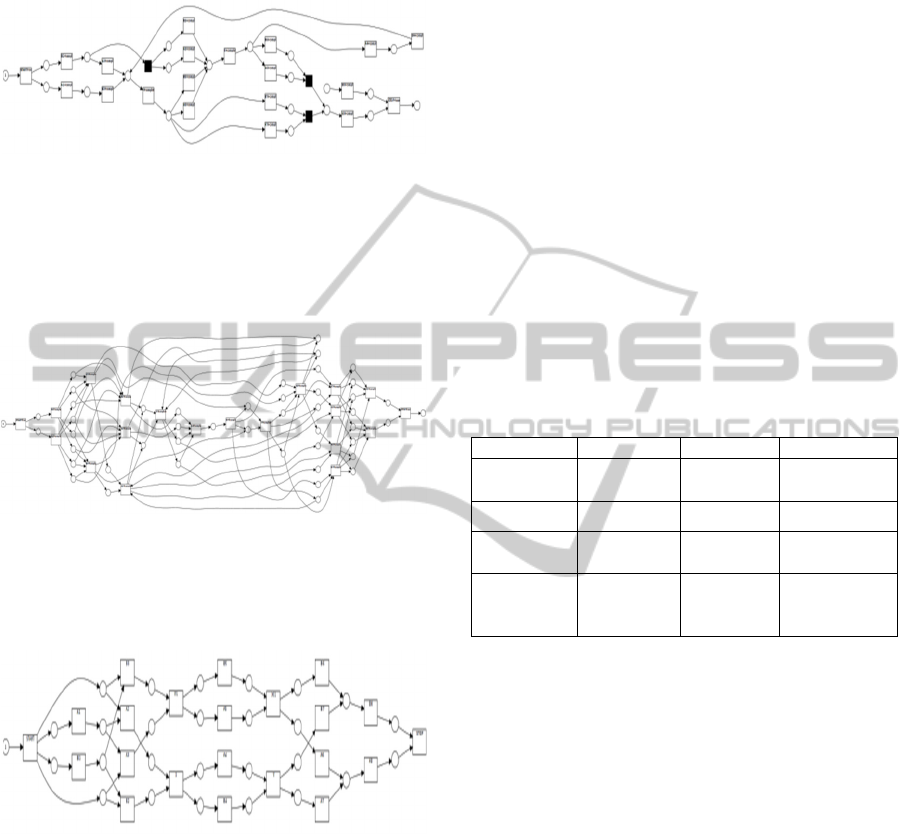
The same log was also processed using the

heuristic process discovery algorithm, and the

resulting model is presented in fig. 3.

Figure 5: Process model generated using the Heuristic

Miner.

Using the original two-step process mining

discovery method, with states represented by sets of

events with no limit in size, the process model from

fig. 6 is generated.

Figure 6.

The process model that corresponds to the transition

system generated using the method presented in

previous sections is depicted in Fig. 7.

Figure 7.

Excluding the model obtained using the heuristic

miner, that can’t reproduce all the traces in the input

log, from a simple visual inspection it is clear that

the last process model is the simplest.

For each of the discovered process models we

used the “Replay a Log for Conformance Analysis”

and “Measure Precision / Generalization” plugins

from ProM to compute metrics for three quality

dimensions: fitness, precision and generalization. All

three values are computed based on an optimal

alignment between the process model and the event

log (Aalst, 2012). The fitness value measures how

well the discovered model is able to replay the traces

in the event log, with each deviation being

penalized. The value for fitness ranges between 0

and 1, with 1(perfect fitness) meaning that all the

traces in the log can be generated by the model. The

metrics for precision and generalization are

computed using empirical formulas, attempting to

quantify the problems of “under-fitting” and “over-

fitting”. An “under-fitting” process model lacks

precision by allowing “much more” behaviour than

presented in the event log and consequently having a

low value for the precision metric. The

generalization metric is concerned with the opposite

problem, of “over-fitting” models, that are only able

to exhibit the behaviour in the event log. Such

processes will have a low value for the

generalization metric.

The computed values for the 4 process models

are depicted in Table 1. All metrics are normalized

in the [0, 1] interval.

Table 1.

Fitness Precision Generalization

Heuristic

Miner

0.8 0.58028 0.65238

ILPMiner

1 0.83036 0.76173

Transition

system

1 0.93304 0.72432

Enhanced

transition

system

1 0.83185 0.72432

As expected, the precision value for the model

generated from the enhanced transition system is

smaller than the one of the model obtained using the

original approach due to the added states and

transitions.

7 CONCLUSIONS

In the future, a more detailed analysis of the

proposed method is required, one that focuses on

event logs collected from real processes.

Another research direction will need to focus on

relaxing some of the assumptions regarding the

behaviour of the agents involved in the execution of

the process and the exact descriptions of the explicit

actions. It is expected that at least in some cases, the

execution of the process won’t follow an optimal

trajectory. Furthermore, the state description of the

explicit actions may be incomplete, with missing

conditions which lead to the creation of imprecise

(under-fitting) process models.

ModellingandAnalysisofProcessExecutionbasedonDataAcquiredfromSensorsNetworks

623

It was assumed in this paper that all the available

events were correctly partitioned into traces

corresponding to process instances. In real systems

however, the collection and processing of events

may pose an important problem that needs to be

addressed in at least a semi-automatic manner. This

issue needs to be addressed in the future, starting

with existing proposal such as (Rozsnyai, 2011) in

which a method of detection correlations between

events based on the values of their associated

attributes is discussed.

An issue that was not addressed in this paper

concerns the discovery of process models that

contain loops. In order to handle this case, a

different approach for the representation of state is

required.

Finally, the proposed method is based on a set of

explicit descriptions for some of the activities.

Although for simple actions, such as moving from

one area to another, the descriptions can be easily

created, situations in which more complex actions

can occur should be investigated.

The work has been funded by the Sectoral

Operational Programme Human Resources

Development 2007-2013 of the Ministry of European

Funds through the Financial Agreement

POSDRU/159/1.5/S/132397.

REFERENCES

de Leoni, M., & van der Aalst, W. M. (2013, March).

Data-aware process mining: discovering decisions in

processes using alignments. In Proceedings of the 28th

Annual ACM Symposium on Applied Computing (pp.

1454-1461). ACM.

van der Aalst, W. M., Rubin, V., Verbeek, H. M. W., van

Dongen, B. F., Kindler, E., & Günther, C. W. (2010).

Process mining: a two-step approach to balance

between underfitting and overfitting. Software &

Systems Modeling, 9(1), 87-111.

van der Werf, J. M. E., van Dongen, B. F., Hurkens, C. A.,

& Serebrenik, A. (2008). Process discovery using

integer linear programming. In Applications and

Theory of Petri Nets (pp. 368-387). Springer Berlin

Heidelberg.

Weijters, A. J., & van der Aalst, W. M. (2003).

Rediscovering workflow models from event-based

data using little thumb. Integrated Computer-Aided

Engineering, 10(2), 151-162.

Coles, A. J., & Coles, A. (2011). LPRPG-P: Relaxed Plan

Heuristics for Planning with Preferences. In ICAPS.

van der Aalst, W., Adriansyah, A., & van Dongen, B.

(2012). Replaying history on process models for

conformance checking and performance analysis.

Wiley Interdisciplinary Reviews: Data Mining and

Knowledge Discovery, 2(2), 182-192.

Carmona, J., Cortadella, J., & Kishinevsky, M. (2008). A

region-based algorithm for discovering Petri nets from

event logs. In Business Process Management (pp. 358-

373). Springer Berlin Heidelberg.

Tiwari, A., Turner, C. J., & Majeed, B. (2008). A review

of business process mining: state-of-the-art and future

trends. Business Process Management Journal, 14(1),

5-22.

Rozinat, A., Zickler, S., Veloso, M., van der Aalst, W. M.,

& McMillen, C. (2009). Analyzing multi-agent

activity logs using process mining techniques. In

Distributed Autonomous Robotic Systems 8 (pp. 251-

260). Springer Berlin Heidelberg.

Cortadella, J., Kishinevsky, M., Lavagno, L., & Yakovlev,

A. (1998). Deriving Petri nets from finite transition

systems. Computers, IEEE Transactions on, 47(8),

859-882.

Song, M., & van der Aalst, W. M. (2008). Towards

comprehensive support for organizational mining.

Decision Support Systems, 46(1), 300-317.

Rozinat, A., de Jong, I. S., Gunther, C. W., & van der

Aalst, W. M. (2009). Process mining applied to the

test process of wafer scanners in ASML. Systems,

Man, and Cybernetics, Part C: Applications and

Reviews, IEEE Transactions on, 39(4), 474-479.

Günther, C. W., Rozinat, A., & Van Der Aalst, W. M.

(2010, January). Activity mining by global trace

segmentation. In Business process management

workshops (pp. 128-139). Springer Berlin Heidelberg.

Rozsnyai, S., Slominski, A., & Lakshmanan, G. T. (2011,

July). Discovering event correlation rules for semi-

structured business processes. In Proceedings of the

5th ACM international conference on Distributed

event-based system (pp. 75-86). ACM.

Mihnea Moisescu, Ioan Sacala, Towards the Development

of Interoperable Sensing Systems for the Future

Enterprise, Journal of Intelligent Manufacturing,

March 2014, Print ISSN 0956-5515, Online ISSN

1572-8145, DOI 10.1007/s10845-014-0900-0,

Springer Eds.

Dragos Repta, Mihnea Alexandru Moisescu, Ioan Stefan

Sacala, Aurelian Mihai Stanescu, Nicolae Constantin,

Generic Architecture for Process Mining in the

Context of Cyber Physical Systems, Periodical

Applied Mechanics and Materials (Volume 656),

Pages 569-577, ISSN: 1662-7482, DOI

10.4028/www.scientific.net/AMM.656.569.

Repta Dragos, Ioan Stefan Sacala, Mihnea Alexandru

Moisescu „Towards the Development of the Future

Internet based Enterprise in the Context of Cyber-

Physical Systems”, 19th International Conference on

Control Systems and Computer Science, 29-31 May

2013, pp. 405-412, ISBN: 978-1-4673-6140-8.

Alix Vargas, Llanos Cuenca, Andres Boza, Ioan Sacala,

Mihnea Moisescu, Towards the development of the

framework for inter sensing enterprise architecture,

Journal of Intelligent Manufacturing, March 2014,

Print ISSN 0956-5515, Online ISSN 1572-8145, DOI

10.1007/s10845-014-0901-z, Springer Eds.

MODELSWARD2015-3rdInternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment

624

Jardim-Goncalves, R., Grilo, A., Agostinho, C.,

Lampathaki, F., and Charalabidis, Y. (2012)

Systematisation of Interoperability Body of

Knowledge: the foundation for Enterprise

Interoperability as a science, Enterprise Information

Systems, vol. 6, no. 3, pp. 1-26, 2012.

ModellingandAnalysisofProcessExecutionbasedonDataAcquiredfromSensorsNetworks

625