
Business Process Generation by Leveraging Complete Search over a
Space of Activities and Process Goals
Dipankar Deb
1
, Nabendu Chaki
1
and Aditya Ghose
2
1
Dept of Computer Science and Engineering, University of Calcutta, Kolkata, India
2
Decision System Lab, School of Computer Science and Software Engineering, University of Wollongong,
Wollongong, NSW, Australia
Keywords:
Business Process Modeling, Process Redesign, Business Goal, Constraints.
Abstract:
An efficient and flexible business process not only helps an organization to meet the requirements of the
evolving surroundings but also may facilitate a competitive advantage over other companies towards delivering
the desired services. This is even more critical for an emerging paradigm like cloud based deployment. In this
paper, we introduce a novel mechanism to generate the business process suitable for specific organizations.
The approach provides an automated way to build the possible business processes for a given set of tasks
that fulfills the goal and satisfies the constraints of an organization. In step 1, we show how to generate the
finite space of all possible designs for a given set of tasks. Secondly, we accumulate the effect of each step
to deduce the final effect of each possible process design and to ensure that the redesigned set of steps still
realizes the service goal. The designs not meeting the service goals are eliminated from the space. In step 3,
the rest of the designs are checked for the constraint satisfaction subject to some specific cases. The framework
provides a comprehensive, both syntactically and semantically correct, consistent business process generation
methodology that adheres to the target business goals and constraints.
1 INTRODUCTION
There is a need to re-design the business processes
over the cloud based on the requirements so that
services can be offered in an efficient and cost-
effective manner. Different business houses, even in
the same vertical, often have their own set of distinct
goals, policies and constraints. As for example,
two different travel agencies may target customers
of different strata of the society and can set their
goals and constraints accordingly. An appropriate
business process model for a particular organization
should be tailor-made according to these. Given a
set of tasks/activities/services and constraints, this
paper aims to construct a business process for an
organization. The initial set of activities is referred
in rest of the text as capability library. Initially, we
generate all possible set of business process designs
out of these capabilities.
The manuscript is organized as follows: Section 2
presents a survey in the existing literature followed
by a statement on the motivation behind the work.
In section 3, syntactic derivation of the exhaustive
search space is described. This ensures that no pos-
sible design is dropped out during generation of the
intermittent solutions that realize the goals. Section
4 describes the checking for completeness of the
proposed algorithms for generation of all possible
business process models. Semantic extraction of goal
specific business space from the initial syntactically
correct search space followed by a running example
is presented in section 5. Eliminating redundancy
from business space depending on the constraints is
described in section 6. In conclusion, we have dis-
cussed the effectiveness of the proposed approached
in identifying the optimized business process from
the reduced business space. Our approach generates
all the business process designs irrespective of the
business application. However, this is a one-time ex-
ercise depending on the number of tasks and may be
reused for different business verticals. Subsequently,
depending upon the requirements of specific business
houses and their application, the goals and policies
can be imposed on this exhaustive design space to
have client-specific solutions with the most optimal
design. The proposed solution follows the method-
ology of converging to the optimal design from the
exhaustive design space as described in figure 1. The
233
Deb D., Chaki N. and Ghose A..
Business Process Generation by Leveraging Complete Search over a Space of Activities and Process Goals.
DOI: 10.5220/0005408702330240
In Proceedings of the 5th International Conference on Cloud Computing and Services Science (CLOSER-2015), pages 233-240
ISBN: 978-989-758-104-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)
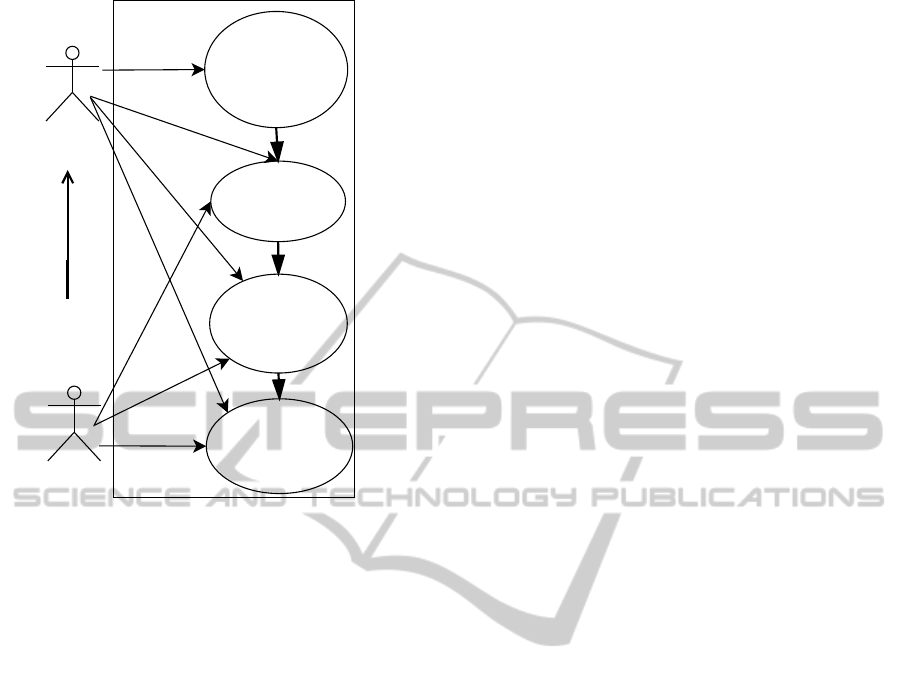
Analyst
User
Generation of
possible process
model out of specific
tasks and
operations
Generation of
goal specific
Business processes
Elimination of
redundancy
depending on
constraints
Identification of
Optimized Business
processes
Specify the number
of tasks
and operation
Specify Goal
Specify
Constraints
Specify Goal
Specify
Constraints
Optimization
criteria
Optimization
criteria
Specify
goal
and
Constraints
Figure 1: Use case for the proposed business process
generation framework.
proposed approach provides an automated way for
business process designs as compared to modeling
with BPMN. The proposed mechanism may be ex-
tended towards deriving a optimal solution based on
one or multiple criteria pertinent to specific clients.
2 RELATED WORK
Services can evolve typically due to changes in struc-
ture, e.g., attributes and operations; or, in behaviour
and policies, e.g., adding new business rules and
regulations, or, in types of business-related events;
and in business protocols as presented by (Papa-
zoglou, 2008). Thus, the issues of service redesign
are very vital. Most of the literatures on business
process redesign(Reijers and Liman Mansar, 2005;
Limam Mansar et al., 2009; Kumar and Bhat, 2011)
do not address the method to arrive at an improved
process from the existing business process. A general
purpose business process modeling language such
as BPMN (BPMN, 2006) or UML activity designs
(UML, 2003) are not designed to support enterprise in
creating models using their own vocabulary and ter-
minology. A business process modeling framework
proposed in (Alotaibi and Liu, 2013) made it easy for
IT people to understand and implement. (Lodhi et al.,
2014) focuses on the relation between evaluation of
business processes and their representation at the
process managerial level.
(Yu et al., 2014) offers a complete methodology
for modeling and validating an e-commerce system
with a third-party payment platform from the view
point of a business process. In another recent work,
(Zhang and Perry, 2014) proposes a technique for
modeling composite activities by including compo-
nents of data, human actors and atomic activities and
represent business processes with composite activ-
ities using process-oriented languages. (Malesevic
and Brdjanin, 2013) presents a software tool for the
automatic visualization of presents a software tool to
automate visualization of the UML activity diagram.
Modeling of medical services based on business pro-
cess model is been described in (Natalia et al., 2013).
A new modular workflow modeling language is pro-
posed in (Combi et al., 2014) allows the designer to
easily express data dependenciesand time constraints.
Verification of Business Process Constraints is been
demonstrated in (Gao et al., 2013). A synchroniza-
tion method for change management between process
models on different abstraction levels is proposed
by (Weidmann et al., 2011). (Macek and Necasky,
2010) derives XML formats for communication links
in the conceptual schema of the business process and
optimizes them. (Wu et al., 2011) proposed to model
the business process based on semantics of business
process models and business vocabulary, then used
the method to transform a plain text rule statement
into BPMN files. The literature survey indicates
some limitations and challenges in the domain of
business process generation such as fulfillment of
user demand, post execution analysis, automated tool
support, provisioning of constraint specification and
end to end solution to provide a model for the analyst.
These motivate us to have an end to end solution
to provide a business process design of a specific
business logic incorporating the goal, constraints and
optimization criteria for the analyst.
3 GENERATION OF
EXHAUSTIVE FINITE SPACE
The process starts with a capability library of n
tasks for an organization and set of possible model
constructs such as XOR-split and AND-split which
can be denoted as < T
1
, T
2
, .....T
n
, ⊗, ⊕ > where
T
1
, T
2
.....T
n
are the capabilities and ⊗, ⊕ denotes an
XOR-split and AND-split respectively.
We generate all possible business process designs
in the form of tree which is elaborately described
in algorithm 1. A business process design tree is a
tree for a given fixed capability library in which the
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
234

root node is an empty business process design, every
leaf node is a syntactically correct business process
designs, every non-leaf node is a partial (incomplete)
business process design and every child node differs
from a parent node by including a single extra process
model construct (either an extra activity, or an extra
event, or an extra gateway). The algorithm generates
the tree considering all possible constraints for com-
plete generation of all possible process models. The
business process designs are generated on traversal of
the paths of the tree. The complete process models in
the tree are all leaf nodes or some intermediate nodes.
The leaf nodes representing XOR-split or AND-split
are followed by XOR-join or AND-join during the
generation of the process tree. A path end with an
XOR-split or AND-split is discarded. Such types of
constraints are identified during the traversal of the
path and are included in the designed algorithm 2.
Figure 2 shows the tree view for the generation of
process models.
Let us take a domain specific example of Car
rental process where the possible subtasks for realiz-
ing the above goal are Register Request(Task1), Re-
view the request(Task2), Reject the request(Task3),
Allocate Car(Task4), Car allocated(Task5) and Per-
form Transportation(Task6) Using the exhaustive ap-
proach we have all possible business process designs
T2
T3
Tn
Ti+1
Ti+2
Ti
Ti+1
Ti+2
Ti
Start
T1
T2
Tn
Figure 2: Process Model Generating Tree for n tasks.
with the above identified tasks T1, T2, T3, T4, T5 and
T6.
4 COMPLETENESS OF
ALGORITHM FOR
GENERATING ALL POSSIBLE
DESIGNS
The exhaustive set of syntactically correct business
process designs refer to the collection of subtrees
where all the artifacts are operated for the valid
set of operations that are syntactically permissible.
We would establish couple of base cases by manual
checking for n=1, n = 2 and n = 3 and shall prove
Lemma 1, Lemma 2 and Lemma 3 by the method of
induction. In figure 4, we find that all the possible
business process designs for n=2 where each of the
two root tasks at level 1, are having a tree with 4
nodes. Each of these two sub-trees generates two
different models. Similarly, by manual checking for
n=3, we find that the algorithm is generating all the
possible business process designs. The corresponding
tree is shown in Figure 5 where each root task at
level 1 is having 19 nodes in its sub-tree. For brevity
we have not shown all the possible business process
designs in the figure. Again, by manual checking
for n = 4, we find that the algorithm is generating
all possible business process designs where each root
task is having tree size=49.
T1
Start
Figure 3: Process design generating tree for a single task.
Lemma 1: If n be the size of the Capability Li-
brary, i.e. the number of tasks in the capability
library, then the height of the tree is equal to
(3n− 4), ∀n ≥ 2.
Proof: We will prove by induction that ∀n ∈ Z and
n ≥ 2 the height of the tree H
n
= 3n− 4.
Base Case: If the size of the Capability Library n=1
We have only one task at level 1 of the tree. In other
words, at level 1 of the tree, we have < T
1
, ⊗, ⊕ >.
The next element for a task at intermediate level is
BusinessProcessGenerationbyLeveragingCompleteSearchoveraSpaceofActivitiesandProcessGoals
235

T1
Start
T2
T2
T1
T1
T2T1
T2
T2
T1
Figure 4: Process Model generating tree where number of
tasks =2.
any of n-k tasks where k is used tasks and the value
of k ranges from 1 to n. Therefore there will be no
expansion for the tree for n=1. The tree is shown
in figure 3. Thus height of the tree is 1. If size of
the Capability Library n=2, then its height H
2
will be
[(3x2) − 4] = 2. Figure 4 shows the height of the tree
is 2. If the size of the Capability Library n=3, then its
height H
3
will be [(3x3) − 4] = 5. Figure 5 shows the
height of the tree is 5.
Inductive Hypothesis
Assume that the theorem is true for number of tasks≤
k.
Inductive Steps: We must prove that the inductive
hypothesisis true for (k+1) numbersof tasks. During
the expansion of the tree with (k + 1) numbers of
tasks, we have the nodes of level 1 of the tree as
< T
1
, T
2
, T
3
, ....T
k
, T
k+1
, ⊗, ⊕ >. The generation of the
tree terminates when the number of possible tasks
at all level is equal to 1. Therefore starting with
k+ 1 number of tasks, the tree expands till used tasks
become (k + 1) and the number of possible tasks for
the next level becomes zero.
We get n numbers of edges for n+1 numbers
of tasks. Thus the height of the subtree for tasks
corresponding to a level with n+1 numbers of tasks
will be n. For each of the XOR or AND split in
the corresponding level with n tasks we have 2 to
[(n + 1) − k + 1] way split where k is used tasks. It
is very obvious that the number of remaining task in
the next level for 3, 4, ....[(n + 1) − k + 1] way split
will be less than that of 2 way split in the same level.
Therefore the height of the subtree for 2 way split will
be more than that of subtrees of 3, 4, ....[(n + 1) − k+
1] way split.The maximum height of the subtree for an
XOR or AND split will correspond to the level with
maximum number of tasks. As the tree expands the
number of tasks will be reduced in increasing level
of the tree. Therefore the corresponding height of the
subtrees for XOR or AND split with lower number of
tasks in the corresponding level will be less than that
Table 1: Height of Subtrees.
No of Tasks No. of Levels Size of Tree
1 1 1
2 2 2
3 5 5
4 8 8
5 11 11
6 14 14
7 17 17
8 20 20
of subtrees for XOR or AND split with higher number
of tasks at corresponding level. Therefore the height
of the tree will be equal to height of subtree created
with 2 way split at level 2. The height of the subtrees
with increasing number of tasks is given in table 1.
Suppose L
Tn
and L
Tn+1
denotes the subtrees created
with 2 way split at level 2 with n and n+1 number of
task respectively. The height of subtree created with
2 way split at level 2 with n+1 number of task From
the above table it is observed that (by the inductive
hypothesis)
L
Tn+1
= L
Tn
+ 3
= (3n− 4) + 3
= 3n− 1
= 3(n+ 1) − 4
Therefore, the height of subtree created with 2 way
split at level 2 with n number of task is 3n-4 and hence
the height of the tree is 3n-4.
Lemma 2: All the subtrees generated with n-1 ca-
pabilities are the subset of the subtrees generated
with n capabilities.
Proof: We will prove by induction that ∀n ∈ Z and
n ≥ 2. T
i
(n−1) is the subtree of T
i
(n) where T
i
(n−1)
and T
i
(n) denotes the tree generated with (n-1) and
n capabilities. Suppose T(n) be the tree generated
with the capability library size n which consists of m
number of subtrees denoted by T
i
such that
[
T
i
= T(n)
The start node is at level 0 has the vertices
T
1
, T
2
, ....T
n
, ⊗, ⊕ i.e. n+2 nodes.
Base Case: If the size of the Capability Library is
n=1, then there will be only one process model. If the
size of the Capability Library is n=2 then from figure
4, we find that T
i
(1) is the subtree of T
i
(2). If the size
of the Capability Library is n=3 then from figure 5,
we find that T
i
(2) is the subtree of T
i
(3).
Inductive Hypothesis
Assume that the theorem is true for k number of tasks
such that k < n , i.e. T
i
(k− 1) is the subtree of T
i
(k).
Inductive Steps: We must prove that the inductive
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
236

T2
Start
T3
T1
T2
T3
T1
T3
T1
T2
T3
T2
T2
T3
T2
T3
T3
T2
T3
T2
T3
T2
T2
T3
T3
T1
T1
T3
T1
T3
T3
T1
T3
T1
Figure 5: Process Model generating tree where number of tasks =3.
hypothesis is true for (k+1) numbers of tasks, i.e.
T
i
(k) is the subtree of T
i
(k + 1). Now, in order to
form the tree for T
k+1
, the start node at level 0 for
T
k
will have the child vertices T
1
, T
2
, ....T
k
, T
k+1
, ⊗, ⊕
i.e., a total k+3 nodes will be there below the start
node. In turn, node T
k
in level 1 of the T
k+1
tree
will have the child vertices T
1
, T
2
, ....T
k
, ⊗, ⊕. These
nodes will again havetheir decedents as per procedure
ExhaustiveModelGenration() i.e., the tree with T
k
as
the root node is essentially a sub-tree of T
k+1
. Hence,
it is proved that if the induction hypothesisholds good
for T
k
, k < n, then it holds good for T
k+1
as well. Thus
the statement of Lemma 2 is proved by induction.
Lemma 3: Tree having the capability library size
n can generate all possible process models.
Proof: We will prove by induction that ∀n ∈ Z
and n ≥ 1, T
i
(n) produces all the possible process
models with n capabilities where T
i
(n) denotes the
tree generated with n capabilities.
Base Case: If the size of the Capability Library is
n=1, then there will be only one process model. If the
size of the Capability Library is n=2 then from figure
4, we find that T
i
(2) produces all the possible process
model. If the size of the Capability Library is n=3
then from figure 5, we find that T
i
(3) produces all the
possible models.
Inductive Hypothesis
Assume that the theorem is true for k number of tasks
such that k < n i.e., T
i
(k) produces all the possible
process model with capability library size=k.
Inductive Steps: We must prove that the inductive
hypothesis is true for (k+1) numbers of tasks, i.e.,
T
i
(k + 1) produces all the possible process model
with capability library size=k+1. As from Lemma
2, it is obvious that T
i
(k) is a subtree of T
i
(k + 1),
therefore having capable of generating all possible
process models for capability library size k with
T
i
(k) with height (3k-4), procedure ExhaustiveModel-
Generation() essentially generate all possible process
model for capability library size=k+1 with T
i
(k + 1)
with height (3(k+1)-4). Thus the statement of Lemma
3 is proved by induction.
Theorem: The proposed Construction Algorithm
generates the exhaustive set of syntactically cor-
rect business process models.
Proof: Lemma 1, Lemma 2 and Lemma 3 establish
that the algorithm is complete in the sense that it gen-
erates all possible business process designs. Hence,
the statement of the theorem is correct.
BusinessProcessGenerationbyLeveragingCompleteSearchoveraSpaceofActivitiesandProcessGoals
237

5 EFFECT ACCUMULATION
The primary aim of this work is to redesign the
business process. This means replacing the existing
process model with an improved one on the basis
of better optimization criteria that confirms to the
business goals and constraints. So it is quite essential
that each of the process models, thus generated
are submitted for goal checking done by effect
accumulation mechanism. The approach is domain
specific. Effect accumulation enables the analyst
to provide with immediate effects after each step,
so as to able to calculate the cumulative effect. To
accumulate the effects of each step, we focus on the
formal effect specifications. Let us define a pair-wise
accumulation operator based on one first introduced
in (Hinge et al., 2009). As defined acc(e1, e2) to be
the set of cumulative effects obtained by executing
a step with effect e2, given a prior set of effects e1.
An effect scenario at a given point in a process is
one consistent set of cumulative effect of a process if
it were to execute up to that point. The first step in
effect accumulation is deriving a Scenario level. To
obtain effect scenario at a given point in a process the
set of scenario level is computed at that point.
Considering the case of Car rental process again
all the possible process models generated by our
method can also be termed as scenario levels. Out of
the automatic generated scenario levels, let us take
a particular scenario level < S, T1, G1, T3, G2, T4 >
where S is the start event.
The effect accumulation stage involves the
process of immediate effect annotation for each
of the tasks listed in the scenario using a pair-wise
operation when the immediate effect of S is combined
with the immediate effect of T1, the result being
the cumulative effect of T1. The cumulative effect
at T1 is then combined with the immediate effect
T2 resulting in the cumulative effect at T2 and so
on up to T6. We express the effect annotations in
conjunctive normal form. Let e1 be the cumulative
effect annotation and e2 be the effect annotation at t2
and t3 respectively. KB be the knowledgebase which
is nothing but a rule set:
e1= request registered and request reviewed.
e2= request accepted.
KB= the request is accepted after the review of the
registered request.
We express the above informal representation
formally in CNL (Control Natural Language) and
also can provide an analyst friendly interface by
means of a software.
e1 = request(x) ∧ request − review(x)
e2 = accept − request(x)
KB = (request(x) ∧ requestreview(x)) →
acceptrequest(x)
≡ ¬(request(x) ∧ requestreview(x)) ∨
acceptrequest(x)
The cumulative effect of the two tasks consists of the
effects of the second task plus as many of the effects
of the first tasks. Two alternative effect scenario
during the cumulative effect at T3 are request (x),
accept-request(x) and request-review(x), accept-
request(x). We proceed this way to gather final effect
annotation at T6. The goal of Car rental process can
be decomposed in CNL (Control Natural Language)
sentences and may be combined to form a logic
sentence. Let F be the set of final effect scenarios
after effects are accumulated across all the steps in
a service. Let G be the formal representation of the
goals associated with the service. We require that the
constraint F |= G be satisfied. Methodologically, the
redesign of the steps can involve search through a
space of alternative sets of steps (including deletion
or replacement of existing steps, addition of new ones
and so on) provided the constraints are satisfied.
6 CONSTRAINT SPECIFICATION
Relation is an abstract association and connection
that holds between two or more conceptual object.
A constraint is a special kind of relationship that
is restricted or compelled to exist under a given set
of conditions. We have to identify the constraint
between the business processes. A constraint is said
to hold in a given context when the relationship is
maintained in the context. In order to verify whether
a constraint hold for a process we use temporal logic.
Business rules may be annotated as constraints to
specify the behaviors and also to specify the deriva-
tion of conditions that affect the execution flow. These
rules are forms of conditional operations attached to
the process to give data result. The business rules will
be restructured when organizations change the data or
process to accommodate the varying business needs.
When rules are changed, it would be possible to
provide a decision based on the given constraints or
based on business requirements. The correct business
process could also be verified by evaluating or vali-
dating the completeness of the business rule.
However, these rules may lack completeness to
determine the computability of business logic. Thus,
for a specific client, it is necessary to check whether
the rule-set is complete. This can be proved when
the rules are interpreted with temporal logic. We
propose the following steps for constraint satisfaction
checking. First,formally representing the design sets,
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
238

secondly,formally representing the constraints and
finally use Prover9 first-order logic theorem-prover
for performing checking constraint satisfaction. The
constraints are considered as the conditions.The user
may go through several forms to assign values to
different constraints definition by example.
7 CONCLUSIONS
In this paper, we introduce a methodology that sup-
ports client-specific constraint checking towards gen-
erating goal-oriented, efficient business process de-
signs. Subsequently, one may apply suitable criteria
for optimized design. The optimization may consider
issues such as delivery time, cost etc. and remains the
future prospect of our current work.
The main concern about the proposed approach
lies in the computation towards generating the ex-
haustive set of process designs. However, this step
is executed offline and a priori for k numbers of tasks
and offered as the template for the analyst.
Our work paves the way for constraint specifi-
cation and checking. We have done completeness
checking for the proposed solution. We are also in
the process of developing a tool support with which
the analyst can derive the optimized business process
as per his/her scope, business goals and identified
constraints in the environment.
ACKNOWLEDGEMENTS
This publication is an outcome of the research work
undertaken in the CoE on Systems Biology and
Biomedical Engineering at University of Calcutta.
Authors thankfully acknowledgement the support
from the CoE.
REFERENCES
Alotaibi, Y. and Liu, F. (2013). Business process modelling
towards derive and implement it goals. In Industrial
Electronics and Applications (ICIEA), pages 1739–
1744. IEEE.
BPMN (2006). Business process modeling notation specifi-
cation. www.bpmi.org. Final Adopted Specification.
Combi, C., Gambini, M., Migliorini, S., and Posenato, R.
(2014). Representing business processes through a
temporal data-centric workflow modeling language:
An application to the management of clinical path-
ways. IEEE Transactions on Systems, Man, and
Cybernetics: Systems, 44(9):1182 1203.
Gao, J., Chen, W., Wang, Y., Zhao, D., Li, W., and Bo, Z.
(2013). Verification of business process constraints
based on xyz/z. In International Conference on Infor-
mation Technology and Applications (ITA), page 479
482. IEEE.
Hinge, K., Ghose, A., and Koliadis, G. (2009). Process
seer: A tool for semantic effect annotation of business
process models. In Enterprise Distributed Object
Computing Conference, 2009. EDOC’09. IEEE Inter-
national, pages 54–63. IEEE.
Kumar, M. and Bhat, J. M. (2011). Process improvement by
simplification of policy, and procedure and alignment
of organizational structure. In AMCIS’11.
Limam Mansar, S., Reijers, H. A., and Ounnar, F. (2009).
Development of a decision-making strategy to im-
prove the efficiency of bpr. Expert Systems with
Applications, 36(2):3248–3262.
Lodhi, A., K¨oppen, V., Wind, S., Saake, G., and Turowski,
K. (2014). Business process modeling language for
performance evaluation. In 47th Annual Hawaii Inter-
national Conference on System Science (HICSS-47).
IEEE.
Macek, O. and Necasky, M. (2010). An extension of
business process model for xml schema modeling. In
Services (SERVICES-1), 2010 6th World Congress on,
pages 383–390. IEEE.
Malesevic, A. and Brdjanin, D.and Maric, S. (2013). Tool
for automatic layout of business process model repre-
sented by uml activity diagram. In IEEE EUROCON,
page 537 542. IEEE.
Natalia, C., Alexandru, M.M.and Mihai, S., Stefan, S.,
and Munteanu, C. (2013). Medical services mod-
elling based on business process model framework.
In IEEE E-Health and Bioengineering Conference
(EHB), page 1 4. IEEE.
Papazoglou, M. (2008). The challenges of service evolu-
tion. In Advanced Information Systems Engineering,
volume 5074 of LNCS, pages 1–15. Springer.
Reijers, H. A. and Liman Mansar, S. (2005). Best practices
in business process redesign: an overview and qual-
itative evaluation of successful redesign heuristics.
Omega, 33(4):283–306.
UML (2003). Uml 2.0 superstructure specification.
www.omg.org. Final Adopted Specification.
Weidmann, M., Alvi, M., Koetter, F., Leymann, F., Ren-
ner, T., and Schumm, D. (2011). Business process
change management based on process model synchro-
nization of multiple abstraction levels. In Service-
Oriented Computing and Applications (SOCA), pages
1–4. IEEE.
Wu, Z., Yao, S., He, G., and Xue, G. (2011). Rules oriented
business process modeling. In IEEE International
Conference on Internet Technology and Applications
(iTAP), pages 1–4. IEEE.
Yu, W., Yan, C., Ding, Z., Jiang, C., and Zhou, M. (2014).
Modeling and validating e-commerce business pro-
cess based on petri nets. Systems, Man, and Cybernet-
ics: Systems, IEEE Transactions on, 44(3):327–341.
Zhang, Y. and Perry, D. (2014). A goal-directed modeling
technique towards business process. In IEEE 8th
BusinessProcessGenerationbyLeveragingCompleteSearchoveraSpaceofActivitiesandProcessGoals
239

International Symposium on Service Oriented System
Engineering (SOSE), page 110 121. IEEE.
APPENDIX
Algorithm 1: Algorithm for generating tree for n initial
elements.
1: procedure GENERATETREE()
2: Begin
3: Create root for START EVENT at level 0; ⊲
initialization
4: Build level 1 with elements for all of the n distinct
tasks, an XOR split and an AND split;
5: k ← 2 ⊲ variable k represents current level
6: T ← n− k + 1 ⊲ T is the number of remaining tasks
7: repeat
8: ∀task at level k, 2 ≤ k ≤ n+ 1
9: Choose all of the remaining n-k+1 distinct
tasks, an XOR split, and an AND split as possible next
elements;
10: ∀XOR split at level k,
11: Choose the possible next elements in
12: for i = 2 to n−k+1 do
13: Generate all possible ways of i-way split
from n-k+1 task
14: if thenumberof siblingtask 6= NULL then
15: the next element is an XOR join
16: else
17: return NULL
18: end if
19: end for
20: ∀AND split at level k,
21: Choose possible next elements in
22: for i = 2 to n−k+1 do
23: Generate all possible ways of i-way split
from n-k+1 tasks
24: if thenumberof siblingtask 6= NULL then
25: the next element is an AND join
26: else
27: return NULL
28: end if
29: end for
30: ∀XOR join at level k, 2 ≤ k ≤ n+ 1
31: Choose all of the remaining n-k+1 distinct
tasks, an XOR split, and an AND split as possible next
elements;
32: ∀AND join at level k, 2 ≤ k ≤ n+ 1
33: Choose all of the remaining n-k+1 distinct
tasks, an XOR split, and an AND split as possible next
elements;
34: T = T − 1;
35: until number of remaining tasks T < 1
36: End
Algorithm 2: Algorithm for extracting all possible process
from the tree for n initial elements.
1: procedure EXHAUSTIVEMODELGENERATION()
2: Begin
3: mark all nodes in the tree as .NOT. REACHED;
4: count = n ⊲ count stores number of nodes yet to be
processed
5: repeat
6: pick any one of the node, say X, at level 1 as
starting node;
7: mark X as REACHED;
8: place X on READY list;
9: count = count − 1;
10: repeat
11: pick a node A from the READY list;
12: find the child nods for A;
13: if A represents XOR or AND then
14: discard the node;
15: Break;
16: end if
17: if A and its child node represents two con-
secutive XOR or AND split then
18: discard the nodes;
19: Break;
20: end if
21: if node A representing XOR or AND split
that do not have siblings then
22: discard the nodes;
23: Break;
24: end if
25: if the same tasks occurs after XOR or AND
split or join node then then
26: discard the nodes;
27: Break;
28: end if
29: mark the node A as REACHED;
30: add A to READY list;
31: count = count − 1;
32: print the READY list;
33: until READY list is empty;
34: until count < 1
35: End
CLOSER2015-5thInternationalConferenceonCloudComputingandServicesScience
240
