
Time-aware Link Prediction in RDF Graphs
Jaroslav Kucha
ˇ
r, Milan Dojchinovski and Tomas Vitvar
Web Intelligence Research Group, Faculty of Information Technology,
Czech Technical University in Prague, Prague, Czech Republic
Keywords:
Link Prediction, Web APIs, Temporal Information, Semantics, Tensor Factorization.
Abstract:
When a link is not explicitly present in an RDF dataset, it does not mean that the link could not exist in reality.
Link prediction methods try to overcome this problem by finding new links in the dataset with support of a
background knowledge about the already existing links in the dataset. In dynamic environments that change
often and evolve over time, link prediction methods should also take into account the temporal aspects of data.
In this paper, we present a novel time-aware link prediction method. We model RDF data as a tensor and
take into account the time when RDF data was created. We use an ageing function to model a retention of
the information over the time; lower the significance of the older information and promote more recent. Our
evaluation shows that the proposed method improves quality of predictions when compared with methods that
do not consider the time information.
1 INTRODUCTION
Over the last few years the number of published RDF
datasets in the Linked Data cloud has grown signifi-
cantly. One of the key Linked Data publishing prin-
ciples is to use URI references to identify Web re-
sources and links between them
1
. Such link are usu-
ally defined at the time of creation of the datasets and
they are often not updated. However, over the time the
links can get old and loose their significance. Link
prediction algorithms, on the other hand, find new
links in datasets that are not explicitly present but they
implicitly exist due to existing structural patterns.
An increasing amount of datasets and their evo-
lution over time introduce another dimension to link
prediction methods. In this paper we develop a novel
method that is able to predict links in a single dataset
that uses i) the creation time of the links, and ii) the
existing structural patterns in the dataset. We call this
method a time-aware link prediction.
We validate the method on a dataset from Pro-
grammableWeb
2
, a leading Web APIs and mashup
directory, that allows developers to publish informa-
tion about their Web APIs and mashups and to join
a social network of developer fellows. At the time
of creating a Web API or a mashup in the directory,
a developer provides various technical and functional
1
http://www.w3.org/DesignIssues/LinkedData.html
2
http://www.programmableweb.com/
descriptions such as categories, tags and defines links
between APIs and mashups. A link prediction method
applied on the dataset from ProgrammableWeb may
be used to find links to other categories, tags or
Web APIs based on structural patterns in which the
Web APIs, mashups or developers occur. However,
such method would ignore the fact that a Web API
or a mashup can be outdated. Our link prediction
method provides more precise results as it can effec-
tively combine time information with structural pat-
terns. We use i) tensors as an underlying mechanism
to model RDF data, ii) time information and an age-
ing function to model the age of the data and iii) a ten-
sor factorization technique to evaluate an existence
of new links. We adopted a widely used ageing to
simulate the loss of the links’ significance; decrease
the impact of older links and promote the more recent
ones. Our assumption is that older links are less im-
portant due to their age, however, they can still have
an influence on the link prediction due to structural
patterns. We evaluate the method on a real-world
dataset from the Web services domain and we present
its performance and capabilities.
The paper is structured as follows. Section 2 de-
scribes the time-aware link prediction method, its no-
tations, definitions and the supporting algorithm. Sec-
tion 3 describes several experiments we conducted to
evaluate its performance and capabilities. In Section 4
we discuss various aspects of the method. In Section
5 we give an overview of the related work, and finally,
390
Kucha
ˇ
r J., Dojchinovski M. and Vitvar T..
Time-aware Link Prediction in RDF Graphs.
DOI: 10.5220/0005428403900401
In Proceedings of the 11th International Conference on Web Information Systems and Technologies (WEBIST-2015), pages 390-401
ISBN: 978-989-758-106-9
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Example of modelling data.
(a) Tensor Y model without ageing
s
1
s
2
s
3
s
4
m
1
0 0 0 0
m
2
1
(t
0
−t
3
)
0 1
(t
0
−t
1
)
0
m
3
0 0 0 0
m
4
0 1
(t
0
−t
15
)
0 0
(b) Tensor X model with ageing
s
1
s
2
s
3
s
4
m
1
0 0 0 0
m
2
0.97
(t
0
−t
3
)
0 0.99
(t
0
−t
1
)
0
m
3
0 0 0 0
m
4
0 0.86
(t
0
−t
15
)
0 0
Section 6 concludes the paper and presents the future
work.
2 TIME-AWARE LINK
PREDICTION METHOD
2.1 Definitions
Tensor. A multi-dimensional array of numerical
values (Kolda and Bader, 2009). The order of the ten-
sor is the number of dimensions that the tensor uses.
In our method we use a tensor of order three denoted
by Y
I×J×K
, where I,J, K ∈ N and I = J. The (i, j, k)
element of a third-order tensor is denoted as y
i jk
.
Information Ageing. A process of retention of in-
formation in a memory over time. We represent the
relation between time and retention using a forget-
ting curve (Ebbinghaus, 1913); defined as R = e
−λT
where R is the memory retention, T is the amount of
time since the information was received and 1/λ is
the strength of the memory.
Based on the definition of the forgetting curve, we
propose an ageing function
A(t
0
) = A(t
x
) ∗ e
−λt
;t
0
> t
x
,t = t
0
−t
x
(1)
where A(t
0
) is the amount of information at the
time t
0
, A (t
x
) is the amount of information at the
time t
x
when the information was created, λ is age-
ing/retention factor and t is the age of the information.
The information ageing is influenced by the the λ pa-
rameter as the strength of the memory. The higher the
value of the λ parameter is, the faster the loss of in-
formation is. Similarly, the older the information is,
the lower is the amount of held information.
Note that Linked Data community has adopted
several approaches to represent temporal information
(Rula et al., 2012; Gutirrez-Basulto and Klarman,
2012). In this paper we use a single starting time point
t
x
which defines the existence of the link, i.e. the link
exists since t
x
(see Section 4 for discussion). We refer
to this time as the creation time. We have no infor-
mation about the duration of the existence of the link
and we cannot conclude whether it is still valid (Open
World Assumption).
2.2 Tensor-based Model with Temporal
Information
Simple graph structures can be modelled as matrices,
which is preferred for graph structures with one type
of links. However, since RDF data contain more than
one type of links, we use a third-order tensor notation,
which was proposed in (Nickel et al., 2011). We can
project the third-order tensor as a set of incidence ma-
trices, where each matrix contains only links between
entities for a corresponding type of the link.
Let Y ∈ {0,1}
N×N×M
be a tensor representing an
RDF dataset. The tensor consists of two identical di-
mensions N representing a domain of entities (con-
cepts and instances) in the dataset, and the third di-
mension M representing a domain of link types (prop-
erties) that explicitly exist in the dataset. The tensor
element y
i jk
= 1, if the i-th entity has link of a type
k with the j-th entity, for i, j ∈ h0,N) and k ∈ h0, M).
Otherwise, the tensor element y
i jk
= 0. Each tensor
element in the model has a value of 1 or 0 if a link
between two entities exists or does not exist, respec-
tively.
In this paper, we propose an extension of this
model to include also temporal information. We focus
on the situation, when the creation time of the links is
available (see Section 4 for discussion). We use this
information to modify the initial tensor Y such that
values of tensor elements are reduced with respect
to the creation time of the corresponding link. Let
X ∈ R
N×N×M
be a tensor at the time t
0
. We then com-
pute a value of a tensor element x
i jk
using the ageing
function (1) as follows
x
i jk
= y
i jk
∗ e
−λt
(2)
where y
i jk
∈ {0,1} is the initial value of the tensor
element, λ is the ageing factor and t is the link’s age
computed as a distance of the link’s creation time and
the time t
0
(see Section 2.1 for additional details about
the ageing function).
Example 1. Consider an RDF dataset consist-
ing of the four instances of concepts ls:Mashup
Time-awareLinkPredictioninRDFGraphs
391

N
R
R
N
N
N
M
R
R
M
X
k
A A
T
R
k
Figure 1: Visualization of RESCAL (Nickel et al., 2011).
(m1,m2,m3,m4) and wl:Service (s1,s2,s3,s4), and
three links ls:usedAPI that indicate usages of the Web
APIs in the mashups, i.e. (m
2
t
0
−t
3
−−−→ s
1
,m
2
t
0
−t
1
−−−→
s
3
,m
4
t
0
−t
15
−−−→ s
2
). In this formula, each arrow indi-
cates the age of the link as the number of weeks since
t
0
. For example, m
4
t
0
−t
15
−−−→ s
2
indicates that the link
was created 15 weeks ago.
Table 1 shows this information modelled as a ten-
sor, both, with and without ageing (in this example we
set parameter λ = 0.01). Note that the link between
the mashup m
4
and the service s
2
has a lower value
due to the fact that this link was created earlier than
the other two.
2.3 Learning Hidden Latent Factors
We use a tensor factorization technique to perform
structural analysis of an RDF dataset. We propose
an extension of the RESCAL approach (Nickel et al.,
2011) which uses the time information. Each inci-
dence matrix X
k
of a tensor is factorized as
X
k
≈ AR
k
A
T
,k = 0...M (3)
where A is a matrix N × R which models a partic-
ipation of an entity in a latent factor R, and R
k
is a
matrix R × R that models interactions of latent factors
for the k-th relation (Figure 1). The R is a configurable
parameter of the factorization algorithm. It indicates
the number of latent factors to be learned.
The matrix A and the matrices R
k
are computed
by solving the minimum optimization problem
min
c
X
k
k X
k
−
c
X
k
k
F
, where
c
X
k
= AR
k
A
T
(4)
Although there exist other tensor factorization al-
gorithms, RESCAL (Nickel et al., 2011) is the most
suitable method for an analysis of multi–relational
data and link prediction tasks, it scales well for larger
datasets and it shows good performance (Nickel et al.,
2012).
In our extension of the algorithm, we use a tensor
with elements as real positive numbers; lower values
for older links and higher values for newer links. By
using this tensor, latent factors can learn regularities
s
1
s
2
s
3
s
4
m
1
0 0 0 0
m
2
0.95
(t
0
−t
3
)
0.04 0.98
(t
0
−t
1
)
0
m
3
0 0 0 0
m
4
0.11 0.83
(t
0
−t
15
)
0.18 0
Figure 2: Example of reconstructed tensor X (R = 3).
in the model while reconstructed values are approx-
imately the same as the original values. The extra
non-zero values in the reconstructed matrices reflect
the temporal information and the higher values are in-
fluenced by the higher values in the original model.
The higher values represent the predicted links influ-
enced by the recent links in the original model.
2.4 Time-aware Link Prediction
The link prediction task evaluates a possible existence
of a link between a pair of entities by using structural
patterns in the dataset. Our time-aware link prediction
task, on the other hand, evaluates a possible existence
of a link between two entities while taking into ac-
count the age of explicit links in the dataset as well as
structural patterns in the dataset.
To evaluate an existence of a link between i-th and
j-th entity we do a reconstruction
c
X
k
= AR
k
A
T
of a
matrix X
k
for a link of type k. The algorithm solves
a minimum optimization problem with goal to predict
links of type k from domain M from the i-th entity
from domain N. Note that in the following algorithm
the terms source entity, link and target entity refer to
the RDF terminology subject, predicate and object,
respectively.
Inputs:
• An RDF dataset where each link contains infor-
mation when the link was created.
• Ageing constant λ.
• A link of type k and an entity i as a source of links.
• A maximum number of target entities L.
Outputs:
• A set of Top-L entities as targets of links.
Algorithm:
1. Model a tensor X for the input RDF dataset and
the ageing constant λ.
2. Compute factorization for the tensor X with the
extended RESCAL algorithm (see Section 2.3).
3. Reconstruct a matrix
c
X
k
using the latent factor R
k
and a matrix A, where k indicates a link type in
the query.
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
392

ls:usedAPI
foaf:knows
dc:creator
ls:assignedTag
ls:supportedFormat
foaf:Person
ls:Category
ls:Mashup
ls:assignedCategory
ls:Tag
wl:Service
ls:Protocol
ls:Format
ls:assignedTag
rdf:type
ls:assignedTag
#Duvander
#JungleThingy
#Mapping
#XML
#places
#travel
#mapping
"2009-01-13"
"2005-12-05"
"2009-03-07"
"2008-06-26"
dc:created
dc:created
dc:created
dc:created
ls:supportedProtocol
#Google-Maps-API
#JavaScript
ls:assignedTag
#Andres
Figure 3: Excerpt from the extended Linked Web APIs dataset.
4. Read values x
i jk
for the i-th row and each j-th col-
umn. The values indicate whether a link between
the i-th entity and entity in the j-th column should
exist.
5. Sort values in decreasing order and return Top-L
values. These values indicate target entities that
should be linked with the source entity using the
link type k. Note that the Top-L entities can also
be evaluated by comparing x
i jk
> θ, where θ is
some threshold.
Example 2. Consider data from Example 1 as an in-
put RDF dataset. It contains only one type of link
(k = usedAPI) to make it clear. Tensor X on Table
1 corresponds to the first step of the algorithm for
λ = 0.01. The second step factorizes tensor to ma-
trices A,R
k
and the third step provides approxima-
tion of the tensor. Example of the reconstructed ma-
trix
c
X
k
is on Figure 2 (R = 3). For entity i = m
4
the
corresponding row contains three possible candidates
as new links (s
3
,s
1
,s
4
) sorted decreasingly by the re-
constructed value. From the list of candidates can be
selected either a set of Top-L elements or elements
with the value above predefined threshold θ.Please
note that the higher value for s
3
was influenced by
the existing link with higher value, that was created
more recently than the second one.
3 EVALUATION AND
EXPERIMENTS
In this section we demonstrate the time-aware link
prediction method on the real-world dataset from Pro-
grammableWeb.
The questions we address in experiments are as
follows:
• How temporal aspects influence the link predic-
tion?
• How the evolution of dataset structure influences
the link prediction?
On several experiments, we evaluate the quality of the
proposed method when compared with a set of base-
line algorithms. The first experiment shows the differ-
ence of the proposed time-aware link prediction and
a link prediction without temporal information. The
following two experiments clarify the connection be-
tween predicted links, the time information and the
structure of the dataset.
3.1 Linked Web APIs Dataset
For evaluation purposes, we created extended version
of the Linked Web APIs dataset. The dataset is an
RDF representation of the ProgrammableWeb
3
direc-
tory, the largest mashup and Web APIs directory. It
contains information about developers, mashups they
created and Web APIs they used, together with cate-
gories they belong to. In addition, the dataset has in-
formation about tags assigned to each mashup and a
Web API, formats and protocols that Web APIs sup-
port. We also collected information about the time
when users, mashups or Web APIs appeared in the
directory for the first time. The dataset contains in-
formation from June 2005 till the end of March 2013,
it has in total 22 286 entities, 8 types of links and con-
tains approx. 123 000 links.
The dataset (Figure 3) uses several well know
ontologies and vocabularies: FOAF
4
ontology (prefix
foaf ) - concept foaf:Person describes users and
property foaf:knows describes a social relationship
3
http://www.programmableweb.com/
4
http://xmlns.com/foaf/spec/
Time-awareLinkPredictioninRDFGraphs
393

0 50 100 150 200 250 300 350
0.0 0.2 0.4 0.6 0.8 1.0
Age (# weeks)
Ageing function
λ = 0.001
λ = 0.01
λ = 0.1
(a) Ageing function
●
●
●
●
●
●
●
●
10 20 30 40 50 60
0.0 0.1 0.2 0.3 0.4 0.5
Number of latent factors
Average difference of sets
●
●
●
●
●
●
●
●
0 1000 2000 3000 4000
Computation time (s)
Difference
Time
(b) Number of Latent factors
Figure 4: Experiments settings.
between users, WSMO-lite (Vitvar et al., 2008) on-
tology (prefix wl)- concept wl:Service describes Web
APIs, Dublin Core
5
vocabulary - property dc:creator
describes relation between a user and a mashup,
and property dc:created indicates creation date of a
mashup, a user or a Web API, SAWSDL (Kopecky
et al., 2007) vocabulary (prefix sawsdl) - property
sawsdl:modelReference describes a tag or a category
of a Web API or a mashup. Additionally, we create
new concepts and properties (prefix ls): ls:Protocol
that identifies a protocol, ls:Format that identifies
data format, and ls:Tag and ls:Category which iden-
tify a tag or a category respectively. We also create
following new properties: ls:usedAPI - between con-
cepts ls:Mashup and wl:Service, ls:supportedFormat,
ls:supportedProtocol - between concepts wl:Service
and ls:Format or ls:Protocol, ls:assignedTag
and ls:assignedCategory - between concepts
wl:Service/ls:Mashup and ls:Tag/ls:Category.
3.2 Experiments Settings
Implementation. We implemented the proposed
method in R. It contains functionalities to construct
a tensor with temporal aspects, RESCAL factoriza-
tion algorithm, link prediction method and a running
example
6
.
Time Information. Our dataset does not contain the
time information for each link. Therefore, we derive
this information from < n,dc : created,t
cn
>, where
n represents a mashup, a Web API or a person and
t
cn
denotes the time the entity was created. Since all
entity links are created in our dataset at the same time
as the entity is created, we propagate t
cn
as a creation
time to all the links of the entity n.
5
http://dublincore.org/documents/
6
https://github.com/jaroslav-kuchar/Time-Aware-Link-
Prediction
Snapshots. For purposes of analysing data over dif-
ferent time periods we prepared 22 snapshots of the
dataset. The first snapshot contains data from June
2005 until January 2008. It contains approx. 21 000
links which is a significant portion of the total num-
ber of links while it is a sufficient information for the
link prediction. We then created subsequent snap-
shots with a step of 3 months where each snapshot
always contains the data of a previous snapshot. In
order to compare capabilities of the time-aware link
prediction and the link prediction that does not use
time information we modelled all 22 snapshots as ten-
sors with and without time information. The ageing
function parameter t
0
(see Formula (1)) denotes the
end of a snapshot.
Setting the Ageing Constant. In the experiments,
we set the ageing constant empirically to λ = 0.01
and the age period t in weeks. Figure 4(a) depicts
the influence of the ageing function for different λ.
Value λ = 0.01 provides a distribution of values over
the whole seven years period. Note that a higher λ
value (i.e. λ = 0.1) promotes less than the last 50
weeks while a lower λ value (i.e. λ = 0.001) does not
provide significant change of values over the period.
This is a configurable parameter that can be used to
control the forgetting rate and it depends on specific
requirements and dataset. Since we want all data in
the dataset to participate in our experiments, the value
λ = 0.01 provides us with the best setting. The results
from the evaluation also supports this setting in terms
of overall quality of the predictions.
Setting the Tensor Factorization. In the tensor fac-
torization, we experimentally set the number of latent
factors to 40. We terminate the factorization when a
change of the factor matrices between two iterations
is < 1. This is a terminating condition for the mini-
mum optimization problem which means that the so-
lution found during the iteration will not change in
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
394
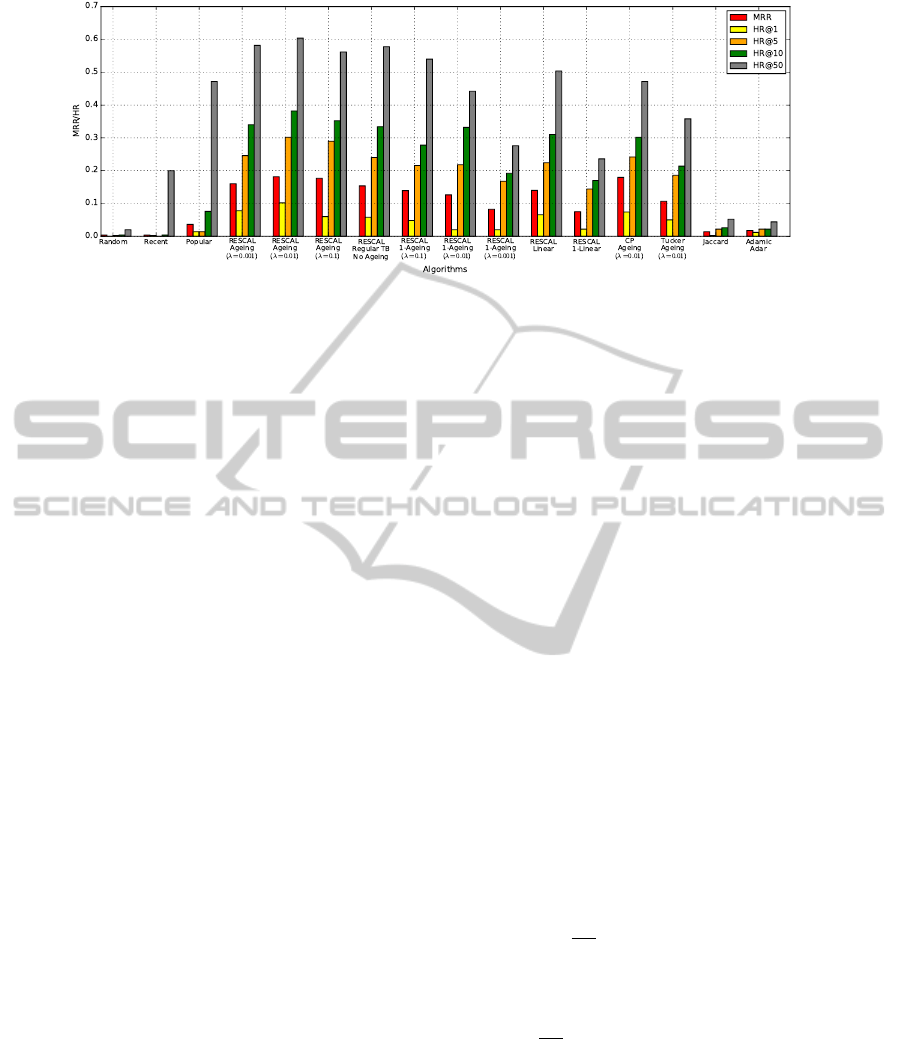
Figure 5: Mean Reciprocal Rank (MRR), HitRatio at top-k (HR@k).
subsequent iterations. Figure 4(b) depicts the impact
of various settings on the method. We performed 10
runs on the same model and measured the difference
of predicted sets of links. The same figure also il-
lustrates a computation time on a computer with 1,6
GHz Intel Core i5 and 4GB RAM. Note that in this
paper we do not focus on the performance and scala-
bility of the algorithm. We refer the reader to (Nickel
et al., 2011) for more details on the performance of
the RESCAL factorization.
3.3 Evaluation
In this section, we describe the results from the ex-
perimental evaluation where the goal is to measure
the quality of the time-aware link prediction. We cre-
ated two sets, namely a training set and a testing set,
from the whole dataset. We randomly selected 1%
of the newest links from the last snapshot (the last 3
months) and put them to the testing set. The rest of
the data we put to the training set. We performed re-
peated random sub-sampling cross-validation.
We evaluated our method (including different
functions and parameters for ageing) compared to the
following set of algorithms.
• Random: for each source of a link in the testing
set, randomly choose a set of targets that corre-
spond to the type of the link. For example, for a
Mashup and a link usedAPI it randomly chooses
a set of Web APIs.
• Recent: select targets from the testing set that are
connected to the newest links in the training set.
• Most Popular: select targets from the testing set
that are connected to the highest number of links
in the training set.
• Regular TB Link Prediction: a tensor model with-
out ageing and the original RESCAL tensor fac-
torization.
• Time-aware Link Prediction with Ageing: our pro-
posed method with different values of λ parameter
for ageing function. “Linear” decreases impor-
tance of older links linearly over the whole time
period, “1 − Ageing” and “1 − Linear” promotes
older links.
• CP and Tucker: tensor decomposition CP (CAN-
DECOMP/PARAFAC) and Tucker (Kolda and
Bader, 2009) using tensor model with ageing
function and λ = 0.01.
• Jaccard and Adamic Adar: baseline graph based
methods for link prediction in social networks
(Oyama et al., 2011) that use node neighbour-
hoods to predict new links.
Note that the Recent and Most Popular are ex-
ploited as recommendation methods in the Pro-
grammableWeb service repository.
Since we only have one relevant target for each
testing item, and we measure a position of a predicted
link, we did not perform evaluation related to Preci-
sion and Recall. Instead, we measured Mean Recipro-
cal Rank (MRR), which is appropriate for evaluation
tasks with a single target. It is computed as a recip-
rocal value of a position at which the relevant target
was evaluated and is averaged across all testing items
(T I): MRR =
1
|T I|
∑
|T I|
i=1
1/position
i
.
The second metric we evaluate is HitRatio at top-
k (HR@k) that indicates whether the relevant link oc-
curs in the top-k predicted links. It is computed as
HR@k =
1
|T I|
∑
|T I|
i=1
hit
k
i
, where hit
k
i
= 1 if the relevant
link is in top-k predicted links, otherwise it is 0.
Figure 5 shows results from the evaluation. Ran-
dom neither works with structural nor temporal infor-
mation and has the lowest values for all metrics. Re-
cent has slightly better results since it takes into ac-
count temporal aspects. Taking into account popular-
ity leads to better results with Most Popular. Regular
Link Prediction has good results since it considers the
data structure. Time-Aware Link Predictions based on
Time-awareLinkPredictioninRDFGraphs
395

2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
realestate
sports
uk
reference
food
transit
events
science
education
politics
trivia
geography
gps
social
travel
photo
video
search
shopping
news
government
location
mobile
visualization
geocoding
deadpool
geolocation
transportation
gis
(a) Without Ageing
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
realestate
sports
uk
reference
food
transit
events
science
education
politics
trivia
geography
gps
social
travel
photo
video
search
shopping
news
government
location
mobile
visualization
geocoding
deadpool
geolocation
transportation
gis
(b) With Ageing
Figure 6: Visualization of positions for each snapshot.
Linear, 1 − Linear or 1 − Ageing do not show better
results than the Regular Link prediction since they do
not reflect properly temporal aspects of links in the
dataset. Jaccard and Adamic Adar does not perform
well since they consider only information about the
closest neighbourhood of each node in graph and they
do not take into account types of nodes or semantics
of links. CP decomposition achieved comparable re-
sults with RESCAL in terms of MRR but lower re-
sults in HR@k. Tucker decomposition has good re-
sults since it takes into account structure but does not
have better results than Regular Link Prediction with
RESCAL. Our time-aware link prediction based on
RESCAL (λ = 0.01) outperforms other baseline al-
gorithms in MRR and HR@1, HR@5, HR@10. It
is able to predict links on better positions (lower k)
than the other algorithms. In the following experi-
ments, we focus on the Time-Aware Link Predictions
with ageing function (λ = 0.01).
3.4 Significance of Time-aware Link
Prediction
In this experiment we test how the time information
influences items and their position in a list of top-L
predicted links. To study the influence of time, we
focused on a simple tagging task. The goal is to find
a set of tags which should be assigned to a specific
API (predicted links to tags can be used to improve
description of APIs). We run this experiment for the
well-known Google Maps API.
Table 2 shows results using the tensor models with
Table 2: Top 10 tags for Google Maps API on the 1st April
2013.
Position Without Ageing With Ageing
1 travel geolocation
2 realestate location
3 sports travel
4 reference government
5 uk geocoding
6 location visualization
7 transit transportation
8 food gis
9 science weather
10 government deadpool
and without ageing for the last snapshot. The column
Without ageing contains a list of tags representing tar-
gets of predicted top-10 links. This list is influenced
only by structural patterns in the whole dataset, since
the snapshot without ageing is used. The column With
Ageing contains a list of tags, which is not only influ-
enced by structural patterns, but also by time. Some
of the predicted tags are the same in both sets, but on
different positions. For example travel lost the first
position, but location or government moved up to bet-
ter positions.
In order to explore differences in both sets we run the
same experiment over time (i.e., by using the 22 snap-
shots). Figures 6(a),6(b) depict positions of tags in a
top-10 set for each snapshot. The position is repre-
sented by a color on a scale from white to black where
a darker color corresponds to a better position of a
tag. Figure 6(a) depicts positions when the ageing is
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
396

●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
●
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
0 50 100 150 200 250 300
Distance in weeks
Time
(a) No Ageing
●
●
●
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
0 20 40 60
Distance in weeks
Time
(b) Ageing
Figure 7: Distance of predicted Mashups from the ending time of snapshot.
not used. It can be observed that a position of tags do
not change very much over time once a tag gets to a
certain position (e.g., realestate, travel). This is influ-
enced by global structural patterns that the algorithm
uses once they appear in the dataset. Note that each
snapshot always contains data of a previous snapshot
(see Snapshots paragraph in Section 4).
Figure 6(b) depicts positions when the ageing is
used. There is a group of tags (food, reference, uk,
sports, realestate) that were on better positions in
the past (the darker colors in the bottom-left corner),
however, they lost significance in recent time. On the
other hand, a group of tags (e.g., geolocation, geocod-
ing, location) had no significance in the past but is
more preferred in recent time (darker colors in the
top-right corner). This is caused by evolution of the
structure of the dataset over time. Intuitively, this also
proves the fact that mapping APIs and mashups (i.e,
tags geocoding, location, geolocation) started to gain
a popularity only 5 years ago and travel mashups and
APIs are all-time popular. Please also refer to experi-
ment in Section 3.6 for more details.
3.5 Influence of Time Information on
Prediction
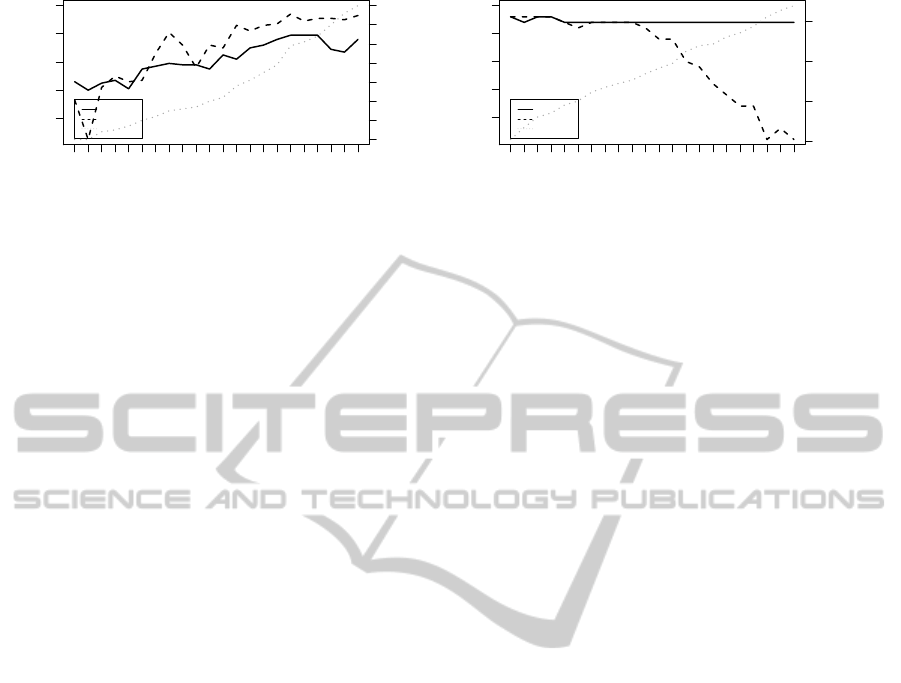
In this experiment, we present a relation of predicted
links and time information of entities which partici-
pate in the predicted links. This experiment is moti-
vated by a need to predict links between mashups and
APIs. For example, to find top-10 mashups that could
benefit from the Flicker API.
We run the experiment for all 22 snapshots. Fig-
ures 7(a) and 7(b) depict a distance in weeks of top 10
mashups from t
0
of every snapshot. We use a standard
box plot to examine distributions of distances graphi-
cally. Figure 7(b) presents much lower distances than
Figure 7(a). These results support our assumption that
predicted entities in top-10 lead to links between enti-
ties with time information closer to t
0
(i.e., the present
time of a particular snapshot) than the link prediction
that does not use time information.
We also performed a quantitative experiment of
this prediction task. We randomly selected 100
tags and predicted top-10 APIs that should be as-
signed to each tag. At the same time we randomly
selected 1000 Mashups and predicted top-10 APIs
which should be used in the specific Mashup. The
mean value of distance is 33 weeks for the time-aware
link prediction and 184 weeks for the link prediction
that does no use time information.
3.6 Impact of Evolution of Structure
In this experiment, we demonstrate how the pro-
posed method takes into account the evolution of the
datasets’ structure when predicting new links.
We run the prediction for two tags realestate and
geocoding and evaluate their positions in top-L pre-
dicted links over time for the well-known Google
Maps API. Figure 8(a) and 8(b) depict an evolution of
the position for both tags on the left axis and a num-
ber of usages of the tags on the right axis (a usage of a
tag means that an explicit link between an entity and
the tag exists in the dataset).
Figures 8(b) shows a high position of the tag
realestate when no ageing is used. This is influenced
by the high number resources (APIs and mashups)
Time-awareLinkPredictioninRDFGraphs
397
80 60 40 20 0
no ageing
ageing
usage
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
10 30 50 70
Position
# usage
Time
(a) Position of tag geocoding
20 15 10 5 0
no ageing
ageing
usage
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
150 200 250 300
Position
# usage
Time
(b) Position of tag realestate
Figure 8: Evolution of position over time for a specific tag.
tagged with this tag and the supporting structural pat-
terns that exist throughout the history. However, when
ageing is applied, the tag is gradually loosing its posi-
tion since the structural patterns were created earlier
in the past rather than in recent time (in a snapshot’s
time t
0
). Figure 8(a) shows that the tag geocoding gets
to slightly better positions when ageing is applied.
This is caused by the fact that supportive structural
patterns for this tag appeared in recent time. The next
paragraph describes an example of elementary struc-
tural patterns that may influence positions of tags in
link prediction.
Significant Sub-graphs. Our method is based on
identification of hidden patterns in the structure of
data (tensor factorization) in connection to the time
information and ageing. Identified hidden patterns are
used to predict new links in data. In order to find such
significant patterns we can use an existing local prop-
erty of graphs, called motifs. Motifs are defined as
recurrent and statistically significant sub-graphs. We
adopted the idea of motifs in this experiment as an
”evidence” of influence of structure and temporal in-
formation in tensor factorization with ageing. The
goal of this experiment is to some extent provide an
explanation of results from the previously described
experiment in this section.
New links for Google Maps API can be predicted
only when a similar pattern exists in the data and
the pattern contains information related or similar
to the Google Maps API structure. Based on the
dataset structure, we define several elementary pat-
terns which may influence the link prediction of the
tags realestate and geocoding for the Google Maps
API. By looking at the Google Maps API structure,
we can see that it is a service, it has assigned a cate-
gory mapping, a tag mapping, and supports JavaScript
protocol. We breakdown this structure to the follow-
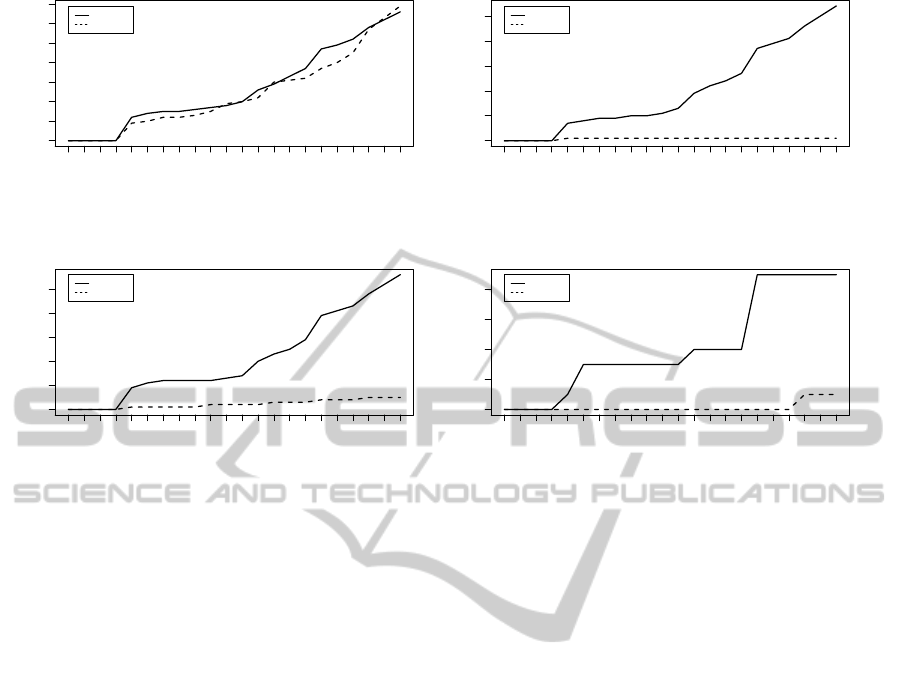
ing queries (that we call patterns), where X can be
either realestate or geocoding. We then measure the
number of occurrences for each of the 8 patterns in
the 22 snapshots.
1. ?var rdf:type wl:Service AND
?var ls:assignedTag ?X
2. ?var ls:assignedCategory ls:Mapping AND
?var ls:assignedTag ?X
3. ?var ls:assignedTag ls:mapping AND
?var ls:assignedTag ?X
4. ?var ls:supportedProtocol ls:JavaSript AND
?var ls:assignedTag ?X
Figures 9(a)-9(d) depict a number of occurrences
for each pattern over time (i.e., for each of the 22
snapshots). The tag geocoding has a higher number
of occurrences of the patterns than the tag realestate.
This means that there are more structures similar to
the Google Maps API structure that have assigned
tag geocoding rather than the tag realestate. Al-
though this does not provide much evidence for the
tag realestate and its high positions when no age-
ing is used (in Figure 8(b)) which is influenced by
other structural patterns not shown here, it shows
that a higher presence of the patterns in recent time
promotes the tag geocoding to better positions when
compared to positions when no ageing is used (Figure
8(a)).
4 DISCUSSION
Robustness. Although we evaluated our method on a
domain-specific dataset from ProgrammableWeb, the
method is capable to predict links in a dataset from
any other domain. We have chosen the dataset from
ProgrammableWeb as it contains sufficient informa-
tion about creation time of entities that we can propa-
gate to relevant links. We plan to evaluate our method
on different datasets in our future work.
Temporal Information. Due to the nature of the
data from ProgrammableWeb we deal with a specific
form of time assigned to an entity as the created time
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
398
0 10 20 30 40 50 60 70
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
geocoding
realestate
# occurences of pattern
Time
(a) Pattern 1
0 10 20 30 40 50
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
geocoding
realestate
# occurences of pattern
Time
(b) Pattern 2
0 10 20 30 40 50
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
geocoding
realestate
# occurences of pattern
Time
(c) Pattern 3
0 2 4 6 8
2008−01−01
2008−04−01
2008−07−01
2008−10−01
2009−01−01
2009−04−01
2009−07−01
2009−10−01
2010−01−01
2010−04−01
2010−07−01
2010−10−01
2011−01−01
2011−04−01
2011−07−01
2011−10−01
2012−01−01
2012−04−01
2012−07−01
2012−10−01
2013−01−01
2013−04−01
geocoding
realestate
# occurences of pattern
Time
(d) Pattern 4
Figure 9: Number of occurrences for each pattern.
(see also Section 3 for information how we propa-
gate this time to corresponding links). We understand
the created time as a starting time from which the
link exists in the dataset and we have no information
about a duration of the link’s existence. It is our fu-
ture work to study various representations of time in
linked datasets and incorporate them into the time-
aware link prediction method.
Further, there are two basic types of expressing an
existence of data - an explicitly defined time point us-
ing a document-centric and a fact-centric information
(e.g., reification, N-ary relationships, snapshots of
graphs, provenance, PROV-O, Memento etc.) (Rula
et al., 2012) or deduced from other facts in an RDF
dataset. The first category can be immediately used
in our model. Since the availability of temporal in-
formation in Linked Data is still limited (Rula et al.,
2012), especially for links, we derive the temporal re-
strictions from available data in dataset.
The types of links that never evolve or should not
evolve (e.g. dc:creator, rdf:type) can be excluded
from the temporal extension of tensor using value 1.
Ageing Function. Our goal was to show that time
information is a very important aspect for link pre-
diction and how a method to predict links can be ex-
tended with time information by modelling a retention
of information using the ageing function. The for-
mula we use for the ageing function is inspired by a
representation of forgetting and retention mechanisms
in the human mind.
Structural Patterns. Results of the time-aware link
prediction highly depend on a structure of the RDF
graph and a time when links were created. In Section
3.6 we identified simple structural patterns that may
influence the link prediction in this specific dataset.
However, there is no reason to assume that there can-
not be present also other, more complex structural pat-
terns that influence the link prediction. In our future
work we plan to explore methods for automatic detec-
tion of more complex patterns.
Snapshot Creation. We have chosen the size of snap-
shots so that they have a sufficient amount of data for
learning. Note that the data of some snapshots can
be differently distributed with respect to time. Some
snapshots might have data normally distributed but in
some snapshots the majority of the data can be at the
start or at end of the snapshot. Such distribution of
the data has an impact on the link prediction.
5 RELATED WORK
There are two main topics closely related to our time-
aware link prediction method, namely tensor factor-
ization and relational learning. The models and meth-
ods covered by these topics are used to model multi-
relational data and to perform the link prediction.
Time-awareLinkPredictioninRDFGraphs
399

Most researches in relational learning are based on
a statistical relational learning. These approaches are
build upon the Bayesian or Markov networks (Fried-
man et al., 1999; Khosravi and Bina, 2010) or their
combinations with tensor representations (Gao et al.,
2012).
There is a growing interest in tensor models and
factorizations in multi-relational data modelling. An
overview of tensor factorizations and their applica-
tions is in (Kolda and Bader, 2009). There are
two basic approaches, namely link-information-based
approaches and node-information-based approaches.
We adopted a model from link-information-based ap-
proaches by (Nickel et al., 2011), where each frontal
slice of a tensor represents a relation. A similar model
was also used in (London et al., 2013). These mod-
elling approaches, however, do not work with time
information. They only take into account entities and
relations among them.
On the other hand, node-information-based ap-
proaches, take into account attributes of entities
(Taskar et al., 2003; Raymond and Kashima, 2010).
An extension of this work in (Nickel et al., 2012) is
able to work with attributes (time attribute can also be
included) and combine both approaches.
There are also existing approaches related to
frameworks LIMES (Ngomo and Auer, 2011) and
SILK (Bizer et al., 2009) that are focused on link dis-
covery between different datasets. Our approach is
focused on link prediction within one dataset.
There are existing researches, that use time for
predicting links. In (Spiegel et al., 2012), the authors
use the third-order tensor factorization, where two di-
mensions are used to represent relations and the third
dimension represents time. This approach is however
suitable only for one type of relation. A similar work
was done in (Acar et al., 2009; Dunlavy et al., 2011;
Ermis et al., 2012) where authors also work with a
dataset with one type of a relation.
There are also other approaches that use either
multi-modal representation of graph or temporal in-
formation for link prediction in Social Networks,
e.g. prediction links in asynchronous communication
(Oyama et al., 2011), prediction based on hypergraph
(Li et al., 2013), prediction in multi-modal networks
(Symeonidis and Perentis, 2014), however, they are
less relevant to our work.
6 CONCLUSION AND FUTURE
WORK
The popularity of publishing RDF datasets as Linked
Data is significantly growing in recent time. A rich
dataset contains a sufficient amount of links, however,
not all links may explicitly exist in the dataset while
some existing links may not be valid. Link prediction
algorithms can be used to find links that do not explic-
itly exist in the dataset. Although there exists a num-
ber of sophisticated approaches for link prediction,
there is still a lack of methods that can work with time
information. The time information is important to
work with datasets in dynamic environments and for
the link prediction it helps to provide more relevant
results. In this paper, we proposed the time-aware
link prediction method that extends the tensor fac-
torization to solve link prediction task with temporal
information about existence of links. While existing
methods use either multi-relational data or data with
one type of relation and time information, our method
utilizes both, the multi-relational data and time infor-
mation in order to create tensor-based model. The re-
sults from the experiments on the real world dataset
from ProgrammableWeb show, that the method effec-
tively exploits both the structure of the datasets and
the temporal information.
In our future work, we want to focus on the eval-
uation of the method on other datasets from Linked
Data Cloud that incorporate links across data sources.
We also plan to investigate other sources for tempo-
ral information. Further, we plan to explore different
applications of the method. In particular, we want to
evaluate the performance of the method in evaluation
of existing links.
ACKNOWLEDGEMENTS
This work was supported by the Grant Agency of
the Czech Technical University in Prague, grant No.
SGS14/104/OHK3/1T/18. We also thank to Pro-
grammableWeb.com for supporting this research.
REFERENCES
Acar, E., Dunlavy, D. M., and Kolda, T. G. (2009). Link
prediction on evolving data using matrix and tensor
factorizations. In Proceedings of the 2009 IEEE In-
ternational Conference on Data Mining Workshops,
ICDMW ’09, pages 262–269, Washington, DC, USA.
IEEE Computer Society.
Bizer, C., Volz, J., Kobilarov, G., and Gaedke, M. (2009).
Silk - a link discovery framework for the web of data.
In 18th International World Wide Web Conference.
Dunlavy, D. M., Kolda, T. G., and Acar, E. (2011). Tempo-
ral link prediction using matrix and tensor factoriza-
WEBIST2015-11thInternationalConferenceonWebInformationSystemsandTechnologies
400

tions. ACM Trans. Knowl. Discov. Data, 5(2):10:1–
10:27.
Ebbinghaus, H. (1913). Memory: A contribution to ex-
perimental psychology. Number 3. Teachers college,
Columbia university.
Ermis, B., Acar, E., and Cemgil, A. T. (2012). Link pre-
diction via generalized coupled tensor factorisation.
CoRR, abs/1208.6231.
Friedman, N., Getoor, L., Koller, D., and Pfeffer, A. (1999).
Learning probabilistic relational models. In In IJCAI,
pages 1300–1309. Springer-Verlag.
Gao, S., Denoyer, L., and Gallinari, P. (2012). Proba-
bilistic latent tensor factorization model for link pat-
tern prediction in multi-relational networks. CoRR,
abs/1204.2588.
Gutirrez-Basulto, V. and Klarman, S. (2012). Towards a
unifying approach to representing and querying tem-
poral data in description logics. In Krtzsch, M. and
Straccia, U., editors, Web Reasoning and Rule Sys-
tems, volume 7497 of Lecture Notes in Computer Sci-
ence, pages 90–105. Springer Berlin Heidelberg.
Khosravi, H. and Bina, B. (2010). A survey on statistical
relational learning. In Proceedings of the 23rd Cana-
dian conference on Advances in Artificial Intelligence,
AI’10, pages 256–268, Berlin, Heidelberg. Springer-
Verlag.
Kolda, T. G. and Bader, B. W. (2009). Tensor decomposi-
tions and applications. SIAM Rev., 51(3):455–500.
Kopecky, J., Vitvar, T., Bournez, C., and Farrell, J. (2007).
Sawsdl: Semantic annotations for wsdl and xml
schema. Internet Computing, IEEE, 11(6):60 –67.
Li, D., Xu, Z., Li, S., and Sun, X. (2013). Link prediction
in social networks based on hypergraph. In Proceed-
ings of the 22Nd International Conference on World
Wide Web Companion, WWW ’13 Companion, pages
41–42, Republic and Canton of Geneva, Switzerland.
International World Wide Web Conferences Steering
Committee.
London, B., Rekatsinas, T., Huang, B., and Getoor, L.
(2013). Multi-relational learning using weighted
tensor decomposition with modular loss. CoRR,
abs/1303.1733.
Ngomo, A.-C. N. and Auer, S. (2011). Limes: A time-
efficient approach for large-scale link discovery on the
web of data. In Proceedings of the Twenty-Second In-
ternational Joint Conference on Artificial Intelligence
- Volume Volume Three, IJCAI’11, pages 2312–2317.
AAAI Press.
Nickel, M., Tresp, V., and Kriegel, H.-P. (2011). A three-
way model for collective learning on multi-relational
data. In Getoor, L. and Scheffer, T., editors, Proceed-
ings of the 28th International Conference on Machine
Learning (ICML-11), ICML ’11, pages 809–816, New
York, NY, USA. ACM.
Nickel, M., Tresp, V., and Kriegel, H.-P. (2012). Factorizing
yago: scalable machine learning for linked data. In
Proceedings of the 21st international conference on
World Wide Web, WWW ’12, pages 271–280, New
York, NY, USA. ACM.
Oyama, S., Hayashi, K., and Kashima, H. (2011). Cross-
temporal link prediction. In Proceedings of the 2011
IEEE 11th International Conference on Data Mining,
ICDM ’11, pages 1188–1193, Washington, DC, USA.
IEEE Computer Society.
Raymond, R. and Kashima, H. (2010). Fast and scalable al-
gorithms for semi-supervised link prediction on static
and dynamic graphs. In Balczar, J., Bonchi, F., Gio-
nis, A., and Sebag, M., editors, Machine Learning and
Knowledge Discovery in Databases, volume 6323 of
Lecture Notes in Computer Science, pages 131–147.
Springer Berlin Heidelberg.
Rula, A., Palmonari, M., Harth, A., Stadtmller, S., and
Maurino, A. (2012). On the diversity and availabil-
ity of temporal information in linked open data. In
Cudr-Mauroux, P., Heflin, J., Sirin, E., Tudorache, T.,
Euzenat, J., Hauswirth, M., Parreira, J., Hendler, J.,
Schreiber, G., Bernstein, A., and Blomqvist, E., edi-
tors, The Semantic Web ISWC 2012, volume 7649 of
Lecture Notes in Computer Science, pages 492–507.
Springer Berlin Heidelberg.
Spiegel, S., Clausen, J., Albayrak, S., and Kunegis, J.
(2012). Link prediction on evolving data using ten-
sor factorization. In Proceedings of the 15th interna-
tional conference on New Frontiers in Applied Data
Mining, PAKDD’11, pages 100–110, Berlin, Heidel-
berg. Springer-Verlag.
Symeonidis, P. and Perentis, C. (2014). Link prediction in
multi-modal social networks. In Calders, T., Espos-
ito, F., Hllermeier, E., and Meo, R., editors, Machine
Learning and Knowledge Discovery in Databases,
volume 8726 of Lecture Notes in Computer Science,
pages 147–162. Springer Berlin Heidelberg.
Taskar, B., fai Wong, M., Abbeel, P., and Koller, D. (2003).
Link prediction in relational data. In in Neural Infor-
mation Processing Systems.
Vitvar, T., Kopeck
´
y, J., Viskova, J., and Fensel, D. (2008).
WSMO-Lite Annotations for Web Services. In ESWC,
pages 674–689.
Time-awareLinkPredictioninRDFGraphs
401
