Determination of Direction and Velocity of the Objects

Vasiliy N. Kruglov, Artem V. Kruglov and Uriy V. Chiryshev

Ural Federal University named after the first President of Russia B. N. Yeltsin, 19 Mira Street, Yekaterinburg, Russia

Keywords: Machine Vision, Control Systems, Image Processing, Fast Fourier Transform, Video Sequence, Frame

Matching, Correlation Surface, Motion Vectors, Movement Direction, Movement Velocity, Scene Depth.

Abstract: In this paper the analysis of methods for determination the direction and velocity of the objects is given. As

applied to the problem of geometry assessment for round timber the optimum by the ratio of accuracy and

performance is phase correlation method. Nonetheless the pointed problem requires better accuracy and

validity, so we had to improve this method and adapt it to the concrete conditions. Modified algorithm was

tested on the image database of real technological process of round timber movement on the conveyer belt.

The offered method has shown its high effectiveness and validity.

1 INTRODUCTION

Determining the direction and velocity of the objects

is possible by combining two adjacent frames in the

video sequence. For two given images:





∶  → ,



∶  → ,, ⊂ 



(1)

where d is dimension of the images (usually d=2),

the task of combining the images is to find such a

spatial transform ∶→ and brightness transform

∶→which allow to convert one image to

another so that a correspondence points of these

images match each other:



























,∈,∈

(2)

That is, every frame is processed by the certain

mathematical apparatus, which allows to determine

the movement of the scene’s object between the

current and previous frames in the sequence of

images.

The most promising methods for the problem

under investigation are: method of determining the

displacement on the basis of cross-correlation

functions (CCF) (Jänne, 2007), the method based on

the phase correlation (Gonzalez and Woods, 2005)

and Lucas-Kanade method based on the optical flow

(Lucas and Kanade, 1981). Although a number of

methods discussed in this article are not complete,

they are typical representatives of the motion

analysis technique, commonly used in practice. Each

of these methods has advantages and disadvantages

as well as they require the optimum conditions,

which depend on the particular application.

2 BODY OF ARTICLE

Method based on the cross-correlation functions of

the two images is calculated according to the

formula:

11 11

00 00

[( , ) ( , )]

(, ) ,

(, ) ( , )

0, 1, 0, 1

NM NM

yx yx

Ix y Tx xy y

Cxy

xy T x xy y

xKMyLN







 

 

 

  





  







 

(3)

With this method it is possible to select section of

one image on another and the difference between the

location of these sections on the images is equal to

displacement of the object against the camera

occurred at the time of a new frame arrival. Among

the shortcomings of the method based on CCF

should be noted the instability to rotations and affine

distortions, as well as high sensitivity to brightness

variations.

Lucas-Kanade method searches for the bias in

the vicinity of the singular point (Shi and Tomasi,

1994). This approach is often called differential as it

is based on the calculation of the partial derivatives

by horizontal and vertical directions of the image. In

case of founding the bias in the vicinity of the

singular point, its position updates for further search.

Otherwise, the singular point is excluding from

103

N. Kruglov V., V. Kruglov A. and V. Chiryshev U..

Determination of Direction and Velocity of the Objects.

DOI: 10.5220/0005431501030107

In Proceedings of the 5th International Workshop on Image Mining. Theory and Applications (IMTA-5-2015), pages 103-107

ISBN: 978-989-758-094-9

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

further analyses. By its nature, this method is local,

that is, the area only around the pixel is taken into

account for the determination of the particular pixel

displacement. As a consequence, it is impossible to

sufficiently determine the bias within the large

uniformly colored sections of the frame.

Fast Fourier Transform method (FFT) for the

phase correlation function is based on the

assumption that if the signal has spatial and temporal

shift, the frequencies and amplitudes of the

harmonic components remain constant, only the

initial phases change (phase-frequency spectrum),

and the phase of each harmonic component varies

proportional to the frequency and shift of the signal

at that.

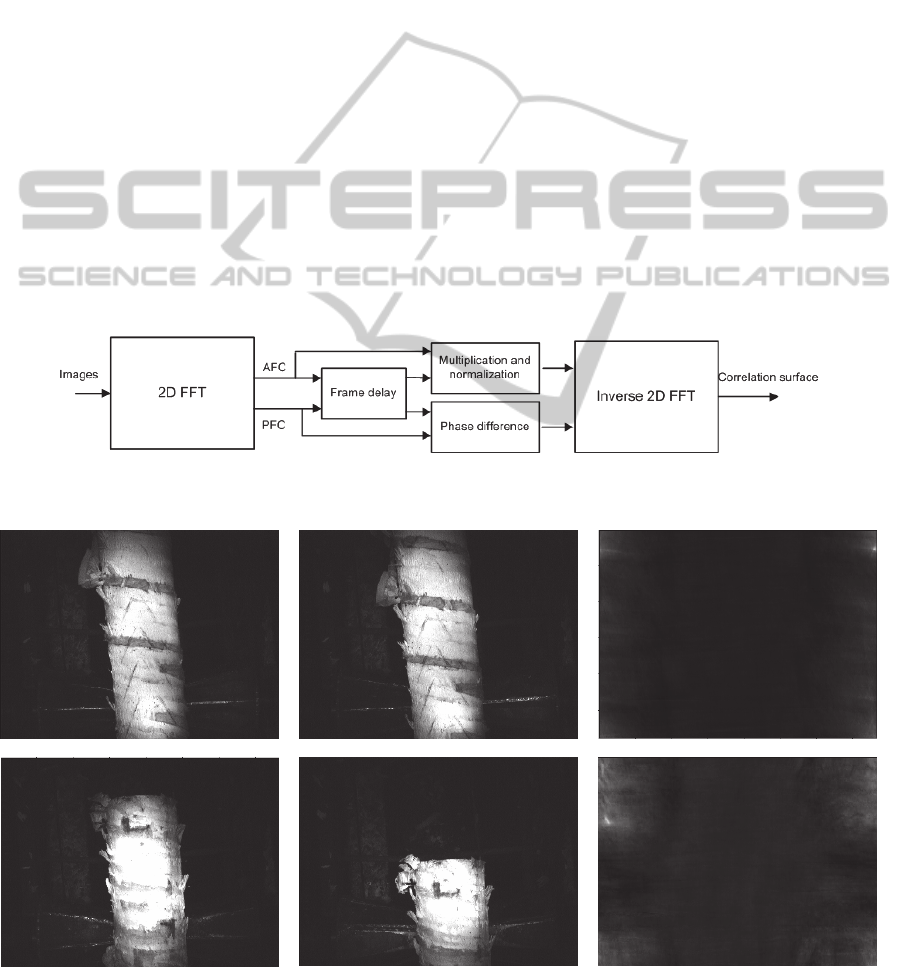
Block diagram of moving vectors receiving by

the phase correlation method is shown on the Figure

The result of transformation is a correlation

surface which is function of two spatial values on

the image plane. If there was no movement the

difference of phase spectra is equal to zero. In this

case spectral components sum up during the

synthesis in phase. It results in surge with spike in

origin of coordinates. When the object moved

several number of maximums appear on the

correlation surface.

Figures 2-3 present results of transforming by

phase correlation obtained with the help of Image

Processing Toolbox.

Transformation was applied to the whole image

and as a result we have one vector (spike)

correspond to the direction of object’s movement.

Disadvantages of this method are

 Impossibility of determination the value of

movement in case of several moving objects on

the frame

 High noise susceptibility

In case of intense noise on the one of the frames

(e.g. camera noise) the dedicated spike may

correspond to the noise (Figure 4), so the

information about direction and velocity of

movement will be inconsistent. In the problem of

geometry assessment of round timber target object

(log) is measured 180-250 times during scan, so

propagation error leads to incorrect result, which is

unacceptable for this task.

Figure 1: Block diagram of FFT phase correlation workflow (AFC – amplitude-frequency characteristic, PFC – phase-

frequency characteristic).

a) previous image b) current image c) correlation surface

d) previous image e) current image f) correlation surface

Figure 2: Phase correlation method for two pairs of frames (a-b and d-e).

IMTA-52015-5thInternationalWorkshoponImageMining.TheoryandApplications

104

Figure 3: 3D-images of correlation surfaces from figures 2,c and 2,f respectively.

Moreover, phase correlation method is not

capable to carry out analysis of several objects in

general case because each object (log on the

conveyer belt) has its own direction and velocity of

movement which don’t match with these

characteristics of other objects.

Figure 4: 3D-image of correlation surface with intense

noise.

Unfortunately, each of these methods has

limitations so the use of any one for this task

becomes difficult. Method based on the CCF is not

resistant to the affine distortions and rotations, and

leaves out of account a particular texture. Lucas-

Canada method is not resistant to affine distortions,

highly sensitive to changes in brightness and shows

insufficient result in the absence relief sections on

the image. FFT phase correlation algorithm has a

lower performance compared to the previous ones,

but it is more accurate.

Thus, based on these findings, an algorithm that

adapt to the scene conditions and the features of the

objects on the image in order to operate with

maximum efficiency for solving the motion

estimation of roundwood on the conveyor was

developed.

This method is as follows. At the first stage of

the frame processing the selection of the front-stage

objects is carried. Then, several sections (7-15 pcs.)

are taken on each selected object, and each section

of the current frame F

(t) is compared with the

corresponding block of the previous frame F

(t-1),



(0,n) by FFT phase correlation as follows:





,









, ∙ 

∗

,





∙

(4)

where R(u,v) is a spectral unit function which phase

is equal to the phase difference between the

functions

and

. Variables u and vare angular

frequencies. Further the inverse Fourier transform is

computed via the function of mutual phase

spectrum:

(, ) [ (,)]Pxy F Ruv





(5)

Function P(x,y)gives a clear peak which determines

the measure of similarity of the images, and the peak

position corresponds to the shift of one picture

relative to another. The basic idea of this step is to

identify the most informative sections within each

region F

(t) and to establish by them matching with

the region on the previous frame. In this case, it is

necessary that each section contains enough

information (relief texture) to establish a correct

match. To achieve this, the procedure of stacking the

measuring sections by elliptical curve relative to the

center of the field F

(t) with subsequent

measurement of the value reflecting the information

content of each section is implemented. Information

content is measured in the horizontal E

and vertical

DeterminationofDirectionandVelocityoftheObjects

105

directions as follows:

(, ) ( , ) (, )

HtijH

VtijV

Exy Ixiay jaSij

Exy Ixiay j aSij













(6)

where S

, S

are Sobel functions for horizontal and

vertical directions which applied to the image I

the point (x,y) and





,



 – tie point in kernel

coordinates

10 1 1 2 1

202 000

10 1 1 2 1



 

 



 



 

(7)

It is necessary to make a number of adjustments to

the current step, concerning certain aspects of the

algorithm. Firstly, the search sections for each

region of interest are stacked along the elliptic curve

within each log (blue dots in Figure 5).

Figure 5: Visualisation of sectional FFT phase correlation

in video sequence in the task of roundwood analysis.

Centers of each section of the objects are marked with

blue dots.

This step is stipulated by the necessity of

compact and uniform distribution of the regions of

interest within each log. It is this method will be by

far the best in terms of uniform stacking of sections

due to the fact that the logs have the elongated along

the motion’s direction profile with a relief texture on

the image. Secondly, the magnitude of the

information content of each section in fact is

meaning of the contrast ratio within a region of

interest so it provides a priori information for

solving the problem of searching the best vector. In

other words, the contrast value establishes a

connection, i.e. indirectly affect the probability of a

correct definition of the shift. Intuitively, the more

contrasting matching sections, the higher probability

that the motion vector for this section will be the

most correspond to the real shift.

With this approach the matching is performed in

two stages. At first, the discrete correlation function

is computed and its "rough" maximum is

determined, then the peak position is adjusted by the

intensity interpolation method (Gonzalez and

Woods, 2005). In the next step, among formed

candidate vectors search for the best one, which

value is considered as the shift of the object, is

implemented by heuristic search method.

This process has three important features. Firstly,

the subpixel search of the peak position of the

correlation surface would greatly increase the

accuracy of determining the shift of the objects.

Secondly, the search operator is applied not to the

entire image, but to the regions where objects were

detected. Thirdly, due to the exhaustive search

within a few number of motion vectors (for the

current task which characterized by objects with

feebly marked relief and possible lack of the specific

features the number of candidates is 7 for each

object) and parallel processing (Kruglov et al.,

2013), a high speed of the algorithm is achieved

(Figure 5).

Tracking objects assumes the establishment of

correspondence between the objects of the previous

frame and the objects detected in the current frame

(Kruglov and Kruglov, 2013). Correspondence

between the objects considered to be established if

these objects are spatially close, displacement is

small and both are sufficiently similar. Proximity

criterion is the fulfillment of the following

conditions:

 the Euclidean distance between the centers of

mass of the objects is small;

 the size of the object does not vary much from

one frame to another (also by the Euclidean

distance).

The resulting algorithm for determination the

direction and velocity of the logs on the basis of the

phase correlation method was tested on the images

database of the actual video sequence process

(435,000 frames). The size of the sections for phase

correlation was 64 * 64 pixels, the number of blocks

- 7 for each selected front-stage object. Test was

carried out in MATLAB framework on the IBM PC

IntelCore i7 2.8GHz. The results of the test are

shown in Table 1.

IMTA-52015-5thInternationalWorkshoponImageMining.TheoryandApplications

106

Table 1: Performance of the algorithm.

1 object

7 sections

2 objects

14 sections

3 objects

21 sections

Without

multithreading

15 ms 28 ms 40 ms

With multithreading

(OpenMP)

7 ms 11 ms 14 ms

According to the results, it should be noted that

offered method for determination the direction and

velocity of the objects based on the phase correlation

demonstrates high efficiency on the test images.

Reliability and performance of the algorithm fully

comply with the conditions of use in machine vision

systems for real-time control of technological

processes associated with the analysis of fast-

moving objects.

3 CONCLUSIONS

As is known from mechanics, solid body moving in

three-dimensional space, can have a six degrees of

freedom maximum: three translational and three

rotational. Degrees of freedom are a set of

coordinates that certainly defines the position of an

object in an associated coordinate system.

Log, like a solid body moving in the plane of the

conveyor, has four degrees of freedom (two

rotational and two translational) This limitation

should be considered in solving the problem of

measuring the volume of logs by observing their

movement in front of the camera. It is possible to

simplify the problem by assuming that the log

moves along rigid rails, i.e. it does not have the

ability to move sideways and rotate, then it has only

one degree of freedom. When using such

simplification, in the sequence of images would be

observed the shift with a constant orientation,

wherein only the instant amplitude varies from

frame to frame. But the fact is that in the real

conditions of logs transportation such ideal type of

movement does not exist. Therefore, it is recognized

as necessary that the log has four degrees of freedom

and all four components of the movement must be

taken into account to accurately measure log’s

length; or at least we can consider the log as material

point with one degree of freedom in the main

approximation (and make corrections due to its

vibrations in other directions when its main

movement is calculated with proper accuracy).

Task of determining the movement of the log can

be formulated as follows: if the log’s shift on the

image is defined by offered method for two

neighboring frames, and its value can be written as a

vector with coordinates (x, y), then how the value

characterizing the physical movement of the log can

be obtained from the resulting vector? How to get

the four-dimensional vector from the two-

dimensional? How to solve a system of two

equations and four unknowns?

In the photo and video camera, an image is

formed under the law of the central projection. As

we know, such a mapping of three-dimensional

space on a plane is not unambiguous because all

three-dimensional points lying along a single ray are

projected at one point on two-dimensional image. In

other words, once we got the log’s image, i.e. from

three-dimensional space transformed into a two-

dimensional, we lost a lot of information related to

the depth of the observed scenes and objects in it.

Recovering of this information is not possible

while using only one camera. The only way of

further developing for this task is to use multiple

cameras for reconstruction of the log in three-

dimensional space. In that case the information

about the depth of the scene and objects on the

image allows to convert the value of the motion

vector, obtained by the offered method, to the

physical movement of the log.

REFERENCES

Jänne B., 2007. Digital image processing, Technospera.

Moscow,5

edition.

Rafael C. Gonzalez, Richard E. Woods 2005. Digital

image processing.Technospera.Moscow,3

edition.

Dvorkovich A. V., Dvorkovich V. P., Zubarev J. B.,

Sokolov A., 1998. A method for analyzing motion

vector components in dynamic images. Patent of the

Russian Federation, the application of 15 July 1998.

Dvorkovich V. P., Nechepaev V. V., 1998. Motion

compensation using the Fourier transform. 1st Int.

Conf. Digital Signal Processing and its Application.

Moscow, ICSTI.

J. Shi, C. Tomasi, 1994. Good features to track. Proc.

IEEE Comput. Soc. Conf. Comput. Vision and Pattern

Recognition.

B. D. Lucas, T. Kanade, 1981. An iterative image

registration technique with an application to stereo

vision. IJCAI'81 Proceedings of the 7th international

joint conference on Artificial intelligence - Volume 2.

Kruglov V. N., Kruglov A. V., Chiryshev U. V.,

Chiryshev A. V., 2013. Application of intensive

algorithms in real time machine vision systems.

Fundamental research. № 10.

Kruglov V. N., Kruglov A. V., 2013. A way to estimate

the discharge of the melt jet flowing out of a melting

furnace. Pattern recognition and image analysis, № 4.

DeterminationofDirectionandVelocityoftheObjects

107