
Central Model Predictive Control of a Group of Domestic Heat Pumps
Case Study for a Small District
R. P. van Leeuwen
1,2
, J. Fink
1
and G. J. M. Smit
1
1
Department of Computer Science, Mathematics and Electrical Engineering, University of Twente,
P.O. Box 217, 7500 AE Enschede, The Netherlands
2
Sustainable Energy Group, Saxion University of Applied Sciences, P.O. Box 70.000, 7500 KB Enschede, The Netherlands
Keywords:
Heat Pump, Smart Grid Control, Domestic Hot Water, Floor Heating, Thermal Storage, Model Predictive
Control, Optimization.
Abstract:
In this paper we investigate optimal control of a group of heat pumps. Each heat pump provides space heating
and domestic hot water to a single household. Besides a heat pump, each house has a buffer for domestic hot
water and a floor heating system for space heating. The paper describes models and algorithms used for the
prediction and planning steps in order to obtain a planning for the heat pumps. The optimization algorithm
minimizes the maximum peak electricity demand of the district. Simulated results demonstrate the resulting
aggregated electricity demand, the obtained thermal comfort and the state of charge of the domestic hot water
storage for an example house. Our results show that a model predictive control outperforms conventional
control of individual heat pumps based on feedback control principles.
1 INTRODUCTION
In the Netherlands, approximately 40% of the total
domestic energy consumption is related to space heat-
ing and domestic hot water (ECN, 2014). To this date,
most Dutch houses rely on natural gas supply and gas
boilers. Heat pumps powered by renewable electric
energy are a possible way to make the transition to-
wards integration of renewable energy in the build-
ing environment (Janssen-Visschers and Lee, 2013),
(Scheepers et al., 2007). In the small city Meppel,
a new district is under construction with an almost
100% renewable energy supply (Meppelenergie, ND).
A biogas CHP provides heat for houses connected to
district heating and electric power for other houses
with a heat pump. Imports and exports of electric en-
ergy from and to the national grid are possible, but the
heat pumps should use the electricity from the CHP
as much as possible. Development of a smart grid
control system is the joined task of a project group
formed by University of Twente, University of Delft,
the utility Rendo, Meppel city council and system in-
tegrator i-NRG.
The Meppel case explores local sustainability, not
only due to the employed energy system, but also due
to the legal aspects. The entire district heating and
cooling system including the heat pumps which are
placed at some of the houses, are owned by a utility
company which is founded specifically for this dis-
trict. Only the supply of hot water for space heating
and domestic hot water is sold by the utility company
to the households, either delivered by the district heat-
ing system, or the heat pumps. The utility company
is not allowed to supply households electricity for do-
mestic appliances, e.g. TV’s and washing machines.
Hence, electric power supply to the heat pumps is
through a separated cable. As a consequence, it is
possible that the utility company controls starting and
stopping of each heat pump on a central level.
Our previous paper (Fink et al., 2014) was aimed
at developing a mathematical approach to solve the
large scale central optimization problem in an effi-
cient way. In that paper solving one big instance
of MILP (Mixed Integer Linear Program) for every
time step of 15 minutes is compared with a more effi-
cient method called time scale MILP. However, a pre-
calculated data table is used for the prediction of heat
demand of 100 households. With this table, the rela-
tion between the heat pump planning and the achieved
thermal comfort within the households cannot be in-
vestigated. In this paper, model predictive control re-
places the pre-calculated data table.
Main contributions of this paper are: describing
a method for model predictive control for planning
136
van Leeuwen R., Fink J. and J. M. Smit G..
Central Model Predictive Control of a Group of Domestic Heat Pumps - Case Study for a Small District.
DOI: 10.5220/0005434301360147
In Proceedings of the 4th International Conference on Smart Cities and Green ICT Systems (SMARTGREENS-2015), pages 136-147
ISBN: 978-989-758-105-2
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

of heat pumps in a district, demonstrating the qual-
ity of the heat pump planning for minimizing the
peak electricity consumption and demonstrating the
achievable thermal comfort within the households.
Furthermore, comparing this result with conventional
feedback control of individual heat pumps.
The paper is structured as follows. Section 2 con-
siders related work to heat pump planning in smart
micro grids and model predictive control. In Section
3, models are formulated for prediction of space heat-
ing and domestic hot water demand and input data for
the Meppel case is described. Section 4 formulates
the general control and optimization problem. Sec-
tion 5 shows results on the achievable aggregated en-
ergy consumption profile of the heat pumps. Also, the
resulting thermal comfort of the households is shown.
Finally, conclusions are given in Section 6, including
a discussion on future work.
2 RELATED WORK
Planning of electric devices in micro-grids is a re-
cent investigation area. In this paper, Triana, a multi-
commodity and optimization tool is employed. Dif-
ferent forms of energy (e.g. electricity, heat, biogas)
can be simulated in relation to a single optimization
objective. Triana is developed at the University of
Twente, the Netherlands.
To obtain flexibility within a smart grid, it is re-
quired that (a) devices are controllable or (b) the func-
tion of the device can be shifted in time without un-
acceptable consequences for the customer. Such de-
vices are batteries, (dish)washing machines, dryers,
fridges and heat pumps. (Bosman, 2012) developed
specific planning algorithms for smart micro grids,
while (Bakker, 2011) and (Molderink et al., 2010) in-
vestigate various case applications like the planning
of a group of fridges in relation to varying electric-
ity price schemes, due to renewable energy produc-
tion by solar PV. (Claessen et al., 2014) compare two
smart grid control approaches, i.e. Triana and Intel-
ligator. The Triana approach contains three steps to
control devices: prediction on the device level, plan-
ning based on price signals from the aggregator and
real time control by the device controller. The Intelli-
gator approach is based on the Powermatcher concept
(Kok et al., 2005) which uses a multi-agent electric-
ity market. Device agents send bids to a central auc-
tioneer agent. The price signal from the auctioneer
clears the market with the purpose to adjust the bids
in such a way that the market equilibrium (and con-
sumption) is steered towards the optimization objec-
tive. Claessen demonstrates that both approaches are
able to reach certain objectives but also demonstrates
the improvement which is possible when predictions
are part of the approach.
In this paper, the Triana approach without market
based steering principles is applied. In the Meppel
case it is possible to simplify the control method and
let a central controller directly determine the planning
of the heat pumps based on heat demand predictions
for each household. Hence, the planning and real time
control steps are basically the same. The planning
step considers planning of the heat pumps from 2 up
to 24 hours ahead, whereas the real time control step
considers planning of the heat pumps for the actual
time up to 1 or 2 hours ahead. This approach leads
to a method called ”time scale MILP” in (Fink et al.,
2014). The central controller has to solve one large
optimization problem every time step of 15 minutes
with a time window of 24 hours ahead. However, the
size of the problem is reduced by considering larger
time steps for moments further in time. In this way,
the planning is more and more approximated, the fur-
ther it looks into the future.
A heat pump is an electric appliance with a low
temperature thermal input and higher temperature
thermal output which is used for space heating or do-
mestic hot water (Mitchel and Braun, 2013), (Hep-
basli and Kalinci, 2009). Model predictive control
(MPC) of heat pumps in the building environment is
a recent investigation area. MPC is investigated ei-
ther for building climate control to minimize energy
consumption, or for power balancing of smart micro
grids. Early work on MPC for building climate con-
trol is performed by Madsen et al (Madsen and Holst,
1995). Recent investigations which include experi-
mental results are carried out by (Oldewurtel et al.,
2012), (
ˇ
Sirok
´
y et al., 2011) and (Pr
´
ıvara et al., 2011).
(Halvgaard et al., 2012) investigates the use of MPC
for the control of a domestic heat pump in relation
to minimizing energy costs for heating a house, for
which Nordic spot market electricity prices are taken
as input data. (Dar et al., 2014) demonstrates how a
domestic heat pump can be controlled by MPC such
that self consumption of PV-generated electricity is
increased.
The previously mentioned research on MPC con-
siders climate control of single buildings with em-
phasis on the quality of model predictions and the
quality of reaching the objectives, i.e. minimizing
costs or energy consumption. Based on this work,
the conclusion is justified that MPC is a promising
control method which outperforms conventional feed-
back control methods when the control system has
more objectives than room temperature control. Our
main interest, however, is not on the optimal control
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
137

of a single building or heat pump, but the application
of MPC to control many houses with heat pumps in
a district. The main goal and contribution of this pa-
per is to demonstrate the quality of reaching multiple
objectives for a smart micro grid with MPC controlled
heat pumps, i.e. minimizing peak loads on the electric
network, maintaining thermal comfort in the houses
and adequate charge states of domestic hot water stor-
ages.
3 PREDICTIVE MODELS
3.1 Model of the Energy System
In Figure 1, a schematic overview of the energy sys-
tem is given. The picture shows a range of houses
(labeled 1 to n, in which n is the number of houses).
Each house has a heat pump (HP) which is connected
to two types of thermal buffers: (a) a floor heating
system and (b) a hot water storage for domestic hot
water (DHW). The ability of the floor heating to store
thermal energy and possible consequences on thermal
comfort and costs is demonstrated in (Leeuwen et al.,
2014). The energy inputs to the heat pumps are: (a)
low temperature source energy from an underground
thermal storage and (b) electric energy from a biogas
Combined Heat and Power system (CHP), which due
to the constant biogas flow runs continuously. The
CHP is also connected to the main electricity grid.
Heat produced by the CHP is distributed via a large,
centrally located thermal storage to a district heating
network which involves much more houses than the
number of houses with a heat pump.
This energy system is a combination and further
development of two common types of local renew-
able energy systems: district heating based on bio-
gas co-generation and heat pumps combined with un-
derground thermal storage. In the Netherlands, Ger-
many and Denmark there are numerous regional ar-
eas where biogas from waste water treatment plants is
used as a source for co-generation of heat and power
which is distributed to local consumers through a dis-
trict heating network and a local electricity grid which
has a connection to the larger grid. A large scale ex-
ample of this is Apeldoorn Zuidbroek (Dreijerink and
Uitzinger, 2013) where 2500 houses are heated in this
way.
An aquifer underground thermal storage is used as
a source for cooling and for heat pumps. An aquifer
is an underground groundwater reservoir at a depth of
around 60-120 meters. The temperature of the wa-
ter is around 15
◦
C, which is used as source energy
for heat pump evaporators during the heating sea-
Figure 1: Schematic picture of the energy system.
son. During the summer, the groundwater is used
to cool the houses, which also regenerates the reser-
voir temperature after the heat pumps have cooled the
reservoir down during the heating season. In recent
years, this type of storage is commonly applied for
new larger buildings and urban areas in North West-
ern Europe. The increasing use of heat pumps in new
building projects combined with suitable soil condi-
tions and existence of large underground aquifers al-
most anywhere in the Netherlands, result in increas-
ing applications of this type of storage.
In general, the purpose of the energy system is
to provide the new district with almost 100% renew-
able energy for heating and cooling of houses. As
the energy system is a combination of existing op-
tions which are proven in practice, more cases with
a similar energy system are expected to be developed
in the future.
The energy system is configured in such a way that
the average electric production of the CHP equals the
average required electric input by all heat pumps on
the coldest possible day. Furthermore, there are only
two energy prices, arranged by contract with the grid
operator. A low price for selling electricity from the
CHP to the grid and a high price for buying electricity
from the grid. Hence, the objectives for the heat pump
control are:
• maintain thermal comfort for space heating within
each house
• maintain sufficient state of charge of the hot water
buffer to cover DHW demand of each house
• use electricity of the CHP as much as possi-
ble locally for the heat pumps and avoid buying
electricity from the grid. This objective can be
reached when the electric demand is flattened to-
wards the average. Also, investments in electric-
ity cables throughout the district and transformers
at the energy house are minimal when the peak
electric demand is as low as possible. Therefore,
the control objective is formulated as: minimize
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
138

Figure 2: 2R2C model.
peaks of the aggregated heat pump electricity de-
mand.
Following the area plan of the Meppel building
project, 104 houses with a heat pump are studied. At
this stage, the houses involved are not yet built and
hence, the study involves simulations based on spe-
cific models which are discussed in the following sub-
sections.
3.2 Household Space Heating Demand
Model
In (Fink et al., 2014), a data table per house is used as
predictive information for the space heating demand.
However, a data table should be based on relevant re-
lations between space heating demand and influences
such as weather conditions or occupancy. For this,
a simulation model can be used or an online model
which learns relations from measurement data. With-
out a model as integral part of the control system,
it is impossible to estimate the consequences on the
thermal comfort when storage flexibility of the house
structure (thermal mass) is exploited to optimize the
control. Applying a model instead of a data table
has the advantage that temperatures which are rele-
vant for people’s comfort are pre-calculated during
the planning phase and deviations with real-time mea-
surements can be corrected during an online real-time
control phase. Therefore, a model is used to predict
space heating demand for each house in this paper.
For the model of space heating demand in relation
to ambient conditions, the following general 2R2C
thermal network model shown in Figure 2 is adopted
which contains a thermal mass term (C
f
) for the floor
heating and internal zone of the house (C
z
). The
model contains the following parameters (Table 1):
The generalized model equation is given by:
dT
dt
= AT + Bq (1)
In which the vector T contains the thermal mass and
ambient temperatures and vector q contains direct
heat gains to or loss terms from the thermal masses,
Table 1: Model parameters.
R
f
resistance between floor heating and zone
C
f
capacitance of floor heating
R
e
thermal resistance of house envelope
C
z
capacitance of the zone
A
w
window area on each side of the building
q
s
solar energy on building planes with windows
q
h
heating energy injected into floor heating
q
gain
thermal gains by occupants and appliances
q
vent
heat loss by ventilation air flow
q
in f
heat loss by infiltration air flow
i.e. heating input to the floor heating and solar en-
ergy gains to the zone. Matrix A characterizes sys-
tem dynamics and contains thermal capacitance and
resistance parameters. Matrix B specifies how the di-
rect heat gains and losses enter the respective thermal
masses.
Model parameters are estimated for 4 types of ref-
erence houses (AgentschapNL, 2013) for which sim-
ulated response data is generated in TRNSYS (TESS,
ND). The accuracy of this approach is investigated in
detail in (Leeuwen et al., 2015). The parameters for
the 4 house types are given in Table 2 in which: TH-
Terraced House, CH-Corner House, SDH-Semi De-
tached House, DH-Detached House.
Table 2: Estimated 2R2C model parameters.
unit TH CH SDH DH
R
f
K/kW 3.26 2.81 1.69 1.66
C
f
kWh/K 3.61 3.61 4.56 5.08
R
e
K/kW 11.01 8.23 8.67 7.17
C
z
kWh/K 10.62 16.74 20.34 22.48
The window areas for each building plane are
given in (AgentschapNL, 2013). Effective solar trans-
mission through the window into the house is calcu-
lated by multiplying the window area of each building
plane with the incident total radiation on the plane
and a transmission factor. The houses are oriented
according to the district area plan into the 4 major
wind directions. Incident total solar radiation on each
building plane is calculated from measured horizontal
total radiation, i.e. from weather station Hoogeveen
of the Royal Dutch weather institute, which is near
to the city of Meppel. The calculation of diffuse
and beam radiation is based on theory outlined in
(Duffie and Beckman, 1980). To calculate the amount
of diffuse radiation from total horizontal radiation
measurements, a correlation proposed in (Erbs et al.,
1982) is used.
In total, there are 104 houses. At present, the pos-
sible types of occupancy (families, couples, etc.) in
relation to the types of houses is not known. Based
on a comparative study of a recent built district in
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
139

the Netherlands (Blokker and Poortema, 2007), the
following 3 types of occupancy and distribution over
104 households are defined: young family (52%), el-
der couple (15%) and young couple (33%). For the
house orientation, indicated by the facing direction
of the front facade, and the distribution of occupant
types over the different house types, the following is
listed, in which the relation between occupant type
and house orientation is assumed to be random:
• 41 terraced houses with the following number of
houses in combination with the front plane direc-
tion: 20-North/4-East/7-South/10-West. Number
of households in combination with occupant-type:
12-young family/2-elder couple/27-young couple.
• 20 corner houses: 10-North/2-East/4-South/4-
West. Households and occupant-type: 18-young
family/0-elder couple/2-young couple.
• 26 semi detached houses: 0-North/10-East/4-
South/12-West. Households and occupant-type:
16-young family/6-elder couple/4-young couple.
• 17 detached houses: 0-North/8-East/8-South/1-
West. Households and occupant-type: 8-young
family/8-elder couple/1-young couple.
3.3 Occupancy Related Thermal Losses
or Gains
For each type of occupancy, hourly schedules are de-
fined for working days and days of the weekend for
relevant thermal events. The schedules are related to
common behavioral patterns of working people. For
this paper, statistical backgrounds of schedules are not
investigated. For each occupancy type, basic sched-
ules are defined including randomization of some of
the time points at which thermal events occur. In the
following, the basic approach for the programming in-
volved is explained. For the occupancy type: young
family, a working weekday schedule is shown in Fig-
ure 3. Further in the paper, a young family is also
considered when discussing the results. The figure
shows relative to a defined maximum, the following
thermal events:
• Occupancy: thermal gains by occupants present
in the house. Schedules consist of a number of
time points at which the number of occupants
which are present in the house are defined. Based
on (Mitchel and Braun, 2013) the thermal gain
by people is on average 40 W per person during
sleeping hours and 110 W per person during day
and evening hours. Figure 3 shows the number of
occupants present in the house.
• Ventilation rates: typically, ventilation schedules
depend on: (a) the time of the day, (b) the num-
ber of occupants present in the house, (c) cooking
events which require higher ventilation rates, (d)
shower or bath events in the bathroom which re-
quire higher ventilation rates. The ventilation sys-
tem has 4 states for the ventilation rate: (1) cook-
ing, (2) high, (3) medium, (4) low. This relates to
typical existing Dutch house ventilation systems.
Figure 3 shows ventilation rates for each hour.
• Appliance thermal gains: Four appliance classes
are defined: (1) computers/television, (2) light-
ing, (3) fridge/freezer, (4) background appliances
like pumps, fans and standby electronic equip-
ment. The total yearly electricity consumption of
the schedule in Figure 3 is approximately equiv-
alent to Dutch average consumption figures pub-
lished by (Milieucentraal, ND).
• DHW (Domestic Hot Water) demand: for a single
household this is determined by several events at
certain timepoints each day. In total, 6 possible
events are defined, each with a specific amount
of required water of 40
◦
C: (1) shower, (2) bath,
(3) hand cleaning, (4) small dish wash, (5) large
dish wash and (6) body washing. Figure 3 shows
the water amounts for a number of events. The
amount of water per event and the time points are
slightly randomized.
In the same way, schedules are worked out for other
occupancy types, both for working days and weekend
days.
3.4 Heat Pump Model
Heat pump performance is approximated as a constant
relation between electric input and thermal output of
the heat pump for two operational modes: space heat-
ing mode with an output temperature of 35
◦
C and
thermal storage mode with an output temperature of
65
◦
C. Hence, the heat pump has 3 operational states:
(1) off, (2) space heating, (3) thermal storage. The
relation is given in table 3 which is based on supplier
data (Alpha-Innotec, 2014).
Table 3: Heat pump energy specification.
state unit input output
off kW 0.0 0.0
space heating kW 1.3 6.0
thermal storage kW 1.8 5.0
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
140

Figure 3: Example weekday thermal event schedule.
4 CONTROL ALGORITHMS
In (Fink et al., 2014) a general approach for off-
line and on-line heat pump central control problems
is introduced. This paper concerns an off-line prob-
lem because the weather and occupancy related data
are known beforehand as forecasts. The optimiza-
tion process is explained in more detail in (Fink
and Hurink, 2015). For the simulation, the predic-
tive models, house type definitions, occupant related
schedules, weather calculation module, reference and
optimization control algorithms are defined as Python
script files. The Triana simulation environment, de-
veloped at the University of Twente is written in C++.
MILP instances are solved by the CPLEX solver
package.
4.1 Optimized Control
Following the Triana smart grid method, planning of
the heat pumps is determined in two calculation steps:
a prediction step and a planning step. The Triana
method also contains a third step: real time control,
but for this type of off-line problem, this step is irrel-
evant: it is assumed for now that there is no deviation
between the prediction and the simulated reality. On
the other hand, if an on-line control problem is stud-
ied, the real time control step involves a comparison
between measurements in real time and predictions
for the short term, resulting in adjustment of the short
term heat pump control planning to reduce possible
deviations.
The control objective to minimize peak electric
demand is formulated as:
Minimize max
t∈T
∑
op
∑
c
E
op
· X
c,op,t
X
c,op,t
∈
{
0, 1
}
(2)
In which E
op
is the electric demand of a heat pump
converter. op ∈
{
sh, dhw
}
denotes an operational
mode of the heat pump within a set of operational
modes, in this case space heating (sh) or domestic hot
water (dhw). X
c,op,t
is the control state for each heat
pump converter.
c ∈
{
1, 2, . . . , n
}
denotes a heat pump converter
for each house within a set of heat pump converters
which totals the number of houses (n). The time in-
terval t ∈ T denotes that all time intervals t are within
the planning period T . Each heat pump is either ”on”
(X
c,op,t
= 1) or ”off” (X
c,op,t
= 0). However, two op-
erational modes for one heat pump cannot be ”on” at
the same time, that is
∑
op
X
c,op,t
≤ 1. For this we in-
troduce additional control variables.
Let x, y and z be control states for which: x, y, z ∈
X. Let x
c,t
be the control variable for space heating
during the prediction phase, y
c,t
be the control vari-
able for space heating during the planning phase and
z
c,t
be the control variable for DHW during the plan-
ning phase. The first stage heat pump planning x
c,t
for space heating is determined in the first phase of
the calculation, i.e. the prediction phase optimizes:
Minimize
∑
t
X
c,op,t
0 ≤ X
c,op,t
≤ 1
subject to the following constraints:
• T z
t
≥ T
pre f ,t
for all t ∈ T where T
pre f ,t
is the set-
point operative temperature.
• the thermal load of a house is modeled with (1)
which relates the floor heating temperatures and
zone temperatures to heat losses to the ambient
and to heat gains and heat input from the heat
pumps.
• pre-calculation of occupancy related thermal
gains and ventilation losses based on schedules.
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
141

• pre-calculation of solar gains.
The output of the prediction phase is a first stage plan-
ning of the heat pumps in order to exactly match the
space heating demand of each house.
During the second phase of the calculation, i.e. the
planning phase, the first stage planning of the space
heating converters is re-calculated but now the op-
timization includes a space heating thermal buffer.
Also, calculation of the planning now includes the
DHW demand prediction and the State of Charge of
the DHW thermal buffer. Equation (2) is now subject
to the following constraints:
• 0 ≤
∑
t
i=1
(y
c,i
− x
c,i
) ≤
SH
max
q
hp,sh
∆t
in which y
c,i
sig-
nifies the re-planned control states of each con-
verter for space heating and q
hp,sh
the thermal out-
put of the heat pump for space heating: q
hp,sh
=
X
c,sh,t
· output
c,sh
in which output
c,sh
is the ther-
mal output of the heat pump specified in Table 3.
∆t signifies the incremental length of the time in-
terval t and SH
max
the maximum capacity of the
space heating buffer. This capacity is determined
in (Leeuwen et al., 2014).
• 0 ≤ SoC
t
≤ DHW
max
in which SoC
t
signifies the
State of Charge of the DHW buffer and DHW
max
the maximum capacity of the DHW buffer, i.e. de-
termined by the water volume and fully charged
average temperature.
• SoC
t+1
= SoC
t
+ z
c,t
· q
hp,dhw
− D
t,dhw
which
yields the control states of the heat pump convert-
ers z
c,t
for the DHW operation mode. q
hp,dwh
sig-
nifies the heat pump thermal output and D
t,dhw
the
DHW demand during time period t. Heat loss of
the heat buffer is not modeled, but could be incor-
porated in D
t,dhw
.
4.2 Reference Control
The reference control is based on a simple set of feed-
back control rules which results in approximately the
same behavior as individual PID control of each heat
pump. At each time interval, the following is evalu-
ated for each house:
• For space heating, the operative temperature T z
t
is compared with T
pre f ,t
which is the minimum
allowed temperature defined in schedules. If the
operative temperature is below this value, the heat
pump is on. If it is above this value plus a positive
deadband value, the heat pump is off.
• For DHW, the State of Charge of the buffer SoC
t
is compared with a minimum allowed value. If
the SoC is below this value, the heat pump is on.
If it is above a value close to the maximum SoC,
the heat pump is off.
Figure 4: Input weather data.
Figure 5: Aggregated electrical energy demand.
• Operation of the heat pump for DHW has priority
over space heating: y
c,t
= 0 if z
c,t
= 1.
5 CASE STUDY RESULTS
5.1 Results for a Cold Week
To discuss the quality of the obtained results, the cold-
est week of the year 2012 is investigated first. This
week has the highest average heat demand and there-
fore the longest peak load duration is expected during
this week. The input weather data, i.e. the ambient
temperature (Ta) and global horizontal solar radiation
(G
t,h
) are shown in Figure 4.
In Figure 5 the electrical energy demand is
shown for the reference control (ref control) and op-
timized control. The sorted values from high to low
(ref control s and optimized s) demonstrate the qual-
ity of the peak minimization by the optimized con-
trol. The peak for the reference control is 162 kW.
This is the peak electric consumption when all heat
pumps have their own on/off controlled thermostats.
The peak for the optimized control is 108 kW. The
average electricity power for the shown period is 74
kW. Compared to this average, the maximum peak of
the reference control is 119% higher and of the opti-
mized control 46% higher.
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
142

Figure 6: Example indoor operative and floor heating tem-
peratures.
Figure 6 shows an example of the indoor operative
and floor heating temperatures for the reference and
optimized control. The example concerns a detached
house occupied by a young family. Other households
show similar results. Tz setpoint relates to the de-
sired setpoint temperature which is set at 18
◦
C during
the night and 20
◦
C during the day. Tz ref control re-
lates to the indoor operative temperature in case of
reference control. Tz relates to the optimized con-
trol. Notice that the reference control is not able to
keep the operative temperatures at the desired daytime
setpoints. This is due to the sharp contrast between
daylight hours with a relatively high amount of solar
gains and nighttime hours with low ambient tempera-
tures. The reference control has no knowledge of the
upcoming heat loss during the night. When it reacts,
the floor heating system gives a slow response due to
its inertia, which is seen on the Tf ref control line.
In contrast, the optimized control is based on
weather forecasts and controls the indoor operative
temperatures such that the desired temperatures are
reached exactly at the first moment when they are
needed, i.e. each morning around 07.00 hours.
The average floor heating temperature (Tf) and av-
erage operative temperature during this week are thus
higher than for the reference control. On some days,
the operative temperatures reach 22
◦
C, which is due
to solar gains. The optimized control has knowledge
of this, but it evaluates the setpoint temperatures as
the minimum allowed temperatures and there are no
upper limits on the operative temperature during the
heating season, to avoid unnecessary cooling.
Figure 6 also shows the operative temperatures
which are calculated as result of the prediction step
(Tz pred). The result of the planning step (Tz) is
only slightly different which is caused by the rela-
tively small size of the space heating buffer, i.e. 12
time periods of 15 minutes continuous charging with
the heat pump output for space heating. This equals a
storage capacity of 12 ·
15
60
· 6.0 = 18 kWh. When this
buffer is larger (24 time periods instead of 12 time pe-
riods) the result is that the electrical energy demand is
Figure 7: Floor heating and DHW buffer state of charge.
Figure 8: Heat pump operational states.
pushed more towards the average for the whole week,
but the real operative temperatures (Tz) differ more
from the first stage control which is the result of the
prediction step.
In Figure 7 the state of charge (SoC) of the buffers
for space heating (floor buffer, dimensionless) and
DHW (DHW buffer, MJ) with the DHW demand
(DHW demand, MJ) for the example household are
shown. The space heating SoC has a relation with the
floor heating temperature and operative zone tempera-
ture shown in Figure 6. In general, the SoC increases
when the zone temperatures are higher than the set-
point and decreases when the zone temperatures ap-
proach the setpoint values.
Figure 7 also shows the relation between the SoC
of the DHW buffer and the DHW demand. The SoC
increases due to heat input from the heat pump. Cor-
responding operational states of the heat pump are
shown in Figure 8. In this case, the DHW buffer
is large enough to supply the largest short time de-
mand peaks, i.e. for filling a bath. The states of the
heat pump are indicated as 0 (off) or 1 (on). For im-
proved visibility, the heat pump state for space heat-
ing is scaled different than for DHW in Figure 8.
5.2 Broader Analyses of Results
Heat Pump On/off Switching Behavior
As Figure 8 shows, the heat pump switches on and off
frequently, which is undesirable for the service life of
the heat pump. Therefore two possibilities to reduce
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
143

the amount of switching are considered:
1. defining a minimum running time constraint for
the heat pump control, like half an hour or charge
until the domestic hot water storage is fully
charged. However, this limits the amount of feasi-
ble solutions considerably and increases the time
to solve the optimization problem.
2. increasing the time interval of the simulation to
half an hour. This decreases the number of vari-
ables and decreases the time to solve the optimiza-
tion problem. Therefore we prefer this method.
When the latter method is applied, the load duration
curves are similar to the results which are shown in
Figure 5. The interior temperatures have a minor dif-
ference, which is shown in Figure 9. In this Fig-
ure, the subscripts 15 and 30 indicate a 15 minute
and 30 minute time interval during simulation respec-
tively. The advantage of the 30 minute time interval
is shown in Figure 10, which shows the amount of
on/off switches in relation to the amount of uninter-
rupted running time intervals of the heat pump. For
the investigated week, the total amount of switches
reduces from 92 to 53. A further reduction can be ex-
pected when an additional charging constraint is in-
cluded for the domestic hot water storage, as most of
the heat pump switches are related to short charging
periods of this storage.
By comparison, the reference control switches
only 11 times. This is perhaps an advantage for the
service life of the heat pump, but Figure 6 demon-
strates drawbacks on the experienced comfort. The
on/off thermostats programmed for reference control
of the space heating and the domestic hot water stor-
age, cause too much cooling down of the house and
of the hot water storage, which results in long periods
of heating demand afterwards. This is observed from
the high number of intervals of uninterrupted opera-
tion of the heat pump in case of reference control in
Figure 10. For the reference control the longest pe-
riod is 65 time intervals of 15 minutes or 16.25 hours,
for the optimized control this is 19 time intervals of
30 minutes or 9.5 hours. In practice, a PID controller
to control the space heating demand would probably
perform better than the on/off reference control and
result in less cooling down of the house and more fre-
quent switching of the heat pumps. This should also
result in shorter operating times and possibly some re-
duction of the aggregated peak electrical loads com-
pared to the reference control.
Results for Periods with Less Heat Demand
As shown in Figure 5 and discussed on Section 5.1,
the peak electrical load is reduced significantly for the
Figure 9: Temperature response for 15 and 30 minute time
intervals.
Figure 10: Amount of heat pump on/off switches related to
uninterrupted operation time intervals.
optimized control. It is interesting to verify if a simi-
lar result is found for periods with less heat demand.
In Figure 11, weather data of a different week for the
same location and climatic year is shown. The ag-
gregated electrical energy demand for the optimized
and reference control is shown in Figure 12. The in-
door temperatures (floor heating temperature Tf and
interior zone temperature Tz) for the same detached
house are shown in Figure 13.
During this week, the domestic hot water demand
dominates the aggregated electrical energy demand,
while the space heating demand is largely concen-
trated on one day between 72 and 96 hours. Due to
approximately 80% simultaneity in the operation of
the heat pumps for domestic hot water, the reference
control shows a high peak electrical demand of 145
kW. The optimized control reduces this to 45 kW.
Notice that the interior zone temperatures are ap-
proximately similar for the reference and optimized
control. The slightly increasing temperatures above
the setpoints which is seen on the last two days are
due to relatively high solar gains. The short term
up and down movement of the floor heating tempera-
tures from 0 up to 84 hours indicates frequent on/off
switching of the heat pump. Also in this case, the
heat pump switching is more frequent for the opti-
mized control than for the reference control. The total
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
144
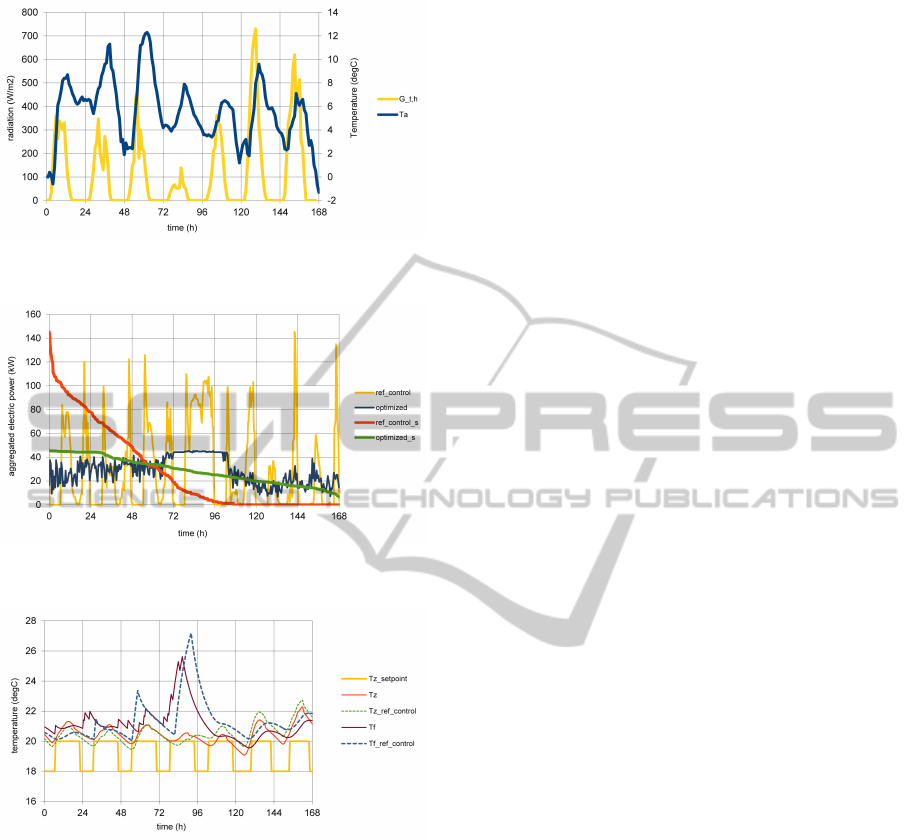
Figure 11: Input weather data for a week with less heat de-
mand.
Figure 12: Aggregated electrical energy demand for a week
with less heat demand.
Figure 13: Indoor temperatures for a week with less heat
demand.
amount of switches for this week is 32 for the opti-
mized control and 10 for the reference control. How-
ever, the longest period of uninterrupted heat pump
operation is 3 hours for the optimized control and
10.25 hours for the reference control, which increases
the chance for simultaneity and hence explains the
high peak electrical load of the reference control. This
also has a relation with the schedules shown in Figure
3. As young families and young couples dominate
the district’s population and the applied schedules for
domestic hot water demand and interior temperature
setpoints of these occupancy types are approximately
similar, the chance for simultaneity is high. A com-
monly used hot water storage contains a single tem-
perature sensor. Within the storage, a good degree of
temperature stratification of hot and cold water layers
is present. In that case, a PID controller would not
perform much better than the simple on/off reference
control.
Optimality of the Control
The main objective for the optimization is to mini-
mize peak electricity consumption. Besides this ob-
jective, there are some hard constraints on the thermal
comfort, i.e. a minimum temperature, maximum size
of the flexible space heating storage and minimum
hot water storage state of charge. Besides that, a 30
minute time interval is introduced during optimization
to avoid excessive on/off switching of the heat pumps.
Hence, the definition of what is in this case really ”op-
timum” for the control is not so obvious. As our re-
sults show, the peak electricity decreases significantly
as the result of the optimized control, but there is a
trade off between the quality of this objective, reach-
ing comfort temperatures in the house which are close
to the setpoints and limiting the amount of heat pump
on/off switches.
6 CONCLUSIONS AND FUTURE
WORK
Optimal control on a central or aggregated level of a
group of heat pumps used for providing space heating
and domestic hot water is investigated. It is demon-
strated that model predictive control is required in
order to anticipate on changing weather conditions
and occupancy related thermal gains and losses. The
developed control algorithm is very well capable to
reach multiple objectives, i.e. minimize peak electri-
cal demands and maintain adequate thermal comfort
levels for each household in terms of comfortable, de-
sired operative temperatures and sufficient charging
states of the buffers to supply domestic hot water.
For the simulation case which involves 104
houses, it takes 100 seconds to compute the heat
pump planning for 7 days in advance with 15 minute
time intervals, on a PC with Intel quad core processor
and 8 GB internal memory. Thus acceptable com-
putational effort for this type of control is demon-
strated. For larger district scales, the computational
time can be limited further by shorter planning hori-
zons, a larger time interval and applying the more ef-
ficient time scale MILP algorithm.
A comparison with simulated results using a ref-
erence control algorithm which equals existing non-
optimized, individual heat pump control, demon-
strates for the optimized, central control, a substan-
tial decrease of the aggregated electricity demand
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
145

peaks and improved thermal comfort for the residents.
However, the optimized control causes a significant
increase of the amount of heat pump on/off switches,
which can be decreased by increasing the time period
of the optimization and by defining additional con-
straints on charging the domestic hot water storage.
Future work is aimed at developing predictive
models for home space heating and domestic hot wa-
ter demand in which online learning is incorporated
and at studying cases which involve cooling during
the summer months. We will also apply the devel-
oped simulation environment to applications which
are more complex and require additional control al-
gorithms. Besides that, we will further compare
the quality of central control with individual control
where optimization is based on auction principles.
ACKNOWLEDGEMENT
The authors would like to thank the Dutch national
program TKI-Switch2SmartGrids for supporting the
project Meppelenergy and the STW organization for
supporting the project I-Care 11854.
REFERENCES
AgentschapNL (2013). Reference houses 2013 (in
dutch: Referentiewoningen nieuwbouw 2013).
http://www.rvo.nl/sites/default/files/2013/09/ Refer-
entiewoningen.pdf, visited October 2014.
Alpha-Innotec (2014). Alpha-Innotec instruction and
user manual WZS series brine/water heat pumps (in
Dutch).
Bakker, V. (2011). Triana: a control strategy for Smart
Grids: Forecasting, planning & real-time control.
PhD thesis, University of Twente.
Blokker, E. and Poortema, K. (2007). Effect study domestic
hot water (in dutch: Effecten levering warm tapwater
door derden). Technical report, KIWA.
Bosman, M. (2012). Planning in Smart Grids. PhD thesis,
University of Twente.
Claessen, F., Claessens, B., Hommelberg, M., Molderink,
A., Bakker, V., and Toersche, H. (2014). Comparative
analysis of tertiary control systems for smart grids us-
ing the flex street model. Renewable energy, 69:260–
270.
Dar, U. I., Sartori, I., Georges, L., and Novakovic, V.
(2014). Advanced control of heat pumps for improved
flexibility of net-zeb towards the grid. Energy and
Buildings, 69:74–84.
Dreijerink, L. and Uitzinger, J. (2013). Socio-economic
evaluation report apeldoorn. Technical report, IVAM
University of Amsterdam. EU SORCER project.
Duffie, J. A. and Beckman, W. A. (1980). Solar engineering
of thermal processes. Wiley, New York.
ECN (2014). Energy trends 2014 (in dutch: En-
ergie trends 2014). Technical report, ECN.
http://energietrends.info/, visited December 2014.
Erbs, D. G., Klein, S. A., and Duffie, J. A. (1982). Estima-
tion of the diffuse radiation fraction for hourly, daily
and monthly-average global radiation. Solar Energy,
28(4):293–302.
Fink, J. and Hurink, J. L. (2015). Minimizing costs is easier
than minimizing peaks when supplying the heat de-
mand of a group of houses. European journal of op-
erational research, 242(2):644–650.
Fink, J., Leeuwen, R. v., Hurink, J., and Smit, G. (2014).
Linear programming control of a group of heat pumps.
ESEIA 2014 conference, submitted to Journal Energy,
Sustainability and Society.
Halvgaard, R., Poulsen, N., Madsen, H., and Jorgensen, J.
(2012). Economic model predictive control for build-
ing climate control in a smart grid. Proceedings of
2012 IEEE PES innovative Smart Grid Technologies
(ISGT).
Hepbasli, A. and Kalinci, Y. (2009). A review of heat pump
water heating systems. Renewable and Sustainable
Energy Reviews, 13(6):1211–1229.
Janssen-Visschers, I. and Lee, G. v. d. (2013). Vision on
electricity sector production and tax development (in
dutch: Visie op productie- en belastingontwikkelingen
in de elektriciteitssector). Technical report, Tennet.
Kok, J., Warmer, C., and Kamphuis, I. (2005). Power-
matcher: multiagent control in the electricity infras-
tructure. In Proceedings of the fourth international
joint conference on Autonomous agents and multia-
gent systems, pages 75–82.
Leeuwen, R. v., Fink, J., Wit, J. d., and Smit, G. (2014).
Thermal storage in a heat pump heated living room
floor for urban district power balancing, effects on
thermal comfort, energy loss and costs for residents.
In Smartgreens 2014, Barcelona. INSTICC.
Leeuwen, R. v., Wit, J. d., Fink, J., and Smit, G. (2015).
Low-energy house thermal model parameter estima-
tion for smart grid control. submitted to conference
IEEE-Powertech 2015.
Madsen, H. and Holst, J. (1995). Estimation of continuous-
time models for the heat dynamics of a building. En-
ergy and Buildings(1995) 67-79.
Meppelenergie (ND). Meppel energy (in dutch: Meppel
energie). http://www.meppelenergie.nl/nieuwveense-
landen, visited March 2014.
Milieucentraal (ND). Insights into energy consump-
tion (in dutch: Inzicht in uw energiereken-
ing). http://www.milieucentraal.nl/, visited December
2014.
Mitchel, J. W. and Braun, J. E. (2013). Principles of Heat-
ing, Ventilation, and Air Conditioning in buildings.
Wiley, New York.
Molderink, A., Bakker, V., Bosman, M. G., Hurink, J. L.,
and Smit, G. J. (2010). A three-step methodology
to improve domestic energy efficiency. In Innova-
tive Smart Grid Technologies (ISGT), 2010, pages 1–
8. IEEE.
Oldewurtel, F., Parisio, A., Jones, C. N., Gyalistras, D., Gw-
erder, M., Stauch, V., Lehmann, B., and Morari, M.
SMARTGREENS2015-4thInternationalConferenceonSmartCitiesandGreenICTSystems
146

(2012). Use of model predictive control and weather
forecasts for energy efficient building climate control.
Energy and Buildings, 45:15–27.
Pr
´
ıvara, S.,
ˇ
Sirok
´
y, J., Ferkl, L., and Cigler, J. (2011).
Model predictive control of a building heating sys-
tem: The first experience. Energy and Buildings,
43(2):564–572.
Scheepers, M., Seebregts, A., Hanschke, C., and Nieuwen-
hout, F. (2007). Influence of innovative technology on
the future electricity infrastructure (in dutch: Invloed
van innovatieve technologie op de toekomstige elek-
triciteitsinfrastructuur). Technical report, ECN.
ˇ
Sirok
´
y, J., Oldewurtel, F., Cigler, J., and Pr
´
ıvara, S. (2011).
Experimental analysis of model predictive control for
an energy efficient building heating system. Applied
Energy, 88(9):3079–3087.
TESS (ND). Trnsys transient system simulation tool.
http://www.trnsys.com/, visited December 2014.
CentralModelPredictiveControlofaGroupofDomesticHeatPumps-CaseStudyforaSmallDistrict
147
